Fixed- and Variable-Temperature Kinetic Models to Predict Evaporation of Petroleum Distillates for Fire Debris Applications
Abstract
:1. Introduction
2. Theory
3. Materials and Methods
3.1. Evaporation of Petroleum Distillates
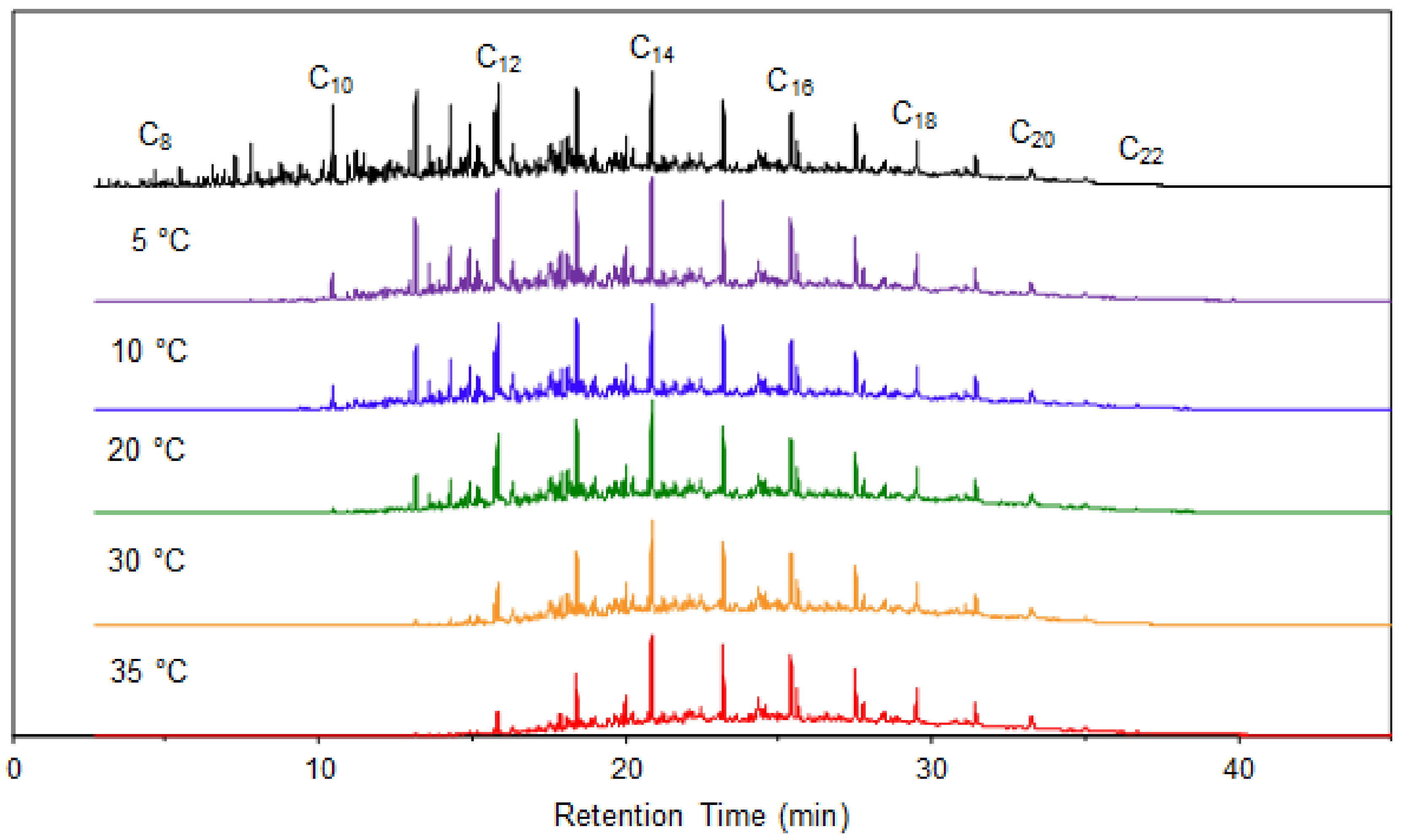
3.2. Gas Chromatography-Mass Spectrometry Analysis
3.3. Model Development and Validation
4. Results and Discussion
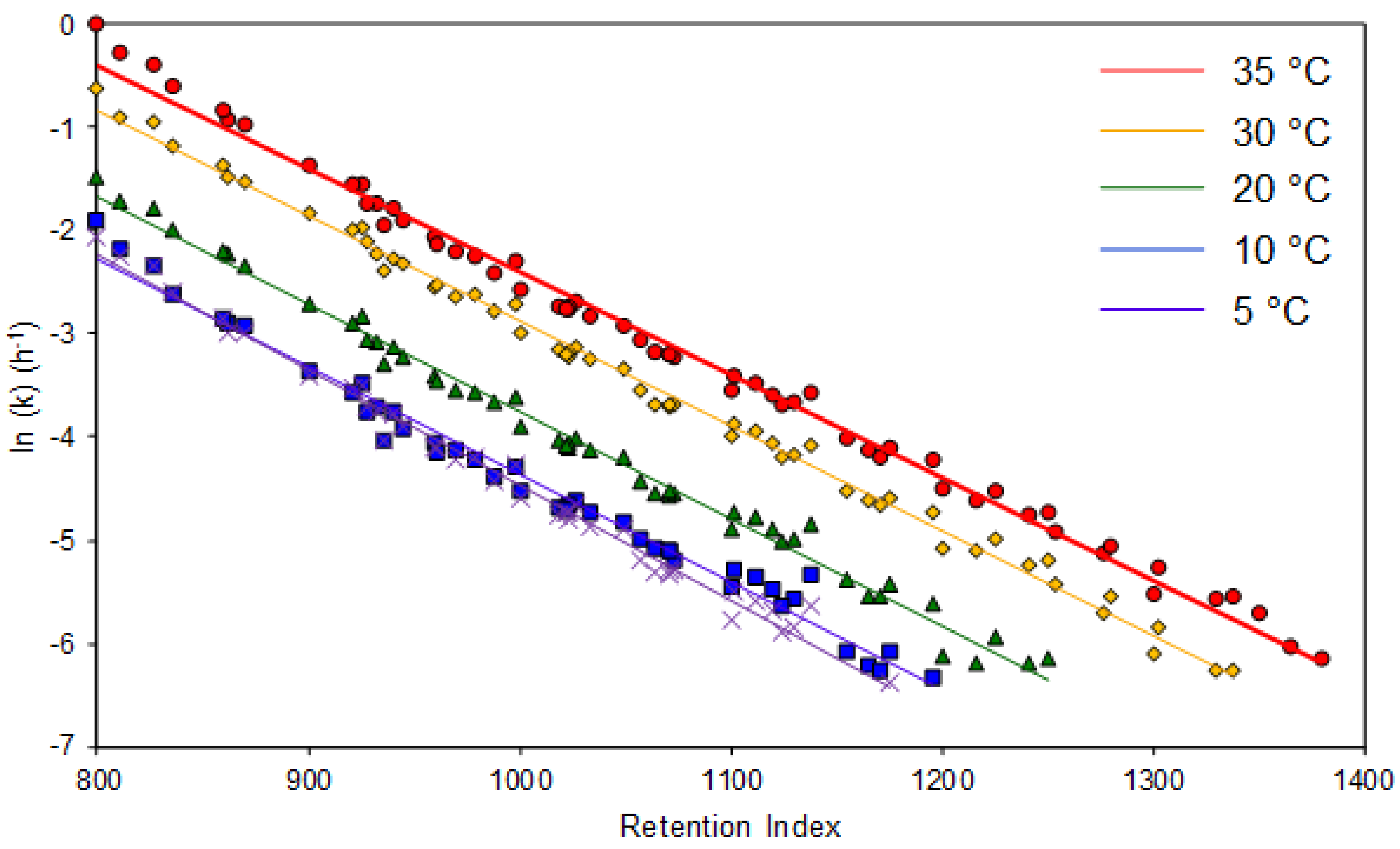
4.1. Fixed-Temperature Models
4.2. Variable-Temperature Model
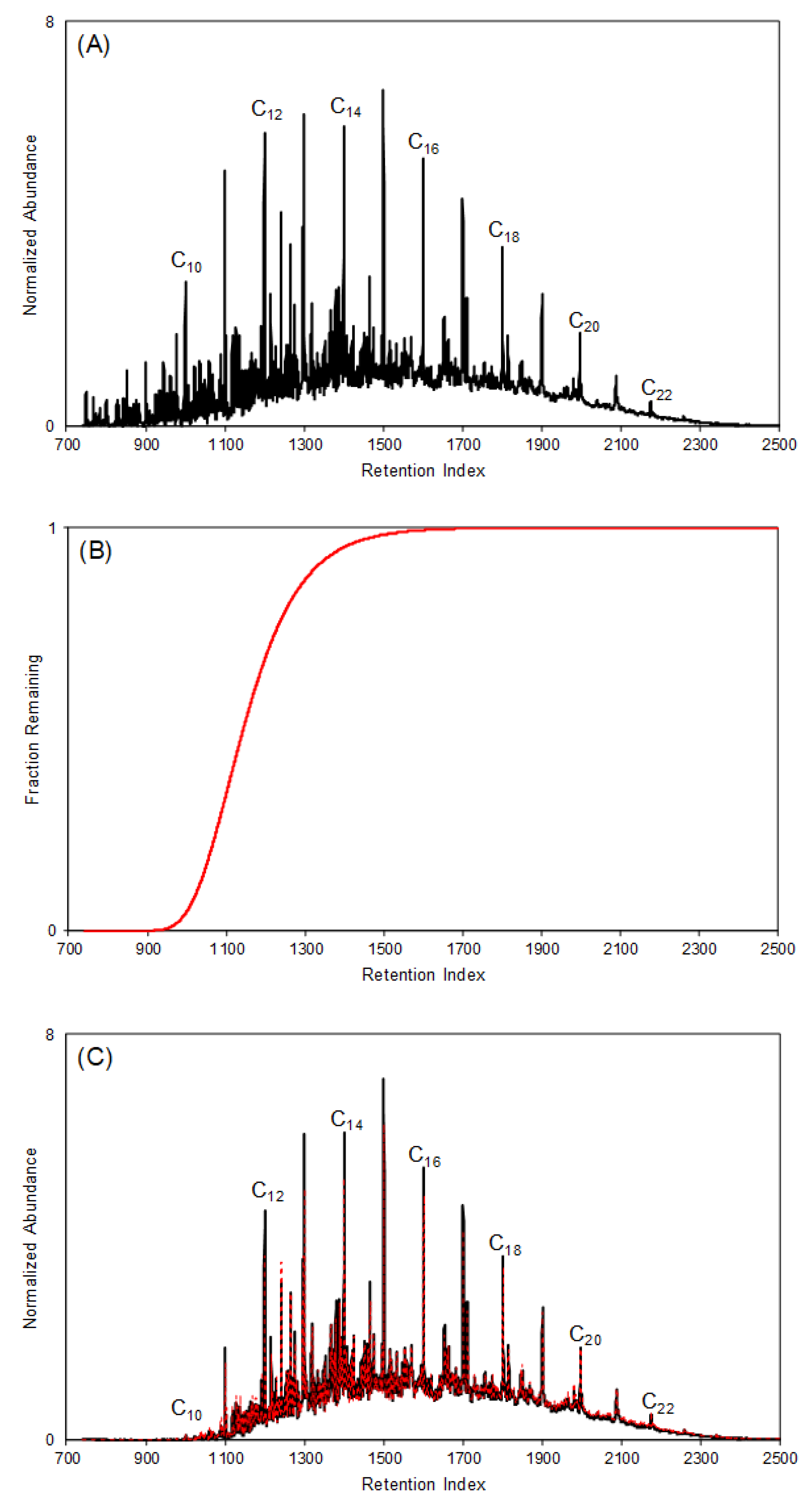
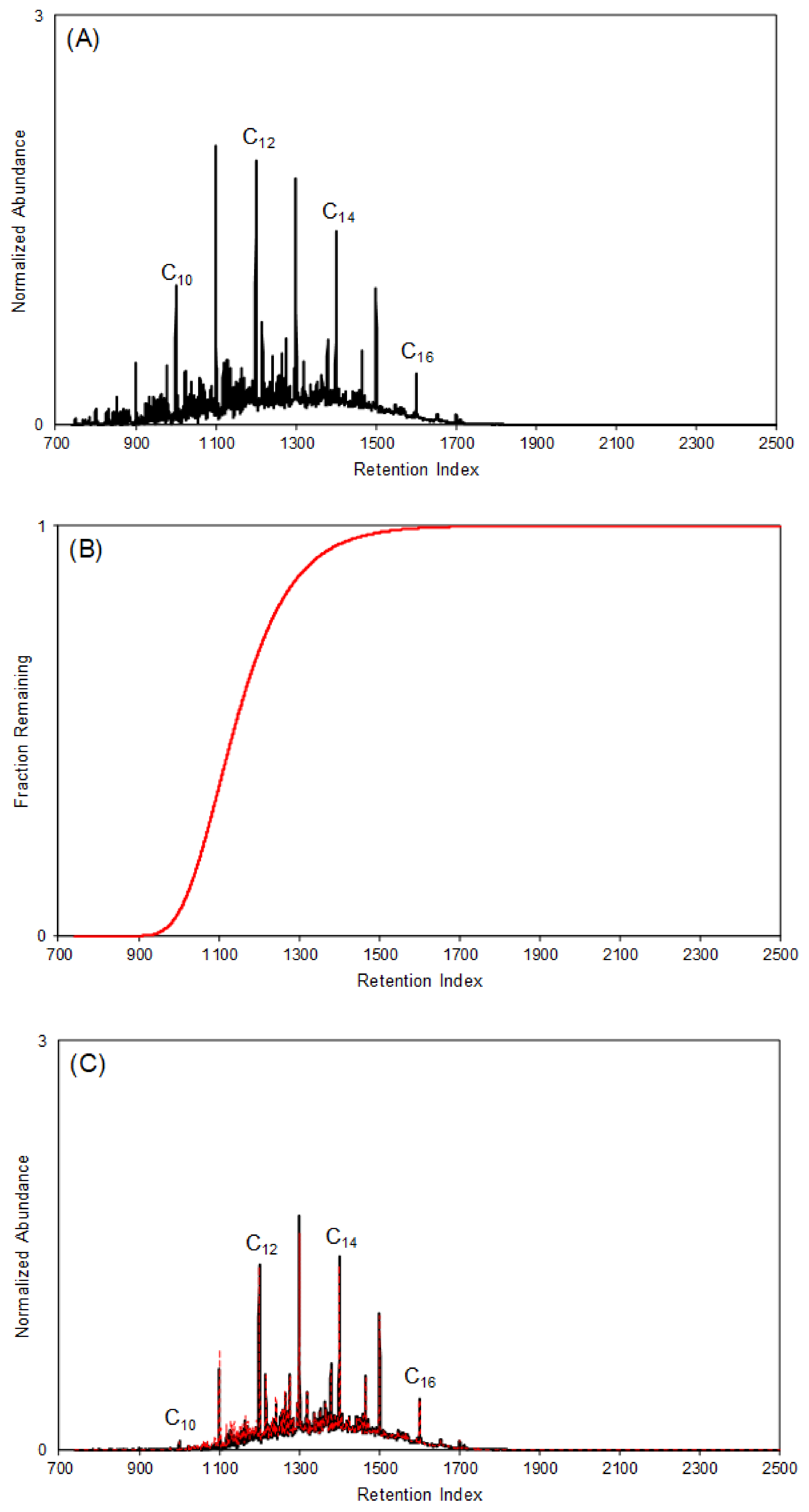
4.3. Applications of Variable-Temperature Model
4.3.1. Predicting the Fraction Remaining of Petroleum Distillates at a Given Time and Temperature
4.3.2. Generating Modeled Reference Collection to Identify Ignitable Liquids in Fire Debris
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- E 1618-14: Standard Test Method for Ignitable Liquid Residues in Extracts from Fire Debris Samples by Gas Chromatograpy-Mass Spectrometry; ASTM International: West Conshohocken, PA, USA, 2014.
- E1388-12: Standard Practice for Sampling of Headspace Vapors from Fire Debris Sample; ASTM International: West Conshohocken, PA, USA, 2012.
- E1413-13: Standard Practice For Separation of Ignitable Liquid Residues from Fire Debris Samples by Dynamic Headspace Concentration; ASTM International: West Conshohocken, PA, USA, 2013.
- E1386-15: Standard Practice for Separation of Ignitable Liquid Residues from Fire Debris Samples by Solvent Extraction; ASTM International: West Conshohocken, PA, USA, 2015.
- E2154-15a: Standard Practice for Separation and Concentration of Ignitable Liquid Residues from Fire Debris Samples by Passive Headspace Concentration with Solid Phase Microextraction (SPME); ASTM International: West Conshohocken, PA, USA, 2015.
- E1412-16: Standard Practice for Separation of Ignitable Liquid Residues From Fire Debris Samples by Passive Headspace Concentration with Activated Charcoal; ASTM International: West Conshohocken, PA, USA, 2016.
- Stauffer, E.; Dolan, J.A.; Newman, R. Fire Debris Analysis; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Hetzel, S.S. Survey of American gasolines (2008). J. Forensic Sci. 2015, 60, S197–S206. [Google Scholar] [CrossRef] [PubMed]
- Hirz, R. Gasoline brand identification and individualization of gasoline lots. J. Forensic Sci. Soc. 1989, 29, 91–101. [Google Scholar] [CrossRef]
- Newman, R.; Gilbert, M.; Lothridge, K. GC-MS Guide to Ignitable Liquids; CRC Press: New York, NY, USA, 1998. [Google Scholar]
- Sandercock, P.M.L.; Du Pasquier, E. Chemical fingerprinting of gasoline. 2. Comparison of unevaporated and evaporated automotive samples. Forensic Sci. Int. 2004, 140, 43–59. [Google Scholar] [PubMed]
- Fingas, M. Evaporation modeling. In Oil Spill Science and Technology; Fingas, M., Ed.; Elsevier: Burlington, MA, USA, 2011. [Google Scholar]
- Fingas, M.F. Studies on the evaporation of crude oil and petroleum products: I. The relationship between evaporation rate and time. J. Hazard. Mater. 1997, 56, 227–236. [Google Scholar]
- Jones, R.K. A simplified pseudo-component oil evaporation model. In Proceedings of the Environmental Canada Twentieth Arctic and Marine Oilspill Program Technical Seminar, Ottawa, ON, Canada, 1997; Volume 1, pp. 43–61. [Google Scholar]
- Stiver, W.; Mackay, D. Evaporation rates of spills of hydrocarbons and petroleum mixtures. Environ. Sci. Technol. 1984, 18, 834–840. [Google Scholar] [CrossRef] [PubMed]
- Stiver, W.; Shiu, W.Y.; Mackay, D. Evaporation times and rates of specific hydrocarbons in oil spills. Environ. Sci. Technol. 1989, 23, 101–105. [Google Scholar] [CrossRef]
- McIlroy, J.W.; Jones, A.D.; McGuffin, V.L. Gas chromatographic retention index as a basis for predicting rates of evaporation of complex mixtures. Anal. Chim. Acta 2014, 852, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Regnier, Z.R.; Scott, B.F. Evaporatoin rates of oil components. Environ. Sci. Technol. 1975, 9, 469–472. [Google Scholar] [CrossRef]
- Smith, R.L. Predicting evaporation rates and times for spills of chemical mixtures. Ann. Occup. Hyg. 2001, 45, 437–445. [Google Scholar] [CrossRef]
- Yim, U.H.; Ha, S.Y.; An, J.G.; Won, J.H.; Han, G.M.; Hong, S.H.; Kim, M.; Jung, J.H.; Shim, W.J. Fingerprint and weathering characteristics of stranded oils after the hebei spirit oil spill. J. Hazard. Mater. 2011, 197, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Waddell Smith, R.; Brehe, R.J.; McIlroy, J.W.; McGuffin, V.L. Mathematically modeling chromatograms of evaporated ignitable liquids for fire debris applications. Forens. Chem. 2016, 2, 37–45. [Google Scholar] [CrossRef]
- Birks, H.L.; Cochran, A.R.; Williams, T.J.; Jackson, G.P. The surprising effect of temperature on the weathering of gasoline. Forens. Chem. 2017, 4, 32–40. [Google Scholar] [CrossRef]
- IUPAC. Compendium of Chemical Terminology (the "Gold Book"); Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Ulrich, N.; Schuurmann, G.; Brack, W. Prediction of gas chromatographic retention indices as classifier in non-target analysis of environmental samples. J. Chromatogr. A 2013, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Vandendool, H.; Kratz, P.D. A generalization of retention index system including linear temperature programmed gas-liquid partition chromatography. J. Chromatogr. 1963, 11, 463–471. [Google Scholar] [CrossRef]
- Atkins, P.; De Paula, J. Physical Chemistry, 9th ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Makridakis, S. Accuracy measures-theoretical and practical concerns. Int. J. Forecast. 1993, 9, 527–529. [Google Scholar] [CrossRef]
- DeVore, J.L. Probability and Statistics for Engineering and the Sciences; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
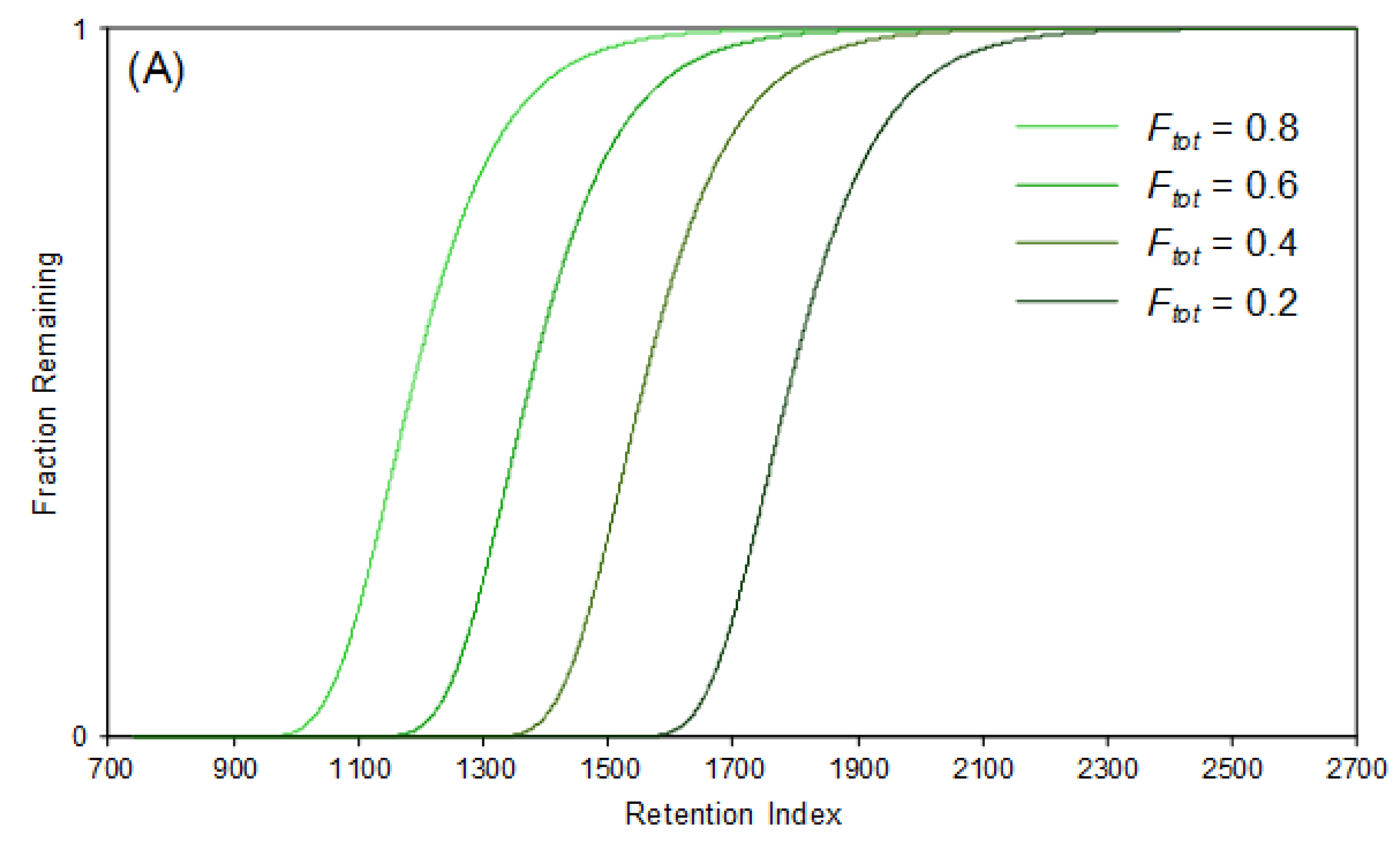
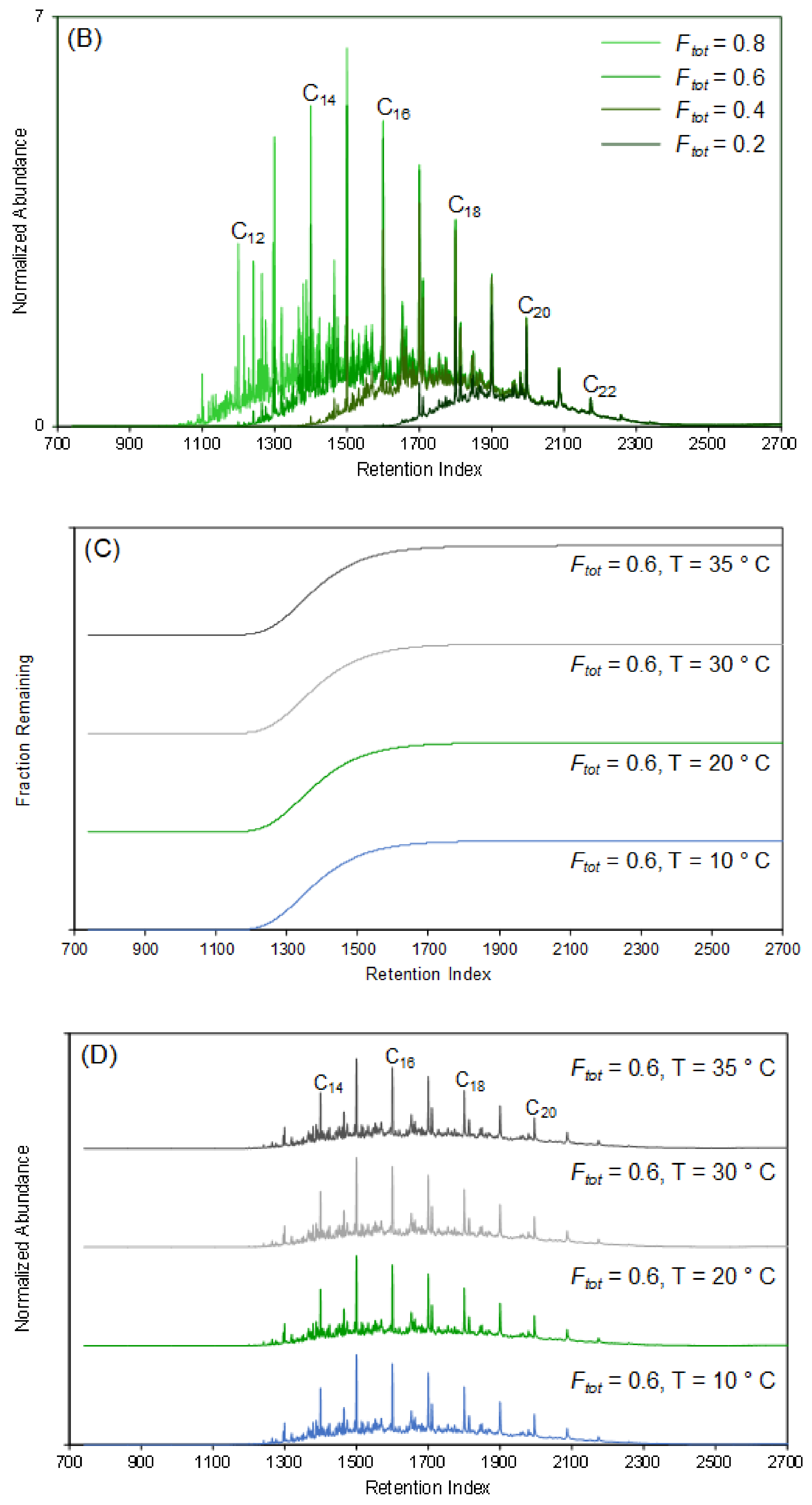
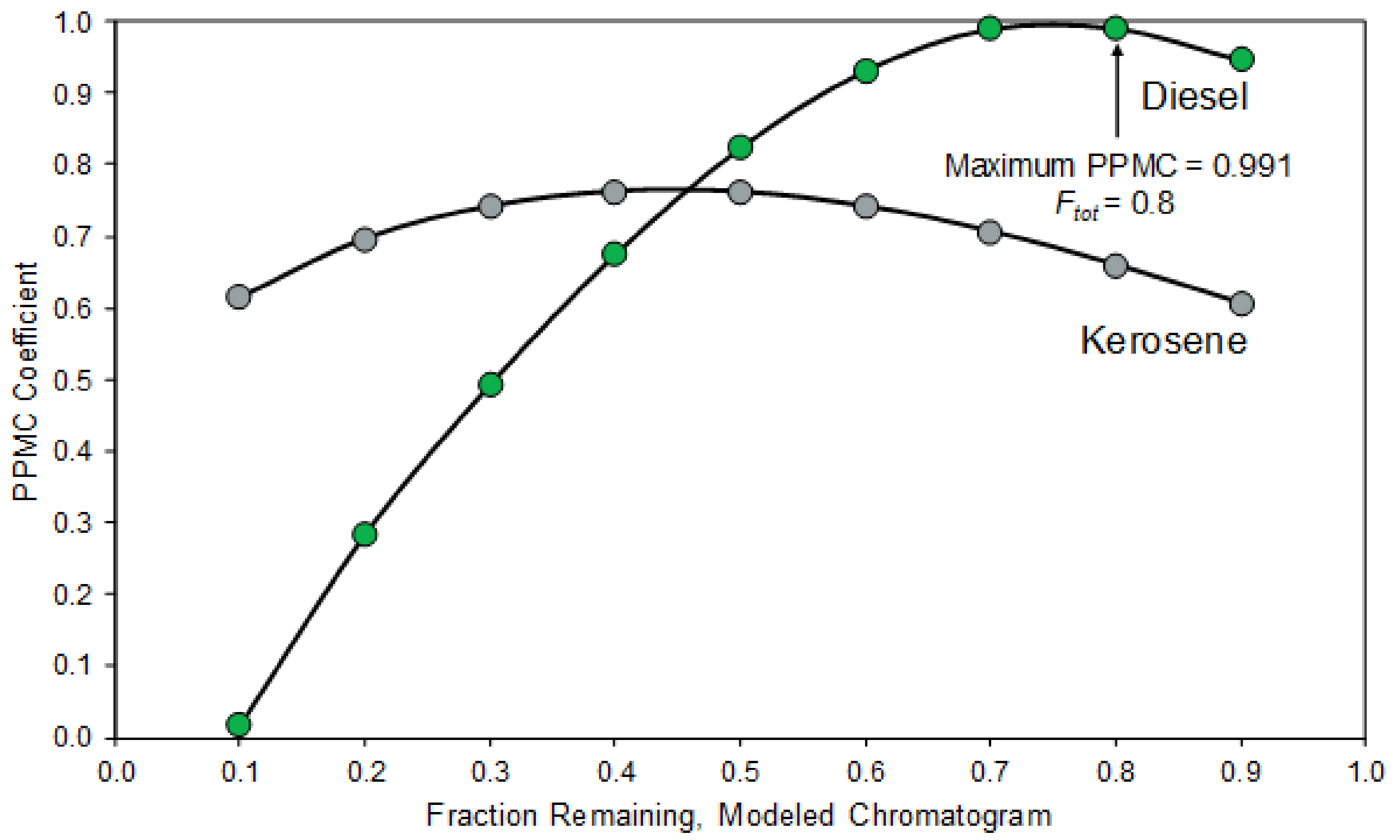
| Temperature (K) | n | m | B | R2 | MAPE(%) Fixed-T Model | MAPE(%) Variable-T Model |
|---|---|---|---|---|---|---|
| 278 | 42 | −1.12 × 10−2 | 6.78 | 0.987 | 9.6 | 19 |
| 283 | 46 | −1.05 × 10−2 | 6.17 | 0.982 | 10.8 | 16 |
| 293 | 51 | −1.05 × 10−2 | 6.71 | 0.990 | 10.3 | 26 |
| 303 | 58 | −1.02 × 10−2 | 7.35 | 0.995 | 8.6 | 9.4 |
| 308 | 61 | −1.00 × 10−2 | 7.62 | 0.993 | 10.5 | 13 |
| Average | 10.0 | 16.4 | ||||
| Temperature (K) | kexp (h−1) | kpred (h−1) Fixed-T Model | APE (%) | kpred(h−1) Variable-T Model | APE (%) |
|---|---|---|---|---|---|
| 278 | 8.41 × 10−3 | 6.95 × 10−3 | 17 | 5.87 × 10−3 | 30 |
| 283 | 8.78 × 10−3 | 7.93 × 10−3 | 9.6 | 8.80 × 10−3 | 0.3 |
| 293 | 1.60 × 10−2 | 1.48 × 10−2 | 7.6 | 1.84 × 10−2 | 15 |
| 303 | 3.92 × 10−2 | 3.58 × 10−2 | 8.7 | 3.69 × 10−2 | 5.8 |
| 308 | 5.87 × 10−2 | 5.84 × 10−2 | 0.5 | 5.15 × 10−2 | 12 |
| Average | 8.8 | 13 | |||
| Temperature (K) | MAPE (%) Fixed-T Model | MAPE (%) Variable-T Model |
|---|---|---|
| 278 | 13.4 | 16.7 |
| 283 | 9.3 | 17.9 |
| 293 | 7.6 | 27.5 |
| 303 | 9.2 | 10.8 |
| 308 | 10.8 | 11.3 |
| Average | 10.1 | 16.8 |
| Test Set 1 Chromatograms | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.5 h | 3 h | 7 h | 30 h a | 30 h b | 30 h c | 70 h A | 70 h B | 150 h | 300 h | |
| Ftot experimental | 0.99 | 0.99 | 0.97 | 0.90 | 0.87 | 0.92 | 0.85 | 0.81 | 0.73 | 0.63 |
| Max. PPMC (35 °C) | 0.980 | 0.988 | 0.995 | 0.993 | 0.993 | 0.993 | 0.994 | 0.991 | 0.993 | 0.992 |
| Max. PPMC (30 °C) | 0.979 | 0.988 | 0.995 | 0.992 | 0.992 | 0.993 | 0.994 | 0.991 | 0.993 | 0.992 |
| Max. PPMC (20 °C) | 0.980 | 0.989 | 0.996 | 0.993 | 0.993 | 0.993 | 0.994 | 0.990 | 0.993 | 0.992 |
| Max. PPMC (10 °C) | 0.979 | 0.988 | 0.995 | 0.993 | 0.993 | 0.993 | 0.994 | 0.990 | 0.993 | 0.992 |
| Ftot Predicted | 0.9 | 0.9 | 0.9 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.7 | 0.6 |
| Test Set 2 Chromatograms | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.5 h 10 °C | 30 h 10 °C | 70 h 10 °C | 0.5 h 20 °C | 3 h 30 °C | 7 h 30 °C | 70 h 30 °C | 0.5 h 35 °C | 70 h 35 °C | 150 h 35 °C | |
| Ftot experimental | 1.11 | 1.22 | 1.18 | 0.96 | 1.02 | 1.00 | 0.96 | 0.99 | 0.78 | 0.73 |
| Max. PPMC (35 °C) | 0.942 | 0.958 | 0.961 | 0.954 | 0.977 | 0.981 | 0.989 | 0.979 | 0.994 | 0.992 |
| Max. PPMC (30 °C) | 0.942 | 0.958 | 0.961 | 0.954 | 0.977 | 0.981 | 0.989 | 0.979 | 0.994 | 0.992 |
| Max. PPMC (20 °C) | 0.942 | 0.958 | 0.961 | 0.954 | 0.977 | 0.981 | 0.989 | 0.980 | 0.994 | 0.992 |
| Max. PPMC (10 °C) | 0.941 | 0.958 | 0.961 | 0.954 | 0.977 | 0.981 | 0.989 | 0.979 | 0.994 | 0.992 |
| Ftot predicted | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.8 | 0.9 | 0.8 | 0.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McIlroy, J.W.; Smith, R.W.; McGuffin, V.L. Fixed- and Variable-Temperature Kinetic Models to Predict Evaporation of Petroleum Distillates for Fire Debris Applications. Separations 2018, 5, 47. https://doi.org/10.3390/separations5040047
McIlroy JW, Smith RW, McGuffin VL. Fixed- and Variable-Temperature Kinetic Models to Predict Evaporation of Petroleum Distillates for Fire Debris Applications. Separations. 2018; 5(4):47. https://doi.org/10.3390/separations5040047
Chicago/Turabian StyleMcIlroy, John W., Ruth Waddell Smith, and Victoria L. McGuffin. 2018. "Fixed- and Variable-Temperature Kinetic Models to Predict Evaporation of Petroleum Distillates for Fire Debris Applications" Separations 5, no. 4: 47. https://doi.org/10.3390/separations5040047
APA StyleMcIlroy, J. W., Smith, R. W., & McGuffin, V. L. (2018). Fixed- and Variable-Temperature Kinetic Models to Predict Evaporation of Petroleum Distillates for Fire Debris Applications. Separations, 5(4), 47. https://doi.org/10.3390/separations5040047




