Separation Optimization of a Mixture of Ionized and Non-Ionized Solutes under Isocratic and Gradient Conditions in Reversed-Phase HPLC by Means of Microsoft Excel Spreadsheets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
2.2. Buffers and Standard Sample Solutions
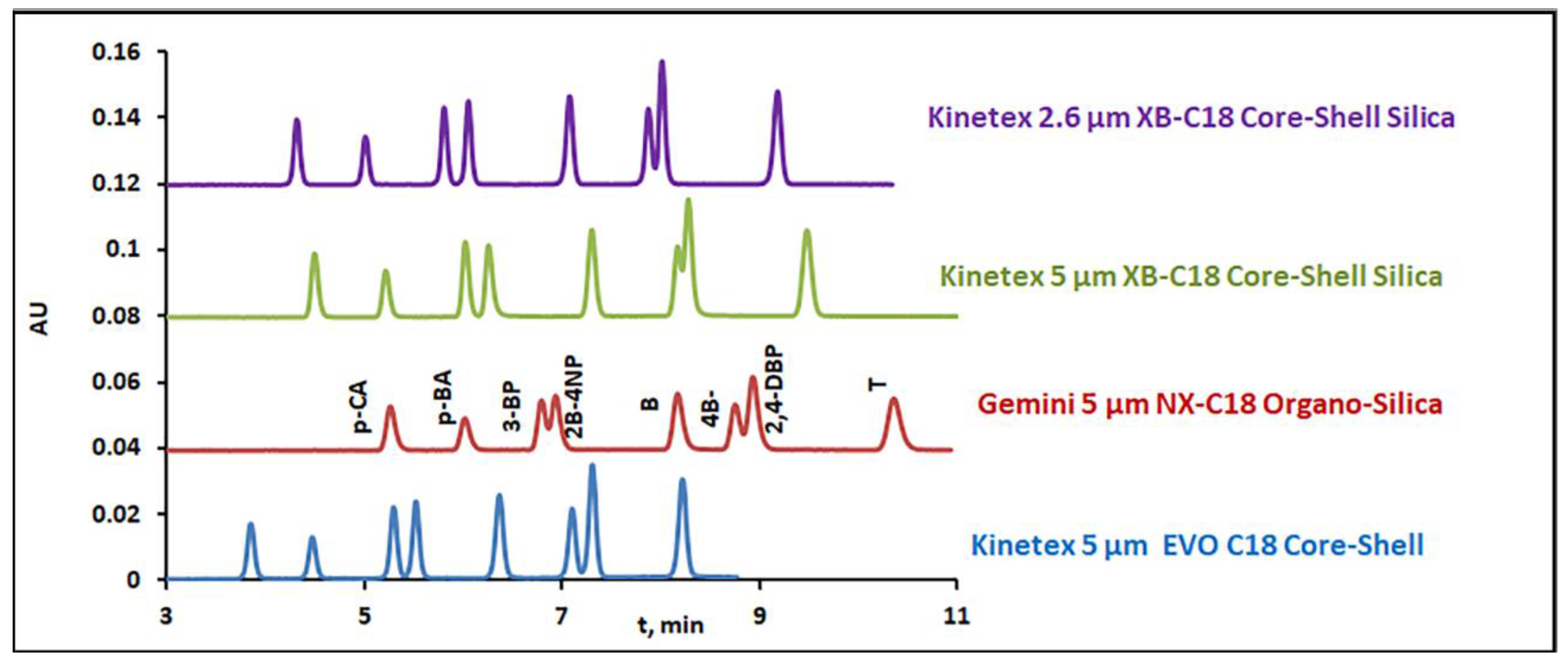
2.3. HPLC System and Conditions
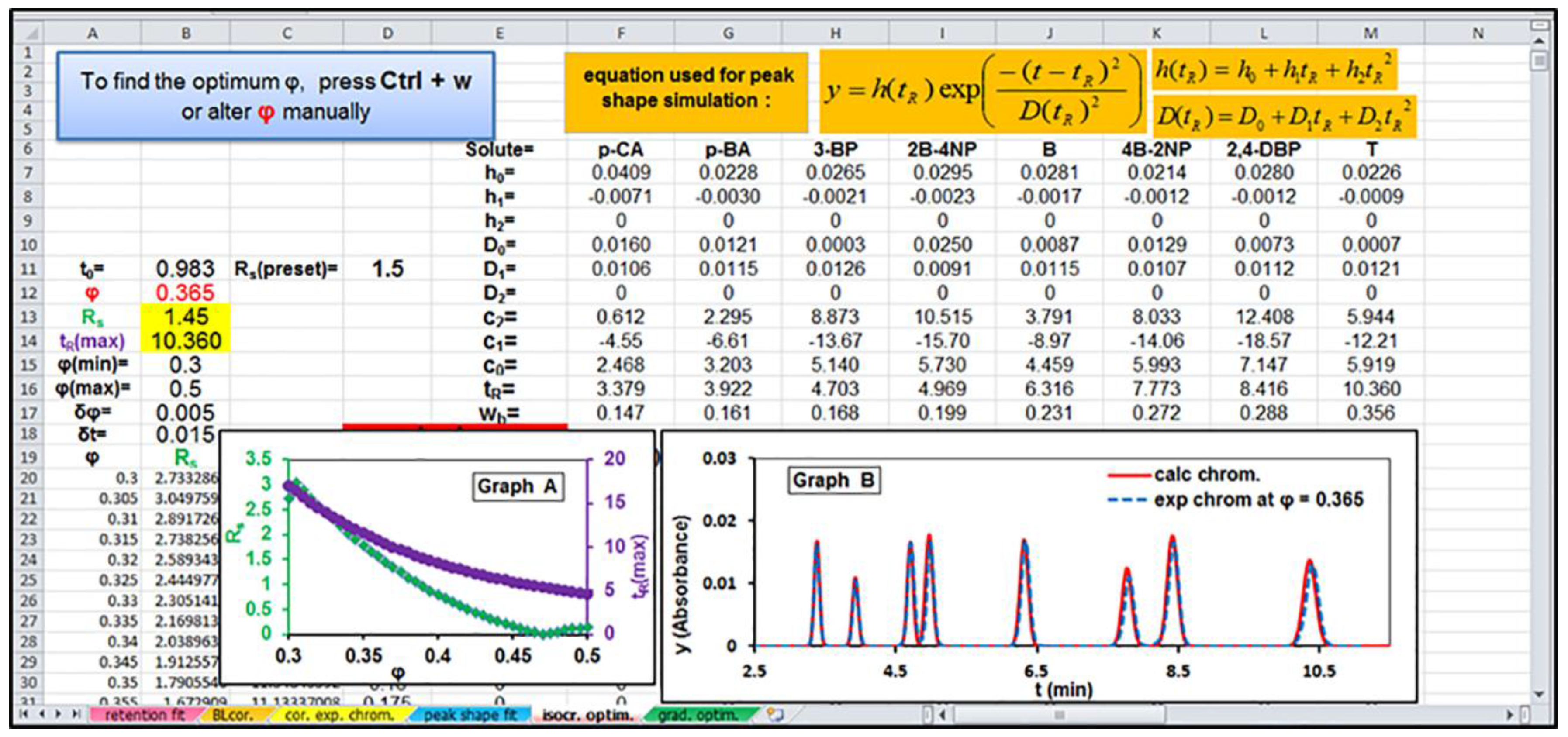
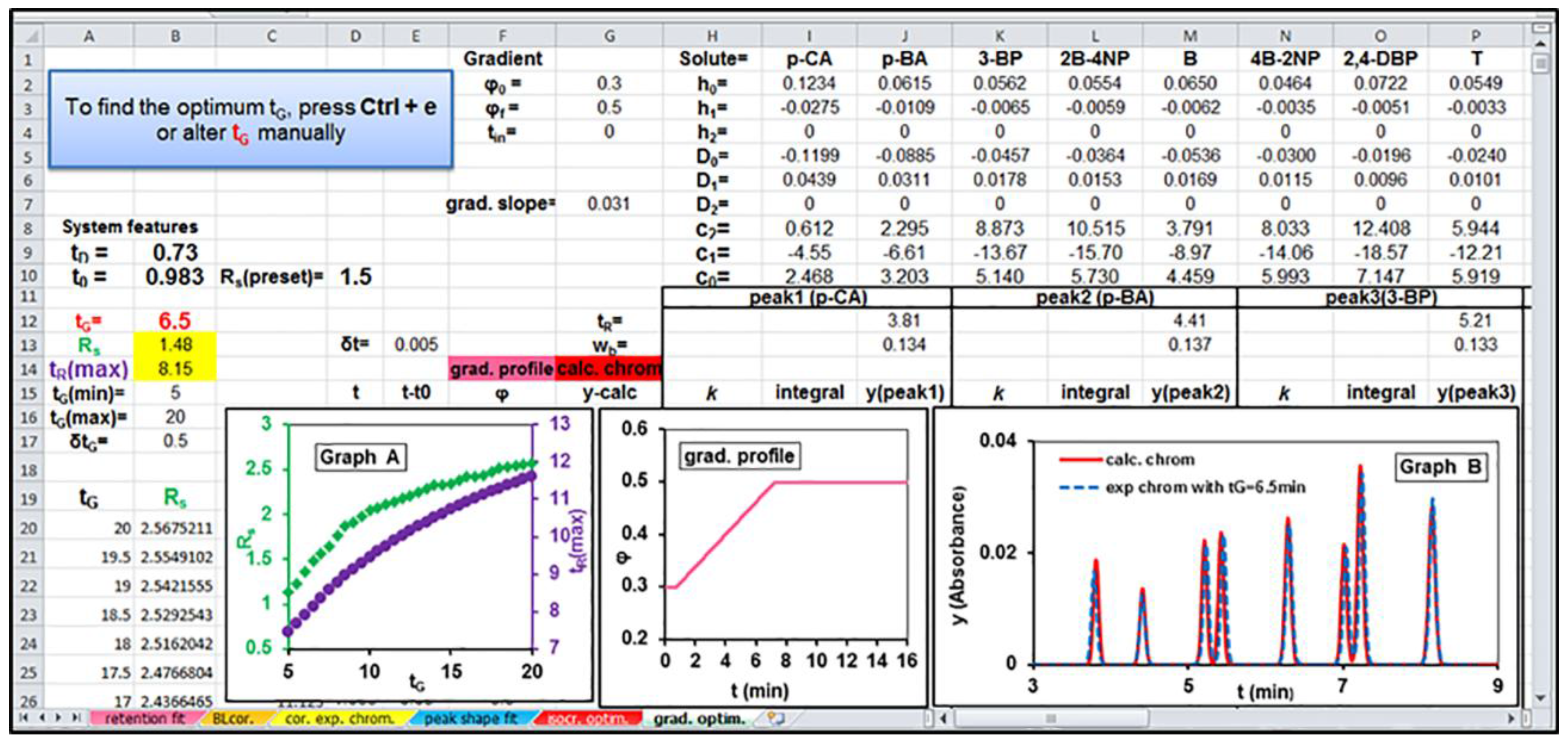
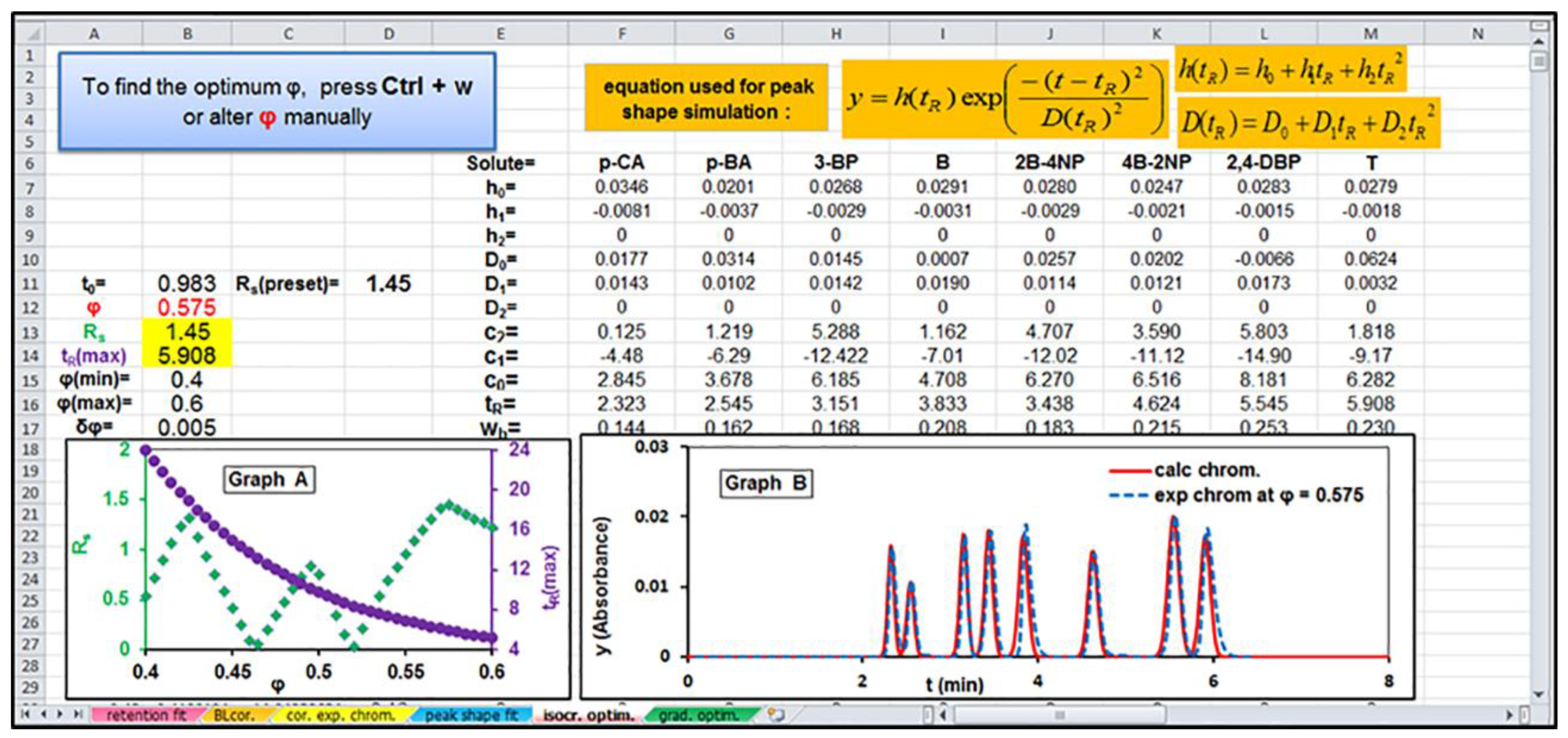
2.4. Excel-Spreadsheet-Based Optimization Software
3. Results
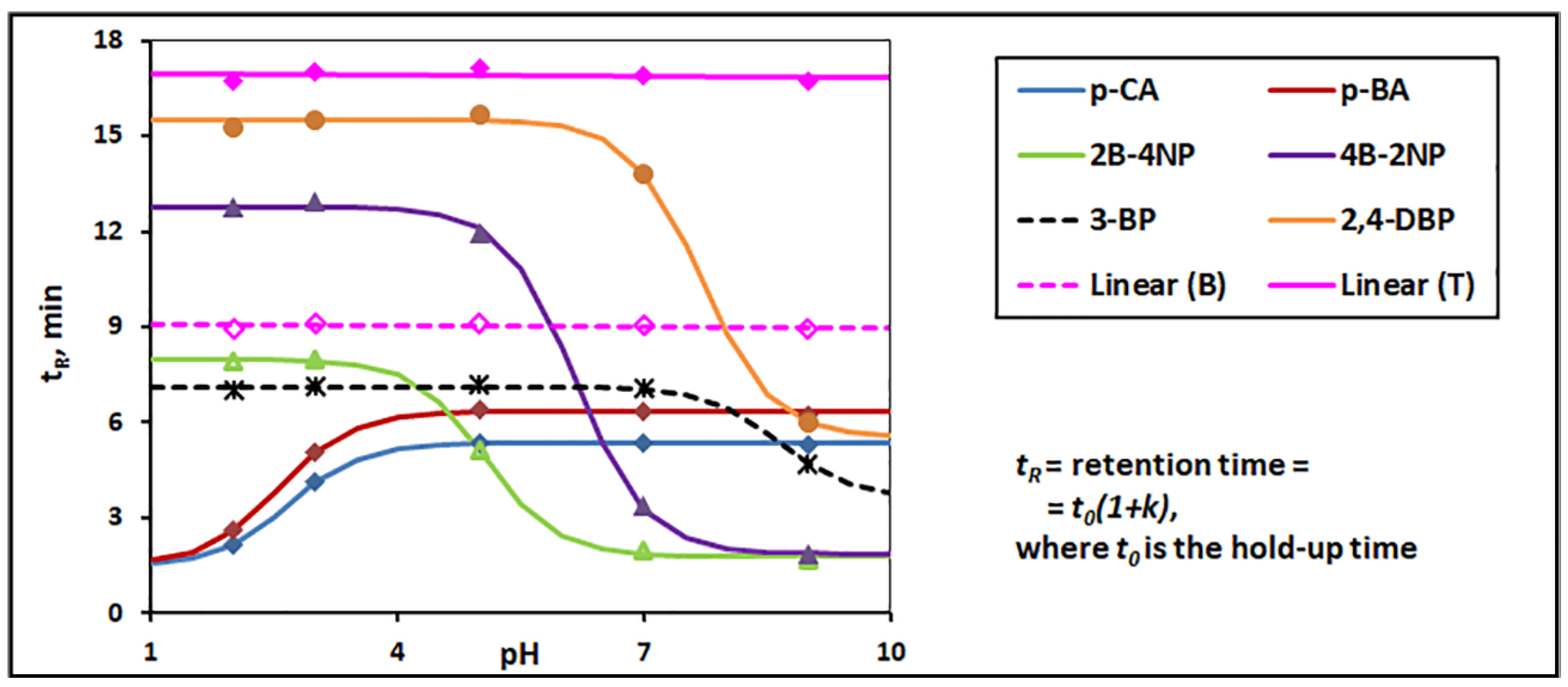
3.1. Effect of the Eluent pH on the Retention of Ionizable Solutes
3.2. Computer-Aided Separation Optimization in Different Eluent pHs
- An initial experimental study of the chromatographic behavior of solutes obtained by the least number of chromatographic runs adequately selected.
- The fitting of the experimental retention data of each solute to a retention model in order to determine its adjustable parameters.
- The modeling of the peak shape of analytes in the form of a preferred function.
- The determination of the optimal separation conditions—i.e., the conditions that lead to the best separation of solutes under consideration—based on the above determined retention and peak shape parameters of solutes.
- The comparison of the simulated chromatogram plotted under the optimal predicted conditions with the corresponding experimental chromatogram recorded under the same conditions in order to test the accuracy of the optimization process.
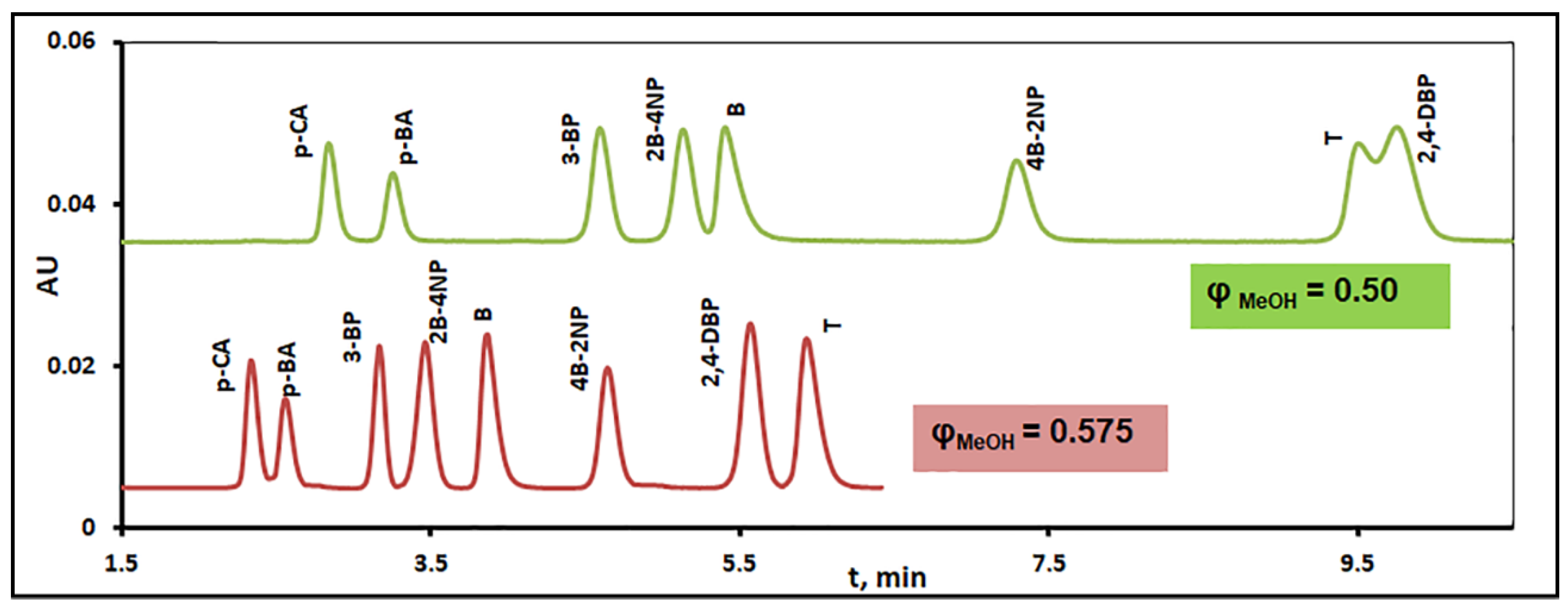
3.3. Utility of Computer-Aided Separation Optimization
4. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Jupille, T.; Snyder, L.; Molnar, I. Optimizing multi-linear gradients in HPLC. LC-GC Eur. 2002, 15, 596–601. [Google Scholar]
- Concha-Herrara, V.; Vivó-Truyols, G.; Torres-Lapasio, J.R.; García-Alvarez-Coque, M.C. Limits of multi-linear gradient optimization in reversed-phase liquid chromatography. J. Chromatogr. A 2005, 1063, 79–88. [Google Scholar] [CrossRef]
- Fasoula, S.; Zisi, C.; Gika, H.; Pappa-Louisi, A.; Nikitas, P. Retention prediction and separation optimization under multilinear gradient elution in liquid chromatography with Microsoft Excel macros. J. Chromatogr. A 2015, 1395, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Debrus, B.; Lebrun, P.; Rozet, E.; Schofield, T.; Mbinze, J.K.; Marini, R.D.; Rudaz, S.; Boulanger, B.; Hubert, P. A new method for quality by design robust method optimization in liquid chromatography. LC-GC Eur. 2013, 26, 370–375. [Google Scholar]
- Tyteca, E.; Liekens, A.; Clicq, D.; Fanigliulo, A.; Debrus, B.; Rudaz, S.; Guillarme, D.; Desmet, G. Predictive elution window shifting and stretching as a generic search strategy for automated method development for liquid chromatography. Anal. Chem. 2012, 84, 7823–7830. [Google Scholar] [CrossRef] [PubMed]
- Fasoula, S.; Nikitas, P.; Pappa-Louisi, A. Teaching simulation and computer-aided separation optimization in liquid chromatography by means of illustrative Microsoft Excel spreadsheets. J. Chem. Educ. 2017, 94, 1167–1173. [Google Scholar] [CrossRef]
- Canals, I.; Valkó, K.; Bosch, E.; Hill, A.P.; Rosés, M. Retention of ionisable compounds on HPLC. 8. Influence of mobile-phase pH change on the chromatographic retention of acids and bases during gradient elution. Anal. Chem. 2001, 73, 4937–4945. [Google Scholar] [CrossRef] [PubMed]
- Andrés, A.; Rosés, M.; Bosch, E. Gradient retention prediction of acid–base analytes in reversed phase liquid chromatography: A simplified approach for acetonitrile–water mobile phases. J. Chromatogr. A 2014, 1370, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Christian, G.D.; Purdy, W.C. The residual current in orthophosphate medium. J. Electroanal. Chem. 1962, 3, 363–367. [Google Scholar] [CrossRef]
- Horvath, C.; Melander, W.; Molnar, I. Liquid chromatography of ionogenic substances with nonpolar stationary Phases. Anal. Chem. 1977, 49, 142–154. [Google Scholar] [CrossRef]
- Wiczling, P.; Kaliszan, R. pH gradient as a tool for the separation of ionizable analytes in reversed-phase high-performance chromatography. Anal. Chem. 2010, 82, 3692–3698. [Google Scholar] [CrossRef] [PubMed]
- Nikitas, P.; Pappa-Louisi, A.; Zisi, C. pH-gradient reversed-phase liquid Chromatography of ionogenic analytes revisited. Anal. Chem. 2012, 84, 6611–6618. [Google Scholar] [CrossRef] [PubMed]
- Fasoula, S.; Zisi, C.; Nikitas, P.; Pappa-Louisi, A. Retention prediction and separation optimization of ionizable analytes in reversed-phase liquid chromatography by organic modifier gradients in different eluent pHs. J. Chromatogr. A 2013, 1305, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Schoenmakers, P.J.; Billiet, H.A.H.; de Galan, L. Description of solute retention over the full range of mobile phase compositions in reversed-phase liquid chromatography. J. Chromatogr. A 1983, 282, 107–121. [Google Scholar] [CrossRef]
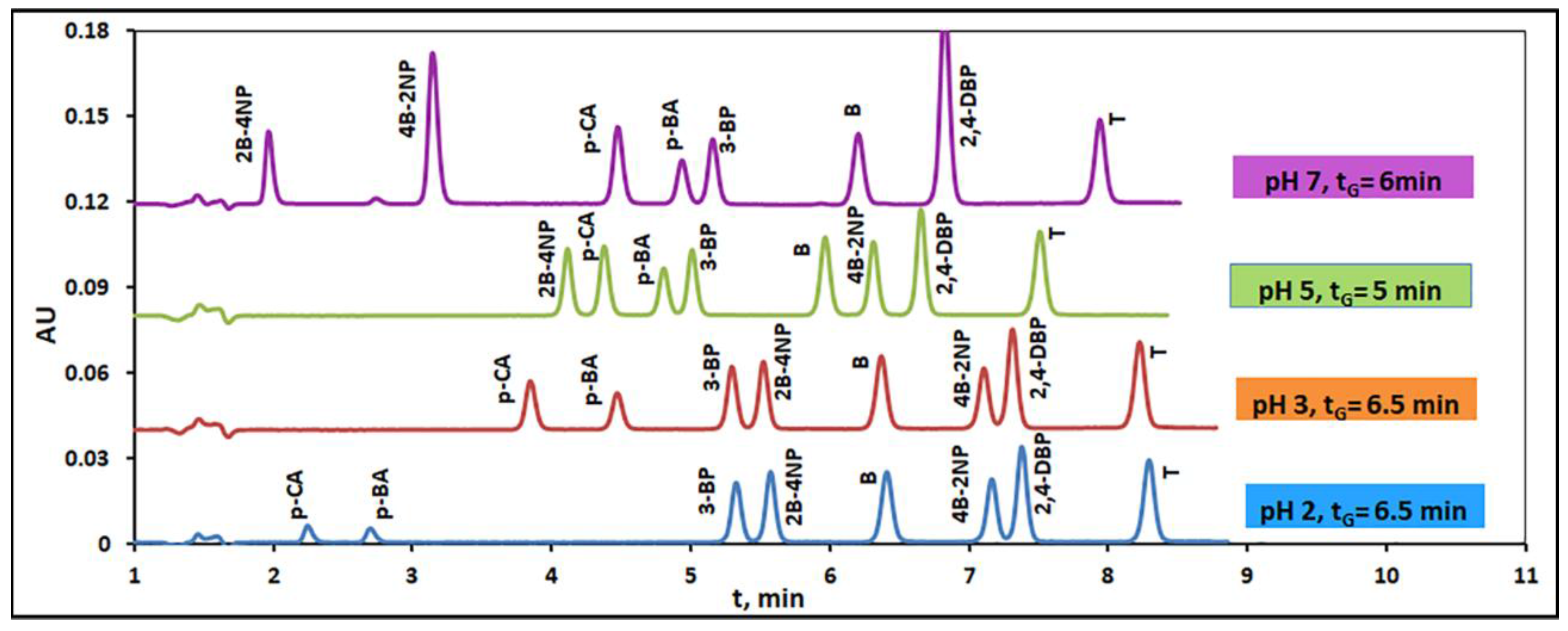
| pH | Optimum Isocratic Conditions in an Eluent Modified with ACN | Optimum Gradient Conditions for the Linear Variation of ϕACN from ϕ0 = 0.3 to ϕf = 0.5 | ||||
|---|---|---|---|---|---|---|
| ϕACN | Rs | tR(max), min | tG, min | Rs | tR(max), min | |
| 2 | 0.370 | 1.41 | 9.87 | 6.5 | 1.47 | 8.10 |
| 3 | 0.365 | 1.45 | 10.96 | 6.5 | 1.48 | 8.15 |
| 5 | 0.365 | 1.38 | 10.40 | 5.0 | 1.43 | 7.46 |
| 7 | 0.370 | 1.42 | 10.07 | 6.0 | 1.42 | 7.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zisi, C.; Mangipa, A.M.; Boutou, E.; Pappa-Louisi, A. Separation Optimization of a Mixture of Ionized and Non-Ionized Solutes under Isocratic and Gradient Conditions in Reversed-Phase HPLC by Means of Microsoft Excel Spreadsheets. Separations 2018, 5, 19. https://doi.org/10.3390/separations5010019
Zisi C, Mangipa AM, Boutou E, Pappa-Louisi A. Separation Optimization of a Mixture of Ionized and Non-Ionized Solutes under Isocratic and Gradient Conditions in Reversed-Phase HPLC by Means of Microsoft Excel Spreadsheets. Separations. 2018; 5(1):19. https://doi.org/10.3390/separations5010019
Chicago/Turabian StyleZisi, Chrysostomi, Athina Maria Mangipa, Eleftheria Boutou, and Adriani Pappa-Louisi. 2018. "Separation Optimization of a Mixture of Ionized and Non-Ionized Solutes under Isocratic and Gradient Conditions in Reversed-Phase HPLC by Means of Microsoft Excel Spreadsheets" Separations 5, no. 1: 19. https://doi.org/10.3390/separations5010019
APA StyleZisi, C., Mangipa, A. M., Boutou, E., & Pappa-Louisi, A. (2018). Separation Optimization of a Mixture of Ionized and Non-Ionized Solutes under Isocratic and Gradient Conditions in Reversed-Phase HPLC by Means of Microsoft Excel Spreadsheets. Separations, 5(1), 19. https://doi.org/10.3390/separations5010019




