An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators
Abstract
1. Introduction
2. Materials and Methods
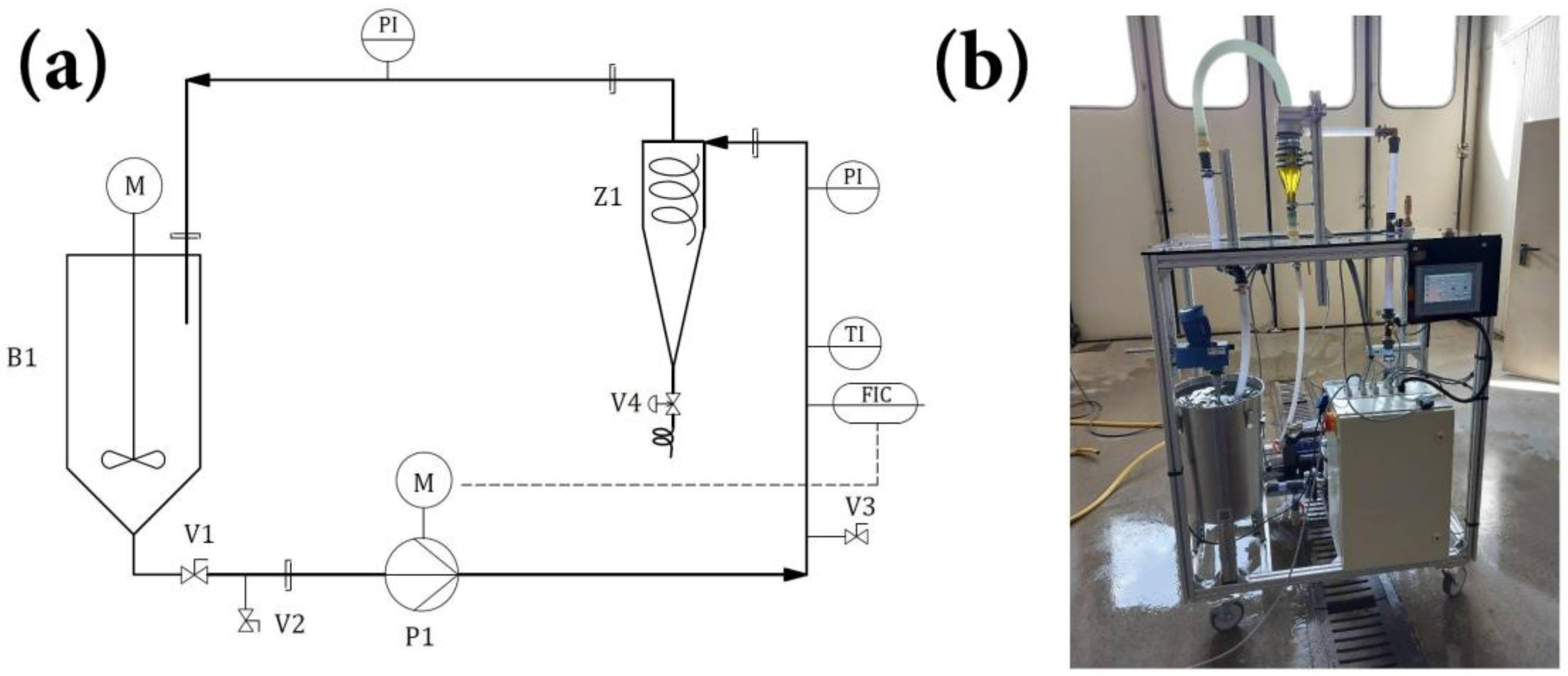
2.1. Experimental Setup
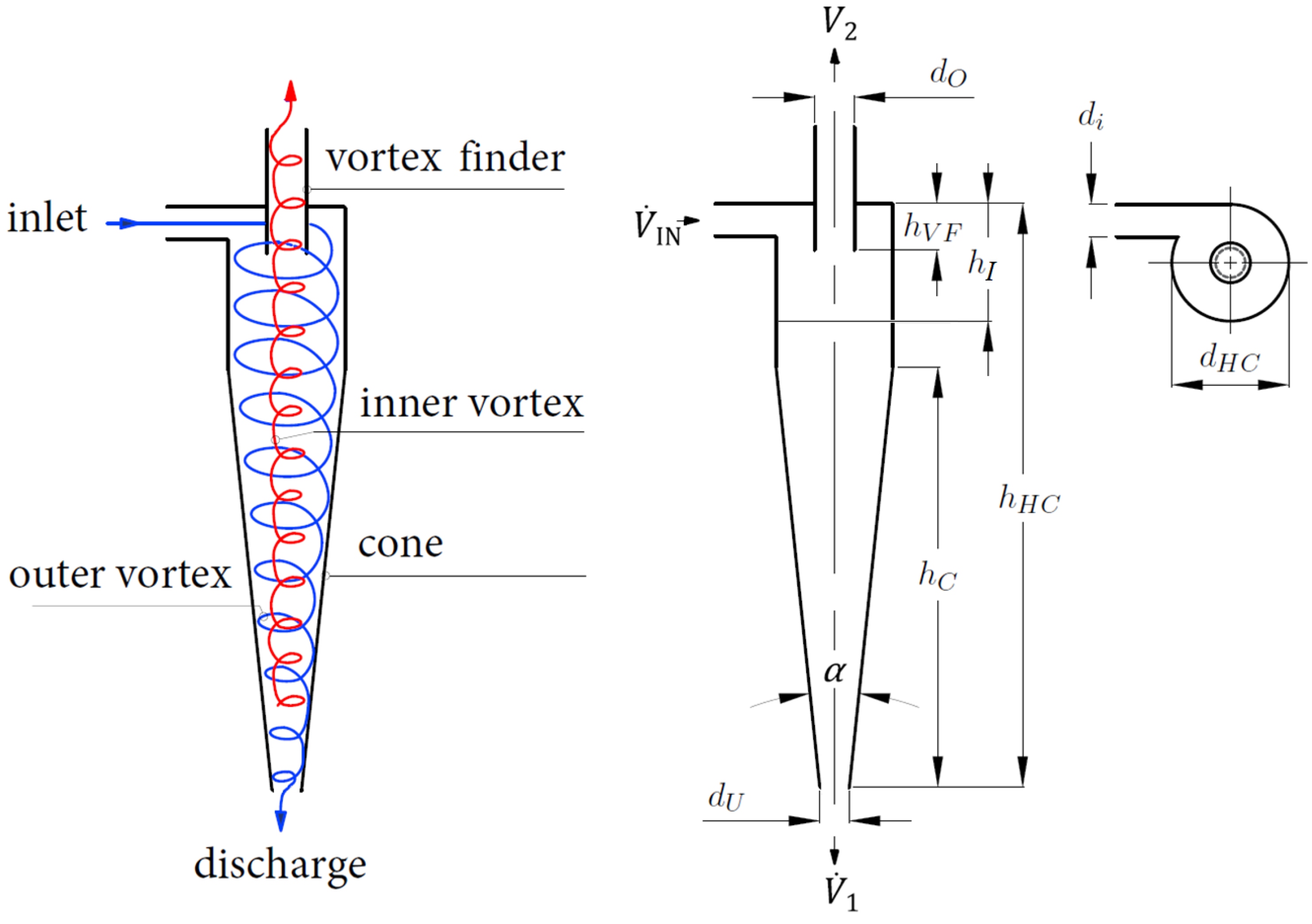
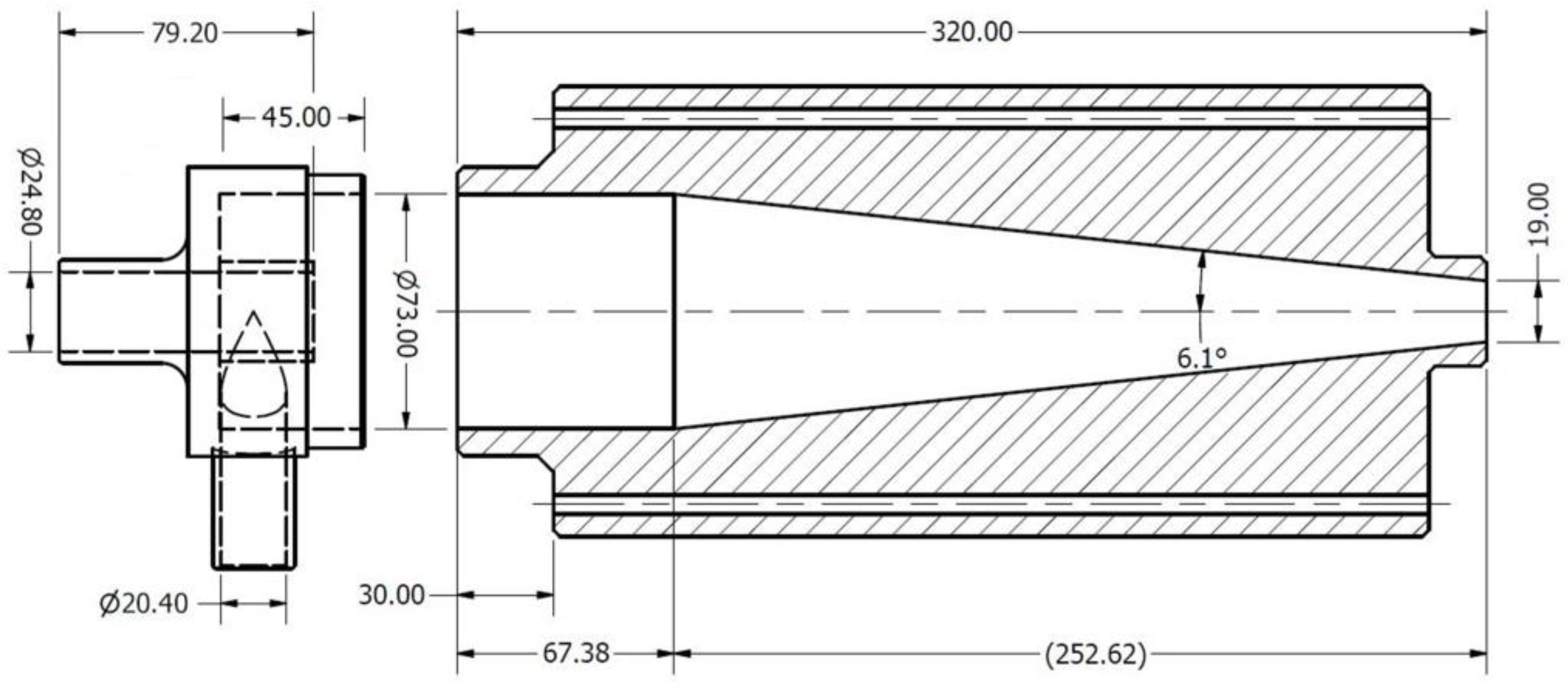
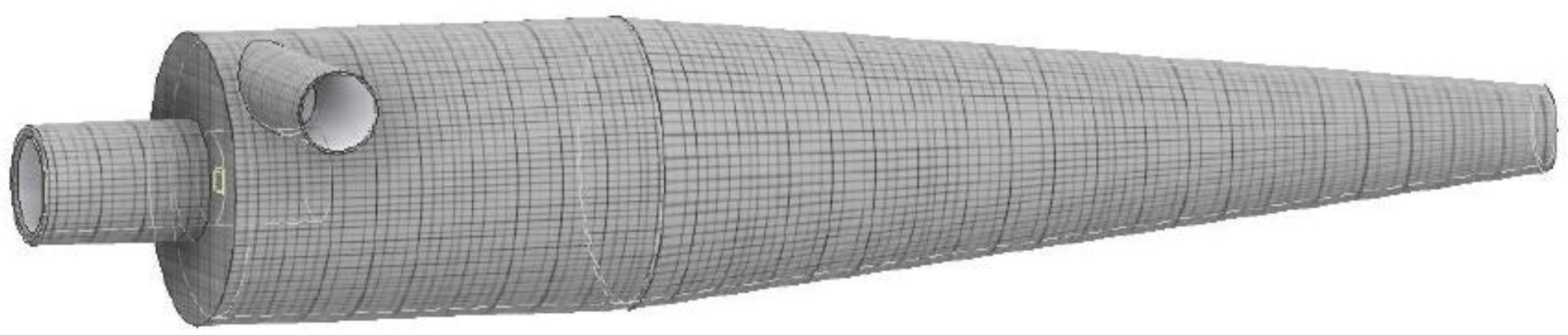
2.2. Separation Chamber, Connecting System and Inlet Section
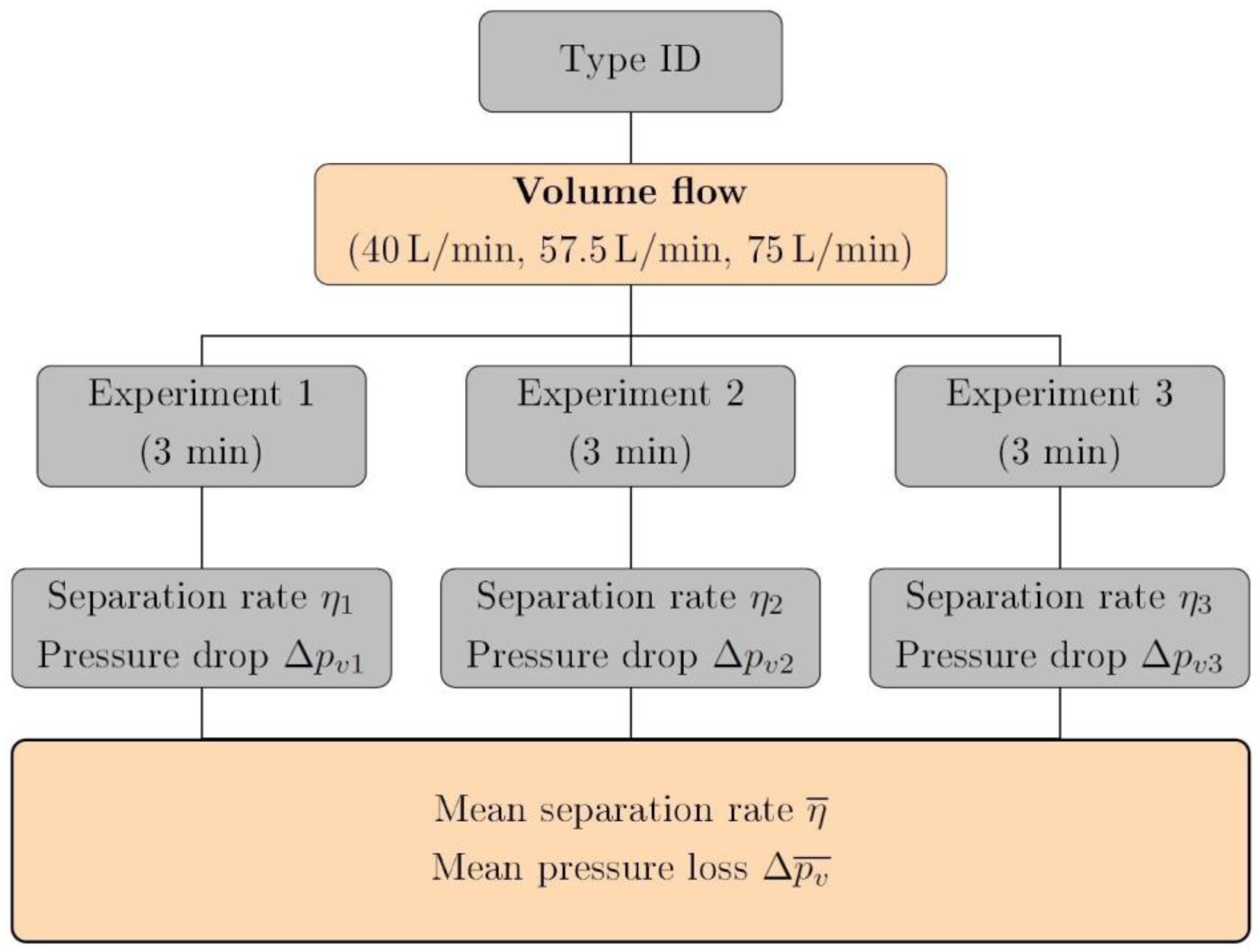
2.3. Operational Parameters and Experimental Procedure
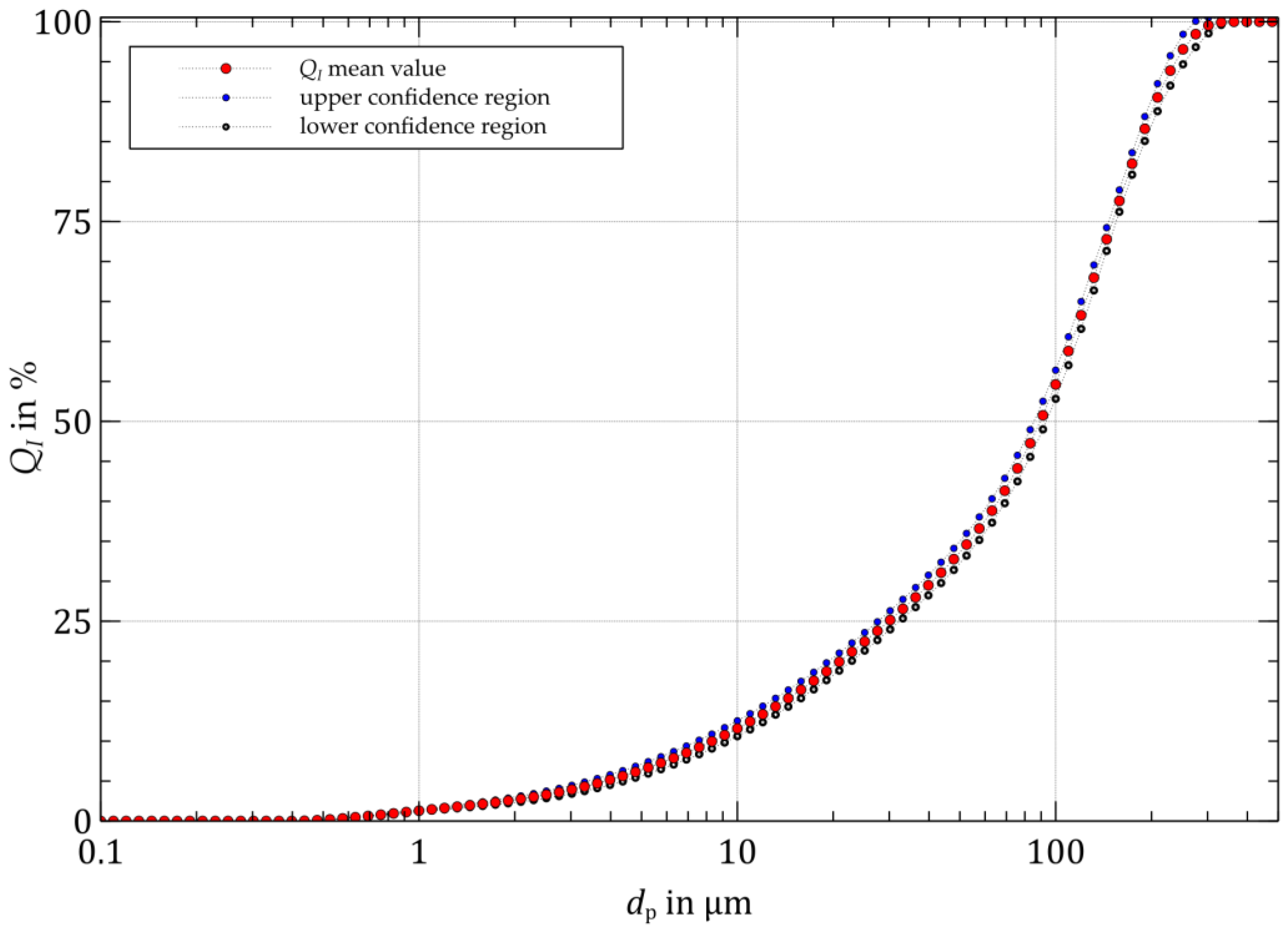
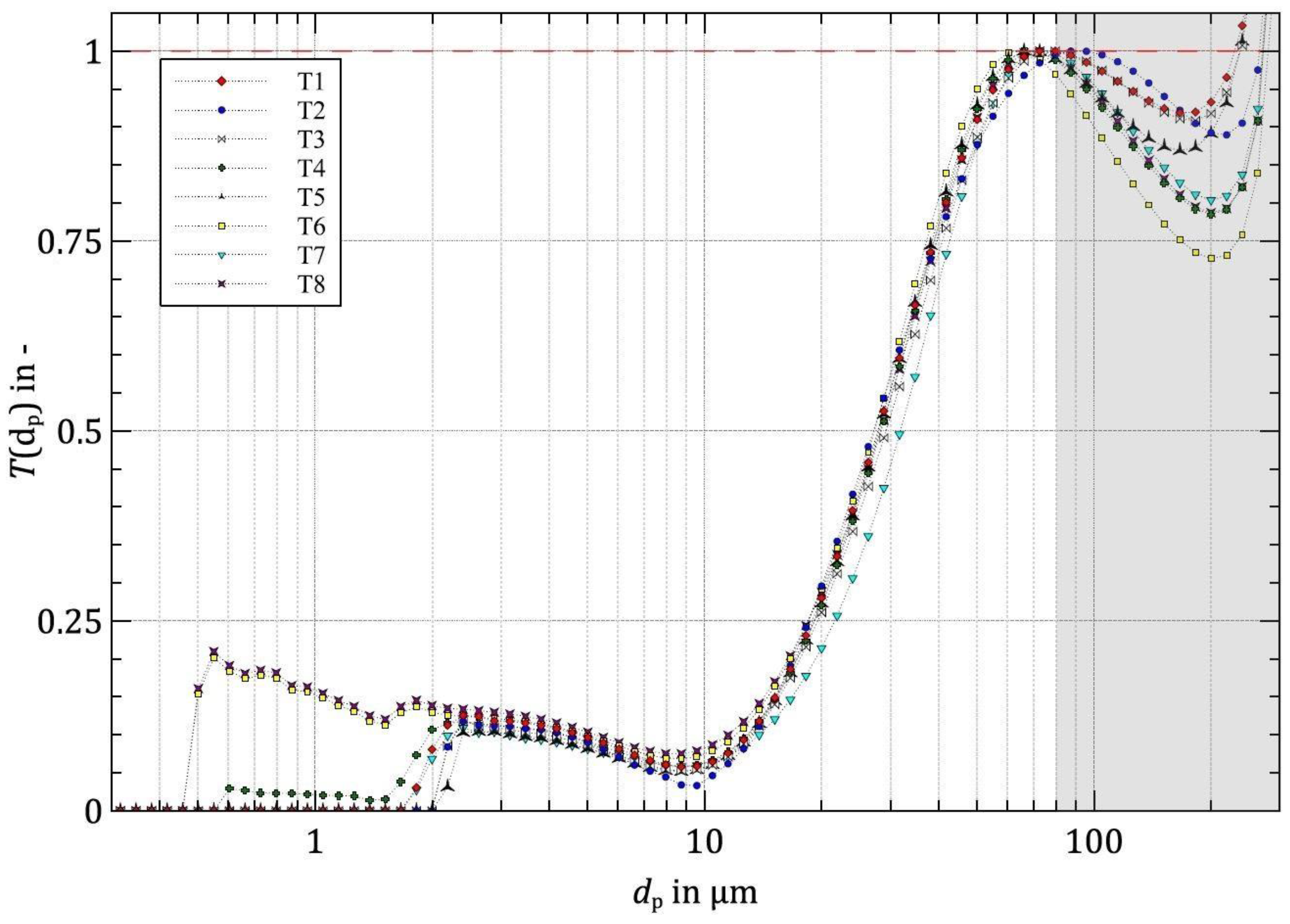
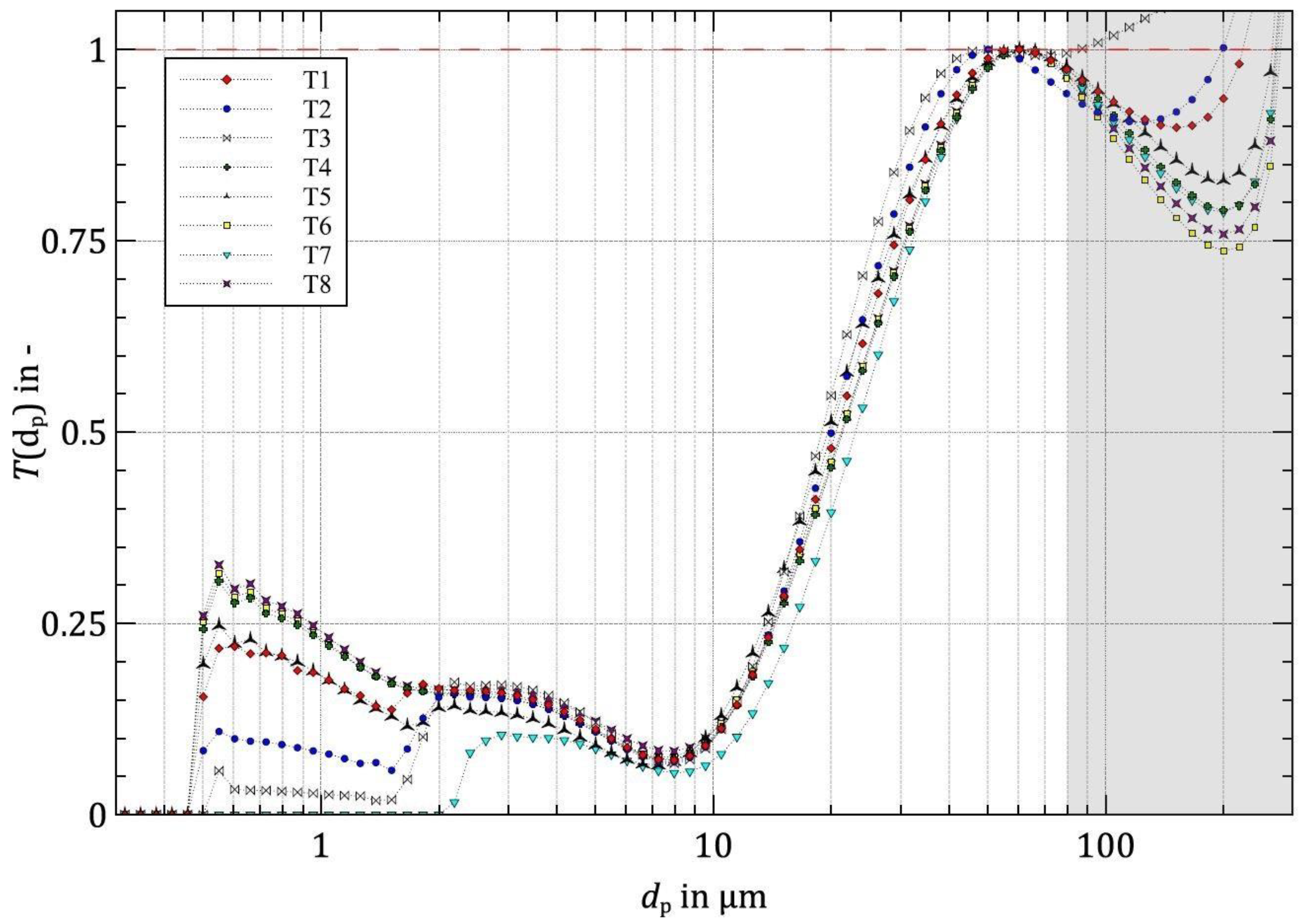
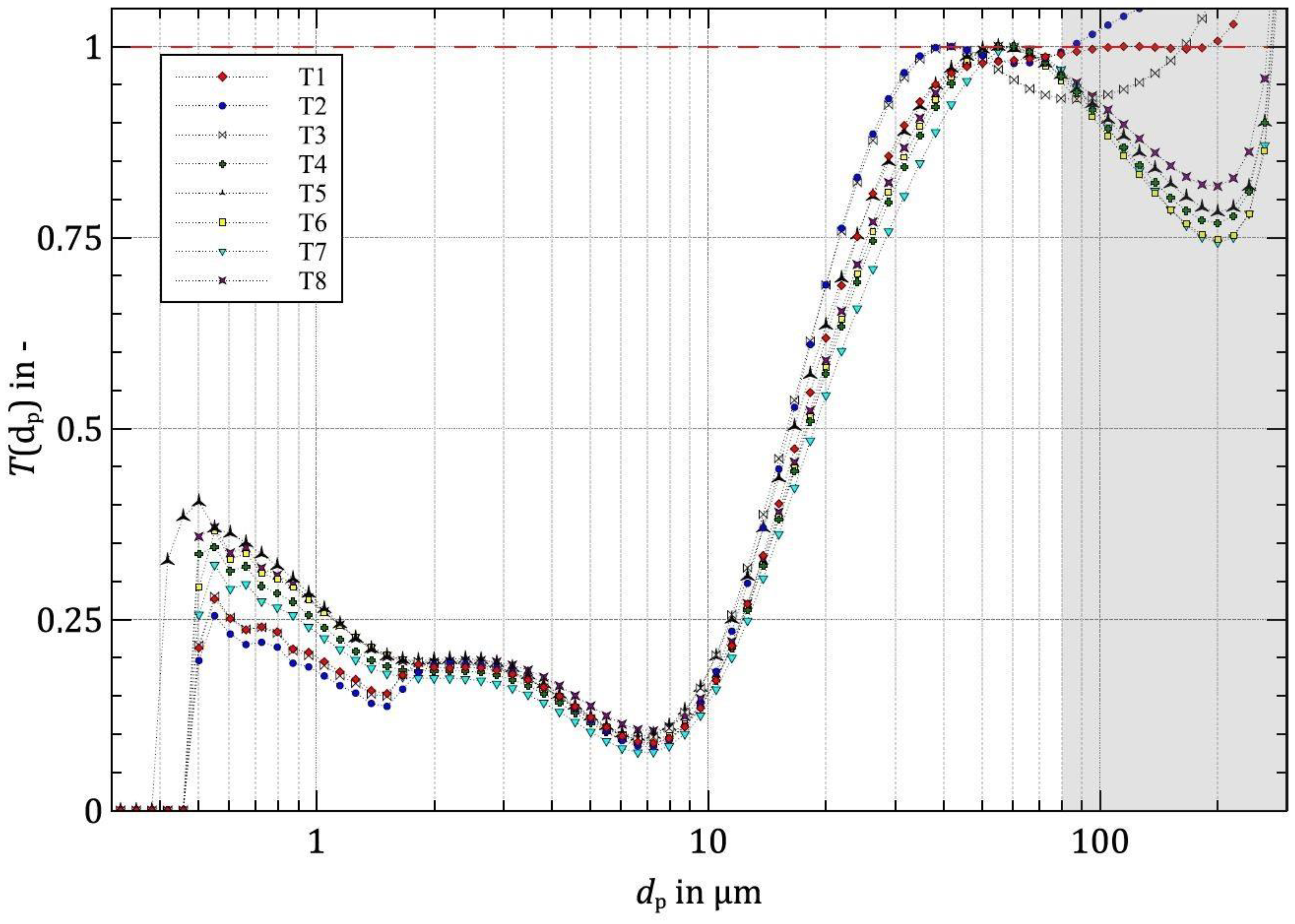
3. Results
Boundary Conditions of Hydrocyclones
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dallmann, W. Handbuch Der Mechanischen Fest-Flüssig-Trennung; Luckert, K., Ed.; Vulkan-Verlag: Essen, Germany, 2004; ISBN 3-8027-2196-9. [Google Scholar]
- Muschelknautz, U. Zyklone zum Abscheiden fester Partikel aus Gasen, VDI Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bradley, D. The Hydrocyclone; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Rietema, K. Performance and Design in Hydrocyclones—III. Chem. Eng. Sci. 1961, 15, 310–319. [Google Scholar] [CrossRef]
- Schubert, H. Handbuch Der Mechanischen Verfahrenstechnik, 1st ed.; Schubert, H., Ed.; Wiley-VCH: Weinheim, Germany, 2002; ISBN 978-3-527-30577-3. [Google Scholar]
- Gundelach, W.; Trawinski, H.F. Der Hydrozyklon. Ein Einfaches und Billiges Gerät für das Klassieren und Eindicken. Chem.-Ing.-Tech. 1960, 32, 279–284. [Google Scholar] [CrossRef]
- Svarovsky, L.; Thew, M.T. Hydrocyclones Analysis and Applications, 1st ed.; Springer Science + Business Media: Dordrecht, The Netherlands, 1992; ISBN 978-94-015-7981-0. [Google Scholar]
- Saidi, M.; Maddahian, R.; Farhanieh, B. Numerical Investigation of Cone Angle Effect on the Flow Field and Separation Efficiency of Deoiling Hydrocyclones. Heat Mass Transf. Stoffuebertragung 2013, 49, 247–260. [Google Scholar] [CrossRef]
- Senfter, T. Kontinuierliche Störstoffabscheidung in Der Klärschlamm-Co-Fermentation Mittels Zentrifugalabscheider. Ph.D. Thesis, University of Innsbruck, Innsbruck, Austria, 2019. [Google Scholar]
- Andritschke, N. Das Aus für Mikroplastik: Mit 1500 g Ins Wirbelzentrum. Wasserwirtsch. Wassertech. 2021, 70, 6–7. [Google Scholar] [CrossRef]
- Ji, L.; Paul, P.; Shanbhag, B.K.; Dixon, I.; Kuang, S.; He, L. Emerging Application of Hydrocyclone in Biotechnology and Food Processing. Sep. Purif. Technol. 2023, 309, 122992. [Google Scholar] [CrossRef]
- FLSmidth GMAX® Hydrozyklone Feinere Partikeltrennung Mit Patentierter Technologie. FLSmidth 2018. Available online: https://www.flsmidth.com/-/media/brochures/brochures-products/centrifugation-and-classification/2019/krebs-gmax-cyclone_brochure_german.pdf (accessed on 10 May 2024).
- Akw, G. Hydrozyklone AKA-VORTEX. Available online: https://de.akwauv.de/hydrozyklone-aka-vortex-2/ (accessed on 10 May 2024).
- Stieß, M. Mechanische Verfahrenstechnik—Partikeltechnologie 1, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-32551-2. [Google Scholar]
- Jiang, L.; Liu, P.; Zhang, Y.; Li, X.; Yang, X.; Xu, H.; Wang, H. Experimental Study of the Separation Performance of a Hydrocyclone with a Compound Curve Cone. Powder Technol. 2022, 409, 117829. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, H.; Liu, Y.; Li, Z. Solid/Liquid Separation Performance of Hydrocyclones with Different Cone Combinations. Sep. Purif. Technol. 2010, 74, 271–279. [Google Scholar] [CrossRef]
- Ghodrat, M.; Kuang, S.B.; Yu, A.B.; Vince, A.; Barnett, G.D.; Barnett, P.J. Numerical Analysis of Hydrocyclones with Different Conical Section Designs. Miner. Eng. 2014, 62, 74–84. [Google Scholar] [CrossRef]
- Vimal, A.; Thalaieswaran, S.; Kannan, N.H.; Ganeshan, P.; Venkatesh, S. A Review on the Investigation of Hydrocyclone Performance by Shape Optimization. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2023; Volume 405. [Google Scholar] [CrossRef]
- Ni, L.; Tian, J.; Song, T.; Jong, Y.; Zhao, J. Optimizing Geometric Parameters in Hydrocyclones for Enhanced Separations: A Review and Perspective. Sep. Purif. Rev. 2019, 48, 30–51. [Google Scholar] [CrossRef]
- Yoshida, H.; Takashina, T.; Fukui, K.; Iwanaga, T. Effect of Inlet Shape and Slurry Temperature on the Classification Performance of Hydro-Cyclones. Powder Technol. 2004, 140, 1–9. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, D.; Cui, B.; Li, T.; Luo, N. Effects of Curvature Radius on Separation Behaviors of the Hydrocyclone with a Tangent-Circle Inlet. Powder Technol. 2017, 305, 156–165. [Google Scholar] [CrossRef]
- Chlebnikovas, A.; Jasevičius, R. Investigation of the Interaction of Particulate Matter and Its Separation from the Gas Flow in a Multi-Channel Cyclone with Recirculation. Granul. Matter 2022, 24, 98. [Google Scholar] [CrossRef]
- Raimondas Jasevičius Pranas Baltrėnas, R.K.; Grubliauskas, R. DEM Simulation of the Impact of Ultrafine Glass Particles on the Partition Wall of the Multichannel Cyclone. Part. Sci. Technol. 2014, 32, 576–587. [Google Scholar] [CrossRef]
- Chlebnikovas, A.; Paliulis, D.; Kilikevičienė, K.; Kilikevičius, A. Experimental Research of Gaseous Emissions Impact on the Performance of New-Design Cylindrical Multi-Channel Cyclone with Adjustable Half-Rings. Sustainability 2022, 14, 902. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhong, S.; Li, L. Characteristics and Mechanisms of Particle Adhesion Patterns in an Aerodynamic Cyclone. Aerosol Sci. Technol. 2017, 51, 1313–1323. [Google Scholar] [CrossRef]
- Zhou, Y.; See, T.; Zhong, S.; Liu, Z.; Li, L. A Massive Reduction of Dust Particle Adhesion in a Cyclone by the Introduction of a Wedge. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 3102–3114. [Google Scholar] [CrossRef]
- Zhou, Y.; See, T.; Zhong, S.; Liu, Z.; Li, L. A 2D Mesh-Free Simulation of the Particle Adhesion in a Plastic Cyclone. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 095440621875879. [Google Scholar] [CrossRef]
- Rietema, K. Performance and Design of Hydrocyclones-IV Design of Hydrocyclones. Chem. Eng. Sci. 1961, 15, 320–825. [Google Scholar] [CrossRef]
- Bonfig, K.W. Taschenbuch Der Messtechnik, 7th ed.; Jörg, H., Ed.; Carl Hanser Verlag: Munich, Germany, 2015; ISBN 978-3-446-44271-9. [Google Scholar]
- Neeße, T.; Schubert, H.; Graichen, K. Praktische und Theoretische Aspekte Der Dichtstromklassierung. Aufb.-Technol. 1991, 32, 459–472. [Google Scholar]
- Trawinski, H.F. Practical Aaspects of the Design and Industrial Applications of the Hydrocyclone. Filtr. Sep. 1969, 6, 361–367. [Google Scholar]
- Hemming, W. Verfahrenstechnik, 8th ed.; Vogel Buchverlag: Landsberg, Germany, 1999; ISBN 3-8023-1774-2. [Google Scholar]
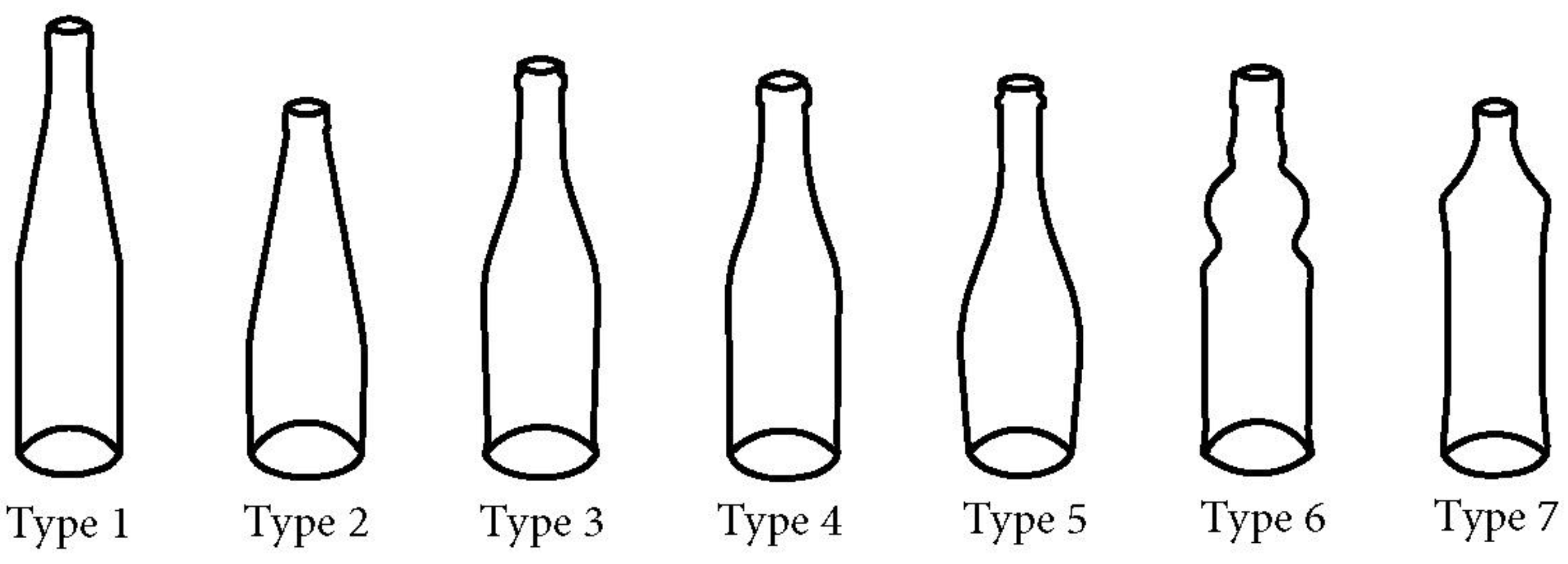


| Bottle Type | Shape | Volume | ||
|---|---|---|---|---|
| - | - | mm | mm | mL |
| Type 1 | Conical | 69 | 315 | 747 |
| Type 2 | Conical | 77 | 255 | 737 |
| Type 3 | Curved | 72 | 286 | 722 |
| Type 4 | Curved | 74 | 275 | 761 |
| Type 5 | Curved | 72 | 271 | 758 |
| Type 6 | Cylindrical | 71 | 281 | 751 |
| Type 7 | Cylindrical | 71 | 254 | 757 |
| Type 8 | Rietema | 73 | 320 | 750 |
| Cyclone Model | |||||
|---|---|---|---|---|---|
| Rietema | 5 | 0.28 | 0.34 | 0.40 | - |
| Bradley | - | 0.14 | 0.20 | 0.33 | 0.5 |
| Type | η | cF | ||||
|---|---|---|---|---|---|---|
| - | L min−1 | L min−1 | % | bar | % | g L−1 |
| Type 1 | 40.0 57.5 75.0 | 0.44 0.61 0.77 | 1.12 1.08 1.03 | 0.086 0.182 0.320 | 64.0 71.0 78.5 | 0.90 0.73 0.54 |
| Type 2 | 40.0 57.5 75.0 | 0.36 0.53 0.69 | 0.92 0.94 0.93 | 0.088 0.186 0.334 | 64.2 70.9 78.4 | 0.90 0.73 0.54 |
| Type 3 | 40.0 57.5 75.0 | 0.40 0.59 0.75 | 1.00 1.03 1.01 | 0.080 0.198 0.330 | 62.4 70.4 77.9 | 0.94 0.74 0.55 |
| Type 4 | 40.0 57.5 75.0 | 0.39 0.57 0.73 | 0.98 1.00 0.98 | 0.082 0.192 0.322 | 62.2 70.2 76.6 | 0.95 0.75 0.59 |
| Type 5 | 40.0 57.5 75.0 | 0.37 0.58 0.74 | 0.92 1.03 1.00 | 0.090 0.190 0.356 | 59.9 71.9 76.4 | 1.00 0.70 0.59 |
| Type 6 | 40.0 57.5 75.0 | 0.44 0.63 0.78 | 1.12 1.10 1.05 | 0.082 0.184 0.326 | 61.7 70.5 76.5 | 0.96 0.74 0.59 |
| Type 7 | 40.0 57.5 75.0 | 0.38 0.56 0.72 | 0.95 0.98 0.96 | 0.082 0.182 0.336 | 62.4 69.1 75.5 | 0.94 0.77 0.61 |
| Type 8 | 40.0 57.5 75.0 | 0.53 0.69 0.83 | 1.30 1.21 1.12 | 0.074 0.178 0.304 | 65.4 71.3 78.0 | 0.87 0.72 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senfter, T.; Neuner, T.; Bachmann, C.; Berger, M.; Mayerl, C.; Kofler, T.; Kraxner, M.; Pillei, M. An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators. Separations 2024, 11, 230. https://doi.org/10.3390/separations11080230
Senfter T, Neuner T, Bachmann C, Berger M, Mayerl C, Kofler T, Kraxner M, Pillei M. An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators. Separations. 2024; 11(8):230. https://doi.org/10.3390/separations11080230
Chicago/Turabian StyleSenfter, Thomas, Thomas Neuner, Christian Bachmann, Manuel Berger, Christian Mayerl, Tobias Kofler, Michael Kraxner, and Martin Pillei. 2024. "An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators" Separations 11, no. 8: 230. https://doi.org/10.3390/separations11080230
APA StyleSenfter, T., Neuner, T., Bachmann, C., Berger, M., Mayerl, C., Kofler, T., Kraxner, M., & Pillei, M. (2024). An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators. Separations, 11(8), 230. https://doi.org/10.3390/separations11080230






