Investigation of a Hydraulic Channel for Plastic Particles Sorting via Experimental and Numerical Tools

Abstract

In recent decades, the versatility of fossil-based polymers has led them to become one of the most used materials for the production of several consumer goods. The destiny of post-consumer plastics is crucial for environmental sustainability. Two are the alternatives to landfilling: (i) energy recovery, i.e., replacement of traditional fuel with plastic litter, and (ii) recycling, i.e., processing of plastic wastes to produce secondary raw materials that may substitute primary raw materials. This work presents the investigation of a device for the hydraulic separation of heterogeneous plastic wastes, which, when properly upscaled, may be efficiently used within recycling plants. This apparatus is suitable for the separation of granules or flakes of plastics with a density higher than 1000 Kg/m³ and may replace existing technologies for mechanical recycling. The purpose of the device is to separate the useful fraction from a mixture of plastics and water introduced inside. The separation procedure efficacy relies on the difference in density, dimension, and shape of the processed plastic particles and on the flow features within the device. Experiments were carried out to test the efficacy of the device as a function of those factors. To increase the range of variation in the key parameters influencing the apparatus’s working principles, Computational Fluid Dynamics was employed to build a numerical model of the device. The validated numerical model suitable to fully characterize the apparatus performance features a hybrid grid with an inner mesh of 3·10⁻³ m size, a careful modeling of the near-wall region, and the k-ω SST turbulent model.

1. Introduction

It is hard to imagine that the world one century ago contained almost no plastics, whereas 100 years later, they have infiltrated many aspects of human activities, such as packaging, electric equipment, clothing, buildings, automobiles, and hygiene [1,2]. However, the great success of plastics in bringing major benefits to our lives has some drawbacks. The constant increase in demand and therefore in the production of plastic materials inevitably leads to a continuous increase in plastic waste to be reckoned with. The probability of impacting the ecosystems is strictly related to the recurring careless disposal of plastics [3,4]. As a synthetic material, plastics perform remarkable chemical stability in natural media where plastic wastes are subject to natural processes of shredding, which produce macro- to micro-elements threatening human health.

Since the 1950s, the global production of plastic products has grown at an average annual rate of 9% [5]. According to the records of Plastics Europe, global plastics production increased to 390.7 million tons in 2021. China is the largest global plastic producer (accounting for about 26%), followed by North America and Europe [6].

In 2020, 29.5 million tons of post-consumer plastic waste were collected in the EU27+3. Efficient recycling prescribes raising the value of recycled products and reducing waste disposal [7]. Plastic recycling can be achieved via mechanical, chemical, or energy recycling. In 2020, 77% of plastic waste was handled via recycling and energy recovery processes, while 23% ended up in landfills.

Plastics comprise two distinct categories, i.e., thermoplastics and thermosetting plastics. The former includes plastics (polyethylene terephthalate (PET), low-density polyethylene (LDPE), polyvinyl chloride (PVC), high-density polyethylene (HDPE), polypropylene (PP), and polystyrene (PS), among others) that can be heated up to form products and, if needed, can be reheated, and melted again for new forms. Conversely, the latter includes plastics (polyurethane (PUR), polyesters, phenolic and acrylic resins, silicone, etc.) that can be melted and formed but unlike thermoplastics, they cannot be remelted. This issue must be considered when arranging a recycling process. The most diffused polymers are PP, LDPE, HDPE, PVC, PUR, PET, and PS. Such polymers are also the most abundant in plastic wastes, with some variations according to the different lifespans of products.

Over the years, different technologies have been developed for recycling plastic waste and reusing potentially useful materials. Mechanical recycling remains the first choice for plastic waste management allowing the recovery of secondary raw materials potentially suitable for the manufacture of new goods. Nevertheless, the recovery of high-quality plastics from wastes requires recycling processes able to efficiently sort different polymers and remove contaminants, generally accepted in small amounts.

Key plastic characteristics, i.e., density, spectral properties, surface wettability, solubility, hardness, and surface chargeability, may be employed for their separation. Typically, efficient sorting technologies convert waste plastics into reclaimable fractions via a two-step process, which makes it possible for the removal of contaminants first (plastic liberation) and the real sorting afterward (plastic separation).

Separation can occur in wet conditions, such as with flotation, dense sorting (sink/float), and cyclones [8,9], or in dry conditions, such as with electrostatic separation and optical methods [10,11,12]. Density separation relies on the difference among the densities of polymers, and it is probably the most extensive process reported in the literature. A medium of intermediate density is employed, and plastic granules of higher density are expected to sink, whereas the ones of lower density float [13]. The separation efficiency depends also on surface texture, particle appearance, surface wettability, particle size, medium viscosity, and particle concentration [9,14]. Cyclone separators, magnetic projection, jigging, projectile separators, and fluidized beds are devices employing density as the key parameter for the sorting process of waste plastics [15].

The cost-effectiveness and efficacy of density separation with respect to other sorting technologies are well recognized. However, density separation may be limited by the small density differences among plastic samples. Furthermore, some technologies may be energy-consuming; separation efficiency can be affected by the occurrence of air bubbles and/or contaminants on polymer surfaces, by polymer alteration, fillers, and additives. Finally, the separating medium disposal may pose environmental hazards issues.

This work presents the investigation of a device for the hydraulic separation of heterogeneous plastic wastes, which, when properly upscaled, may be efficiently used within recycling plants. The hydraulic separator allows for the recovery of homogeneous plastic fractions fulfilling the most limiting standards in the secondary raw materials market. Polymers with a density greater than 1000 Kg/m³ can be treated within the apparatus, and plain water without chemical additives is employed. The separation process depends on the difference in the polymer density, dimensions, and shape and on the characteristic flow pattern developing inside the device.

To investigate the efficacy of the device, separation tests were conducted at different flow rates, using both one-polymer samples (mono-material tests) and two-polymer samples (multi-material tests) [16]. Furthermore, an image analysis technique was used to characterize the velocity flow field within the device and to study its connection with the separation capability.

Computational Fluid Dynamics (CFD) was employed to fully characterize the device. First, the velocity field within the apparatus was simulated in different operating conditions. Subsequently, CFD was used to investigate the properties of the two-phase flow (working fluid–solid plastic particles to be sorted) and their coupling regime. The advantage of this approach compared to the experimental investigation is the possibility to simulate a larger number of operating conditions faster than with other approaches, reducing the total effort required in the laboratory. On the other hand, the numerical tool requires experimental data for its validation. A combination of different methodologies is certainly the best approach for carrying out the investigation.

Different literature contributions investigated the use of CFD to predict the separation efficiency of solid particles within hydrodynamic particle separators. In several studies, a Eulerian–Lagrangian approach was employed, where the fluid phase was modeled as a continuum, and the solid phase was tracked as individual particles. Refs. [17,18] used this approach to model sedimentation and solid separation in sewer detention tanks. Ref. [19] investigated the influence of particle characteristics (density and diameter) on the trapping efficiency of a hydrodynamic separator. The specific issues behind the coupling between the two phases were considered by [20], where the effect of solid particles on a gas flow field was studied. Also, ref. [21] analyzed the effect of particles on the hydrodynamic separator. Past literature contributions demonstrated that the boundary conditions are fundamental to properly reproduce the separation efficiency of an apparatus. ANSYS Fluent, employed for the numerical simulations presented in this paper, provides boundary conditions that may not be suitable to reproduce the particle behavior at the bottom of the apparatus under investigation. For this reason, user-defined boundary conditions must be implemented to ensure reproducibility of separation efficiency and sediment distribution. Ref. [17] used a boundary condition based on bed shear stress, according to which a particle was trapped when a critical value of the quantity was reached. Otherwise, the particle was resuspended. Ref. [18] employed different wall conditions for different water depths based on both bed shear stress and bed turbulent kinetic energy. In this study, a user-defined “trapped or reflect” boundary condition was implemented. This condition allows for the sedimentation of particles after a fixed number of reflections on the bottom wall. The novelty of the contribution lies in the original boundary condition implemented within the numerical model and in the systematic comparison among numerical results and experiment outcomes, which allows the numerical model to be validated for further extensive use.

2. Materials and Methods

2.1. Experimental Setup

The hydraulic separator’s geometrical and technical characteristics and its operating conditions are described in detail in [22]. Here, the principal features are highlighted. The device structure is the result of the combination of two profiles realized with eight half-cylinders each to form a sequence of eight equal chambers (C_i, with i = 1, …, 8). Shifting the upper profile with respect to the lower one, the shape of the chambers may be changed, making it possible to investigate different geometric arrangements. Experiments described in [16] demonstrated that the apparatus with internal geometry named “arrangement ASYM” (Figure 1), with L1/L2 roughly equal to 2, turned out to be the most effective in separating plastic samples. Then, the ASYM geometry was implemented in the CFD model for numerical investigation.

The separator is fed using eight input ducts (I_j, with j = 1, …, 8) located along the first chamber, with axes normal to the semi-cylindrical tubes. A tank filled with water up to a certain height is connected to all eight inlet ducts and ensures a constant discharge. The inlet duct I4 is used to insert the plastic sample within the separator. In the last chamber, eight outlet ducts (O_k, with k = 1, …, 8) are located. Finally, the bottom of each chamber presents a collecting duct (R_z, z = 1, …, 8), allowing for the extraction of the material settled in each chamber at the end of the separation process.

To guarantee optical access, the separator was realized in Plexiglas. In fact, an extensive experimental investigation was devoted to the reconstruction of the fluid velocity field. It is worth noting that these data are mandatory for the validation of the numerical model. Hybrid Lagrangian Particle-Tracking (HLPT) [23,24] was employed for such a task. This image analysis technique simultaneously provides particle centroids and correspondent velocity predictors via the solution of the optical flow equation. Trajectories of both the passive tracer seeding the fluid phase and of plastic particles were reconstructed to determine the main features of the flow field and to compare the carrier and the dispersed phase kinematic behaviors. Image analysis techniques prescribe digital images to be acquired and stored for further processing. The acquisition system comprised two high-speed (400 Hz), high-resolution (1280 × 1024 pixels) cameras (Mikrotron EoSens, Unterschleißheim, Germany) equipped with Nikon (Tokyo, Japan) lenses with a focal length of 105 × 10⁻³ m; and two high-speed Camera Link Digital Video Recorders operating in full configuration (IO Industries DVR Express^® Core, London, ON, Canada) to synchronize recordings from the two cameras and manage data acquisition and storage. Proper illumination was ensured using an LED-based Linescan Illuminator (COBRA Slim, Boston, MA, USA) placed above the upper surface. A light sheet 0.40 m long and 0.01 m thick oriented in the longitudinal direction, i.e., parallel to the mean flow field, was generated. A well-reflecting neutrally buoyant passive tracer, “VESTOSINT 2157 natural”, with a density of 1016 Kg/m³ and an average size of 56·10⁻⁶ m, was used.

The flow rate depends on the feeding tank height and on the number of the opened outlet ducts, hereinafter hydraulic configuration. Nine combinations of tank heights and opened outlet ducts were tested; in each case, the flow rate was determined by estimating the time required to fill a known water volume output from the outlet ducts. The measurement was repeated at least three times, and the average value was calculated. The discharge ranged from 0.72 × 10⁻³ m³/s to 1.36 × 10⁻³ m³/s.

2.2. Separation Tests

Experimental separation tests were conducted on mono- and multi-material samples. To ensure the material would enter the apparatus, polymers with a density larger than water, i.e., PET, PVC, and PC, were employed. Each type of material was characterized in the following ways: geometrically, to identify the particle size and shape; physically, to determine the density; and spectrally, in the near-infrared region [25].

The purpose of mono-material tests is to investigate the efficacy of the apparatus as a function of the flow rate and plastic typology. The result of a test consists of two products: the fraction expelled from the separator and the fraction settled within the apparatus chambers. The response of each sample is different according to its physical property (shape, size, and density) and separator hydraulic operating conditions. As a matter of fact, each sample may (i) settle within the separator chambers, (ii) be expelled from the apparatus, or (iii) partially settle and partially be expelled.

The purpose of multi-material tests is to evaluate the effectiveness of the experimental apparatus in a realistic separation process.

2.3. CFD Model

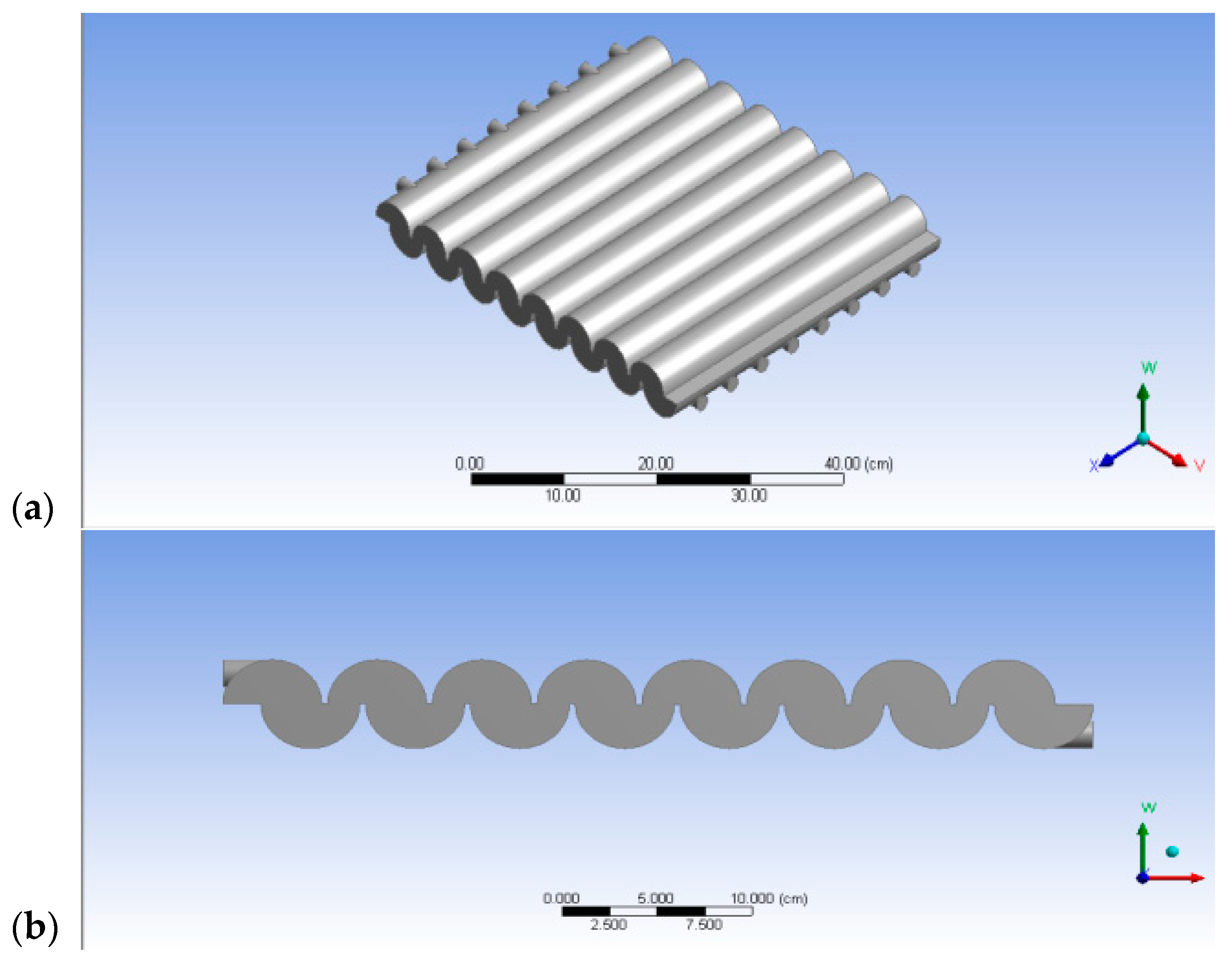
2.3.1. Geometry Creation and Grid Generation

The first step for a numerical simulation is the creation of the system geometry, which involves the reconstruction of the channel containing the flow under investigation via a model as similar as possible to reality. This step can be carried out with a CAD package. The model pictured in Figure 2 represents the separation channel provided with eight inner nozzles and eight outflow conduits imported in ANSYS Fluent. All the elements are on a real scale.

The following step is the domain discretization by using the grid generation tool. In ANSYS Fluent, three kinds of grids may be chosen: structured, unstructured, and hybrid. The choice must take into account the fluid/flow characteristics. The simulations presented in this contribution were performed using a hybrid grid with an internal unstructured mesh with tetrahedral elements and a refinement in the wall-normal direction using quadrilateral elements.

The near-wall modeling significantly impacts the reliability of numerical solutions. In fact, turbulent flows are significantly affected by the presence of walls in non-trivial ways. Very close to the wall, viscous damping reduces the tangential velocity fluctuations, while kinematic blocking reduces the normal fluctuations. Then, toward the outer part of the near-wall region, turbulence is rapidly increased by the production of turbulence kinetic energy due to the large gradients of the mean velocity. Therefore, the accurate representation of the flow in the near-wall region determines successful predictions of wall-bounded turbulent flows [26,27].

For our simulations, near-wall modeling was a particularly challenging issue because of the shape of the channel and the large surface of contact. In this region, several quantities can be introduced: friction velocity U_T, viscous stress on the wall τ_W, and non-dimensional distance from the first grid point to wall y⁺ (assuming y is orthogonal to the wall).

Traditionally, there are two approaches to model the near-wall region. According to the first one, semi-empirical formulas called “wall functions” are used to bridge the viscosity-affected inner region (viscous sublayer and buffer layer) and the fully turbulent region. According to the second approach, namely “near-wall modeling”, turbulence models are modified to enable the viscosity-affected region to be resolved. In this case, the mesh covers the entire domain up to the wall and then includes the “viscous sublayer”. The grid resolution near the wall must be very small (y⁺ ≈ 1) [27]. When a near-wall modeling approach is used, high-quality numerical results for the wall boundary layer may be expected if the overall resolution of the boundary layer is sufficient. The minimum number of cells to accurately cover a boundary layer is around 10, but a larger value is desirable. The associated increase in accuracy is typically well worth the additional computing costs. Conversely, wall functions save computational effort.

For our simulations, the standard ANSYS Fluent wall functions were employed, and an empirical formula [28] was used to calculate y⁺ for all the investigated cases [29]. The structured grid comprises 10 layers, with a distance increase of 20% between adjacent layers. Experimental data were used to compute the average horizontal velocity component values required to compute y⁺. To do so, two different regions of the model were considered: the inlet ducts and the area above the lower cusp at the entrance of chamber C3.

To define the internal unstructured grid, the max face size parameter (hereinafter MFS) is used. Using the same thickness of the structured grid on the wall, three MFS sizes were tested, i.e., 3·10⁻³ m, 4·10⁻³ m, and 5·10⁻³ m (Figure 3;

Table 1. Number of nodes and number of elements of the different grids used in the simulations.

Case #	MFS 10−3 m	Number of Nodes	Number of Elements
1	5	411,066	1,045,074
5	5	419,254	1,085,413
9	5	421,273	1,105,216
1	4	592,709	1,528,616
5	4	599,365	1,587,456
9	4	605,730	1,628,975
1	3	981,525	2,555,892
5	3	995,874	2,595,413
9	3	1,001,148	2,671,870

).

The investigated discharges were 0.72 l/s (case #1), 1.08 l/s (case #5), and 1.36 l/s (case #9).

2.3.2. Fluid Phase Modeling

Due to its speed in performing the simulations and reduced computational costs, the Reynolds-averaged Navier–Stokes (RANS) approach was used. RANS equations have the same general form as the instantaneous Navier–Stokes equations, with velocity components and other variables representing ensemble-averaged (or time-averaged) values. Turbulent models are used to describe the effect of the fluctuating velocity components on the mean flow. The Reynolds stresses $-\rho \overline{{u^{\prime }}_i{u^{\prime }}_j}$ appearing in the equations, where ${u^{\prime }}_i$ is the fluctuating velocity component in the direction i (i = 1, 2, 3 are the three directions of the reference system) and the overline denotes the average is considered, are unknown additional terms that represent the effects of turbulence [27]. ANSYS Fluent employs the Boussinesq hypothesis to relate the Reynolds stresses to the mean velocity gradients. The advantage of this approach is the relatively low computational cost associated with the computation of the turbulent viscosity ${\mu }_t$. The disadvantage of the Boussinesq hypothesis is that it assumes ${\mu }_t$ is an isotropic scalar quantity, which is not strictly true [27].

From the experiments, it can be found that the Reynolds number, $\mathit{Re}=\frac{\dot{\rho }{U}_F{d}_F}{\mu }$, where $\mu$ is the dynamic fluid viscosity, $\dot{\rho }$ the continuous phase material density, $d_F$ the characteristic dimension of the flow, and $U_F$ the mean velocity, ranges between 1950 and 3400 [22]. Therefore, a laminar model was implemented first. In addition to that, a few different RANS turbulent models were tested, namely k-ε, k-ω and k-ω SST, and modeling results were compared with experiment outcomes for proper validation.

The k-ω (SST) model developed by the authors of [30] blends the robust and accurate formulation of the k-ω model in the near-wall region with the free-stream independence of the k-ε model in the far field. In [27,31], details about the conversion of the k-ε model into a k-ω formulation are provided, as well as the refinements of the SST model with respect to the standard k-ω model.

Simulations were run in steady-state mode. The default convergence criterion available in Fluent was employed. This criterion requires that the scaled residuals decrease to 10⁻³ for the three velocity components, the equation of continuity, and the turbulent model variables.

2.3.3. Solid Phase Modeling

Separation tests were characterized by a solid phase volume fraction, defined as the ratio of the total volume of the dispersed phase and the total volume of the mixture, around 10⁻⁵. This value denotes a discrete phase regime. Then, a Euler–Lagrange approach is suggested for the simulations, i.e., the fluid phase is treated as a continuum by solving the Navier–Stokes equations, while the dispersed phase is solved by tracking a large number of particles, bubbles, or droplets via the calculated flow field. The dispersed phase can exchange momentum, mass, and energy with the fluid phase. When the dispersed phase occupies a low volume fraction and particle-particle interactions can be neglected, this approach is considerably simpler. The particle trajectories are computed individually at specified intervals during the fluid phase calculation. This makes the model appropriate for the modeling of any application where the volume fraction of the second phase cannot be neglected.

2.3.4. Boundary Conditions

For the fluid phase simulation, adequate boundary conditions were set at the inlet, outlet, and wall boundaries. The boundary conditions for the discrete phase simulation take into account the interactions of the particles with the channel. A wall-jet condition was set to simulate the entrance of the particles through I4. The outlet ducts were defined as escapes to simulate the exit of the particles that do not settle in the apparatus.

The challenging issue for the simulations presented herein was the proper modeling of the particle behavior close to the bottom wall. In this zone, the particles can belong to the lower recirculation zone or to the transport current, and, consequently, they can settle or follow the fluid flow. ANSYS Fluent allows “trapped” or “reflect” conditions to be set at the wall, but the former may overestimate the separation efficiency while the latter may underestimate it. Then, in this study, a user-defined “trapped or reflect” condition was implemented. Using this condition, when the particle reaches the bottom wall, it is inserted again in the domain with the same impact velocity but with the opposite horizontal component. This is allowed until a certain number of touches at the lower bottom is reached. When the number of touches overcomes the set threshold, the particle is captured. The user-defined “trapped or reflect” condition was not applied at the first and last chamber, where a reflecting condition was rather chosen. The upper wall of the chambers was set as a reflecting surface.

3. Results

3.1. Experimental Results

Hybrid Lagrangian Particle-Tracking allowed for the qualitative visualization and quantitative estimation of the flow field within each chamber. For all Re numbers, three characteristic flow regions were recognized in chambers C2 to C7, namely a transport current, a lower recirculation zone, and an upper recirculation area. Due to the strong influence of the inner and outlet ducts, the flow appeared less structured in the first and last chambers of the apparatus.

In the transport current, the fluid presents a positive value of the velocity component along the x axis. The transport flow is responsible for the displacement of particles from one chamber to the next; solid material is eventually driven to the outlet nozzles without separation. The lower recirculation zone is localized below the transport current; its clockwise rotating motion is suitable for capturing particles from the principal current (Figure 4). It is observed that plastic particles captured in this way may behave in one of the following ways: (i) they settle within the chamber if sufficiently heavy; or (ii) they follow the upward portion of the rotating motion without reaching the main transport current, due to the fact that they are too heavy to perform a complete rotation; or (iii) they execute a complete rotation and are recaptured by the principal transport current moving toward the following chamber. The upper recirculation zone is localized above the main transport current. Its motion is counterclockwise. The upper recirculation zone may subtract particles from the main transport current. Particles may rotate within the upper recirculation zone, may be recaptured by the principal current, or may reach the lower recirculation area of the chamber after crossing the principal current [32,33].

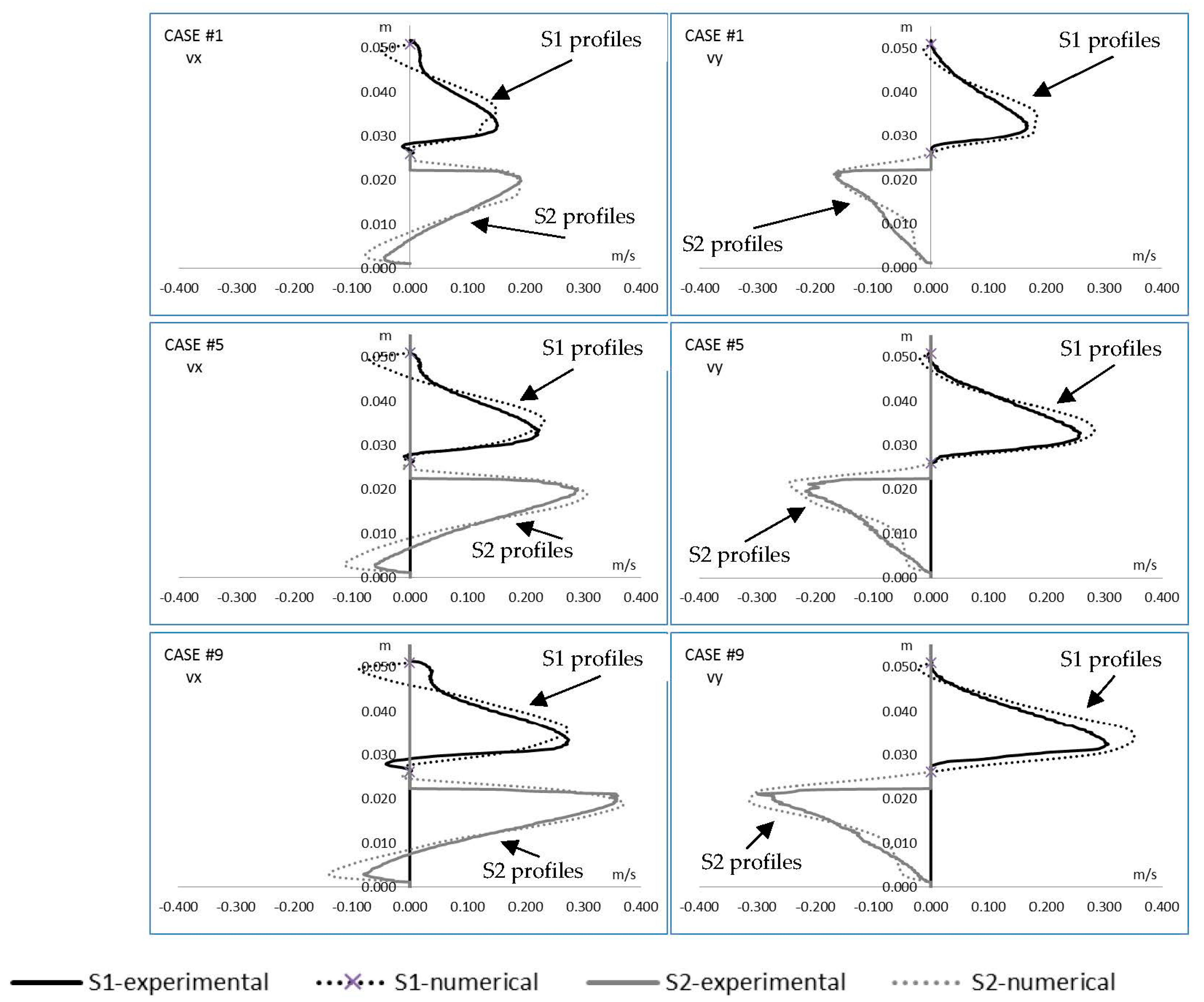
3.2. Numerical Results

To validate the numerical model, i.e., to choose mesh size and RANS turbulent model, several simulations were carried out. For each simulation, the validation procedure prescribed the extraction of two velocity profiles and comparison with the experimental results along the same sections. Specifically, sections S1 and S2 were chosen within chamber 3 (Figure 5). S1 is placed in correspondence to the lower cusp, at the entrance to the chamber, S2 corresponds to the upper cusp. Both vertical and horizontal velocity components were reconstructed.

It is worth recalling that Reynolds numbers computed from experiments ranged between 1950 and 3400, highlighting a transitional flow regime. For this reason, in addition to turbulent models, the flow simulation was also carried out with a laminar model. It turned out that laminar velocity profiles underestimate experimental data. Subsequently, RANS turbulent models were considered. Realizable k-ε model outcomes compared to experimental profiles also showed an underestimation of the velocity components profiles from the numerical model. This can be justified considering that k-ε models are usually employed for completely developed turbulent regimes.

k-ω and k-ω SST (Shear Stress Transport) models were further investigated. Even though they provided similar results, the k-ω SST model performed better in terms of computation time. Figure 6 presents the comparison between numerical results with the SST k-ω model and experimental profiles. The remarkable match between numerical and experimental profiles suggests that the model can be profitably employed for further investigations.

In addition to velocity profiles, the color maps of the velocity components were extrapolated from numerical simulations. Figure 7 and Figure 8 show streamlines overlapped to the color maps of the horizontal and vertical velocity components for the k-ω SST RANS turbulence models and the hydraulic configurations denoted as case #1 and case #9.

As expected, the velocity magnitude increases with increasing flow rate. The horizontal velocity component is positive along the principal transport current, negative on the left side of the lower recirculation zone, and on the right side of the upper one due to the rotation of the vortices. Instead, the vertical velocity component presents positive values and increases in the zone between the lower cusps and the right side of the upper vortex; vice versa, it has negative values and decreases in the zone between the upper cusps and the left side of the lower vortex.

Once the flow field was validated, further simulations were conducted to test the separation performance of the device. Results from numerical simulations were compared to the experimental data presented in [22]. Mono-material tests shown in [22] were conducted employing samples of 6.21 × 10⁻⁶ m³ solid volume, and the sedimentation efficacy, defined as the ratio between the amount of material settled in the apparatus chambers and the material treated within the separator, was presented for increasing fluid flow rate. The samples were constituted by particles of nearly spherical or cylindrical shape with rather regular and homogeneous sizes. The PET sample belonged to the size class I, i.e., 2.00 × 10⁻³ m < d < 3.36 × 10⁻³ m, whereas the PC and PVC samples belonged to the size class II, i.e., 3.36 × 10⁻³ m < d < 4.76 × 10⁻³ m. For the numerical simulations, a total of 100 spherical particles were injected through inlet input I4, and the number of particles leaving the apparatus, if any, was evaluated. This made it possible to easily compute the separation efficacy and make comparisons between experimental and numerical results. Figure 9 presents the distribution, at the end of the simulation, of a sample of 100 particles mimicking PET 2-V behavior (for the polymer nomenclature, refer to [22]) and for the hydraulic configuration denoted case #1. Each particle is associated with a color.

Table 2. Mono-material separation test results expressed in terms of sedimentation efficacy for virgin material samples of PC, PET and PVC for increasing flow rate.

Polymer Name	Sedimentation Efficacy from Experiments (%)			Sedimentation Efficacy from Numerical Simulations (%)
	Case #1	Case #5	Case #9	Case #1	Case #5	Case #9
PC 1-V	82.8	0.0	0.0	77.6	0.0	0.0
PET 2-V	99.2	0.0	0.0	94.0	0.0	0.0
PVC 2-V	100	31.5	0.0	98.7	35.0	0.0

presents the complete set of mono-material separation test results expressed in terms of sedimentation efficacy for virgin material samples of PC, PET, and PVC and for increasing flow rate.

The above-mentioned user-defined boundary condition appears effective in reproducing the sedimentation efficacies observed during the experiments.

4. Conclusions

The numerical model of the hydraulic separator apparatus was realized by using AutoCAD, and different hybrid grids of diverse mesh sizes were tested. To reproduce the experimental operating conditions, appropriate boundary conditions were imposed. For each simulation, the fluid (water) was introduced via the eight inlet ducts with the correct flow rate value, whereas the opened ducts were set as outflows according to the different experimental hydraulic configurations.

The comparison between experimental and numerical results suggested the following:

• A mesh of size 3·10⁻³ m was suitable for reproducing the observations;
• Laminar and different turbulent models, i.e., k-ε and k-ω, were employed and validated with experimental results; the k-ω SST model turned out to be the one providing results remarkably similar to the experimental ones and was then chosen to test the behavior of the particles within the apparatus;
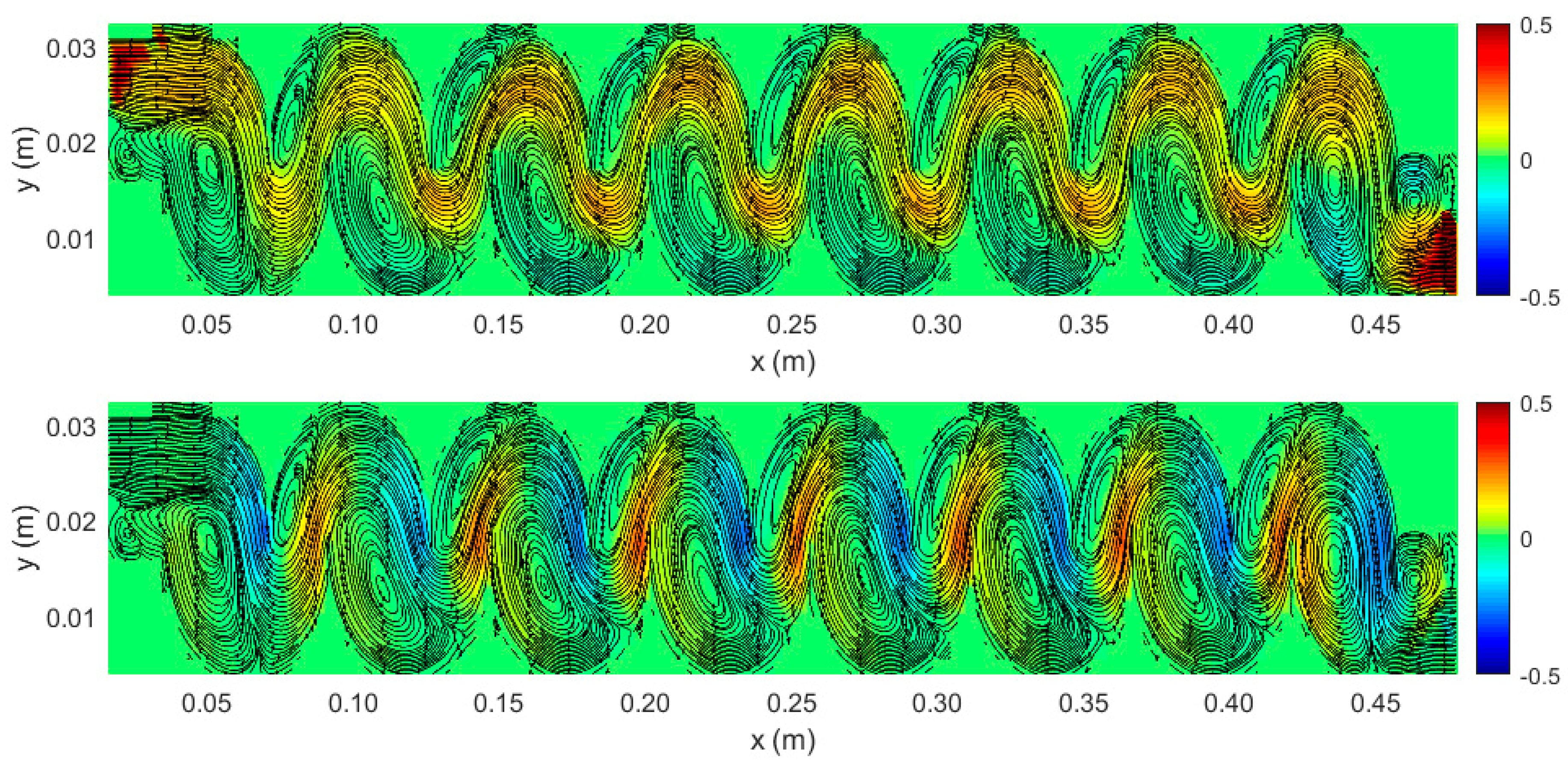
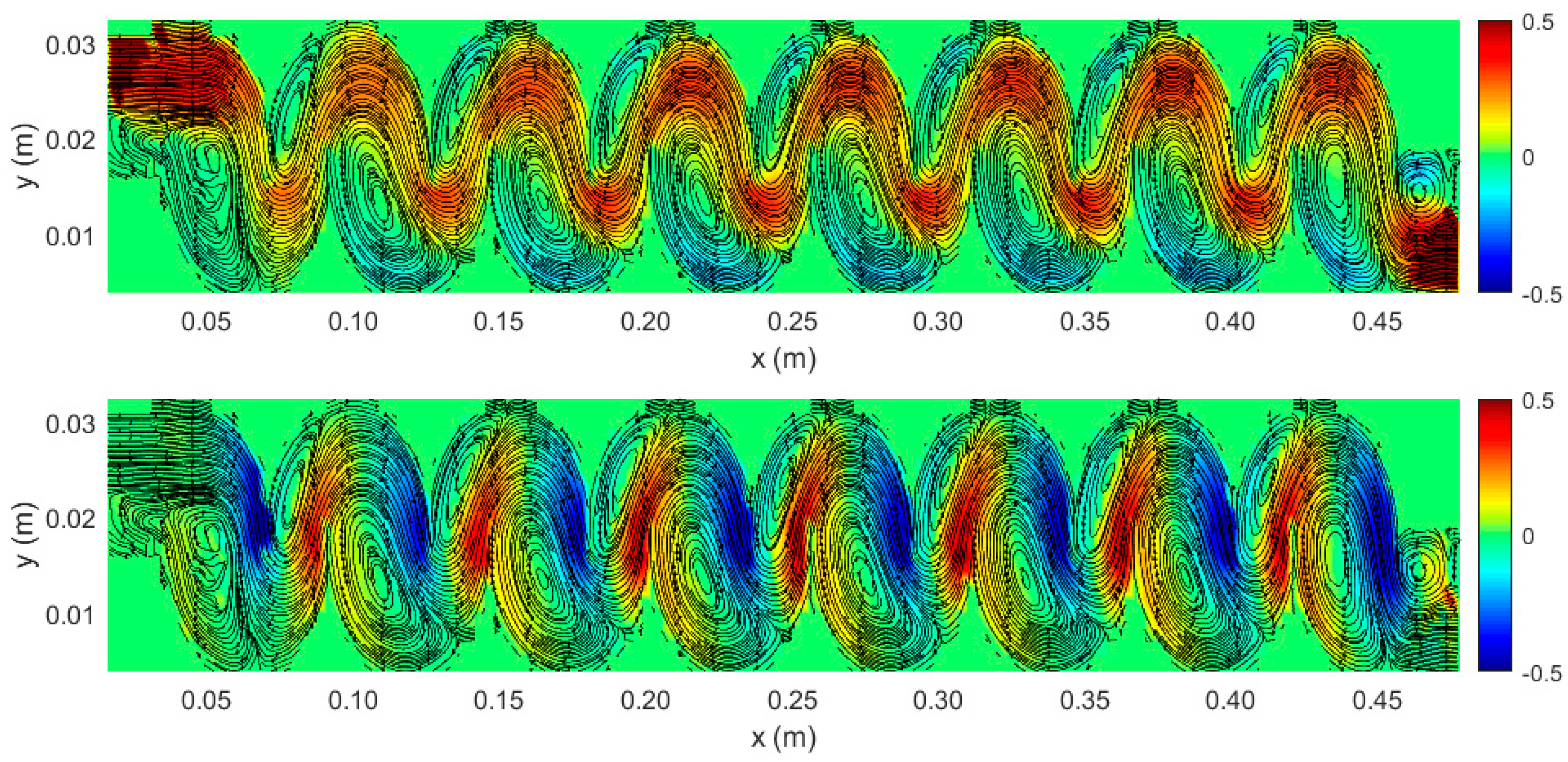
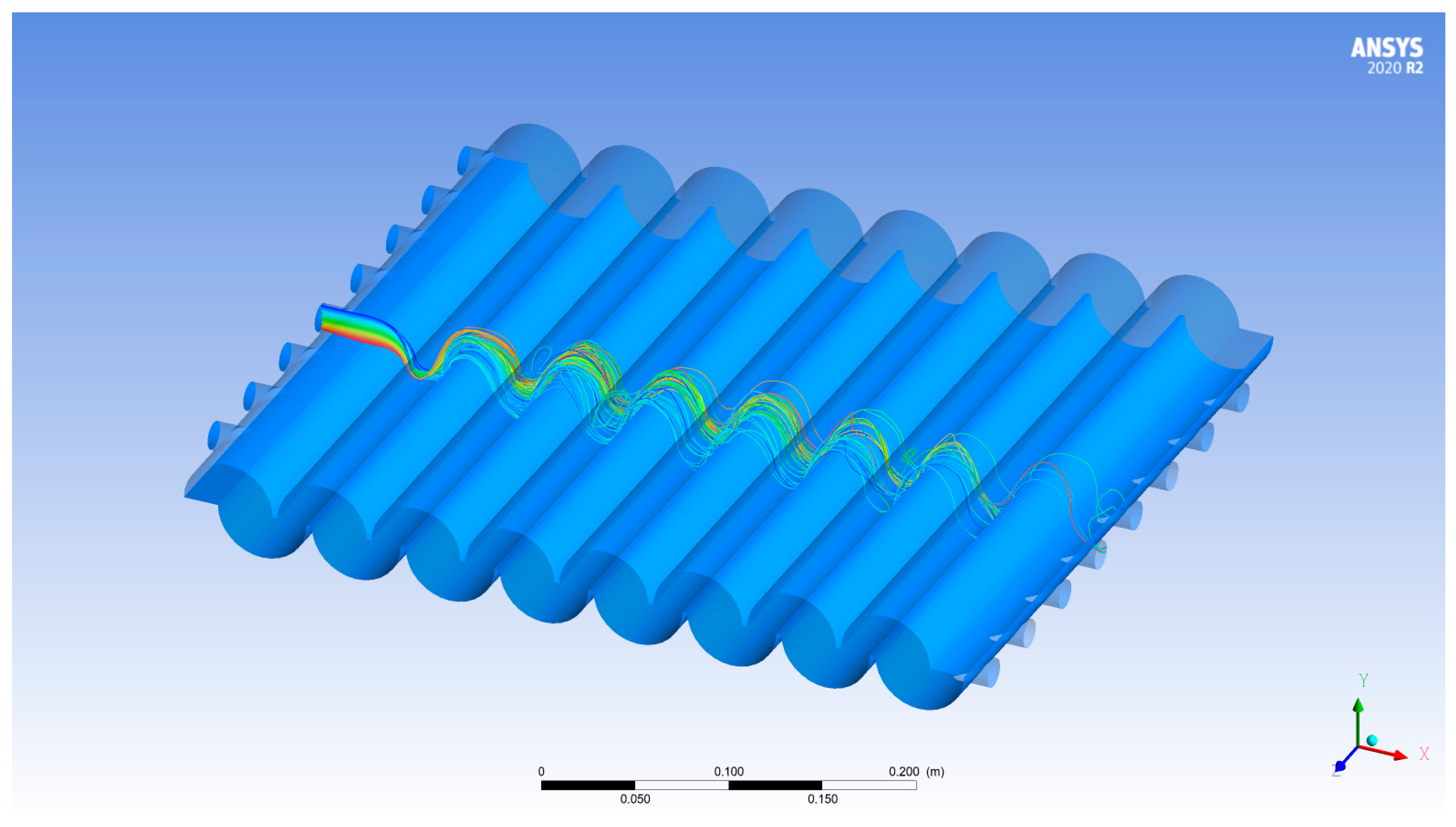
• The qualitative representation of the velocity field makes it possible to identify three different characteristic flow structures within the separator channel: (i) a principal transport current along the entire longitudinal section that may drag the material inside the device according to its size, density, and shape, and, in each chamber, (ii) a lower recirculation zone that may subtract particle from the main current or from the bottom of the chamber and (iii) an upper recirculation zone that may capture particles from the main current slowing down their settling with the chamber or their displacement within the apparatus;
• The user-defined boundary condition for solid particles was demonstrated to be effective in reproducing the results of mono-material separation tests. As already demonstrated with experiments, encouraging separation results can be achieved using several combinations of polymers, namely PET-PVC, PET-PC, and PVC-PC, and appropriate hydraulic conditions.

The validated numerical tool can be effectively used to verify the device performance for a wide range of hydraulic configurations, geometric arrangements, and solid particle features.