Abstract
The direct use of nanosorbents for water purification is limited due to their aggregation and the lack of techniques for their recovery from natural waters. To overcome these problems, the affixation of nanomaterials onto bulk, non-mobile supports has been proposed. However, a method to simulate the efficiency of these sorbents under realistic conditions is still not available. To address this need, this work describes a method for evaluating the sorption efficiency of nanosorbent materials incorporated on bulk supports under non-equilibrium conditions. The method combines the principles of passive sampling, an environmental monitoring technique that is based on passive diffusion of dissolved contaminants from water to a sorbent, with batch sorption experiments that measure sorption under equilibrium conditions, to determine the parameters associated with water purification. These parameters are the maximum sorption capacity of the sorbent and the sampling rate, which is the volume of contaminated water treated per unit of time. From these variables, the deployment time of the sorbent until reaching saturation is proposed as an alternative indicator of sorbent efficiency. As proof-of-principle, the removal of oxyanions from a Zr-metal-organic framework (MOR−1) immobilized on cotton textiles was investigated. The results show that the sorption capacity under passive diffusion uptake conditions, is approximately 20 mg/g for As(VI) and 36 mg/g Se(IV), which is 10 to 30 times lower compared to that determined in batch sorption studies, indicating that conventional equilibrium sorption overestimates the efficiency of the sorbents under realistic conditions. The application of the method to a worst-case scenario, involving the severe contamination of freshwaters with arsenate species, is also demonstrated.
1. Introduction
In recent decades, there has been a rapid growth in research associated with the development of new sorbent materials for the removal of organic and inorganic contaminants from water [1,2,3]. On most occasions, these sorbents are produced in micro- or nano-sized form, offering significant advantages compared to their bulk counterparts (such as higher sorption capacity and faster sorption kinetics) due to their high specific surface area, tunable sorption sites (pore size, surface functionalization, etc.) and short intra-particle diffusion distance [1,2,4,5,6,7,8]. However, their small size is also a bottleneck in the practical application of these materials in natural waters. Upon addition into water (eco)systems, micro-/nano-sized particles aggregate, precipitate to sediments, or adhere to physical obstacles (e.g., rocks, plant roots, etc.) and are removed from the water column [9,10]. Even more, nanosized particles may be uptaken by organisms causing toxic effects [11]. All these processes compromise the performance of the materials and render their collection and retrieval from the water phase practically impossible.
To overcome these limitations and enable the realistic use of nano sorbent materials in water purification, recent reports propose the immobilization of nanosorbents onto less-mobile, bulk structures that can be immersed into water to “trap” the target contaminants and then recovered as bulk material [10,12]. Sponges [13], polyurethane foam [14], cotton textiles [15] and cellulose-based composite membranes [16] are some of the scaffolds that have been proposed as potential bulk supports of nano-sized adsorbents for the removal of contaminants from aqueous media.
Although the affixation of nanomaterials in bulk supports may overcome some of the difficulties associated with the use of nanomaterials in natural waters, the determination of their performance in real-world applications is a challenge. That is because there is no method to determine the effectiveness of a sorbent under realistic conditions, and as a result, batch sorption studies are still used as the “gold standard” method to evaluate sorbents’ efficiency. However, batch sorption is performed under controlled laboratory conditions that are significantly different than those encountered in natural waters. Specifically, in batch sorption studies, the sorbent is added to a given volume of contaminated aqueous phase (usually spiked distilled water) and mixed under vigorous stirring until equilibrium is reached between the concentration of the contaminants in the aqueous and the sorbent phase. In natural waters, the hydrodynamic and physicochemical conditions are significantly different in several ways: (a) the bulk-supported sorbent cannot be mixed and maintained in suspension. Instead, it can only be held static inside the water column. (b) Water is a dynamic medium that is continually renewed under variable flow velocity and mixing conditions (usually turbulent), which range from a few m/h in lake waters to several m/s in river waters. Therefore, the water-sorbent contact time is significantly lower (a few seconds) than the contact time during batch sorption (a few minutes to hours). (c) The concentration of contaminants is not constant and exhibits diurnal variation. (d) The concentration of ubiquitous water components (such as dissolved organic matter, anions, cations, chlorophyll, etc.) that may compete for the available sorption sites is significantly higher than the concentration of dissolved contaminants, and these components exhibit diurnal, seasonal and spatial variability. Under these conditions, batch sorption may not provide a realistic evaluation of the sorption kinetics and the maximum sorption capacity.
In recent decades, considerable research efforts have been devoted to the development of devices that can be used to passively uptake dissolved contaminants from water ecosystems for environmental monitoring purposes. These devices, called passive samplers, consist of a sorbent medium (usually surrounded by a membrane and encased within a protective housing or cage) that is immersed and statically exposed to an environmental medium for several days or weeks to retain contaminants into the sorbent phase [17,18,19,20]. Therefore, there are many similarities between passive samplers and bulk-supported sorbents for water remediation. In this regard, we reasoned that the principles of passive sampling could be useful also in describing water remediation with bulk-supported nano-sorbent materials.
In this work, we report a new experimental protocol to model water remediation with bulk-supported nanosorbents. The protocol combines the experimental procedures used for the calibration of passive samplers with that employed in batch sorption studies to determine the main parameters (sorption capacity and sampling rate) associated with sorption under dynamic, non-equilibrium conditions. From these parameters, the employment time of the sorbent, before reaching saturation, can be calculated as an indicator of sorbent performance. As a proof-of-concept, the uptake of As(V) and Se(IV) oxyanions from natural waters with a porous metal-organic framework (as nanosorbent) impregnated on cotton textiles (as bulk support) was used to assess efficiency of water purification.
2. Materials and Methods
2.1. Materials
Zirconium chloride (99.5%+, metal basis) and 2-amino terephthalic (99%) (NH2-H2BDC) were purchased from Alfa-Aesar. Arsenic(V) and selenium(IV) AAS-grade standard solutions (Certipur, 1000 mg/L in 0.5 M HNO3) were purchased from Sigma-Aldrich. Pure cotton textiles were purchased from local stores. The textiles were washed with water and acetone to remove any impurities and dried at 60 °C.
2.2. Fabrication of MOR−1@Cotton Fabric
The fabrication of the MOR−1@cotton fabric sorbent was performed in two steps according to our previous works [15,21]. Briefly, a piece of cotton fabric (25.12 cm2 total surface area on both sides) was modified with hydroxytyraminium chloride (0.05 g) in 20 mL tris-base 10 mM under stirring for 3 h. Then, the PDA-coated fabric was refluxed under acidic conditions with 0.54 mmol ZrCl4 and 0.75 mmol NH2-H2BDC. Reflux was performed twice with fresh reagents to ensure maximum coverage of the fabric with MOR−1. After synthesis, the MOR−1-cotton fabric was thoroughly rinsed with distilled water and acetone, ultrasonicated in 0.4 M HCl to remove any unreacted reagents, and deprotonated by stirring in distilled water until the pH of the solution was neutral, to avoid the release of acid during the experiments that could reduce the pH of the samples.
2.3. Characterization of the Sorbent
The sorbent was characterized via (a) ATR-IR using an Agilent Cary 630 FTIR, (b) PXRD diffraction patterns recorded on a Bruker D2 Phaser X-ray diffractometer (CuKα radiation, wavelength = 1.54184 Å) and (c) Scanning Electron Microscopy (SEM) performed on FEG-SEM Zeiss SUPRA 35VP (resolution 1.7 nm at 15 kV).
The determination of As(V) and Se(VI) in water samples was performed with electrothermal atomic absorption spectrometry (Shimadzu AA-6800) using hollow cathode lamps with self-reversal and D2 background correction at 20 and 12 mA, respectively. The measurement of As(V) and Se(IV) concentrations was performed in the peak area mode at 193.7 nm and 242.8 nm, respectively.
2.4. Experimental Procedure for Oxyanion Uptake Studies
Genuine water samples (river and lake water) were retrieved in polyethylene bottles, filtered through 0.45 μm filters to remove suspended solids (that could sorb part of the analytes) and spiked with NaN3 to prevent biological growth.
Oxyanion uptake experiments were performed for 20 consecutive days by the static renewal of the contaminated water. In detail, a semi-circular MOR−1@cotton fabric of 12.56 cm2 surface area (on both sides) was fixed on a framed mesh and added to 1 L of a genuine water sample, artificially contaminated with 150 μg of As(V) and Se(IV) species. A graphical illustration of the experimental setup is shown in Figure 1.
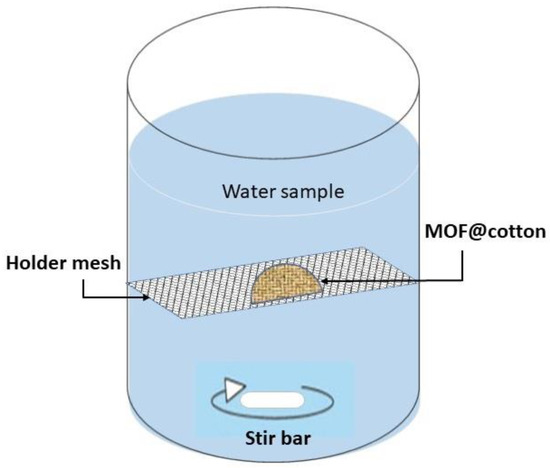
Figure 1.
Experimental setup for passive diffusion sorption of contaminants on a static sorbent.
After 24 h, the holder with the MOR−1-fabric was removed and placed in a freshly prepared genuine water sample fortified with both oxyanion species at the same concentration level (i.e., 150 μg/L). The concentration of oxyanions was measured at the beginning and the end of each experiment (i.e., at 0 and 24 h) and the difference in the aqueous concentration of oxyanions were used to determine the amount of oxyanions removed by the sorbent. The mixing rate was controlled by a magnetic stirring rod at two stirring rates (50 and 150 rpm) corresponding to 0.28 and 0.86 m/s flow velocity, respectively, to simulate horizontal (linear) flow velocity conditions in lakes and rivers, respectively [22,23].
The stirring rate was converted to flow velocity (u, m/s) using the formula:
where r is the rod length in meters and N is the angular velocity in rpm. Control experiments were also performed without MOR−1@cotton fabric to assess the potential loss of analytes that is unrelated to MOR−1@cotton fabric uptake and subtracted from the sorbed concentration of oxyanions. The average loss of analytes that was not related to MOR−1@cotton fabric uptake was negligible (≤2.5%, n = 50).
3. Results
3.1. Characterization of MOR−1@Cotton Fabric
In our previous work, we reported the immobilization of a microporous Zr4+-MOF with ammonium functional groups (MOR−1 or UiO-66-NH3+) on cotton fabric via an in situ coating method [15]. The successful immobilization of MOF on the fabric was confirmed via PXRD, ATR-IR and SEM studies (Figure 2). The PXRD pattern of MOR−1@cotton shows diffraction peaks at 2θ of 7.3°, 8.5° and 12°, corresponding to the (111), (200) and (220) planes of MOR−1, respectively [24]. The IR bands at 1570 and 1385 cm−1, assigned to the νas(COO–) and νs(COO–) modes of MOR−1, respectively, are an additional indication of the successful immobilization of MOR−1 on the cotton surface. Finally, the inspection of FE-SEM images of the cotton’s surface (Figure 2c) clearly shows the coverage with MOR−1 particles (Figure 2d).
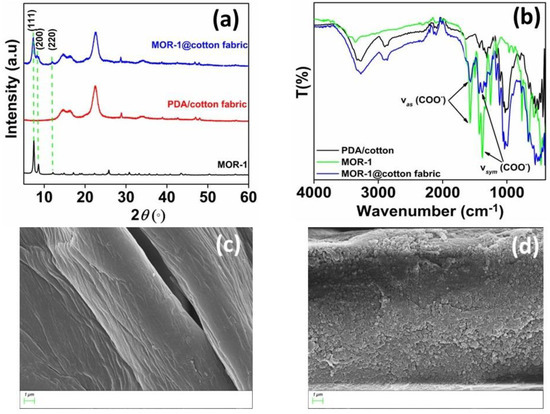
Figure 2.
(a) PXRD pattern of MOR−1, PDA/cotton fabric, and MOR−1@cotton fabric, (b) FT−IR of MOR−1, PDA/cotton fabric, and MOR−1@cotton fabric and SEM images of (c) PDA/cotton fabric and (d) MOR−1@cotton fabric.
3.2. Principles of Passive Sampling for Modeling Contaminants’ Uptake by a Sorbent
In passive sampling, the free flow, passive diffusion of molecules or ions from water to a sorbent, and the accumulation of the compounds inside the sorbent are described by Fick’s first law of diffusion following first-order kinetics [20,25]. According to this approach, the sorption of contaminants occurs in three consecutive regimes: an initial (integrative) uptake regime where the uptake rate increases linearly with time, a curvilinear increase in which the uptake rate progressively slows down, and the (near) equilibrium phase in which the uptake rate is reduced to almost zero [20,26]. The overall process can be represented by a first-order one-compartment model which includes the kinetics between the water and the sorbent [18,27]:
where Cs and Cw are the (volume-based) contaminant concentrations in the sorbent and water, respectively, Vs vs. is the sorbent volume, A is the sorbent surface area, Rs is the sampling rate (L/d), which is defined as the volume of water cleared of the contaminant in a unit of time, and Ksw is the sorbent–water partition coefficient, which represents the compound’s partition coefficient between the sorbent and the water medium [28,29].
For short periods, corresponding to the linear uptake phase and assuming that Cw is constant, Equation (2) reduces to
while for long exposure times corresponding to the equilibrium phase, Equation (2) is further simplified to:
Equation (3) relates the mass of contaminants accumulated into the sorbent phase (Cs × Vs. = M) to the concentration of contaminants in water (Cw) in the initial uptake phase, where M increases linearly with time. Therefore, to calculate Cw, it is necessary to determine the values of M and Rs. The value of M is determined experimentally by extracting the contaminants accumulated in the sorbent over the specified period (t), while Rs is calculated by calibration because it depends on the properties of the sorbent and the environmental conditions (i.e., temperature, pH, salinity, flow rate, etc.) [28].
One popular procedure for the calibration of passive samplers is through static water renewal experiments. In these experiments, a set of devices (6 or more) are exposed simultaneously to a contaminated water medium that is refreshed (batch-wise) at frequent time intervals [18,28,30,31,32]. At specified periods (usually a few days) one of the devices is removed and extracted to determine the accumulated mass of contaminants (M). This procedure continues until all devices are gradually removed from the water. The Rs is then calculated as the slope of the linear part of the curve produced by plotting M/Cw versus time in the linear uptake phase.
3.3. Repurposing Passive Sampling (Diffusion) Modeling to Water Remediation
To evaluate the efficiency of the sorbent in water remediation under realistic conditions, a new calibration protocol that combines static water renewal with batch sorption studies was developed. The experimental procedure involved the exposure of a sorbent to a contaminated water sample that was refreshed daily. The mass of oxyanions sorbed on MOR−1@cotton fabric was determined by the difference in the aqueous concentration of the oxyanions at the beginning and the end of the experiment (i.e., 0 h and 24 h). This approach is based on static renewal calibration of passive samplers but adopts two modifications as employed in batch sorption studies: (a) the mass of sorbent remains constant during sorption. Ιnstead, for the calibration of passive samplers, several sorbent devices are immersed into the sample solution. At specific time intervals, one device is retrieved, until all devices have been removed. Therefore, the total mass of sorbent is reduced with increasing remediation time. (b) The mass of contaminants accumulated in the sorbent is determined from the mass of contaminants removed from water (instead of the mass of contaminants uptaken by the sorbent). This method facilitates the determination of the kinetics of removal within short time intervals (i.e., 24 h or less), as opposed to passive sampling calibration, where the accumulation is monitored over several days to ensure an adequate mass of contaminants has been uptaken by the sorbent. Moreover, all experiments were performed in genuine water samples, thus accounting for the presence of matrix components that could affect sorption.
Based on the modified experimental design, the uptake kinetic curves obtained for both oxyanions are depicted in Figure 3 and Figure 4. The curves follow an uptake profile that resembles that observed in the passive sampling of oxyanions [33,34,35]. However, on some occasions, the mass of analytes that is accumulated in the sorbent increases exponentially with time, while in others, a decline is observed, indicating the potential release of the contaminants. Such patterns are not common during the calibration of passive samplers’ and may be related to (a) the variability of water composition, (b) the properties of the sorbent and (c) the experimental conditions (e.g., static use of the sorbent). However, in all experiments, an initial linear increase was observed. Therefore, as a compromise, the sorption capacity and, consequently, the remediation time were determined from the linear uptake phase. This inherently leads to an underestimation of both maximum sorption capacity and sorption kinetics but minimizes the influence of unpredicted (non-systematic) variables that may affect sorption after the linear uptake phase.
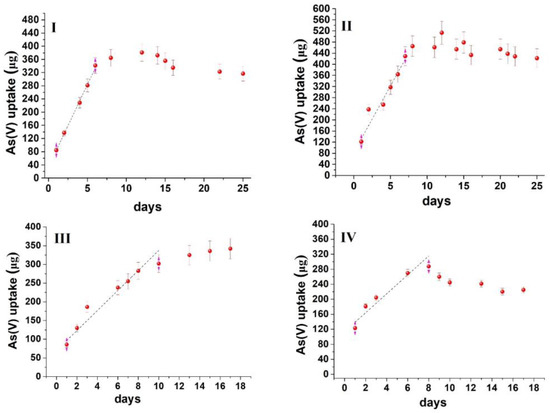
Figure 3.
Time series uptake data of As(V) oxyanion on MOR−1@cotton fabric. (I) River water mixed at 50 rpm, (II) River water mixed at 150 rpm, (III) Lake water mixed at 50 rpm, (IV) Lake water mixed at 150 rpm.
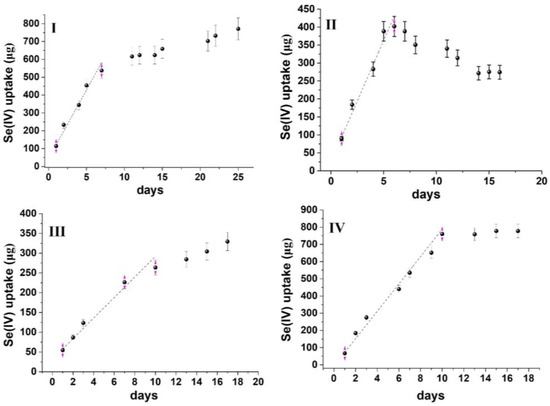
Figure 4.
Time series uptake data of Se(IV) oxyanion on MOR−1@cotton fabric. (I) River water mixed at 50 rpm, (II) River water mixed at 150 rpm, (III) Lake water mixed at 50 rpm, (IV) Lake water mixed at 150 rpm.
From the data presented in Figure 3 and Figure 4, it can be calculated that the sorption capacity at the end of the linear uptake phase ranges from 13.7–19.6 mg/g for As(V) and 12.6–36.2 mg/g for Se(IV) (Table 1), which is at least an order of magnitude lower than the maximum sorption capacity calculated from batch sorption studies with the same sorbent (459 mg/g for As(V) and 325 mg/g for Se(IV)) [15]. The lower sorption capacity, compared to batch sorption studies, can be attributed to the following: (a) the competition from ubiquitous water constituents (e.g., inorganic anions, dissolved organic matter, chlorophyll-a, etc.) that are present in natural waters at concentrations higher than As(V) and Se(IV) oxyanions (a similar observation has also been made during the field deployment of passive sampling devices for the uptake of oxyanions, [33,34,35,36]); (b) the static use of the sorbent (instead of its orbital and intense mixing during batch sorption), which reduces the diffusion rate of the contaminants from water to the sorbent and concurrently the mass transfer rate. This also explains why the sorbent could not accomplish the complete removal of the contaminants, even though the aqueous concentration of oxyanions was below the maximum sorption capacity of the sorbent. Therefore, to accomplish complete removal, scaling up of the sorbent would be required to ensure a larger mass transfer from the aqueous to the sorbent phase.

Table 1.
Parameters of passive diffusion uptake of As(V) and Se(IV) from genuine water samples on MOR−1@cotton fabric at the linear uptake phase.
Although the sorption capacity per mass of sorbent is lower than that determined from batch sorption studies [15], it is higher than other sorbent phases used for the passive sampling of oxyanions [20,33,34,35,36]. Specifically, the sorption capacity per sorbent surface area is comparable to other sorbent materials in distilled water but offers at least an order of magnitude higher sorption efficiency in natural waters (Table 2). The higher sorption capacity in natural waters may be attributed to: (a) the high surface area of the Zr4+ MOF (~581 m2/g for the MOF immobilized to cotton fabric) [15], (b) the porosity of the fabric that facilitates the penetration of water through the fabric pores, enhancing the contact with the MOR−1 particles [15,21] and, (c) to some extent, the greater surface area exposed to water compared to passive samplers and, hence, to the higher number of available sorption sites. These features indicate that the sorbent is suitable for water remediation applications.

Table 2.
Comparison of the sorption capacity of MOR−1@cotton fabric with other sorbent phases used for the passive sampling of As and Se oxyanions in freshwaters.
3.4. Method Demonstration
The approach described above was evaluated, as a proof-of-concept, in a scenario involving the severe contamination of lake water, having a nominal flow velocity (0.28 m/s), with 1 mg/L of As(V) species. The experimental setup was the same as shown in Figure 1. From eq. 3 and the data of Table 1, it can be calculated that under such severe conditions, a sorbent of 12.56 cm2 will reach equilibrium in less than 3 days of exposure. Indeed, on the third day, the amount of As(V) that was removed from the MOR−1@fabric (12.56 cm2, 21 mg MOF) was approximately 380 μg (Figure 5; black line) suggesting that the sorbent has reached saturation (according to Table 1, the calculated sorption capacity at the end of the linear phase is 301 μg and approximately 350 μg at the end of the curvilinear phase). Such a situation is impractical for real applications as it would require the frequent renewal of the sorbent.
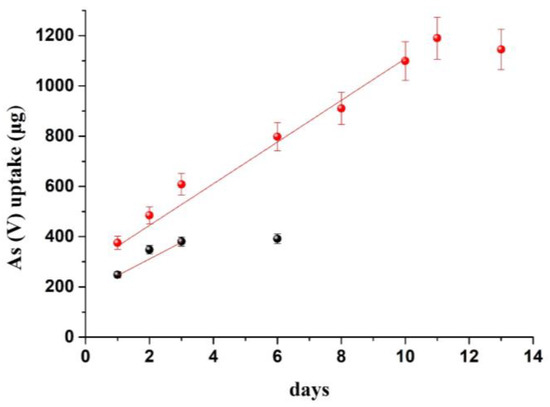
Figure 5.
Kinetic update data of 1 mg/L of As(V) from lake water. Black line: uptake on 12.56 cm2 MOR−1@cotton fabric. Red line: uptake on 45 cm2 MOR−1@cotton fabric.
To extend the linear uptake time to 8 days, which is a reasonable remediation time for replacing the sorbent, Equation (4) advises that the sorbent should accumulate approximately 1100 μg of As(V). To accomplish that, it is necessary to scale up the sorbent to increase the sorption capacity. From the data in Table 2, it can be extrapolated that 77 mg of sorbent are needed to accomplish this value of sorption capacity. Considering that 21 mg of MOF are immobilized in 12.56 cm2 of fabric, the fabric surface area will have to be increased to ~46 cm2. To test the validity of these calculations we repeated the same experiment by adding 45 cm2 of the MOR−1@cotton and measuring the concentration of As(V) for 15 days. According to the measured concentrations of As(V), the uptake phase was linear up to 11 days (Figure 5; red line) which is in agreement with the deployment time expected from the data of Table 1 (10 days). Therefore, the proposed approach offers a tool to predict sorbent employment time before sorbent replacement is necessary.
4. Conclusions
This work demonstrates a new experimental protocol to estimate the performance of free-standing nanosorbents incorporated on macrostructured supports for water decontamination. The protocol enables us to determine the sorption of contaminants by passive diffusion on a static sorbent under continuous water renewal conditions, which are reminiscent to those encountered in natural waters. Based on this protocol, the sorbent deployment time is proposed as a new parameter related to sorbent efficiency. The data from a proof-of-concept demonstration, using a porous Zr4+ MOF immobilized on cotton textiles to remove dissolved oxyanions from water, show that the classic method of batch sorption may provide overoptimistic predictions of the performance of bulk-supported nanosorbents in realistic conditions. Although the first results seem promising, further research is needed to validate this approach as a tool for assessing the efficiency of sorbents during water remediation of natural ecosystems. Beyond experimental validation, theoretical considerations are also needed to obtain a better understanding of the sorption mechanisms and obtain accurate calibration results. As the properties of the bulk support materials (such as density, morphology, surface distribution of reactive sites, etc.) can affect the activity and performance of the nanosorbents, there is a need to evaluate the efficiency of the model to various macrostructured support phases. Field deployment studies are also important to unravel the potential of the method in real-world applications.
Author Contributions
E.M.: investigation, validation. A.D.P.: investigation, data Curation, M.J.M.: conceptualization, writing—review and editing. D.L.G.: conceptualization, writing—review and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The research project was supported by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “First Call for H.F.R.I. Research Projects to support Faculty members and Researchers and the procurement of high-cost research equipment grant” (Project Number: 348).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to gratefully thank the Laboratory of X-ray Diffraction and Microscopy of FORTH/ICE-HT for the FE-SEM and EDS measurements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grumezescu, A.M. (Ed.) Water Purification; Elsevier B.V.: Amsterdam, The Netherlands, 2017; ISBN 9780128043714. [Google Scholar]
- Lahnsteiner, J. (Ed.) Handbook of Water and Used Water Purification; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-319-66382-1. [Google Scholar]
- Singh, N.B.; Nagpal, G.; Agrawal, S.; Rachna. Water Purification by Using Adsorbents: A Review. Environ. Technol. Innov. 2018, 11, 187–240. [Google Scholar] [CrossRef]
- Santhosh, C.; Velmurugan, V.; Jacob, G.; Jeong, S.K.; Grace, A.N.; Bhatnagar, A. Role of Nanomaterials in Water Treatment Applications: A Review. Chem. Eng. J. 2016, 306, 1116–1137. [Google Scholar] [CrossRef]
- Lu, H.; Wang, J.; Stoller, M.; Wang, T.; Bao, Y.; Hao, H. An Overview of Nanomaterials for Water and Wastewater Treatment. Adv. Mater. Sci. Eng. 2016, 2016, 4964828. [Google Scholar] [CrossRef]
- Manos, M.J.; Kanatzidis, M.G. Metal Sulfide Ion Exchangers: Superior Sorbents for the Capture of Toxic and Nuclear Waste-Related Metal Ions. Chem. Sci. 2016, 7, 4804–4824. [Google Scholar] [CrossRef]
- Kumar, P.; Pournara, A.; Kim, K.-H.; Bansal, V.; Rapti, S.; Manos, M.J. Metal-Organic Frameworks: Challenges and Opportunities for Ion-Exchange/Sorption Applications. Prog. Mater. Sci. 2017, 86, 25–74. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Zhao, G.; Chen, C.; Chai, Z.; Alsaedi, A.; Hayat, T.; Wang, X. Metal–Organic Framework-Based Materials: Superior Adsorbents for the Capture of Toxic and Radioactive Metal Ions. Chem. Soc. Rev. 2018, 47, 2322–2356. [Google Scholar] [CrossRef]
- Gehrke, I.; Geiser, A.; Somborn-Schulz, A. Innovations in Nanotechnology for Water Treatment. Nanotechnol. Sci. Appl. 2015, 8, 1–17. [Google Scholar] [CrossRef]
- Westerhoff, P.; Alvarez, P.; Li, Q.; Gardea-Torresdey, J.; Zimmerman, J. Overcoming Implementation Barriers for Nanotechnology in Drinking Water Treatment. Environ. Sci. Nano 2016, 3, 1241–1253. [Google Scholar] [CrossRef]
- Mauter, M.S.; Zucker, I.; Perreault, F.; Werber, J.R.; Kim, J.-H.; Elimelech, M. The Role of Nanotechnology in Tackling Global Water Challenges. Nat. Sustain. 2018, 1, 166–175. [Google Scholar] [CrossRef]
- Borovik, A.; Karanikola, V.; Zucker, I. Platform Selection of Engineered Nanomaterials for Water Decontamination Applications. Environ. Sci. Nano 2020, 7, 3641–3654. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, H.; Yu, F.; Liu, Y.; Jia, L.; Zhao, W.; Li, P.; Wang, H.; Zhu, P.; Li, B. Blow Spinning of Polyimide/SiO2 Composite Fibrous Sponges with Excellent Adsorption Capacity and Recyclability. ACS Appl. Polym. Mater. 2022, 4, 8487–8495. [Google Scholar] [CrossRef]
- Bouraie, M.E.; Abdelghany, A. Sorption Features of Polyurethane Foam Functionalized with Salicylate for Chlorpyrifos: Equilibrium, Kinetic Models and Thermodynamic Studies. Polymers 2020, 12, 2036. [Google Scholar] [CrossRef]
- Pournara, A.D.; Moisiadis, E.; Gouma, V.; Manos, M.J.; Giokas, D.L. Cotton Fabric Decorated by a Zr4+ MOF for Selective As(V) and Se(IV) Removal from Aqueous Media. J. Environ. Chem. Eng. 2022, 10, 107705. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, G.; Dai, H.; Yang, M.; Fu, Y.; Ying, Y.; Li, Y. Biomineralization-Mimetic Preparation of Hybrid Membranes with Ultra-High Loading of Pristine Metal–Organic Frameworks Grown on Silk Nanofibers for Hazard Collection in Water. J. Mater. Chem. A 2018, 6, 3402–3413. [Google Scholar] [CrossRef]
- Godlewska, K.; Stepnowski, P.; Paszkiewicz, M. Pollutant Analysis Using Passive Samplers: Principles, Sorbents, Calibration and Applications. A Review. Environ. Chem. Lett. 2021, 19, 465–520. [Google Scholar] [CrossRef]
- Booij, K.; Vrana, B.; Huckins, J.N. Chapter 7. Theory, Modelling and Calibration of Passive Samplers Used in Water Monitoring. In Comprehensive Analytical Chemistry; Greenwood, R., Mills, G., Vrana, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 48, pp. 141–169. [Google Scholar]
- Gong, X.; Li, K.; Wu, C.; Wang, L.; Sun, H. Passive Sampling for Monitoring Polar Organic Pollutants in Water by Three Typical Samplers. Trends Environ. Anal. Chem. 2018, 17, 23–33. [Google Scholar] [CrossRef]
- Salim, F.; Górecki, T. Theory and Modelling Approaches to Passive Sampling. Environ. Sci. Process. Impacts 2019, 21, 1618–1641. [Google Scholar] [CrossRef]
- Gouma, V.; Pournara, A.D.; Manos, M.J.; Giokas, D.L. Fabric Phase Sorpitive Extraction and Passive Sampling of Ultraviolet Filters from Natural Waters Using a Zirconium Metal Organic Framework-Cotton Composite. J. Chromatogr. A 2022, 1670, 462945. [Google Scholar] [CrossRef]
- Gartner, J.W.; Wellman, R.E.; Wood, T.M.; Cheng, R.T. Water Velocity and Suspended Solids Measurements by In-Situ Instruments in Upper Klamath Lake, Oregon; U.S. Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Schulze, K.; Hunger, M.; Döll, P. Simulating River Flow Velocity on Global Scale. Adv. Geosci. 2005, 5, 133–136. [Google Scholar] [CrossRef]
- Rapti, S.; Pournara, A.; Sarma, D.; Papadas, I.T.; Armatas, G.S.; Hassan, Y.S.; Alkordi, M.H.; Kanatzidis, M.G.; Manos, M.J. Rapid, Green and Inexpensive Synthesis of High Quality UiO-66 Amino-Functionalized Materials with Exceptional Capability for Removal of Hexavalent Chromium from Industrial Waste. Inorg. Chem. Front. 2016, 3, 635–644. [Google Scholar] [CrossRef]
- Kot-Wasik, A.; Zabiegała, B.; Urbanowicz, M.; Dominiak, E.; Wasik, A.; Namieśnik, J. Advances in Passive Sampling in Environmental Studies. Anal. Chim. Acta 2007, 602, 141–163. [Google Scholar] [CrossRef]
- Roll, I.B.; Halden, R.U. Critical Review of Factors Governing Data Quality of Integrative Samplers Employed in Environmental Water Monitoring. Water Res. 2016, 94, 200–207. [Google Scholar] [CrossRef]
- Kaserzon, S.L.; Kennedy, K.; Hawker, D.W.; Thompson, J.; Carter, S.; Roach, A.C.; Booij, K.; Mueller, J.F. Development and Calibration of a Passive Sampler for Perfluorinated Alkyl Carboxylates and Sulfonates in Water. Environ. Sci. Technol. 2012, 46, 4985–4993. [Google Scholar] [CrossRef]
- Męczykowska, H.; Kobylis, P.; Stepnowski, P.; Caban, M. Calibration of Passive Samplers for the Monitoring of Pharmaceuticals in Water-Sampling Rate Variation. Crit. Rev. Anal. Chem. 2017, 47, 204–222. [Google Scholar] [CrossRef]
- Morin, N.; Miège, C.; Coquery, M.; Randon, J. Chemical Calibration, Performance, Validation and Applications of the Polar Organic Chemical Integrative Sampler (POCIS) in Aquatic Environments. TrAC Trends Anal. Chem. 2012, 36, 144–175. [Google Scholar] [CrossRef]
- Harman, C.; Allan, I.J.; Vermeirssen, E.L.M. Calibration and Use of the Polar Organic Chemical Integrative Sampler—A Critical Review. Environ. Toxicol. Chem. 2012, 31, 2724–2738. [Google Scholar] [CrossRef]
- Arditsoglou, A.; Voutsa, D. Passive Sampling of Selected Endocrine Disrupting Compounds Using Polar Organic Chemical Integrative Samplers. Environ. Pollut. 2008, 156, 316–324. [Google Scholar] [CrossRef]
- Mechelke, J.; Vermeirssen, E.L.M.; Hollender, J. Passive sampling of organic contaminants across the water-sediment interface of an urban stream. Water Res. 2019, 165, 114966. [Google Scholar] [CrossRef]
- Ding, S.; Xu, D.; Wang, Y.; Wang, Y.; Li, Y.; Gong, M.; Zhang, C. Simultaneous Measurements of Eight Oxyanions Using High-Capacity Diffusive Gradients in Thin Films (Zr-Oxide DGT) with a High-Efficiency Elution Procedure. Environ. Sci. Technol. 2016, 50, 7572–7580. [Google Scholar] [CrossRef]
- Guan, D.-X.; Williams, P.N.; Luo, J.; Zheng, J.-L.; Xu, H.-C.; Cai, C.; Ma, L.Q. Novel Precipitated Zirconia-Based DGT Technique for High-Resolution Imaging of Oxyanions in Waters and Sediments. Environ. Sci. Technol. 2015, 49, 3653–3661. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, H.; Santner, J.; Davison, W. Performance Characteristics of Diffusive Gradients in Thin Films Equipped with a Binding Gel Layer Containing Precipitated Ferrihydrite for Measuring Arsenic(V), Selenium(VI), Vanadium(V), and Antimony(V). Anal. Chem. 2010, 82, 8903–8909. [Google Scholar] [CrossRef]
- Bennett, W.W.; Teasdale, P.R.; Panther, J.G.; Welsh, D.T.; Jolley, D.F. Speciation of Dissolved Inorganic Arsenic by Diffusive Gradients in Thin Films: Selective Binding of As III by 3-Mercaptopropyl-Functionalized Silica Gel. Anal. Chem. 2011, 83, 8293–8299. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).