Combined Effects of Polyamide Microplastics and Hydrochemical Factors on the Transport of Bisphenol A in Groundwater
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Material
2.2. Material Characterization
2.3. Batch Experiments
2.3.1. Isothermal Adsorption Experiments
2.3.2. Kinetic Adsorption Experiments
2.4. BPA Transport Experiment
2.5. BPA Transport Model
3. Results and Discussion
3.1. Characterization of Materials
3.2. Adsorption
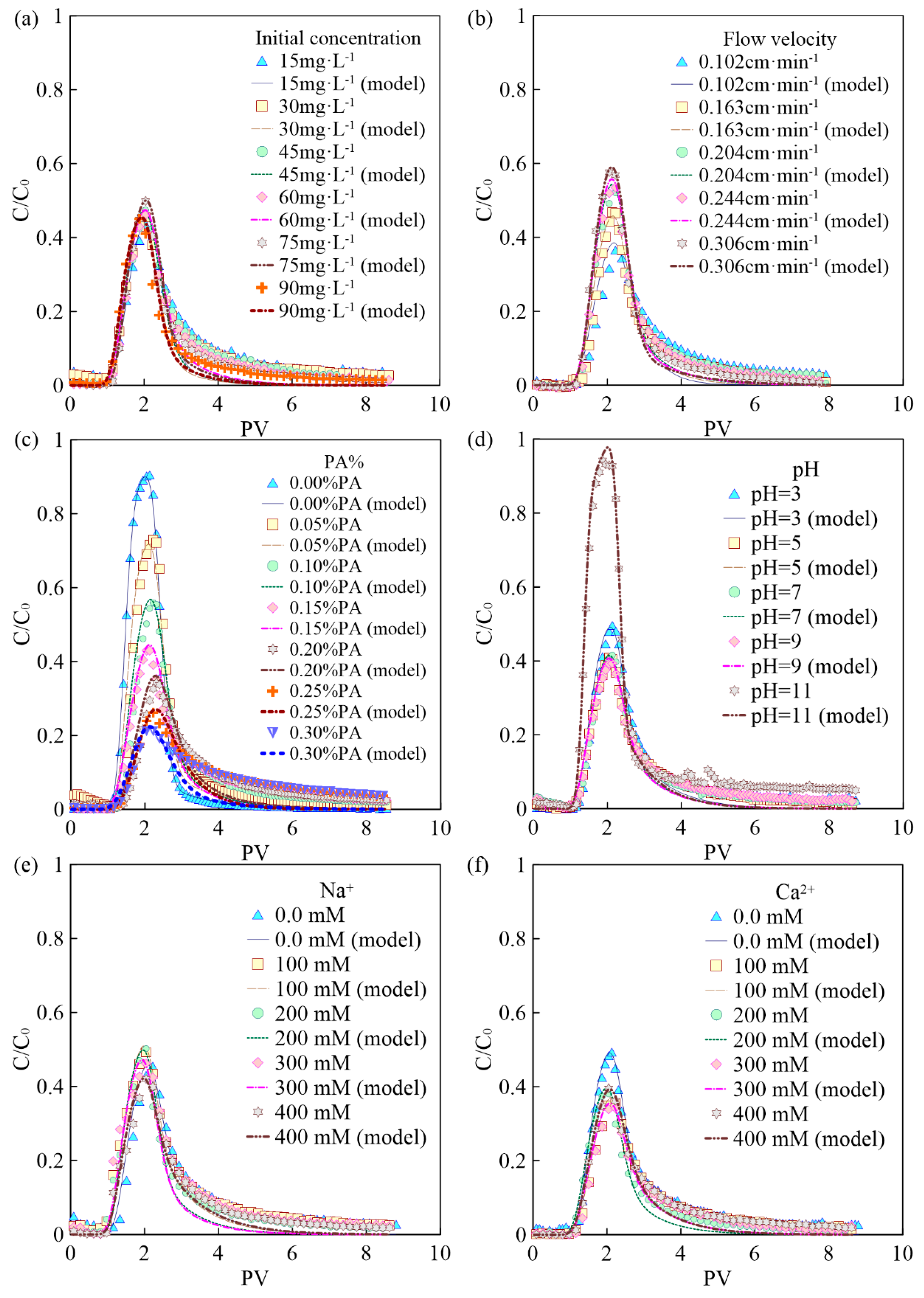
3.3. BPA Transport under Different Conditions
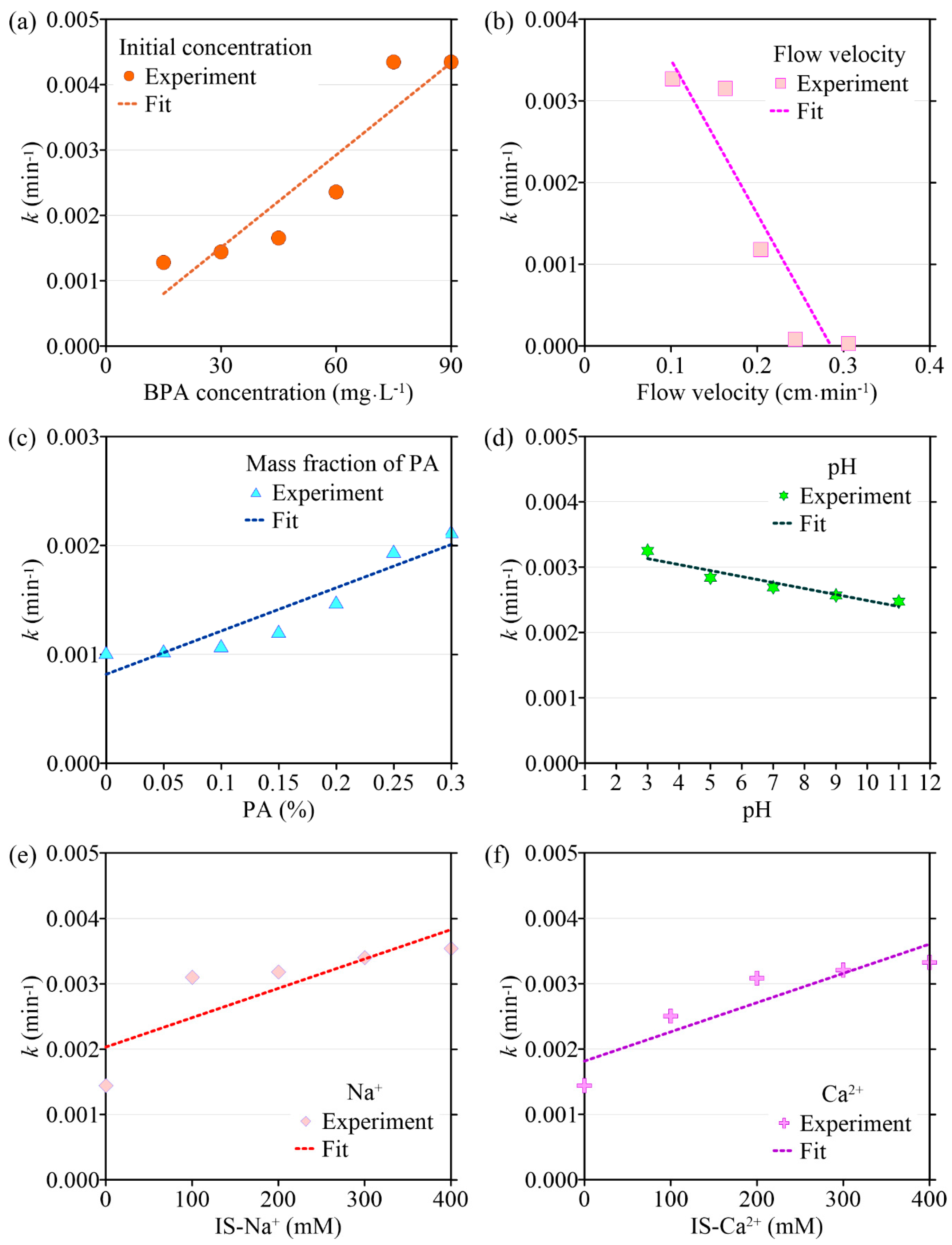
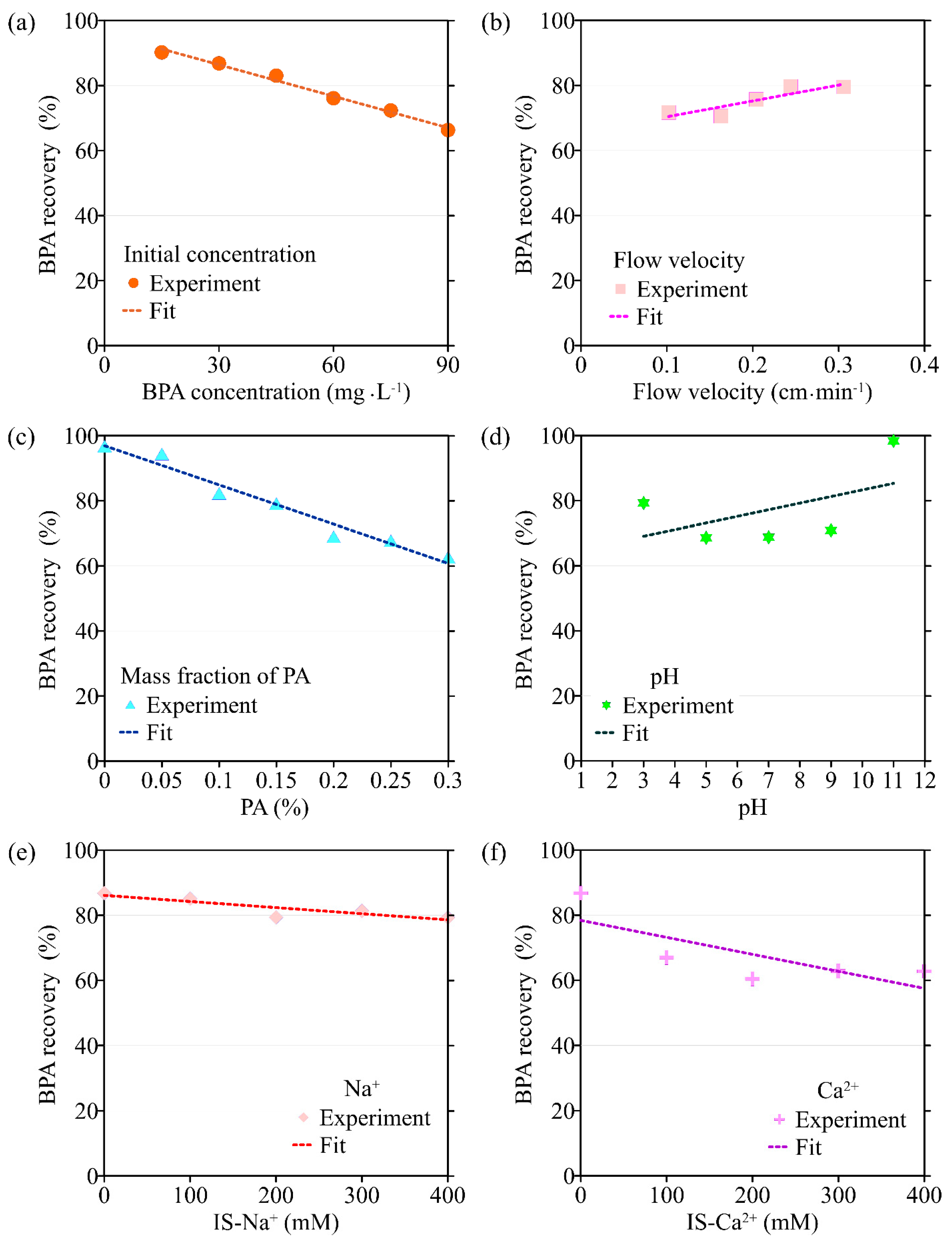
3.3.1. Initial Concentration
3.3.2. Flow Velocity
3.3.3. Mass Fraction of PA
3.3.4. pH
3.3.5. Ionic Types and Strengths
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rillig, M.C. Microplastic in Terrestrial Ecosystems and the Soil? Environ. Sci. Technol. 2012, 46, 6453–6454. [Google Scholar]
- Rochman, C.M. Microplastics research—From sink to source. Science 2018, 360, 28–29. [Google Scholar] [CrossRef]
- Shi, J.Y.; Dong, Y.B.; Shi, Y.Y.; Yin, T.T.; He, W.; An, T.Y.; Tang, Y.L.; Hou, X.W.; Chong, S.J.; Chen, D.N.; et al. Groundwater antibiotics and microplastics in a drinking-water source area, northern China: Occurrence, spatial distribution, risk assessment, and correlation. Environ. Res. 2022, 210, 112855. [Google Scholar] [CrossRef]
- Auta, H.S.; Emenike, C.U.; Fauziah, S.H. Distribution and importance of microplastics in the marine environment: A review of the sources, fate, effects, and potential solutions. Environ. Int. 2017, 102, 165–176. [Google Scholar] [CrossRef]
- Cole, M.; Lindeque, P.; Fileman, E.; Halsband, C.; Goodhhead, R.; Moger, J.L.; Galloway, T.S. Microplastic Ingestion by Zooplankton. Environ. Sci. Technol. 2013, 47, 6646–6655. [Google Scholar]
- Wright, S.L.; Thompson, R.C.; Galloway, T.S. The physical impacts of microplastics on marine organisms: A review. Environ. Pollut. 2013, 178, 483–492. [Google Scholar]
- Kazour, M.; Terki, S.; Rabhi, K.; Jemaa, S.; Khalaf, G.; Amara, R. Sources of microplastics pollution in the marine environment: Importance of wastewater treatment plant and coastal landfill. Mar. Pollut. Bull. 2019, 146, 608–618. [Google Scholar]
- Zhang, Y.; Wu, H.W.; Xu, L.; Liu, H.Z.; An, L.H. Promising indicators for monitoring microplastic pollution. Mar. Pollut. Bull. 2022, 182, 113952. [Google Scholar]
- Mintenig, S.M.; Löder, M.G.J.; Primpke, S.; Gerdts, G. Low numbers of microplastics detected in drinking water from ground water sources. Sci. Total Environ. 2019, 648, 631–635. [Google Scholar]
- Nizzetto, L.; Futter, M.; Langaas, S. Are Agricultural Soils Dumps for Microplastics of Urban Origin? Environ. Sci. Technol. 2016, 50, 10777–10779. [Google Scholar] [CrossRef]
- Teuten, E.L.; Rowland, S.J.; Galloway, T.S.; Thompson, R.C. Potential for Plastics to Transport Hydrophobic Contaminants. Environ. Sci. Technol. 2007, 41, 7759–7764. [Google Scholar]
- Panno, S.V.; Kelly, W.R.; Scott, J.; Zheng, W.; McNeish, R.E.; Holm, N.; Hoellein, T.J.; Baranski, E.L. Microplastic Contamination in Karst Groundwater Systems. Groundwater 2019, 57, 189–196. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Wong, C.K.C.; Zheng, J.S.; Bouwman, H.; Barra, R.; Wahlström, B.; Neretin, L.; Wong, M.H. Bisphenol A (BPA) in China: A review of sources, environmental levels, and potential human health impacts. Environ. Int. 2012, 42, 91–99. [Google Scholar] [CrossRef]
- Česen, M.; Lenarčič, K.; Mislej, V.; Levstek, M.; Kovačič, A.; Cimrmančič, B.; Uranjek, N.; Kosjek, T.; Heath, D.; Dolenc, M.S.; et al. The occurrence and source identification of bisphenol compounds in wastewaters. Sci. Total Environ. 2018, 616–617, 744–752. [Google Scholar]
- Ballesteros-Gómez, A.; Rubio, S.; Pérez-Bendito, D. Analytical methods for the determination of bisphenol A in food. J. Chromatogr. A 2022, 182, 113952. [Google Scholar] [CrossRef]
- Vandenberg, L.N.; Hauser, R.; Marcus, M.; Olea, N.; Welshons, W.V. Human exposure to bisphenol A (BPA). Reprod. Toxicol. 2007, 24, 139–177. [Google Scholar] [CrossRef]
- Li, D.; Zhou, Z.; Qing, D.; He, Y.; Wu, T.; Miao, M.; Wang, J.; Weng, X.; Ferber, J.R.; Herrinton, L.J.; et al. Occupational exposure to bisphenol-A (BPA) and the risk of Self-Reported Male Sexual Dysfunction. Hum. Reprod. 2010, 25, 519–527. [Google Scholar]
- Gerona, R.R.; Woodruff, T.J.; Dickenson, C.A.; Pan, J.; Schwartz, J.M.; Sen, S.; Friesen, M.W.; Fujimoto, V.Y.; Hunt, P.A. Bisphenol-A (BPA), BPA Glucuronide, and BPA Sulfate in Midgestation Umbilical Cord Serum in a Northern and Central California Population. Environ. Sci. Technol. 2013, 47, 12477–12485. [Google Scholar]
- Careghini, A.; Mastorgio, A.F.; Saponaro, S.; Sezenna, E. Bisphenol A, nonylphenols, benzophenones, and benzotriazoles in soils, groundwater, surface water, sediments, and food: A review. Environ. Sci. Pollut. Res. 2015, 22, 5711–5741. [Google Scholar]
- Ahmadzadeh, S.; Dolatabadi, M. Modeling and kinetics study of electrochemical peroxidation process for mineralization of bisphenol A; a new paradigm for groundwater treatment. J. Mol. Liq. 2018, 254, 76–82. [Google Scholar]
- Shi, Y.F.; Sun, Y.Y.; Gao, B.; Xu, H.X.; Shi, X.Q.; Wu, J.C. Retention and Transport of Bisphenol A and Bisphenol S in Saturated Limestone Porous Media. Water Air Soil Pollut. 2018, 229, 260. [Google Scholar]
- Shi, Y.F.; Gao, B.; Sun, Y.Y.; Xu, H.X.; Wu, J.C. Effect of Residual NAPLs on the Transport of Bisphenol A and Bisphenol S in Saturated Porous Media. Water Air Soil Pollut. 2019, 230, 185. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using Hydrus. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- Teijón, G.; Candela, L.; Šimůnek, J.; Tamoh, K.; Valdes-Abellán, J. Fate and transport of naproxen in a sandy aquifer material: Saturated column studies and model evaluation. Soil Sediment Contam. 2014, 23, 736–750. [Google Scholar]
- Zakari, S.; Liu, H.; Tong, L.; Wang, Y.; Liu, J.F. Transport of bisphenol-A in sandy aquifer sediment: Column experiment. Chemosphere 2016, 144, 1807–1814. [Google Scholar]
- Wu, M.; Chen, Y.N.; Cheng, Z.; Hao, Y.R.; Hu, B.X.; Mo, C.M.; Li, Q.S.; Zhao, H.M.; Xiang, L.; Wu, J.F.; et al. Effects of polyamide microplastic on the transport of graphene oxide in porous media. Sci. Total Environ. 2022, 843, 157042. [Google Scholar] [CrossRef]
- Liu, X.M. Interaction and Mechanism between Microplastics and Typical Environmental Endocrine Disrupting Compounds. Master’s Thesis, East China Normal University, Shanghai, China, 2020. (In Chinese with English abstract). [Google Scholar]
- Chen, Y.N.; Wu, M.; Cheng, Z.; Hu, X.N. Effects of typical microplastics on migration of ciprofloxacin in porous media. J. Agro-Environ. Sci. 2021, 40, 400–407, (In Chinese with English abstract). [Google Scholar]
- Wei, X.; Shao, M.; Du, L.; Horton, R. Humic acid transport in saturated porous media: Influence of flow velocity and influent concentration. J. Environ. Sci. 2014, 26, 2554–2561. [Google Scholar] [CrossRef]
- Cai, L.; Zhu, J.H.; Hou, Y.L.; Tong, M.P.; Kim, H.J. Influence of gravity on transport and retention of representative engineered nanoparticles in quartz sand. J. Contam. Hydrol. 2015, 181, 153–160. [Google Scholar]
- Song, S.; Song, Y.; Shi, M.; Hu, Z.; Li, T.; Lin, S. Transport and numerical simulation of Cu2+ in saturated porous medium in the presence of magnetic nanoparticles. Environ. Sci. Pollut. R. 2019, 26, 35827–35837. [Google Scholar] [CrossRef]
- Liang, Y.; Bradford, S.A.; Simunek, J.; Vereecken, H.; Klumpp, E. Sensitivity of the transport and retention of stabilized silver nanoparticles to physicochemical factors. Water Res. 2013, 47, 2572–2582. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, B.; Bradford, S.A.; Wu, L.; Chen, H.; Shi, X.; Wu, J. Transport, retention, and size perturbation of graphene oxide in saturated porous media:effects of input concentration and grain size. Water Res. 2015, 68, 24–33. [Google Scholar]
- Wang, D.; Shen, C.; Jin, Y.; Su, C.; Chu, L.; Zhou, D. Role of solution chemistry in the retention and release of graphene oxide nanomaterials in uncoated and iron oxide-coated sand. Sci. Total Environ. 2016, 579, 776–785. [Google Scholar] [CrossRef]
- Zhao, X.Q. The removal of bisphenol compiunds in water environment by coconut shell biochar immobilized TTNP3. Master’s Thesis, Nanjing University, Nanjing, China, 2018. (In Chinese with English abstract). [Google Scholar]
- Yang, D. The adsorption mechanism of bisphenol A and its substitute on graphene. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2021. (In Chinese with English abstract). [Google Scholar]
- Ye, X.; Cheng, Z.; Wu, M.; Hao, Y.; Lu, G.P.; Hu, B.X.; Mo, C.H.; Li, Q.S.; Wu, J.F.; Wu, J.C. Effects of Clay Minerals on the Transport of Polystyrene Nanoplastic in Groundwater. Water Res. 2022, 223, 118978. [Google Scholar]



| No. | CBPA 1 (mg·L−1) | ν 2 (cm·min−1) | PPA 3 (%) | pH | IS 4 (mM) | PC/C0 5 | RC 6 (%) | Model Results | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Na+ | Ca2+ | k7 (min−1) | Smax 8 (mg·g−1) | R2 | |||||||
| 1 | 15 | 0.204 | 0.1 | 7 | \ | \ | 0.437 | 90.2 | 1.28 × 10−3 | 0.693 | 0.942 |
| 2 | 30 | 0.204 | 0.1 | 7 | \ | \ | 0.465 | 86.8 | 1.44 × 10−3 | 1.48 | 0.928 |
| 3 | 45 | 0.204 | 0.1 | 7 | \ | \ | 0.474 | 83.0 | 1.65 × 10−3 | 2.36 | 0.923 |
| 4 | 60 | 0.204 | 0.1 | 7 | \ | \ | 0.462 | 76.1 | 2.35 × 10−3 | 3.81 | 0.958 |
| 5 | 75 | 0.204 | 0.1 | 7 | \ | \ | 0.499 | 72.3 | 4.35 × 10−3 | 6.63 | 0.977 |
| 6 | 90 | 0.204 | 0.1 | 7 | \ | \ | 0.454 | 66.3 | 4.34 × 10−3 | 7.01 | 0.976 |
| 7 | 30 | 0.102 | 0.1 | 7 | \ | \ | 0.366 | 71.7 | 3.27 × 10−3 | 3.90 | 0.913 |
| 8 | 30 | 0.163 | 0.1 | 7 | \ | \ | 0.468 | 70.5 | 3.15 × 10−3 | 3.00 | 0.958 |
| 9 | 30 | 0.244 | 0.1 | 7 | \ | \ | 0.543 | 79.7 | 8.21 × 10−5 | 2.88 | 0.981 |
| 10 | 30 | 0.306 | 0.1 | 7 | \ | \ | 0.593 | 79.5 | 2.75 × 10−5 | 2.79 | 0.987 |
| 11 | 30 | 0.204 | 0.0 | 7 | \ | \ | 0.905 | 96.7 | 1.02 × 10−3 | 1.51 | 0.997 |
| 12 | 30 | 0.204 | 0.05 | 7 | \ | \ | 0.730 | 94.3 | 1.03 × 10−3 | 2.01 | 0.947 |
| 13 | 30 | 0.204 | 0.15 | 7 | \ | \ | 0.430 | 79.1 | 1.21 × 10−3 | 3.04 | 0.953 |
| 14 | 30 | 0.204 | 0.2 | 7 | \ | \ | 0.344 | 69.0 | 1.48 × 10−3 | 3.09 | 0.904 |
| 15 | 30 | 0.204 | 0.25 | 7 | \ | \ | 0.262 | 67.7 | 1.95 × 10−3 | 3.16 | 0.859 |
| 16 | 30 | 0.204 | 0.3 | 7 | \ | \ | 0.217 | 62.7 | 2.13 × 10−3 | 4.11 | 0.779 |
| 17 | 30 | 0.204 | 0.1 | 3 | \ | \ | 0.496 | 79.2 | 3.25 × 10−3 | 4.16 | 0.974 |
| 18 | 30 | 0.204 | 0.1 | 5 | \ | \ | 0.409 | 68.7 | 2.84 × 10−3 | 4.11 | 0.983 |
| 19 | 30 | 0.204 | 0.1 | 9 | \ | \ | 0.393 | 70.9 | 2.56 × 10−3 | 3.91 | 0.979 |
| 20 | 30 | 0.204 | 0.1 | 11 | \ | \ | 0.944 | 98.4 | 2.47 × 10−3 | 2.65 | 0.991 |
| 21 | 30 | 0.204 | 0.1 | 7 | 100 | \ | 0.493 | 85.1 | 3.10 × 10−3 | 4.39 | 0.985 |
| 22 | 30 | 0.204 | 0.1 | 7 | 200 | \ | 0.502 | 79.4 | 3.18 × 10−3 | 4.76 | 0.977 |
| 23 | 30 | 0.204 | 0.1 | 7 | 300 | \ | 0.462 | 81.3 | 3.40 × 10−3 | 5.34 | 0.964 |
| 24 | 30 | 0.204 | 0.1 | 7 | 400 | \ | 0.425 | 79.3 | 3.54 × 10−3 | 5.77 | 0.974 |
| 25 | 30 | 0.204 | 0.1 | 7 | \ | 100 | 0.362 | 67.0 | 2.50 × 10−3 | 3.85 | 0.965 |
| 26 | 30 | 0.204 | 0.1 | 7 | \ | 200 | 0.390 | 60.4 | 3.08 × 10−3 | 4.31 | 0.986 |
| 27 | 30 | 0.204 | 0.1 | 7 | \ | 300 | 0.349 | 62.8 | 3.21 × 10−3 | 4.73 | 0.960 |
| 28 | 30 | 0.204 | 0.1 | 7 | \ | 400 | 0.396 | 62.7 | 3.32 × 10−3 | 5.04 | 0.982 |
| Parameter | k1 (min−1) | Smax 2 (mg·g−1) | PC/C0 3 | RC 4 (%) |
|---|---|---|---|---|
| CBPA 5 (mg·L−1) | (R2 = 0.863) | (R2 = 0.951) | (R2 = 0.368) | (R2 = 0.989) |
| ν 6 (cm·min−1) | (R2 = 0.848) | (R2 = 0.704) | (R2 = 0.953) | (R2 = 0.784) |
| PPA7 (%) | (R2 = 0.881) | (R2 = 0.941) | (R2 = 0.956) | (R2 = 0.963) |
| pH | (R2 = 0.904) | (R2 = 0.659) | (R2 = 0.354) | (R2 = 0.378) |
| ISNaCl 8 (mM) | (R2 = 0.775) | (R2 = 0.993) | (R2 = 0.313) | (R2 = 0.276) |
| ISCaCl2 9 (mM) | (R2 = 0.851) | (R2 = 0.968) | (R2 = 0.336) | (R2 = 0.295) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Lin, X.; Wu, M.; Lu, G.; Hao, Y.; Mo, C.; Li, Q.; Wu, J.; Wu, J.; Hu, B.X. Combined Effects of Polyamide Microplastics and Hydrochemical Factors on the Transport of Bisphenol A in Groundwater. Separations 2023, 10, 123. https://doi.org/10.3390/separations10020123
Cheng Z, Lin X, Wu M, Lu G, Hao Y, Mo C, Li Q, Wu J, Wu J, Hu BX. Combined Effects of Polyamide Microplastics and Hydrochemical Factors on the Transport of Bisphenol A in Groundwater. Separations. 2023; 10(2):123. https://doi.org/10.3390/separations10020123
Chicago/Turabian StyleCheng, Zhou, Xuanhao Lin, Ming Wu, Guoping Lu, Yanru Hao, Cehui Mo, Qusheng Li, Jianfeng Wu, Jichun Wu, and Bill X. Hu. 2023. "Combined Effects of Polyamide Microplastics and Hydrochemical Factors on the Transport of Bisphenol A in Groundwater" Separations 10, no. 2: 123. https://doi.org/10.3390/separations10020123
APA StyleCheng, Z., Lin, X., Wu, M., Lu, G., Hao, Y., Mo, C., Li, Q., Wu, J., Wu, J., & Hu, B. X. (2023). Combined Effects of Polyamide Microplastics and Hydrochemical Factors on the Transport of Bisphenol A in Groundwater. Separations, 10(2), 123. https://doi.org/10.3390/separations10020123







