Numerical Characterization of Acoustic Cavitation Bubbles with Respect to the Bubble Size Distribution at Equilibrium
Abstract
1. Introduction
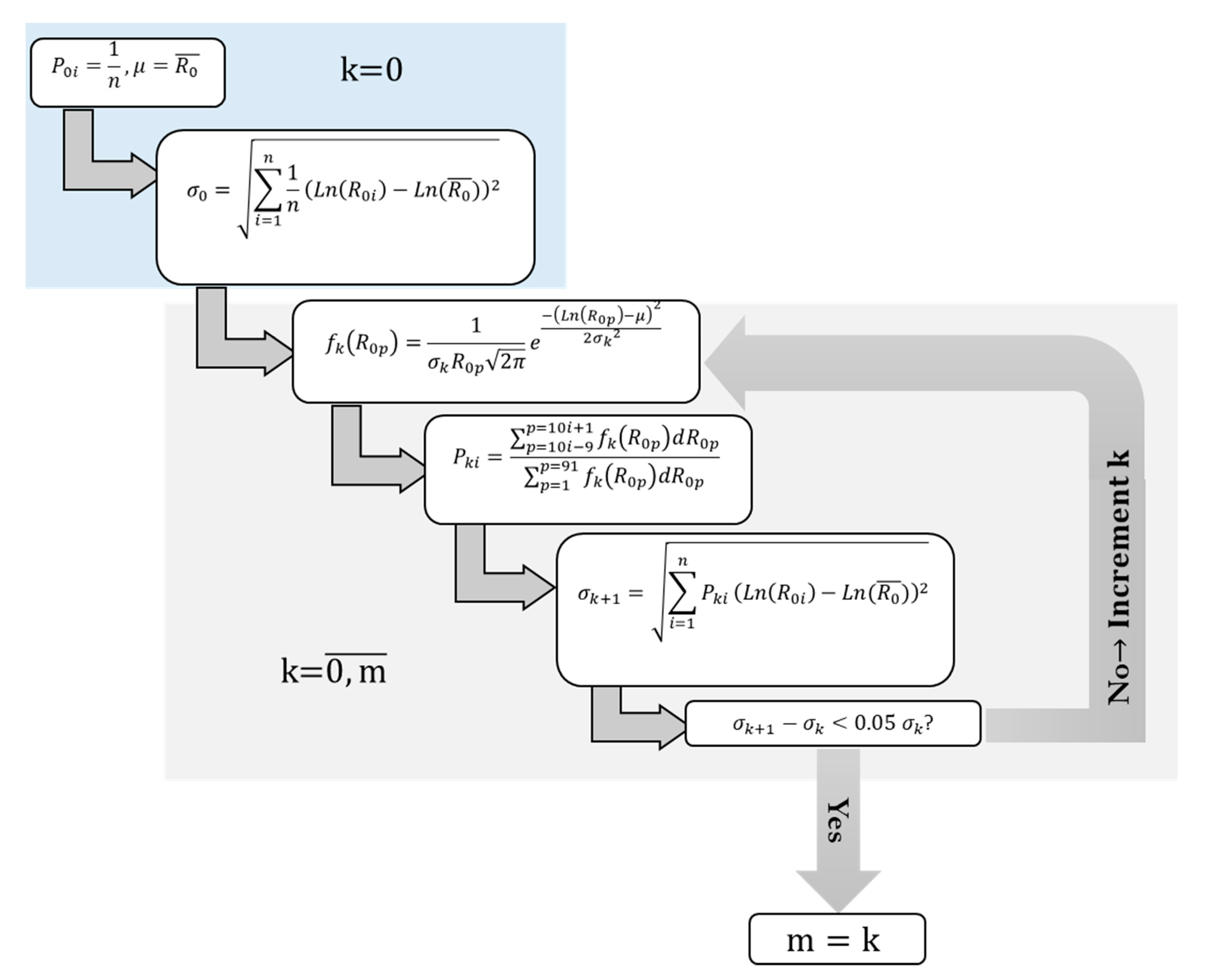
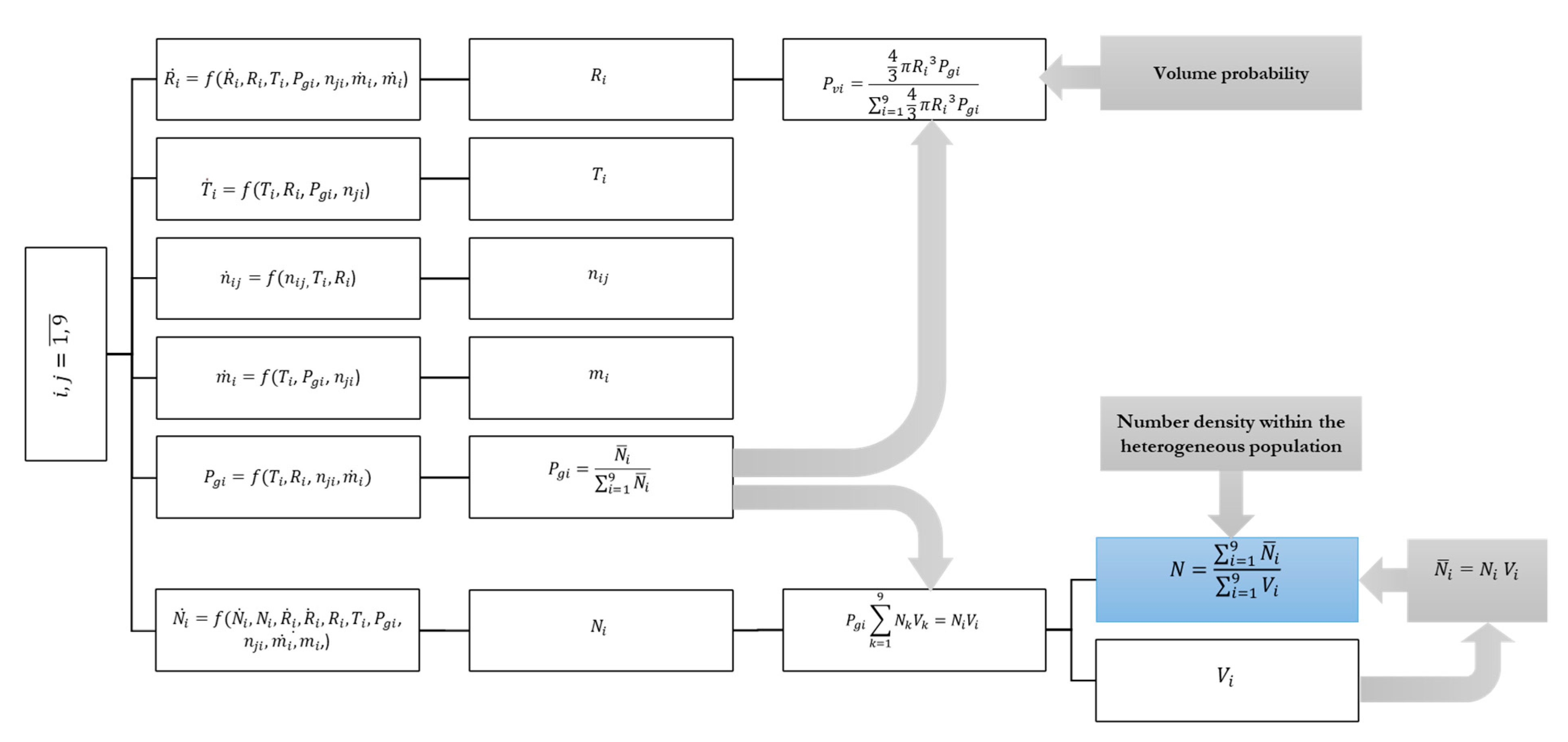
2. Numerical Methods
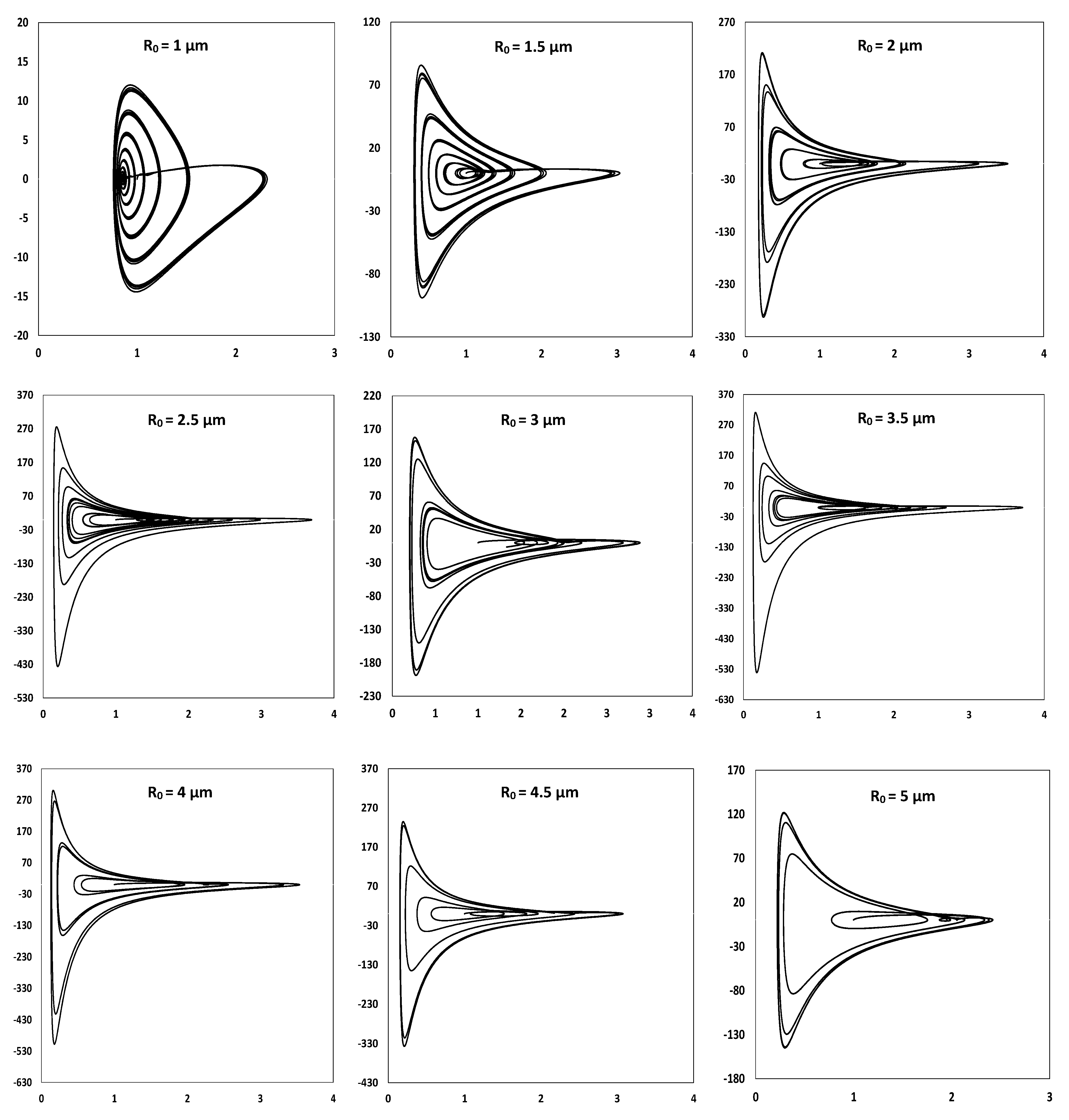
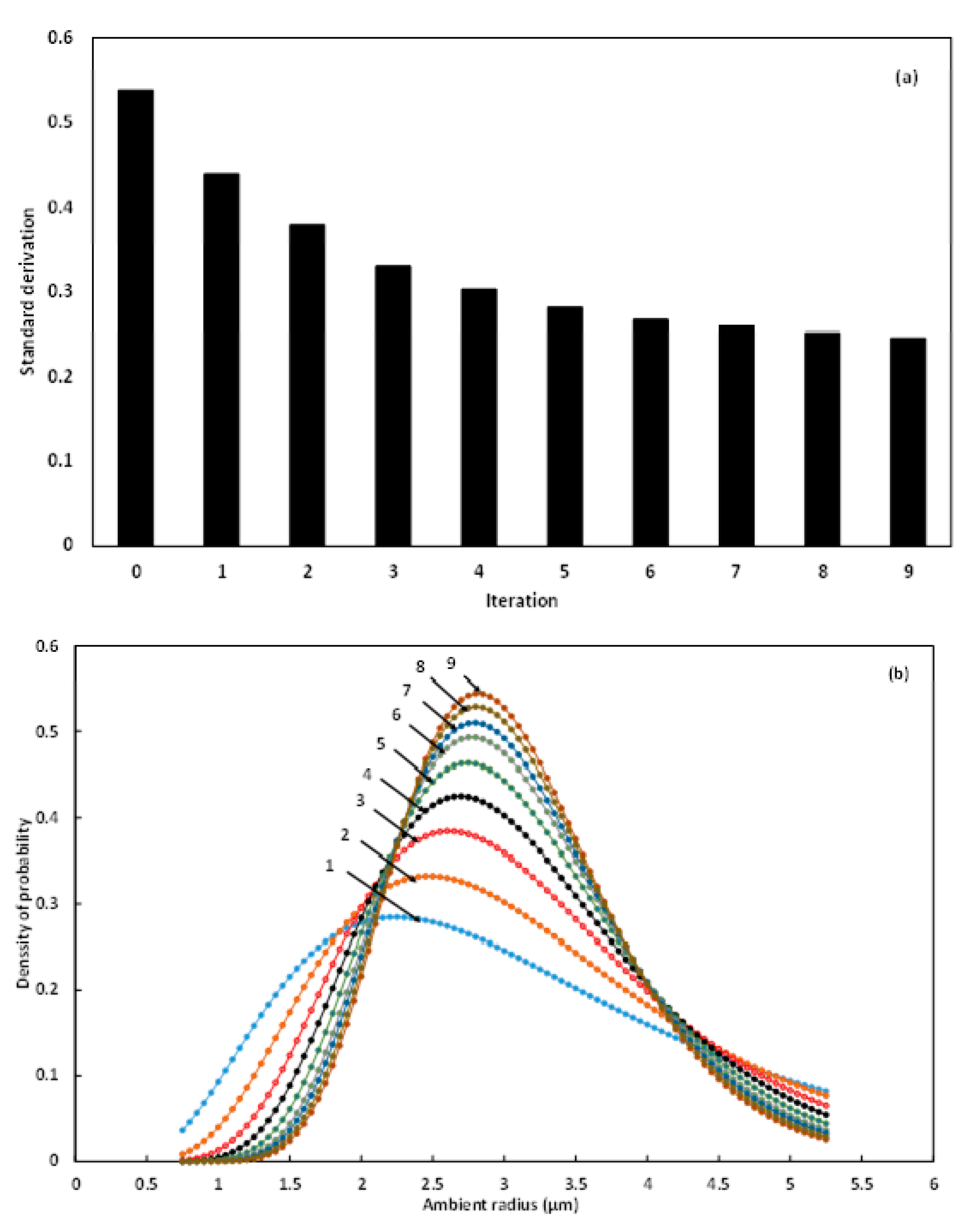
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yasui, K. Acoustic Cavitation and Bubble Dynamics; Pollet, B.G., Ashokkumar, M., Eds.; Springer Briefs in Molecular Science: Ultrasound and Sonochemistry: Nagoya, Japan, 2017. [Google Scholar]
- Kentish, S.; Ashokkumar, M. The Physical and Chemical Effects of Ultrasound. In Ultrasound Technologies for Food and Bioprocessing; Elsevier: New York, NY, USA, 2010; pp. 1–19. [Google Scholar]
- Grieser, F.; Choi, P.-K.; Enomoto, N.; Harada, H.; Okitsu, K.; Yasui, K. Sonochemistry and the Acoustic Bubble; Elsevier: Amesterdam, The Netherlands, 2015. [Google Scholar]
- Gong, C.; Hart, D.P. Ultrasound induced cavitation and sonochemical yields. J. Acoust. Soc. Am. 1998, 104, 2675–2682. [Google Scholar] [CrossRef]
- Thompson, L.H.; Doraiswamy, L.K. Sonochemistry: Science and Engineering. Ind. Eng. Chem. Res. 1999, 38, 1215–1249. [Google Scholar] [CrossRef]
- Lim, M.; Son, Y.; Khim, J. Frequency effects on the sonochemical degradation of chlorinated compounds. Ultrason. Sonochemistry 2011, 18, 460–465. [Google Scholar] [CrossRef]
- Merouani, S.; Hamdaoui, O.; Saoudi, F.; Chiha, M.; Pétrier, C. Influence of bicarbonate and carbonate ions on sonochemical degradation of Rhodamine B in aqueous phase. J. Hazard. Mater. 2010, 175, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Navarro, N.M.; Chave, T.; Pochon, P.; Bisel, I.; Nikitenko, S.I. Effect of Ultrasonic Frequency on the Mechanism of Formic Acid Sonolysis. J. Phys. Chem. B 2011, 115, 2024–2029. [Google Scholar] [CrossRef] [PubMed]
- Anto, T.; Bauchat, P.; Foucaud, A.; Fujita, M.; Kimura, T.; Sohmiya, H. Sonochemical switching from ionic to radical pathways in the reactions of styrene and trans-β-Methylstyrene with lead tetraacetate. Tetrahedron Lett. 1991, 32, 6379–6382. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O.; Islam, M.H.; Alghyamah, A.; Hansen, H.E.; Pollet, B.G. Low carbon ultrasonic production of alternate fuel: Operational and mechanistic concerns of the sonochemical process of hydrogen generation under various scenarios. Int. J. Hydrogen Energy 2021, 46, 26770–26787. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O.; Alghyamah, A. Energy balance of high-energy stable acoustic cavitation within dual-frequency sonochemical reactor. Ultrason. Sonochemistry 2021, 73, 105471. [Google Scholar] [CrossRef]
- Merouani, S.; Hamdaoui, O.; Rezgui, Y.; Guemini, M. Computational engineering study of hydrogen production via ultrasonic cavitation in water. Int J. Hydrogen Energy 2016, 41, 832–844. [Google Scholar] [CrossRef]
- Yasui, K. Alternative model of single-bubble sonoluminescence. Phys. Rev. E 1997, 56, 6750–6760. [Google Scholar] [CrossRef]
- Sivasankar, T.; Moholkar, V.S. Physical insights into the sonochemical degradation of recalcitrant organic pollutants with cavitation bubble dynamics. Ultrason. Sonochemistry 2009, 16, 769–781. [Google Scholar] [CrossRef]
- Merouani, S.; Ferkous, H.; Hamdaoui, O.; Rezgui, Y.; Guemini, M. A method for predicting the number of active bubbles in sonochemical reactors. Ultrason. Sonochemistry 2015, 22, 51–58. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Void fraction, number density of acoustic cavitation bubbles, and acoustic frequency: A numerical investigation. J. Acoust. Soc. Am. 2019, 146, 2240–2252. [Google Scholar] [CrossRef] [PubMed]
- Kerboua, K.; Hamdaoui, O.; Alghyamah, A. Predicting the Sonochemical Efficiency for Water Decontamination: An Upscaled Numerical Approach. Chem. Eng. Technol. 2020, 44, 273–282. [Google Scholar] [CrossRef]
- Hao, Y.; Oguz, H.N.; Prosperetti, A. The action of pressure-radiation forces on pulsating vapor bubbles. Phys. Fluids 2001, 13, 1167–1177. [Google Scholar] [CrossRef][Green Version]
- Mettin, R.; Akhatov, I.; Parlitz, U.; Ohl, C.D.; Lauterborn, W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. Phys. Rev. E 1997, 56, 2924–2931. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S. The secondary Bjerknes force between two gas bubbles under dual-frequency acoustic excitation. Ultrason. Sonochemistry 2016, 29, 129–145. [Google Scholar] [CrossRef]
- Iida, Y.; Ashokkumar, M.; Tuziuti, T.; Kozuka, T.; Yasui, K.; Towata, A.; Lee, J. Bubble population phenomena in sonochemical reactor: II. Estimation of bubble size distribution and its number density by simple coalescence model calculation. Ultrason. Sonochemistry 2010, 17, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Influence of ultrasonic frequency on multibubble sonoluminescence. J. Acoust. Soc. Am. 2002, 112, 1405–1413. [Google Scholar] [CrossRef] [PubMed]
- Colonius, T.; Hagmeijer, R.; Ando, K.; Brennen, C.E. Statistical equilibrium of bubble oscillations in dilute bubbly flows. Phys. Fluids 2008, 20, 040902. [Google Scholar] [CrossRef]
- Ida, M. Multibubble cavitation inception. Phys. Fluids 2009, 21, 113302. [Google Scholar] [CrossRef]
- Yasui, K.; Iida, Y.; Tuziuti, T.; Kozuka, T.; Towata, A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E 2008, 77, 016609. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, L.; Wu, Y.; Chen, W. The role of the bubble–bubble interaction on radial pulsations of bubbles. Ultrason. Sonochemistry 2021, 73, 105535. [Google Scholar] [CrossRef]
- D’Hondt, L.; Cavaro, M.; Payan, C.; Mensah, S. Acoustical characterisation and monitoring of microbubble clouds. Ultrasonics 2019, 96, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Desai, P.D.; Ng, W.C.; Hines, M.J.; Riaz, Y.; Tesar, V.; Zimmerman, W.B. Comparison of Bubble Size Distributions Inferred from Acoustic, Optical Visualisation, and Laser Diffraction. Colloids Interfaces 2019, 3, 65. [Google Scholar] [CrossRef]
- Brotchie, A.; Grieser, F.; Ashokkumar, M. Effect of Power and Frequency on Bubble-Size Distributions in Acoustic Cavitation. Phys. Rev. Lett. 2009, 102, 084302. [Google Scholar] [CrossRef] [PubMed]
- Avvaru, B.; Pandit, A.B. Oscillating bubble concentration and its size distribution using acoustic emission spectra. Ultrason. Sonochemistry 2009, 16, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Zong, Y.; Li, W.; Zhang, S.; Wan, M. Bubble size distribution in acoustic droplet vaporization via dissolution using an ultrasound wide-beam method. Ultrason. Sonochemistry 2014, 21, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Reuter, F.; Lesnik, S.; Ayaz-Bustami, K.; Brenner, G.; Mettin, R. Bubble size measurements in different acoustic cavitation structures: Filaments, clusters, and the acoustically cavitated jet. Ultrason. Sonochemistry 2019, 55, 383–394. [Google Scholar] [CrossRef]
- Calvisi, M.L.; Lindau, O.; Blake, J.R.; Szeri, A.J. Shape stability and violent collapse of microbubbles in acoustic traveling waves. Phys. Fluids 2007, 19, 47101. [Google Scholar] [CrossRef]
- Akhatov, I.S.; Konovalova, S.I. Regular and chaotic dynamics of a spherical bubble. J. Appl. Math. Mech. 2005, 69, 575–584. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Y.; Du, X. Stability mechanisms of oscillating vapor bubbles in acoustic fields. Ultrason. Sonochemistry 2018, 40, 808–814. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Chaotic oscillations of gas bubbles under dual-frequency acoustic excitation. Ultrason. Sonochemistry 2018, 40, 151–157. [Google Scholar] [CrossRef]
- Hegedűs, F.; Lauterborn, W.; Parlitz, U.; Mettin, R. Non-feedback technique to directly control multistability in nonlinear oscillators by dual-frequency driving: GPU accelerated topological analysis of a bubble in water. Nonlinear Dyn. 2018, 94, 273–293. [Google Scholar] [CrossRef]
- Klapcsik, K.; Hegedűs, F. Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochemistry 2019, 54, 256–273. [Google Scholar] [CrossRef]
- Klapcsik, K.; Hegedűs, F. The effect of high viscosity on the evolution of the bifurcation set of a periodically excited gas bubble. Chaos Solitons Fractals 2017, 104, 198–208. [Google Scholar] [CrossRef][Green Version]
- Kerboua, K.; Hamdaoui, O. Numerical investigation of the effect of dual frequency sonication on stable bubble dynamics. Ultrason. Sonochemistry 2018, 49, 325–332. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Oxidants Emergence under Dual-Frequency Sonication within Single Acoustic Bubble: Effects of Frequency Combinations. Iran. J. Chem. Chem. Eng. 2021, 40, 323–332. [Google Scholar] [CrossRef]
- Burdin, F.; Tsochatzidis, N.; Guiraud, P.; Wilhelm, A.; Delmas, H. Characterisation of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochemistry 1999, 6, 43–51. [Google Scholar] [CrossRef]
- Duraiswami, R.; Prabhukumar, S.; Chahine, G.L. Bubble counting using an inverse acoustic scattering method. J. Acoust. Soc. Am. 1998, 104, 2699–2717. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O.; Alghyamah, A. Acoustic frequency and optimum sonochemical production at single and multi-bubble scales: A modeling answer to the scaling dilemma. Ultrason. Sonochemistry 2021, 70, 105341. [Google Scholar] [CrossRef]
- Wayment, D.G.; Casadonte, D.J. Frequency effect on the sonochemical remediation of alachlor. Ultrason. Sonochemistry 2002, 9, 251–257. [Google Scholar] [CrossRef]
- Koda, S.; Kimura, T.; Kondo, T.; Mitome, H. A standard method to calibrate sonochemical efficiency of an individual reaction system. Ultrason. Sonochemistry 2003, 10, 149–156. [Google Scholar] [CrossRef]
- Mark, G.; Tauber, A.; Laupert, R.; Schuchmann, H.-P.; Schulz, D.; Mues, A.; von Sonntag, C. OH-radical formation by ultrasound in aqueous solution–Part II: Terephthalate and Fricke dosimetry and the influence of various conditions on the sonolytic yield. Ultrason. Sonochemistry 1998, 5, 41–52. [Google Scholar] [CrossRef]
- Chiha, M.; Hamdaoui, O.; Baup, S.; Gondrexon, N. Sonolytic degradation of endocrine disrupting chemical 4-cumylphenol in water. Ultrason. Sonochemistry 2011, 18, 943–950. [Google Scholar] [CrossRef]
- Didenko, Y.T.; Suslick, K.S. The energy efficiency of formation of photons, radicals and ions during single-bubble cavitation. Nature 2002, 418, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.Y.; Byun, K.-T.; Kwak, H.-Y. Temperature and pressure fields due to collapsing bubble under ultrasound. Chem. Eng. J. 2007, 132, 125–135. [Google Scholar] [CrossRef]
- Merouani, S.; Hamdaoui, O.; Haddad, B. Acoustic cavitation in 1-butyl-3-methylimidazolium bis(triflluoromethyl-sulfonyl)imide based ionic liquid. Ultrason. Sonochemistry 2018, 41, 143–155. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas-liquid systems. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Pandit, A.B.; Varley, J.; Thorpe, R.B.; Davidson, J. Measurement of bubble size distribution: An acoustic technique. Chem. Eng. Sci. 1992, 47, 1079–1089. [Google Scholar] [CrossRef]
- Xu, W.; Tzanakis, I.; Srirangam, P.; Terzi, S.; Mirihanage, W.U.; Eskin, D.G.; Mathiesen, R.H.; Horsfield, A.P.; Lee, P.D. In Situ Synchrotron Radiography of Ultrasound Cavitation in a Molten Al-10Cu Alloy. In Proceedings of the TMS 2015 Annual Meeting Supplemental Proceedings TMS (The Minerals, Metals & Materials Society), Orlando, FL, USA, 15–19 March 2015; pp. 61–66. [Google Scholar]
- Merouani, S.; Hamdaoui, O.; Rezgui, Y.; Guemini, M. Effects of ultrasound frequency and acoustic amplitude on the size of sonochemically active bubbles-Theoretical study. Ultrason Sonochemistry 2013, 20, 815–819. [Google Scholar] [CrossRef] [PubMed]
- Caruthers, J.W. Lognormal bubble size distributions. J. Acoust. Soc. Am. 2017, 142, 2534. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Ultrasonic waveform upshot on mass variation within single cavitation bubble: Investigation of physical and chemical transformations. Ultrason. Sonochemistry 2018, 42, 508–516. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Variation of Liquid Temperature at Bubble Wall near the Sonoluminescence Threshold. J. Phys. Soc. Jpn. 1996, 65, 2830–2840. [Google Scholar] [CrossRef]
- Fuster, D.; Hauke, G.; Dopazo, C. Influence of the accommodation coefficient on nonlinear bubble oscillations. J. Acoust. Soc. Am. 2010, 128, 5–10. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Sonochemistry in Green Processes: Modeling, Experiments, and Technology. In Sustainable Green Chemical Processes and Their Allied Applications; Springer: Cham, Switzerland, 2020; p. 603. [Google Scholar]
- Kerboua, K.; Hamdaoui, O. Sonochemical production of hydrogen: Enhancement by summed harmonics excitation. Chem. Phys. 2019, 519, 27–37. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Lee, J.; Kozuka, T.; Towata, A.; Iida, Y. The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions. J. Chem. Phys. 2008, 128, 184705. [Google Scholar] [CrossRef] [PubMed]


| r | Reaction r | Ar | br | Er/Rg (K) | ΔHr (kJ/mol) |
|---|---|---|---|---|---|
| 1 | H + O2 ⇒ O + ●OH | 1.92 × 108 | 0 | 8270 | 69.17 |
| 2 | O + H2 ⇒ H● + ●OH | 5.08 × 10−2 | 2.67 | 3166 | 8.23 |
| 3 | ●OH + H2 ⇒ H● + H2O | 2.18 × 102 | 1.51 | 1726 | −64.35 |
| 4 | ●OH + ●OH ⇒ H2O + O | 2.1 × 102 | 1.4 | 200 | −72.59 |
| 5 | H2 + M ⇒ H● + H● + M; Coef. H2: 2.5, H2O: 16.0 | 4.58 × 1013 | −1.4 | 52,500 | 444.47 |
| 6 | O + O + M ⇒ O2 + M; Coef. H2: 2.5, H2O: 16.0 | 6.17 × 103 | −0.5 | 0 | −505.4 |
| 7 | O + H● + M ⇒ ●OH + M; Coef. H2O: 5.0 | 4.72 × 105 | −1.0 | 0 | −436.23 |
| 8 | H● + ●OH + M ⇒ H2O + M; Coef. H2: 2.5, H2O: 16.0 | 2.25 × 1010 | −2.0 | 0 | −508.82 |
| 9 | H● + O2 + M ⇒ HO2● + M; Coef. H2: 2.5, H2O: 16.0 | 2.00 × 103 | 0 | −500 | −204.8 |
| 10 | H● + HO2● ⇒ O2 + H2 | 6.63 × 107 | 0 | 1070 | −239.67 |
| 11 | H● + HO2● ⇒ ●OH + ●OH | 1.69 × 108 | 0 | 440 | −162.26 |
| 12 | O + HO2● ⇒ O2 + ●OH | 1.81 × 107 | 0 | −200 | −231.85 |
| 13 | ●OH + HO2● ⇒ O2 + H2O | 1.45 × 1010 | −1.0 | 0 | −304.44 |
| 14 | HO2● + HO2● ⇒ O2 + H2O2 | 3.0 × 106 | 0 | 700 | −175.35 |
| 15 | H2O2 + M ⇒ ●OH + ●OH + M; Coef. H2: 2.5, H2O: 16.0 | 1.2 × 1011 | 0 | 22,900 | 217.89 |
| 16 | H2O2 + H● ⇒ H2O + ●OH | 3.2 × 108 | 0 | 4510 | −290.93 |
| 17 | H2O2 + H● ⇒ H2 + HO2● | 4.82 × 107 | 0 | 4000 | −64.32 |
| 18 | H2O2 + O ⇒ ●OH + HO2● | 9.55 | 2 | 2000 | −56.08 |
| 19 | H2O2 + ●OH ⇒ H2O + HO2● | 1.00 × 107 | 0 | 900 | −128.67 |
| 20 | O3 + M ⇒ O2 + O + M; Coef. O2: 1.64; Coef. O2: 1.63, H2O: 15 | 2.48 × 108 | 0 | 11,430 | 109.27 |
| 21 | O3 + O ⇒ O2 + O2 | 5.2 × 106 | 0 | 2090 | −396.14 |
| 22 | O3 + ●OH ⇒ O2 + HO2● | 7.8 × 105 | 0 | 960 | −164.92 |
| 23 | O3 + HO2● ⇒ O2 + O2 + ●OH | 1 × 105 | 0 | 1410 | −121.92 |
| 24 | O3 + H● ⇒ HO2● + O | 9 × 106 | 0.5 | 2010 | −135.65 |
| 25 | O3 + H● ⇒ O2 + ●OH | 1.6 × 107 | 0 | 0 | −96.2 |
| 26 | O + ●OH ⇒ H + O2 | 7.18 × 105 | 0.36 | −342 | −69.17 |
| 27 | H● + ●OH ⇒ O + H2 | 2.64 × 10−2 | 2.65 | 2245 | −8.23 |
| 28 | H● + H2O ⇒ ●OH + H2 | 1.02 × 103 | 1.51 | 9370 | 64.35 |
| 29 | H2O + O ⇒●OH + ●OH | 2.21 × 103 | 1.4 | 8368 | 72.59 |
| 30 | H● + H● + M ⇒ H2 + M; Coef. H2: 2.5, H2O: 16.0 | 2.45 × 108 | −1.78 | 480 | −444.47 |
| 31 | O2 + M ⇒ O + O + M; Coef. H2: 2.5, H2O: 16.0 | 1.58 × 1011 | −0.5 | 59,472 | 505.4 |
| 32 | ●OH + M ⇒ O + H● + M; Coef. H2O: 5.0 | 4.66 × 1011 | −0.65 | 51,200 | 436.23 |
| 33 | H2O + M ⇒ H● + ●OH + M; Coef. H2: 2.5, H2O: 16.0 | 1.96 × 1016 | −1.62 | 59,700 | 508.82 |
| 34 | HO2● + M ⇒ H● + O2 + M; Coef. H2: 2.5, H2O: 16.0 | 2.46 × 109 | 0 | 24,300 | 204.8 |
| 35 | O2 + H2 ⇒ H● + HO2● | 2.19 × 107 | 0.28 | 28,390 | 239.67 |
| 36 | ●OH + ●OH ⇒ H● + HO2● | 1.08 × 105 | 0.61 | 18,230 | 162.26 |
| 37 | O2 + ●OH ⇒ O + HO2● | 3.1 × 106 | 0.26 | 26,083 | 231.85 |
| 38 | O2 + H2O ⇒ ●OH + HO2● | 2.18 × 1010 | −0.72 | 34,813 | 304.44 |
| 39 | O2 + H2O2 ⇒ HO2● + HO2● | 4.53 × 108 | −0.39 | 19,700 | 175.35 |
| 40 | ●OH + ●OH + M ⇒ H2O2 + M; Coef. H2: 2.5, H2O: 16.0 | 9.0 × 10−1 | 0.90 | −3050 | −217.89 |
| 41 | H2O + ●OH ⇒ H2O2 + H● | 1.14 × 103 | 1.36 | 38,180 | 290.93 |
| 42 | H2 + HO2● ⇒ H2O2 + H● | 1.41 × 105 | 0.66 | 12,320 | 64.32 |
| 43 | ●OH + HO2● ⇒ H2O2 + O | 4.62 × 10−3 | 2.75 | 9277 | 56.08 |
| 44 | H2O + HO2● ⇒ H2O2 + ●OH | 2.8 × 107 | 0 | 16,500 | 128.67 |
| 45 | O2 + O + M ⇒ O3 + M; Coef. O2: 1.64; Coef. O2: 1.63, H2O: 15 | 4.1 | 0 | −1057 | −109.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerboua, K.; Hamdaoui, O.; Alghyamah, A. Numerical Characterization of Acoustic Cavitation Bubbles with Respect to the Bubble Size Distribution at Equilibrium. Processes 2021, 9, 1546. https://doi.org/10.3390/pr9091546
Kerboua K, Hamdaoui O, Alghyamah A. Numerical Characterization of Acoustic Cavitation Bubbles with Respect to the Bubble Size Distribution at Equilibrium. Processes. 2021; 9(9):1546. https://doi.org/10.3390/pr9091546
Chicago/Turabian StyleKerboua, Kaouther, Oualid Hamdaoui, and Abdulaziz Alghyamah. 2021. "Numerical Characterization of Acoustic Cavitation Bubbles with Respect to the Bubble Size Distribution at Equilibrium" Processes 9, no. 9: 1546. https://doi.org/10.3390/pr9091546
APA StyleKerboua, K., Hamdaoui, O., & Alghyamah, A. (2021). Numerical Characterization of Acoustic Cavitation Bubbles with Respect to the Bubble Size Distribution at Equilibrium. Processes, 9(9), 1546. https://doi.org/10.3390/pr9091546







