Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review
Abstract
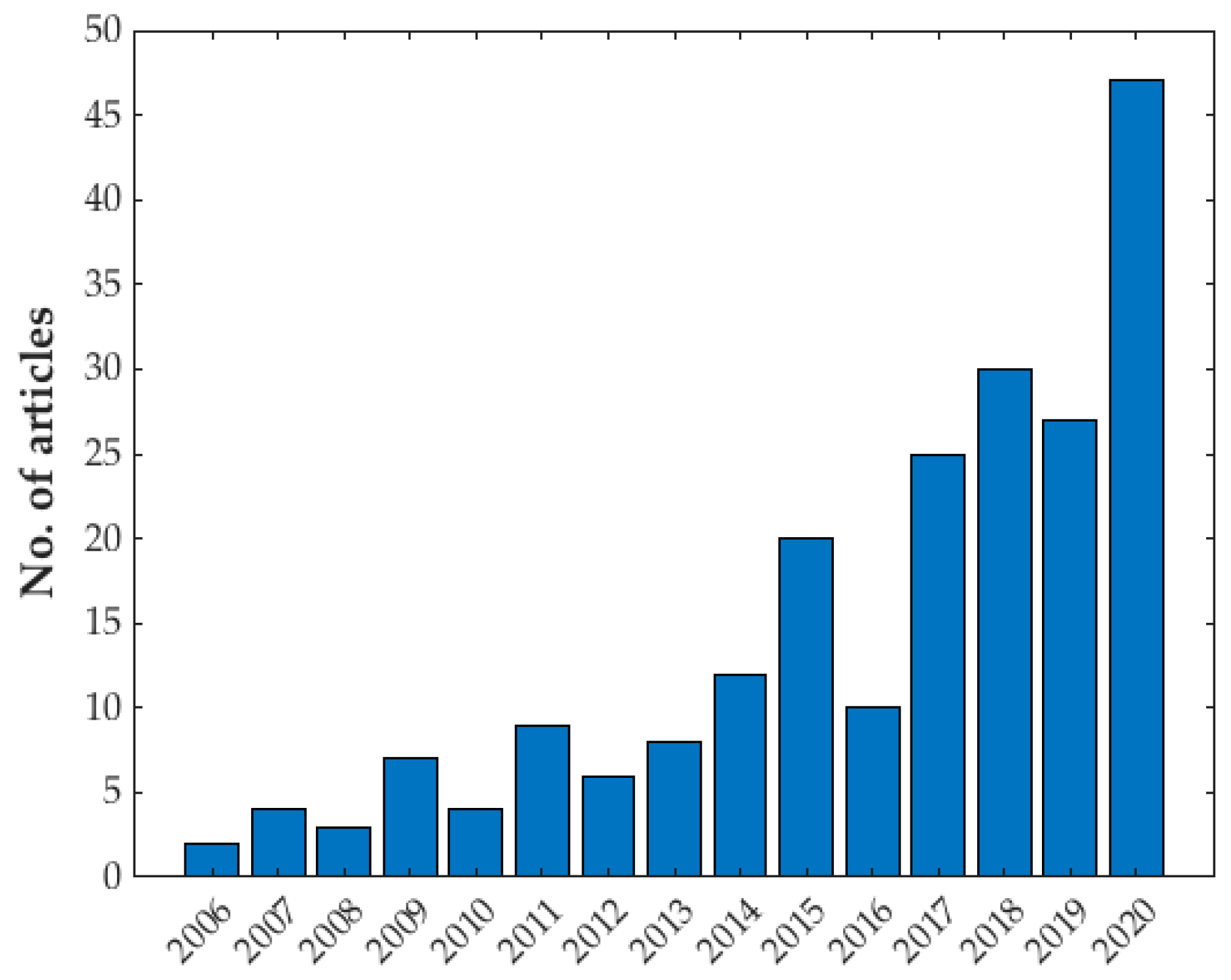
1. Introduction
2. Conventional Approach
2.1. CFD-DEM Modelling for Fluidized Beds
2.2. Contact Models
2.3. Hydrodynamic Interaction Models
2.4. Cohesive Forces
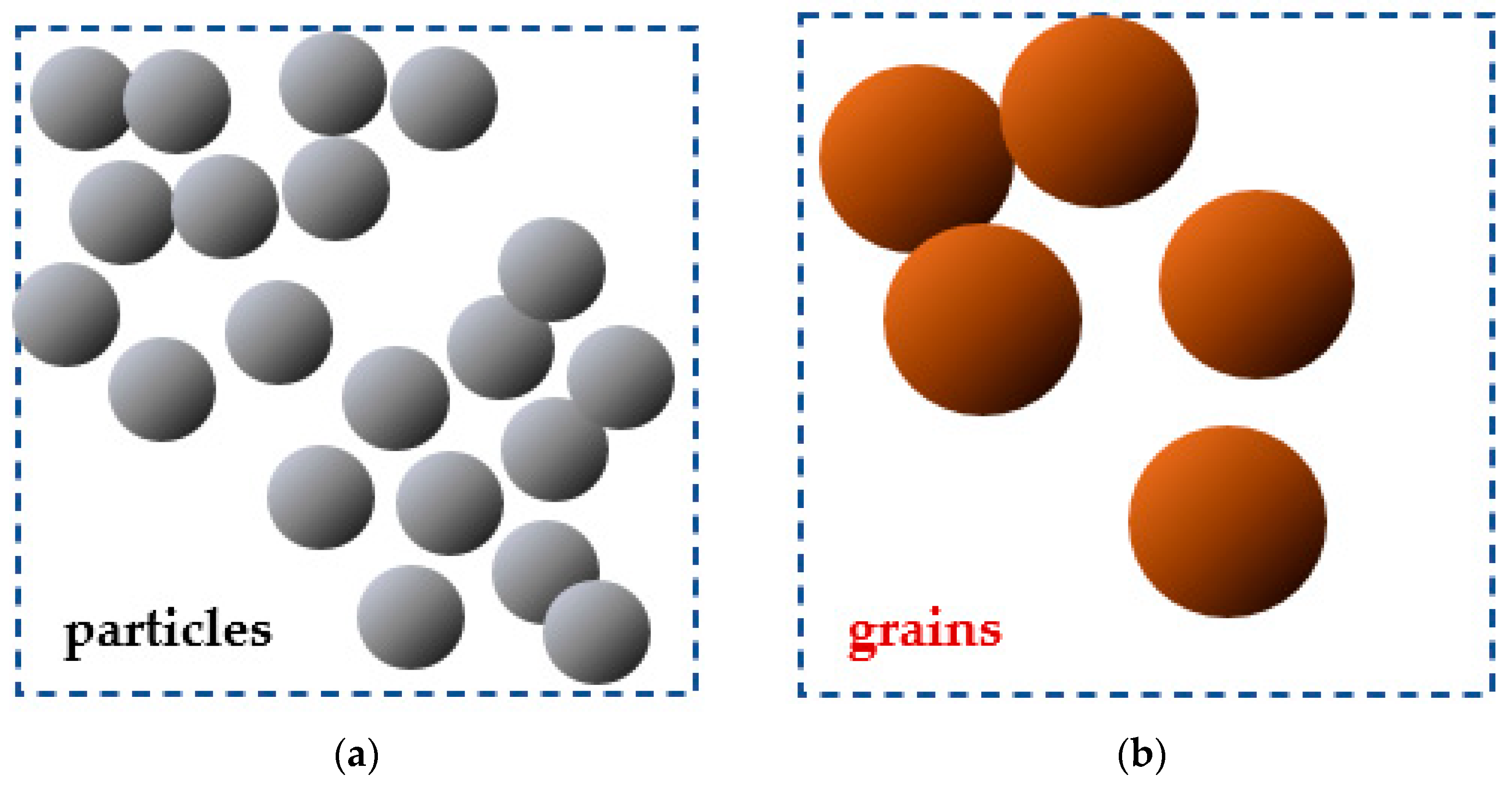
3. From Real to Computational Particles (Grains)
3.1. Context of the Early Coarse-Graining Approaches
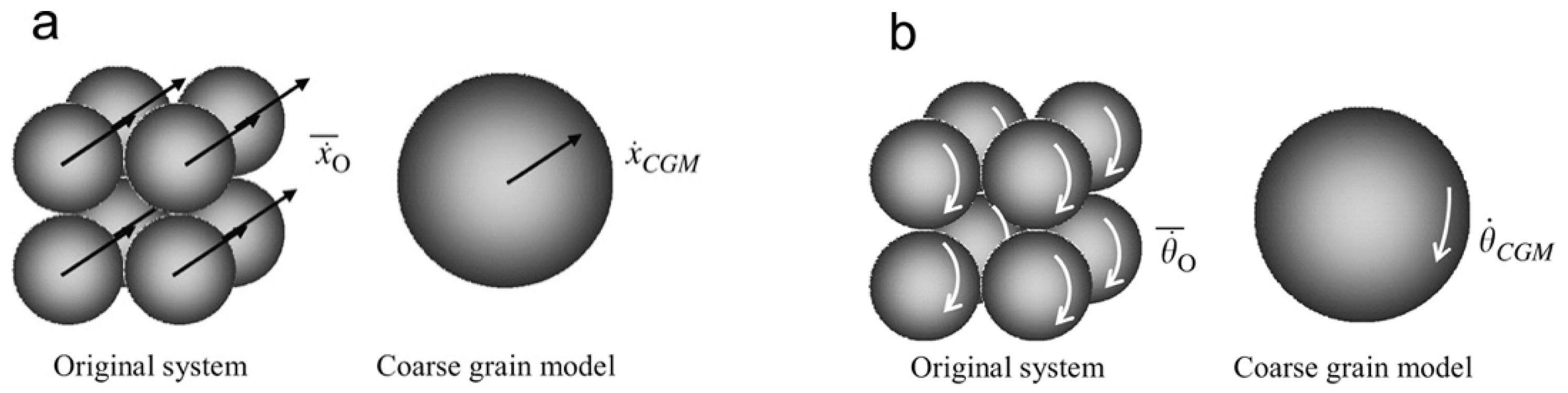
3.2. General Particle and Bed Properties
3.2.1. Compact Grains
3.2.2. Porous Grains
3.3. Contact Interaction: Linear Spring-Dashpot-Slider Model
3.3.1. Constant Absolute Overlap Models
3.3.2. Constant Relative Overlap Models
3.3.3. Contact between Porous Grains
3.3.4. Summary of Coarse Graining Approaches for the Linear Model
3.4. Contact Interaction: Hertz-Based Modelling
3.5. Hydrodynamic (Drag and Pressure Gradient) Forces
3.6. Cohesive Force Modelling
4. Computational Savings
5. Applications to Bubbling/Spouted Beds
5.1. Bubbling/Spouted/Liquid Fluidized Beds
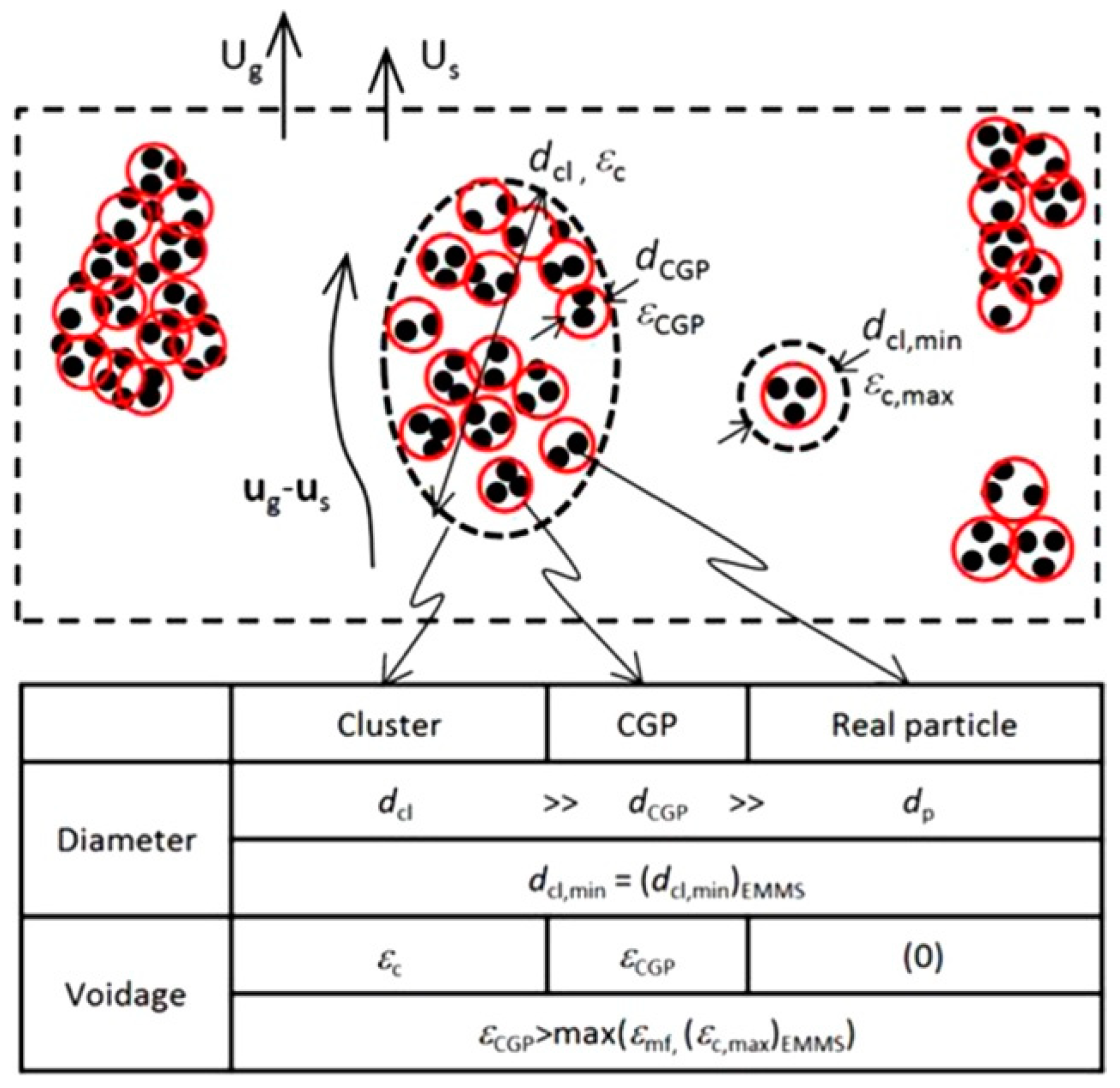
5.2. Circulating Fluidized Beds and Cyclones
6. Recent Promising Extensions and Open Problems
6.1. Physical Models
6.2. Computational Improvements
6.3. Open Problems
- Coarse graining of non-spherical particles;
- Rotational motion and rolling friction for applications e.g., in cyclones;
- Further testing on multi-component polydisperse particles, with coarse-graining of polydisperse drag;
- Hydrodynamic interactions in dilute regions (collisional regime) at extreme coarse graining degrees and with coarse grids;
- Further development of adaptive coarse graining;
- Scaling for mass transfer, chemical reactions and other cohesive interactions, e.g., triboelectric charging.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Units | Description |
| diameter | ||
| Sauter mean diameter | ||
| - | coefficient of restitution | |
| elastic energy | ||
| - | coarse grain factor | |
| - | function of the coefficient of restitution in Equation (76) | |
| generalized buoyancy force | ||
| contact forces | ||
| drag force | ||
| fluid-particle interphase momentum transfer per unit volume | ||
| gravity force | ||
| hydrodynamic force | ||
| cohesive/adhesive force | ||
| particle shear modulus | ||
| gravity acceleration | ||
| Hamaker constant | ||
| - | heterogeneity index | |
| moment of inertia | ||
| inter-particle distance | ||
| spring stiffness constant | ||
| mass | ||
| total solid mass | ||
| - | number | |
| - | number of contacts | |
| - | coarse grain number | |
| - | Number of particles | |
| pressure | ||
| contact heat transfer | ||
| particle-fluid-wall heat transfer | ||
| radius | ||
| separation distance | ||
| rupture distance | ||
| torque contributions generated by non-collinear collisions | ||
| fluid-particle torque | ||
| polling friction torque | ||
| gas velocity | ||
| particle velocity | ||
| volume | ||
| initial collision velocity | ||
| final collision velocity | ||
| liquid bridge volume | ||
| total volume mass | ||
| work of adhesion per unit contact area | ||
| - | volume fraction of the particle size class | |
| - | i-th local polydispersion index | |
| time step | ||
| Greek Symbols | ||
| angular acceleration | ||
| coefficient in the drag expression | ||
| displacements between the contacting particles | ||
| - | void fraction | |
| - | specification coefficient in polydisperse drag | |
| dashpot damping coefficient | ||
| Hertz dissipative coefficient in Bierwisch et al. [24] | ||
| Hertz dissipative coefficient | ||
| angle | ||
| - | tangential to normal spring stiffness ratio | |
| - | coulomb friction coefficient | |
| gas viscosity | ||
| - | particle Poisson’s ratio | |
| density | ||
| stress deviatoric tensor | ||
| angular velocity | ||
| Subscripts | ||
| grain in EMMS-DPM model | ||
| equivalent | ||
| fluid | ||
| grain (i.e., parcel) | ||
| internal “hard-core” diameter | ||
| i-th, j-th particle | ||
| k | cohesive | |
| l | liquid bridge | |
| minimization fluidization | ||
| normal | ||
| particle | ||
| tangential | ||
References
- Grace, J.R.; Bi, X.; Ellis, N. Essentials of Fluidization Technology; Wiley-VCH: Weinheim, Germany, 2020; ISBN 9783527340644. [Google Scholar]
- Figaro, S.; Pereira, U.; Rada, H.; Semenzato, N.; Pouchoulin, D.; Paullier, P.; Dufresne, M.; Legallais, C. Optimizing the Fluidized Bed Bioreactor as an External Bioartificial Liver. Int. J. Artif. Organs 2017, 40, 196–203. [Google Scholar] [CrossRef] [PubMed]
- Naghib, S.D.; Pandolfi, V.; Pereira, U.; Girimonte, R.; Curcio, E.; Di Maio, F.P.; Legallais, C.; Di Renzo, A. Expansion properties of alginate beads as cell carrier in the fluidized bed bioartificial liver. Powder Technol. 2017, 316, 711–717. [Google Scholar] [CrossRef]
- Anderson, T.B.; Jackson, R. A Fluid Mechanical Description of Fluidized Beds. Equations of Motion. Ind. Eng. Chem. Fundam. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press Inc.: Boston, MA, USA, 1994; ISBN 0122824709. [Google Scholar]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Deen, N.G.; van Sint Annaland, M.; van der Hoef, M.A.; Kuipers, J.A.M. Review of discrete particle modeling of fluidized beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Yu, A.B.; Xu, B.H. Particle-scale modelling of gas-solid flow in fluidisation. J. Chem. Technol. Biotechnol. 2003, 78, 111–121. [Google Scholar] [CrossRef]
- van der Hoef, M.A.; van Sint Annaland, M.; Deen, N.G.; Kuipers, J.A.M. Numerical Simulation of Dense Gas-Solid Fluidized Beds: A Multiscale Modeling Strategy. Annu. Rev. Fluid Mech. 2008, 40, 47–70. [Google Scholar] [CrossRef]
- Golshan, S.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N.; Blais, B.; Kuipers, J.A.M. Review and implementation of CFD-DEM applied to chemical process systems. Chem. Eng. Sci. 2020, 221, 115646. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Pietsch, S.; Dosta, M.; Heinrich, S. Possibilities and Limits of Computational Fluid Dynamics–Discrete Element Method Simulations in Process Engineering: A Review of Recent Advancements and Future Trends. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 397–422. [Google Scholar] [CrossRef]
- Kuang, S.; Zhou, M.; Yu, A. CFD-DEM modelling and simulation of pneumatic conveying: A review. Powder Technol. 2020, 365, 186–207. [Google Scholar] [CrossRef]
- Tsuji, T.; Yabumoto, K.; Tanaka, T. Spontaneous structures in three-dimensional bubbling gas-fluidized bed by parallel DEM–CFD coupling simulation. Powder Technol. 2008, 184, 132–140. [Google Scholar] [CrossRef]
- Jajcevic, D.; Siegmann, E.; Radeke, C.; Khinast, J.G. Large-scale CFD–DEM simulations of fluidized granular systems. Chem. Eng. Sci. 2013, 98, 298–310. [Google Scholar] [CrossRef]
- Ge, W.; Wang, L.; Xu, J.; Chen, F.; Zhou, G.; Lu, L.; Chang, Q.; Li, J. Discrete simulation of granular and particle-fluid flows: From fundamental study to engineering application. Rev. Chem. Eng. 2017, 33, 551–623. [Google Scholar] [CrossRef]
- Lu, L.; Xu, J.; Ge, W.; Yue, Y.; Liu, X.; Li, J. EMMS-based discrete particle method (EMMS–DPM) for simulation of gas–solid flows. Chem. Eng. Sci. 2014, 120, 67–87. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Stepanek, F.; Munjiza, A. A study on adjusted contact force laws for accelerated large scale discrete element simulations. Particuology 2010, 8, 161–175. [Google Scholar] [CrossRef]
- Sakano, M.; Yaso, T.; Nakanishi, H. Numerical simulation of two-dimensional fluidized bed using discrete element method with imaginary sphere model. Jpn. J. Multiph. Flow 2000, 14, 66–73. [Google Scholar] [CrossRef]
- Kuwagi, K.; Takeda, H.; Horio, M. Similar Particle Assembly (SPA) Model. An Approach to Large-Scale Discrete Element (DEM) Simulation. In Proceedings of the Fluidization XI, Ischia, Italy, 9–14 May 2004; pp. 243–250. [Google Scholar]
- Kuwagi, K.; Mokhtar, M.A.; Okada, H.; Hirano, H.; Takami, T. Numerical Experiment of Thermoset Particles in Surface Modification System with Discrete Element Method (Quantization of Cohesive Force Between Particles by Agglomerates Analysis). Numer. Heat Transf. Part A Appl. 2009, 56, 647–664. [Google Scholar] [CrossRef]
- Sakai, M.; Koshizuka, S.; Takeda, H. Development of Advanced Representative Particle Model-Application of DEM Simulation to Large-scale Powder Systems. J. Soc. Powder Technol. Jpn. 2006, 43, 4–12. [Google Scholar] [CrossRef][Green Version]
- Patankar, N.A.; Joseph, D.D. Modeling and numerical simulation of particulate flows by the Eulerian–Lagrangian approach. Int. J. Multiph. Flow 2001, 27, 1659–1684. [Google Scholar] [CrossRef]
- Sakai, M.; Koshizuka, S. Large-scale discrete element modeling in pneumatic conveying. Chem. Eng. Sci. 2009, 64, 533–539. [Google Scholar] [CrossRef]
- Bierwisch, C.; Kraft, T.; Riedel, H.; Moseler, M. Three-dimensional discrete element models for the granular statics and dynamics of powders in cavity filling. J. Mech. Phys. Solids 2009, 57, 10–31. [Google Scholar] [CrossRef]
- Radl, S.; Radeke, C.; Khinast, J.G.; Sundaresan, S. Parcel-Based Approach For The Simulation Of Gas-Particle Flows. In Proceedings of the 8th Interantional Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 21–23 June 2011. paper no. CFD11-124. [Google Scholar]
- Hilton, J.E.; Cleary, P.W. Comparison of resolved and coarse grain DEM models for gas flow through particle beds. In Proceedings of the Ninth International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 10–12 December 2012; pp. 1–6. [Google Scholar]
- Hilton, J.E.; Cleary, P.W. Comparison of non-cohesive resolved and coarse grain DEM models for gas flow through particle beds. Appl. Math. Model. 2014, 38, 4197–4214. [Google Scholar] [CrossRef]
- Di Maio, F.P.; Di Renzo, A. Verification of scaling criteria for bubbling fluidized beds by DEM–CFD simulation. Powder Technol. 2013, 248, 161–171. [Google Scholar] [CrossRef]
- van Ommen, J.R.; Teuling, M.; Nijenhuis, J.; van Wachem, B.G.M. Computational validation of the scaling rules for fluidized beds. Powder Technol. 2006, 163, 32–40. [Google Scholar] [CrossRef]
- Feng, Y.T.; Owen, D.R.J. Discrete element modelling of large scale particle systems—I: Exact scaling laws. Comput. Part. Mech. 2014, 1, 159–168. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Ranjith, P.G.; Yang, W.M.; Shi, S.S.; Wei, C.C.; Li, Z.H. A new set of scaling relationships for DEM-CFD simulations of fluid–solid coupling problems in saturated and cohesiveless granular soils. Comput. Part. Mech. 2019, 6, 657–669. [Google Scholar] [CrossRef]
- Baran, O.; Kodl, P.; Aglave, R. DEM Simulations of Fluidized Bed using a Scaled Particle Approach. In Proceedings of the 2013 AIChE Annual Meeting, San Francisco, CA, USA, 3–8 November 2013. [Google Scholar]
- Jurtz, N.; Kruggel-Emden, H.; Baran, O.; Aglave, R.; Cocco, R.; Kraume, M. Impact of Contact Scaling and Drag Calculation on the Accuracy of Coarse-Grained Discrete Element Method. Chem. Eng. Technol. 2020, 43, 1959–1970. [Google Scholar] [CrossRef]
- Ostermeier, P.; Fischer, F.; Fendt, S.; DeYoung, S.; Spliethoff, H. Coarse-grained CFD-DEM simulation of biomass gasification in a fluidized bed reactor. Fuel 2019, 255, 115790. [Google Scholar] [CrossRef]
- Stroh, A.; Daikeler, A.; Nikku, M.; May, J.; Alobaid, F.; von Bohnstein, M.; Ströhle, J.; Epple, B. Coarse grain 3D CFD-DEM simulation and validation with capacitance probe measurements in a circulating fluidized bed. Chem. Eng. Sci. 2019, 196, 37–53. [Google Scholar] [CrossRef]
- Dietiker, J. MFIX 20.4 Release Announcement. Available online: https://mfix.netl.doe.gov/mfix-20-4-release-announcement/ (accessed on 20 December 2020).
- Weinhart, T.; Labra, C.; Luding, S.; Ooi, J.Y. Influence of coarse-graining parameters on the analysis of DEM simulations of silo flow. Powder Technol. 2015, 293, 138–148. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. Diffusion-based coarse graining in hybrid continuum–discrete solvers: Theoretical formulation and a priori tests. Int. J. Multiph. Flow 2015, 77, 142–157. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Di Maio, F.P.; Di Renzo, A. Modelling Particle Contacts in Distinct Element SimulationsLinear and Non-Linear Approach. Chem. Eng. Res. Des. 2005, 83, 1287–1297. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. An improved integral non-linear model for the contact of particles in distinct element simulations. Chem. Eng. Sci. 2005, 60, 1303–1312. [Google Scholar] [CrossRef]
- Antypov, D.; Elliott, J.A. On an analytical solution for the damped Hertzian spring. Europhys. Lett. 2011, 94, 50004. [Google Scholar] [CrossRef]
- Queteschiner, D.; Lichtenegger, T.; Pirker, S.; Schneiderbauer, S. Multi-level coarse-grain model of the DEM. Powder Technol. 2018, 338, 614–624. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Beetstra, R.; van der Hoef, M.A.; Kuipers, J.A.M. Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 2007, 53, 489–501. [Google Scholar] [CrossRef]
- Holloway, W.; Yin, X.; Sundaresan, S. Fluid-particle drag in inertial polydisperse gas-solid suspensions. AIChE J. 2009, 56, 1995–2004. [Google Scholar] [CrossRef]
- Yin, X.; Sundaresan, S. Fluid-particle drag in low-Reynolds-number polydisperse gas-solid suspensions. AIChE J. 2009, 55, 1352–1368. [Google Scholar] [CrossRef]
- Rong, L.W.; Dong, K.J.; Yu, A.B. Lattice-Boltzmann simulation of fluid flow through packed beds of uniform spheres: Effect of porosity. Chem. Eng. Sci. 2013, 99, 44–58. [Google Scholar] [CrossRef]
- Cello, F.; Di Renzo, A.; Di Maio, F.P. A semi-empirical model for the drag force and fluid–particle interaction in polydisperse suspensions. Chem. Eng. Sci. 2010, 65, 3128–3139. [Google Scholar] [CrossRef]
- Tang, Y.; Peters, E.A.J.F.; Kuipers, J.A.M.; Kriebitzsch, S.H.L.; Van der Hoef, M.A. A new drag correlation from fully resolved simulations of flow past monodisperse static arrays of spheres. AIChE J. 2015, 61, 688–698. [Google Scholar] [CrossRef]
- Rong, L.W.; Dong, K.J.; Yu, A.B. Lattice-Boltzmann simulation of fluid flow through packed beds of spheres: Effect of particle size distribution. Chem. Eng. Sci. 2014, 116, 508–523. [Google Scholar] [CrossRef]
- Norouzi, H.R.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2016; ISBN 978-1-119-00513-1. [Google Scholar]
- Liu, P.; LaMarche, C.Q.; Kellogg, K.M.; Hrenya, C.M. Fine-particle defluidization: Interaction between cohesion, Young’s modulus and static bed height. Chem. Eng. Sci. 2016, 145, 266–278. [Google Scholar] [CrossRef]
- Breuninger, P.; Weis, D.; Behrendt, I.; Grohn, P.; Krull, F.; Antonyuk, S. CFD–DEM simulation of fine particles in a spouted bed apparatus with a Wurster tube. Particuology 2019, 42, 114–125. [Google Scholar] [CrossRef]
- Grohn, P.; Lawall, M.; Oesau, T.; Heinrich, S.; Antonyuk, S. CFD-DEM Simulation of a Coating Process in a Fluidized Bed Rotor Granulator. Processes 2020, 8, 1090. [Google Scholar] [CrossRef]
- Pei, C.; Wu, C.-Y.; England, D.; Byard, S.; Berchtold, H.; Adams, M. Numerical analysis of contact electrification using DEM–CFD. Powder Technol. 2013, 248, 34–43. [Google Scholar] [CrossRef]
- Alfano, F.O.; Di Renzo, A.; Di Maio, F.P.; Ghadiri, M. Computational analysis of triboelectrification due to aerodynamic powder dispersion. Powder Technol. 2021, 382, 491–504. [Google Scholar] [CrossRef]
- Mokhtar, M.A.; Kuwagi, K.; Takami, T.; Hirano, H.; Horio, M. Validation of the similar particle assembly (SPA) model for the fluidization of Geldart’s group A and D particles. AIChE J. 2012, 58, 87–98. [Google Scholar] [CrossRef]
- Washino, K.; Hsu, C.-H.; Kawaguchi, T.; Tsuji, Y. Similarity Model for DEM Simulation of Fluidized Bed. J. Soc. Powder Technol. Jpn. 2007, 44, 198–205. [Google Scholar] [CrossRef]
- Sakai, M.; Yamada, Y.; Shigeto, Y.; Shibata, K.; Kawasaki, V.M.; Koshizuka, S. Large-scale discrete element modeling in a fluidized bed. Int. J. Numer. Methods Fluids 2010, 64, 1319–1335. [Google Scholar] [CrossRef]
- Sakai, M.; Abe, M.; Shigeto, Y.; Mizutani, S.; Takahashi, H.; Viré, A.; Percival, J.R.; Xiang, J.; Pain, C.C. Verification and validation of a coarse grain model of the DEM in a bubbling fluidized bed. Chem. Eng. J. 2014, 244, 33–43. [Google Scholar] [CrossRef]
- Sakai, M.; Takahashi, H.; Pain, C.C.; Latham, J.-P.P.; Xiang, J. Study on a large-scale discrete element model for fine particles in a fluidized bed. Adv. Powder Technol. 2012, 23, 673–681. [Google Scholar] [CrossRef]
- Sakai, M. How Should the Discrete Element Method Be Applied in Industrial Systems?: A Review. KONA Powder Part. J. 2016, 33, 169–178. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, T.; Sakai, M.; Shen, Y. Particle-scale study of spout deflection in a flat-bottomed spout fluidized bed. Chem. Eng. Sci. 2019, 205, 121–133. [Google Scholar] [CrossRef]
- Mori, Y.; Wu, C.-Y.Y.; Sakai, M. Validation study on a scaling law model of the DEM in industrial gas-solid flows. Powder Technol. 2019, 343, 101–112. [Google Scholar] [CrossRef]
- Cai, R.; Zhao, Y. An experimentally validated coarse-grain DEM study of monodisperse granular mixing. Powder Technol. 2020, 361, 99–111. [Google Scholar] [CrossRef]
- Benyahia, S.; Galvin, J.E. Estimation of Numerical Errors Related to Some Basic Assumptions in Discrete Particle Methods. Ind. Eng. Chem. Res. 2010, 49, 10588–10605. [Google Scholar] [CrossRef]
- Snider, D. An Incompressible Three-Dimensional Multiphase Particle-in-Cell Model for Dense Particle Flows. J. Comput. Phys. 2001, 170, 523–549. [Google Scholar] [CrossRef]
- Lu, L.; Yoo, K.; Benyahia, S. Coarse-Grained-Particle Method for Simulation of Liquid–Solids Reacting Flows. Ind. Eng. Chem. Res. 2016, 55, 10477–10491. [Google Scholar] [CrossRef]
- Lu, L.; Xu, Y.; Li, T.; Benyahia, S. Assessment of different coarse graining strategies to simulate polydisperse gas-solids flow. Chem. Eng. Sci. 2018, 179, 53–63. [Google Scholar] [CrossRef]
- Nasato, D.S.; Goniva, C.; Pirker, S.; Kloss, C. Coarse graining for large-scale DEM simulations of particle flow—An investigation on contact and cohesion models. In Procedia Engineering; Elsevier: Amsterdam, The Netherlands, 2015; Volume 102, pp. 1484–1490. [Google Scholar]
- O’Rourke, P.J.; Snider, D.M. An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets. Chem. Eng. Sci. 2010, 65, 6014–6028. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of discrete element model parameters for cohesionless and cohesive solid. Powder Technol. 2016, 293, 130–137. [Google Scholar] [CrossRef]
- Chu, K.; Chen, J.; Yu, A. Applicability of a coarse-grained CFD–DEM model on dense medium cyclone. Miner. Eng. 2016, 90, 43–54. [Google Scholar] [CrossRef]
- Lu, B.; Wang, W.; Li, J. Eulerian simulation of gas–solid flows with particles of Geldart groups A, B and D using EMMS-based meso-scale model. Chem. Eng. Sci. 2011, 66, 4624–4635. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Luo, C.; Moghtaderi, B. Influence of void fraction calculation on fidelity of CFD-DEM simulation of gas-solid bubbling fluidized beds. AIChE J. 2014, 60, 2000–2018. [Google Scholar] [CrossRef]
- Radl, S.; Sundaresan, S. A drag model for filtered Euler–Lagrange simulations of clustered gas–particle suspensions. Chem. Eng. Sci. 2014, 117, 416–425. [Google Scholar] [CrossRef]
- Lu, L.; Konan, A.; Benyahia, S. Influence of grid resolution, parcel size and drag models on bubbling fluidized bed simulation. Chem. Eng. J. 2017, 326, 627–639. [Google Scholar] [CrossRef]
- Mu, L.; Buist, K.A.; Kuipers, J.A.M.; Deen, N.G. Scaling method of CFD-DEM simulations for gas-solid flows in risers. Chem. Eng. Sci. X 2020, 6, 100054. [Google Scholar] [CrossRef]
- Ozel, A.; Kolehmainen, J.; Radl, S.; Sundaresan, S. Fluid and particle coarsening of drag force for discrete-parcel approach. Chem. Eng. Sci. 2016, 155, 258–267. [Google Scholar] [CrossRef]
- Hærvig, J.; Kleinhans, U.; Wieland, C.; Spliethoff, H.; Jensen, A.L.; Sørensen, K.; Condra, T.J. On the adhesive JKR contact and rolling models for reduced particle stiffness discrete element simulations. Powder Technol. 2017, 319, 472–482. [Google Scholar] [CrossRef]
- Chen, X.; Elliott, J.A. On the scaling law of JKR contact model for coarse-grained cohesive particles. Chem. Eng. Sci. 2020, 227, 115906. [Google Scholar] [CrossRef]
- Chan, E.L.; Washino, K. Coarse grain model for DEM simulation of dense and dynamic particle flow with liquid bridge forces. Chem. Eng. Res. Des. 2018, 132, 1060–1069. [Google Scholar] [CrossRef]
- Tausendschön, J.; Kolehmainen, J.; Sundaresan, S.; Radl, S. Coarse graining Euler-Lagrange simulations of cohesive particle fluidization. Powder Technol. 2020, 364, 167–182. [Google Scholar] [CrossRef]
- Takabatake, K.; Mori, Y.; Khinast, J.G.; Sakai, M. Numerical investigation of a coarse-grain discrete element method in solid mixing in a spouted bed. Chem. Eng. J. 2018, 346, 416–426. [Google Scholar] [CrossRef]
- Lu, L.; Benyahia, S.; Li, T. An efficient and reliable predictive method for fluidized bed simulation. AIChE J. 2017, 63, 5320–5334. [Google Scholar] [CrossRef]
- Lu, L.; Gopalan, B.; Benyahia, S. Assessment of Different Discrete Particle Methods Ability To Predict Gas-Particle Flow in a Small-Scale Fluidized Bed. Ind. Eng. Chem. Res. 2017, 56, 7865–7876. [Google Scholar] [CrossRef]
- Hu, C.; Luo, K.; Wang, S.; Sun, L.; Fan, J. Influences of operating parameters on the fluidized bed coal gasification process: A coarse-grained CFD-DEM study. Chem. Eng. Sci. 2019, 195, 693–706. [Google Scholar] [CrossRef]
- Qi, T.; Lei, T.; Yan, B.; Chen, G.; Li, Z.; Fatehi, H.; Wang, Z.; Bai, X.-S. Biomass steam gasification in bubbling fluidized bed for higher-H2 syngas: CFD simulation with coarse grain model. Int. J. Hydrogen Energy 2019, 44, 6448–6460. [Google Scholar] [CrossRef]
- Lu, L.; Gao, X.; Shahnam, M.; Rogers, W.A. Bridging particle and reactor scales in the simulation of biomass fast pyrolysis by coupling particle resolved simulation and coarse grained CFD-DEM. Chem. Eng. Sci. 2020, 216, 115471. [Google Scholar] [CrossRef]
- Lu, L.; Gao, X.; Gel, A.; Wiggins, G.M.; Crowley, M.; Pecha, B.; Shahnam, M.; Rogers, W.A.; Parks, J.; Ciesielski, P.N. Investigating biomass composition and size effects on fast pyrolysis using global sensitivity analysis and CFD simulations. Chem. Eng. J. 2020, 127789. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Gao, X.; Xu, Y.; Shahnam, M.; Rogers, W.A. Coupling reduced-order modeling and coarse-grained CFD-DEM to accelerate coal gasifier simulation and optimization. AIChE J. 2021, 67, e17030. [Google Scholar] [CrossRef]
- Lu, L.; Yu, J.; Gao, X.; Xu, Y.; Shahnam, M.; Rogers, W.A. Experimental and numerical investigation of sands and Geldart A biomass co-fluidization. AIChE J. 2020, 66, e16969. [Google Scholar] [CrossRef]
- Lu, L.; Gao, X.; Shahnam, M.; Rogers, W.A. Coarse grained computational fluid dynamic simulation of sands and biomass fluidization with a hybrid drag. AIChE J. 2020, 66, e16867. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Lu, L.; Gao, X.; Tebianian, S.; Grace, J.R.; Chaouki, J.; Leadbeater, T.W.; Jafari, R.; Parker, D.J.; et al. Development and confirmation of a simple procedure to measure solids distribution in fluidized beds using tracer particles. Chem. Eng. Sci. 2020, 217, 115501. [Google Scholar] [CrossRef]
- Jiang, Z.; Rai, K.; Tsuji, T.; Washino, K.; Tanaka, T.; Oshitani, J. Upscaled DEM-CFD model for vibrated fluidized bed based on particle-scale similarities. Adv. Powder Technol. 2020, 31, 4598–4618. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Ge, W.; Lu, B.; Wang, W. Long-time simulation of catalytic MTO reaction in a fluidized bed reactor with a coarse-grained discrete particle method—EMMS-DPM. Chem. Eng. J. 2020, 389, 124135. [Google Scholar] [CrossRef]
- Lan, B.; Xu, J.; Zhao, P.; Zou, Z.; Zhu, Q.; Wang, J. Long-time coarse-grained CFD-DEM simulation of residence time distribution of polydisperse particles in a continuously operated multiple-chamber fluidized bed. Chem. Eng. Sci. 2020, 219, 115599. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Pietsch, S.; Höfert, M.; Schönherr, M.; Heinrich, S.; Kleine Jäger, F. Influence of gas inflow modelling on CFD-DEM simulations of three-dimensional prismatic spouted beds. Powder Technol. 2018, 329, 167–180. [Google Scholar] [CrossRef]
- Otto, H.; Kerst, K.; Roloff, C.; Janiga, G.; Katterfeld, A. CFD–DEM simulation and experimental investigation of the flow behavior of lunar regolith JSC-1A. Particuology 2018, 40, 34–43. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Alghamdi, Y.A.; Shah, K.; Luo, C.; Moghtaderi, B. CFD–DEM simulation of solid circulation rate in the cold flow model of chemical looping systems. Chem. Eng. Res. Des. 2015, 95, 262–280. [Google Scholar] [CrossRef]
- Nikolopoulos, A.; Stroh, A.; Zeneli, M.; Alobaid, F.; Nikolopoulos, N.; Ströhle, J.; Karellas, S.; Epple, B.; Grammelis, P. Numerical investigation and comparison of coarse grain CFD-DEM and TFM in the case of a 1 MWth fluidized bed carbonator simulation. Chem. Eng. Sci. 2017, 163, 189–205. [Google Scholar] [CrossRef]
- Stroh, A.; Alobaid, F.; von Bohnstein, M.; Ströhle, J.; Epple, B. Numerical CFD simulation of 1 MWth circulating fluidized bed using the coarse grain discrete element method with homogenous drag models and particle size distribution. Fuel Process. Technol. 2018, 169, 84–93. [Google Scholar] [CrossRef]
- Chu, K.W.; Wang, B.; Yu, A.B.; Vince, A.; Barnett, G.D.; Barnett, P.J. CFD–DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone. Miner. Eng. 2009, 22, 893–909. [Google Scholar] [CrossRef]
- Lu, L.; Xu, J.; Ge, W.; Gao, G.; Jiang, Y.; Zhao, M.; Liu, X.; Li, J. Computer virtual experiment on fluidized beds using a coarse-grained discrete particle method—EMMS-DPM. Chem. Eng. Sci. 2016, 155, 314–337. [Google Scholar] [CrossRef]
- Lu, L.; Morris, A.; Li, T.; Benyahia, S. Extension of a coarse grained particle method to simulate heat transfer in fluidized beds. Int. J. Heat Mass Transf. 2017, 111, 723–735. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, Y. CFD-DEM simulation of fluidized bed with an immersed tube using a coarse-grain model. Chem. Eng. Sci. 2021, 231, 116290. [Google Scholar] [CrossRef]
- Washino, K.; Chan, E.L.; Tanaka, T. DEM with attraction forces using reduced particle stiffness. Powder Technol. 2018, 325, 202–208. [Google Scholar] [CrossRef]
- Lin, J.; Luo, K.; Wang, S.; Hu, C.; Fan, J. An augmented coarse-grained CFD-DEM approach for simulation of fluidized beds. Adv. Powder Technol. 2020, 31, 4420–4427. [Google Scholar] [CrossRef]
- Queteschiner, D.; Lichtenegger, T.; Schneiderbauer, S.; Pirker, S. Coupling resolved and coarse-grain DEM models. Part. Sci. Technol. 2018, 36, 517–522. [Google Scholar] [CrossRef]
- Wang, X.; Chen, K.; Kang, T.; Ouyang, J. A Dynamic Coarse Grain Discrete Element Method for Gas-Solid Fluidized Beds by Considering Particle-Group Crushing and Polymerization. Appl. Sci. 2020, 10, 1943. [Google Scholar] [CrossRef]
- Lu, L.; Benyahia, S. Method to estimate uncertainty associated with parcel size in coarse discrete particle simulation. AIChE J. 2018, 64, 2340–2350. [Google Scholar] [CrossRef]

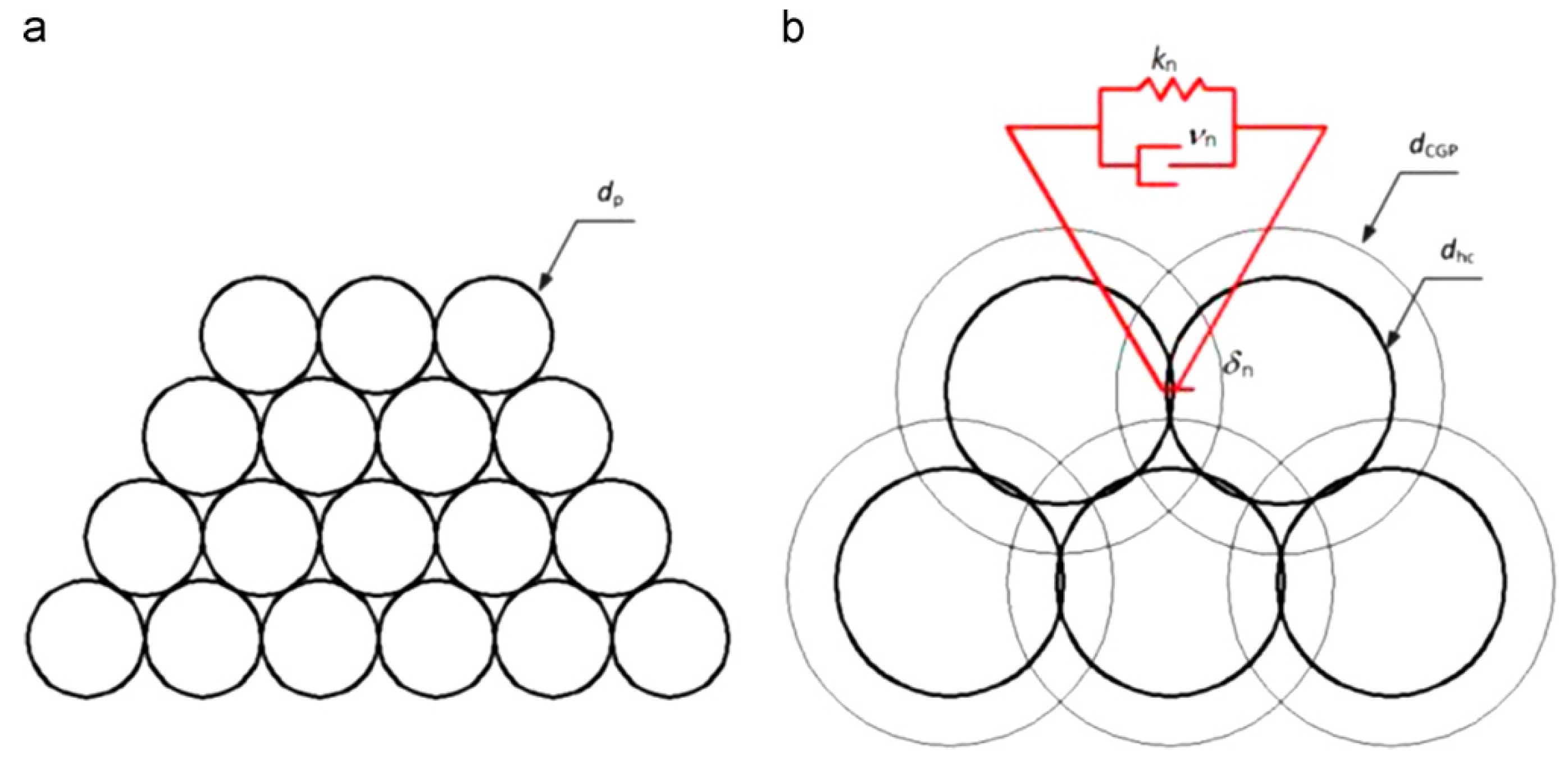

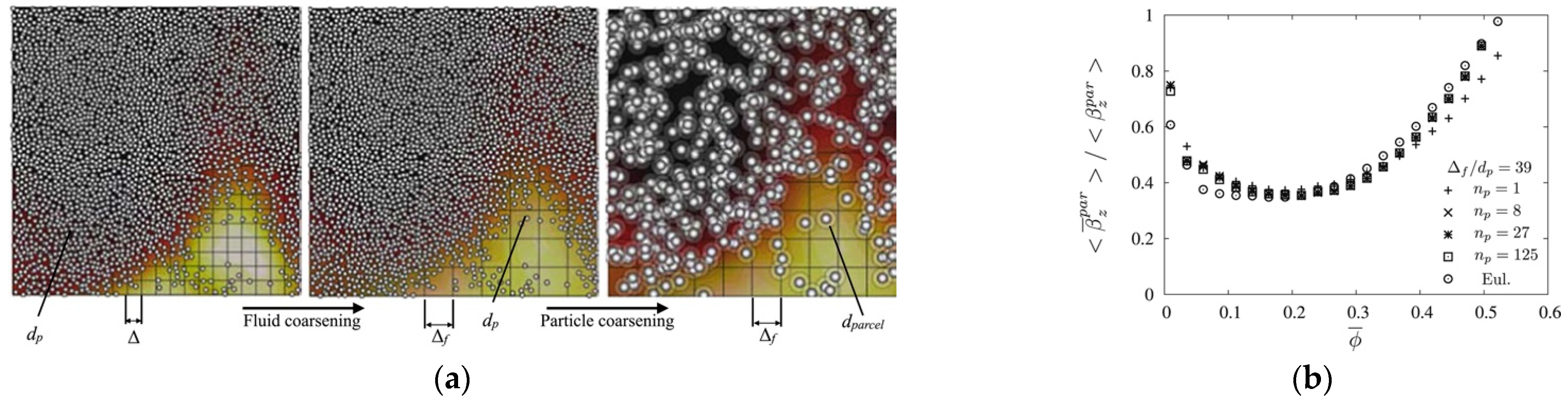

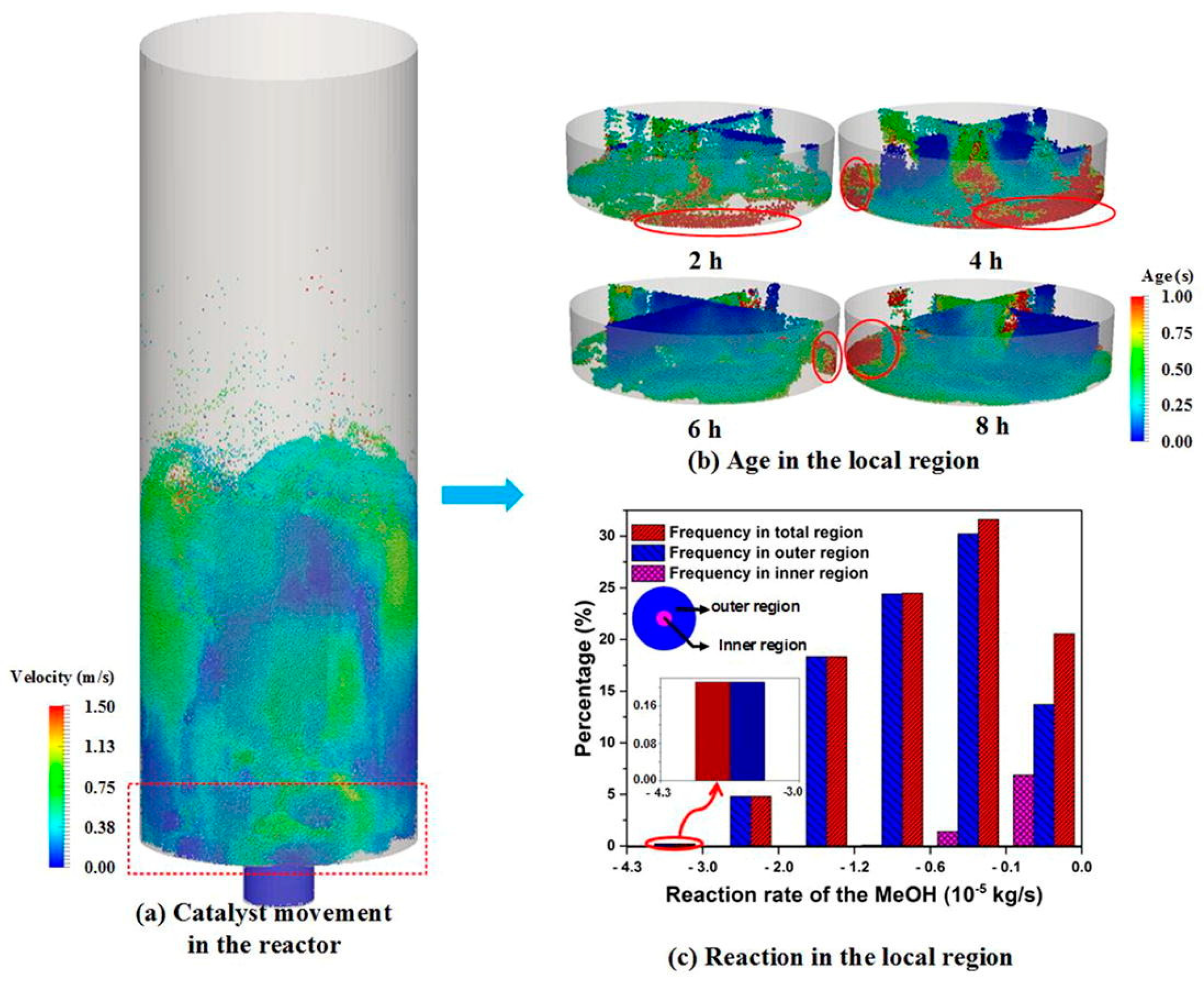
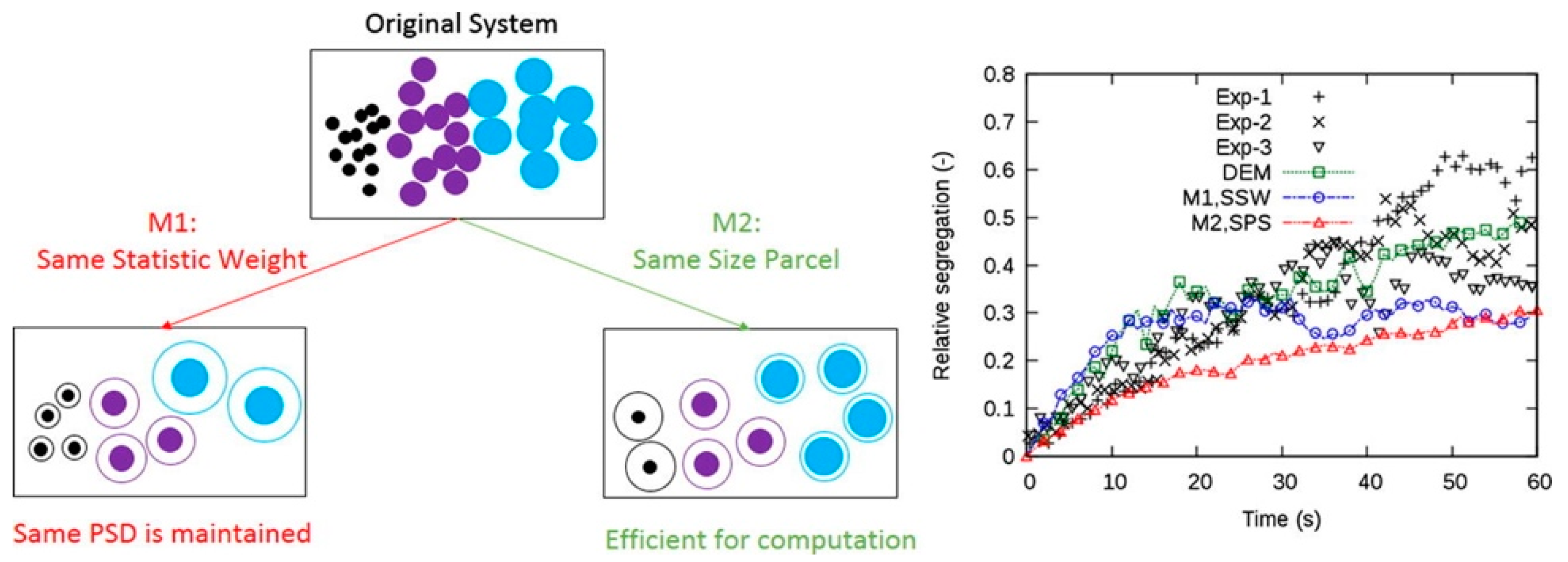

| Variable, [Units] | Description |
|---|---|
| , [–] | coarse grain factor, grain-to-particle size ratio |
| , [–] | coarse grain number, number of particles in a grain |
| Equal Dissipation Approaches, i.e., | |||||
| Stiffness (N) | Damping (N) | Stiffness (T) | Damping (T) | Friction | |
| Constant absolute overlap models (see, among others, [23,26,68]) | |||||
| Constant relative overlap models (see, among others, [25,72]) | |||||
| Additional (intra-grain) dissipation approaches, i.e., | |||||
| altered dissipation | notes | ||||
| Simplified dissipation scaling (Benyahia and Galvin (2010) [68]) | valid if , otherwise see Equation (47) | ||||
| KTGF based scaling (Lu et al. (2018) [71]) | from the KTGF; limited by | ||||
| EMMS-DPM (Lu et al. (2014) [16]) | from CG in EMMS; valid for grains with “porosity” | ||||
| Reference | Investigated CG Range | Typical Performance |
|---|---|---|
| [19] | speed-up = 15 (), 50 () | |
| [60] | ||
| [20] | 8 k grains for 64 billion particles | |
| [24] | at , 66 k grains for 60 M particles | |
| [68] | Shear flow: = 1,2,5,10 ( Periodic riser: = 10, 20, 50, 100 (relative ) | speed-up: 1, 3.6, 26, 102 relative speed-up *: 1, 3.3, 11, 15 |
| [61] | speed-up: 1, 3, 4.3, | |
| [26] | speed-up: 4.2, 15.7, 68.6 | |
| [16] | 48 k grains for 1.6 M particles 190 k grains for 4.1 M particles 14 M grains for a real CFB loop | |
| [86] | speed-up = 8.2, 29 | |
| [87] | at f = 5, speed-up = 625 (estimated); for the relative f* = 2, speed-up = 6. | |
| speed-up * = 1, 35, 131 | ||
| [80] | speed-up | |
| [85] | speed-up = 14, 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Renzo, A.; Napolitano, E.S.; Di Maio, F.P. Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes 2021, 9, 279. https://doi.org/10.3390/pr9020279
Di Renzo A, Napolitano ES, Di Maio FP. Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes. 2021; 9(2):279. https://doi.org/10.3390/pr9020279
Chicago/Turabian StyleDi Renzo, Alberto, Erasmo S. Napolitano, and Francesco P. Di Maio. 2021. "Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review" Processes 9, no. 2: 279. https://doi.org/10.3390/pr9020279
APA StyleDi Renzo, A., Napolitano, E. S., & Di Maio, F. P. (2021). Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes, 9(2), 279. https://doi.org/10.3390/pr9020279







