Large Eddy Simulation of Film Cooling Involving Compound Angle Holes: Comparative Study of LES and RANS
Abstract
1. Introduction
2. Numerical Methods and Validation
2.1. Computational Domain and Boundary Conditions
2.2. Governing Equations and Turbulence Models
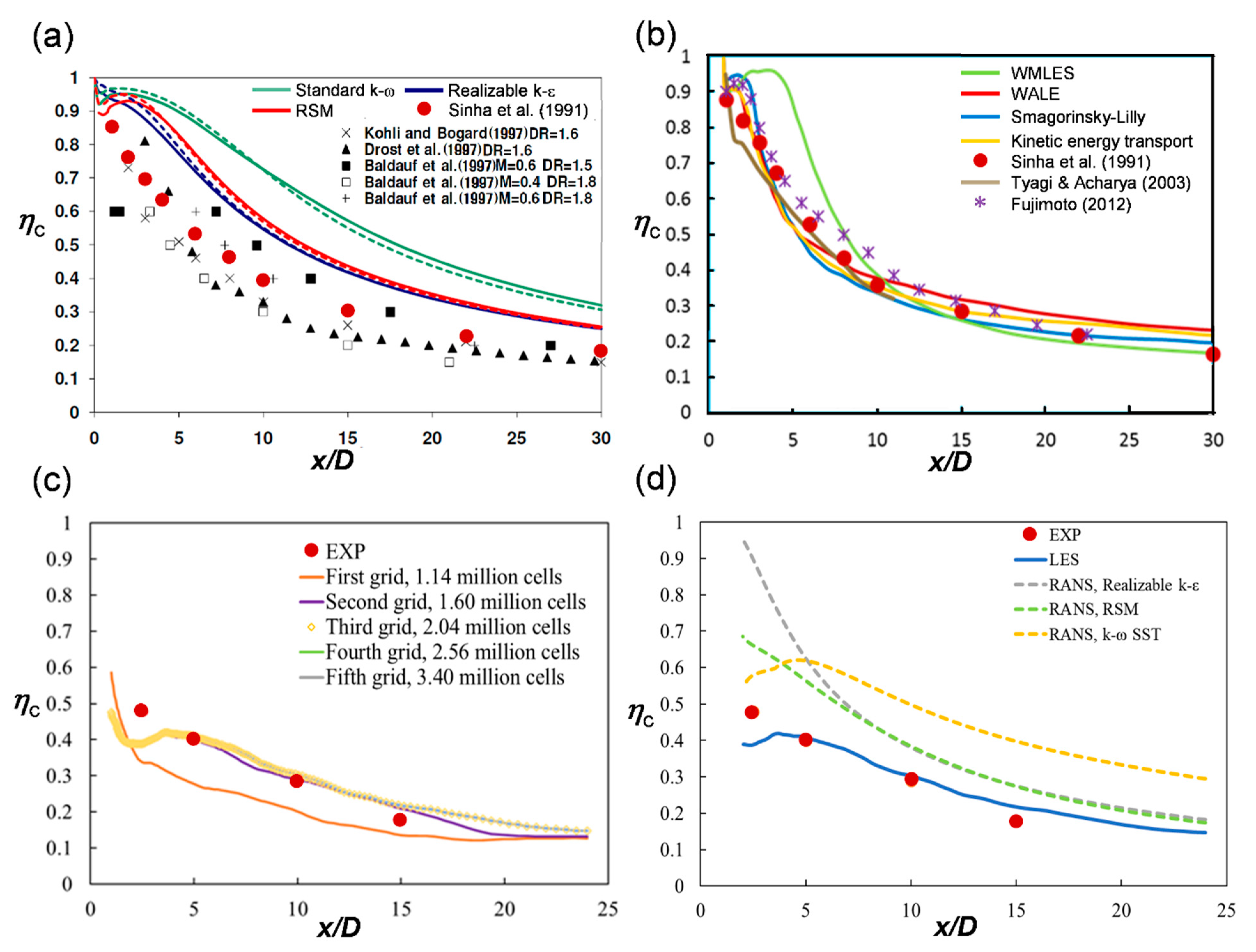
2.3. Code Validation
3. Results and Discussion
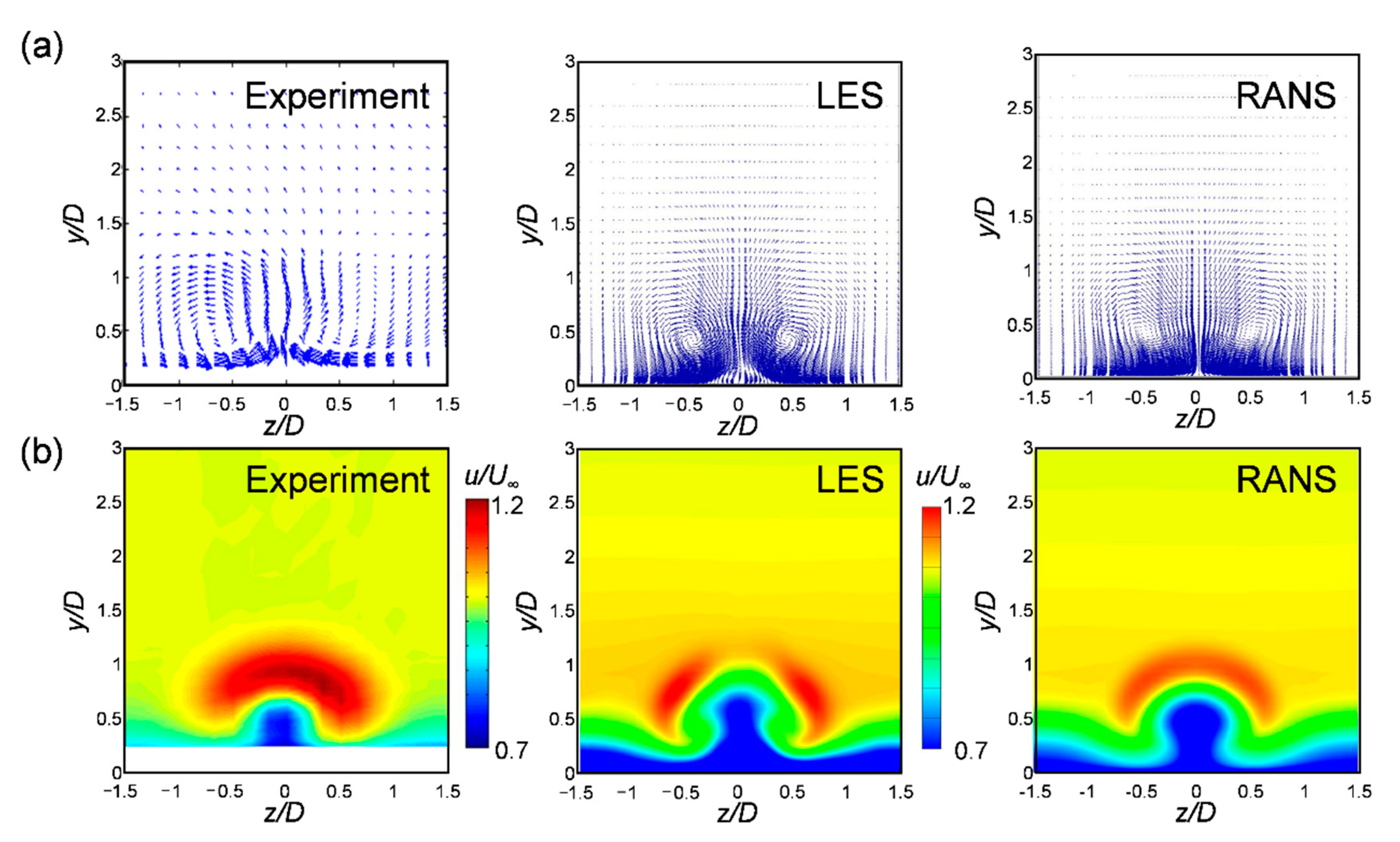
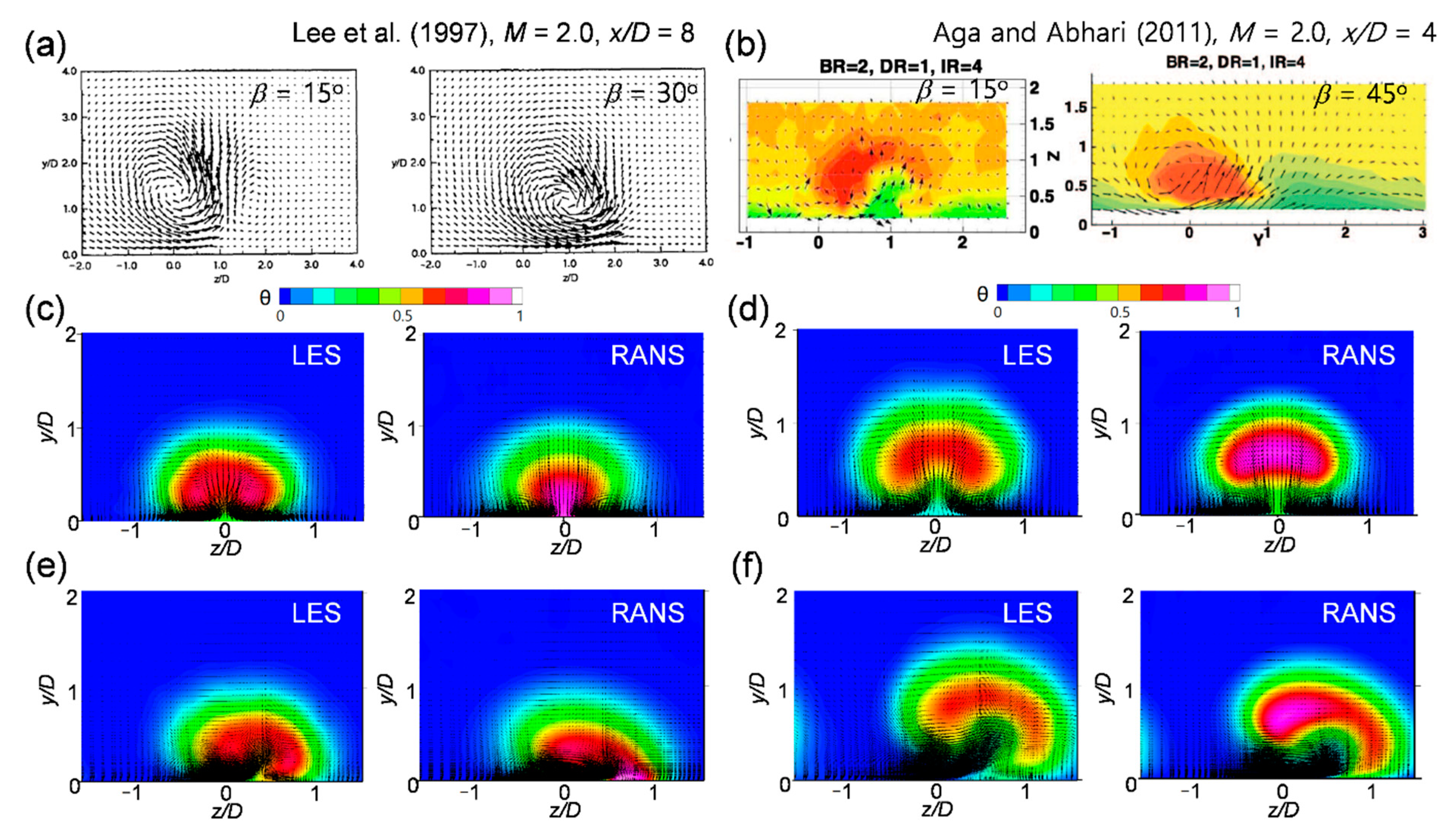
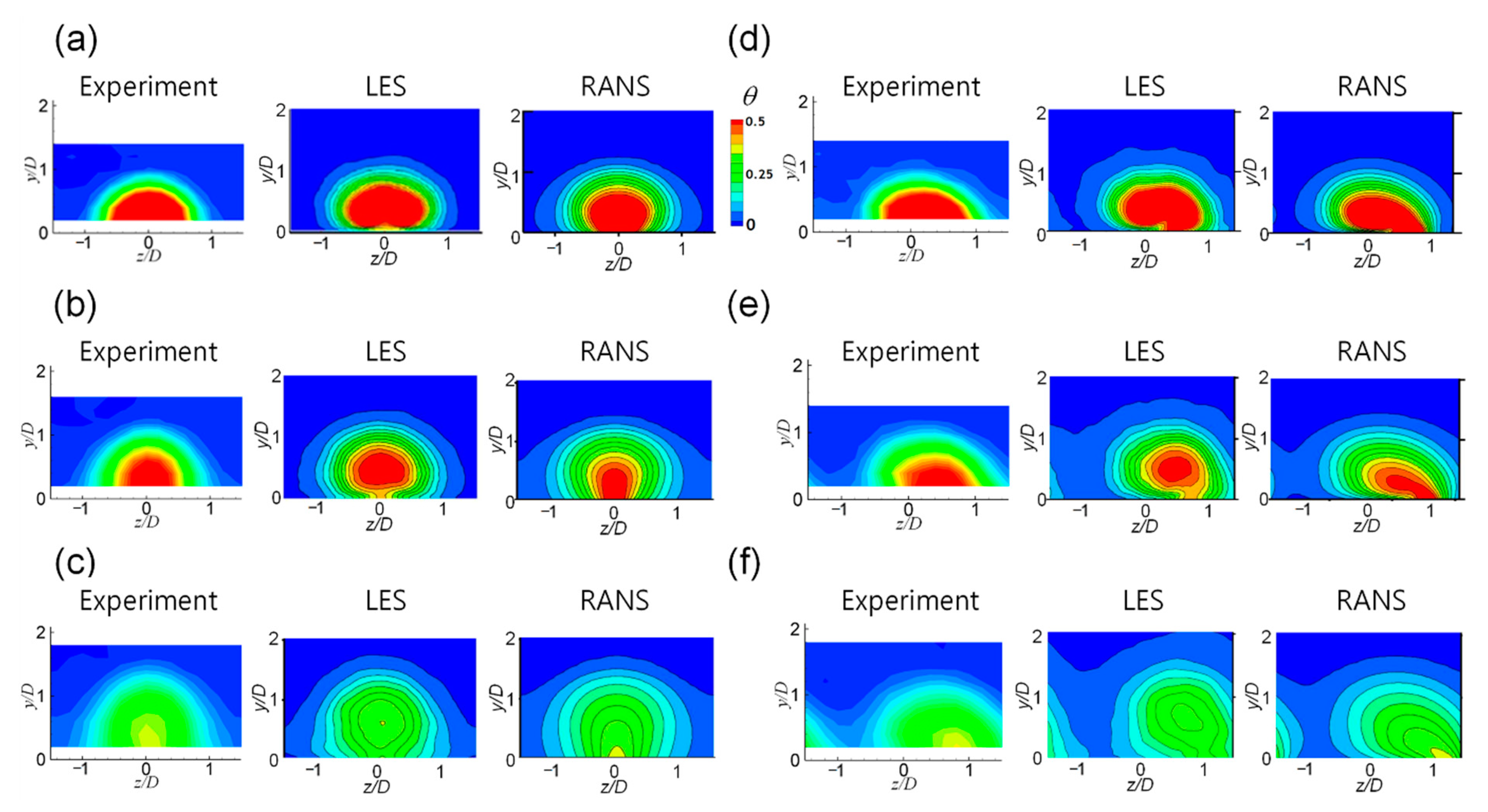
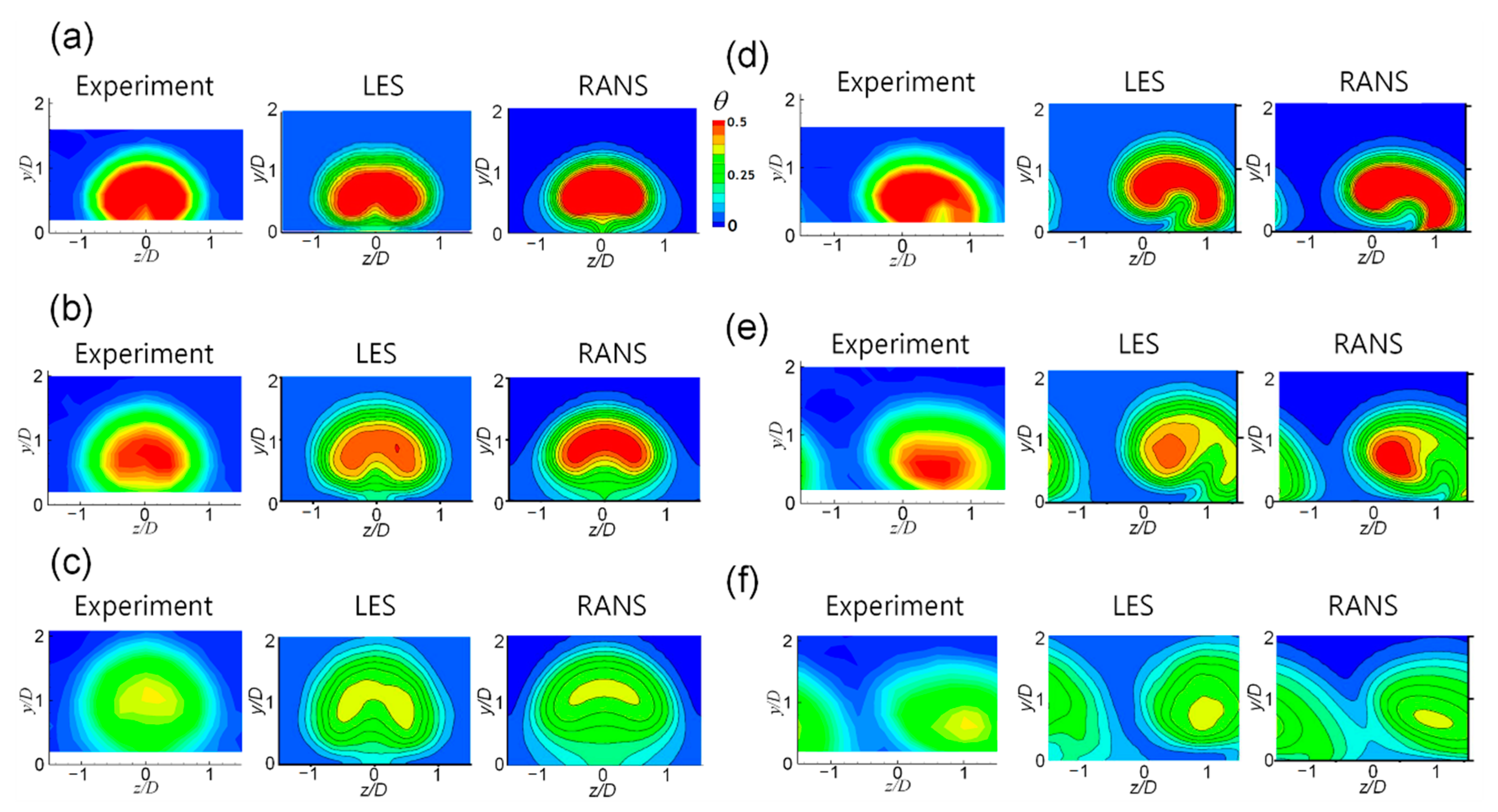
3.1. Time-Averaged Flow and Thermal Fields
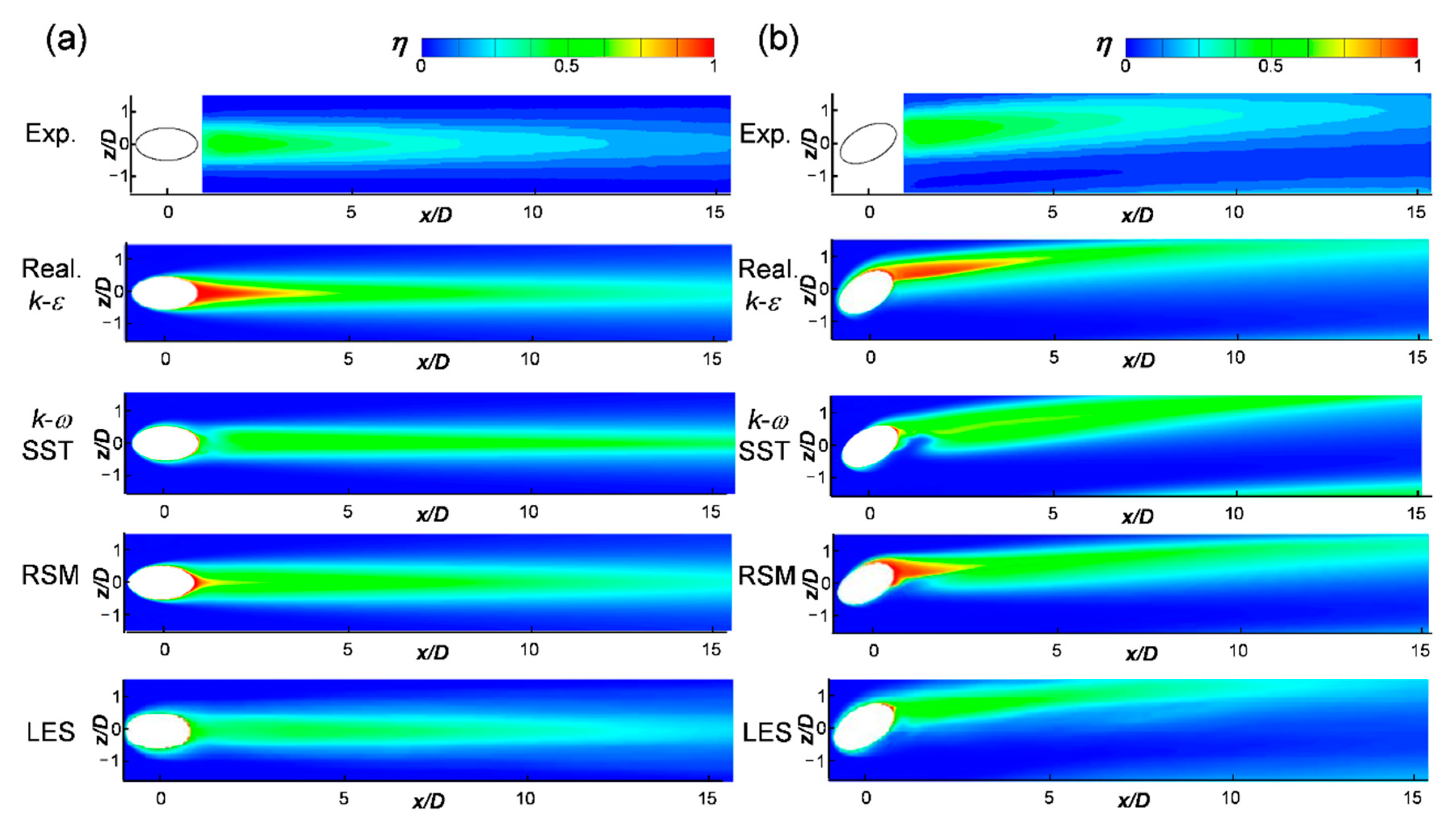
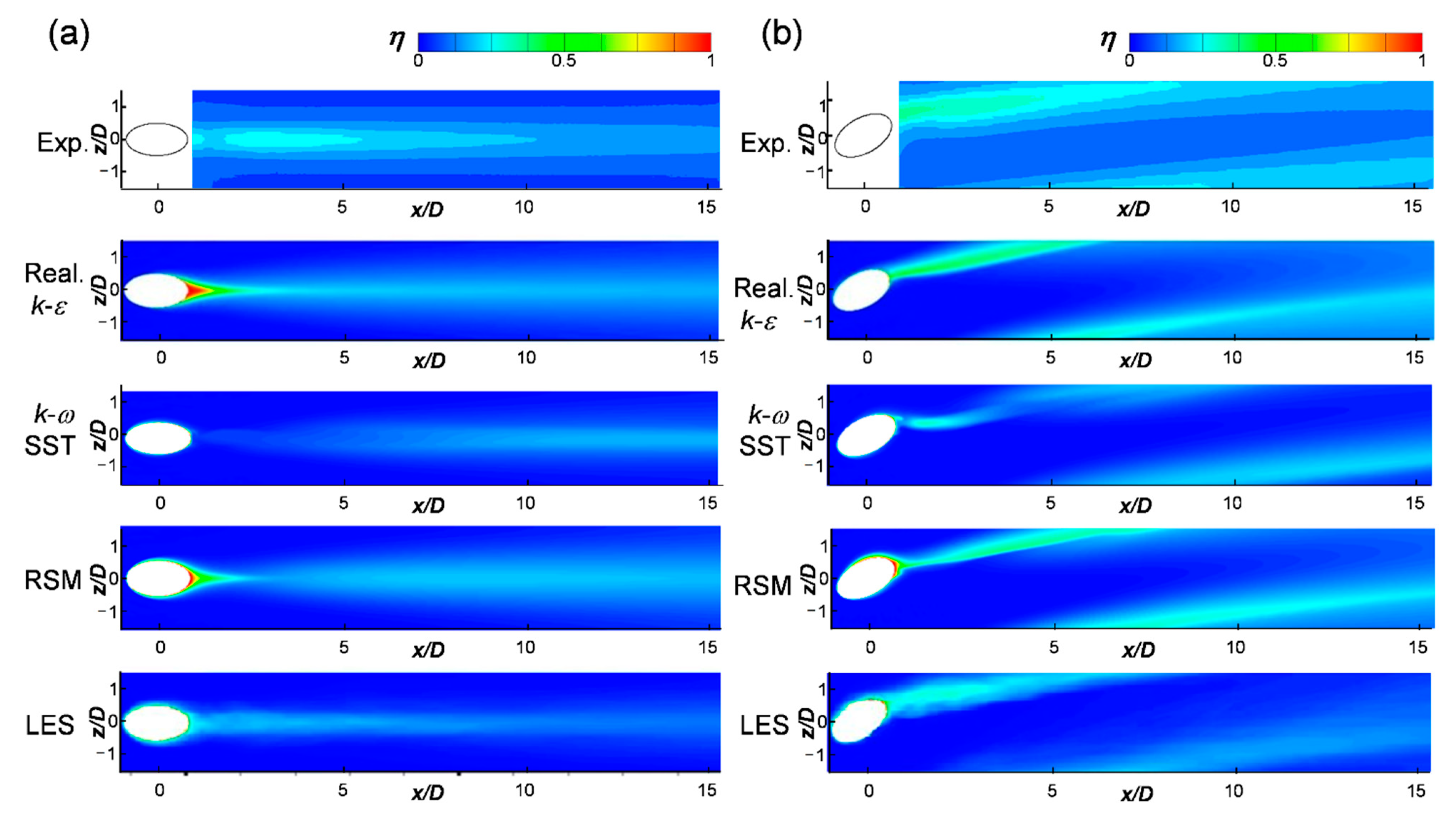
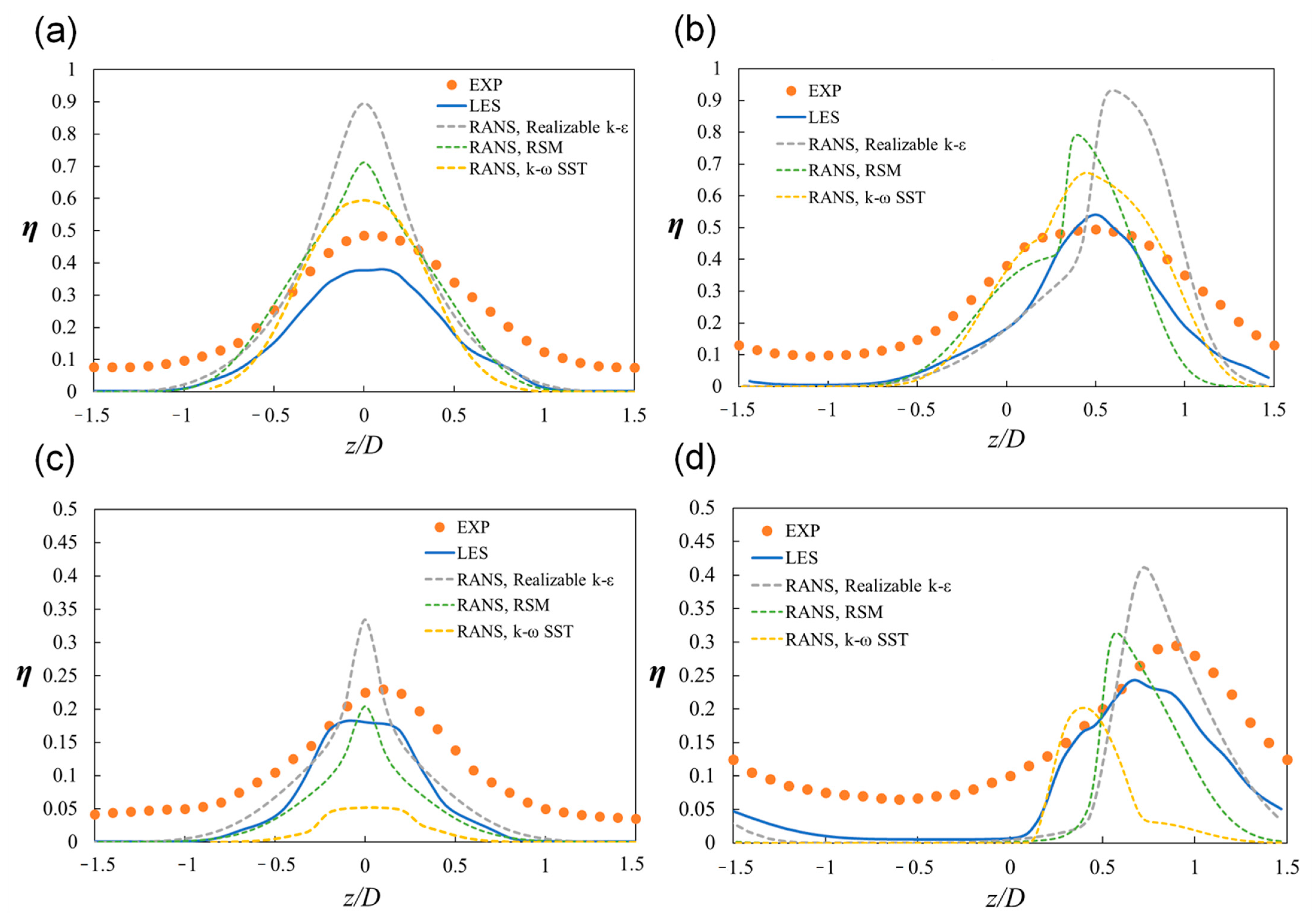
3.2. Adiabatic Film Cooling Effectiveness
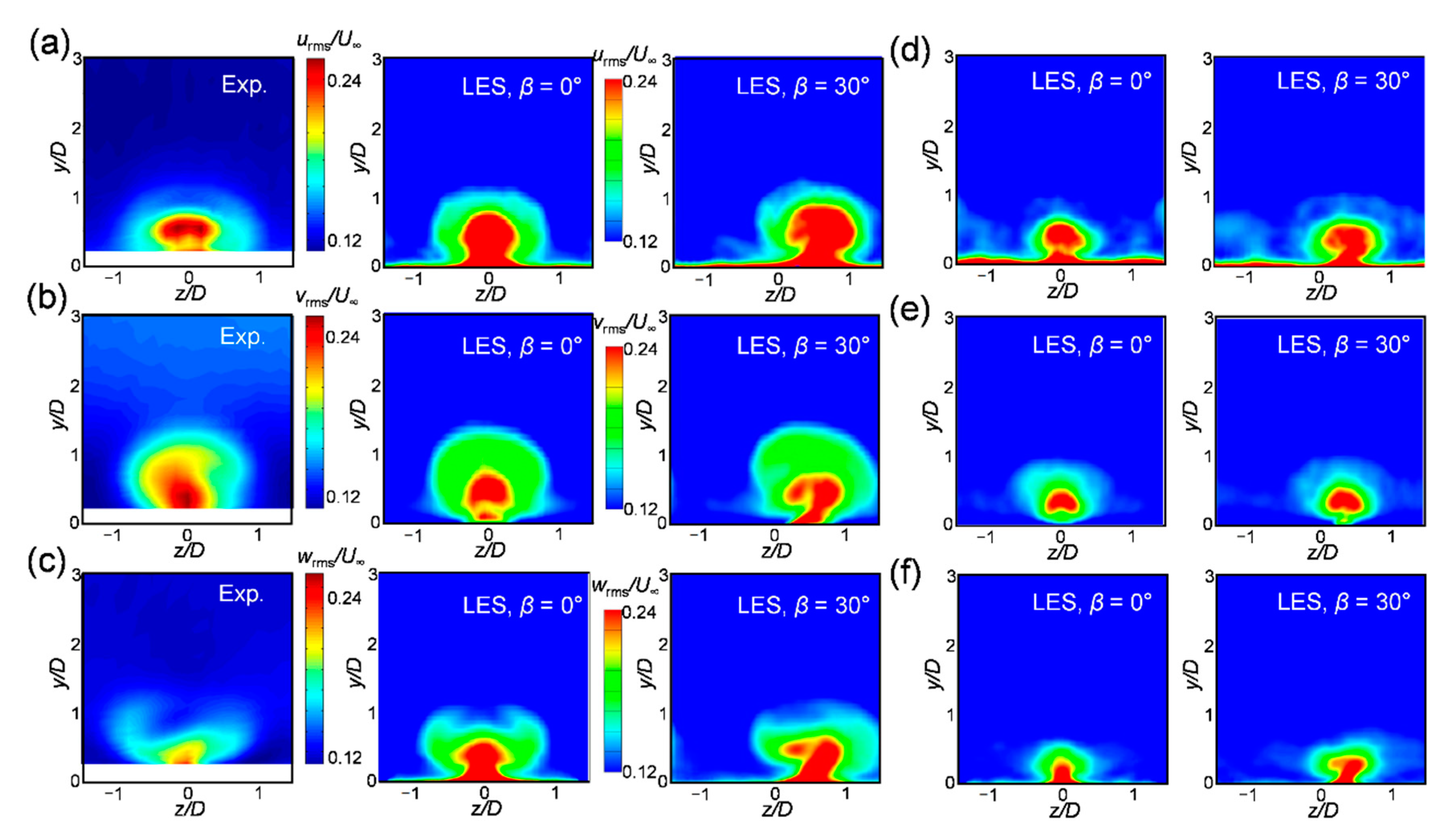
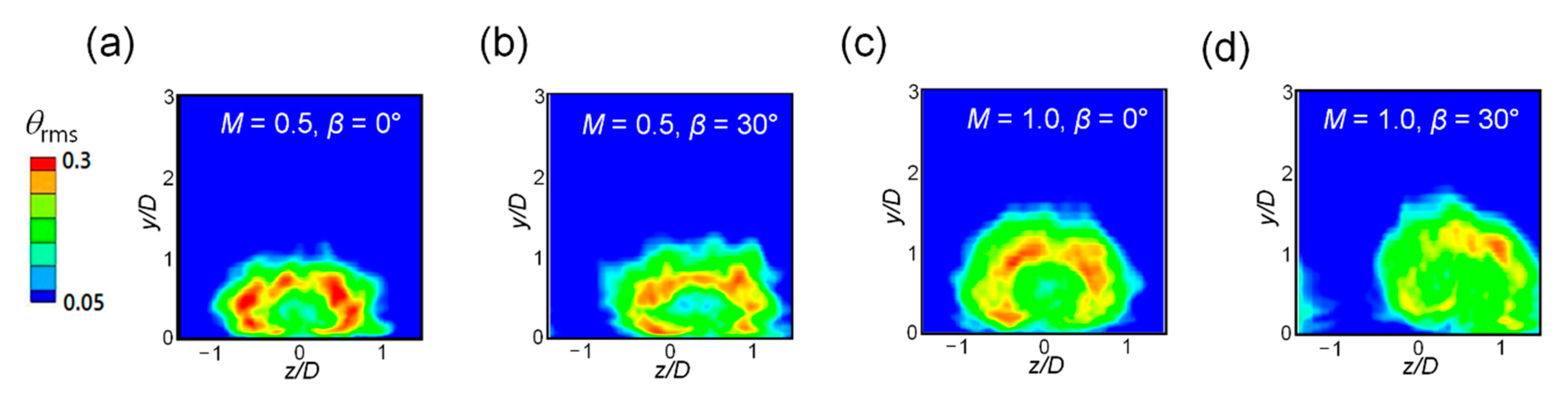
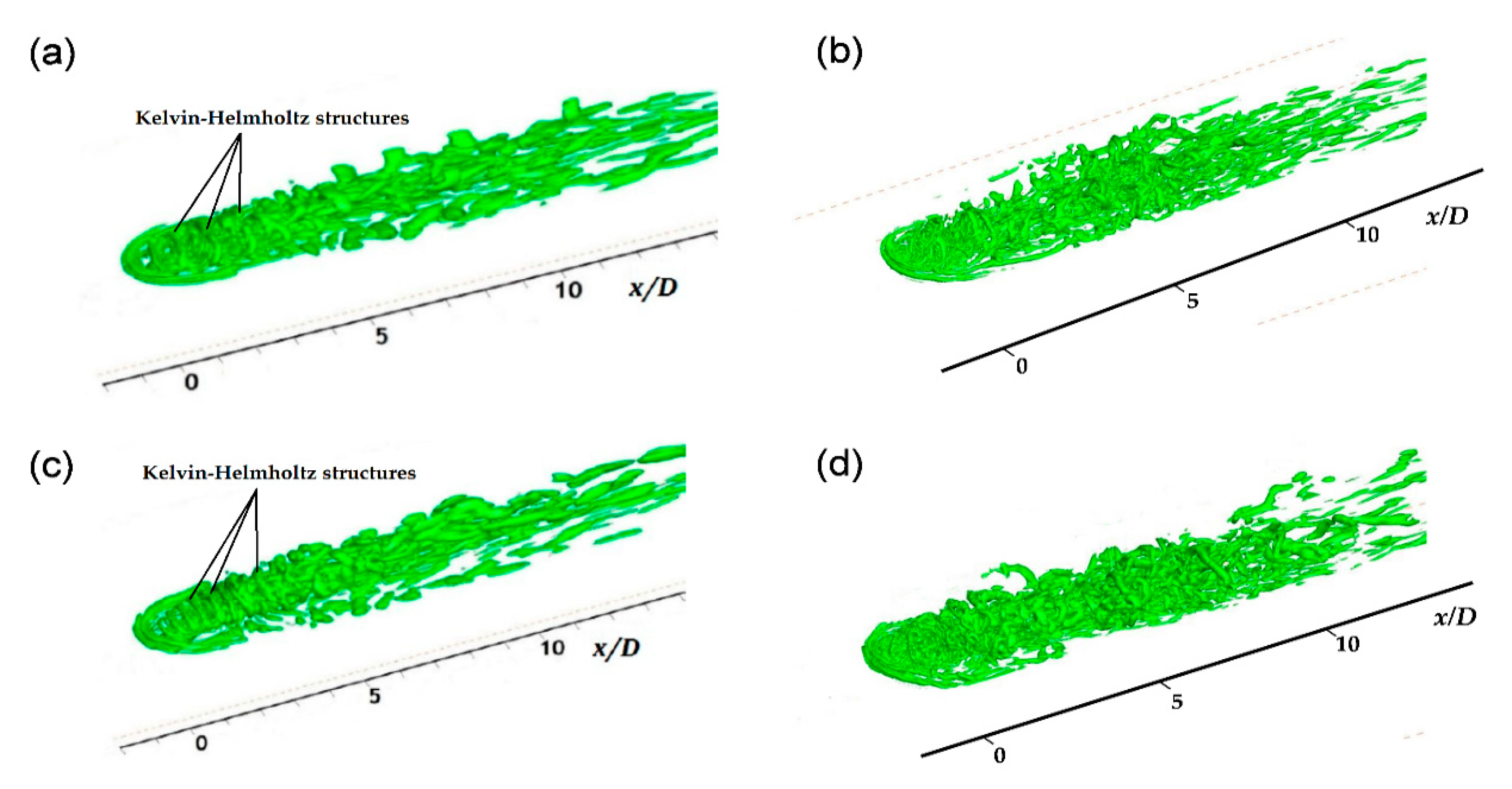
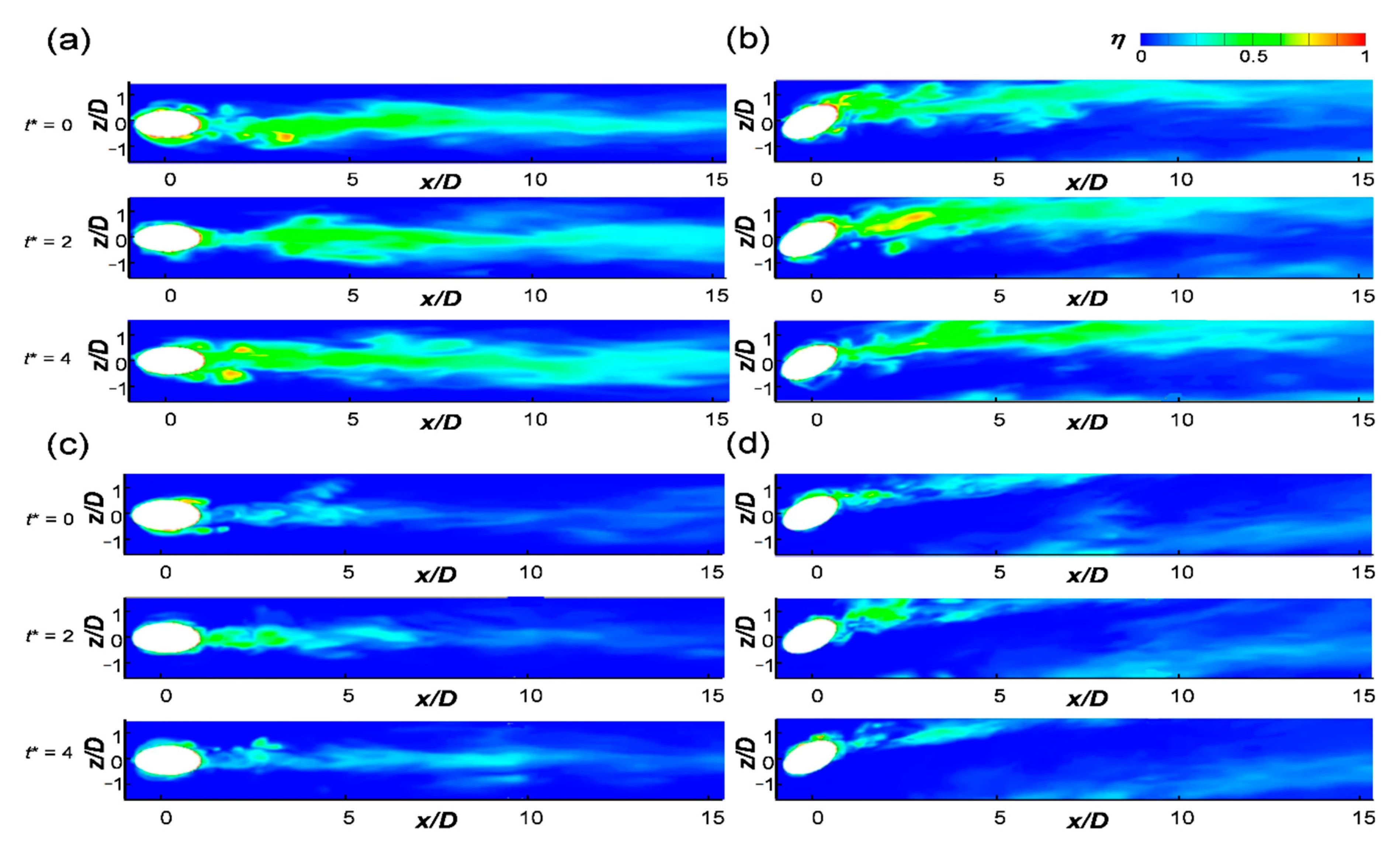
3.3. Turbulence Statistics and Instantaneous Flow Fields
4. Conclusions
- In the time-averaged flow field, the RANS data exhibited a difference from the experiment and LES in terms of the rising point of the CRVP as the vortices collided with each other on the wall. When the injection ratio was 0.5 and the orientation angle is 30°, the LES predicted that the counter-rotating vortex remained weak and the RANS predicted that the vortex completely changed to a single vortex;
- The RANS did not accurately predict the lift-off of the injectant or mixing with the main flow, and thus, it could not accurately predict the film cooling performance. The corresponding predictions obtained using the LES were better. The reattachment of the injectant at the blowing ratio of 1.0 was better predicted by the RANS in the compound angle case than that in the case of the simple angle;
- The turbulence intensity was large in the region in which the upward flow of the vortex in the injectant was generated and the temperature fluctuation was large at the boundary of the turbulent intensity peak. The temperature fluctuation slightly decreased when the injectant was supplied at a compound angle;
- In the compound angle case, the insulation film was eliminated near the leeward rim of the film cooling hole due to the influence of the single vortex however, at the injection ratio of 1.0, the injectant flowed along the wall more smoothly than that in the simple injection angle, thereby enhancing the downstream film cooling performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cs | Smagorinsky constant |
| Cp | Specific heat [J/(kgK)] |
| D | diameter of a single hole [mm] |
| d | wall distance [mm] |
| L | delivery tube length [mm] |
| Ls | mixing length of subgrid scales = |
| M | blowing ratio = |
| P | pitch of the holes [mm] |
| qj | heat flux [W/mm2] |
| T | emperature [K] |
| t | time [s] |
| t* | non-dimensional time = U∞ t/D |
| U | time-averaged flow velocity [m/s] |
| U∞ | freestream velocity [m/s] |
| u | streamwise velocity [m/s] |
| v | wall-normal velocity [m/s] |
| w | panwise velocity [m/s] |
| x | streamwise coordinate |
| y | wall-normal coordinate |
| z | spanwise coordinate |
| Greek symbols | |
| α | thermal diffusivity [m2/s] |
| adiabatic film cooling effectiveness = | |
| centerline film cooling effectiveness | |
| thermal conductivity [W/(mK)] | |
| density [kg/m3] | |
| τij | subgrid-scale turbulent stress = |
| μt | subgrid-scale turbulent viscosity [kg/(m·s)] |
| Δ | local grid scale |
| θ | dimensionless temperature = |
| Subscripts | |
| aw | adiabatic wall |
| c | centerline |
| C | coolant |
| G | mainstream gas |
| rms | root mean square value |
References
- Lakshminarayana, B. Fluid Dynamics and Heat Transfer of Turbomachinery; Wiley: Hoboken, NJ, USA, 1996; pp. 315–322. [Google Scholar]
- Goldstein, R.J. Film Cooling. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1971; Volume 7, pp. 321–379. [Google Scholar]
- Goldstein, R.J.; Eckert, E.R.G.; Ramsey, J.W. Film Cooling with Injection through Holes: Adiabatic Wall Temperatures Downstream of a Circular Hole. J. Eng. Power 1968, 90, 384–393. [Google Scholar] [CrossRef]
- Pedersen, D.R.; Eckert, E.R.G.; Goldstein, R.J. Film Cooling with Large Density Differences between the Mainstream and the Secondary Fluid Measured by the Heat-Mass Transfer Analogy. J. Heat Transf. 1977, 99, 620–627. [Google Scholar] [CrossRef]
- Sinha, A.K.; Bogard, D.G.; Crawford, M.E. Film-Cooling Effectiveness Downstream of a Single Row of Holes with Variable Density Ratio. J. Turbomach. 1991, 113, 442–449. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, J.S.; Ro, S.T. Experimental Study on the Flow Characteristics of Streamwise Inclined Jets in Crossflow on Flat Plate. J. Turbomach. 1994, 116, 97–105. [Google Scholar] [CrossRef]
- Coletti, F.; Benson, M.; Ling, J.; Elkins, C.J.; Eaton, J. Turbulent transport in an inclined jet in crossflow. Int. J. Heat Fluid Flow 2013, 43, 149–160. [Google Scholar] [CrossRef]
- Schmidt, D.L.; Sen, B.; Bogard, D.G. Film Cooling with Compound Angle Holes: Adiabatic Effectiveness. J. Turbomach. 1996, 118, 807–813. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Lee, J.S. Film Cooling from a Single Row of Compound Angle Holes at High Blowing Ratios. Int. J. Rotating Mach. 1996, 2, 259–267. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, Y.B.; Lee, J.S. Flow Characteristics and Aerodynamic Losses of Film-Cooling Jets with Compound Angle Orientations. J. Turbomach. 1997, 119, 310–319. [Google Scholar] [CrossRef]
- Jung, I.S.; Lee, J.S. Effects of Orientation Angles on Film Cooling over a Flat Plate: Boundary Layer Temperature Distributions and Adiabatic Film Cooling Effectiveness. J. Turbomach. 1999, 122, 153–160. [Google Scholar] [CrossRef]
- Aga, V.; Rose, M.; Abhari, R.S. Experimental Flow Structure Investigation of Compound Angled Film Cooling. J. Turbomach. 2008, 130, 031005. [Google Scholar] [CrossRef]
- Aga, V.; Abhari, R.S. Influence of Flow Structure on Compound Angled Film Cooling Effectiveness and Heat Transfer. J. Turbomach. 2011, 133, 031029. [Google Scholar] [CrossRef]
- McGovern, K.T.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics: Part II—Compound-Angle Injection with Cylindrical Holes. J. Turbomach. 2000, 122, 113–121. [Google Scholar] [CrossRef]
- Harrison, K.L.; Bogard, D.G. Comparison of RANS Turbulence Models for Prediction of Film Cooling Performance. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. GT2008-51423. [Google Scholar]
- Yu, F.; Yavuzkurt, S. Near-Field Simulations of Film Cooling with a Modified DES Model. Inventions 2020, 5, 13. [Google Scholar] [CrossRef]
- Tyagi, M.; Acharya, S. Large Eddy Simulation of Film Cooling Flow from an Inclined Cylindrical Jet. J. Turbomach. 2003, 125, 734–742. [Google Scholar] [CrossRef]
- Ziefle, J.; Kleiser, L. Numerical Investigation of a Film-Cooling Flow Structure: Effect of Crossflow Turbulence. J. Turbomach. 2013, 135, 041001. [Google Scholar] [CrossRef]
- Sakai, E.; Takahashi, T.; Watanabe, H. Large-eddy simulation of an inclined round jet issuing into a crossflow. Int. J. Heat Mass Transf. 2014, 69, 300–311. [Google Scholar] [CrossRef]
- Dai, C.; Jia, L.; Zhang, J.; Shu, Z.; Mi, J. On the flow structure of an inclined jet in cross flow at low velocity ratios. Int. J. Heat Fluid Flow 2016, 29, 1–17. [Google Scholar]
- Rozati, A.; Tafti, D. Large-eddy simulations of leading edge film cooling: Analysis of flow structures, effectiveness, and heat transfer coefficient. Int. J. Heat Fluid Flow 2008, 29, 1–17. [Google Scholar] [CrossRef]
- Ahn, J.; Schobeiri, M.; Han, J.-C.; Moon, H.-K. Effect of rotation on leading edge region film cooling of a gas turbine blade with three rows of film cooling holes. Int. J. Heat Mass Transf. 2007, 50, 15–25. [Google Scholar] [CrossRef]
- Lakehal, D.; Theodoridis, G.; Rodi, W. Three-dimensional flow and heat transfer calculations of film cooling at the leading edge of a symmetrical turbine blade model. Int. J. Heat Fluid Flow 2001, 22, 113–122. [Google Scholar] [CrossRef]
- Graf, L.; Kleiser, L. Large-Eddy Simulation of double-row compound-angle film cooling: Setup and validation. Comput. Fluids 2011, 43, 58–67. [Google Scholar] [CrossRef]
- Ahn, J.; Jung, I.S.; Lee, J.S. Film cooling from two rows of holes with opposite orientation angles: Injectant behavior and adiabatic film cooling effectiveness. Int. J. Heat Fluid Flow 2003, 24, 91–99. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Ren, J.; Jiang, H. Large eddy simulation of compound angle hole film cooling with hole length-to-diameter ratio and internal crossflow orientation effects. Int. J. Therm. Sci. 2017, 121, 410–423. [Google Scholar] [CrossRef]
- McClintic, J.; Klavetter, S.; Winka, J.; Anderson, J.; Bogard, D.; Dees, J.; Laskowski, G.; Briggs, R. The effect of internal cross-flow on the adiabatic effectiveness of compound angle film cooling holes. J. Turbomach. 2015, 137, 071006. [Google Scholar] [CrossRef]
- Stratton, Z.; Shih, T.; Laskowski, G.; Barr, B.; Briggs, R. Effects of Crossflow in an Internal-Cooling Channel on Film Cooling of a Flat Plate through Compound-Angle Holes. In Proceedings of the ASME Turbo Expo Proceeding, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Baek, S.I.; Yavuzkurt, S. Effects of Flow Oscillations in the Mainstream on Film Cooling. Inventions 2018, 3, 73. [Google Scholar] [CrossRef]
- Baek, S.I.; Ahn, J. Large Eddy Simulation of Film Cooling with Triple Holes: Injectant Behavior and Adiabatic Film-Cooling Effectiveness. Processes 2020, 8, 1443. [Google Scholar] [CrossRef]
- ANSYS Fluent Theory Guide Version 19. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 December 2020).
- Tannehill, J.; Anderson, D.; Pletcher, R. Computational Fluid Mechanics and Heat Transfer, 2nd ed.; Taylor & Francis: New York, NY, USA, 1997. [Google Scholar]
- Fujimoto, S. Large Eddy Simulation of Film Cooling Flows Using Octree Hexahedral Meshes. In Proceedings of the ASME Turbo Expo 2012, Copenhagen, Denmark, 11–15 June 2012. GT2012-70090. [Google Scholar]
- Burd, S.W.; Kaszeta, R.W.; Simon, T.W. Measurements in Film Cooling Flows: Hole L/D and Turbulence Intensity Effects. J. Turbomach. 1998, 120, 791–798. [Google Scholar] [CrossRef]
- Khojasteh, A.R.; Wang, S.F.; Peng, D.; Yavuzkurt, S.; Liu, Y. Structure analysis of adiabatic film cooling effectiveness in the near field of a single inclined jet: Measurement using fast-response pressure-sensitive paint. Int. J. Heat Mass Transf. 2017, 110, 629–642. [Google Scholar] [CrossRef]
- Kolář, V. Vortex identification: New requirements and limitations. Int. J. Heat Fluid Flow 2007, 28, 638–652. [Google Scholar] [CrossRef]
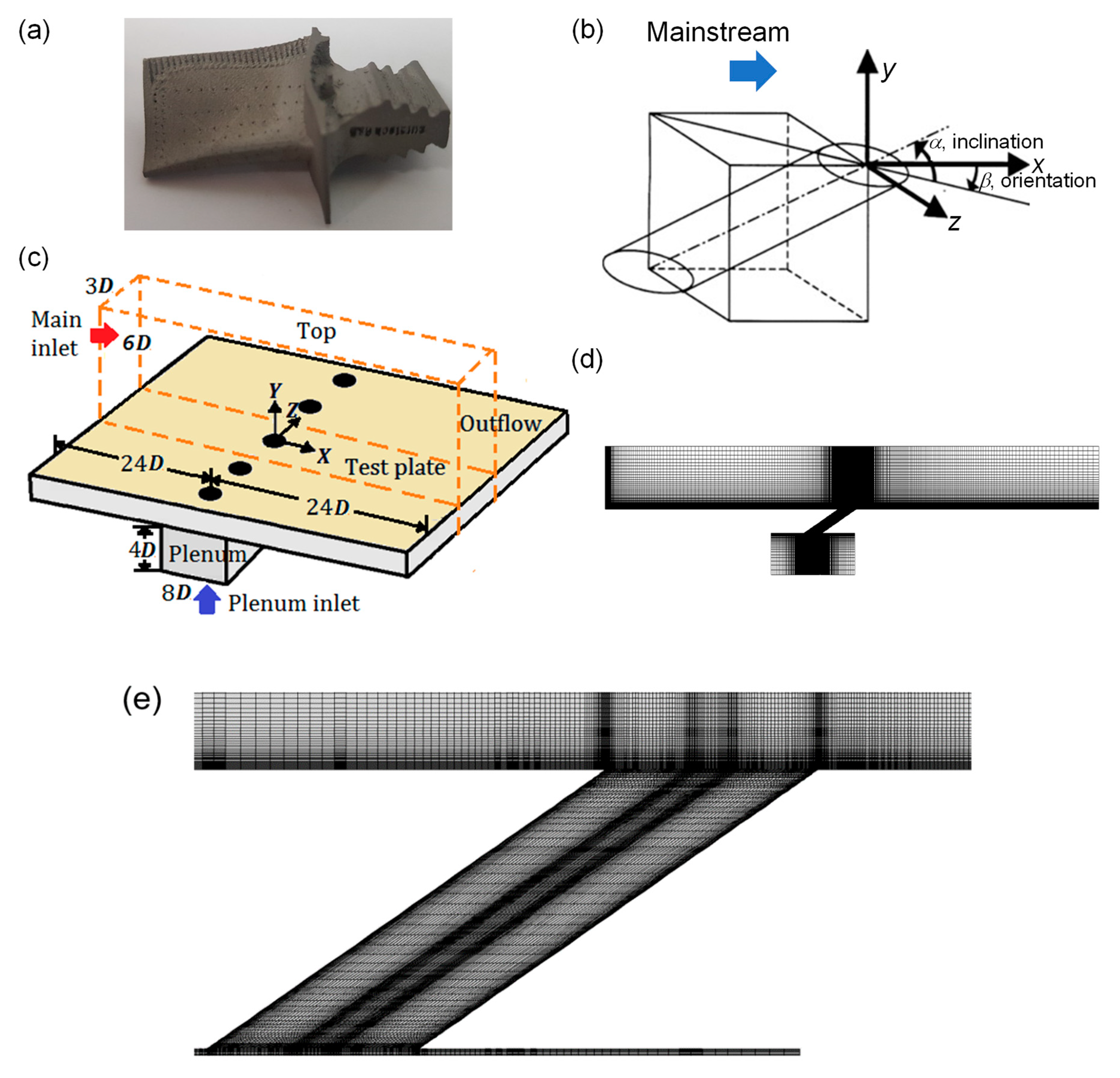
| Surface | Boundary Condition |
|---|---|
| Main inlet | Velocity inlet (u = constant) |
| Plenum inlet | Velocity inlet (u = constant) |
| Top | Symmetry () |
| Test plate | Adiabatic wall (u = v = w = 0) |
| Outflow | Pressure outlet |
| Main sides | Periodic (u (x, y, z, t) = u (x, y, z + P, t), ΔP = 0) |
| Sides of plenum | Wall (u = v = w = 0) |
| Tube wall | Wall (u = v = w = 0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S.I.; Ahn, J. Large Eddy Simulation of Film Cooling Involving Compound Angle Holes: Comparative Study of LES and RANS. Processes 2021, 9, 198. https://doi.org/10.3390/pr9020198
Baek SI, Ahn J. Large Eddy Simulation of Film Cooling Involving Compound Angle Holes: Comparative Study of LES and RANS. Processes. 2021; 9(2):198. https://doi.org/10.3390/pr9020198
Chicago/Turabian StyleBaek, Seung Il, and Joon Ahn. 2021. "Large Eddy Simulation of Film Cooling Involving Compound Angle Holes: Comparative Study of LES and RANS" Processes 9, no. 2: 198. https://doi.org/10.3390/pr9020198
APA StyleBaek, S. I., & Ahn, J. (2021). Large Eddy Simulation of Film Cooling Involving Compound Angle Holes: Comparative Study of LES and RANS. Processes, 9(2), 198. https://doi.org/10.3390/pr9020198






