Grand Tour Algorithm: Novel Swarm-Based Optimization for High-Dimensional Problems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Iterative Optimization Processes: A General View
2.2. Particle Swarm Optimization (PSO)
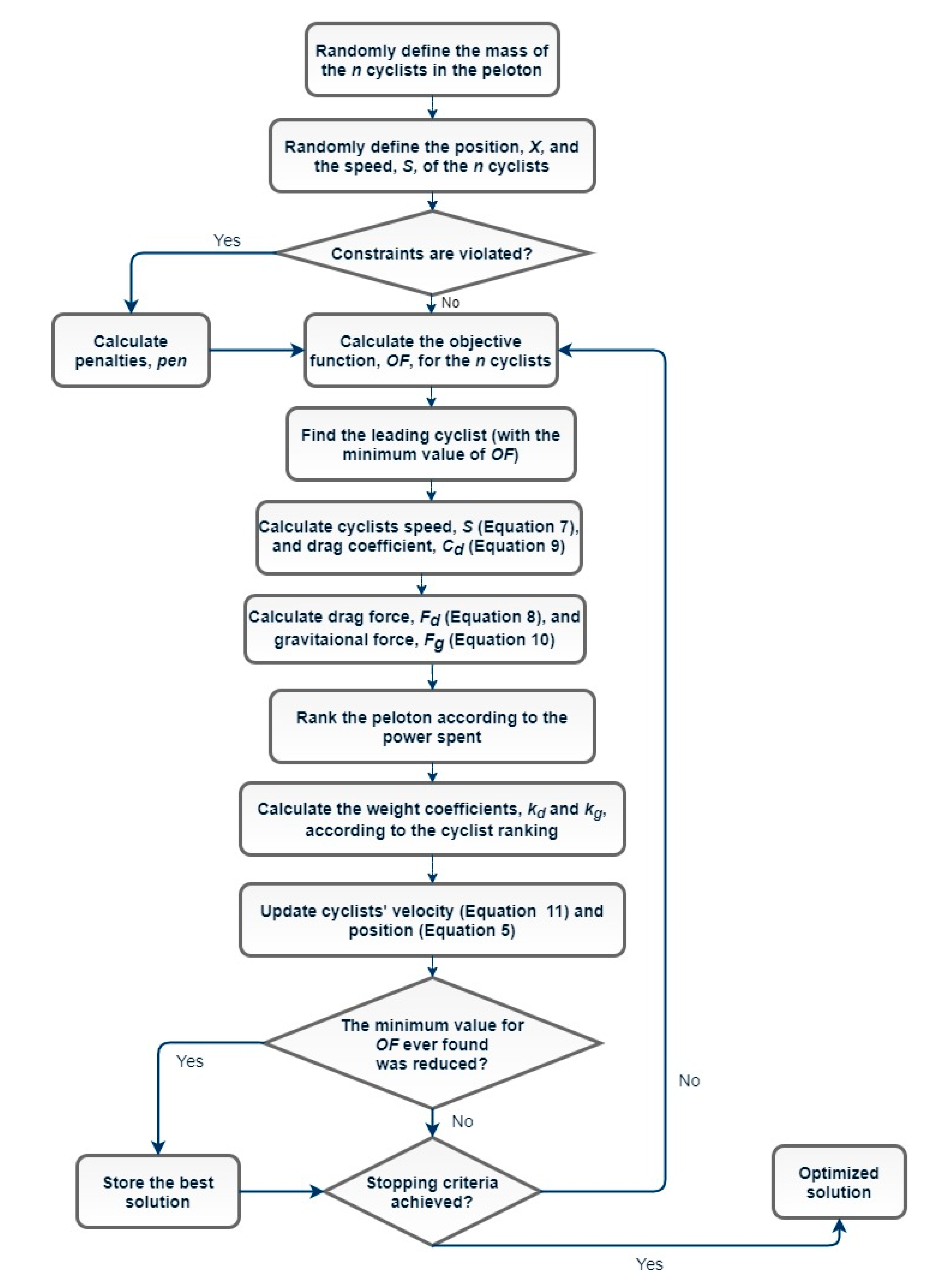
2.3. Grand Tour Algorithm (GTA)
2.3.1. GTA Fundamentals
2.3.2. Calculation of Drag Force
2.3.3. Calculation of Gravitational Force
2.3.4. Velocity and Position Updating
2.4. Test Conditions
3. Results
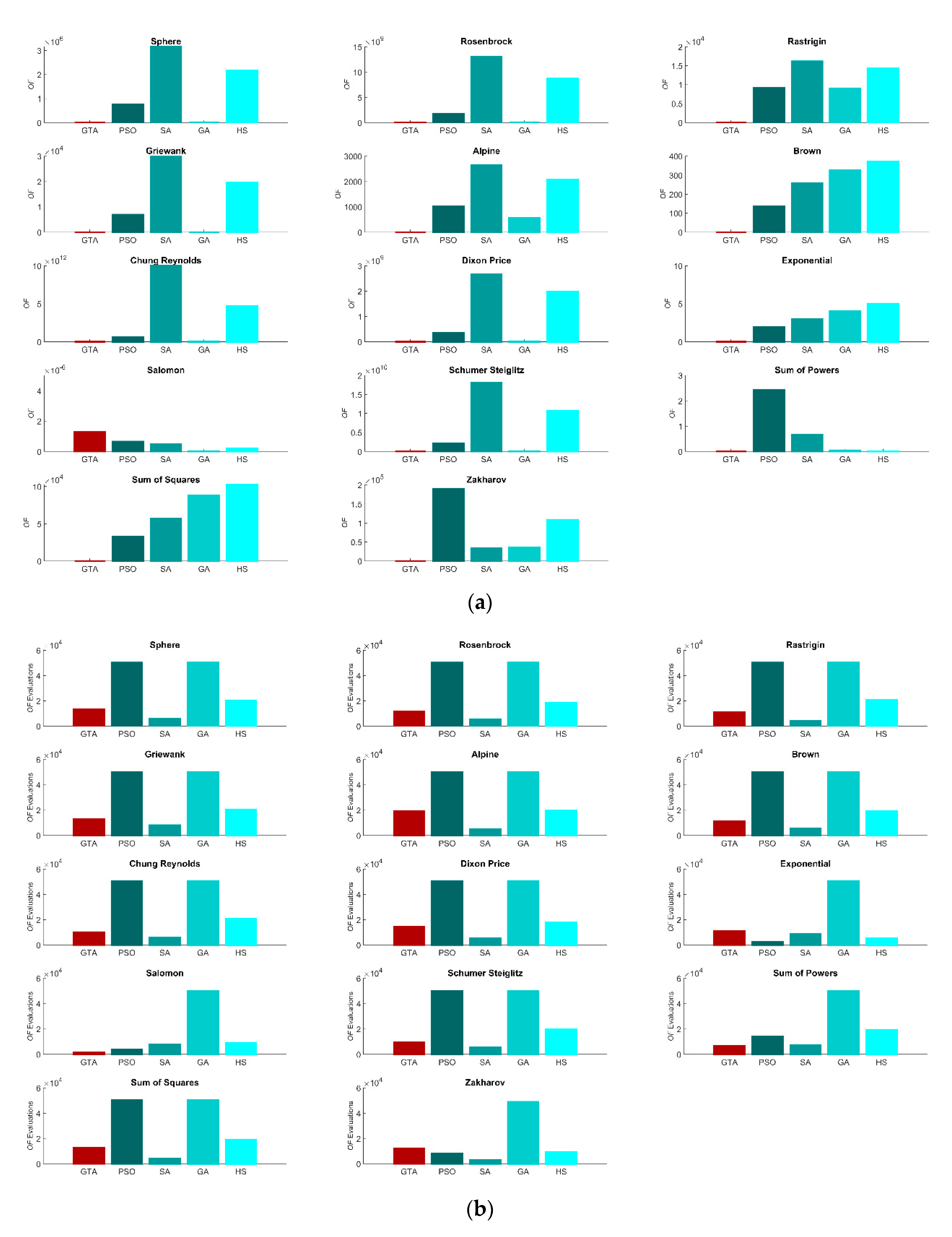
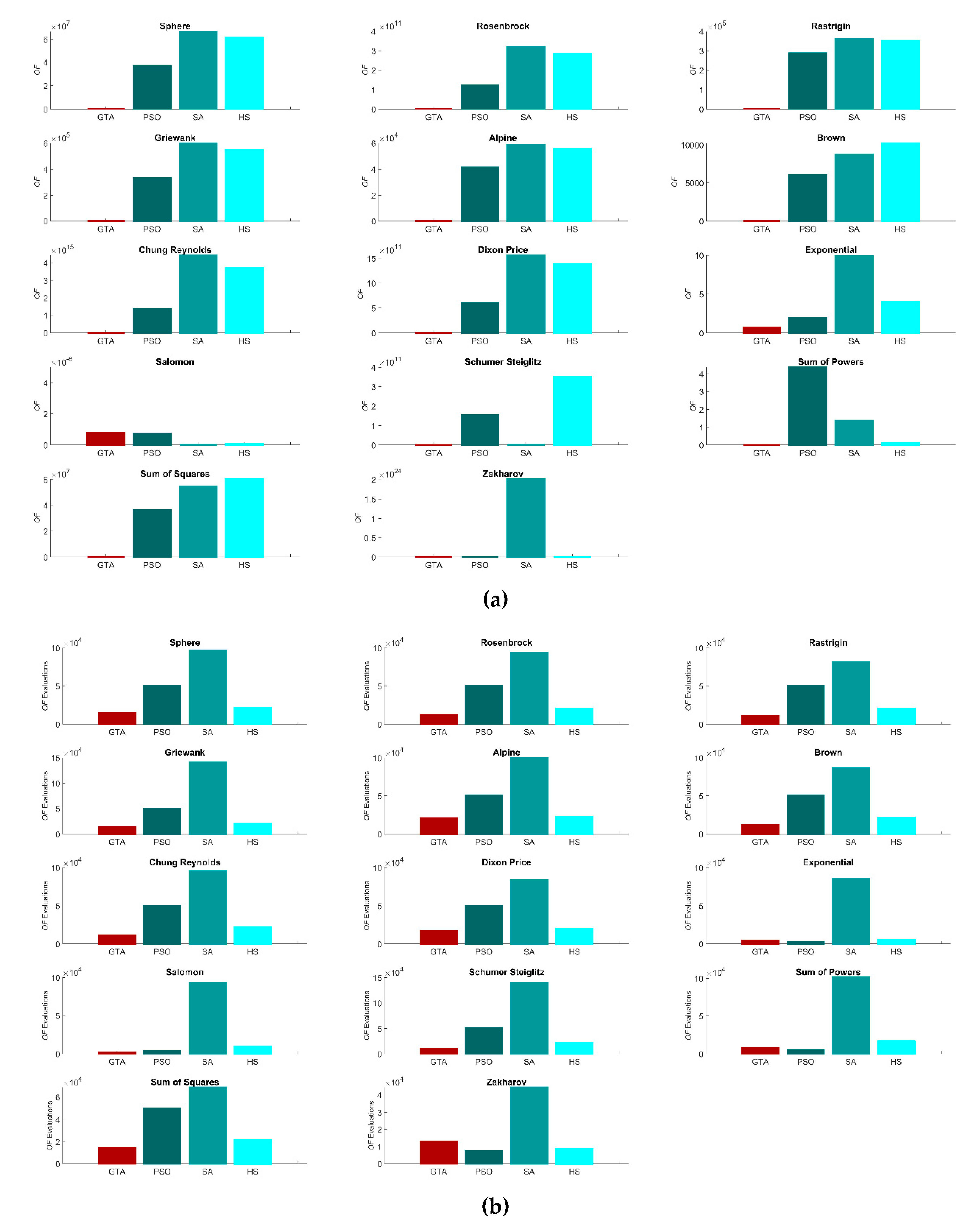
3.1. Performance
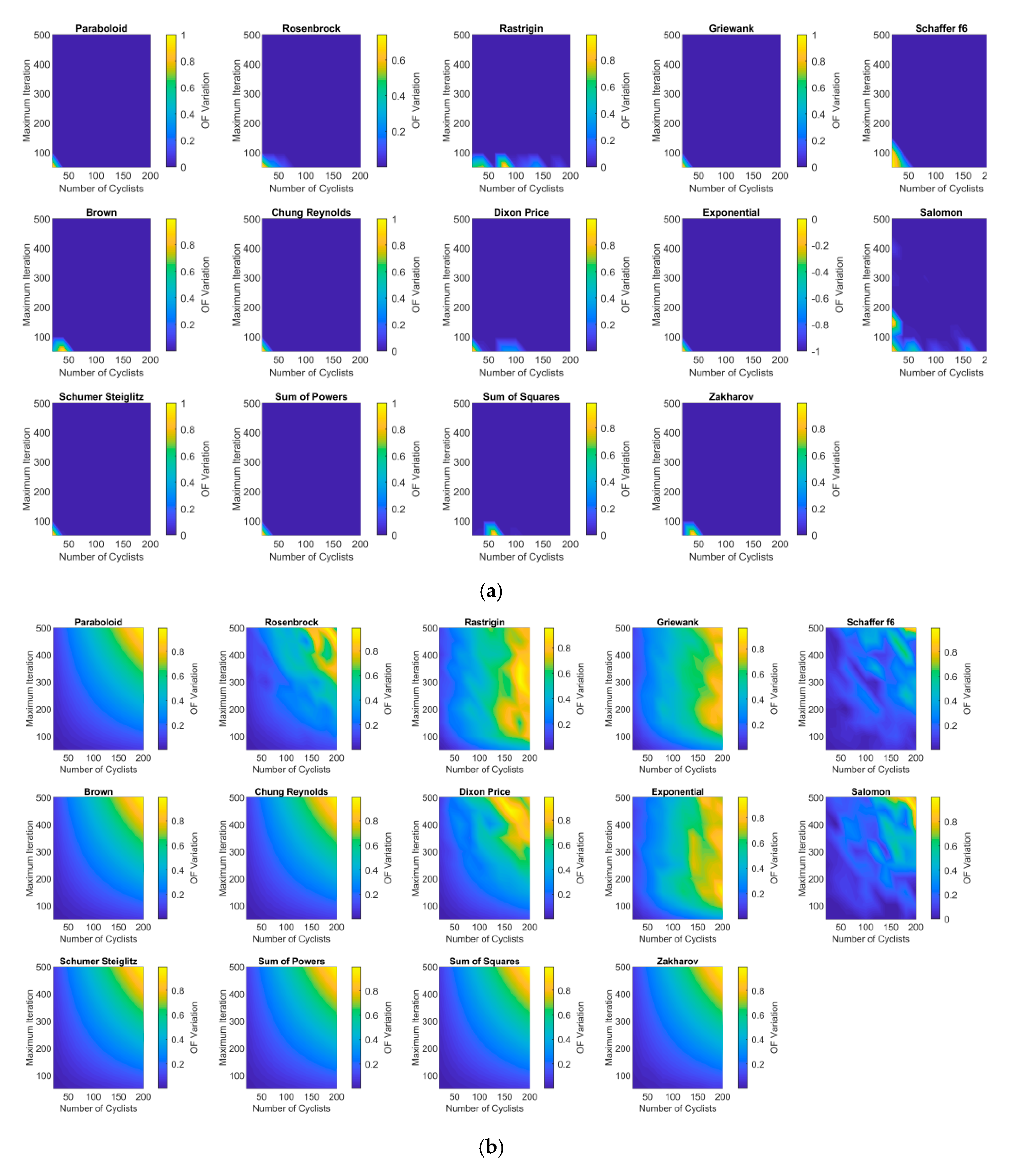
3.2. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cyb. 2019, 11, 1501–1529. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Soft. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Global Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE Intern Conf Neural Net, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Gonzalez-Fernandez, Y.; Chen, S. Leaders and followers—A new metaheuristic to avoid the bias of accumulated information. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 776–783. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization method for constrained optimization problems. Intell. Tech. Theory Appl. New Trends Intell. Tech. 2002, 76, 214–220. [Google Scholar]
- Wu, Z.Y.; Simpson, A.R. A self-adaptive boundary search genetic algorithm and its application to water distribution systems. J. Hydr. Res. 2002, 40, 191–203. [Google Scholar] [CrossRef] [Green Version]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Brentan, B.; Meirelles, G.; Luvizotto, E., Jr.; Izquierdo, J. Joint operation of pressure-reducing valves and pumps for improving the efficiency of water distribution systems. J. Water Res. Plan. Manag. 2018, 144, 04018055. [Google Scholar] [CrossRef] [Green Version]
- Freire, R.Z.; Oliveira, G.H.; Mendes, N. Predictive controllers for thermal comfort optimization and energy savings. Ener. Build. 2008, 40, 1353–1365. [Google Scholar] [CrossRef]
- Banga, J.R.; Seider, W.D. Global optimization of chemical processes using stochastic algorithms. In State of the Art in Global Optimization; Springer: Boston, MA, USA, 1996; pp. 563–583. [Google Scholar]
- Waziruddin, S.; Brogan, D.C.; Reynolds, P.F. The process for coercing simulations. In Proceedings of the 2003 Fall Simulation Interoperability Workshop, Orlando, FL, USA, 14–19 September 2003. [Google Scholar]
- Carnaham, J.C.; Reynolds, P.F.; Brogan, D.C. Visualizing coercible simulations. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; Volume 1. [Google Scholar]
- Bollinger, A.; Evins, R. Facilitating model reuse and integration in an urban energy simulation platform. Proc. Comput. Sci. 2015, 51, 2127–2136. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Chui, T.F.M. Developing a Flexible Simulation-Optimization Framework to Facilitate Sustainable Urban Drainage Systems Designs through Software Reuse. In Proceedings of the International Conference on Software and Systems Reuse, Cincinnati, OH, USA, 26–28 June 2019. [Google Scholar] [CrossRef]
- Yazdani, C.; Nasiri, B.; Azizi, R.; Sepas-Moghaddam, A.; Meybodi, M.R. Optimization in Dynamic Environments Utilizing a Novel Method Based on Particle Swarm Optimization. Int. J. Artif. Intel. 2013, 11, A13. [Google Scholar]
- Wang, Z.-J.; Zhan, Z.-H.; Du, K.-J.; Yu, Z.-W.; Zhang, J. Orthogonal learning particle swarm optimization with variable relocation for dynamic optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Lib, C.; Yang, S. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. Swarm Evol. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Gore, R.; Reynolds, P.F.; Tang, L.; Brogan, D.C. Explanation exploration: Exploring emergent behavior. In Proceedings of the 21st International Workshop on Principles of Advanced and Distributed Simulation (PADS’07), San Diego, CA, USA, 12–15 June 2007; IEEE: Washington, DC, USA, June 2007. [Google Scholar] [CrossRef] [Green Version]
- Gore, R.; Reynolds, P.F. Applying causal inference to understand emergent behavior. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; IEEE: Washington, DC, USA, December 2008. [Google Scholar] [CrossRef]
- Kim, V. A Design Space Exploration Method for Identifying Emergent Behavior in Complex Systems. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, December 2016. [Google Scholar]
- Hybinette, M.; Fujimoto, R.M. Cloning parallel simulations. ACM Trans. Model. Comput. Simul. (TOMACS) 2001, 11, 378–407. [Google Scholar] [CrossRef]
- Hybinette, M.; Fujimoto, R. Cloning: A novel method for interactive parallel simulation. In Proceedings of the WSC97: 29th Winter Simulation Conference, Atlanta, GA, USA, 7–10 December 1997; pp. 444–451. [Google Scholar] [CrossRef]
- Chen, D.; Turner, S.J.; Cai, W.; Gan, B.P. Low MYH Incremental HLA-Based Distributed Simulation Cloning. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; IEEE: Washington, DC, USA, December 2004. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Yan, Y.; Li, Z. PS–ABC: A hybrid algorithm based on particle swarm and artificial bee colony for high-dimensional optimization problems. Exp. Syst. Appl. 2015, 42, 8881–8895. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Pérez-García, R.; Herrera, M. Water distribution system computer-aided design by agent swarm optimization. Comput. Aided Civil Infrastr. Eng. 2014, 29, 433–448. [Google Scholar] [CrossRef]
- Maringer, D.G. Portfolio Management with Heuristic Optimization; Springer Science & Business Media: Boston, MA, USA, 2006. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Blocken, B.; van Druenen, T.; Toparlar, Y.; Malizia, F.; Mannion, P.; Andrianne, T.; Marchal, T.; Maas, G.J.; Diepens, J. Aerodynamic drag in cycling pelotons: New insights by CFD simulation and wind tunnel testing. J. Wind Eng. Ind. Aerod. 2018, 179, 319–337. [Google Scholar] [CrossRef]
- MATLAB 2018; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation—CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 84–88. [Google Scholar]
- GAMS World, GLOBAL Library. Available online: http://www.gamsworld.org/global/globallib.html (accessed on 29 April 2020).
- Gould, N.I.M.; Orban, D.; Toint, P.L. CUTEr, A Constrained and Un-Constrained Testing Environment, Revisited. Available online: http://cuter.rl.ac.uk/cuter-www/problems.html (accessed on 29 April 2020).
- GO Test Problems. Available online: http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm (accessed on 29 April 2020).
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Num. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef] [Green Version]
- Sharma, G. The Human Genome Project and its promise. J. Indian College Cardiol. 2012, 2, 1–3. [Google Scholar] [CrossRef]
- Li, W. On parameters of the human genome. J. Theor. Biol. 2011, 288, 92–104. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, November 2016. [Google Scholar]
- Hughes, M.; Goerigk, M.; Wright, M. A largest empty hypersphere metaheuristic for robust optimisation with implementation uncertainty. Comput. Oper. Res. 2019, 103, 64–80. [Google Scholar] [CrossRef]
- Zaeimi, M.; Ghoddosian, A. Color harmony algorithm: An art-inspired metaheuristic for mathematical function optimization. Soft Comput. 2020, 24, 12027–12066. [Google Scholar] [CrossRef]
- Singh, G.P.; Singh, A. Comparative Study of Krill Herd, Firefly and Cuckoo Search Algorithms for Unimodal and Multimodal Optimization. J. Intel. Syst. App. 2014, 2, 26–37. [Google Scholar] [CrossRef]
- Taheri, S.M.; Hesamian, G. A generalization of the Wilcoxon signed-rank test and its applications. Stat. Papers 2013, 54, 457–470. [Google Scholar] [CrossRef]


| Algorithm | Settings |
|---|---|
| GTA | Drag and Gravitational Coefficients = range from 0.5 to 1.0 |
| PSO | Cognitive and Social Coefficients = 1.49 Inertia coefficient = varying from 0.1 to 1.1, linearly, |
| SA | Initial Temperature = 100 °C Reanneling Interval = 100 |
| GA | Crossover Fraction = 0.8 Elite Count = 0.05 Mutation rate = 0.01 |
| HS | Harmony Memory Considering Rate = 0.8 Pitching Adjust Rate = 0.1 |
| General | Maximum iterations = 500 Population Size = 100 Tolerance = 10−12 Maximum Stall Iteration = 20 |
| Function | Equation | Global Minimum | |
|---|---|---|---|
| Sphere | 0 | ||
| Rosenbrock | 0 | ||
| Rastrigin | 0 | ||
| Griewank | 0 | ||
| Alpine | 0 | ||
| Brown | 0 | ||
| Chung Reynolds | 0 | ||
| Dixon Price | 0 | ||
| Exponential | 0 | ||
| Salomon | 0 | ||
| Schumer Steiglitz | 0 | ||
| Sum of Powers | 0 | ||
| Sum of Squares | 0 | ||
| Zakharov | 0 |
| Function | Sphere | Rosenbrock | Rastrigin | Griewank | Alpine | Brown | Chung Reynolds | Dixon Price | Exponential | Salomon | Schumer Steiglitz | Sum of Powers | Sum of squares | Zakharov | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | GTA | 4.4 × 10–18 | 9.9 × 102 | 0.0 × 100 | 0.0 × 100 | 1.6 × 10–15 | 8.9 × 10–18 | 5.0 × 10–23 | 1.0 × 100 | 0.0E × 100 | 6.7 × 10–10 | 1.4 × 10–23 | 1.3 × 10–22 | 2.4 × 10–18 | 1.3 × 10–17 |
| PSO | 6.4 × 105 | 1.3 × 109 | 8.4 × 103 | 5.8 × 103 | 9.0 × 102 | 1.1 × 102 | 3.9 × 1011 | 2.5 × 108 | 1.0 × 100 | 2.5 × 10–12 | 1.5 × 109 | 1.1 × 100 | 2.6 × 104 | 2.4 × 104 | |
| SA | 2.9 × 106 | 1.1 × 1010 | 1.5 × 104 | 2.7 × 104 | 2.4 × 103 | 2.1 × 102 | 8.7 × 1012 | 2.2 × 109 | 1.0 × 100 | 1.0 × 10–10 | 1.6 × 1010 | 6.4 × 10–2 | 4.5 × 104 | 3.1 × 104 | |
| GA | 8.2 × 102 | 2.6 × 105 | 8.3 × 103 | 1.1 × 100 | 5.2 × 102 | 2.9 × 102 | 6.8 × 105 | 3.8 × 106 | 1.0 × 100 | 0.0 × 100 | 2.0 × 103 | 5.3 × 10–3 | 7.7 × 104 | 1.0 × 103 | |
| HS | 2.1 × 106 | 7.9 × 109 | 1.4 × 104 | 1.8 × 104 | 2.0 × 103 | 3.6 × 102 | 4.2 × 1012 | 1.8 × 109 | 1.0 × 100 | 1.4 × 10–13 | 1.0 × 1010 | 2.4 × 10–3 | 9.5 × 104 | 3.0 × 104 | |
| Mean | GTA | 2.3 × 10–15 | 1.0 × 103 | 0.0 × 100 | 1.6 × 10–15 | 6.9 × 10–14 | 3.3 × 10–15 | 8.1 × 10–18 | 1.0 × 100 | 0.0 × 100 | 1.3 × 10–6 | 1.3 × 10–17 | 1.5 × 10–16 | 3.4 × 10–15 | 1.7 × 10–15 |
| PSO | 7.5 × 105 | 1.7 × 109 | 9.1 × 103 | 6.9 × 103 | 1.0 × 103 | 1.4 × 102 | 5.9 × 1011 | 3.6 × 108 | 1.0 × 100 | 6.4 × 10–7 | 2.1 × 109 | 2.4 × 100 | 3.3 × 104 | 1.9 × 105 | |
| SA | 3.2 × 106 | 1.3 × 1010 | 1.6 × 104 | 3.0 × 104 | 2.6 × 103 | 2.6 × 102 | 1.0 × 1013 | 2.6 × 109 | 1.0 × 100 | 4.5 × 10–7 | 1.8 × 1010 | 6.5 × 10–1 | 5.7 × 104 | 3.4 × 104 | |
| GA | 9.2 × 102 | 3.1 × 105 | 8.9 × 103 | 1.2 × 100 | 5.6 × 102 | 3.2 × 102 | 8.5 × 105 | 5.0 × 106 | 1.0 × 100 | 7.7 × 10–13 | 2.5 × 103 | 4.0 × 10–2 | 8.8 × 104 | 3.5 × 104 | |
| HS | 2.2 × 106 | 8.6 × 109 | 1.4 × 104 | 1.9 × 104 | 2.1 × 103 | 3.7 × 102 | 4.7 × 1012 | 2.0 × 109 | 1.0 × 100 | 1.9 × 10–7 | 1.1 × 1010 | 1.2 × 10–2 | 1.0 × 105 | 1.1 × 105 | |
| Standard deviation | GTA | 5.3 × 10–15 | 9.1 × 10–1 | 0.0 × 100 | 3.4 × 10–15 | 9.3 × 10–14 | 1.3 × 10–14 | 2.9 × 10–17 | 4.3 × 10–6 | 0.0 × 100 | 3.2 × 10–6 | 6.5 × 10–17 | 5.3 × 10–16 | 8.7 × 10–15 | 4.4 × 10–15 |
| PSO | 5.1 × 104 | 1.9 × 108 | 3.2 × 102 | 5.1 × 102 | 4.5 × 101 | 9.7 × 100 | 9.4 × 1010 | 4.7 × 107 | 3.0 × 10–38 | 1.7 × 10–6 | 2.8 × 108 | 4.6 × 10–1 | 2.7 × 103 | 1.2 × 106 | |
| SA | 8.9 × 104 | 5.4 × 108 | 4.4 × 102 | 8.1 × 102 | 8.6 × 101 | 2.3 × 101 | 5.8 × 1011 | 1.5 × 108 | 1.4 × 10–36 | 2.6 × 10–6 | 7.7 × 108 | 3.9 × 10–1 | 5.2 × 103 | 1.3 × 103 | |
| GA | 4.4 × 101 | 2.6 × 104 | 2.6 × 102 | 3.8 × 10–2 | 1.7 × 101 | 1.2 × 101 | 7.4 × 104 | 5.7 × 105 | 2.1 × 10–39 | 5.3 × 10–12 | 2.9 × 102 | 3.7 × 10–2 | 4.5 × 103 | 3.3 × 104 | |
| HS | 3.7 × 104 | 2.4 × 108 | 1.6 × 102 | 4.1 × 102 | 3.2 × 101 | 7.2 × 100 | 1.9 × 1011 | 6.2 × 107 | 3.0 × 10–49 | 6.8 × 10–7 | 2.7 × 108 | 6.2 × 10–3 | 2.5 × 103 | 3.8 × 105 | |
| Success rate | GTA | 100 | 0 | 100 | 100 | 100 | 100 | 100 | 0 | 100 | 12 | 100 | 100 | 100 | 100 |
| PSO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 0 | 0 | 0 | |
| SA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | |
| GA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | |
| HS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 31 | 0 | 0 | 0 | 0 | |
| evaluations | GTA | 13,401 | 11,605 | 10,920 | 12,686 | 19,352 | 11,234 | 9983 | 14,314 | 10,764 | 1701 | 9273 | 6757 | 12,573 | 11,933 |
| PSO | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 2200 | 3874 | 50,100 | 14,016 | 50,100 | 8064 | |
| SA | 5562 | 5132 | 4272 | 8002 | 5142 | 5632 | 5532 | 5002 | 8342 | 7622 | 5352 | 6972 | 4002 | 3032 | |
| GA | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 50,100 | 48,817 | |
| HS | 19,956 | 18,340 | 20,824 | 20,365 | 19,457 | 19,251 | 20,315 | 17,935 | 5010 | 8965 | 19,430 | 19,385 | 18,770 | 8976 | |
| Score | GTA | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| PSO | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| SA | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| GA | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| HS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Comparison | GTA vs PSO | GTA vs SA | GTA vs AG | GTA vs HS |
|---|---|---|---|---|
| GTA [%] | 95.65 | 94.96 | 92.86 | 94.54 |
| Algorithm [%] | 4.12 | 4.74 | 6.29 | 5.06 |
| Equal [%] | 0.24 | 0.31 | 0.86 | 0.39 |
| -value | 0 | 0 | 0 | 0 |
| Function | Best | Standard Deviation | Sucess Rate | ||
|---|---|---|---|---|---|
| Sphere | 2.14 × 10–18 | 1.88 × 10–15 | 3.73 × 10–15 | 100 | 14,328 |
| Rosenbrock | 1.99 × 104 | 2.00 × 104 | 2.53 × 101 | 0 | 11,195 |
| Rastrigin | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 100 | 10,488 |
| Griewank | 0.00 × 100 | 1.34 × 10–15 | 2.51 × 10–15 | 100 | 13,080 |
| Alpine | 2.44 × 10–15 | 7.19 × 10–14 | 7.22 × 10–14 | 100 | 20,593 |
| Brown | 1.84 × 10–18 | 2.29 × 10–15 | 5.34 × 10–15 | 100 | 12,007 |
| Chung Reynolds | 1.69 × 10–24 | 2.52 × 10–17 | 1.32 × 10–16 | 100 | 10,947 |
| Dixon Price | 1.00 × 100 | 1.00 × 100 | 1.20 × 10–8 | 0 | 16,782 |
| Exponential | 0.00 × 100 | 7.40 × 10–1 | 4.41 × 10–1 | 26 | 4132 |
| Salomon | 2.96 × 10–10 | 7.95 × 10–7 | 1.76 × 10–6 | 12 | 1518 |
| Schumer Steiglitz | 1.20 × 10–22 | 1.00 × 10–17 | 3.86 × 10–17 | 100 | 9657 |
| Sum of Powers | 3.09 × 10–21 | 1.16 × 10–3 | 1.02 × 10–2 | 97 | 8052 |
| Sum of Squares | 1.83 × 10–18 | 2.46 × 10–15 | 6.20 × 10–15 | 100 | 14,238 |
| Zakharov | 5.92 × 10–19 | 2.11 × 10–15 | 4.47 × 10–15 | 100 | 13,075 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meirelles, G.; Brentan, B.; Izquierdo, J.; Luvizotto, E., Jr. Grand Tour Algorithm: Novel Swarm-Based Optimization for High-Dimensional Problems. Processes 2020, 8, 980. https://doi.org/10.3390/pr8080980
Meirelles G, Brentan B, Izquierdo J, Luvizotto E Jr. Grand Tour Algorithm: Novel Swarm-Based Optimization for High-Dimensional Problems. Processes. 2020; 8(8):980. https://doi.org/10.3390/pr8080980
Chicago/Turabian StyleMeirelles, Gustavo, Bruno Brentan, Joaquín Izquierdo, and Edevar Luvizotto, Jr. 2020. "Grand Tour Algorithm: Novel Swarm-Based Optimization for High-Dimensional Problems" Processes 8, no. 8: 980. https://doi.org/10.3390/pr8080980
APA StyleMeirelles, G., Brentan, B., Izquierdo, J., & Luvizotto, E., Jr. (2020). Grand Tour Algorithm: Novel Swarm-Based Optimization for High-Dimensional Problems. Processes, 8(8), 980. https://doi.org/10.3390/pr8080980








