1. Introduction
Process monitoring based on mechanistic nonlinear models combined with atline and online measurement data [
1,
2,
3,
4,
5,
6,
7,
8] enables the detection of undesired deviations over the course of fermentations. This kind of process intelligence is promoted by the Process Analytical Technology (PAT) initiative defined by the United States Food and Drug Administration (FDA) [
9,
10]. With increased precision and availability, Raman [
11,
12,
13] and near-infrared (NIR) [
13,
14,
15,
16,
17] spectroscopy are used more often in recent years for cultivation monitoring. Most of the time, a partial least squares regression (PLS) is used for multivariate data analysis to correlate the analyte, for example, biomass or glucose concentration in the cultivation broth, with the spectroscopic information contained in the spectra. In contrast to process spectroscopy, a nonlinear process model enables model-predictive control or real-time optimization of processes. This has successfully been applied for chemical processes [
18] and is an established state-of-the-art method in chemical industry [
19]. However, fewer examples of its application in the biotechnological sector have been published so far [
1,
20,
21,
22,
23,
24,
25]. One of the very first applications in which the production of an antibiotic by a mycelial organism was optimized was reported in 1993 [
26,
27,
28].
Some authors have performed offline optimization of fed-batch cultivations [
29], but many focus on model-free process improvements [
30] or model-free response surface optimizations using a classical design of experiments [
31]. The biggest obstacle for the use of model-based approaches is the effort of obtaining a suitable biological process model. A possible solution is the automation of this step to facilitate the use of model-based methods. The approach published by Herold and King [
32] can be used to automatically generate structured models of low complexity based on measurement data. After interpolation of all the measured quantities in a cultivation, their change over time is merged in a few distinctive phenomena that are then compared to assign probabilities to model components for example limiting behavior of a substrate. As a result, a family of process models with a descending probability can be created in the form of differential equations in MATLAB code, and their respective model parameters can be estimated using automated code generation [
33].
The organism
Paenibacillus polymyxa (
P.p.), which is used as an example in the current case study, produces macrolactin D under limiting conditions. Macrolactins are of interest because of their antibacterial and, in some cases, antiviral effects [
34,
35]. For further information, see [
36]. Other use cases of
P.p. are the production of enhanced 2,3-Butanediol. For this application, Okonkwo et al. [
37] performed model-free optimization via response-surface methodology. A very basic model of
P.p. was developed by Haughney and Nauman [
38], which cannot necessarily be transferred to other strains of the organism. For the strain of
P.p. used in this publication, a structured model was manually developed by Violet et al. [
39]. Due to the high number of parameters, the identifiability of this model is rather poor. In contrast to the fact that the model is very sophisticated, the dynamics of the macrolactin production could not be captured correctly.
In this publication, a different approach was chosen. The basic model was not developed manually, but via the automated model identification approach presented by Herold [
40]. In this publication, we show how such models can successfully be used for robust optimization. On top of that, we show that this model provides a good basis for model improvement and extension. The refined model is the first published structured model of small size of
P.p. that includes a model for the off-gas concentration and the base consumption. In conclusion, we show that the attained model quality is satisfactory for state estimation and online optimization. Besides a publication that uses
P.p. as an example for cultivation monitoring via flourescence [
41], this is the first publication that applies NIR-spectrsocopy to
P.p. and furthermore integrates the results in a model-based state estimator.
The current paper is organized as follows: After a description of the experimental setup in
Section 2.1, a general model is introduced in
Section 2.2 with a discussion of various uncertainties, i.e., measurement, parameter, and model uncertainties. Multivariate analysis based on NIR data and model-based process optimization are discussed in
Section 2.3 and
Section 2.4, respectively. Optimization is divided up into an offline phase, named trajectory planning, and an online optimization. For optimization, a situation is considered in which a family of possible models is available. A state estimation using a sigma-point Kalman filter is summarized in
Section 2.5 before the results of an online optimization and a discussion are presented in
Section 3.
3. Results and Discussion
3.1. Automatically Generated Model (A)
In Herold’s dissertation [
40], several hundred structured biological models of small size for
P.p. were automatically proposed and built based on an automatically performed analysis of the fermentation data and on a set of rules. The model states are the mass of ammonium (Am), phosphate (Ph), glucose (C), and macrolactin (ML) in the supernatant and the cell-intern masses of active biomass (Xa) and, depending on the model, cell-internal storage compartments for ammonium (AmSt), phosphate (PhSt), and glucose (CSt). All cell compartments are summarized in the biomass (X). The complete model equations and parameters are given in
Appendix A. The parameters were fit to four cultivations. After identification, the models were sorted according to the quality of the parameter identification. For the sake of convenience, only the best eight models with two internal storage compartments (CSt and AmSt) and the best three models with a single internal storage compartment (PhSt) were selected and considered further. Because of the increased number of states and reaction equations, the two-storage models have a significantly higher number of parameters. For each of these models, Herold [
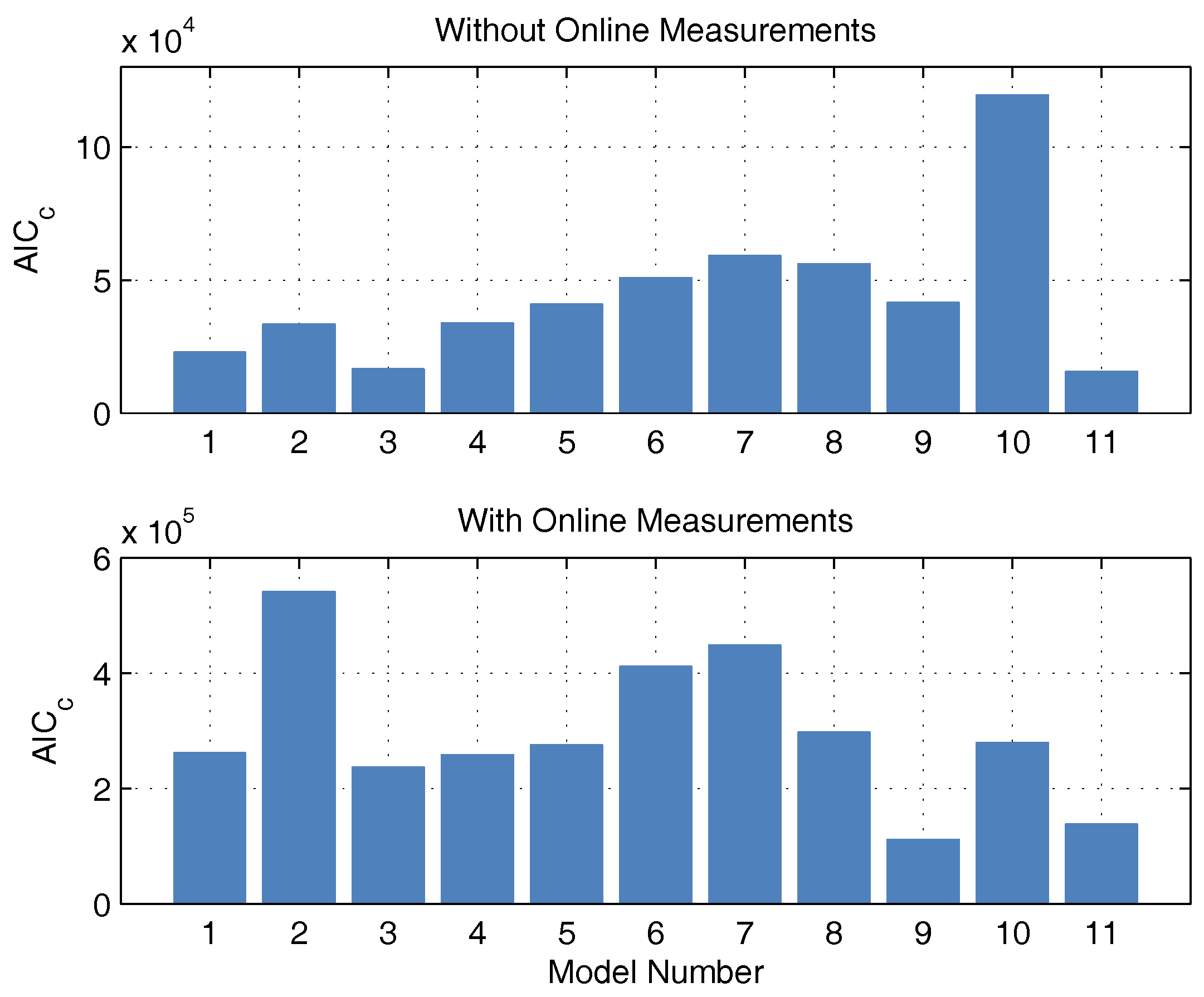
32] calculated the corrected information criterion according to the Akaike AIC
c and the derived model probability
. These are given in
Table 2. The models are numbered by ascending AIC
c, meaning that No. 1 is the most probable.
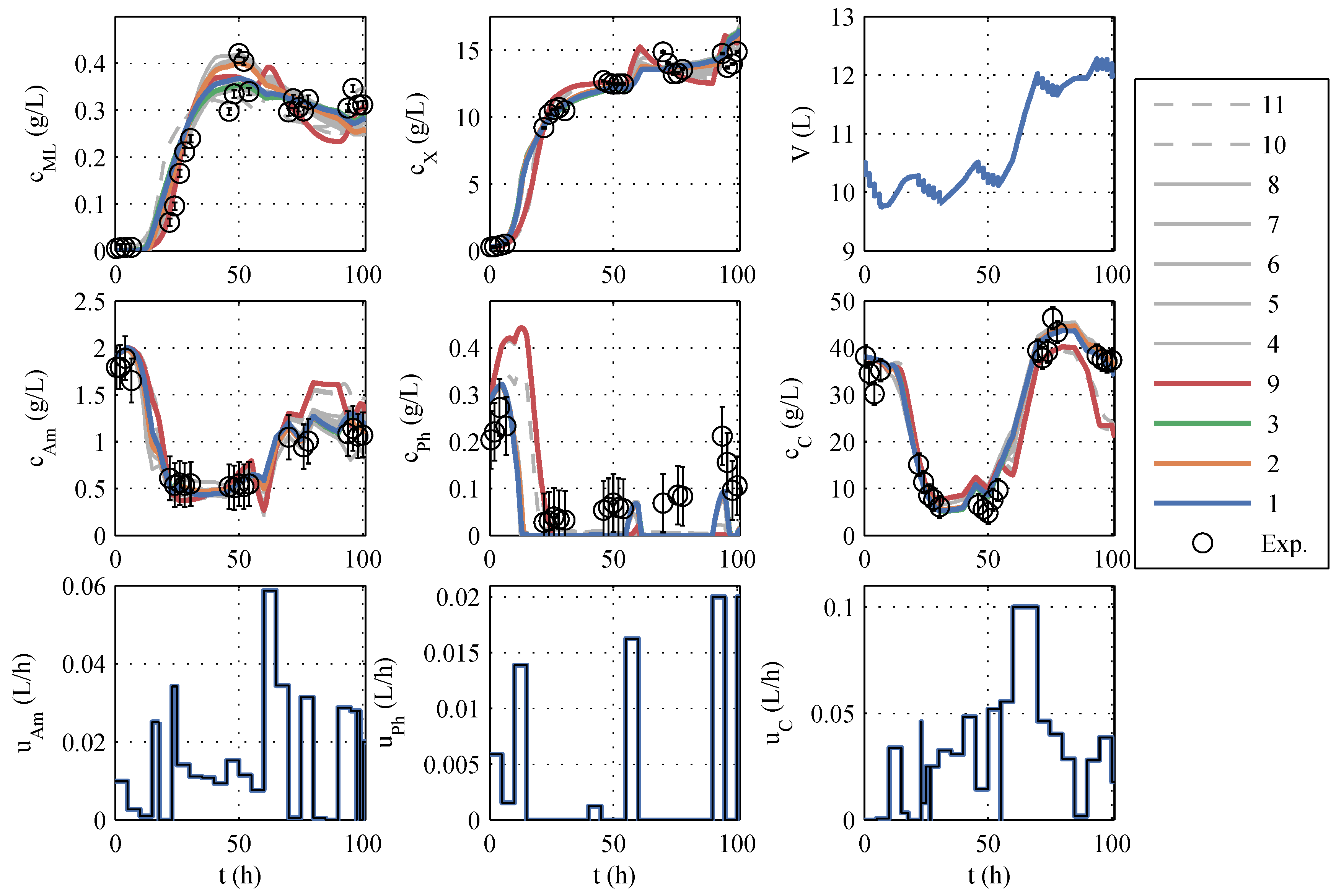
A typical identification experiment is given in
Figure 1. Because phosphate storage in
P.p. is also mentioned in the literature [
39], the best model with a phosphate storage (No. 9) is also taken into account in further planning to cover structural uncertainties, even though Akaike ruled it out. The models to be further used are highlighted in color (red, green, orange, and blue) in
Figure 1 and termed model family A (in
Table A1), and the remaining seven models are colored gray. The differences between the models are similarly large as the differences between the model and measured values. The AIC
c values also support this impression because no single model has a particularly high model probability. In other identification experiments (which are not shown here) the macrolactin simulation performed better. Model 9 was chosen as the best representative of its model structure, containing only a phosphate storage instead of ammonium and glucose storage. It is included in further process planning by manually assignind a model probability of 5%. It has to be noted that the decision to include model 9 was made before the extended model family B was developed. It turned out later that the phosphate storage approach is superior as will be discussed in the next subsection.
Overall, a purely visual differentiation and selection of the “best” model is difficult, and a model-based optimization based on only one seemingly “best”, nominal model would be at least questionable. For this reason, all good models als well as the best model with phosphate storage will be used, as shown below.
3.2. Extended Model (B)
The model family A was constructed fully automatically [
40] and was used in the early modeling stage for robust planning; see
Section 3.3.1 for the results. After performing the optimized experiment and installing process NIR spectroscopy as well as an online off-gas analysis, the new information was used to improve and extend the models towards a model family B.
There are some differences in the structure of model family A and model family B. The initial conditions such as the biomass concentration and the proportion of storage compartments within the cell in the inocolum are subject to disturbances. In model family A, the initial proportion of storage compartments was allowed to differ between experiments. The respective experiment-dependent parameters were found by optimization. The good adaptation that could be achieved in this way came at the expense of poor parameter identifiability. In the model family B, the parameters defining the proportion of storage compartments are set to a single global parameter for each component. The number of parameters that have to be determined by parameter identification is therefore drastically reduced and the identifiability is significantly improved.
Further changes from model family A to B concern biological phenomena. In family A, there is an “active biomass” Xa and there are storage compartments. Xa is degraded via a decay rate . The degraded biomass is not part of the measured biomass and is not converted back into substrates or any other usable form. This behaviour seems strange from a chemical and biological point of view. The source of this formulation could be automatic modelling based on the detection of phenomena.
After manual model checking, this behaviour is corrected in model family B. A state inactivated/deactivated biomass is added to the model, which consists of the cell-intern degraded active biomass.
For the modeling of the carbon dioxide content in the exhaust gas, only active biomass and the maintenance metabolism were taken into account. The dynamic effects of mass transport and storage in the liquid were neglected. This resulted in the CO
2 mass flow entering the gas phase of
The mass balance in the headspace can be written as follows:
It is assumed that ammonium is absorbed in the form of NH
3, so the H
+ of the dissolved NH
must be compensated by the corresponding amount of base added to keep the pH constant [
71]. Further modeling approaches such as the production of organic acids in the context of an overflow metabolism are not considered. The differential equation for the mass of correction fluid base
results in the following:
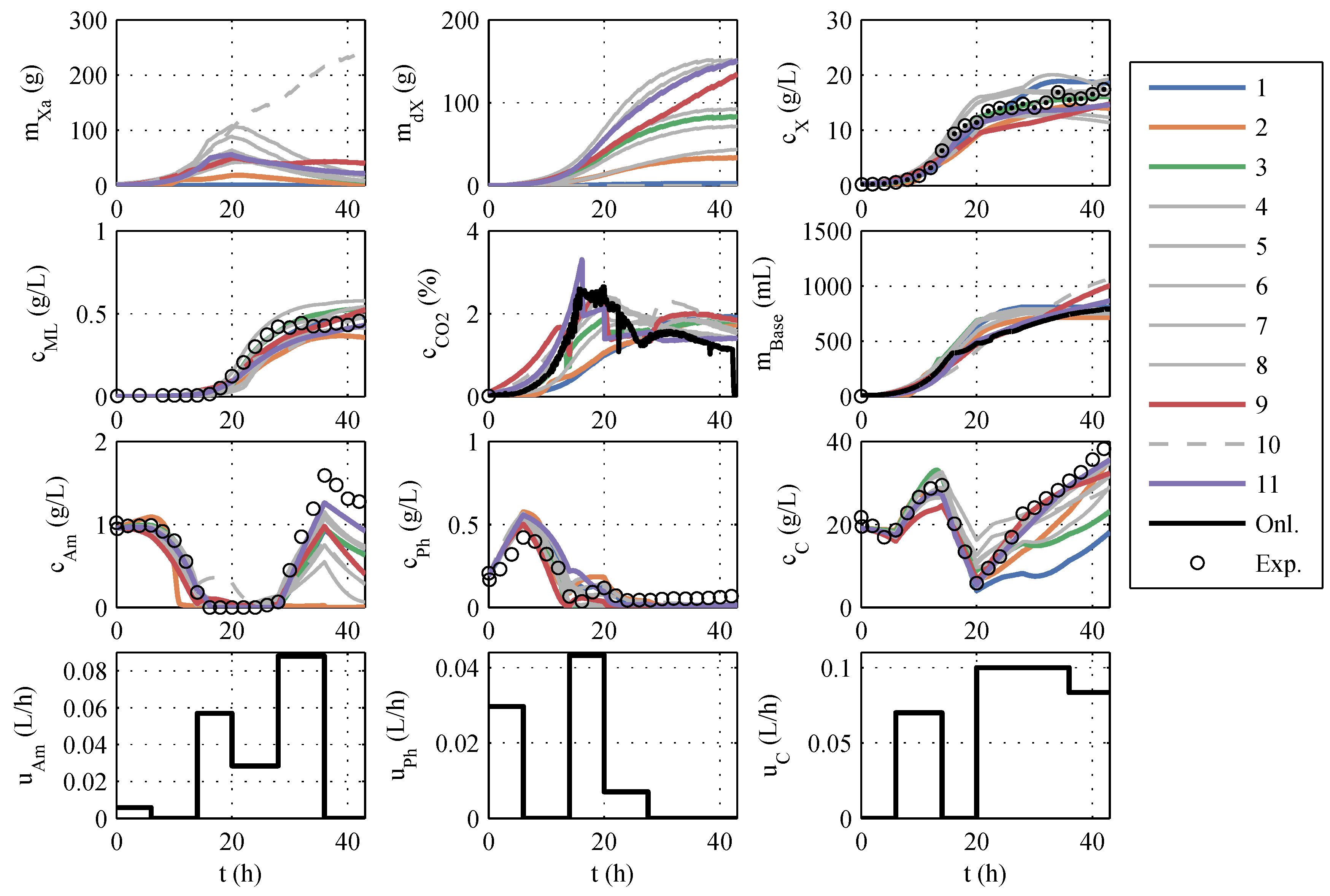
The models developed in this way are based directly on model family A, so the numbering of the models in
Section 3.1 is retained. After implementing the model modifications, another parameter estimation was performed. A typical identification experiment is shown in
Figure 2.
In contrast to the identification experiments of models A, the extended models show very large differences between the different models, especially in the description of CO
2, biomass, and glucose concentration. This could be because the additional measurement information is now available, while the number of parameters has increased only insignificantly. The AIC
c values and the corresponding probabilities are newly calculated. It is debatable whether the measurement data of CO
2 and base are to be considered in the calculation of the AIC
c. Both measured values have no influence on substrate consumption, biomass growth, and macrolactin production, and, therefore, are completely irrelevant for the process optimization. However, the correct description of the online measurements is relevant for the state estimation and should also be taken into account. Consequently, both approaches were pursued and are illustrated in
Figure 3 in the form of AIC
c values. If the model probabilities are calculated without continuous measurement data, there is an Akaike probability of almost 100% for model 11. If online measurements are considered, model 11 also shows good performance because it scores second best with only a narrow distance to the best model but a large distance to the next-best model. Hence, model 11 is used for the online optimization and state estimation.
The differential equations for model 11, the parameter values, and the parameter standard deviations after the subset selection are given in the
Appendix B.
NIR Spectroscopy
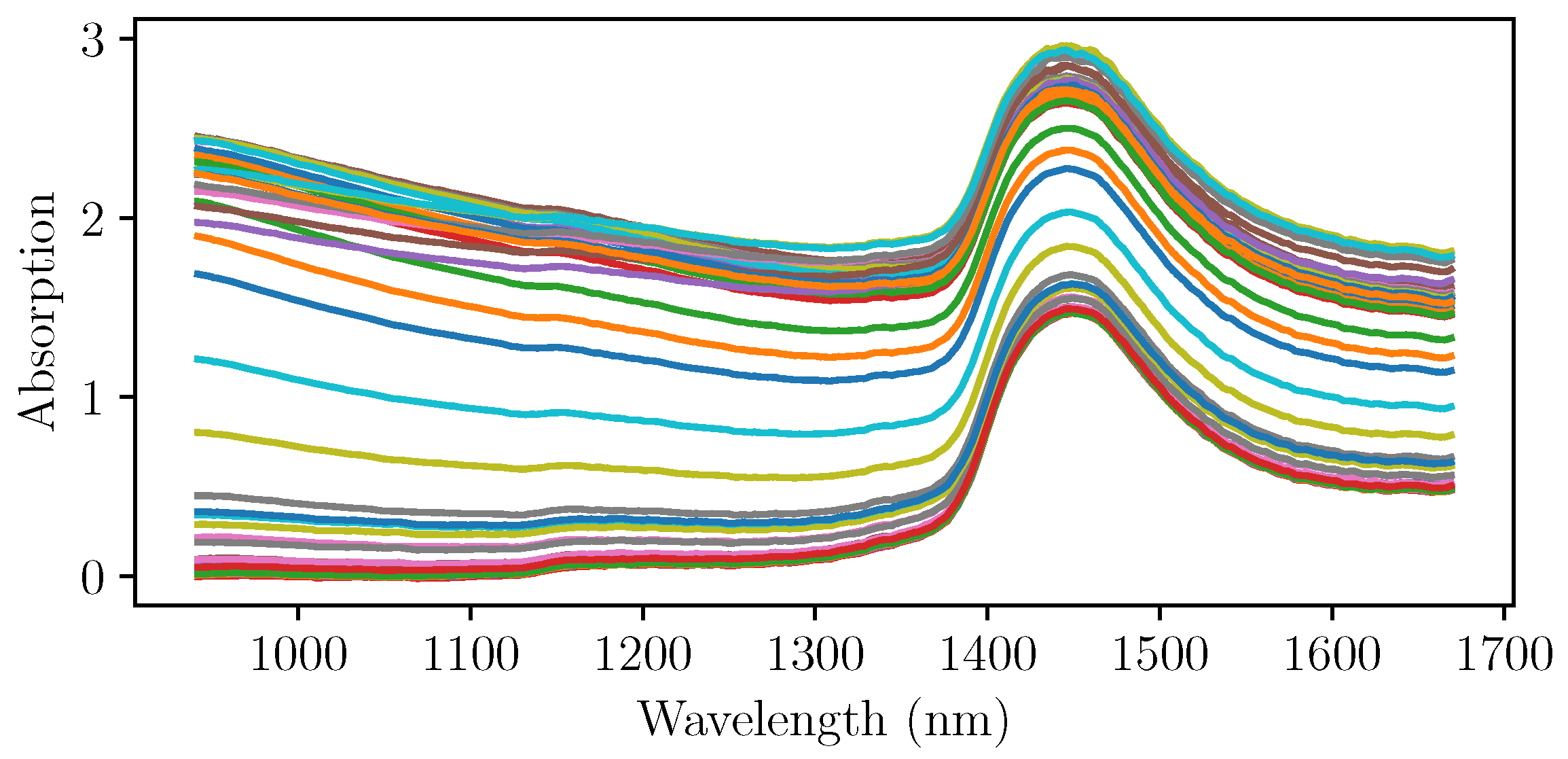
After the initial experiments, four more cultivations were run using NIR spectroscopy as an online measurement of the biomass concentration. The pretreated NIR spectra at the sampling times of the three cultivations that were used for the PLS regression are shown in
Figure 4. It can be seen that the gradient with respect to the wavelength differs strongly, even at the same levels of absorption at wavelengths up to 1400 nm. A simple univariate intepretation that would focus on only one wavelenght would not yield the desired outcome.
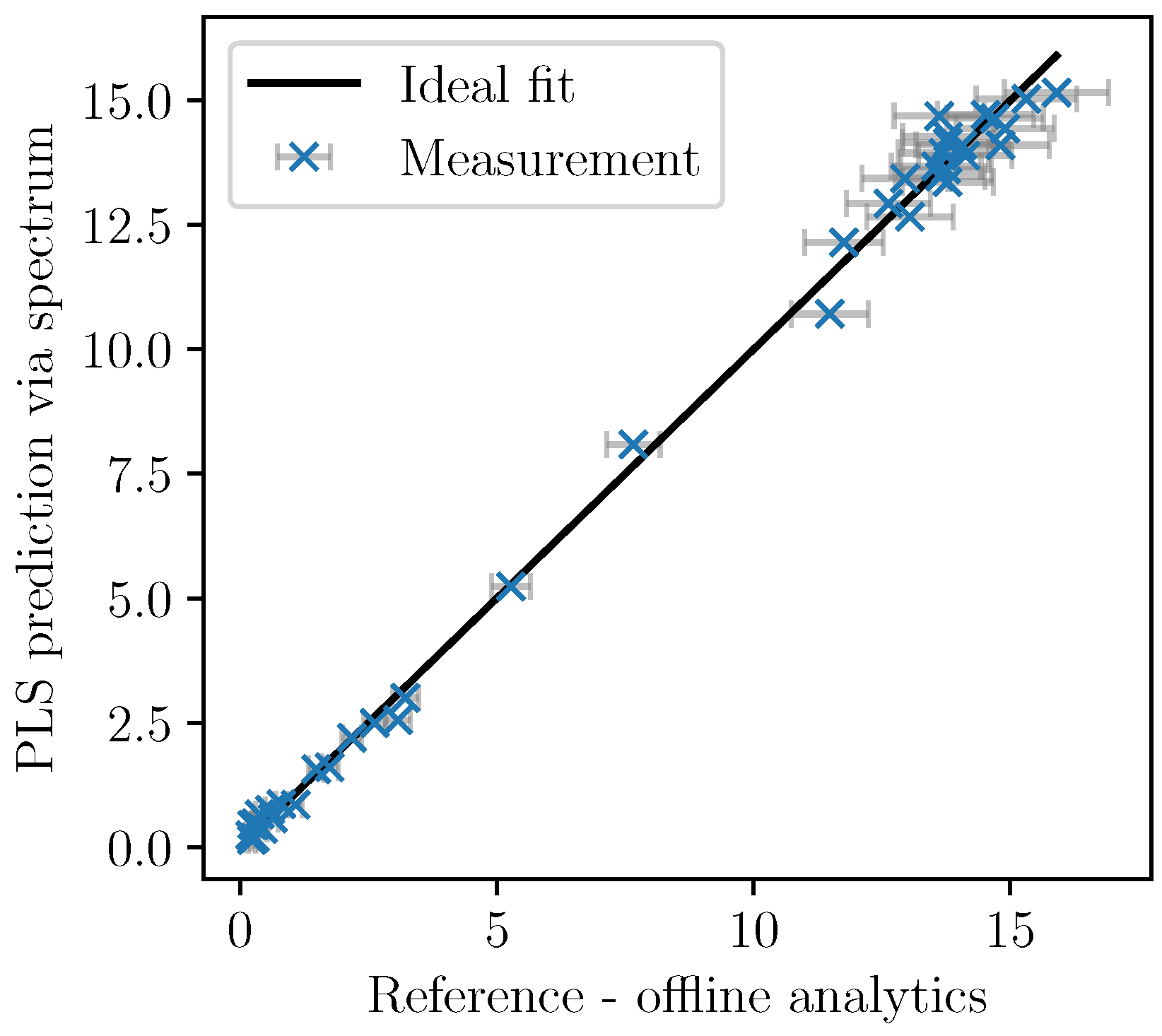
Based on the cross-validation, the number of factors was set to five. In
Figure 5, the cross-validation of the PLSR predictions are plotted over the analytically measured reference values together with the ±2-
error bars of the measurements. The model shows good accordance as the deviation from the ideal fit could be explained by the measurement errors associated with the offline measurements.
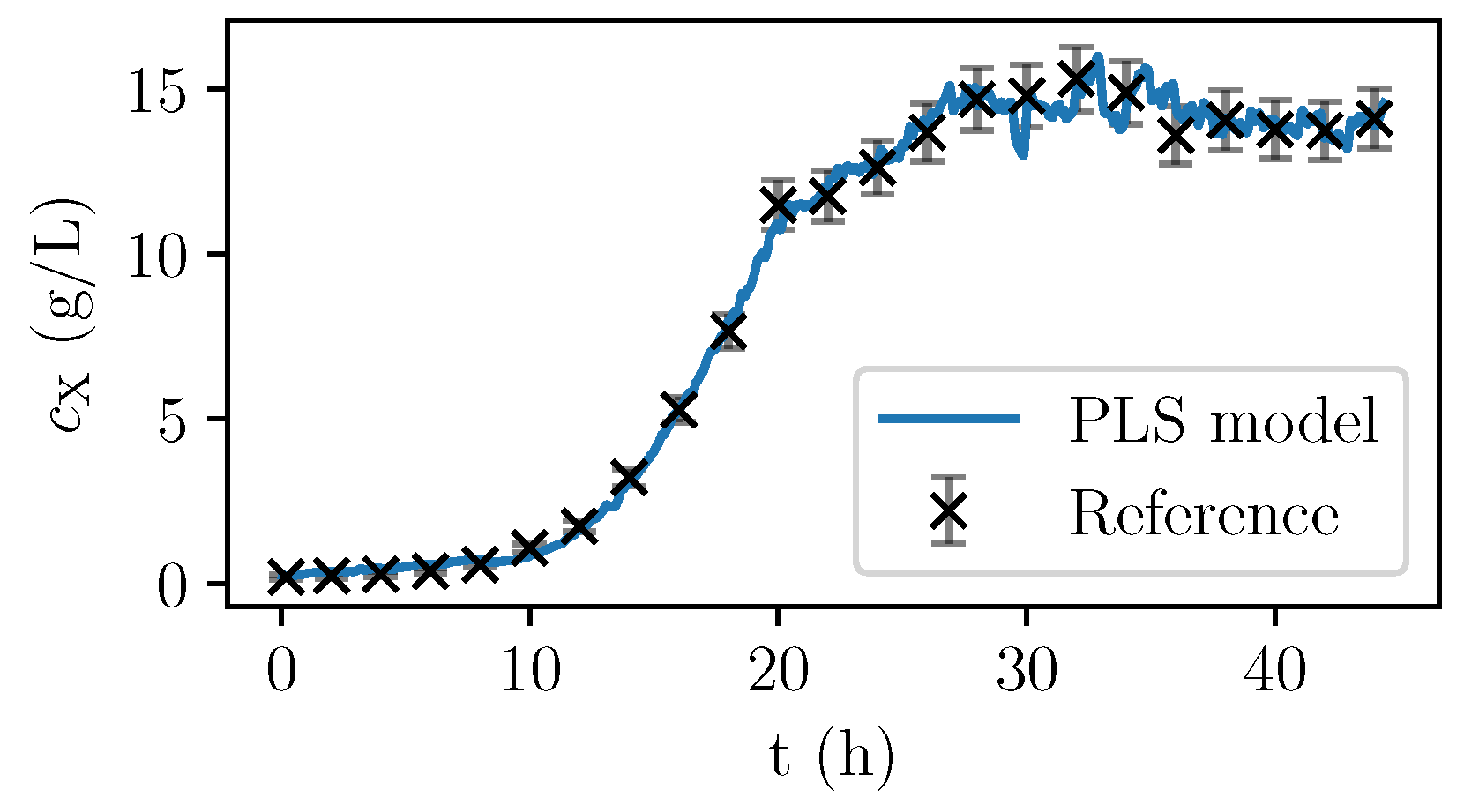
Only the spectra with corresponding offline-measurements were used for the calibration. Once identified, the PLS model can be used to calculate the PLS predictions of the biomass concentration based on the almost continuously recorded NIR spectra. In
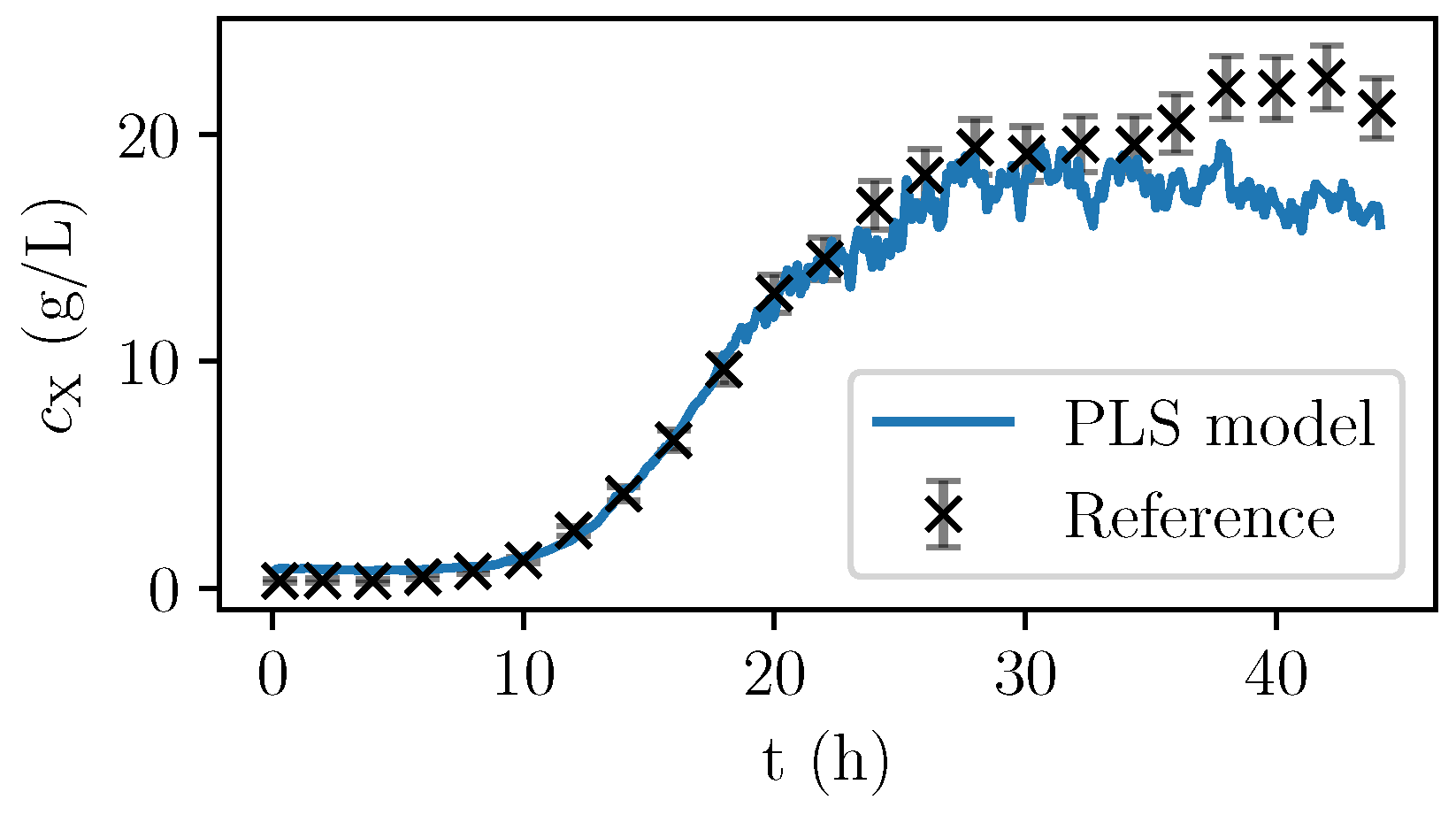
Figure 6, the values are given for a fermentation used for calibration. In
Figure 7, the validation experiment not used for PLSR is depicted. In the validation cultivation, the biomass concentration surpasses the values that were reached in the calibration cultivations, as shown in
Figure 5. Above 15 g/L of
, large deviations occur. Furthermore, in the first eight hours, the prediction deviates significantly from the measurement data. All in all, PLS predictions are rather precise at medium biomass concentrations between 2 and 14 g/L. Therefore, NIR spectroscopy perfectly complements the CO
2 measurements that are more precise in the first part of the exponential growth phase at medium biomass concentrations between 0 and 2 g/L but that lack a good description of the limiting conditions.
No reliable PLS model was found for the substrates and macrolactin D.
3.3. Early-Stage Robust Optimization
The use case of the multi-model trajectory planning (MMTP) is the early process design while the model is still being improved. Only four cultivations were performed prior to the MMTP experiment; the following results are based only on the model family A.
3.3.1. Reference Nominal Process Optimization
Nominal trajectory planning serves as the reference method by choosing the best model of the model family, according to the AICc criterion and using it for offline optimization. To avoid a limitation by the limited oxygen input, a maximum biomass concentration of 20 g/L and a maximum biomass growth of 17 g/h was determined. To prevent the depletion of glucose, even in case of uncertainties, a lower limit of 10 g/L was set for the optimization.
From the covariance matrix
, the predicted uncertainties of the measured variables during the fermentation process were determined via the state sensitivities. The volume, the concentrations of biomass, macrolactin, ammonium, phosphate, and glucose, as well as the control profiles of the optimal trajectory for model 1 and the
-
ranges of uncertainty, are shown in blue in
Figure 8. In comparison, the curves of models 2, 3, and 9 are given, which occur if the manipulated variables optimized with model 1 were used for the simulation. Model 11 was not considered in this early phase, per
Section 3.1.
In contrast to the parameter identification of model family A, the course of the various models differs considerably, shown in
Figure 8. It is particularly noticeable in macrolactin production. The simulated macrolactin concentration with models 2, 3, and 9 is extremely low, whereas the quantity of 1.2 g/L computed with model 1 is significantly higher than the quantities achieved in the identification tests. Furthermore, it is noticeable that the simulation of the three models after 20 h fermentation time is far outside the ±2-
range of model 1 for almost all the measured variables. The range within
standard deviations
comprises about 95% of the possible results. If one had relied solely on model 1, one would assume that macrolactin concentrations of less than 0.5 g/L occur only in 2.5% of the cases. However, all other models predict values below 0.2 g/L. These low macrolactin concentrations would be extremely unlikely according to model 1. However, according to the AIC
c, models 1, 2, and 3 were almost equally likely based on the set of the four first identification experiments. Therefore, it is evident that the parametric uncertainty of model 1 does not cover the uncertainty of the model choice.
3.3.2. Robust Planning and Experimental Validation
To address the problems outlined above, a subset of four models selected via the AIC
c criterion was used in robust planning (multi-model trajectory planning: MMTP) with Equation (
13). For model 9, a probability of 5% was defined, and the other weights were based on their Akaike probability and adjusted accordingly. The simulated courses of substrate, biomass, and macrolactin concentrations are shown together with the experimental results in
Figure 9.
For a comparison with the nominal planning, only simulations are available. The most important parameter here is the product quantity achieved. To compare the MMTP (using models 1, 2, 3, and 9) and nominal planning (using model 1), the respective optimal feeding profile is used for simulations with the models (1, 2, 3, and 9). The resulting macrolactin masses are given in
Table 3. For each case, the minimal and the mean macrolactin mass are determined and compared. Model 2 would yield only 1.1 g using the nominal optimization approach, whereas the smallest amount of macrolactin in the MMTP case is 281% higher. Similarly, the model-weighted mean is 33% higher for the MMTP case compared with the profiles obtained via nominal optimization. In the experimental realization, 6.8 g macrolactin were produced, which is less than the predicted average by the MMTP but still significantly more than the maximum 4.3 g achieved in the identification experiments. Furthermore, the effects of the parameter uncertainties on the fermentation were reduced without being explicitly taken into account. The computing time of the MMTP with an Intel i7 (3.07 GHz) of 72 min is only slightly more than twice as long as with the nominal planning, which requires 32 min.
3.4. Online Optimization
The multi-model approach can be omitted once a final model can be deducted and its parameters identified, which is the case here after four additional cultivations using online measurements of CO2, consumed base, and NIR spectroscopy. From the extended and modified model family B, model 11 is found to be satisfactorily predictive on its own. However, besides the model uncertainty, there are other sources of deviations; for example, the initial biomass in the inoculum. Whereas offline robust optimization can only account for general deviations and leads to a very conservative design, online optimization can deal with the measured or estimated disturbances in the process hence leading to better results.
3.4.1. State Estimation
Only minimal tuning of the SPKF was necessary. The measurement uncertainty of the online measurements is not kept at the values that were determined experimentally. For the state estimation, the relative part
a of Equation (
2) is increased to take into account the deviation between the model value and measured value. The standard deviations of the corresponding measurements are given in
Table 4. The measured value-dependent calculation of
is particularly appropriate here because the CO
2 concentration and the base consumption at low values, i.e., in the exponential growth phase, are a very good indicator of growth, while the model uncertainty is much more pronounced at higher concentrations. The absolute measurement uncertainty of the CO
2 concentration was reduced to 0.1
to take better advantage of this effect. For the NIR spectroscopy, the opposite is the case. High uncertainty was assumed at low biomass levels, while the relative error is smaller compared with the
and base.
No correlation between the measured values was assumed,
R was hence a diagonal matrix with the corresponding variances. For the uncertainties of the initial values, a heuristic approach [
67] yielded a relative deviation of
for the biomass components and a value of
for the remaining states. For the creation of sigma points, the parameter covariance matrix
was used after the subset selection described above instead of
Q. The corresponding standard deviations of the parameters are given in
Table A2.
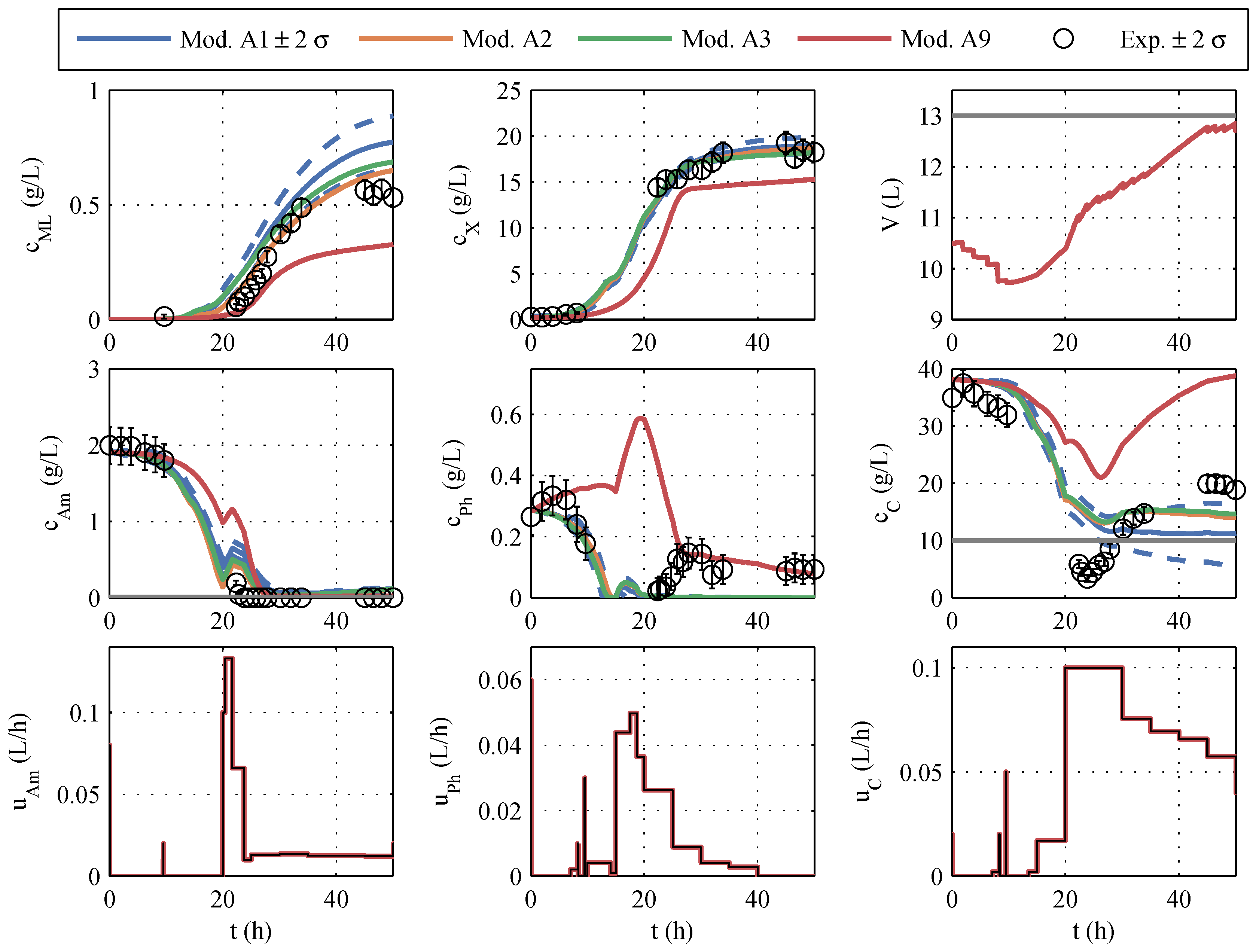
The SPKF was tested with a cultivation, where the effects of large deviations in the inoculation biomass could be observed. Here, temperature fluctuations in the preculture phase led to a change in the inoculation biomass. The planned course of the offline robust process planning (MMTP) with model family A is given together with the experimental results in
Figure 10. For illustration, the SPKF based on the new model B 11 was used to estimate and plot the states. The SPKF combines the complementary online measurements in an optimal way to determine the nonmeasurable states. A more detailed analysis is given in [
8].
Observability
In all models, the rank of the observation matrix is lower than the respective system order, i.e., the number of estimated states. The differential equations obtained from mass balances, as shown in
Appendix B, make it clear that the macrolactin quantity in the cultivation has no effect on the other states. Therefore, it is not possible to infer the macrolactin concentration indirectly via measurements. If one removes the mass of macrolactin from the system description and calculates the observability matrix again, its rank corresponds to the system order of the respective model at any time. Thus, all states save for the macrolactin mass are observable. However, it is not ensured that macrolactin converges with the actual value, but
Figure 10 shows that the prediction nevertheless shows acceptable agreement with the offline measured values.
3.4.2. Experimental Application of Online Optimization
A final cultivation was performed to show the applicability of real-time optimization (RTO) with an SPKF state estimation. Every 0.1 h, a measurement update with the current online measurements was performed. Subsequently, the RTO was performed based on the newly estimated state. The constraints of the concentrations applied formerly to the MMTP were slightly adjusted. For the RTO, the upper biomass limit was removed, and the biomass growth limit was raised to 25 g/h because a better model quality allowed for a more precise estimation of growth and, therefore, fewer safety buffers were needed. The limitation of the glucose concentration to 10 g/L and the volume to 13 L were maintained.
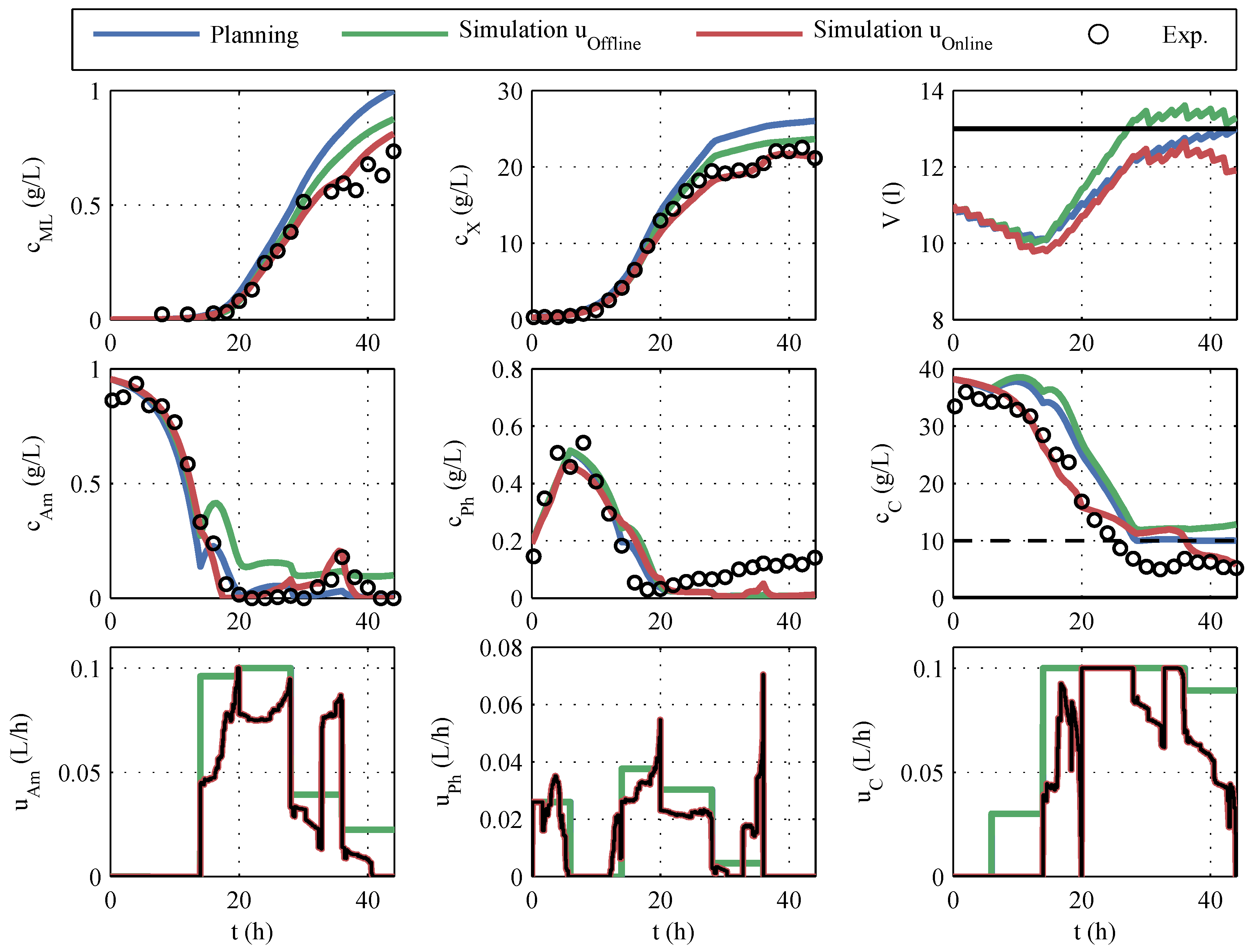
The experimental results of the online optimization are given in
Figure 11. Additionally, different simulations are plotted. The result of the offline optimization is marked with
planning in blue. In the initial offline optimization, the volumes of the correction fluids (acid, base, antifoam agent) were unknown and, therefore, not taken into account. The
simulation in green is obtained by using the offline optimized control variables together with the actually consumed correction fluids and the known sampling volumes for the simulation. The
simulation in red corresponds to
simulation , but the online-optimized control variables are used in the simulation.
The
planning shows the highest predicted macrolactin concentration, but if this planning was to be carried out, the disregard of the correction fluids would result in a lower macrolactin concentration and an unacceptable violation of the volume constraint. The online optimization processes the SPKF’s current estimate of volume and, therefore, complies with the volume constraint but at a 7% lower predicted macrolactin concentration. If one compares the manipulated variable profiles in
Figure 11 with the offline planning, it is noticeable that considerably less feeding volume was added. In
Table 5, the impressive savings of the feeding quantities (28% for glucose) are summarized.
The comparison of hypothetical, simulated macrolactin quantities is only of limited significance. However, if one compares the macrolactin concentrations achieved, the RTO with 0.73 g/L eclipses the maximum concentrations of the offline robust process optimization (0.57 g/L). Because of the reduction of the fermentation duration from 50 h to 44 h, the improvement of the spacetime yield is even more pronounced.
4. Conclusions
The current experimental study showed the high performance of model-based approaches for process improvement. Based on a family of automatically built models (A), robust offline optimization led to increased macrolactin yield while ensuring that the constraints would be met by all the models. The use of nominal optimization based only on the best model would have underestimated the uncertainty of the model selection. Experimental validation confirmed the higher product yield that was achieved via robust process optimization even after only four cultivations. The performed experiments showed great discriminatory potential, leading to the selection of one superior model (B). The relatively simple model with only nine states in total permits good interpretability of the results and a low numerical burden for identification, as well as state estimation and optimization. However, even if the model uncertainty was greatly reduced, the influence of the deviations in the inoculum still had a large impact on the fermentation and its productivity. It has been shown how a SPKF can successfully estimate the course of the cultivation in real time based on the measurements of base consumption for pH control and CO2 concentration in the off-gas. The use of process NIR spectroscopy with PLS regression was incorporated in the SPKF and led to an even more robust estimation because of its complementary measurement information. The use of real-time product maximization was successfully tested for the production of macrolactin D by Paenibacillus polymyxa. Besides reducing the amount of glucose feed by 28% compared with the offline planning, the optimization led to the largest mass of macrolactin compared with all other performed cultivations in the same setting.
Further investigations have to evaluate how well RTO can compensate for disturbances such as feeding pump failure and temperature fluctuations because the focus of the current contribution was on the process of model development and fast deployment of model-based methods in the process development.