Numerical Study of Binary Trickle Flow of Liquid Iron and Molten Slag in Coke Bed by Smoothed Particle Hydrodynamics
Abstract
:1. Introduction
2. Methods
2.1. Basic Formulation of SPH
2.2. Density Approximation
2.3. Fluid Motion Equation and Discretization
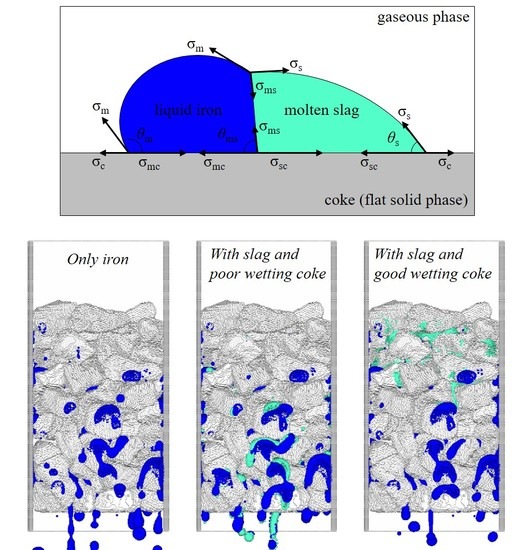
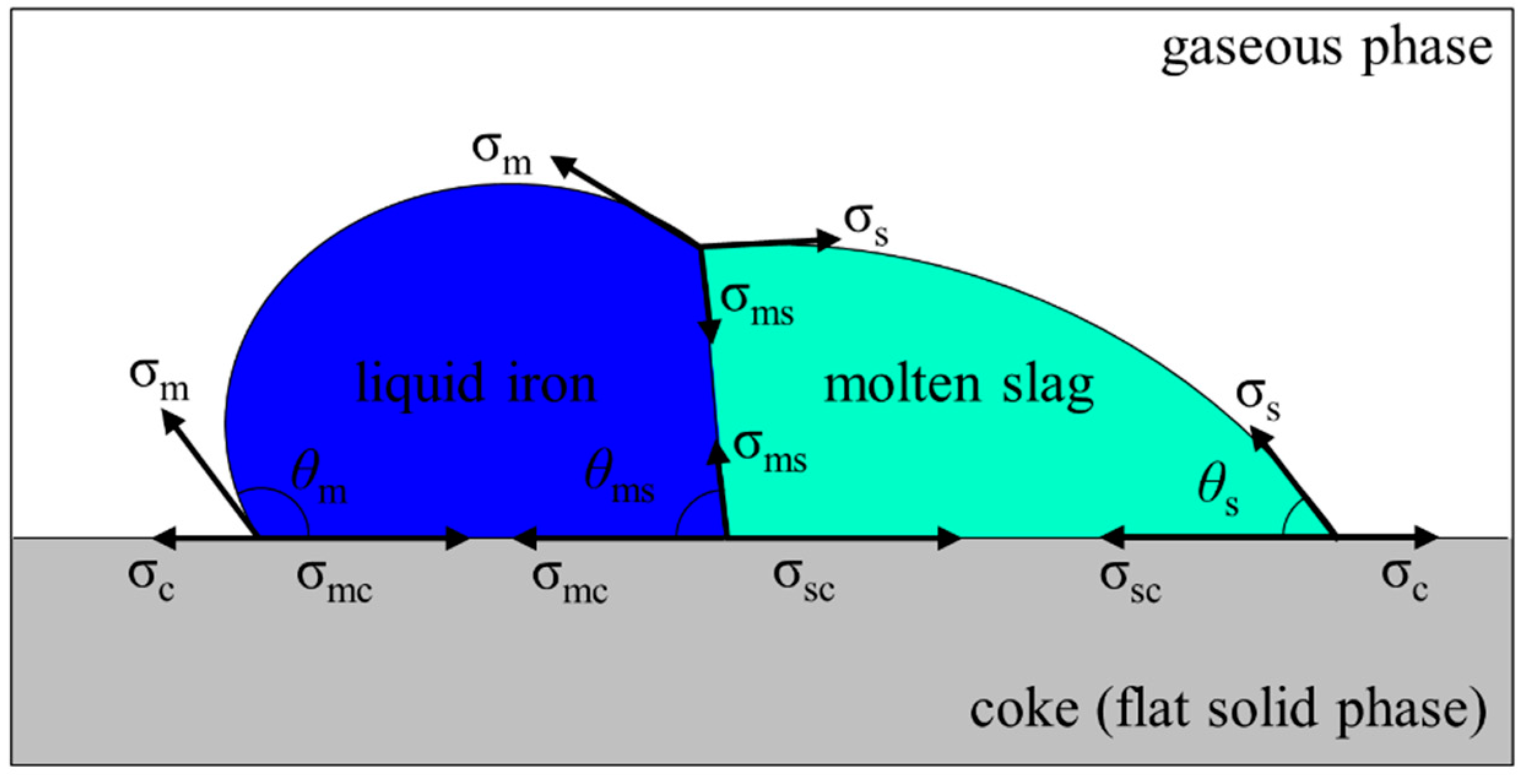
2.4. Interfacial Force Model
2.5. Physical Properties of Liquid Iron and Molten Slag
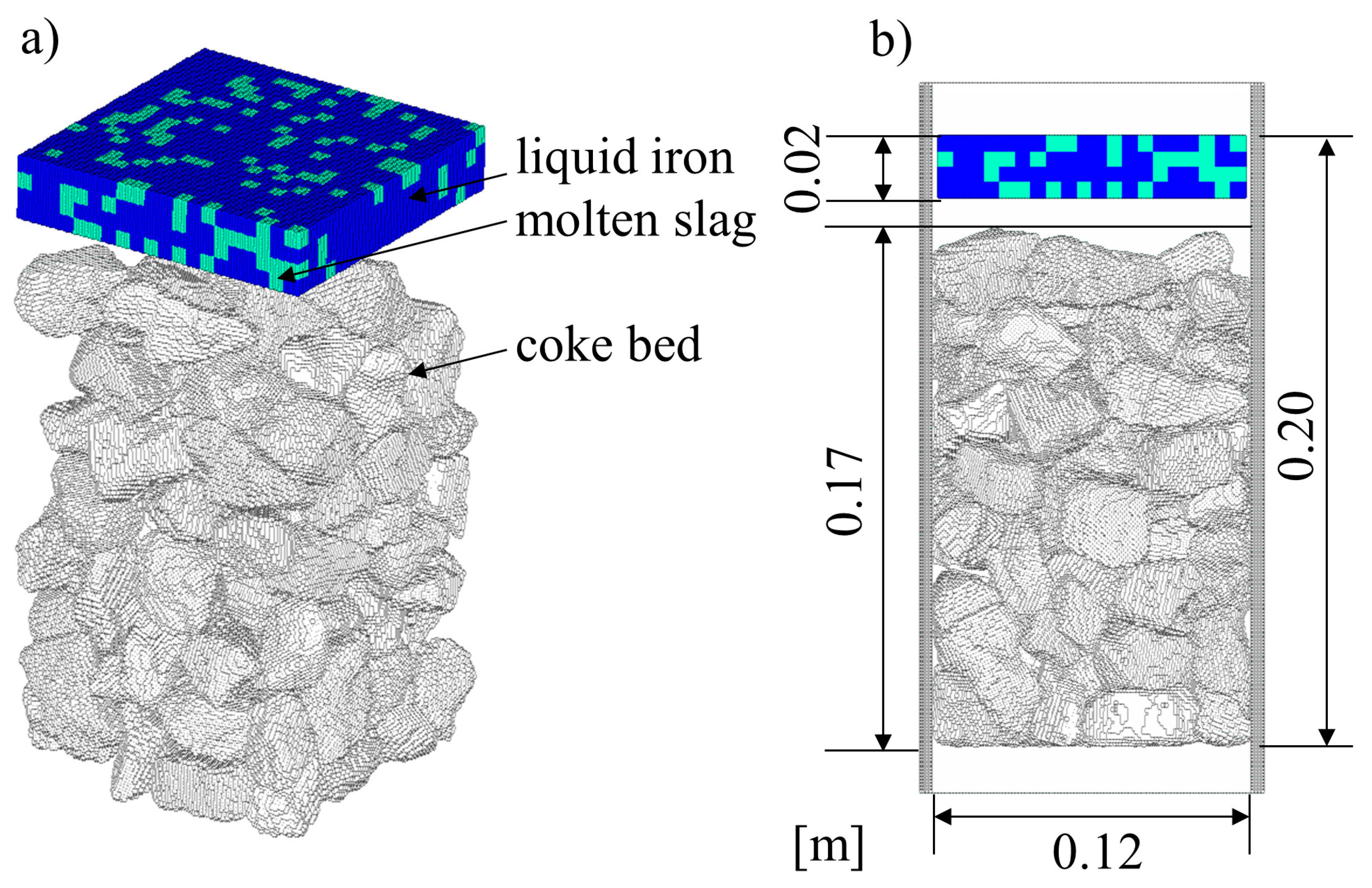
2.6. Calculation Condition
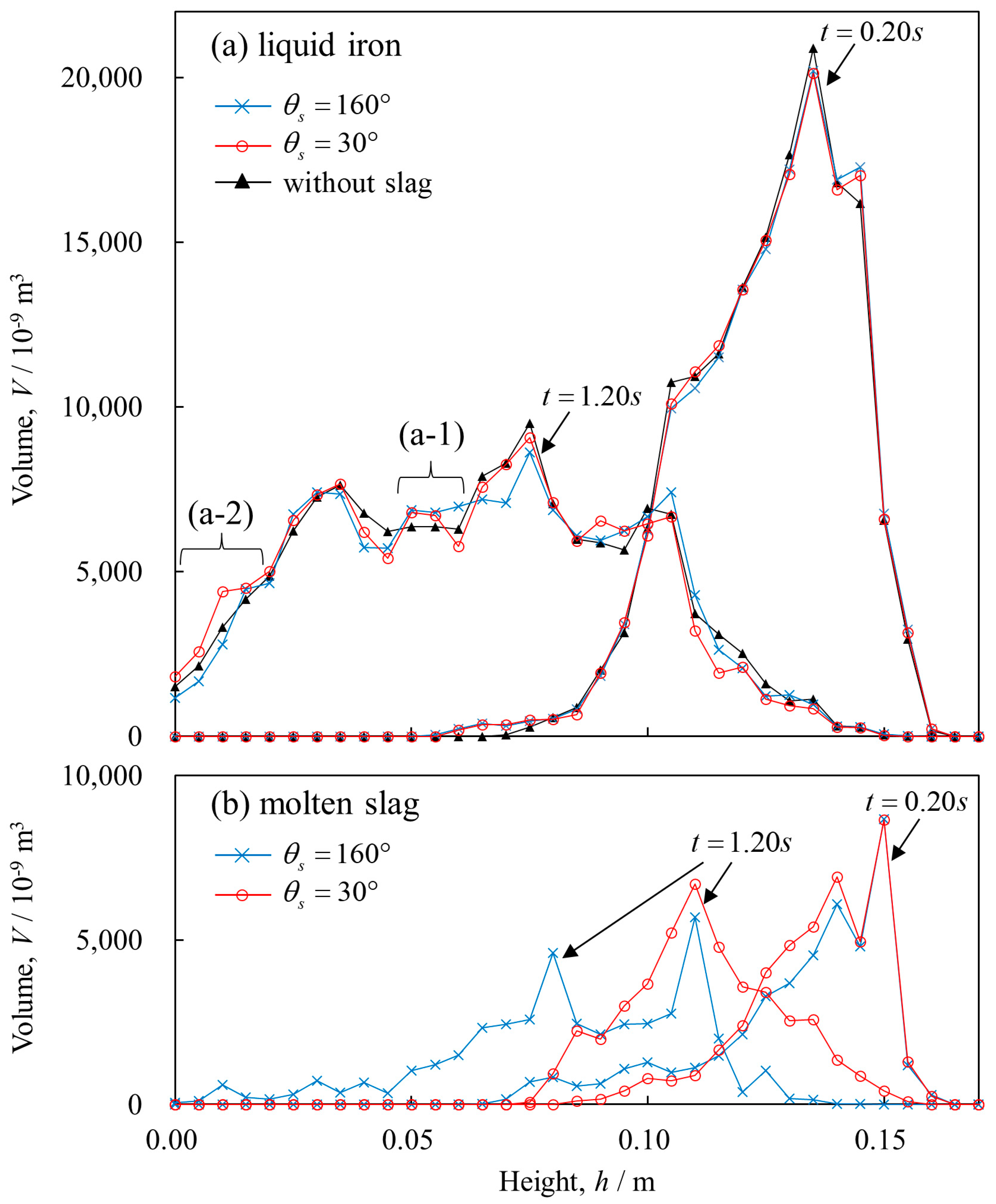
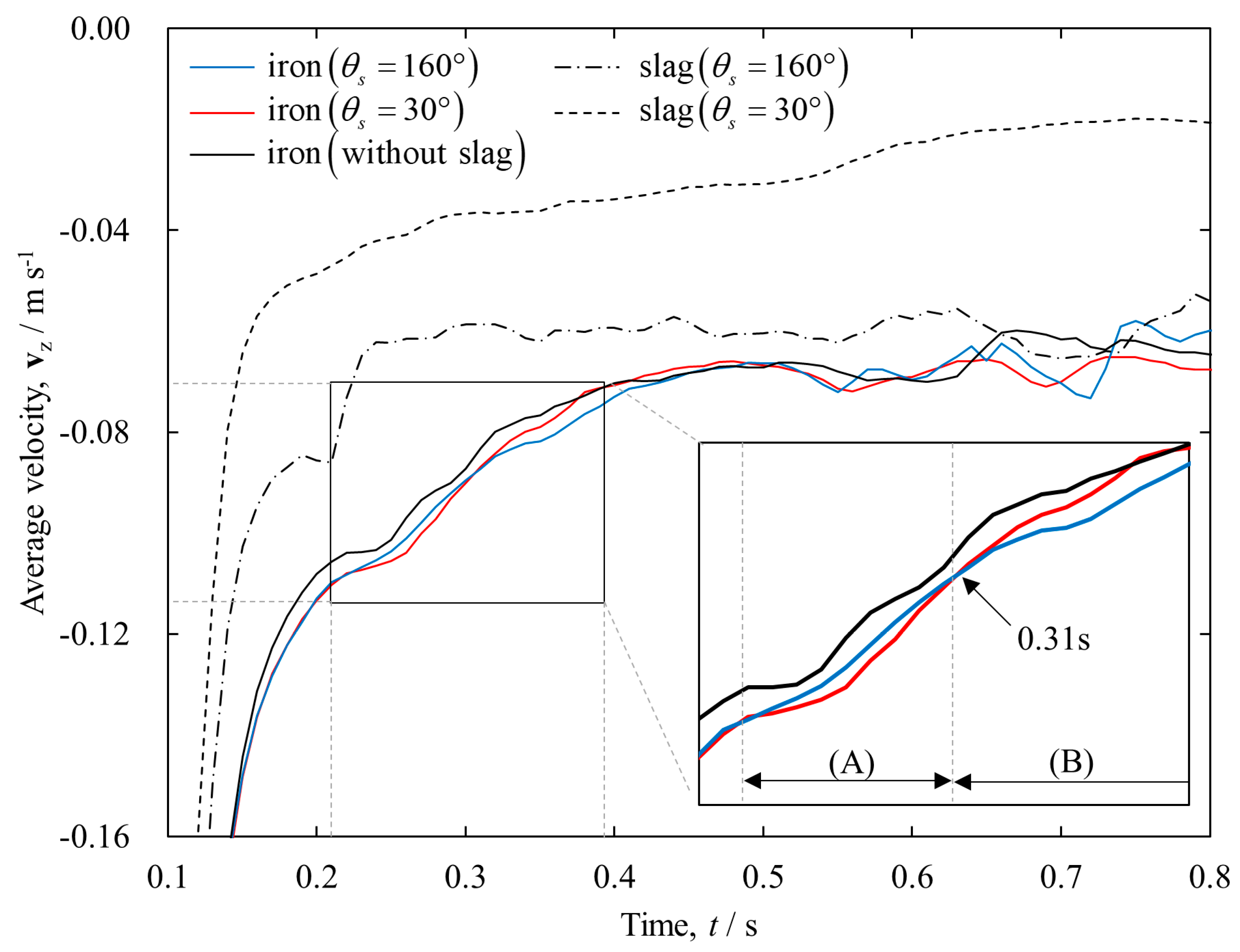
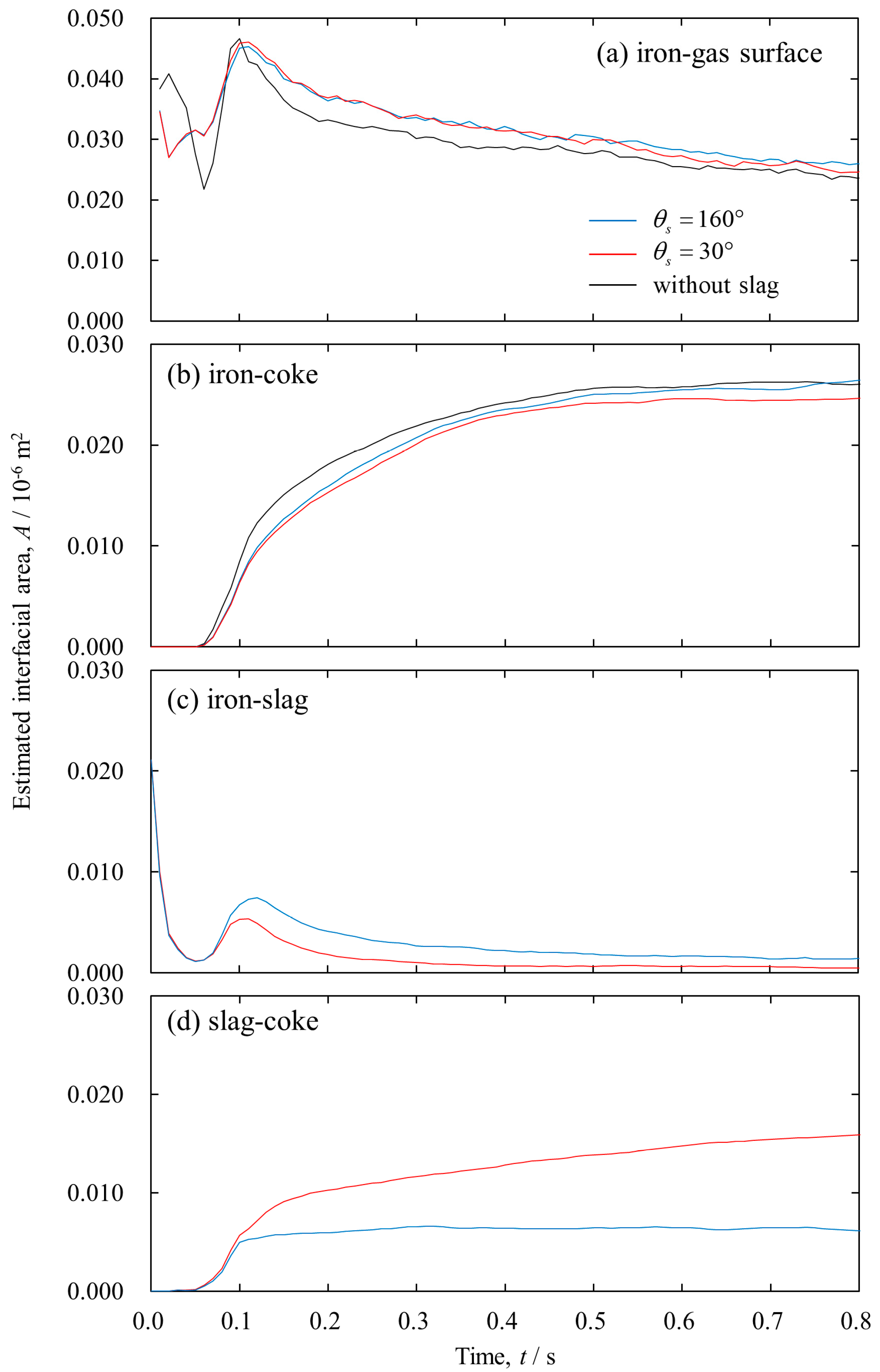
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fukutake, T.; Rajakumar, V. Liquid holdups and abnormal flow phenomena of the gas-liquid counter-current flow in packed beds under simulating conditions of the flow in the dropping zone of a blast furnace. Tetsu-to-Hagané 1980, 66, 1937–1946. [Google Scholar] [CrossRef] [Green Version]
- Chew, S.J.; Zulli, P.; Yu, A. Modelling of liquid flow in the blast furnace. Application in a comprehensive blast furnace model. ISIJ Int. 2001, 41, 1122–1130. [Google Scholar] [CrossRef]
- Kawabata, H.; Shinmyou, K.; Harada, T.; Usui, T. Influence of channeling factor on liquid hold-ups in an initially unsoaked bed. ISIJ Int. 2005, 45, 1474–1481. [Google Scholar] [CrossRef] [Green Version]
- Husslage, W.M.; Bakker, T.; Steeghs, A.G.S.; Reuter, M.A.; Heerema, R.H. Flow of molten slag and iron at 1500 °C to 1600 °C through packed coke beds. Metall. Mater. Trans. B 2005, 36, 765–776. [Google Scholar] [CrossRef]
- Jang, D.; Shin, M.; Oh, J.S.; Kim, H.S.; Yi, S.H.; Lee, J. Static holdup of liquid slag in carbonaceous beds. ISIJ Int. 2014, 54, 1251–1255. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Liu, Y.; Zhou, Z.; Wang, J.; Xue, Q. Static holdup of liquid slag in simulated packed coke bed under oxygen blast furnace ironmaking conditions. JOM 2018, 70, 29–33. [Google Scholar] [CrossRef]
- Ohgusu, H.; Sassa, Y.; Tomita, Y.; Tanaka, K.; Hasegawa, M. Main factors affecting static holdup of molten slag in coke-packed bed. Tetsu-to-Hagané 1992, 78, 1164–1170. [Google Scholar] [CrossRef] [Green Version]
- Oh, J.S.; Lee, J. Composition-dependent reactive wetting of molten slag on coke substrates. J. Mater. Sci. 2016, 51, 1813–1819. [Google Scholar] [CrossRef]
- White, J.F.; Lee, J.; Hessling, O.; Glaser, B. Reactions between liquid CaO-SiO2 slags and graphite substrates. Metall. Mater. Trans. B 2017, 48, 506–515. [Google Scholar] [CrossRef] [Green Version]
- Saito, K.; Ohno, K.I.; Miki, T.; Sasaki, Y.; Hino, M. Behavior of ironmaking slag permeation to carbonaceous material layer. ISIJ Int. 2006, 46, 1783–1790. [Google Scholar] [CrossRef] [Green Version]
- Kang, T.W.; Gupta, S.; Saha-Chaudhury, N.; Sahajwalla, V. Wetting and interfacial reaction investigations of coke/slag systems and associated liquid permeability of blast furnaces. ISIJ Int. 2005, 45, 1526–1535. [Google Scholar] [CrossRef] [Green Version]
- Geleta, D.D.; Siddiqui, M.I.H.; Lee, J. Characterization of Slag Flow in Fixed Packed Bed of Coke Particles. Metall. Mater. Trans. B 2019. [Google Scholar] [CrossRef]
- Vångö, M.; Pirker, S.; Lichtenegger, T. Unresolved CFD-DEM modeling of multiphase flow in densely packed particle beds. Appl. Math. Model. 2018, 56, 501–516. [Google Scholar] [CrossRef]
- Jiao, L.; Kuang, S.; Yu, A.; Li, Y.; Mao, X.; Xu, H. Three-dimensional modeling of an ironmaking blast furnace with a layered cohesive zone. Metall. Mater. Trans. B 2020, 51, 258–275. [Google Scholar] [CrossRef]
- Rabbani, H.S.; Joekar-Niasar, V.; Pak, T.; Shokri, N. New insights on the complex dynamics of two-phase flow in porous media under intermediate-wet conditions. Sci. Rep. 2017, 7, 4584. [Google Scholar] [CrossRef] [PubMed]
- Rabbani, H.S.; Or, D.; Liu, Y.; Lai, C.Y.; Lu, N.B.; Datta, S.S.; Stone, H.A.; Shokri, N. Suppressing viscous fingering in structured porous media. Proc. Natl. Acad. Sci. USA 2018, 115, 4833–4838. [Google Scholar] [CrossRef] [Green Version]
- Natsui, S.; Ishihara, S.; Kon, T.; Ohno, K.; Nogami, H. Detailed Modelling of Packed-bed Gas Clogging Due to Thermal-softening of Iron Ore by Eulerian-Lagrangian Approach. Chem. Eng. J. in press. [CrossRef]
- Alpak, F.O.; Berg, S.; Zacharoudiou, I. Prediction of fluid topology and relative permeability in imbibition in sandstone rock by direct numerical simulation. Adv. Water Resour. 2018, 122, 49–59. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Panchenko, A. Pairwise force smoothed particle hydrodynamics model for multiphase flow: Surface tension and contact line dynamics. J. Comput. Phys. 2016, 305, 1119–1146. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Saxén, H. A simulation study of two-liquid flow in the taphole of the blast furnace. ISIJ Int. 2013, 53, 988–994. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.S.; Kim, J.G.; Sasaki, Y. The role of molten slag in iron melting process for the direct contact carburization: Wetting and separation. ISIJ Int. 2010, 50, 1099–1106. [Google Scholar] [CrossRef] [Green Version]
- Jeong, I.H.; Kim, H.S.; Sasaki, Y. Trickle flow behaviors of liquid iron and molten slag in the lower part of blast furnace. ISIJ Int. 2013, 53, 2090–2098. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Viswanathan, N.N.; Ballal, N.B. Flow phenomena in the dripping zone of blast furnace—A review. Steel Res. Int. 2017, 88, 1600440. [Google Scholar] [CrossRef]
- Kon, T.; Natsui, S.; Ueda, S.; Nogami, H. Analysis of effect of packed bed structure on liquid flow in packed bed using moving particle semi-implicit method. ISIJ Int. 2015, 55, 1284–1290. [Google Scholar] [CrossRef] [Green Version]
- Natsui, S.; Kikuchi, T.; Suzuki, R.O.; Kon, T.; Ueda, S.; Nogami, H. Characterization of liquid trickle flow in poor-wetting packed bed. ISIJ Int. 2015, 55, 1259–1266. [Google Scholar] [CrossRef] [Green Version]
- Natsui, S.; Nashimoto, R.; Takai, H.; Kumagai, T.; Kikuchi, T.; Suzuki, R.O. SPH simulations of the behavior of the interface between two immiscible liquid stirred by the movement of a gas bubble. Chem. Eng. Sci. 2016, 141, 342–355. [Google Scholar] [CrossRef]
- Natsui, S.; Sawada, A.; Kikuchi, T.; Suzuki, R.O. Holdup characteristics of melt in coke beds of different shapes. ISIJ Int. 2018, 58, 1742–1744. [Google Scholar] [CrossRef] [Green Version]
- Natsui, S.; Nashimoto, R.; Kikuchi, T.; Suzuki, R.O.; Takai, H.; Ohno, K.; Sukenaga, S. Capturing the non-spherical shape of granular media and its trickle flow characteristics using fully-Lagrangian method. AIChE J. 2017, 63, 2257–2271. [Google Scholar] [CrossRef]
- Nakano, M.; Ito, K. Three dimensional simulation of lime particle penetration into molten iron bath using smoothed particle hydrodynamics. ISIJ Int. 2016, 56, 1537–1542. [Google Scholar] [CrossRef] [Green Version]
- Tsuboi, M.; Ito, K. Cold model experiment and numerical simulation of flow characteristics of multi-phase slag. ISIJ Int. 2017, 57, 1191–1196. [Google Scholar] [CrossRef] [Green Version]
- Hosono, N.; Karato, S.I.; Makino, J.; Saitoh, T.R. Terrestrial magma ocean origin of the moon. Nat. Geosci. 2019, 12, 418–423. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Kondo, M.; Koshizuka, S.; Suzuki, K.; Takimoto, M. Surface Tension Model Using Inter-particle Force in Particle Method. In Proceedings of the ASME/JSME 2007 5th Joint Fluids Engineering Conference, San Diego, CA, USA, 30 July 2007; American Society of Mechanical Engineers Digital Collection. pp. 93–98. [Google Scholar]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Keverian, J.; Taylor, H.F. Effects of gaseous and solid addition on surface tension and contact angle (on graphite) if various iron-carbon alloys. Trans. AFS 1957, 65, 212–221. [Google Scholar]
- Machin, J.S.; Yee, T.B. Viscosity studies of system CaO-MgO-Al2O3-SiO2: II, CaO-Al2O3-SiO2. J. Am. Ceram. Soc. 1948, 31, 200–204. [Google Scholar] [CrossRef]
- Mukai, K.; Ishikawa, T. Surface tension measurements on liquid slags in CaO-SiO2, CaO-Al2O3 and CaO-Al2O3-SiO2 systems by a pendant drop method. J. Jpn. Inst. Met. 1981, 45, 147. [Google Scholar] [CrossRef] [Green Version]
- Mehta, A.S.; Sahajwalla, V. Influence of composition of slag and carbonaceous materials on the wettability at the slag/carbon interface during pulverised coal injection in a blast furnace. Scand. J. Metall. 2000, 29, 17–29. [Google Scholar] [CrossRef]
- Watakabe, S.; Takeda, K.; Igawa, K. Coke properties and operational conditions of blast furnace to prevent coke degradation in the raceway. Tetsu-to-Hagané 2002, 88, 8–15. [Google Scholar] [CrossRef]
- Natsui, N.; Sawada, A.; Terui, T.; Kashihara, Y.; Kikuchi, T.; Suzuki, R.O. Evaluation of coke degradation effect on flow characteristics in packed bed using 3D scanning for rotational mechanical strength test and solid-liquid-gas three-phase dynamic model analysis. Tetsu-to-Hagané 2018, 104, 347–357. [Google Scholar] [CrossRef] [Green Version]
- Natsui, S.; Ohno, K.I.; Sukenaga, S.; Kikuchi, T.; Suzuki, R.O. Detailed modeling of melt dripping in coke bed by DEM-SPH. ISIJ Int. 2018, 58, 282–291. [Google Scholar] [CrossRef]
- Sugiyama, T.; Nakagawa, T.; Sibaike, H.; Oda, Y. Analysis on liquid flow in the dripping zone of blast furnace. Tetsu-to-Hagané 1987, 73, 2044–2051. [Google Scholar] [CrossRef]
- Natsui, S.; Nashimoto, R.; Kumagai, T.; Kikuchi, T.; Suzuki, R.O. An SPH study of molten matte–slag dispersion. Metall. Mater. Trans. B 2017, 48, 1792–1806. [Google Scholar] [CrossRef]
- Kon, T.; Sukenaga, S.; Ueda, S. Dynamic wettability of liquids on gasified metallurgical cokes. ISIJ Int. 2017, 57, 1166–1172. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natsui, S.; Tonya, K.; Nogami, H.; Kikuchi, T.; Suzuki, R.O.; Ohno, K.-i.; Sukenaga, S.; Kon, T.; Ishihara, S.; Ueda, S. Numerical Study of Binary Trickle Flow of Liquid Iron and Molten Slag in Coke Bed by Smoothed Particle Hydrodynamics. Processes 2020, 8, 221. https://doi.org/10.3390/pr8020221
Natsui S, Tonya K, Nogami H, Kikuchi T, Suzuki RO, Ohno K-i, Sukenaga S, Kon T, Ishihara S, Ueda S. Numerical Study of Binary Trickle Flow of Liquid Iron and Molten Slag in Coke Bed by Smoothed Particle Hydrodynamics. Processes. 2020; 8(2):221. https://doi.org/10.3390/pr8020221
Chicago/Turabian StyleNatsui, Shungo, Kazui Tonya, Hiroshi Nogami, Tatsuya Kikuchi, Ryosuke O. Suzuki, Ko-ichiro Ohno, Sohei Sukenaga, Tatsuya Kon, Shingo Ishihara, and Shigeru Ueda. 2020. "Numerical Study of Binary Trickle Flow of Liquid Iron and Molten Slag in Coke Bed by Smoothed Particle Hydrodynamics" Processes 8, no. 2: 221. https://doi.org/10.3390/pr8020221
APA StyleNatsui, S., Tonya, K., Nogami, H., Kikuchi, T., Suzuki, R. O., Ohno, K.-i., Sukenaga, S., Kon, T., Ishihara, S., & Ueda, S. (2020). Numerical Study of Binary Trickle Flow of Liquid Iron and Molten Slag in Coke Bed by Smoothed Particle Hydrodynamics. Processes, 8(2), 221. https://doi.org/10.3390/pr8020221