A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace
Abstract
1. Introduction
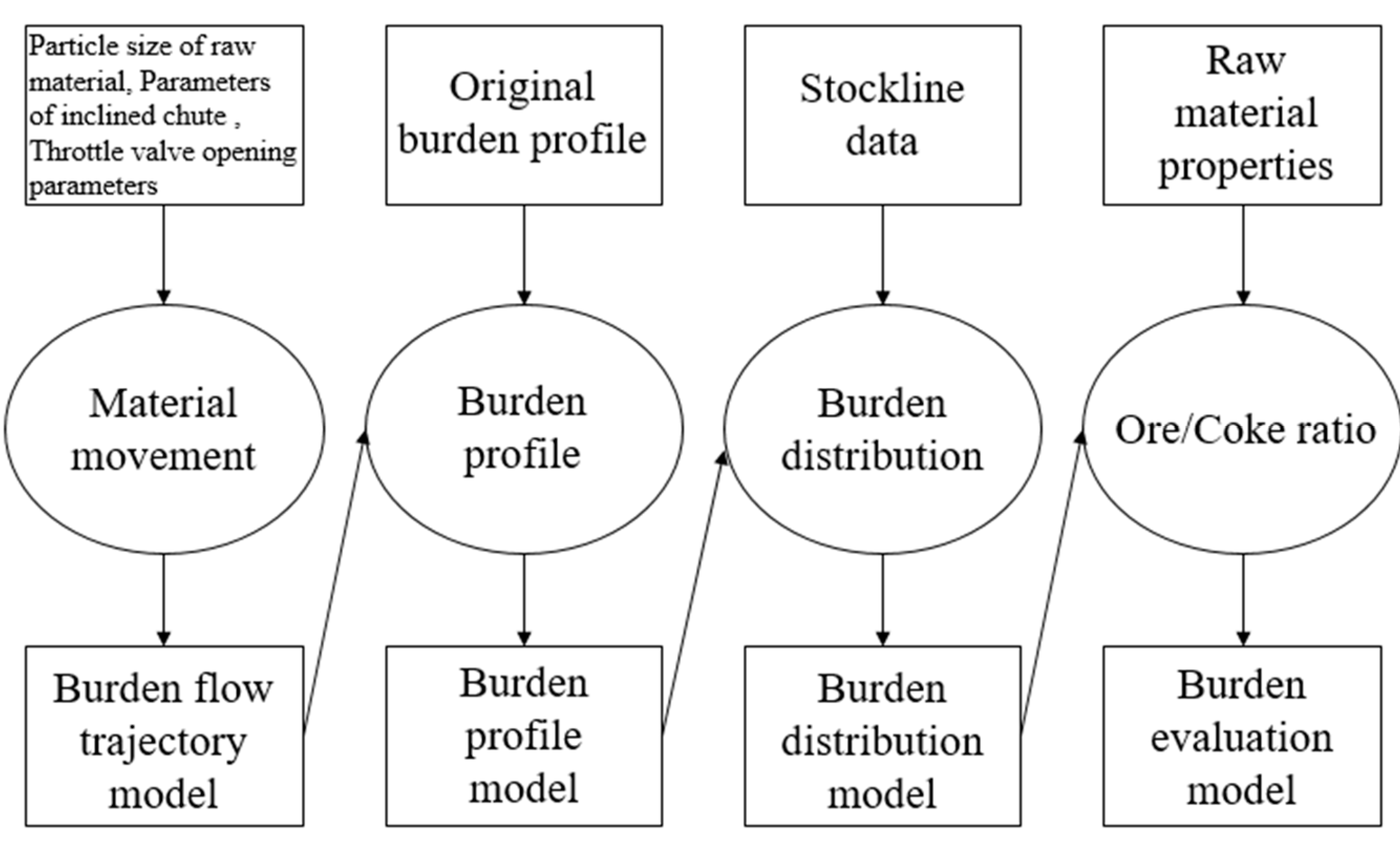
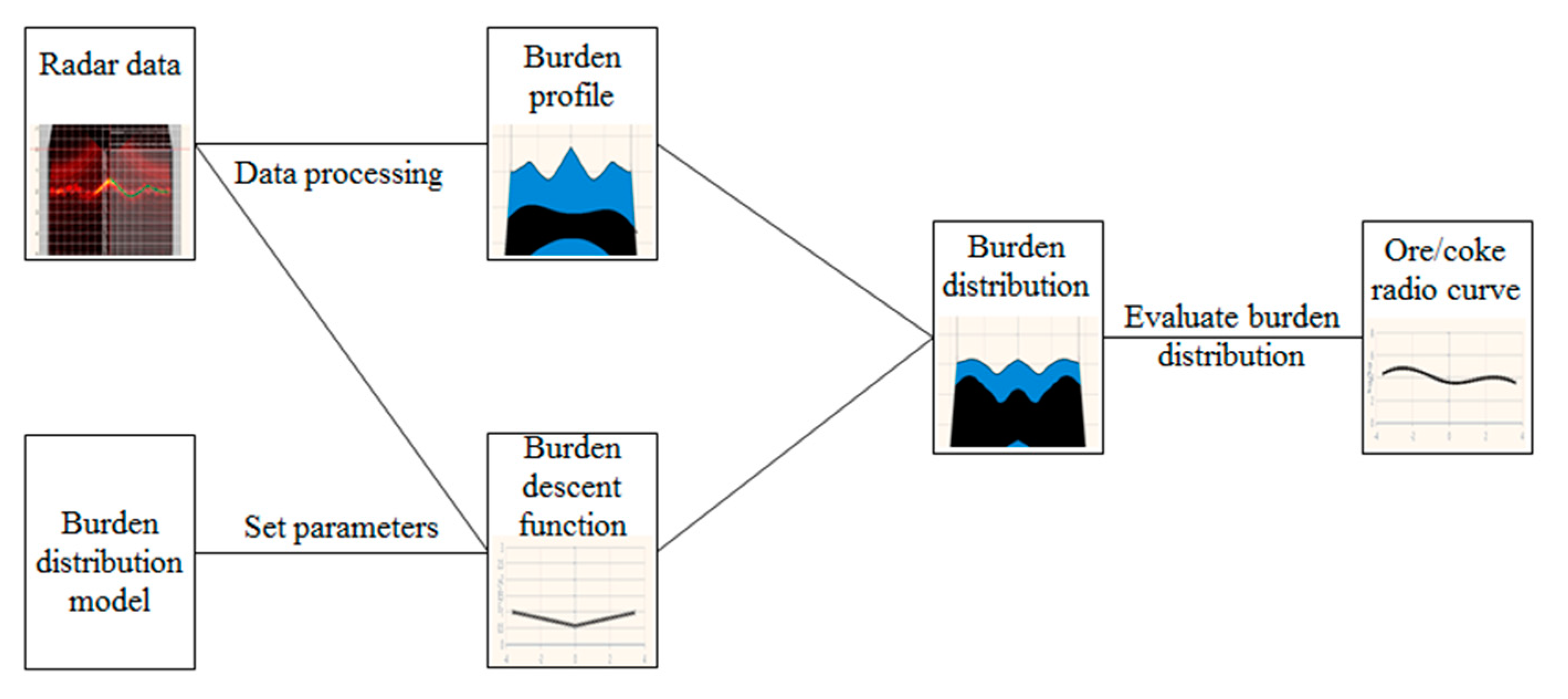
2. Mathematical Model and Radar Data Treatment
2.1. Mathematical Model Structure
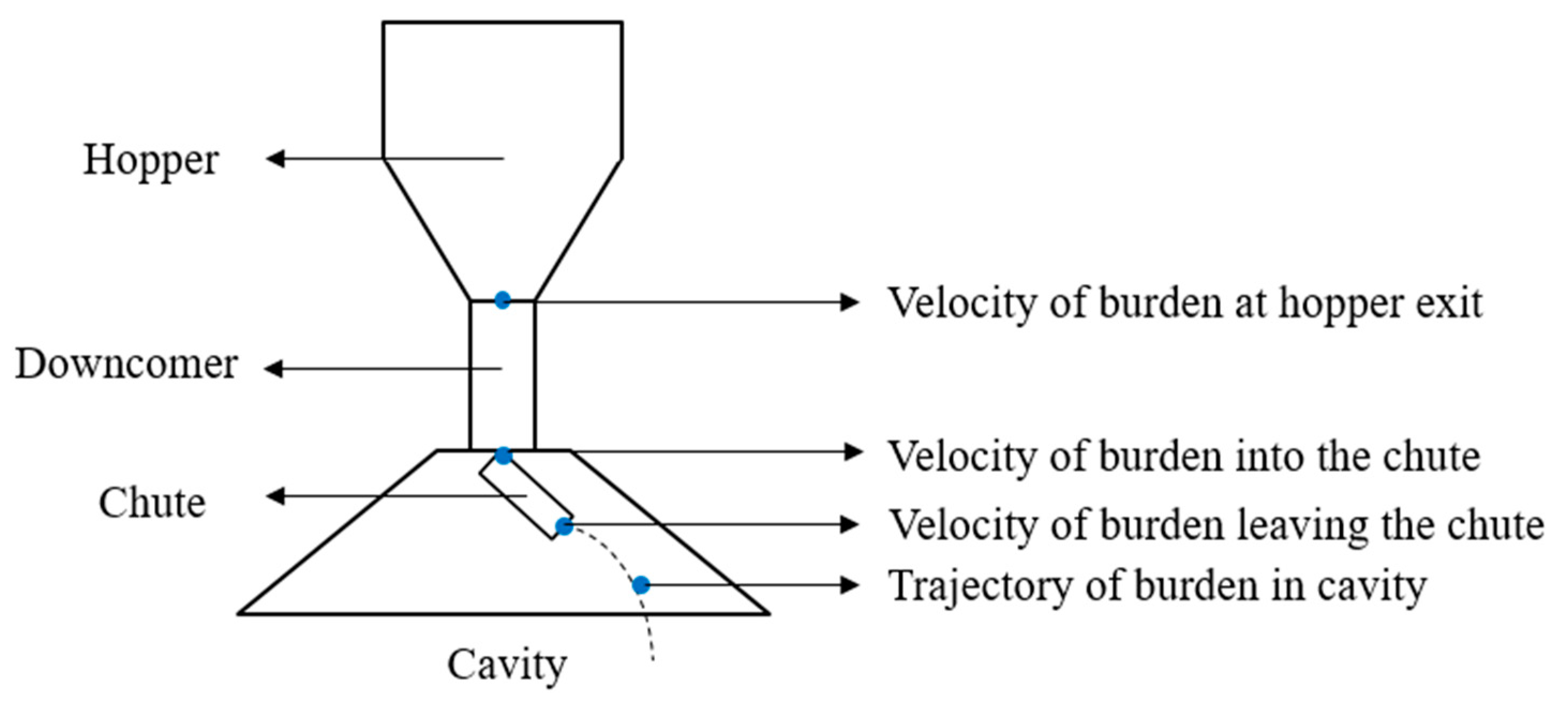
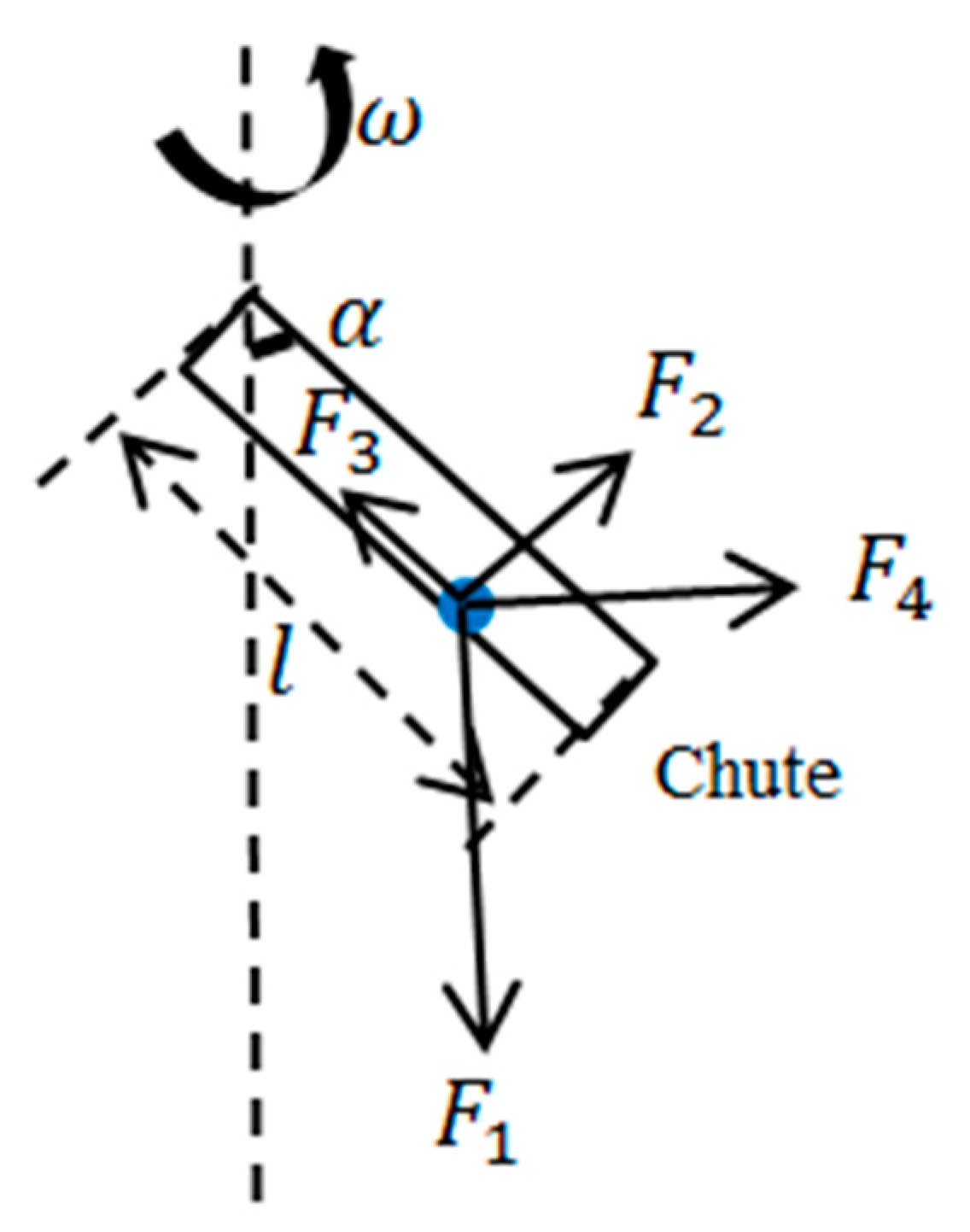
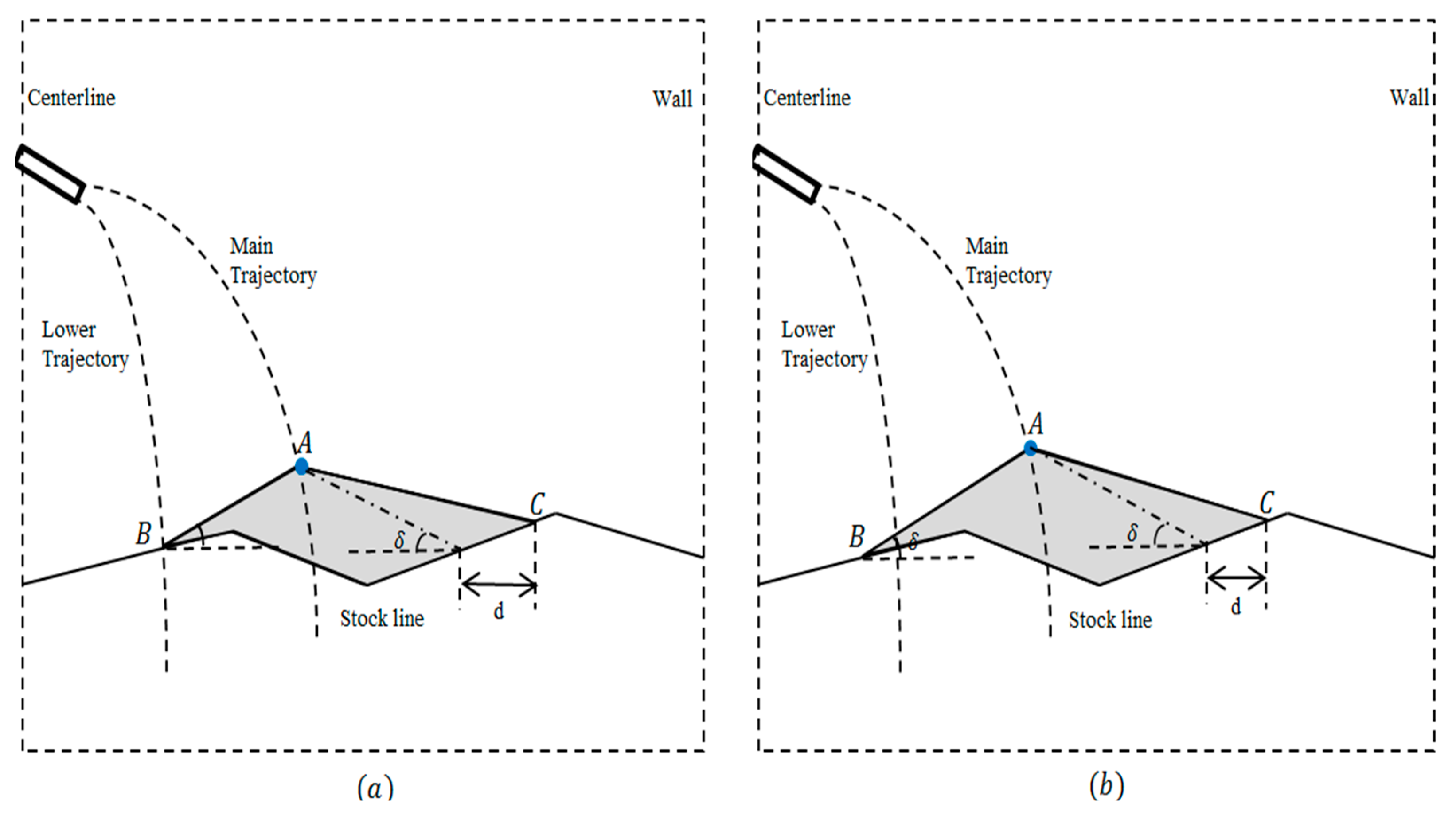
2.1.1. Burden Flow Trajectory Model
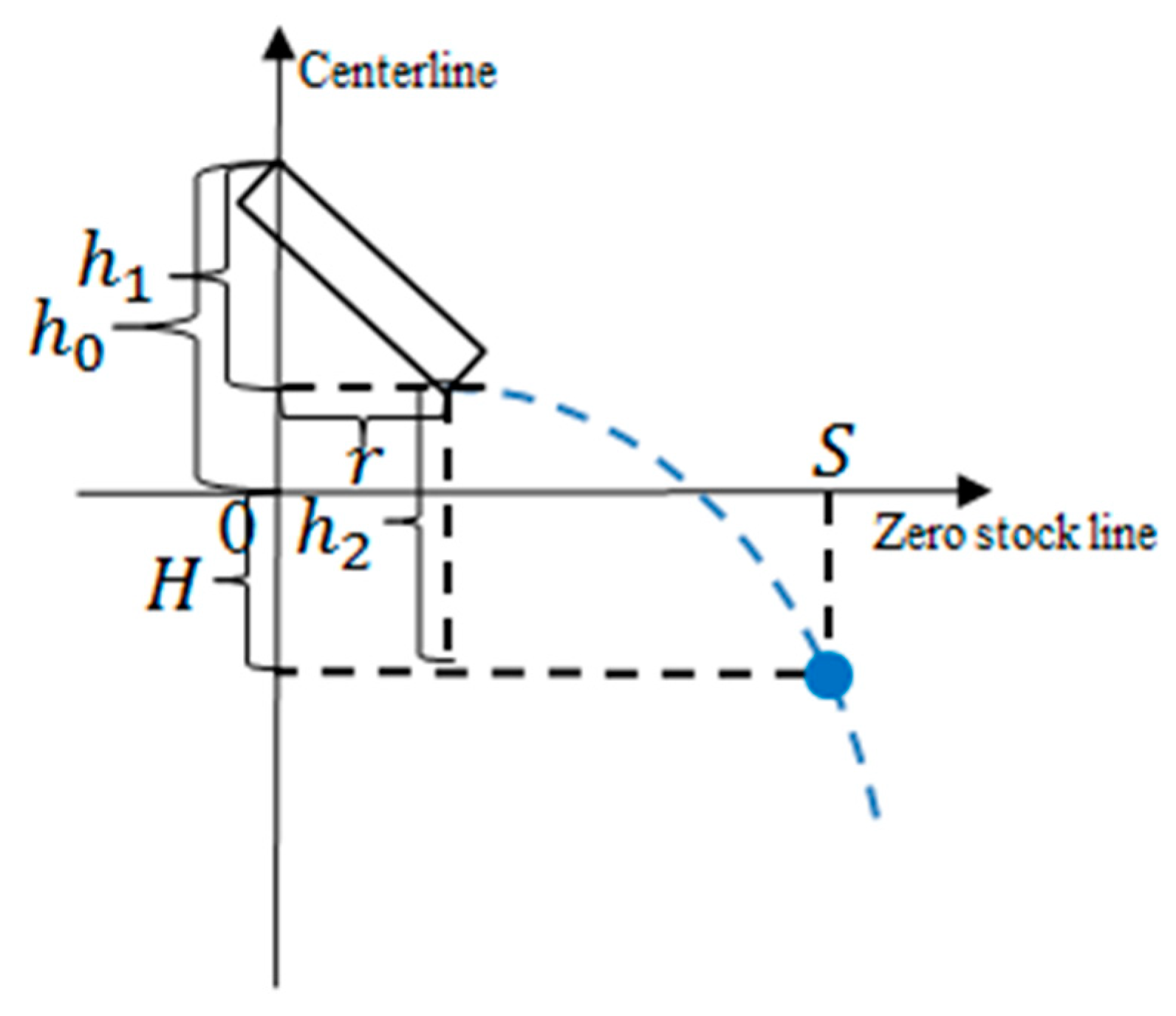
2.1.2. Burden Profile Model
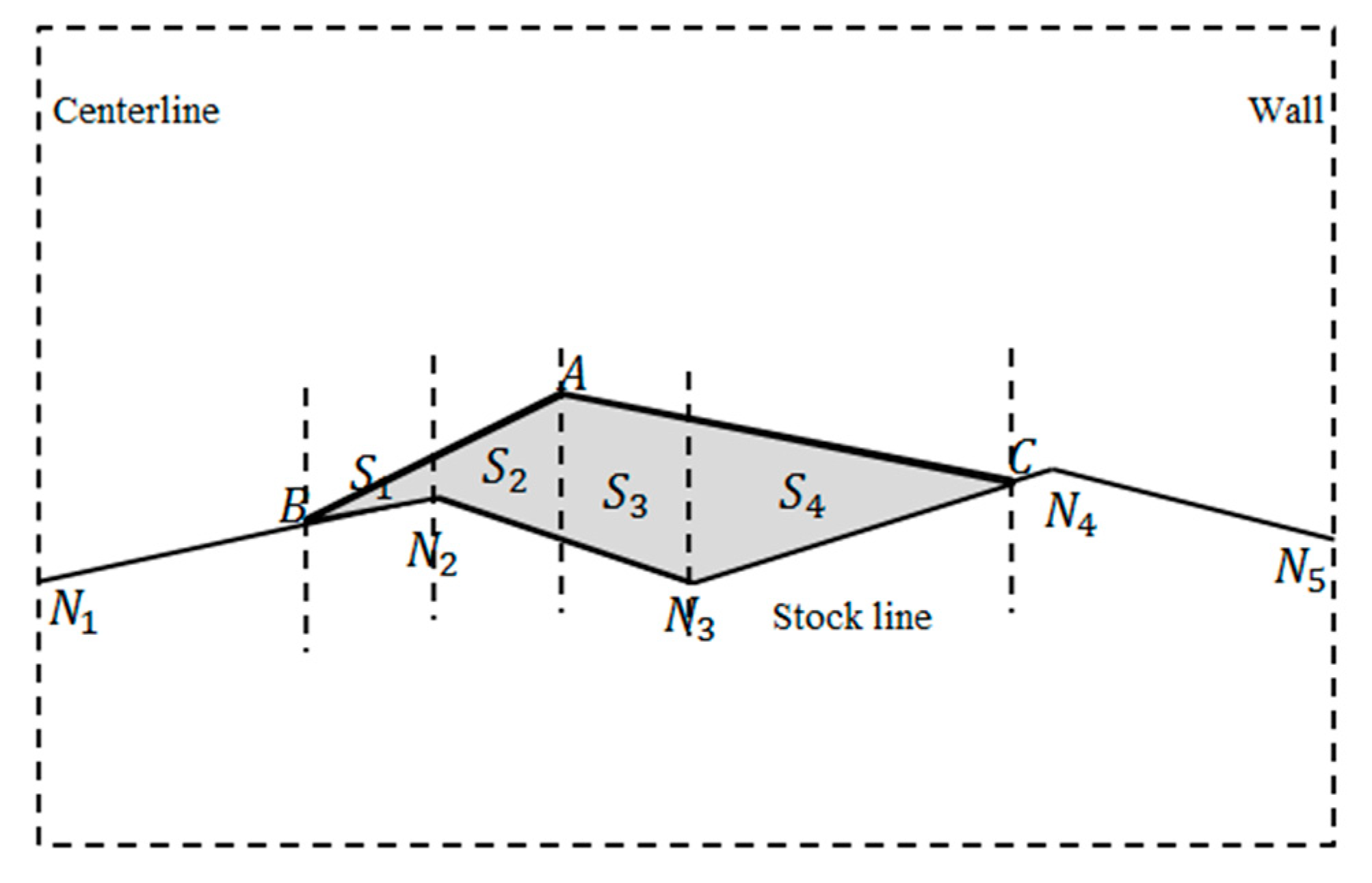
2.1.3. Burden Distribution Model
2.1.4. Burden Evaluation Model
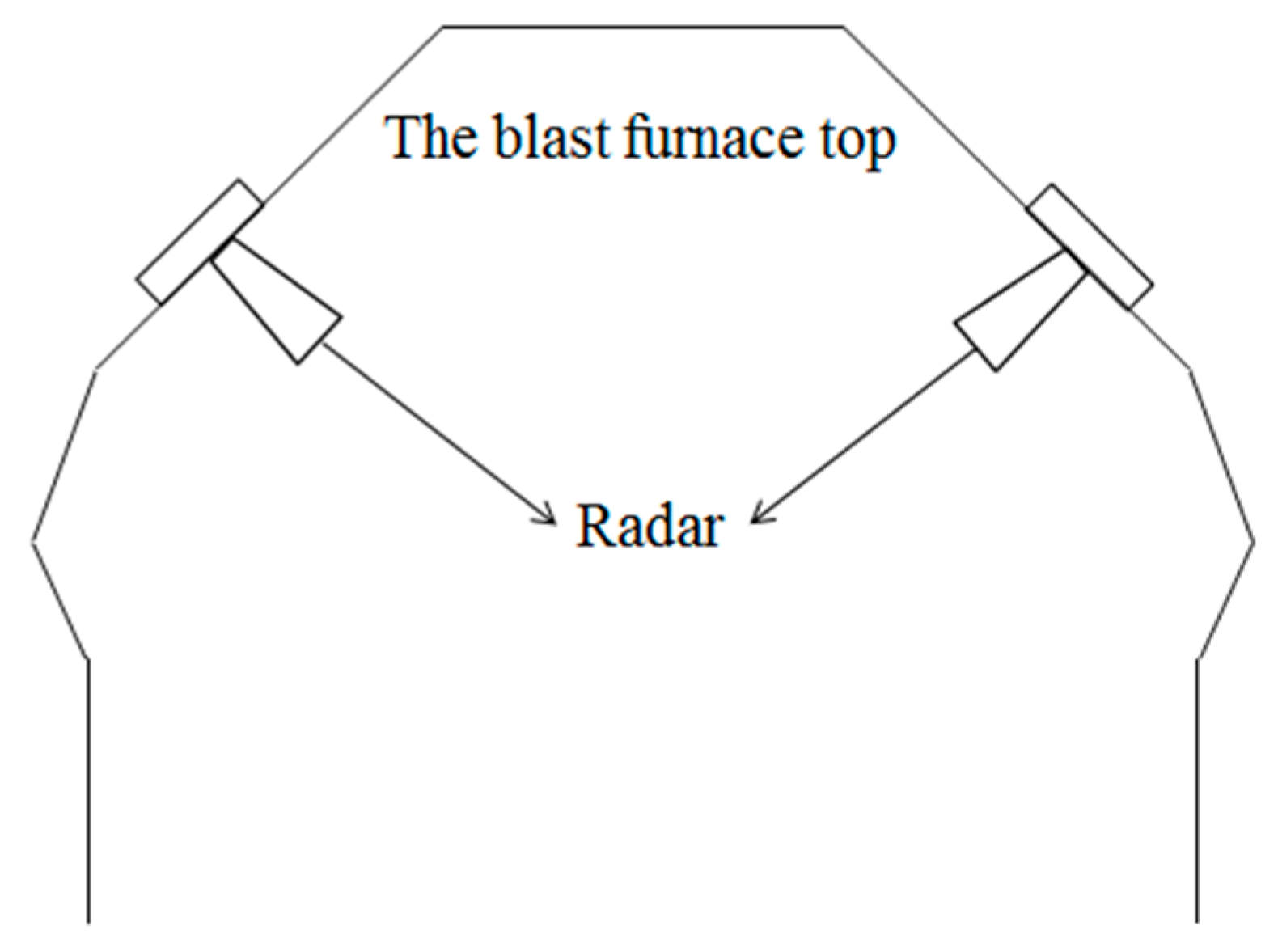
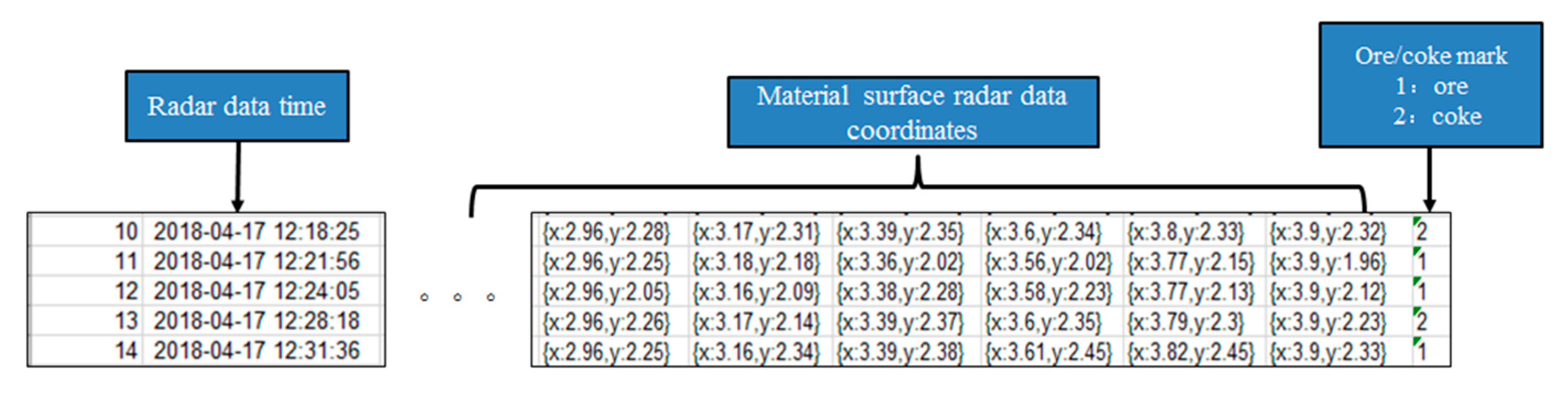
2.2. Radar Detection Measurement
2.2.1. Radar Data Collection
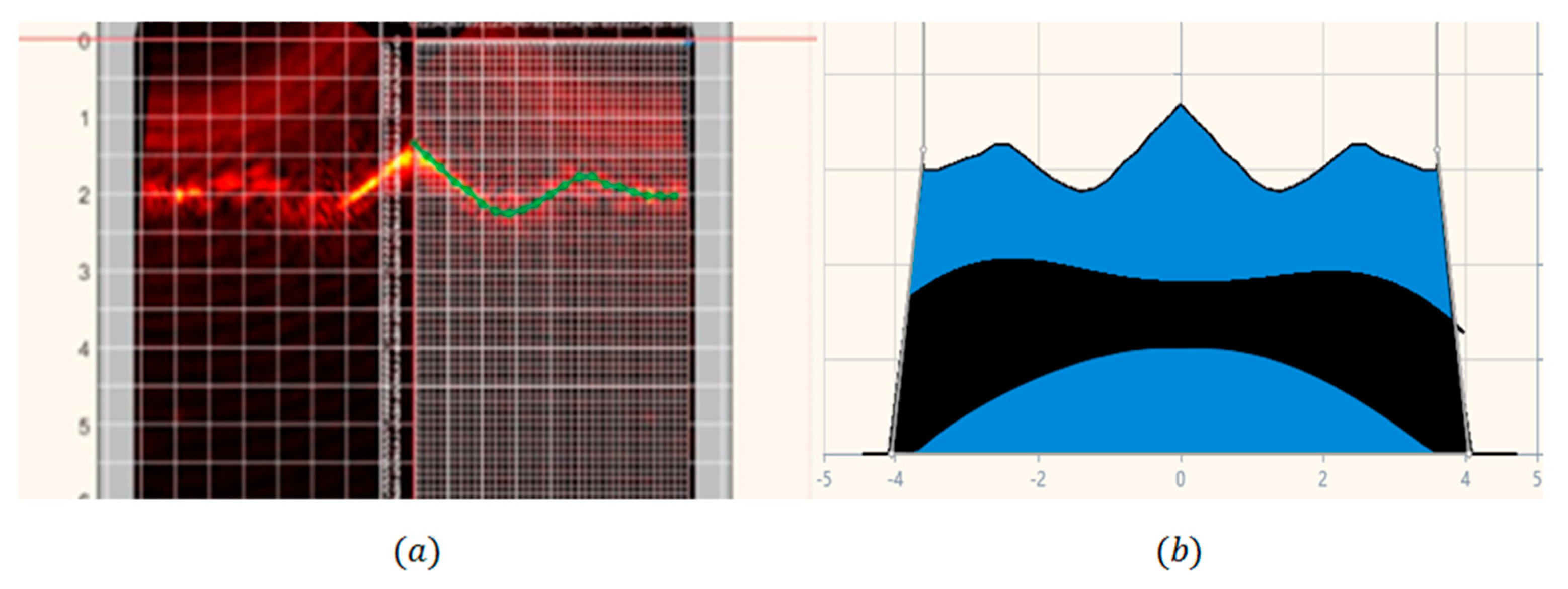
2.2.2. Processing of Radar Data
2.2.3. Burden Distribution Calculation
2.3. Parameters of Blast Furnace and Assumptions of Calculation
3. Application of the Combined Model and Results
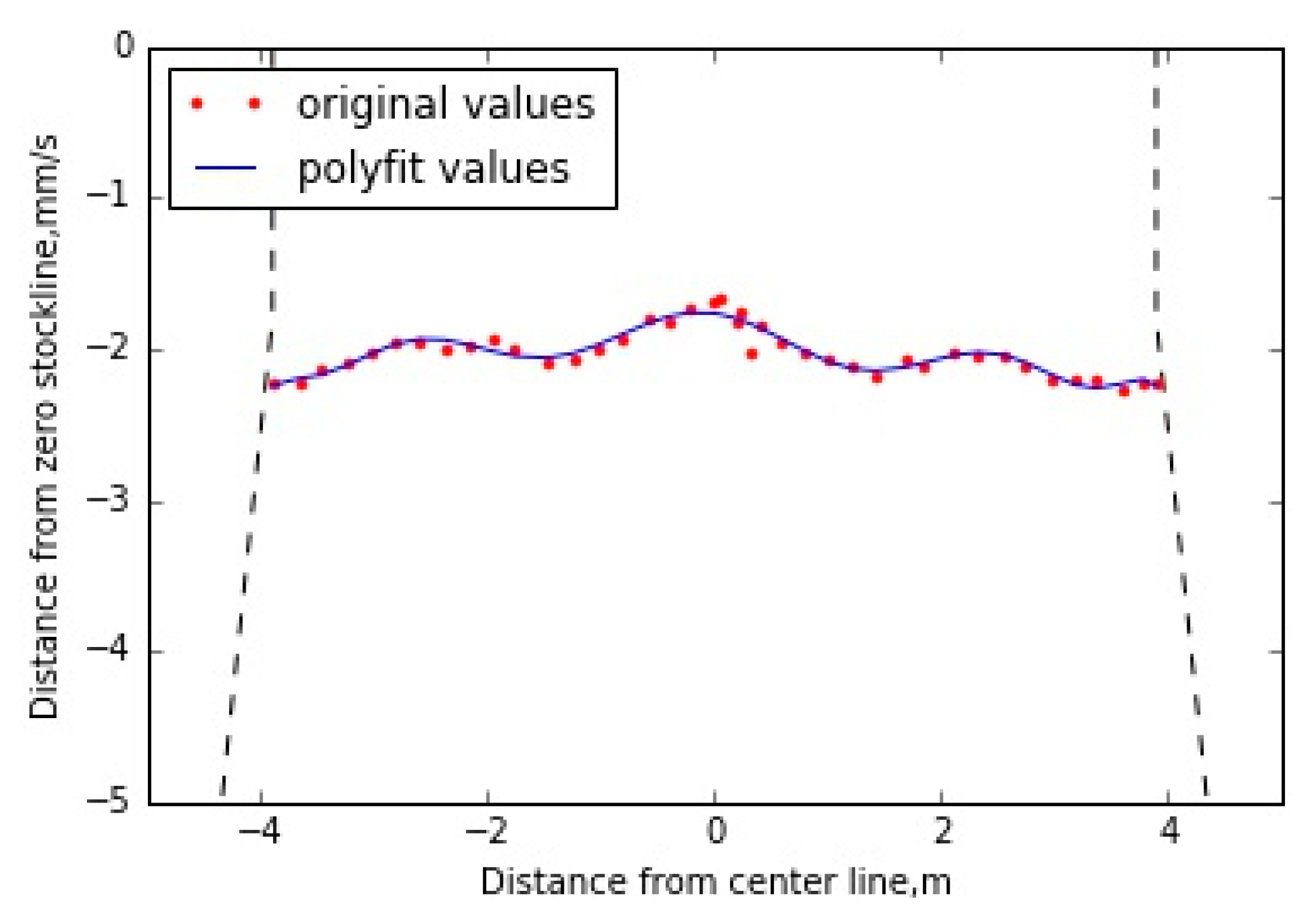
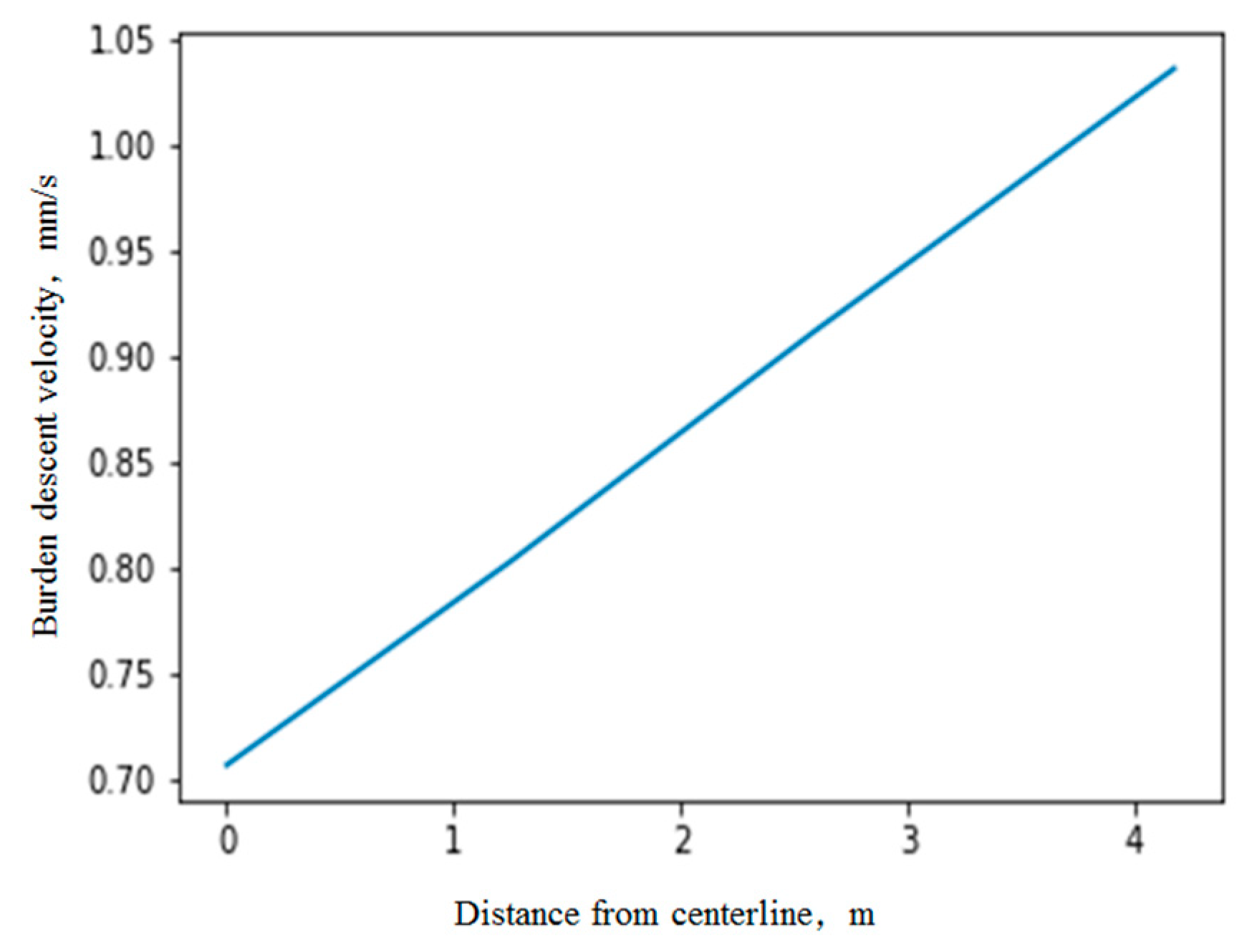
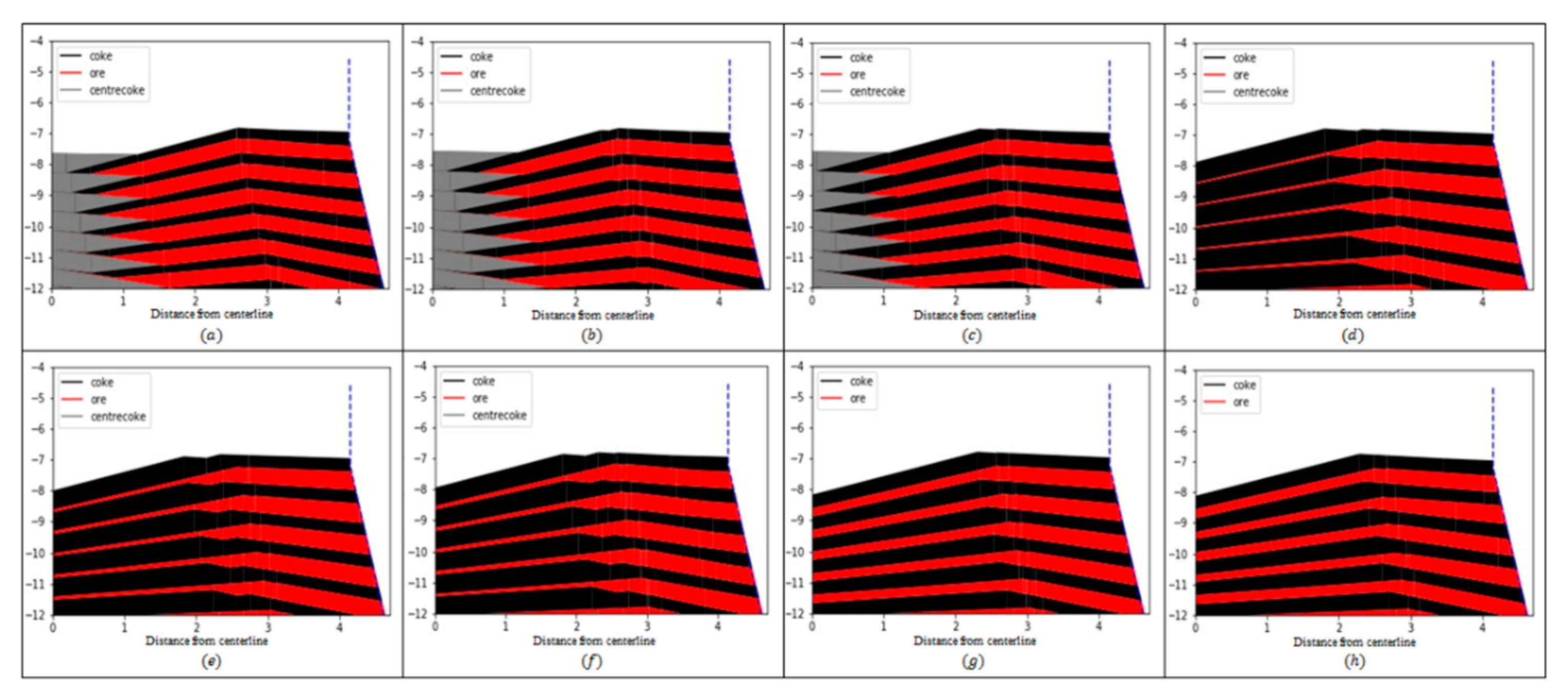
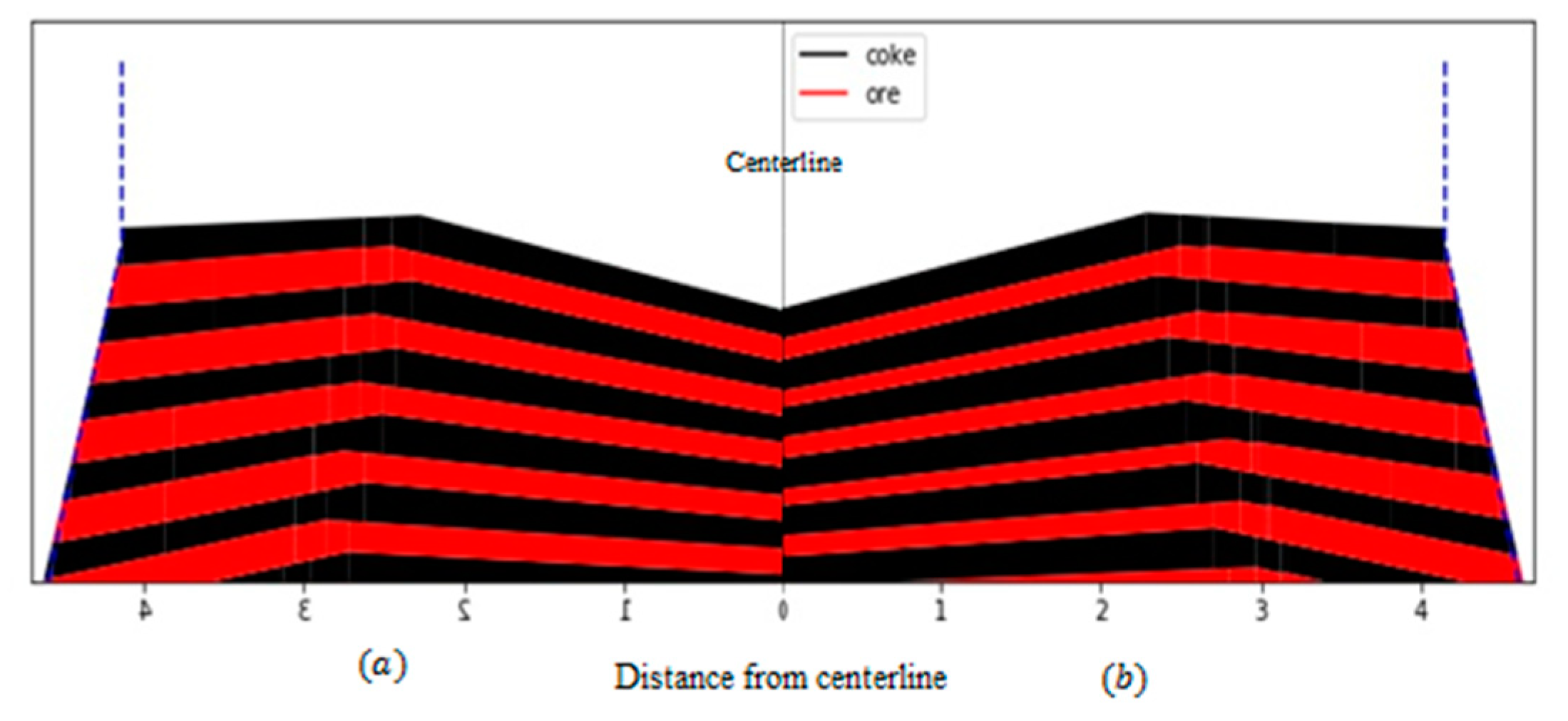
3.1. Mathematical Model Test
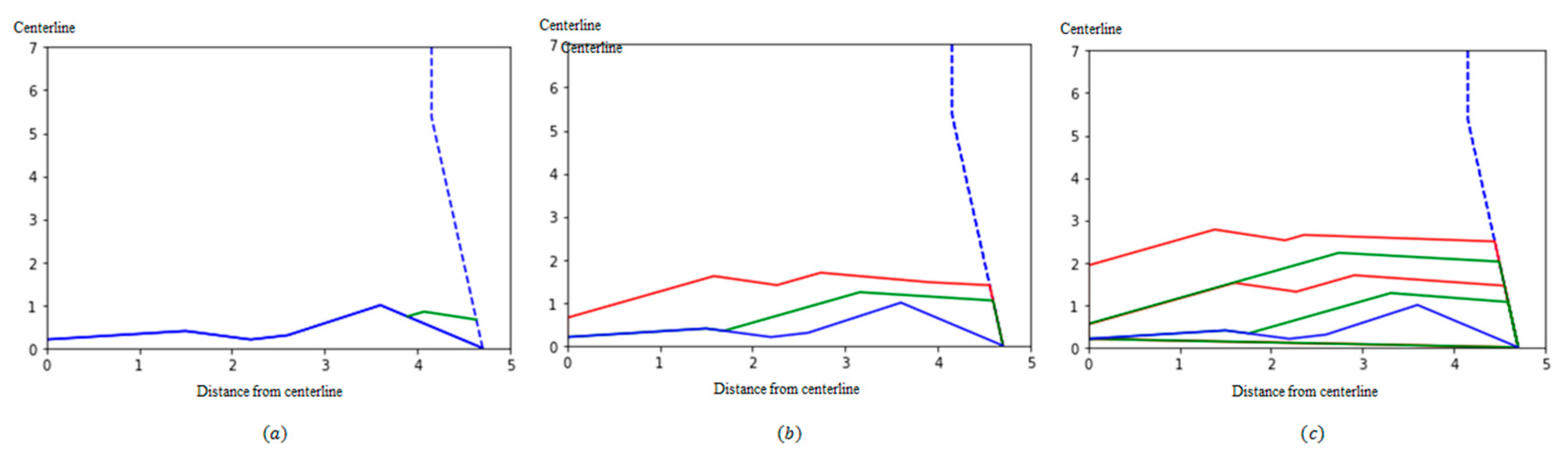
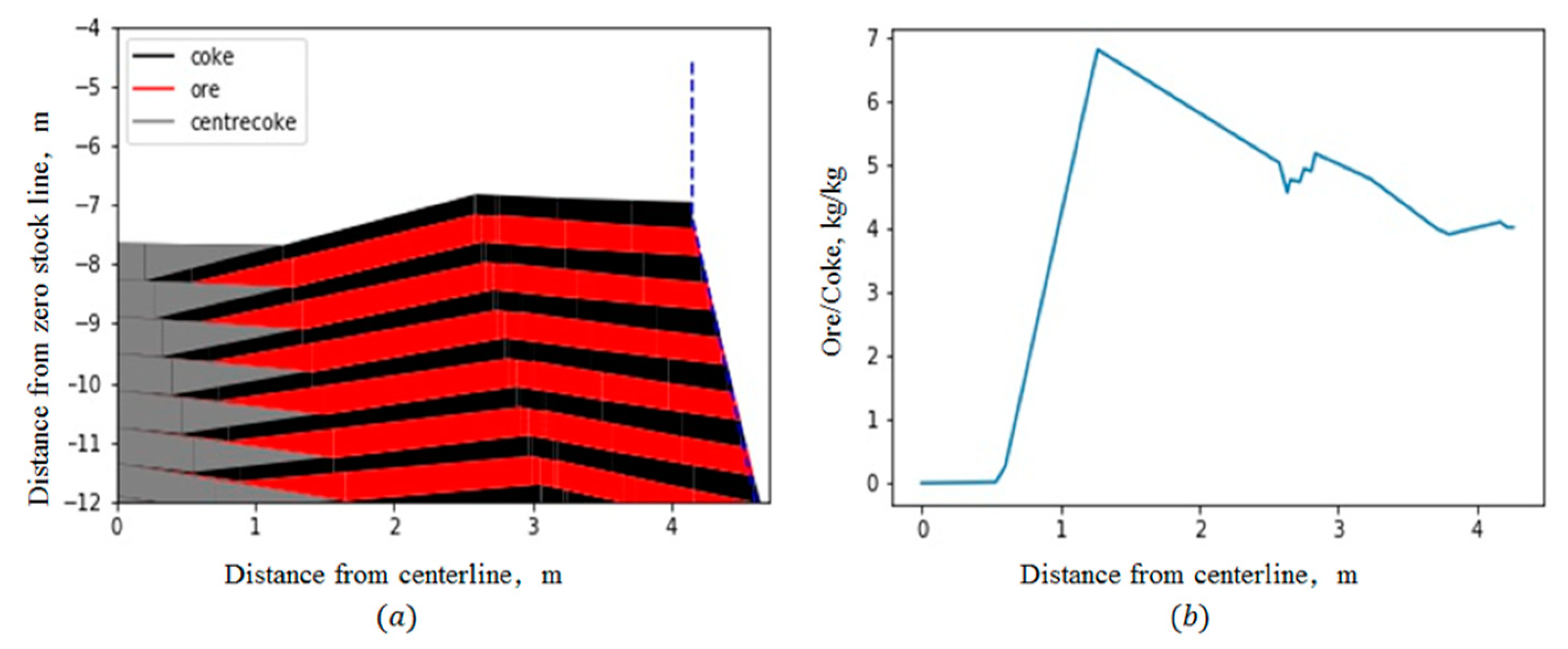
3.2. Combination of the Mathematical Model and Radar Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, L.L.; An, G.; Zhang, Z.G.; Wang, S.T.; Qiu, X.X. Application of making infrares video on blast furnace roof. Hebei Metall. 2007, 6, 35–37. [Google Scholar]
- Venkatesh, V.; Akhil, G.; Liang, G.; Rangarajan, V. Finite Element Based Physical Chemical Modeling of Corrosion in Magnesium Alloys. Metals 2017, 7, 83. [Google Scholar]
- Nishio, H.; Ariyama, T.; Sato, M.; Nakatani, G.; Maki, A.; Saito, N. Development of a Simulation Model Burden Distribution. (Study Burden Distribution Bell-Less Top-II). 1983, 23, p. b319. Available online: https://www.researchgate.net/publication/298277111_DEVELOPMENT_OF_A_SIMULATION_MODEL_OF_BURDEN_DISTRIBUTION_STUDY_ON_BURDEN_DISTRIBUTION_IN_BELL-LESS_TOP_-_II (accessed on 8 December 2019).
- Jung, S.K.; Chung, W.S. Improvement of gas flow through analyzing discharge behavior in the bunker used in blast furnace. ISIJ Int. 2001, 41, 1324–1330. [Google Scholar] [CrossRef][Green Version]
- Radhakrishnan, V.R.; Ram, K.M. Mathematical model for predictive control of the bell-less top charging system of a blast furnace. J. Process Contr. 2001, 11, 565–586. [Google Scholar] [CrossRef]
- Saxén, H.; Hinnelä, J. Model for burden distribution tracking in the blast furnace. Miner. Process. Extr. Metall. Rev. 2004, 25, 1–27. [Google Scholar] [CrossRef]
- Hinnelä, J.; Saxén, H.; Pettersson, F. Modeling of the Blast Furnace Burden Distribution by Evolving Neural Networks. Ind. Eng. Chem. Res. 2003, 42, 2314–2323. [Google Scholar] [CrossRef]
- Nag, S.; Koranne, V.M. Development of material trajectory simulation model for blast furnace compact bell-less top. Ironmak. Steelmak. 2009, 36, 371–378. [Google Scholar] [CrossRef]
- Park, J.I.; Baek, U.H.; Jang, K.S.; Oh, H.S.; Han, J.W. Development of the Burden Distribution and Gas Flow Model in the Blast Furnace Shaft. ISIJ Int. 2011, 51, 1617–1623. [Google Scholar] [CrossRef]
- Nag, S.; Gupta, A.; Paul, S.; Gavel, D.J.; Aich, B. Prediction of Heap Shape in Blast Furnace Burden Distribution. ISIJ Int. 2014, 54, 1517–1520. [Google Scholar] [CrossRef]
- Shi, P.Y.; Zhou, P.; Fu, D.; Zhou, C.Q. Mathematical model for burden distribution in blast furnace. Ironmak. Steelmak. 2016, 43, 74–81. [Google Scholar] [CrossRef]
- Xiao, G.C. Application of rotary radar technology in blast furnace of nanjing steel. In Proceedings of the Workshop on Experience Analysis of Production Organization in Limited Season and Staggered Season of Blast Furnace in 2018, Tai’an, Shandong, China, 18 April 2018; pp. 124–128. [Google Scholar]
- Zhang, S.; Wei, K.D.; Zhang, H.G.; Yin, Y.X.; Chen, X.Z. 3D Surface Reconstrution of Blast Furnace Based on Phased Array Radar Data. In Proceedings of the 11th China Steel Annual Conference, Beijing, China, 21 November 2017; p. 6. Available online: http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGJS201711002143.htm (accessed on 8 December 2019).
- Liu, D.X.; Li, X.L.; Lu, S.T.; Ding, D.W.; Chen, X.Z. Application of Fuzzy Neural Network in Burden Surface Clustering. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23 May 2012; pp. 1094–1099. Available online: https://ieeexplore.ieee.org/document/6244174?tp=&arnumber=6244174&contentType=Conference%20Publications&refinements%3D4291944822%26sortType%3Ddesc_p_Publication_Year%26ranges%3D2012_2012_p_Publication_Year%26pageNumber%3D107%26rowsPerPage%3D100= (accessed on 8 December 2019).
- Gao, Z.K. Innovation and Practices of Blast Furnace Visualization and Simulation Technology. China Metall. 2013, 23, 8–14. [Google Scholar]
- Zhu, Q.; Lu, C.L.; Yin, Y.X.; Chen, X.Z. Burden Distribution Calculation of Bell-Less Top of Blast Furnace Based on Multi-Radar Data. J. Iron Steel Res. Int. 2013, 20, 33–37. [Google Scholar] [CrossRef]
- Li, X.L.; Liu, D.X.; Jia, C.; Chen, X.Z. Multi-model control of blast furnace burden surface based on fuzzy SVM. Neurocomputing 2015, 55, 1146–1156. [Google Scholar] [CrossRef]
- Tian, J.; Tanaka, A.; Hou, Q.; Chen, X. Radar Detection-based Modeling in a Blast Furnace: A Prediction Model of Burden Surface Shape after Charging. ISIJ Int. 2018, 58, 1999–2008. [Google Scholar] [CrossRef]
- Tian, J.; Tanaka, A.; Hou, Q.; Chen, X. Radar Detection-Based Modeling in a Blast Furnace: A Prediction Model of Burden Surface Descent Speed. Metals 2019, 9, 609. [Google Scholar] [CrossRef]
- Miao, L.L.; Chen, X.Z.; Bai, Z.L.; Huang, Y.Q.; Hou, Q.W.; Yin, Y.X. Blast furnace line shape measurement fusion and compensation algorithm based on radar. J. Univ. Sci. Technol. Beijing 2014, 36, 82–88. [Google Scholar]
- Li, H.; Saxén, H.; Liu, W.; Shao, L.; Zou, Z. Model-based analysis of factors affecting the burden layer structure in the blast furnace shaft. Metals 2019, 9, 1003. [Google Scholar] [CrossRef]
- Wang, P. Measurement and analysis of burden flow trajectory and width in bell-less top with two concentric vertical hoppers. Iron Steel 2003, 38, 10–14. [Google Scholar]
- Yu, Y.W. Research and Development on the Model for Bell-Less Charging of Blast Furnace; Chongqin University: Chongqin, China, 2008. [Google Scholar]
- Nishida, T.; Hachiya, S.; Tanaka, K.; Satoh, K.-I.; Inaba, S.-I.; Okimoto, K.-I. Application of the results of a burden distribution experiment on a bell-less scale model to blast furnace operation. Kobe Steel Eng. Rep. Res. Dev. 1982, 32, 73–76. [Google Scholar]




| Property | Value |
|---|---|
| Throat diameter (mm) | 8300 |
| Throat height (mm) | 2600 |
| Shaft angle (°) | 84.15 |
| 1 (mm) | 4010 |
| 2 (mm) | 1030 |
| 3 (mm) | 4601 |
| Property | Value |
|---|---|
| The length of the chute (mm) | 3890 |
| Chute speed () | 0.133 |
| Coefficient of coke friction | 0.758 |
| Coefficient of ore friction | 0.638 |
| Velocity attenuation coefficient of coke | 0.70 |
| Velocity attenuation coefficient of ore | 0.71 |
| Property | Ore | Coke |
|---|---|---|
| Bulk density () | 1800 | 550 |
| Repose angle (°) | 31.5 | 32.5 |
| Chute Angle (°) | 46 | 44 | 41.5 | 39 | 36.5 | 15 |
|---|---|---|---|---|---|---|
| Coke charging ring number | 2 | 2 | 2 | 2 | 2 | |
| Ore charging ring number | 3 | 3 | 2 | 2 |
| Figure No. | Inclination Angle of the Chute (°) | 41 | 39 | 37 | 34 | 31 | 27 | 20 | 12 |
|---|---|---|---|---|---|---|---|---|---|
| a | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 5 | |||
| b | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 1 | 4 | ||
| c | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 2 | 3 | ||
| d | Ore | 2 | 3 | 3 | 2 | ||||
| Coke | 3 | 3 | 3 | 2 | 2 | 3 | |||
| e | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 3 | 2 | ||
| f | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 2 | 2 | ||
| g | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 2 | |||
| Inclination angle of the Chute (°) | 40 | 38 | 36 | 33 | 30 | 27 | |||
| h | Ore | 2 | 3 | 3 | 2 | 1 | |||
| Coke | 3 | 3 | 3 | 2 | 2 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Wei, H.; Ge, Y.; Xiao, G.; Yu, Y. A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace. Processes 2020, 8, 239. https://doi.org/10.3390/pr8020239
Li M, Wei H, Ge Y, Xiao G, Yu Y. A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace. Processes. 2020; 8(2):239. https://doi.org/10.3390/pr8020239
Chicago/Turabian StyleLi, Meng, Han Wei, Yao Ge, Guocai Xiao, and Yaowei Yu. 2020. "A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace" Processes 8, no. 2: 239. https://doi.org/10.3390/pr8020239
APA StyleLi, M., Wei, H., Ge, Y., Xiao, G., & Yu, Y. (2020). A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace. Processes, 8(2), 239. https://doi.org/10.3390/pr8020239






