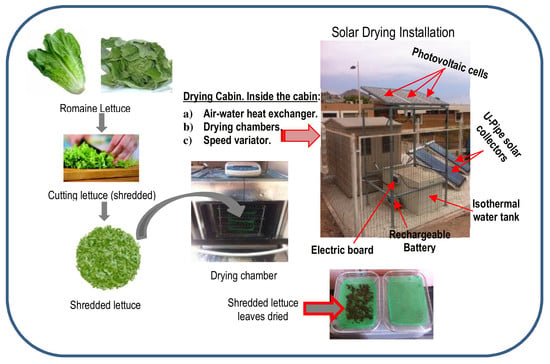
Effect of Drying on Lettuce Leaves Using Indirect Solar Dryer Assisted with Photovoltaic Cells and Thermal Energy Storage
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
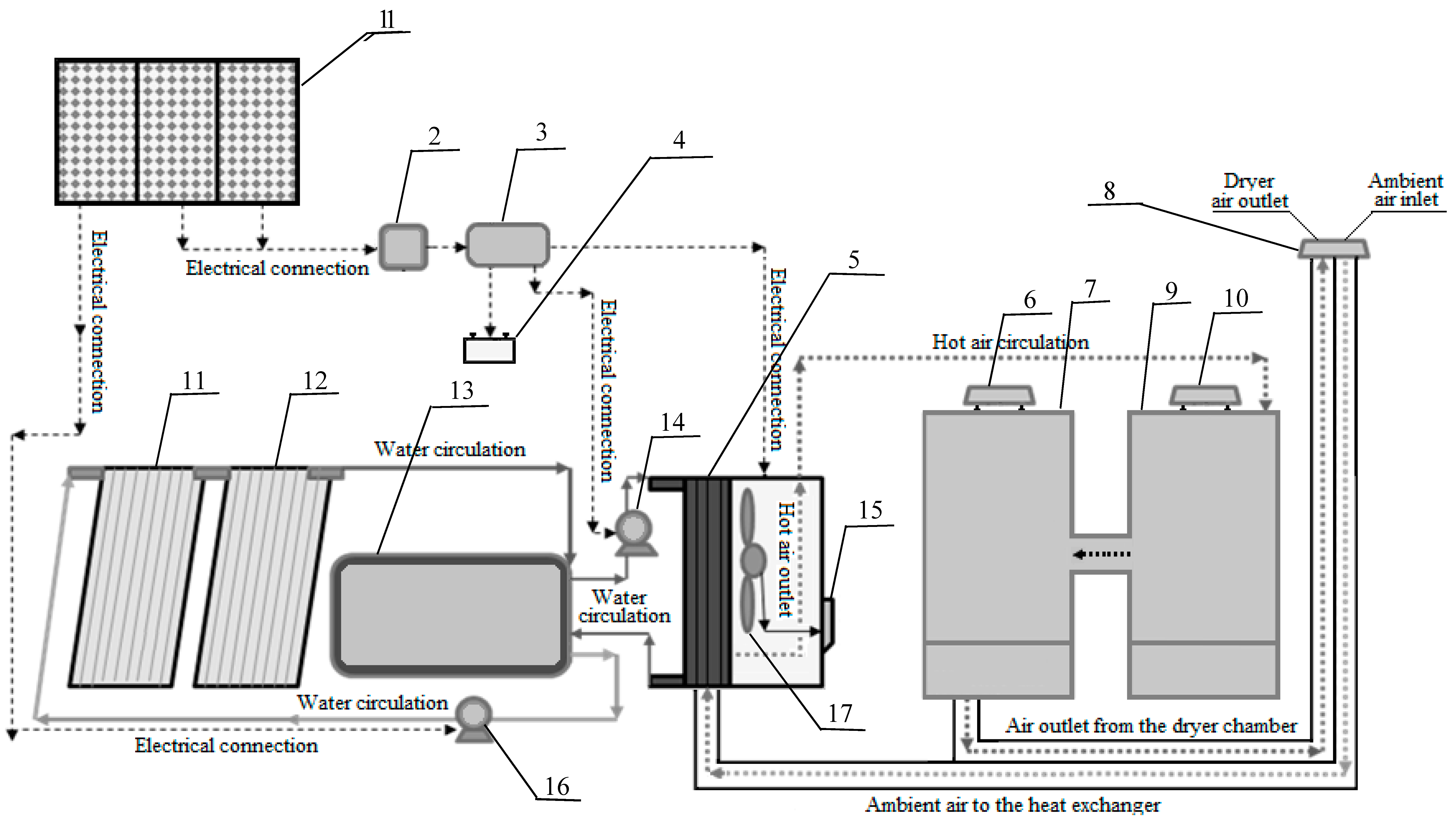
2.2. Solar Drying Equipment
2.3. Experimental Procedures
2.4. Drying Curves
2.5. Calculations for Determining the Drying Curves and Drying Rate
2.6. Modeling of Drying Curves
2.7. Color Analysis
2.8. Calculation of Effective Moisture Diffusivity
2.9. Statistical Analysis
3. Results and Discussion
3.1. Drying Characteristics
3.1.1. Drying Curve
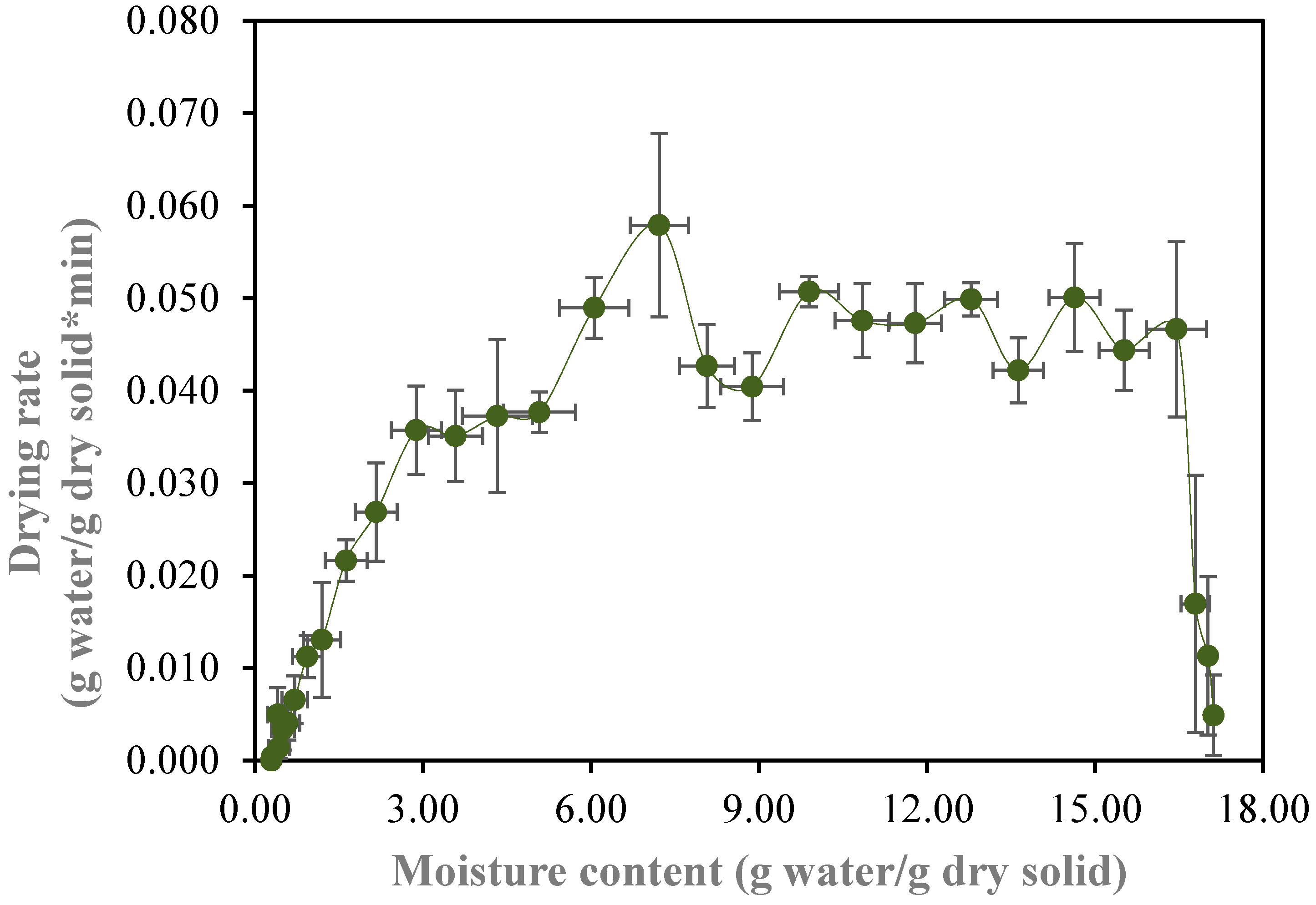
3.1.2. Drying Rate Curve
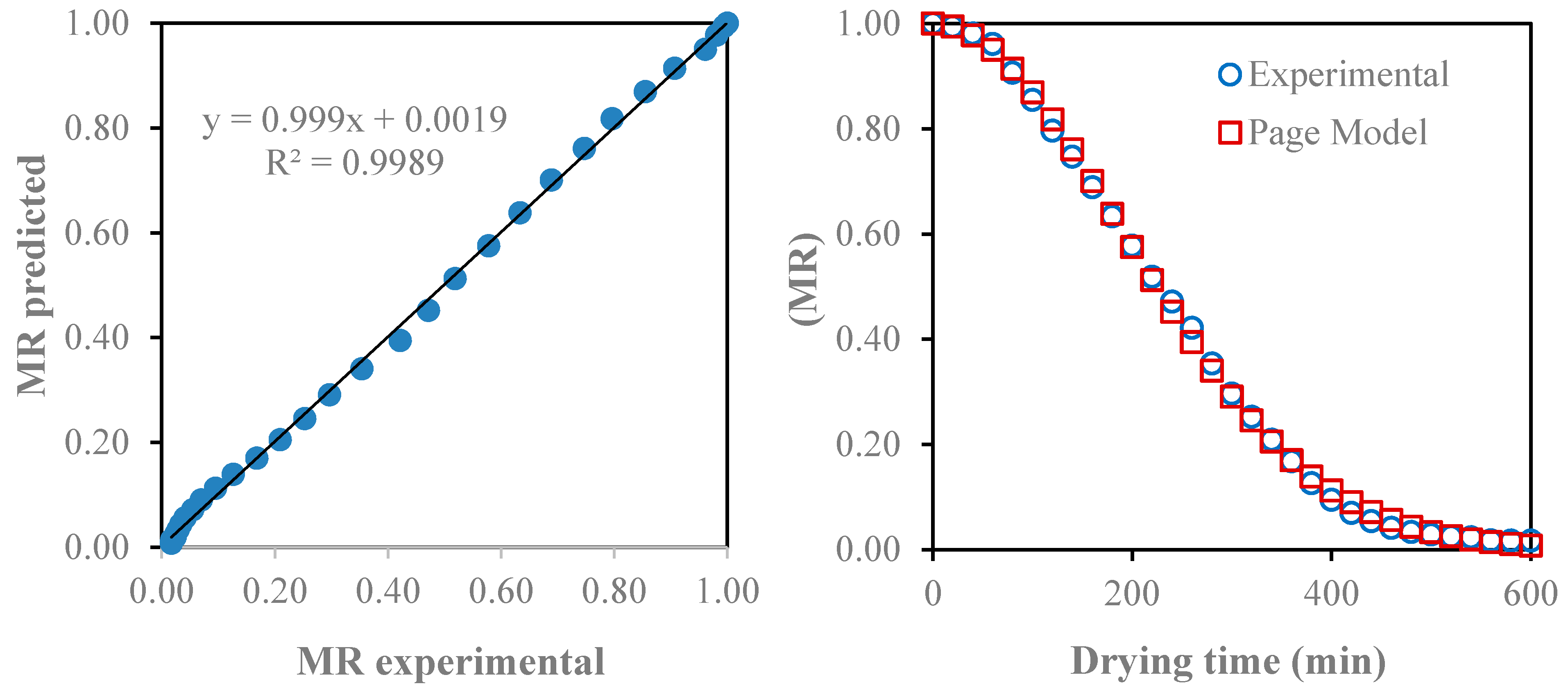
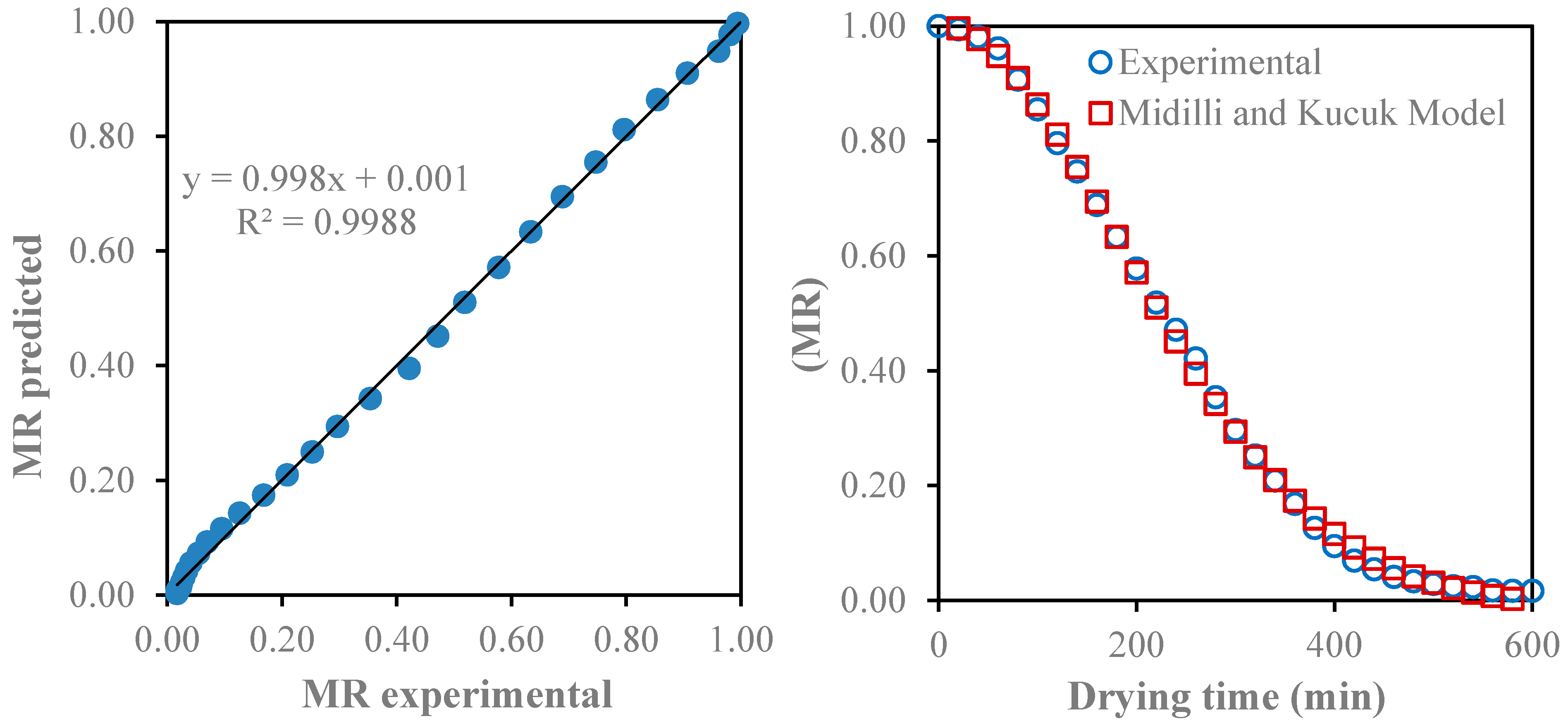
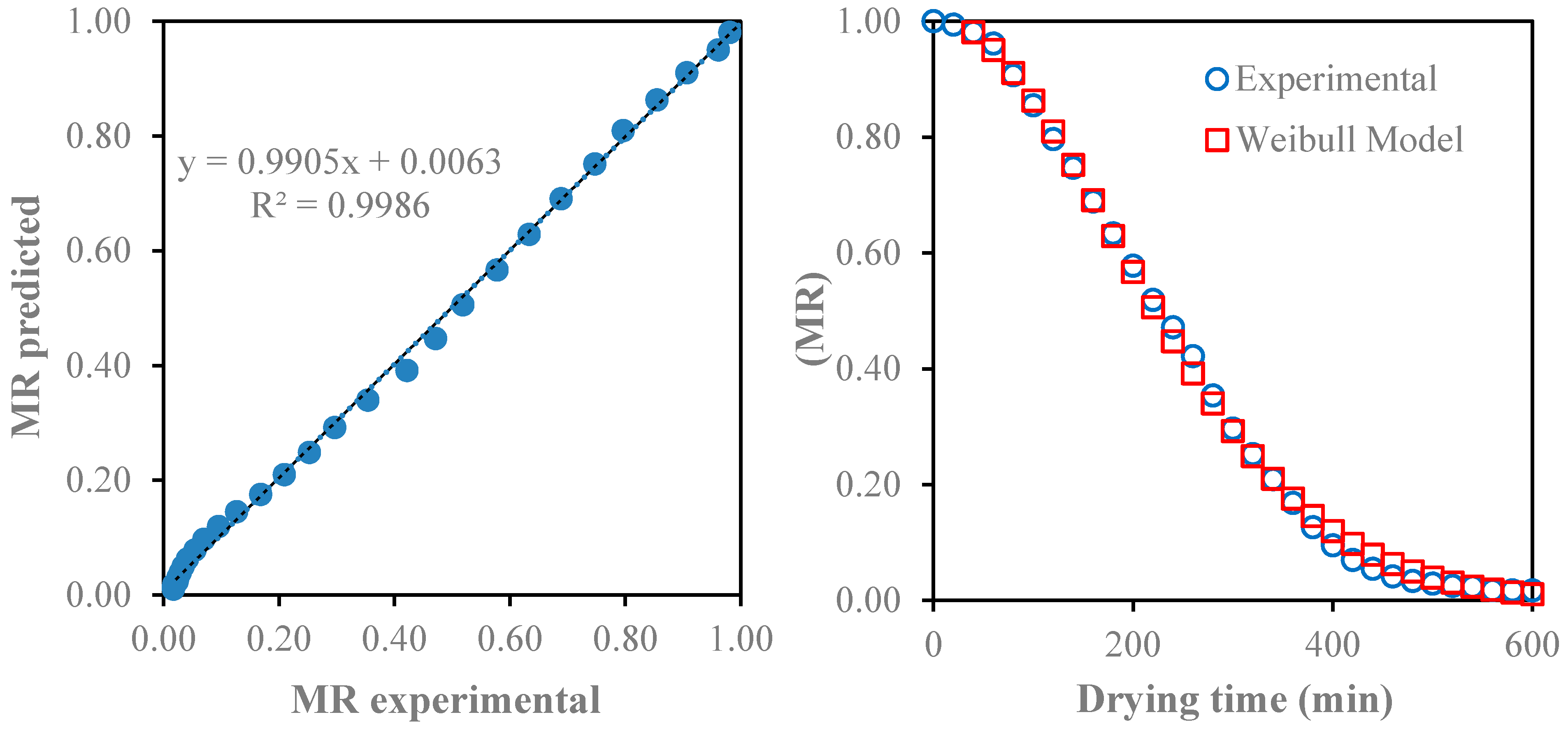
3.2. Modeling of Drying Curves Statistical Parameters
3.3. Model Validation
3.4. Chromatic Coordinates
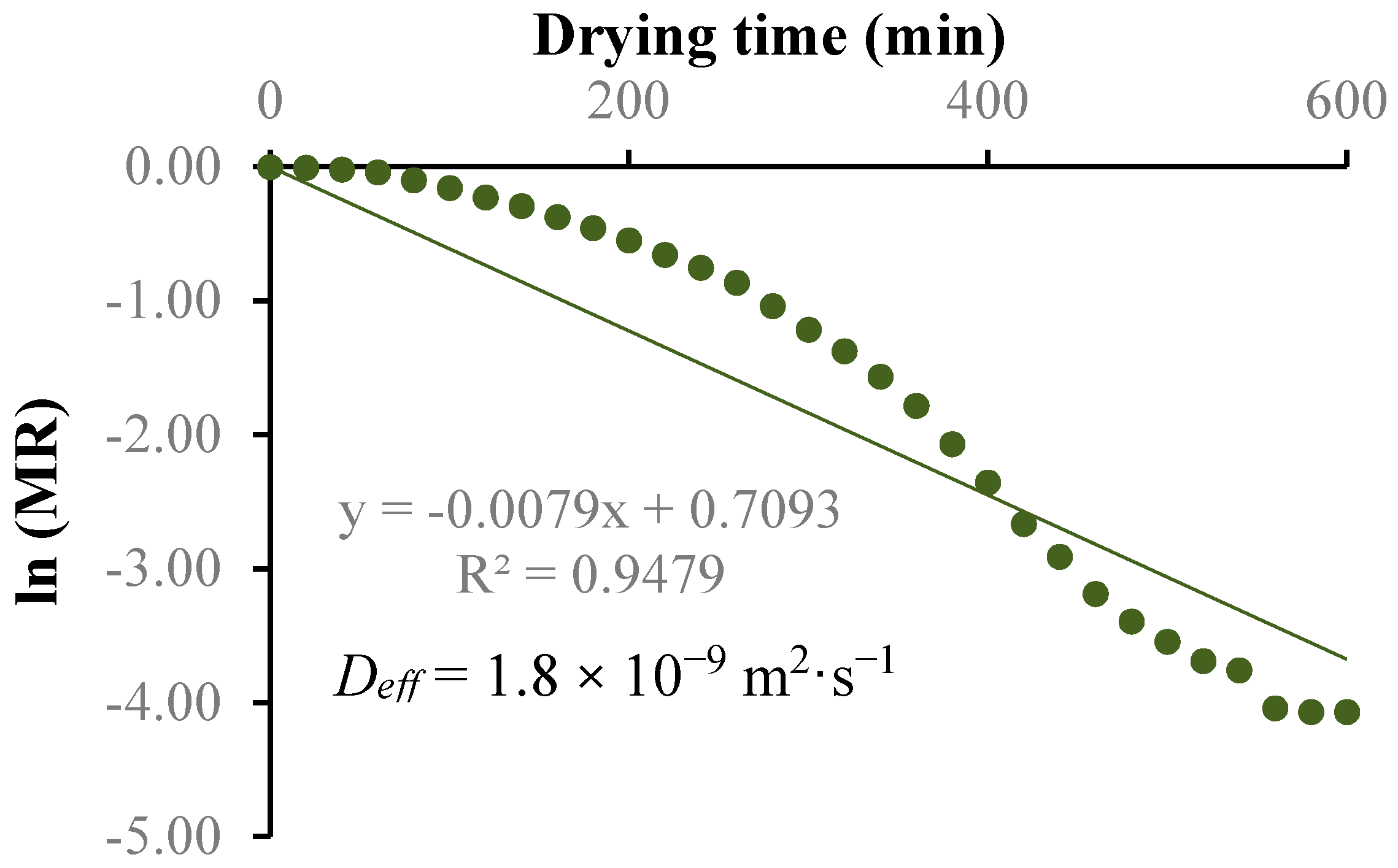
3.5. Effective Moisture Diffusivity (Deff)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karim, M.A.; Hawlader, M.N.A. Mathematical modelling and experimental investigation of tropical fruits drying. Int. J. Heat Mass Tran. 2005, 48, 4914–4925. [Google Scholar] [CrossRef]
- Perumal, R. Comparative Performance of Solar Cabinet, Vacuum Assisted Solar and Open Sun Drying Methods. Master’s Thesis, McGill University, Montreal, Canada, 2007; p. 100. Available online: http://digitool.Library.McGill.CA:80/R/-?func=dbin-jump-full&object_id=18283&silo_library=GEN01 (accessed on 10 October 2020).
- Douglas, R.B.; Román, J.C.; Pantaleón, D.; Moreno-Álvarez, M.; Medina, C.; Ojeda, C. Efecto del secado solar en los contenidos de humedad, carbohidratos, carotenoides totales e índice de peróxidos del mesocarpio de la palma coroba (Attalea spp.). Interciencia 2007, 32, 257–261, ISSN 0378-184. [Google Scholar]
- Jairaj, K.S.; Singh, S.P.; Srikant, K. A review of solar dryers developed for grape drying. Sol. Energy 2009, 83, 1698–1712. [Google Scholar] [CrossRef]
- Kadam, D.M.; Samuel, D.V.K. Convective Flat-plate Solar Heat Collector for Cauliflower Drying. Biosyst. Eng. 2006, 93, 189–198. [Google Scholar] [CrossRef]
- Banout, J.; Ehl, P.; Havlik, J.; Lojka, B.; Polesny, Z.; Verner, V. Design and performance evaluation of a Double-pass solar drier for drying of red chilli (Capsicum annum L.). Sol. Energy 2011, 85, 506–515. [Google Scholar] [CrossRef]
- Chen, X.Y. Moisture Diffusivity in Food and Biological Materials’. Dry. Technol. 2007, 25, 1203–1213. [Google Scholar] [CrossRef]
- Özbek, B.; Dadali, G. Thin-layer drying characteristics and modelling of mint leaves undergoing microwave treatment. J. Food Eng. 2007, 83, 541–549. [Google Scholar] [CrossRef]
- Mou, B. Nutrient Content of Lettuce and its Improvement. Curr. Nutr. Food Sci. 2009, 5, 242–248. [Google Scholar] [CrossRef]
- Gebhardt, S.E.; Thomas, R.G. Nutritive Values of Foods; Home Garden Bulletin; US Government Printing Office: Washington, DC, USA, 2002; p. 90. Available online: http://www.nal.usda.gov/fnic/foodcomp/Data/HG72/hg72_2002 (accessed on 10 October 2020).
- Sánchez-Mongue, E. Flora Agrícola. Taxonomia de las Magnoliofitas (Angiospermas) de Interes Agricola, con Excepcion de las de Aprovechamiento Exclusivamente Ornamental o Forestal, I/II ed.; Ministerio de Agricultura, Pesca y Alimentación: Madrid, Spain, 1991; ISBN 84-7479-901-5. [Google Scholar]
- Kirschmann, J.D.; Dunne, L.J.; Inc. Nutrition Search. Nutrition Almanac, 6th ed.; McGraw Hill Education: New York, NY, USA, 2007; p. 371. ISBN 13-978-0071436588. [Google Scholar]
- Walker, N.W. Fresh Vegetable and Fruit Juices: What’s Missing in Your Body? Book Publishing Co.: Summertown, TN, USA, 1978; p. 118. ISBN 0-89019-06704. [Google Scholar]
- Davidson, A. The Oxford Companion to Food; Oxford University Press: Oxford, UK, 1999; ISBN 0-19-211579-0. [Google Scholar]
- Saltveit, M.E. Physical and physiological changes in minimally processed fruits and vegetables. In Phytochemistry of Fruits and Vegetables; Tomás-Barberán, F.A., Robin, R.D., Eds.; Oxford University Press: Oxford, UK, 1997; pp. 205–220. ISBN 0198577907. [Google Scholar]
- Loiza-Velarde, J.; Tomás-Barberán, F.A.; Saltveit, M.E. Effect of intensity and duration of heat-shock treatments on wound induced phenolic metabolism in iceberg lettuce. J. Am. Soc. Hortic. Sci. 1997, 122, 873–877. [Google Scholar] [CrossRef]
- Degl’innocenti, E.; Guidi, L.; Pardossi, A.; Tognoni, F. Biochemical Study of Leaf Browning in Minimally Processed Leaves of Lettuce (Lactuca sativa L. Var. Acephala). J. Agric. Food Chem. 2005, 53, 9980–9984. [Google Scholar] [CrossRef]
- Cantos, E.; Espin, J.C.; Tomás-Barberán, F. Effect of wounding on phenolic enzymes in six minimally processed lettuce cultivars upon storage. J. Agric. Food Chem. 2001, 49, 322–330. [Google Scholar] [CrossRef]
- Lopez, A.; Iguaz, A.; Esnoz, A.; Virseda, P. Thin-layer Drying behaviour of vegetable wastes from wholesale market. Dry. Technol. 2000, 18, 995–1006. [Google Scholar] [CrossRef]
- Rojano-Aguilar, A.; Santos, A.; Flores, J.; Salazar-Moreno, R.; Ruiz-García, A. Solar drying device tested with lettuce leaves. Acta Hortic. 2017, 1182, 105–110. [Google Scholar] [CrossRef]
- Mahapatra, A.; Tripathy, P.P. Modeling and simulation of moisture transfer during solar drying of carrot slices. J. Food Process Eng. 2018, 41, 1–15. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F.A. Review of thin layer drying of foods: Theory, modeling, and experimental results, critical reviews. Food Sci. Nutr. 2009, 50, 441–464. [Google Scholar] [CrossRef]
- Ayensu, A. Dehydration of food crops using a solar dryer with convective heat flow. Sol. Energy 1997, 59, 121–126. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin Layers. Master’s Thesis, Department of Mechanical Engineering, Prude University, Prude, West Lafayette, IN, USA, January 1949. [Google Scholar]
- Al-Mahasneh, M.A.; Rababah, T.M.; Al-Shbool, M.A. Thin-layer drying kinetics of sesame hulls under forced convection and open sun drying. J. Food Process Eng. 2007, 30, 324–337. [Google Scholar] [CrossRef]
- Henderson, S.M.; Pabis, S. Grain drying theory I: Temperature effect on drying coefficient. J. Agric. Res. Eng. 1961, 6, 169–174. [Google Scholar]
- Karathanos, V.T. Determination of water content of dried fruits by drying kinetics. J. Food Eng. 1999, 39, 337–344. [Google Scholar] [CrossRef]
- Toğrul, T.; Pehlivan, D. Modelling of drying kinetics of single apricot. J. Food Eng. 2003, 58, 23–32. [Google Scholar] [CrossRef]
- Midilli, A.; Kucuk, H.; Yapar, Z. A new model for single layer drying. Dry. Technol. 2002, 20, 1503–1513. [Google Scholar] [CrossRef]
- Henderson, S.M. Progress in developing the thin layer drying equation. Trans. ASAE 1974, 17, 1167–1168. [Google Scholar] [CrossRef]
- Sharaf-Elden, Y.I.; Blaisdell, J.L.; Hamdy, M.Y. A model for ear corn drying. Trans. ASAE 1980, 5, 1261–1265. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Kianmehr, M.H.; Arabhosseini, A.; Nazghelichi, T. Modelling the carrot thin layer drying in a semi-industrial continuous band dryer. Czech. J. Food Sci. 2009, 29, 528–538. [Google Scholar] [CrossRef]
- Verma, L.R.; Bucklin, R.A.; Endan, J.B.; Wratten, F.T. Effects of drying air parameters on rice drying models. Trans. ASAE 1985, 28, 296–301. [Google Scholar] [CrossRef]
- Wang, C.Y.; Singh, R.P. A Single Layer Drying Equation for Rough Rice; Paper No. 78–3001; ASAE: St. Joseph, MI, USA, 1978. [Google Scholar]
- Kucuk, H.; Midilli, A.; Kilic, A.; Dincer, I. A Review on Thin-Layer Drying-Curve Equations. Dry. Technol. 2014, 32, 757–773. [Google Scholar] [CrossRef]
- Babalis, S.T.; Papanicolaou, E.; Kyriakis, N.; Belessiotis, V.G. Evaluation of thin-layer drying models for describing drying kinetics of figs (Ficus carica). J. Food Eng. 2006, 75, 205–214. [Google Scholar] [CrossRef]
- Vega, A.; Lemus, R.; Tello, C.; Miranda, M.; Yagnam, F. Kinetic study of convective drying of blueberry variety O’Neil (Vaccinium corymbosum L.). Chil. J. Agric. Res. 2009, 69, 171–178. [Google Scholar] [CrossRef]
- Ergüneş, G.; Tarha, S. Color retention of red peppers by chemical pretreatments during greenhouse and open sun drying. J. Food Eng. 2006, 76, 446–452. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press, Clarendon Press: Oxford, UK, 1975; ISBN 0 19 853344 6. [Google Scholar]
- Yaldiz, O.; Ertekin, C. Thin layer solar drying of some vegetables. Dry. Technol. 2001, 19, 583–596. [Google Scholar] [CrossRef]
- Akpinar, E.K. Determination of suitable thin layer drying curve model for some vegetables and fruits. J. Food Eng. 2006, 73, 75–84. [Google Scholar] [CrossRef]
- Gunhan, T.; Demir, V.; Hancioglu, E.; Hepbasli, A. Mathematical modeling of drying of bay leaves. Energy Convers. Manag. 2005, 46, 1667–1679. [Google Scholar] [CrossRef]
- Gutiérrez, F.; De La Vara, R. Análisis y Diseño de Experimentos, 3rd ed.; Mc Graw Hill- Interamericana: Madrid, de España, 2012; ISBN 6071507251. [Google Scholar]
- Ali, M.A.; Yusof, Y.A.; Chin, N.L.; Ibrahim, M.N.; Basra, S.M.A. Drying kinetics and colour analysis of Moringa oleifera leaves. Agric. Agric. Sci. Procedia 2014, 2, 394–400. [Google Scholar] [CrossRef]
- Rosa, D.P.; Luna-Solano, G.; Polachini, T.C.; Telis-Romero, J. Mathematical modeling of orange seed drying kinetics. Ciênc. Agrotechol. 2015, 39, 291–300. [Google Scholar] [CrossRef]
- Akpinar, E.K. Mathematical modelling of thin layer drying process under open sun of some aromatic plants. J. Food Eng. 2006, 77, 864–870. [Google Scholar] [CrossRef]
- Alara, O.R.; Abdurahman, N.H.; Mudalip, S.K.A.; Olarere, O.A. Mathematical modeling of thin layer drying using open sun and shade of Vernonia amygdalina leaves. Agric. Nat. Resour. 2018, 52, 53–58. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Bicer, Y.; Cetinkaya, F. Modelling of thin layer drying of parsley leaves in a convective dryer and under open sun. J. Food Eng. 2006, 75, 308–315. [Google Scholar] [CrossRef]
- Sobukola, O.P.; Dairo, O.U.; Sanni, L.O.; Odunewu, A.V.; Fafiolu, B.O. Thin Layer Drying Process of Some Leafy Vegetables under Open Sun. Food Sci. Technol. Int. 2007, 13, 35–40. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Shalaby, S.M. Experimental investigation of an indirect-mode forced convection solar dryer for drying thymus and mint. Energy Convers. Manag. 2013, 74, 109–116. [Google Scholar] [CrossRef]
- Obón, J.M.; Castellar, M.R.; Alacid, M.; Fernández-López, J.A. Production of a red–purple food colorant from Opuntia stricta fruits by spray drying and its application in food model systems. J. Food Eng. 2009, 90, 471–479. [Google Scholar] [CrossRef]
- Hong, S.I.; Han, J.H.; Krochta, J.M. Optical and surface properties of whey protein isolate coatings on plastic films as influenced by substrate, protein concentration, and plasticizer type. J. Appl. Polym. Sci. 2004, 92, 335–343. [Google Scholar] [CrossRef]
- Batu, A. Determination of acceptable firmness and colour values of tomatoes. J. Food Eng. 2004, 61, 471–475. [Google Scholar] [CrossRef]
- Ahmed, J.; Kaur, A.; Shivhare, U. Color degradation kinetics of spinach, mustard leaves, and mixed puree. J. Food Sci. 2002, 3, 1088–1091. [Google Scholar] [CrossRef]
- Doymaz, I. Thin-layer drying behaviour of mint leaves. J. Food Eng. 2006, 74, 370–375. [Google Scholar] [CrossRef]
- Kadam, D.M.; Goyal, R.K.; Singh, K.K.; Gupta, M.K. Thin layer convective drying of mint leaves. J. Med. Plants Res. 2011, 5, 164–170, ISSN: 1996-0875. [Google Scholar]
- Doymaz, I.; Tugrul, N.; Pala, M. Drying characteristics of dill and parsley leaves. J. Food Eng. 2006, 7, 559–565. [Google Scholar] [CrossRef]

| N° | Model Name | Model | References |
|---|---|---|---|
| Models derived from Newton’s law of cooling | |||
| 1 | Newton | MR = exp (−k t) | [23] |
| 2 | Page | MR = exp (−k t n) | [24] |
| 3 | Modified Page I | MR = exp (−k t)n | [25] |
| Models derived from Fick’s second law of diffusion | |||
| 4 | Henderson and Pabis | MR = a exp (−k t) | [26] |
| 5 | Modified Henderson and Pabis. | MR = a exp (−k t) + b exp (−g t) + c exp (−h t) | [27] |
| 6 | Logarithmic | MR = a exp (−k t) + c | [28] |
| 7 | Approximation of diffusion | MR = a exp (−k t) + (1−a) exp (−k b t) | [28] |
| 8 | Midilli and Kucuk | MR = a exp (–k t n) + b t | [29] |
| 9 | Two Term | MR = a exp (−k0 t)+ b exp (−k1 t) | [30] |
| 10 | Two Term exponential | MR = a exp (−k t) + (1−a) exp (−k a t) | [31] |
| 11 | Aghbashlo Model | MR = exp (−(k1 t)/(1 + k2 t)) | [32] |
| 12 | Verma Model | MR = a exp(−k t) + (1−a) exp(−g t) | [33] |
| Empirical models | |||
| 13 | Wang and Sing | MR = 1 + a t + b t2 | [34] |
| 14 | Thompson | MR = exp ((−a −(a2 + 4 b t)0.5)/2b) | [35] |
| 15 | Weibull Distribution | MR = a − b exp (− k t n) | [36] |
| N° | Models | Coefficients | R2 | χ2 | SSE | RMSE | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Newton | k = 3.85 × 10−3 | 0.8995 | 1.32 × 10−2 | 1.28 × 10−2 | 0.11302 | |||||
| 2 | Page | k = 1.53 × 10−5 | n = 1.98128 | 0.9989 | 1.49 × 10−4 | 1.40 × 10−4 | 0.01182 | ||||
| 3 | Modified Page | k = 9.61 × 10−3 | n = 0.40023 | 0.8995 | 1.37 × 10−2 | 1.28 × 10−2 | 0.11203 | ||||
| 4 | Henderson and Pabis | a = 1.20453 | k = 4.58 × 10−3 | 0.9385 | 8.36 × 10−3 | 7.82 × 10−3 | 0.08842 | ||||
| 5 | Modified Henderson & Pabis | a = 0.26382 | b = 0.26382 | c = 0.67678 | k = 4.56 × 10−3 | g = 4.56 × 10−3 | h = 4.58 × 10−3 | 0.9385 | 9.70 × 10−3 | 7.82 × 10−3 | 0.08842 |
| 6 | Logarithm | a = 1.60883 | c = −0.48434 | k = 2.27 × 10−3 | 0.9781 | 3.08 × 10−3 | 2.79 × 10−3 | 0.05277 | |||
| 7 | Approach of diffusion | a = −119.017 | b = 0.98918 | k = 9.31 × 10−3 | 0.9908 | 1.29 × 10−3 | 1.17 × 10−3 | 0.03414 | |||
| 8 | Midilli and Kucuk | a = 1.00374 | b = −1.92 × 10−5 | n = 1.91162 | k = 2.22 × 10−5 | 0.9988 | 1.70 × 10−4 | 1.48 × 10−4 | 0.01217 | ||
| 9 | Two Term | a = 12.7062 | b = −11.7499 | k = 8.93 × 10−3 | k1 = 9.99 × 10−3 | 0.9915 | 1.24 × 10−3 | 1.08 × 10−3 | 0.03284 | ||
| 10 | Two Term Exponential | a = 2.23266 | k = 6.67 × 10−3 | 0.9868 | 1.85 × 10−3 | 1.67 × 10−3 | 0.04093 | ||||
| 11 | Aghbashlo | k1 = 1.85 × 10−3 | k2 = −1.66 × 10−3 | 0.9928 | 9.80 × 10−4 | 9.17 × 10−4 | 0.03028 | ||||
| 12 | Verma | a = 14.6651 | k = 8.05 × 10−4 | g = 6.71 × 10−4 | 0.9650 | 4.93 × 10−3 | 4.45 × 10−3 | 0.06671 | |||
| 13 | Wang and Sing | a = −2.64 × 10−3 | b = 1.42 × 10−6 | 0.9678 | 4.37 × 10−3 | 4.09 × 10−3 | 0.06396 | ||||
| 14 | Thompson | a = −180.062 | b = 0.41438 | 0.9378 | 2.76 × 10−2 | 2.58 × 10−2 | 0.16060 | ||||
| 15 | Weibull Distribution | a = 1.01587 | b = 0.00746 | k = 2.60 × 10−5 | n = 1.88817 | 0.9985 | 2.15 × 10−4 | 1.87 × 10−4 | 0.01368 | ||
| Chromatic Coordinates and Others Parameters | Samples | |
|---|---|---|
| Fresh | Dried | |
| L* | 27.97 ± 0.05 a | 28.92 ± 0.71 a |
| a* | −4.5 ± 0.07 a | 0.8 ± 0.13 b |
| b* | 22.27 ± 0.10 a | 16.5 ± 0.32 b |
| ΔE | - | 8.26 ± 0.18 |
| R = | −0.20 ± 0.00 a | 0.05 ± 0.01 b |
| h° | 101.43 ± 0.15 a | 87.16 ± 0.41 b |
| C | 22.72 ± 0.11 a | 16.07 ± 0.32 b |
| BI | 120.50 ± 0.70 a | 78.99 ± 0.50 b |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerezal Mezquita, P.; Álvarez López, A.; Bugueño Muñoz, W. Effect of Drying on Lettuce Leaves Using Indirect Solar Dryer Assisted with Photovoltaic Cells and Thermal Energy Storage. Processes 2020, 8, 168. https://doi.org/10.3390/pr8020168
Cerezal Mezquita P, Álvarez López A, Bugueño Muñoz W. Effect of Drying on Lettuce Leaves Using Indirect Solar Dryer Assisted with Photovoltaic Cells and Thermal Energy Storage. Processes. 2020; 8(2):168. https://doi.org/10.3390/pr8020168
Chicago/Turabian StyleCerezal Mezquita, Pedro, Aldo Álvarez López, and Waldo Bugueño Muñoz. 2020. "Effect of Drying on Lettuce Leaves Using Indirect Solar Dryer Assisted with Photovoltaic Cells and Thermal Energy Storage" Processes 8, no. 2: 168. https://doi.org/10.3390/pr8020168
APA StyleCerezal Mezquita, P., Álvarez López, A., & Bugueño Muñoz, W. (2020). Effect of Drying on Lettuce Leaves Using Indirect Solar Dryer Assisted with Photovoltaic Cells and Thermal Energy Storage. Processes, 8(2), 168. https://doi.org/10.3390/pr8020168