Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. XRD Analysis
3.2. Thermal Analysis
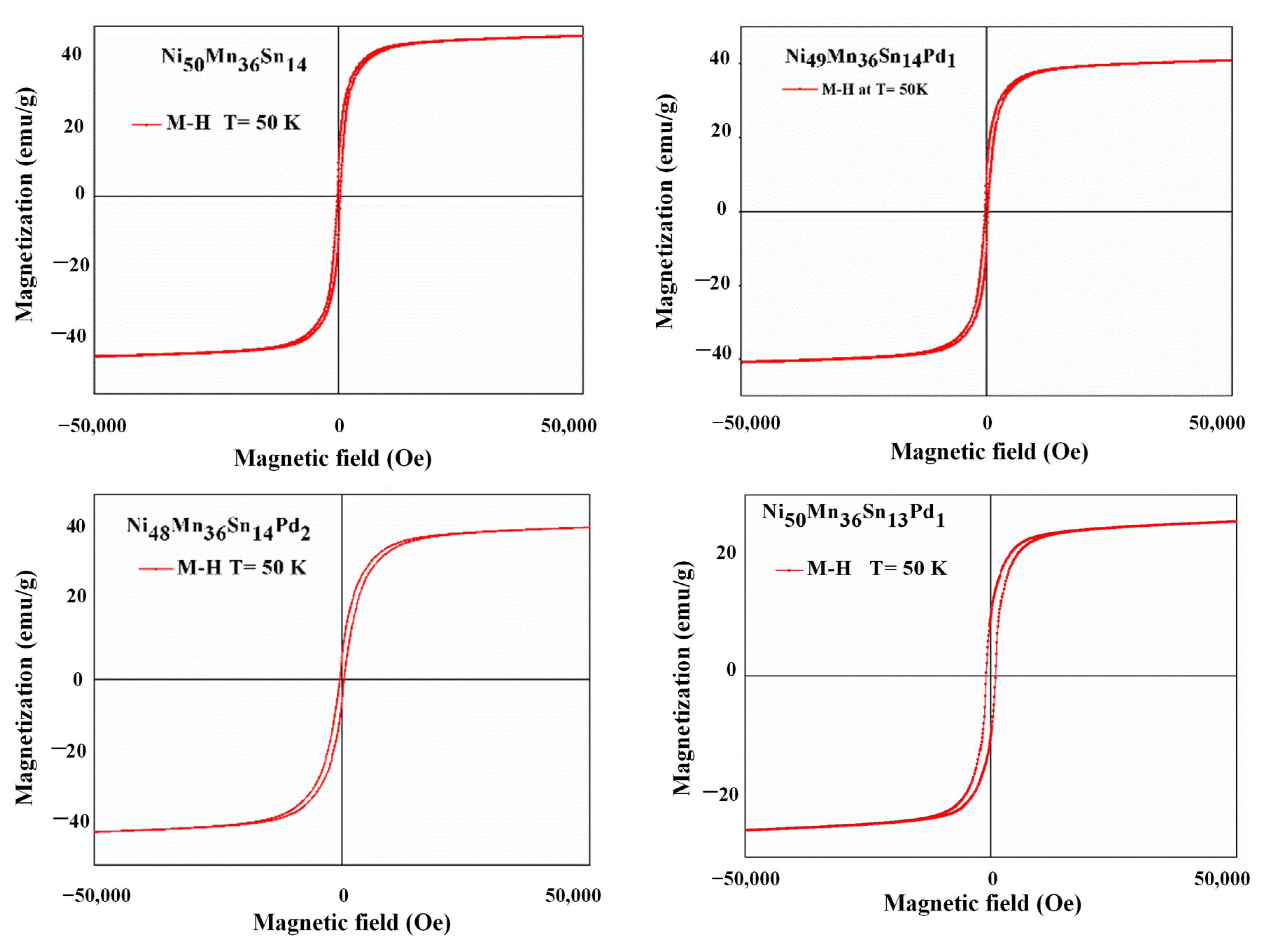
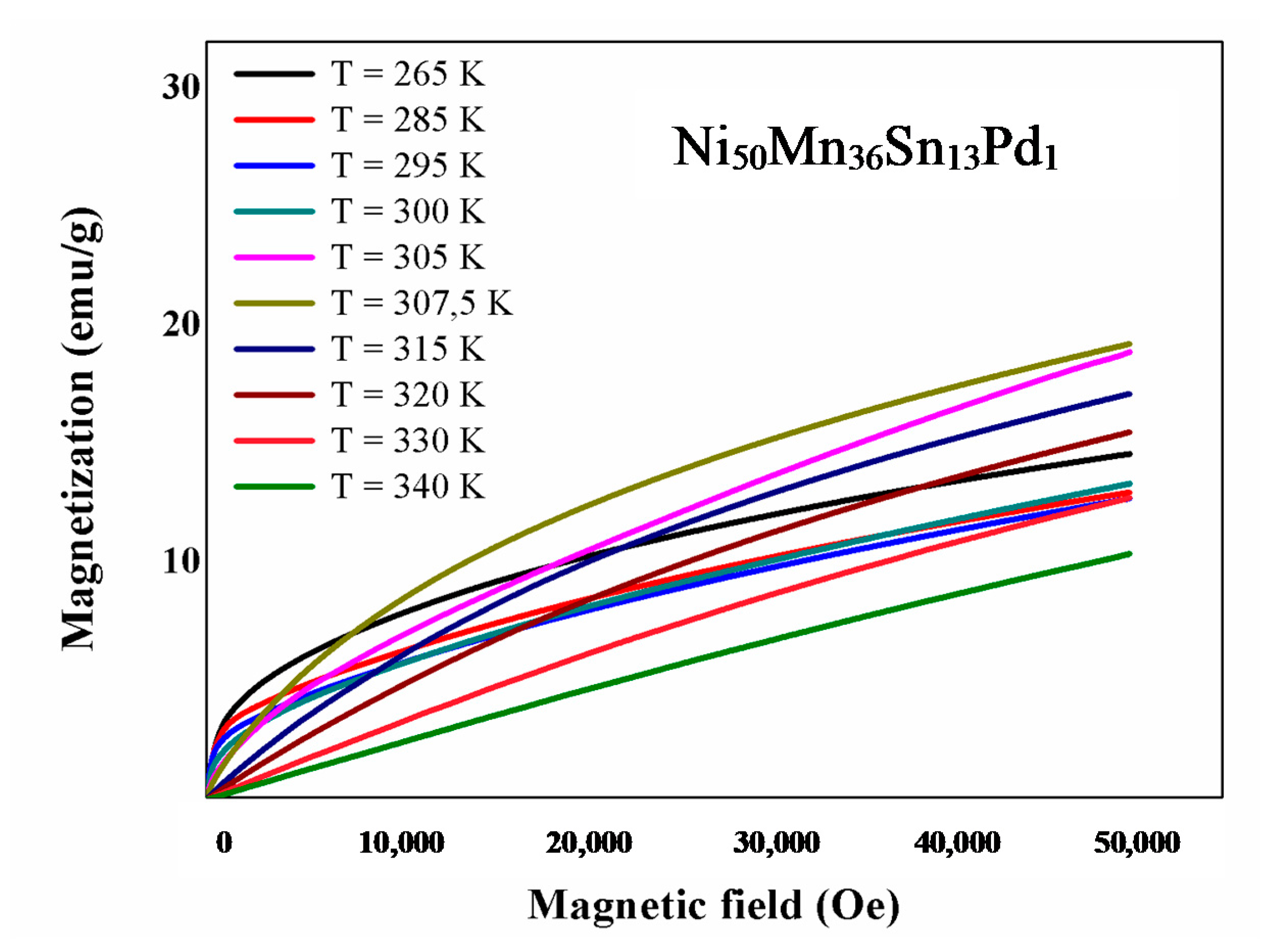
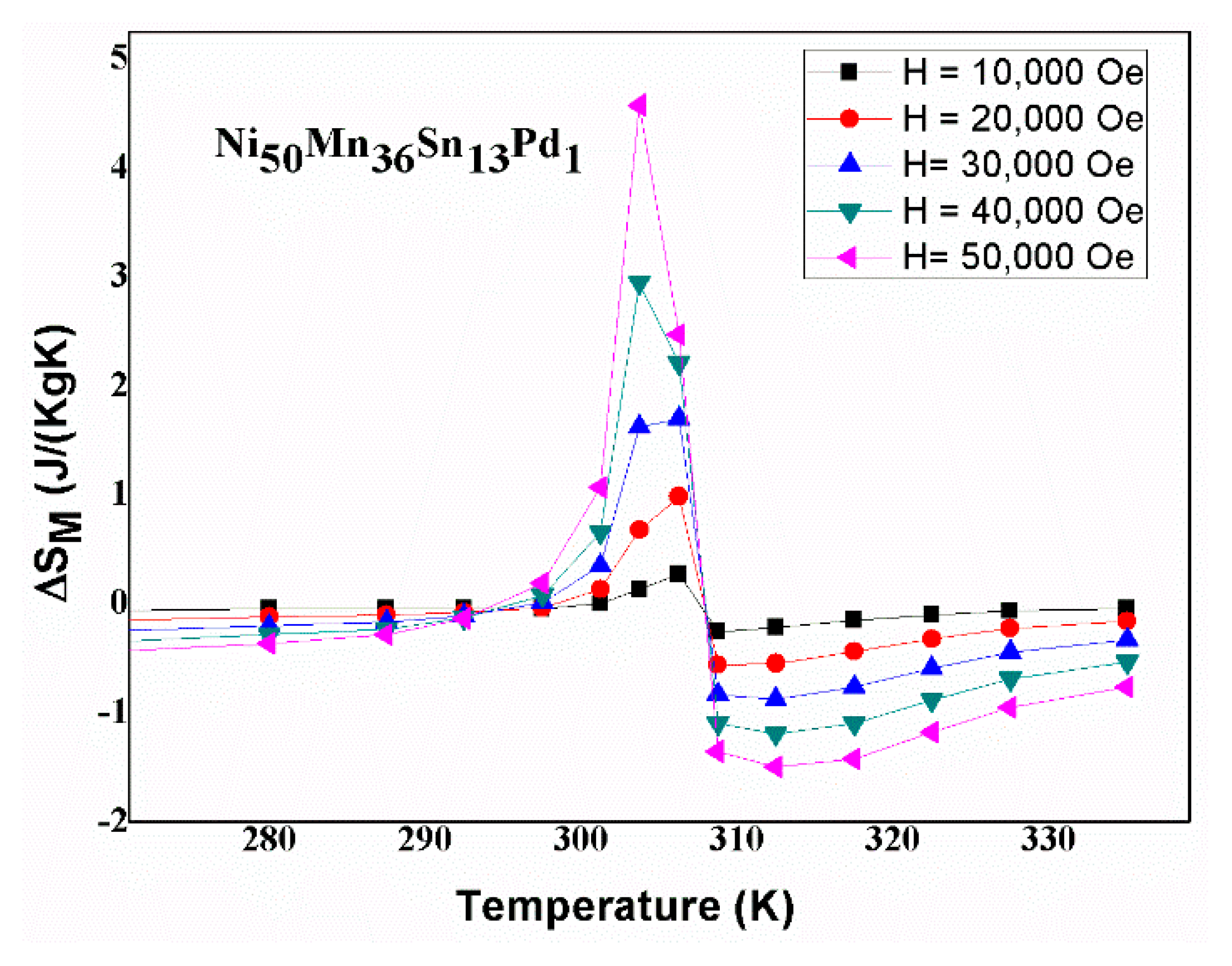
3.3. Magnetic Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kök, M.; Durğun, S.B.; Özen, E. Thermal analysis, crystal structure and magnetic properties of Cr-doped Ni–Mn–Sn high-temperature magnetic shape memory alloys. J. Therm. Anal. Calorim. 2019, 136, 1147–1152. [Google Scholar] [CrossRef]
- Gruner, M.E.; Niemann, R.; Entel, P.; Pentcheva, R.; Rößler, U.K.; Nielsch, K.; Fähler, S. Modulations in martensitic Heusler alloys originate from nanotwin ordering. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Coll, R.; Escoda, L.; Saurina, J.; Sánchez-Llamazares, J.L.; Hernando, B.; Suñol, J.J. Martensitic transformation in Mn-Ni-Sn Heusler alloys. J. Therm. Anal. Calorim. 2010, 99, 905–909. [Google Scholar] [CrossRef]
- Bachaga, T.; Daly, R.; Escoda, L.; Sunol, J.J.; Khitouni, M. Influence of chemical composition on martensitic transformation of MnNiIn shape memory alloys. J. Therm. Anal. Calorim. 2015, 122, 167–173. [Google Scholar] [CrossRef]
- Zhang, K.; Tan, C.; Guo, E.; Feng, Z.; Zhu, J.; Tong, Y.; Cai, W. Simultaneous tuning of martensitic transformation behavior, magnetic and mechanical properties in Ni–Mn–Sn magnetic alloy by Cu doping. J. Mater. Chem. C 2018, 6, 5228–5238. [Google Scholar] [CrossRef]
- Maji, B.; Ray, M.K.; Modak, M.; Mondal, S.; Suresh, K.G.; Banerjee, S. Magnetic properties and large reversible magnetocaloric effect in Er3Pd2. J. Magn. Magn. Mater. 2018, 456, 236–240. [Google Scholar] [CrossRef]
- Pérez-Landazábal, J.I.; Recarte, V.; Sánchez-Alarcos, V.; Beto-López, J.J.; Rodríguez-Velamazán, J.A.; Sánchez-Marcos, J.; Gómez-Polo, E.; Cesari, E. Giant direct and inverse magnetocloric effect linked to the same forward martensitic transformation. Sci. Rep. 2017, 7, 13328. [Google Scholar] [CrossRef]
- Ghosh, A.; Rawat, R.; Bhattacharyya, A.; Mandal, G.; Nigam, A.K.; Nair, S. Measurement independent magnetocaloric effect in Mn-rich Mn-Fe-Ni-Sn(Sb/In) Heusler alloys. J. Magn. Magn. Mater. 2019, 476, 92–99. [Google Scholar] [CrossRef]
- Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morito, H.; Okamoto, S.; Kitakami, O.; Oikawa, K.; Fujita, A.; Kanomata, T.; et al. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar] [CrossRef]
- Li, Z.B.; Yang, B.; Zhang, Y.D.; Esling, C.; Zhao, X.; Zuo, L. Influence of Cu doping on martensitic and magnetic transitions in Ni-Mn-Sn alloys. Mater. Sci. Forum 2017, 879, 1123–1128. [Google Scholar] [CrossRef]
- Wederni, A.; Ipatov, M.; Pineda, E.; Suñol, J.-J.; Escoda, L.; González, J.M.; Alleg, S.; Khitouni, M.; Żuberek, R.; Chumak, O.; et al. Magnetic properties, martensitic and magnetostructural transformations of ferromagnetic Ni–Mn–Sn–Cu shape memory alloys. Appl. Phys. A 2020, 126, 320. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Qian, M.; Geng, L. Enhanced magnetocaloric effect in Ni-Mn-Sn-Co alloys with two successive magnetostructural transformations. Sci. Rep. 2018, 8, 8235. [Google Scholar] [CrossRef]
- Chen, C.; Yu, L.; Zhu, J.; Tan, C. The mechanical properties of Ni-Mn-Sn Alloy thin films with Fe doping. Integr. Ferroelectr. 2020, 207, 156–165. [Google Scholar] [CrossRef]
- Inallu, M.N.; Kameli, P.; Varzaneh, A.G.; Sarsari, I.A.; Salazar, D.; Orue, I.; Chernenko, V.A. Magnetocaloric effect in W-doped Ni-Mn-Sn alloy probed by direct and indirect measurements. J. Phys. D Appl. Phys. 2019, 52. [Google Scholar] [CrossRef]
- Dong, S.Y.; Chen, J.Y.; Han, Z.D.; Fang, Y.; Zhang, L.; Zhang, C.L.; Qian, B.; Jiang, X.F. Intermartensitic transformation and enhanced exchange bias in Pd (Pt)-doped Ni-Mn-Sn alloys. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Katukuri, V.M.; Cococcioni, M. Origin of magnetic interactions and their influence on the structural properties of Ni 2 MnGa and related compounds related content origin of magnetic interactions and their influence on the structural properties of Ni 2 MnGa and related compounds. J. Phys. Condens. Matter 2012, 24, 15. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Nigam, A.K. Room temperature inverse magnetocaloric effect in Pd substituted Ni50Mn37Sn13 Heusler alloys. Phys. B Condens. Matter 2014, 448, 263–266. [Google Scholar] [CrossRef]
- Lutterotti, L.; Matthies, S.; Wenk, H.R. Quantitative phase analysis. Newsl. CPD 1999, 21, 14–15. [Google Scholar]
- Quintana-Nedelcos, A.; Llamazares, J.L.S.; Ríos-Jara, D.; Lara-Rodríguez, A.G.; García-Fernández, T. Effect of quenching rate on the average grain size and martensitic transformation temperature in rapidly solidified polycrystalline Ni50Mn37Sn13 alloy ribbons. Phys. Status Solidi 2013, 210, 2159–2165. [Google Scholar] [CrossRef]
- Krenke, T.; Moya, X.; Aksoy, S.; Acet, M.; Entel, P.; Mañosa, L.; Planes, A.; Elerman, Y.; Yücel, A.; Wassermann, E.F. Electronic aspects of the martensitic transition in Ni–Mn based Heusler alloys. J. Magn. Magn. Mater. 2007, 310, 2788–2789. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Bachaga, T.; Daly, R.; Khitouni, M.; Escoda, L.; Saurina, J.; Suñol, J. Thermal and structural analysis of Mn49.3Ni43.7Sn7.0 Heusler alloy ribbons. Entropy 2015, 17, 646–657. [Google Scholar] [CrossRef]
- Qu, Y.H.; Cong, D.Y.; Sun, X.M.; Nie, Z.H.; Gui, W.Y.; Li, R.G.; Ren, Y.; Wang, Y.D. Giant and reversible room-temperature magnetocaloric effect in Ti-doped Ni-Co-Mn-Sn magnetic shape memory alloys. Acta Mater. 2017, 134, 236–248. [Google Scholar] [CrossRef]
- Emre, B.; Yuce, S.; Bruno, N.M.; Karaman, I. Martensitic transformation and magnetocaloric properties of NiCoMnSn magnetic shape memory alloys. Intermetallics 2019, 106, 65–70. [Google Scholar] [CrossRef]
- Czaja, P.; Kowalczyk, M.; Maziarz, W. On the magnetic contribution to the inverse magnetocaloric effect in Ni-Co-Cu-Mn-Sn metamagnetic shape memory alloys. J. Magn. Magn. Mater. 2019, 474, 381–392. [Google Scholar] [CrossRef]
- Xuan, H.C.; Xie, K.X.; Wang, D.H.; Han, Z.D.; Zhang, C.L.; Gu, B.X.; Du, Y.W. Effect of annealing on the martensitic transformation and magnetocaloric effect in Ni44.1Mn44.2Sn11.7 ribbons. Appl. Phys. Lett. 2008, 92, 242506. [Google Scholar] [CrossRef]
- Xing, C.; Zhang, H.; Long, K.; Xiao, Y.; Zhang, H.; Qiu, Z.; He, D.; Liu, X.; Zhang, Y.; Long, Y. The effect of different atomic substitution at Mn site on magnetocaloric effect in Ni50Mn35Co2Sn13 alloy. Crystals 2018, 8, 329. [Google Scholar] [CrossRef]
- Pataky, G.J.; Ertekin, E.; Sehitoglu, H. Elastocaloric cooling potential of NiTi, Ni2FeGa, and CoNiAl. Acta Mater. 2015, 96, 420–427. [Google Scholar] [CrossRef]
- Louidi, S.; Sunol, J.J.; Ipatov, M.; Hernando, B. Effect of cobalt doping on martensitic transformations and the magnetic properties of Ni 50−x Co x Mn 37 Sn 13 (x = 1, 2, 3) Heusler ribbons. J. Alloys Compd. 2018, 739, 305–310. [Google Scholar] [CrossRef]
- Bachaga, T.; Daly, R.; Suñol, J.J.; Saurina, J.; Escoda, L.; Legarreta, L.G.; Hernando, B.; Khitouni, M. Effects of Co additions on the martensitic transformation and magnetic properties of Ni–Mn–Sn shape memory alloys. J. Supercond. Nov. Magn. 2015, 28, 3087–3092. [Google Scholar] [CrossRef]
- Dubenko, I.; Ali, N.; Stadler, S.; Zhukov, A.; Zhukova, V.; Hernando, B.; Prida, V.; Prudnikov, V.; Gan’shina, E.; Granovsky, A. Magnetic, magnetocaloric, magnetotransport, and magneto-optical properties of Ni–Mn–In-based Heusler alloys: Bulk, ribbons, and microwires. In Novel Functional Magnetic Materials; Springer: Cham, Switzerland, 2016; pp. 41–82. [Google Scholar]
- González-Legarreta, L.; Caballero-Flores, R.; Rosa, W.O.; Ipatov, M.; Escoda, L.; Suñol, J.J.; Prida, V.M.; González, J.; Hernando, B. Heusler alloy ribbons: Structure, martensitic transformation, magnetic transitions, and exchange bias effect. In Novel Functional Magnetic Materials; Springer: Cham, Switzerland, 2016; pp. 83–114. [Google Scholar]
- Wu, Z.; Guo, J.; Liang, Z.; Zhang, Y.; Ye, X.; Zhang, J.; Li, Y.; Liu, Y.; Yang, H. Room temperature metamagnetic transformation of a tough dual-phase Ni–Mn–Sn–Fe ferromagnetic shape memory alloy. J. Alloys Compd. 2020, 829, 154606. [Google Scholar] [CrossRef]
- Hernando, B.; Llamazares, J.L.S.; Santos, J.D.; Sánchez, M.L.; Escoda, L.; Suñol, J.J.; Varga, R.; García, C.; González, J. Grain oriented NiMnSn and NiMnIn Heusler alloys ribbons produced by melt spinning: Martensitic transformation and magnetic properties. J. Magn. Magn. Mater. 2009, 321, 763–768. [Google Scholar] [CrossRef]
- Caron, L.; Ou, Z.Q.; Nguyen, T.T.; Cam Thanh, D.T.; Tegus, O.; Brück, E. On the determination of the magnetic entropy change in materials with first-order transitions. J. Magn. Magn. Mater. 2009, 321, 3559–3566. [Google Scholar] [CrossRef]
- Aguilar-Ortiz, C.O.; Soto-Parra, D.; Álvarez-Alonso, P.; Lázpita, P.; Salazar, D.; Castillo-Villa, P.O.; Flores-Zúñiga, H.; Chernenko, V.A. Influence of Fe doping and magnetic field on martensitic transition in Ni-Mn-Sn melt-spun ribbons. Acta Mater. 2016, 107, 9–16. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, L.; Du, J. Table-like magnetocaloric effect in Gd–Ni–Al amorphous/nanocrystalline composites. J. Phys. D Appl. Phys. 2017, 50, 355601. [Google Scholar] [CrossRef]
- Liu, Z.H.; Aksoy, S.; Acet, M. Influence of Sb on the magnetic and magnetocaloric properties of ferromagnetic shape memory alloy NiMnIn. J. Appl. Phys. 2009, 105. [Google Scholar] [CrossRef]
- Fabbrici, S.; Kamarad, J.; Arnold, Z.; Casoli, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Porcari, G.; Pernechele, C.; et al. From direct to inverse giant magnetocaloric effect in Co-doped NiMnGa multifunctional alloys. Acta Mater. 2011, 59, 412–419. [Google Scholar] [CrossRef]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Inverse magnetocaloric effect in ferromagnetic Ni–Mn–Sn alloys. Nat. Mater. 2005, 4, 450–454. [Google Scholar] [CrossRef]
- Sasioglu, E.; Sandratskii, L.M.; Bruno, P. First-principles calculation of the intersublattice exchange interactions and Curie temperatures of full Heusler alloys Ni2MnX (X = Ga, In, Sn, Sb). Phys. Rev. B Condens. Matter Mater. Phys. 2004, 70. [Google Scholar] [CrossRef]
- Provenzano, V.; Shapiro, A.J.; Shull, R.D. Reduction of hysteresis losses in the magnetic refrigerant Gd 5Ge2Si2 by the addition of iron. Nature 2004, 429, 853–857. [Google Scholar] [CrossRef]
- Modak, R.; Manvel Raja, M.; Srinivasan, A. Enhanced magento-caloric effect upon fourt element (Cu, Fe, Co) substitution in Ni-Mn-Sn thin films. Appl. Phys. A 2019, 125, 57. [Google Scholar] [CrossRef]
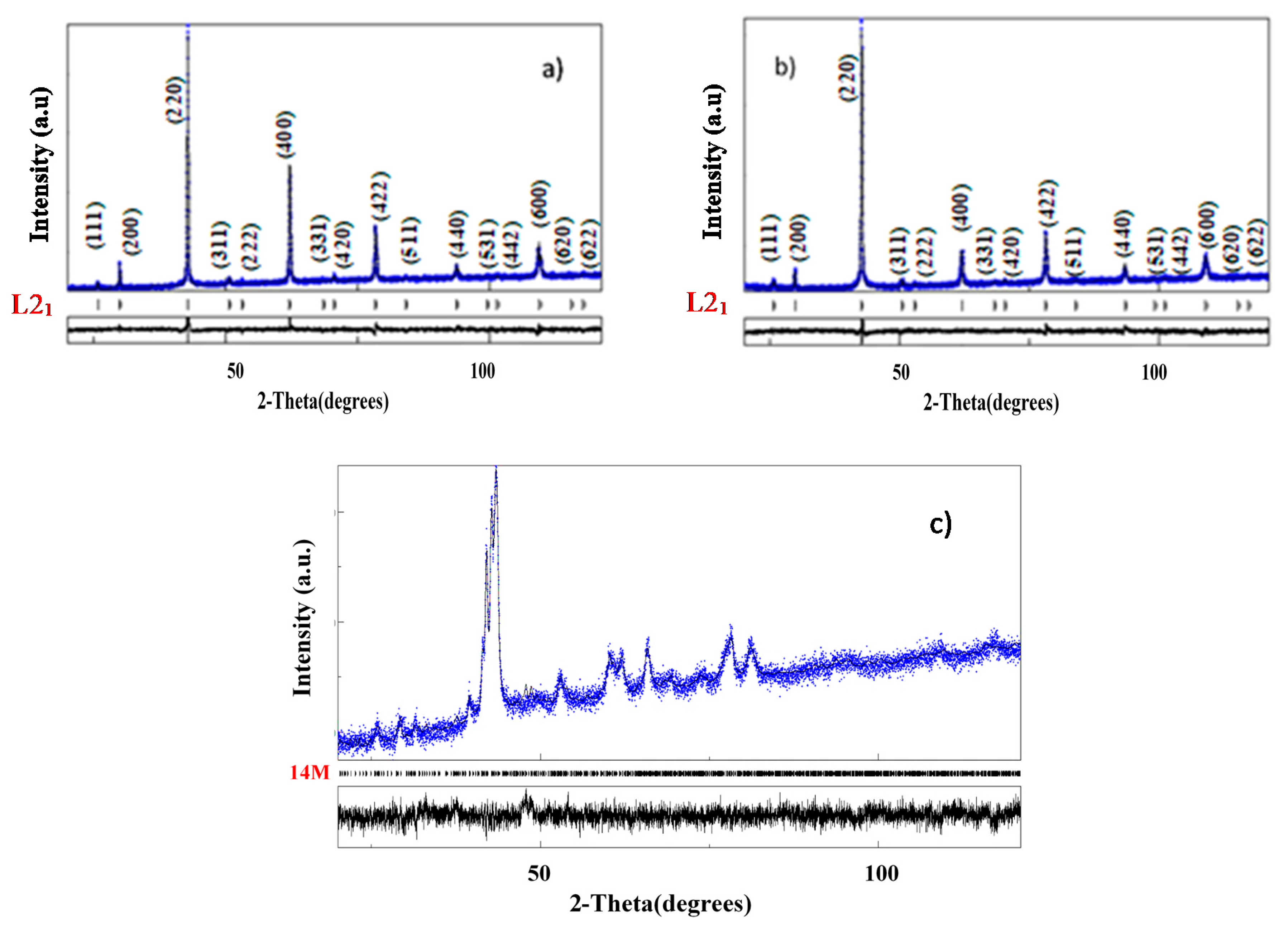
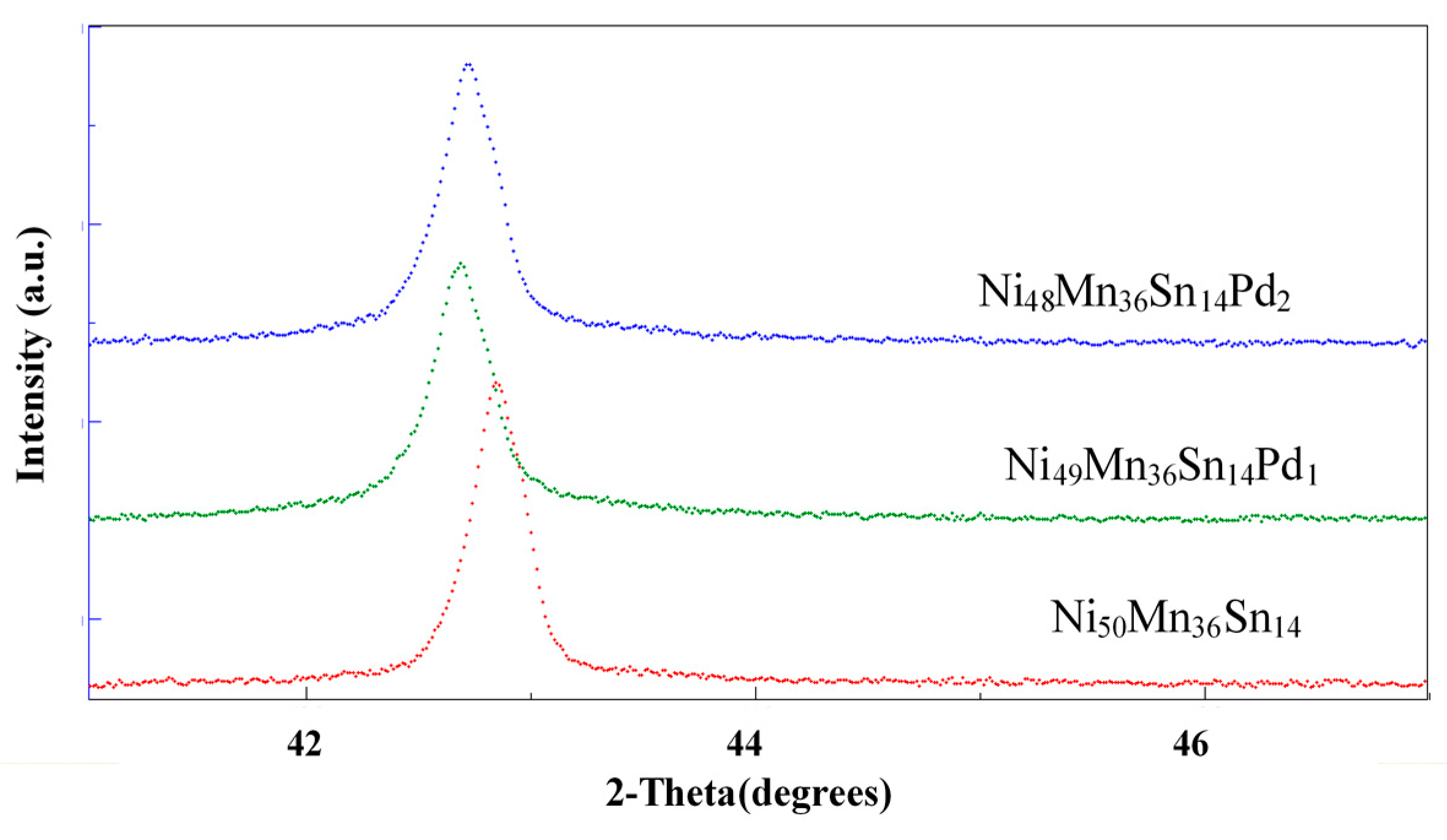
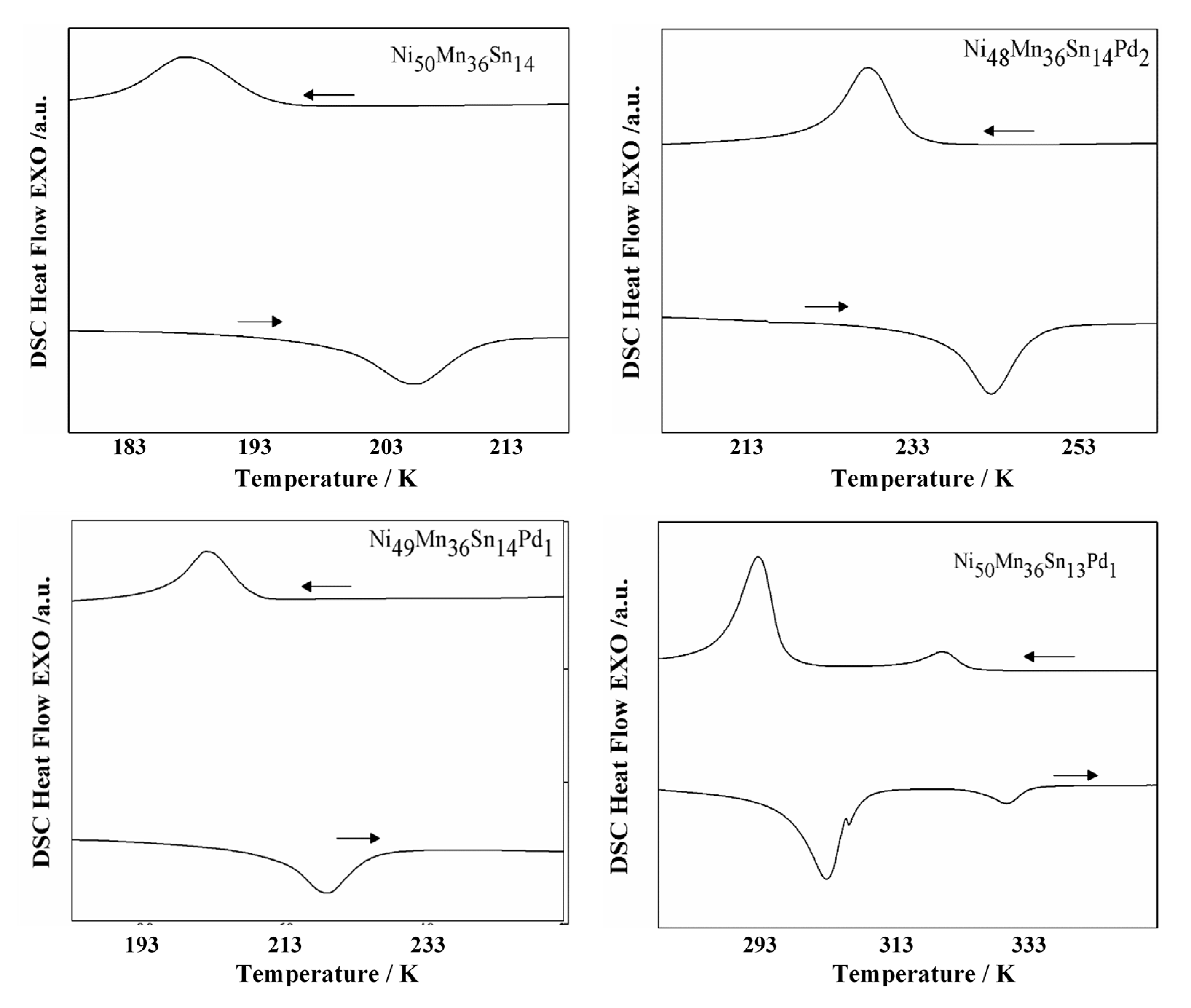
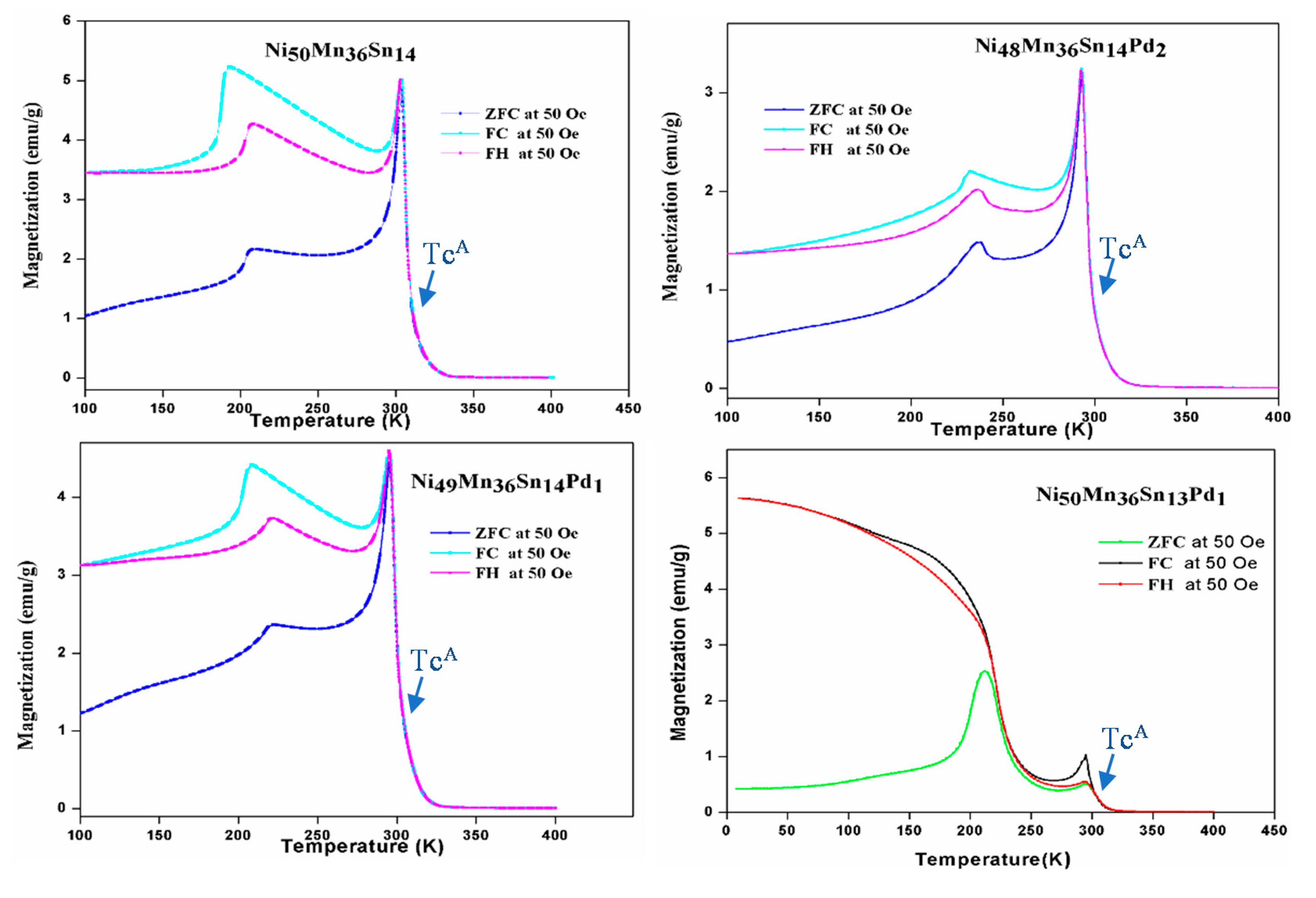

| Alloy | Ms/K | Mf/K | As/K | Af/K | T0/K | ΔH/J g−1 | ΔS/J g−1 K−1 |
|---|---|---|---|---|---|---|---|
| Ni50Mn36Sn14 | 194.09 | 182.75 | 198.89 | 212.75 | 203.42 | (h) 1.573 (c) 1.516 | (h) 0.0078 (c) 0.00758 |
| Ni50Mn36Sn13Pd1 | 295.85 | 286 | 296.6 | 307 | 301.425 | (h) 0.626 (c) 0.612 | (h) 1.595 (c) 1.633 |
| Ni49Mn36Sn14Pd1 | 208.76 | 193 | 211.8 | 225 | 216.88 | (h) 1.539 (c) 1.332 | (h) 0.0035 (c) 0.0030 |
| Ni48Mn36Sn14Pd2 | 233.26 | 219.2 | 219.2 | 247 | 240.13 | (h) 2.939 (c) 2.994 | (h) 0.0122 (c) 0.0124 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wederni, A.; Ipatov, M.; Pineda, E.; Escoda, L.; González, J.-M.; Khitouni, M.; Suñol, J.-J. Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys. Processes 2020, 8, 1582. https://doi.org/10.3390/pr8121582
Wederni A, Ipatov M, Pineda E, Escoda L, González J-M, Khitouni M, Suñol J-J. Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys. Processes. 2020; 8(12):1582. https://doi.org/10.3390/pr8121582
Chicago/Turabian StyleWederni, Asma, Mihail Ipatov, Eloi Pineda, Lluisa Escoda, Julian-Maria González, Mohamed Khitouni, and Joan-Josep Suñol. 2020. "Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys" Processes 8, no. 12: 1582. https://doi.org/10.3390/pr8121582
APA StyleWederni, A., Ipatov, M., Pineda, E., Escoda, L., González, J.-M., Khitouni, M., & Suñol, J.-J. (2020). Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys. Processes, 8(12), 1582. https://doi.org/10.3390/pr8121582







