1. Introduction
Multitubular packed bed reactors are widely used in the chemical and process industry for highly endothermic or exothermic catalytic reactions. They consist of up to thousands of tubes filled with catalyst particles, whereby a heat transfer media, e.g., a molten salt or gas heated by combustion, is circulated around the tubes to either provide or remove the heat of reaction. To ensure an adequate radial heat transfer within the reactor tubes, the tube diameter is usually very low (2–8 cm) [
1]. On the other hand, the pressure drop needs to be kept low, that is why relatively large particles are used, which leads to slender packed beds characterized by a low tube-to-particle diameter ratio
N.
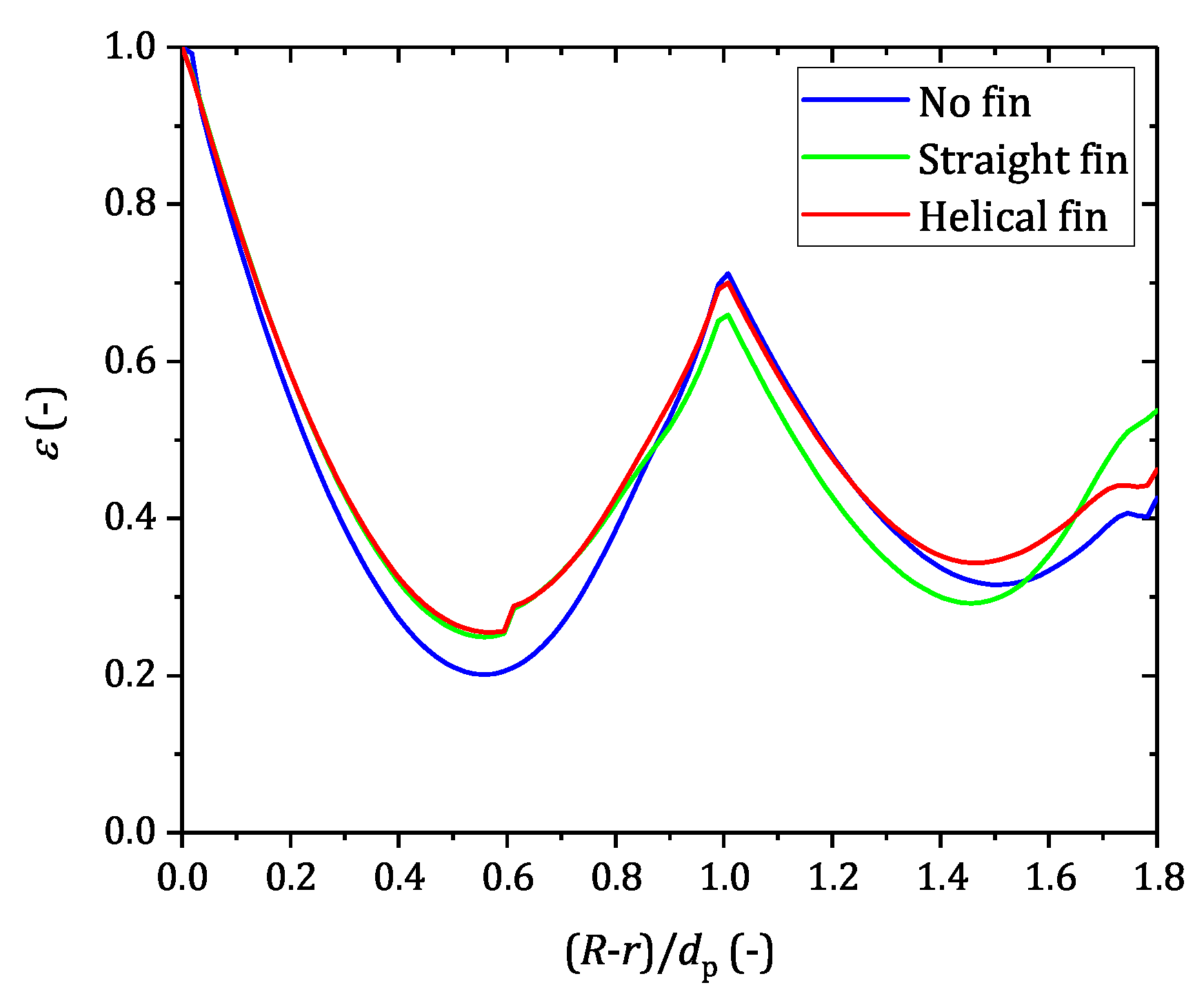
For this reactor configuration the assumption of a homogeneously distributed void fraction does not hold true, as the confining walls exert an ordering effect on the particle structure. This leads to a radial void fraction distribution that is characterized by several distinct minima and maxima, as exemplary shown in
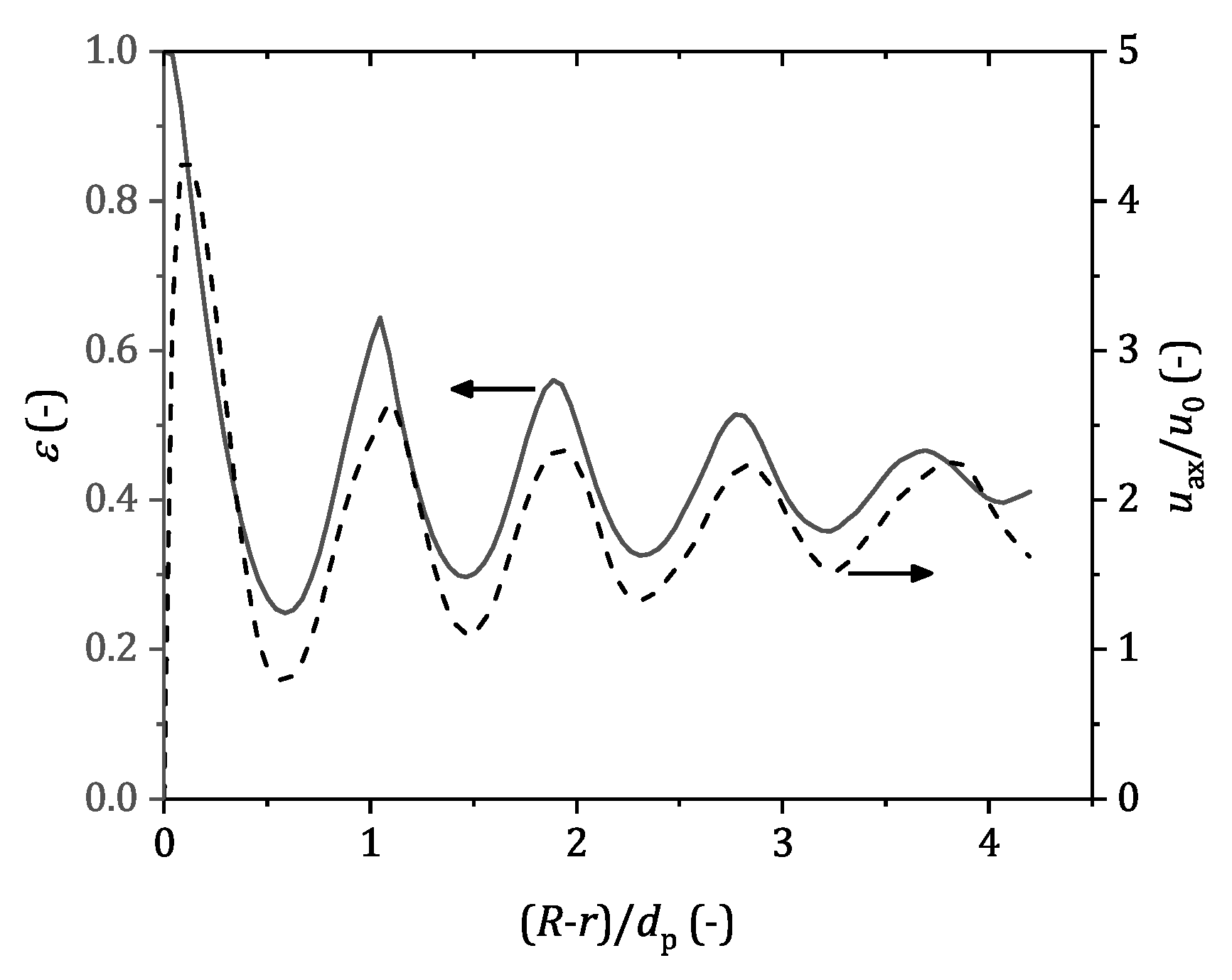
Figure 1 for spheres. Directly at the wall, only a point contact exists between particles and the tube wall, leading to a bed voidage of
. Because of the ordering wall effect, particles tend to build a layer close to the wall. This leads to a global minimum in bed voidage at a distance of half a sphere away from the wall. After a distance of one particle diameter, the first layer of particles ends, leading to a global maximum in bed voidage. With increasing distance from the wall the ordering effect gets more and more lost, leading to a damped oscillatory progression of the radial void fraction distribution. The unevenly distributed bed voidage significantly impacts the fluid dynamics in the bed structure as it can be seen in
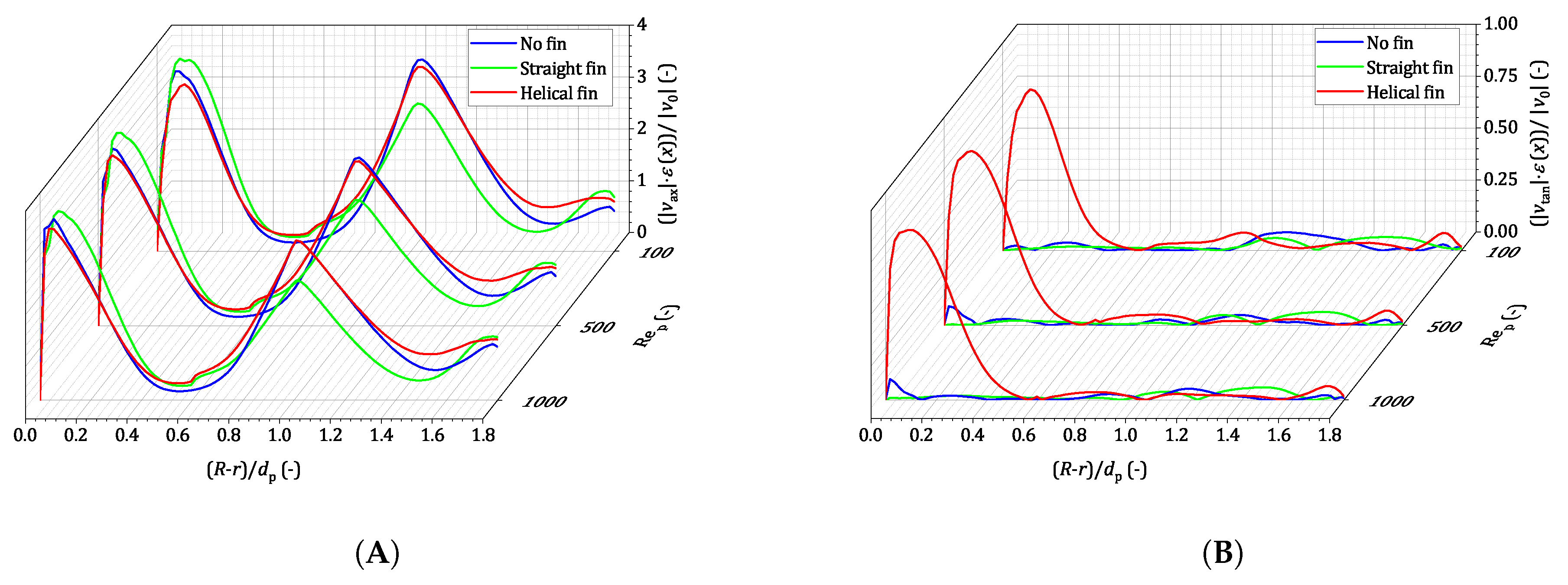
Figure 1 in terms of the radial profile of the average axial velocity normalized by the superficial velocity. The radial velocity profile corresponds to the radial void fraction distribution and shows an increased axial velocity at positions where the bed voidage is high, which is because the flow tends to take the path of the lowest resistance. Close to the reactor wall a global maximum in axial velocity can be seen which is known as the wall channeling effect. It is widely accepted that this effect negatively influences the radial heat transport close to the wall, and, therefore, limits the thermal performance of the overall system. According to Yagi and Kunii [
2], the reduced heat transfer can be attributed to three different effects, which are: (1) the reduced solid conductivity close to the wall as a result of increased voidage, (2) the buildup of a laminar boundary layer at the wall, and (3) a reduced lateral convective mixing.
Recently, several research groups have addressed this topic, investigating reactor concepts to increase the radial heat transfer in gas-solid systems. Some of those concepts are shown illustratively in
Figure 2. The main research focus is on the investigation of the impact of particle shape on fluid dynamics, heat/mass transfer and chemical conversion. The experimental work of Giese et al. [
3] showed that the use of Raschig rings or deformed spheres lead to a more homogeneous radial void fraction distribution and less radial variance in axial velocity in the inner region of the packed bed. However, it was also shown that the wall channeling as such could not fully be avoided. This finding was later verified by the numerical work of Caulkin et al. [
4] and Wehinger et al. [
5]. The former of both authors showed that even for trilobes, although characterized by an almost homogeneous void fraction profile, a wall channeling effect occur, caused by the steep increase of bed voidage close to the wall. Nevertheless, although the wall channeling cannot totally be avoided by the choice of complex particle shapes, it can be at least reduced. Martin and Nilles [
6] demonstrated, that compared to spheres, Raschig rings show a higher wall heat transfer coefficient over a large Reynolds number range. However, the authors also highlighted that cylinder packings show a slightly higher heat transfer coefficient, although the tendency for wall channeling is higher compared to rings. A possible explanation for this is the higher conductive resistance of rings caused by the lower amount of solid material in the system. Although, from a fluid dynamic point of view, complex particle shapes may not solve entirely the radial heat transfer problem, from a reaction engineering point of view, it offers many possibilities as recently shown [
5,
7,
8]. Especially, different catalyst suppliers present very different types of shapes for different applications, e.g., wagon wheels, toothed wheels, flute wheels, daisy-types, tri- or multi-lobes, stars, and many more [
9,
10].
An alternative concept to overcome the radial heat transfer problem in catalytic flow reactors represent periodic open cell structures (POCS), as proposed by the research groups at FAU Erlangen-Nuremberg [
11,
12,
13] and visualized in
Figure 2B. This concept combines the beneficial characteristics of honeycomb monoliths, e.g., low pressure drop and high thermal conductivity, with the high radial mass transfer of open-cell foams. The packings are based on unit cells, e.g., cubic, diamond or tetradecahedron cells, which are arranged periodically and repetitively. POCS are proposed as alternatives to random bed structures or honeycombs in gas-solid or gas-liquid-solid applications [
11,
12,
13]. The latter authors investigated the impact of material, morphology and wall coupling on the thermal performance of POCS. The material, and likewise the solid thermal conductivity, only affected the stagnant part of the effective radial thermal conductivity of the system, leading to a parallel shift of the effective radial thermal conductivity for different materials plotted over superficial gas velocity. The authors found that an increasing voidage leads to a reduced stagnant conductivity, while with decreasing cell density the effective radial thermal conductivity increases faster, if the superficial gas velocity is raised. This reveals one drawback of the concept: Although the specific surface area with respect to the reactor volume is high (
), the absolute available surface area is limited, because the voidage is usually also high (
), and a high cell density (number of void cells per inch) has a negative effect on the effective radial thermal conductivity. The wall coupling seems not to be too critical, as it was found that 10–20% wall coupling is sufficient for an effective wall heat transfer. However, it was shown that in comparison to conventional packed bed reactors with the same specific surface area, POCS are only beneficial for low to moderate superficial velocities of
, which corresponds to a maximum Particle Reynolds number of
. This could limit the throughput under optimal operating conditions and thus leads to larger reactor dimensions, resulting in higher investment costs. Furthermore, there may be limitations on the manufacturability of large scale POCS.
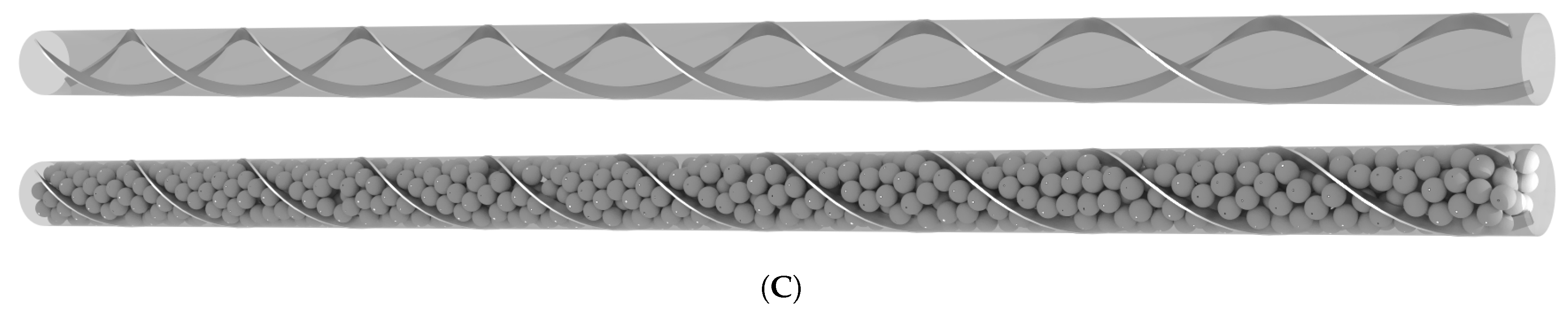
Also inspired by the superior heat transfer characteristic of open-cell foams is the packed foams reactor concept proposed by Ambrosetti et al. [
14] (see schematically
Figure 2C) and the packed-POCS concept by Fratalocchi et al. [
15] and Ambrosetti et al. [
16]. Here, the open-cell foam or POCS are just a carrier to enhance the heat transfer. The catalytic active surface area is provided by traditional pellets that are poured into the reactor and fill the interstices. In their numerical and experimental study, Ambrosetti et al. [
14,
16] found that the packing efficiency (
) is mainly affected by the pore-to-pellet size ratio. For a ratio of
the bed voidage approaches asymptotically the value of conventional packed beds filled with the same type of particles. Furthermore, the authors found that the specific pressure drop of packed foams is in the same order of magnitude as for a packed bed, if the foam has a high void fraction (
). This becomes significantly higher, if the foam voidage decreases. For the reactor design, this results in a trade-off between good thermal conductivity and low pressure drop. Since the foam structure occupies space that is not available for catalyst particles, this leads in an overall higher pressure drop per active catalyst surface area in comparison to conventional packed beds. However, it was shown by Fratalocchi et al. [
15] that for Fischer-Tropsch synthesis, the packed foam concept leads to almost isothermal reaction conditions and higher conversion in comparison to conventional packed beds. In comparison to packed foams, packed-POCS show an increased bulk heat transfer characteristic and wall heat transfer, respectively.
A completely different concept to solve the radial heat transfer problem in packed beds is proposed by Zobel et al. [
17] and Eppinger et al. [
18], see
Figure 2D. They suggest macroscopic wall structures to disturb the regular particle arrangement close to the wall. With that, they achieved a more homogeneous axial and radial void fraction distribution, leading to a more plug-flow-like flow characteristic. Zobel et al. [
17] demonstrated, that, close to the wall, lateral mixing is significantly increased, showing an average radial velocity of up to 30% higher, compared to the case without wall structures. In their numerical study, Eppinger et al. [
18] noticed an up to 40% increase in lateral mixing when using appropriate macroscopic wall structures. They also found that the wall channeling effect can totally be avoided by using specific wall structures, e.g., randomly arranged spherical caps. The concept itself is interesting, because it directly addresses the underlying mechanisms of the radial heat transport problem without changing the reactor type too much. One potential drawback is the manufacturabilty of the specific designs for these wall structures, which depends on the utilized pellet shape and size.
Comparing the different concepts discussed above, one can distinguish between two different mechanisms to increase the radial heat transfer: One can either increase the radial conductive heat transfer, as in the case of POCS and packed foams, or one increases the convective lateral mixing close to the wall, which can be achieved by macroscopic wall structures. A traditional approach to increase the heat transfer from a surface to a surrounding fluid is the use of pin-fins in a wide variety of engineering applications, e.g., cooling of turbine airfoils, electronics, etc. [
19,
20,
21]. In the field of packed bed reactors, however, this is not commonly used, and, therefore, only limited work has previously been conducted in that field. Nakaso et al. [
22] investigated the impact of shell-side fins on the thermal performance of a tube-side heated packed bed and found an up to thirty times higher effective thermal conductivity if spiral-type heat fins are used. The impact of pin-fin heat sinks on the heat transfer in packings of spherical particles were investigated by Jeng et al. [
23], and a significant increase in the Nusselt number was observed, comparing a bottom heated cubic packing of spherical brass particles with heat fins against the configuration without them. The impact of fins in adsorption cooling units was investigated by numerous authors, e.g., [
24,
25], showing beneficial characteristics of heat fins for this kind of application.
To the best of our knowledge, the impact of internal heat fins on the heat transfer inside cylindrical packed bed reactors has not been investigated by now. The basic idea is to bridge the near wall region, that is characterized by low lateral mixing and thermal conductivity, using fins made of highly conductible material. This is similar to the mechanism that leads to the beneficial thermal behavior of open-cell foams or POCS, however, only limited to the region close to the reactor wall, and without changing the general characteristics of a packed bed too much. If a positive effect of internal heat fins can be found, this would offer the possibility of equipping new and already existing units with that device, since the heat fins could be manufactured, for example as a sleeve, that can be inserted into the reactor tubes.
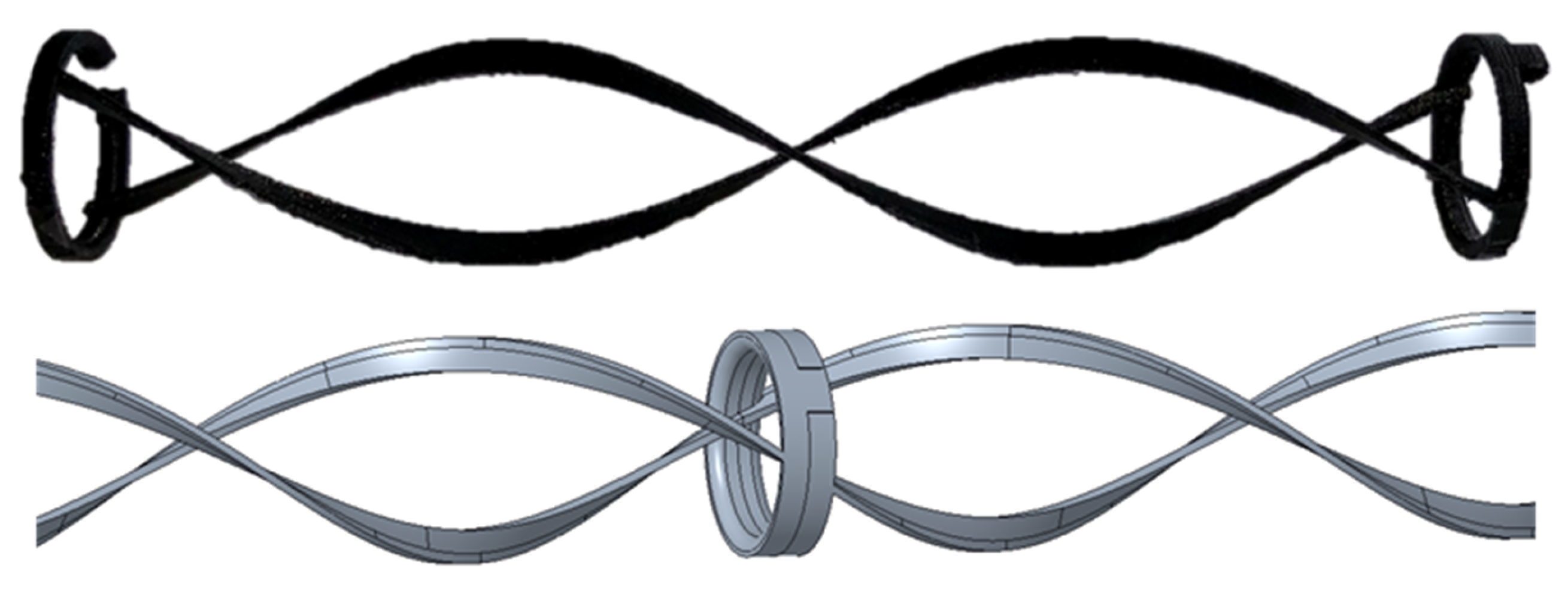
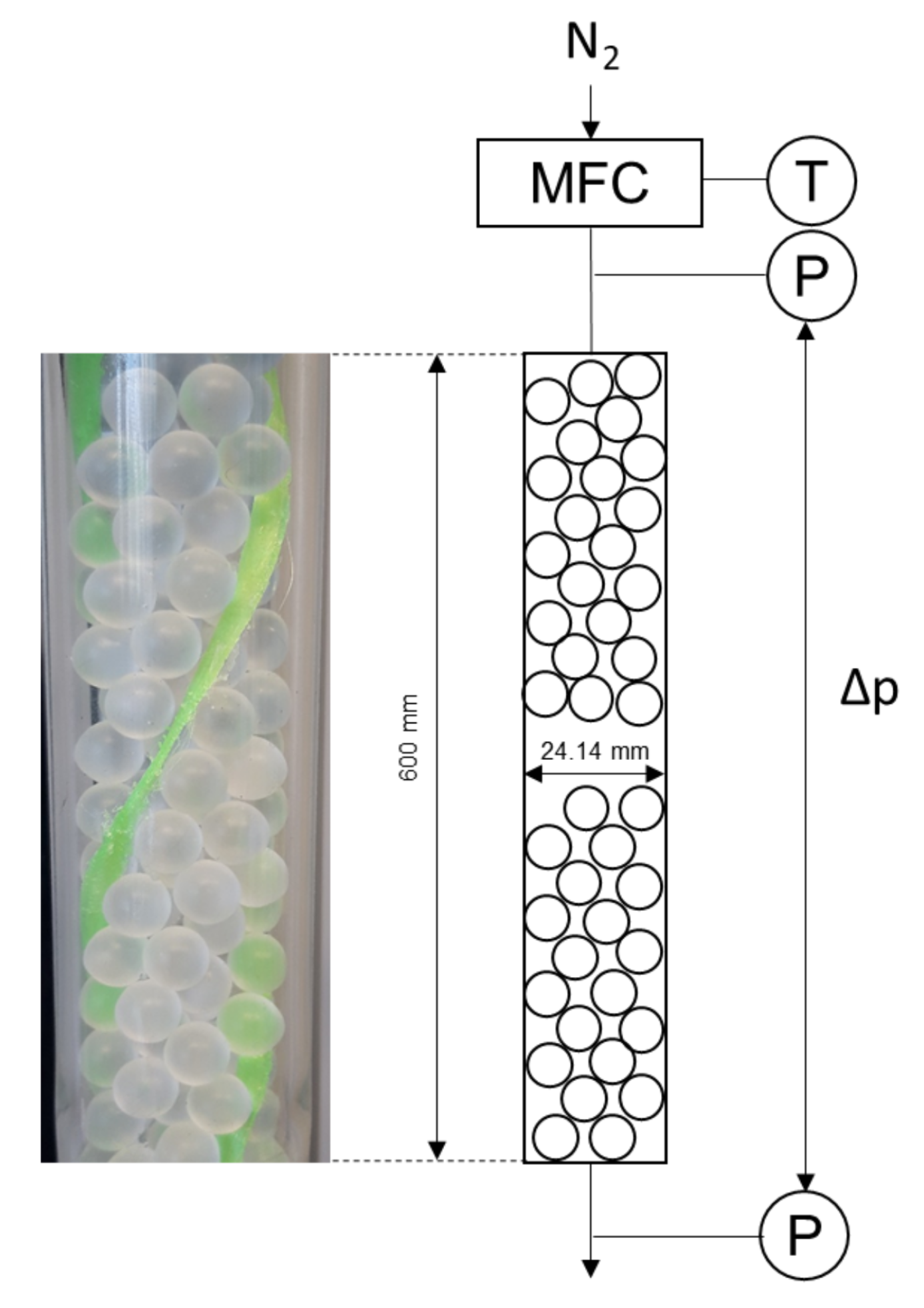
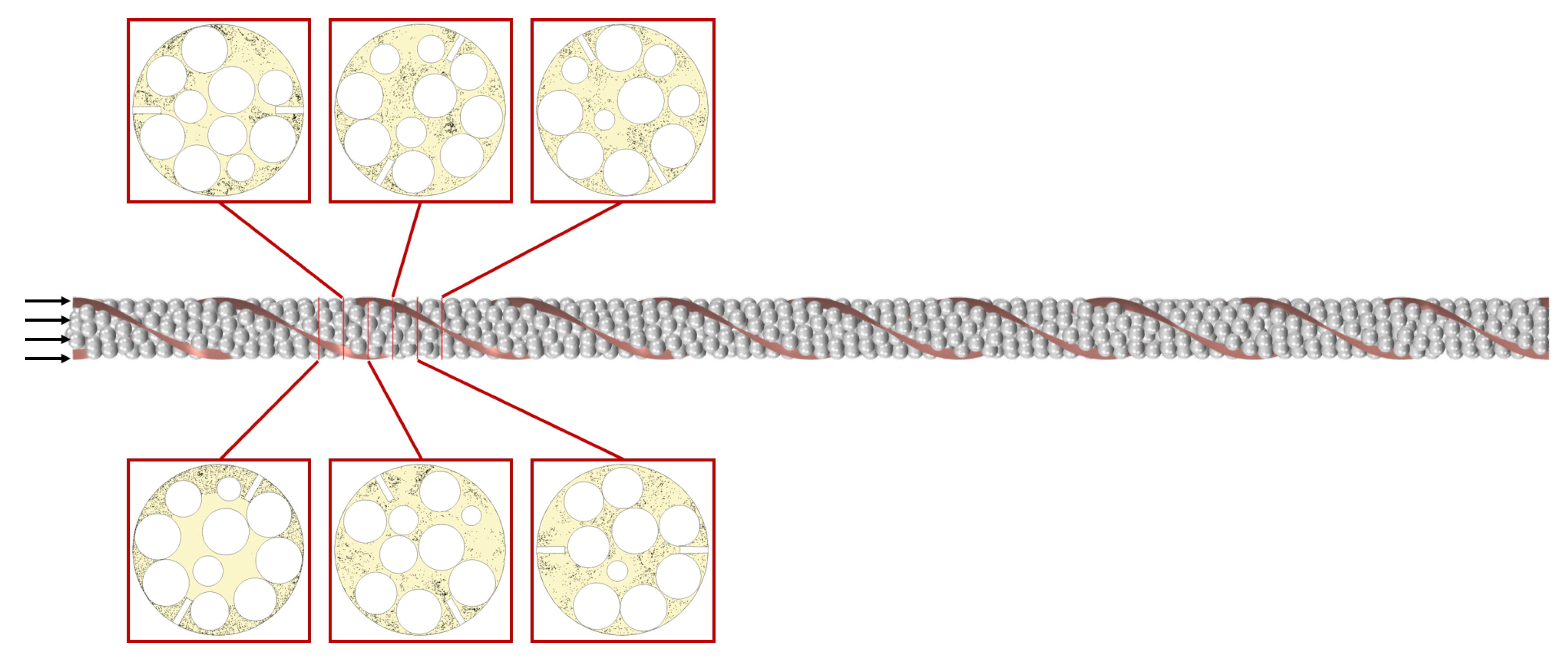
In the first part of this study, details are given about the additive manufacturing process used to produce a helical finned sleeve. Filling experiments are conducted and numerically replicated, using the Discrete Element Method (DEM), to investigate the impact of heat fins on the bed voidage, and with that, the specific surface area of the catalyst particles. In the next part, the impact of the heat fins on the pressure drop is investigated experimentally and numerically, followed by a numerical study examining the impact of internal heat fins on the fluid dynamics and heat transfer. This study is limited to spherical particles. However, other particle shapes of fin shapes and/or dimensions might have an even larger positive effect on the reactor performance.
4. Conclusions
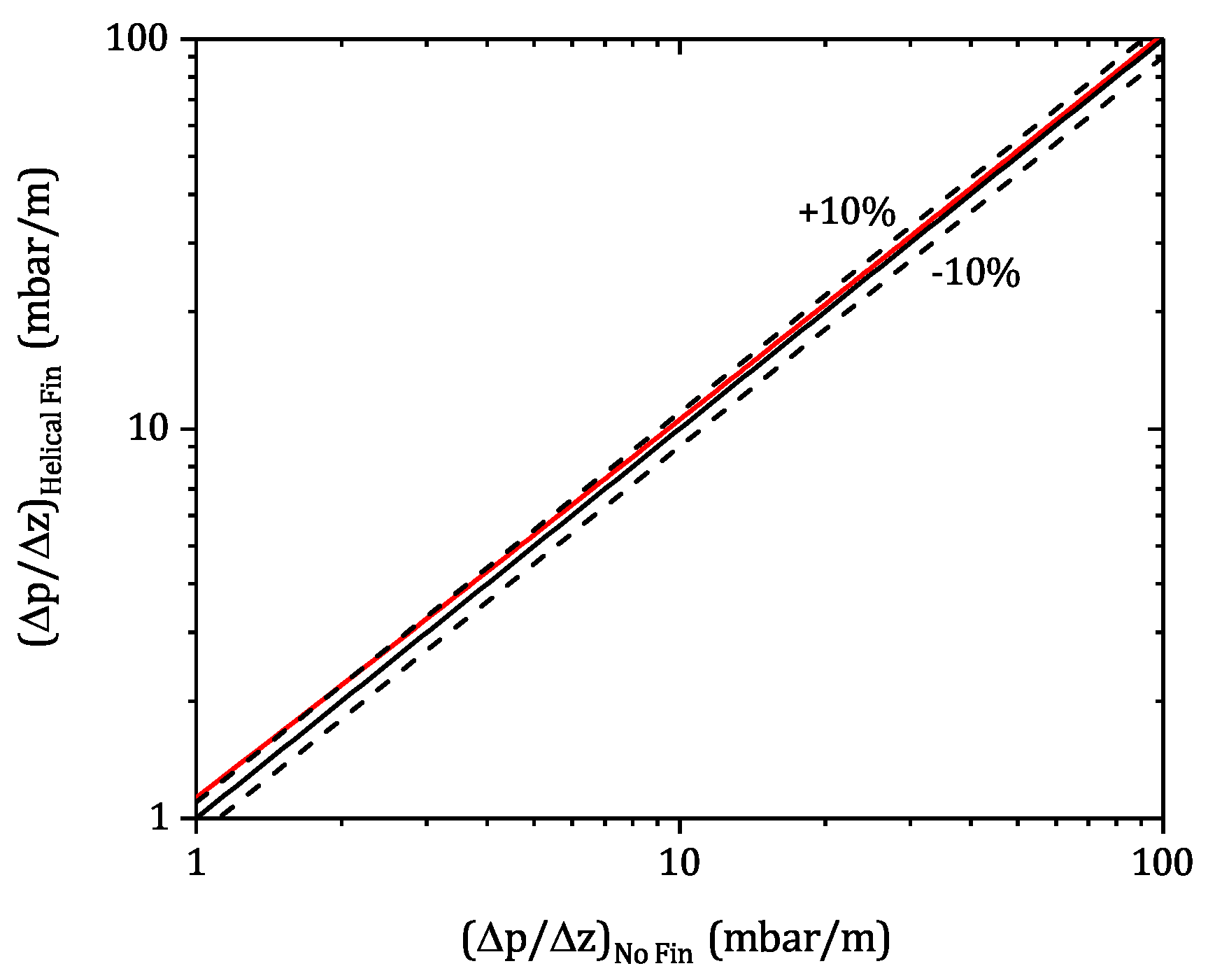
In this work, the impact of internal heat fins on the bed morphology, pressure drop and heat transfer in slender packed bed reactors filled with spherical particles was investigated. Helical fin modules were manufactured using the FLM 3D printing technique. The effect of the fins on bed morphology, in terms of particle count, and specific pressure drop was investigated both, experimentally and numerically, using particle-resolved CFD. An excellent agreement between the CFD results and the experimental measurements were found, indicating that particle-resolved CFD is a reliable and predictive tool that can be used for further design studies, e.g., dimensions, shape, and numbers of internal heat fins. For industrially relevant Reynolds numbers (), the specific pressure drop, caused by the helical heat fins, is below +10% in comparison to the case without fins. However, one needs to keep in mind, that the bed voidage increases due to the presence of the helical fins, resulting in a lower pellet surface area per reactor volume.
In a comparative numerical study, two different heat fin designs (helical and straight fin design) were compared against a reactor without heat fins under wall-heated conditions. While, in accordance with our previously presented results, the specific pressure drop for the helical fin design is only slightly increased, a significant reduction in specific pressure drop of 20% was observed for the straight fin design. To account for the differences in bed voidage, the friction factors were calculated. A decrease of up to 20% can be seen for the straight fin design, which is mainly caused by additional channeling effects that are a result of how the spherical particles arrange around the heat fins. Regarding the helical fin design, a strong swirl occurs close to the tube wall, which is the main driving force for the increase of the friction factor of 30%. Nevertheless, it was found that the flow in this near-wall region is in strong exchange with the flow in the remaining bulk part of the reactor.
Based on the axial temperature profiles, the wall heat transfer coefficients and the effective radial thermal conductivities were calculated. Over the investigated particle Reynolds number range, an increase of 25% to 35% in wall heat transfer coefficient, and of up to almost 90% in effective radial thermal conductivity was found for the helical fin design, respectively. For the straight fin design, the increase of the wall heat transfer coefficient accounts for 8–19%. For the lowest and highest investigated Reynolds number, also for the straight fin design, a significant increase in of up to 30% was found. Overall, the simulation results show the beneficial impact of internal heat fins on the heat transfer characteristics in slender packed bed reactors. In comparison to other presented reactor concepts, the advantages of internal heat fins are:
It is applicable to new and already existing reactors, as the fins are manufactured as replaceable sleeves.
The morphological and fluid dynamic characteristics (bed voidage and pressure drop) change only moderately.
The active catalytic surface area changes only slighty. It is reduced by 7% for the helical and below 5% for the straight fin design, respectively.
Reactor filling and re-filling strategies can stay unaffected.
Nevertheless, we see the following future tasks, to make this a reliable reactor concept:
Although, some publications are available, indicating the accuracy of particle-resolved CFD when it comes to heat transfer simulation, e.g., [
46,
47], broader validation is necessary, to make this a reliable and predictive design tool, especially under industrial conditions, e.g., complex particle shapes, turbulent flows, steep gradients, and coupled with catalytic reactions.
Design parameters, such as number of fins, fin thickness, fin material and fin shape, should be varied to find an optimized fin design that incorporates a beneficial heat transfer characteristic with a reduced impact on bed voidage, active catalytic surface area and pressure drop.
It needs to be evaluated, if a generalized optimized fin design can be found, that is also applicable to other particle shapes than spheres, or if individual solutions must be developed.
Possible limits regarding the manufacturability using 3D printing need to also be evaluated.