Denitrification Control in a Recirculating Aquaculture System—A Simulation Study
Abstract
1. Introduction
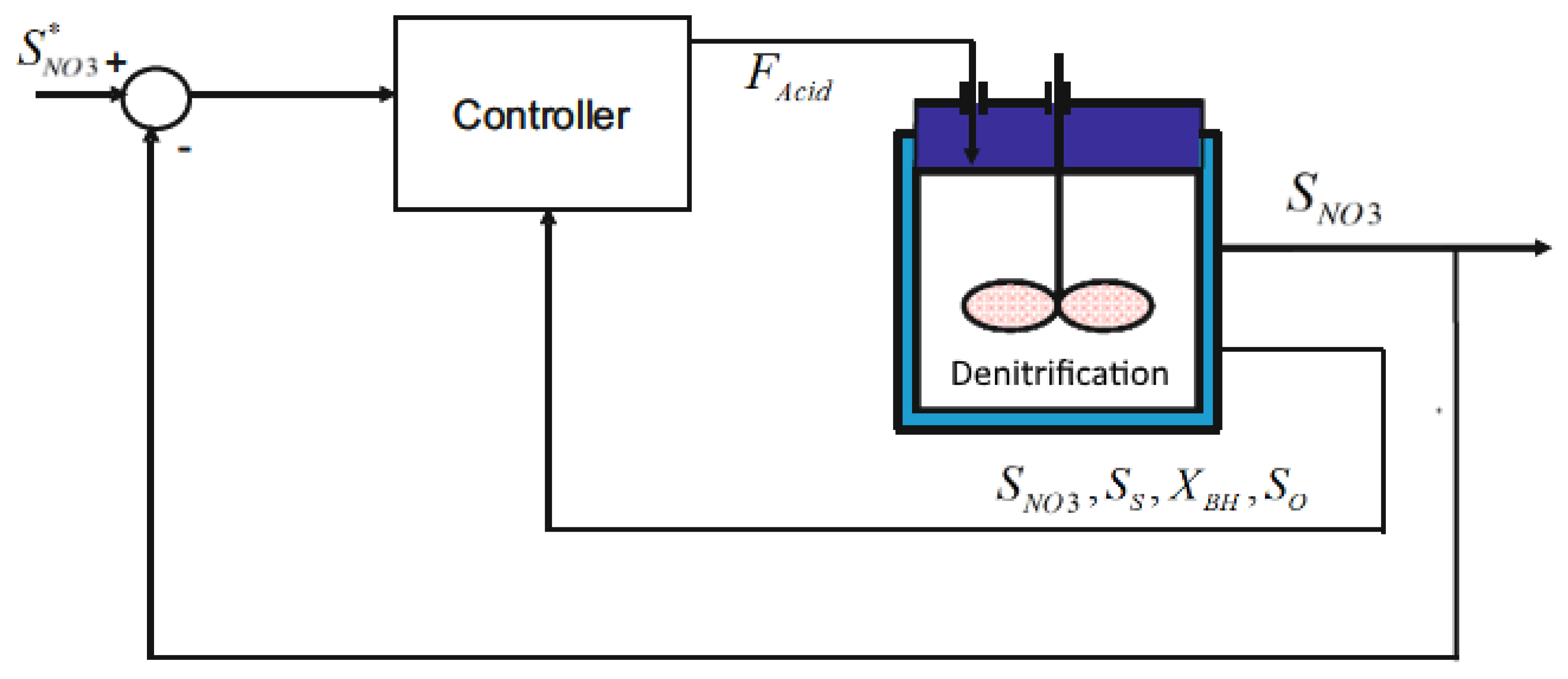
2. Problem Description
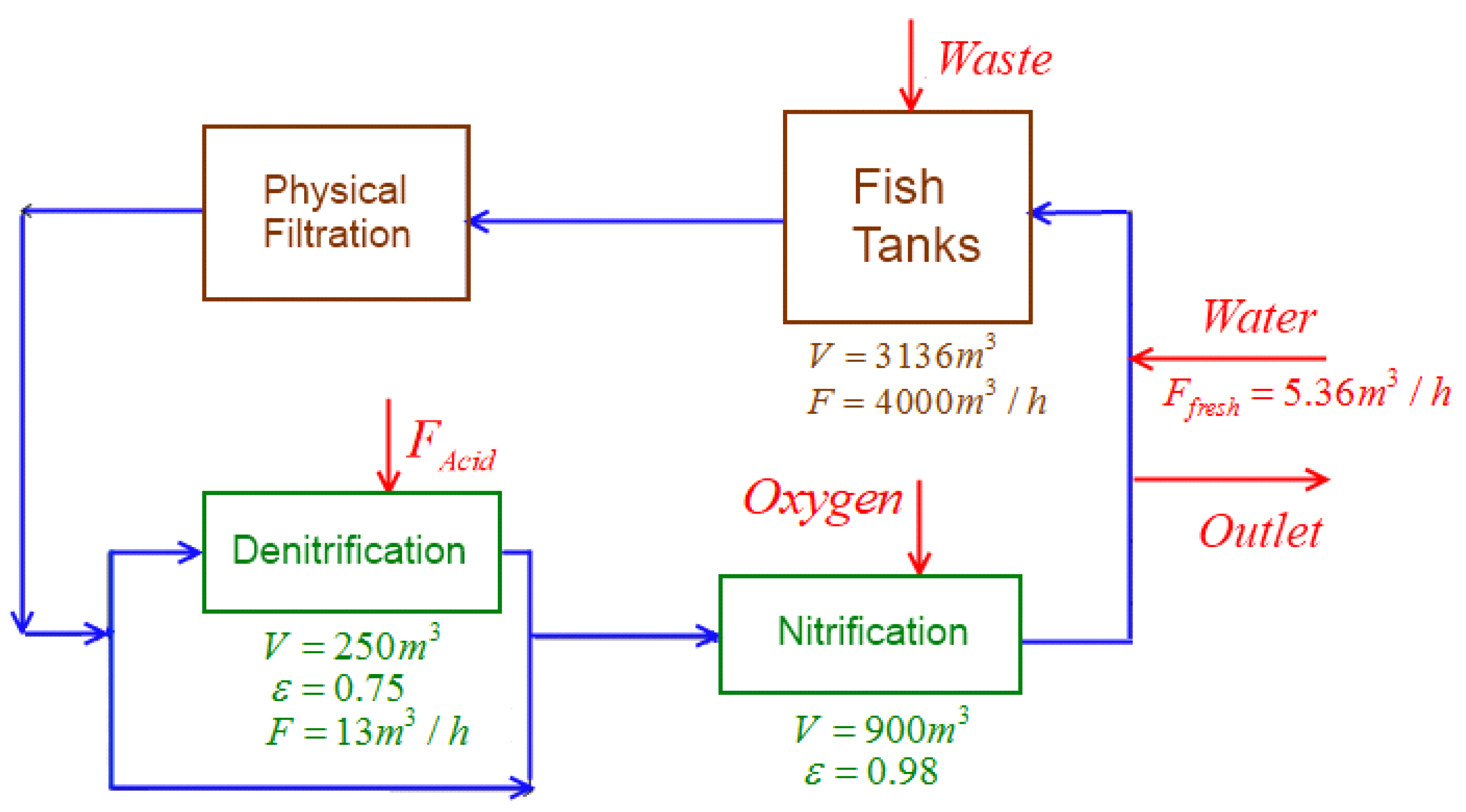
2.1. Industrial Plant
2.2. Model Description
- Fish Tanks:The fish excretion rate is considered with assumed constant fish size and population. It can be translated into ASM variables using the waste matrix reported in [6]. The fish respiration is calculated based on the values reported in [20,21] (see Table 1).The Fish basins are modeled as perfectly mixed tank reactors where no biological reaction occurs, applying mass balances as in:where variable ξ may be used to represent both soluble (S) and particulate (X) waste compounds and V is the fish tank volume. The corresponding waste production rates , all quantified in Table 1, are estimated for an assumed constant fish density of 12 kg/m3 and body weight of 8.5 kg. These rates can also be translated into ASM variables using the waste matrix reported in [6] while the fish respiration is calculated based on the values reported in [20,21] (see Table 1). The fish basin may therefore be modeled by the replication of the generic Equation (1) for each waste component of Table 1.
- Physical particle filter:90% of the particulate components in the inlet are filtered, leading to:where and represent, respectively, the outlet and inlet concentrations of particulate component k.
- Denitrification filter:The denitrification filter consists of a moving bed perfectly-mixed tank reactor. Solubles that exist in the reactor bulk (index b) dissolve into the biofilm (index c) where the main part of the biological reactions occurs. The same ASM model, which is applied for nitrification, is used with the exception that ammonia is not considered as substrate for heterotrophic growth ( is not considered in , and ). Acetic acid is added to this bioreactor (4) as a carbon source for denitrification, which can therefore be modeled as:where is the acetic acid flow rate in , is the coefficient of conversion of acid into easily biodegradable organic matter in and is the production/consumption rate of component ξ, which can be calculated using stoichiometry—that is, the corresponding coefficient (provided in Table S1, in Supplementary Materials) and rate (provided in Table S2, in Supplementary Materials), as in:where w is an index denoting the process referenced in Tables S1 and S2 in Supplementary Materials.
- Nitrification filter:The nitrification filter is hydraulically modeled assuming six sequential perfectly mixed tank reactors filled with solid media. Biologically, a modified ASM1 model with the inclusion of two-step nitrification/denitrification is used (provided in Tables S1 and S2, in Supplementary Materials). This model has been validated using the data from the COST Simulation Benchmark in [22]. It has to be noticed that oxygen is also added to this bioreactor. Particles present in the inlet remain in the outlet. However, the particles already existing in each compartment () do not move to others. The resulting mass balances lead to:where D represents the dilution rate, is the diffusion coefficient in m3/h, is the empty volume of the reactor in m3, and are the consumption/production rates of solubles i and particulates k, calculated from (8), F is the volumetric flowrate in m3/h, is the mass flowrate in g/h, is the detachment coefficient in h−1·m3 and is the oxygen mass transfer coefficient in h−1.
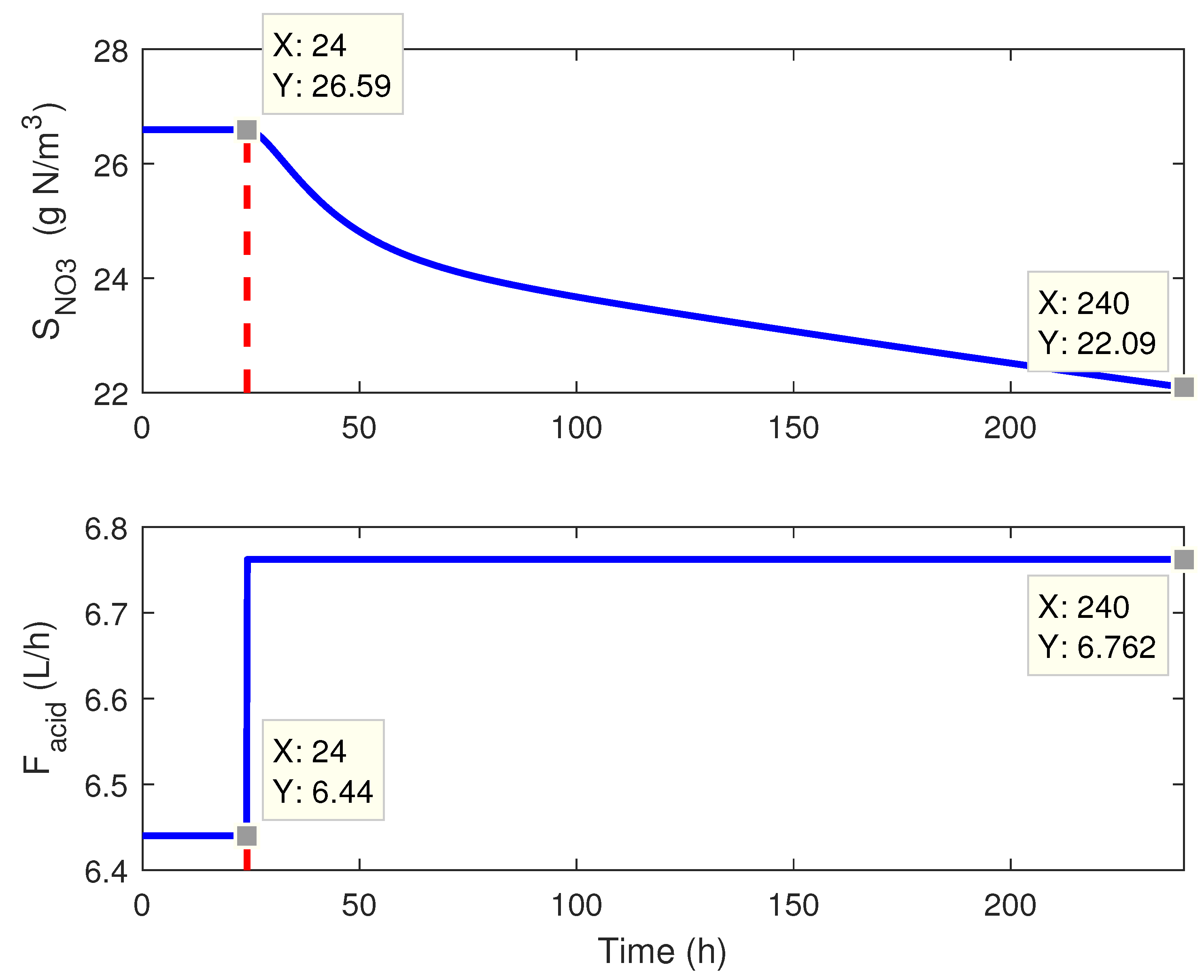
2.3. Plant Dynamics: A Preliminary Study
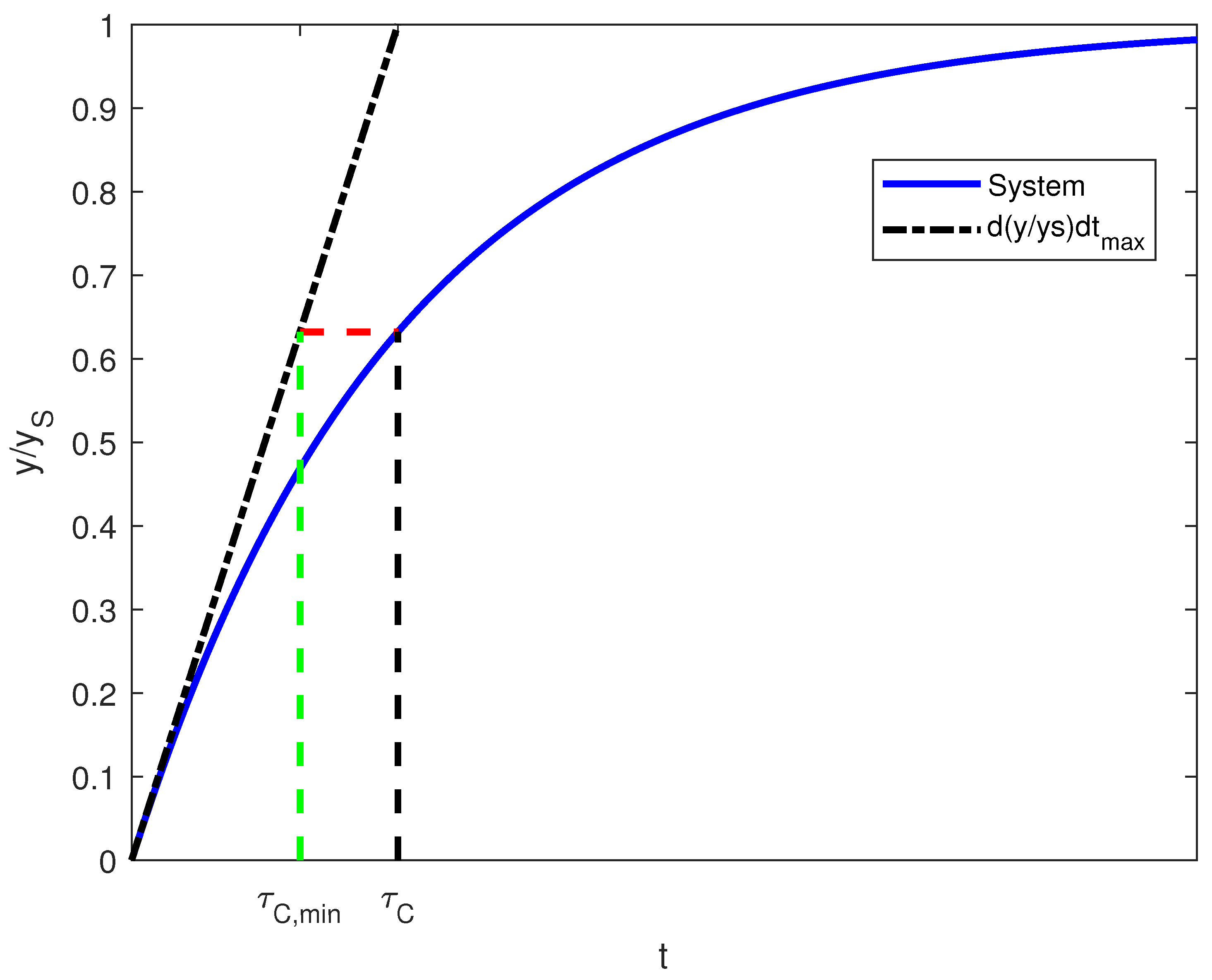
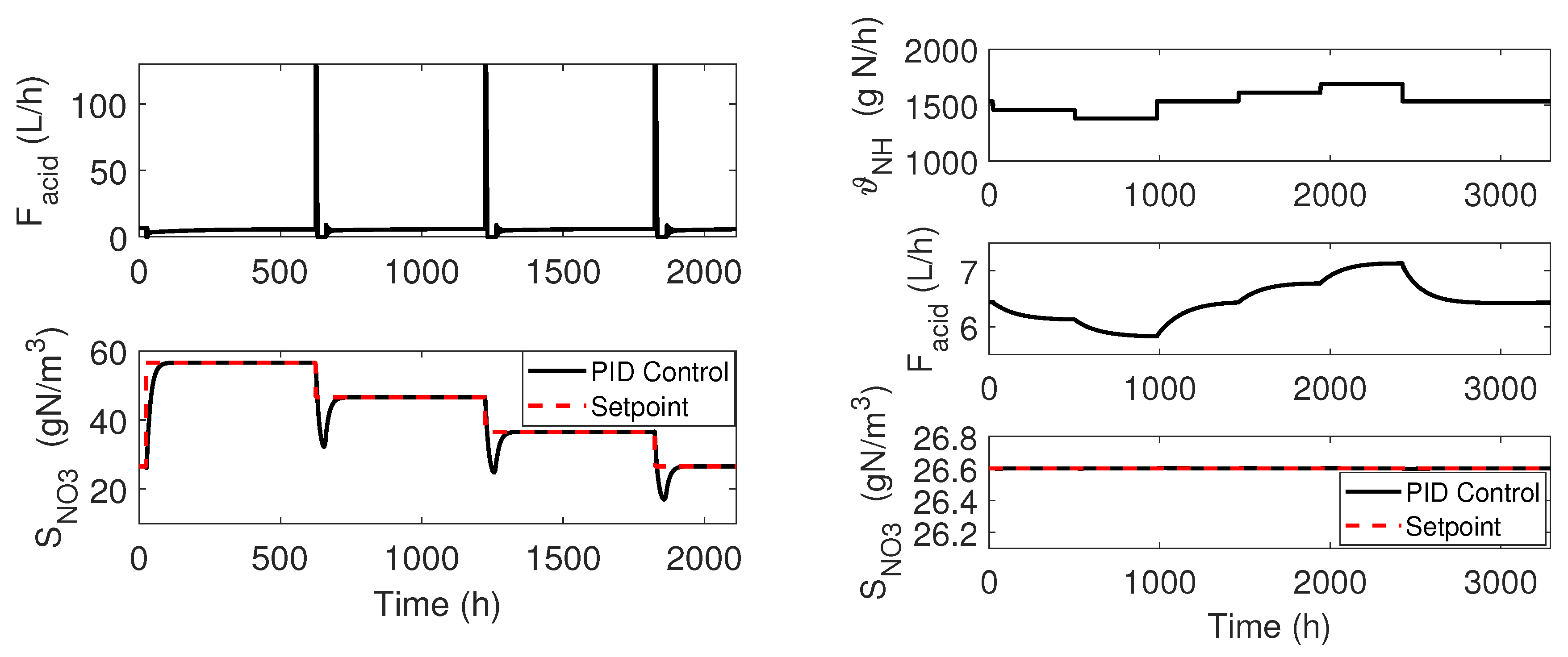
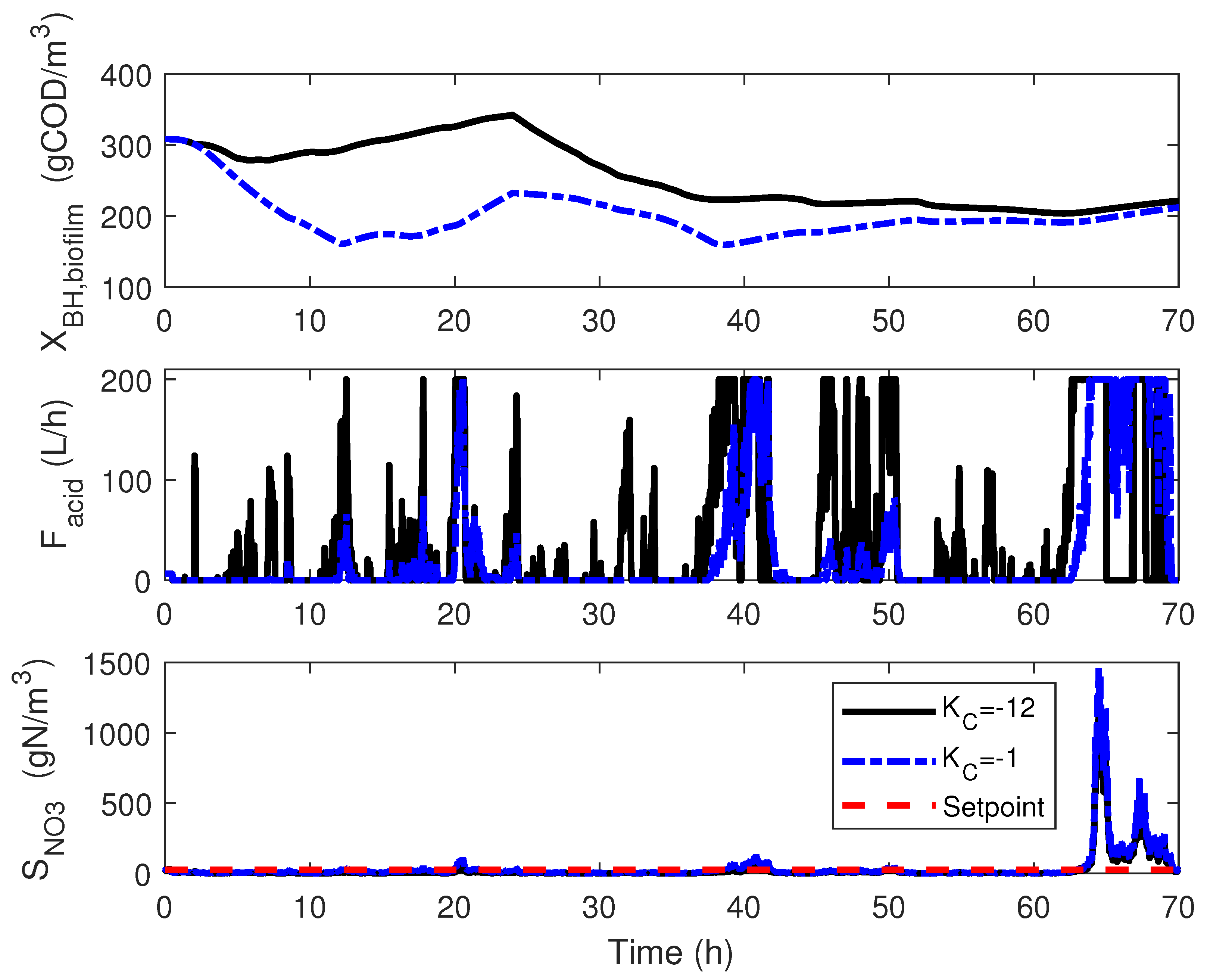
3. Control Implementation: Classical Approach
4. Linearizing Control
- Only the denitrification reactor is considered;
- This reactor only contains heterotrophic bacteria;
- Since the oxygen concentration is low, no nitrification can occur;
- Biomass is retained in the tank ;
- Only three other components besides biomass are considered: oxygen (), easily biodegradable organic matter () and nitrate ();
- Only two reactions are assumed to occur:
- Aerobic growth of heterotrophs:
- Anoxic growth of heterotrophs on nitrate:
- Acid is added as a carbon source and represents the conversion of acid flowrate (, ) into easily biodegradable carbon source flowrate ().
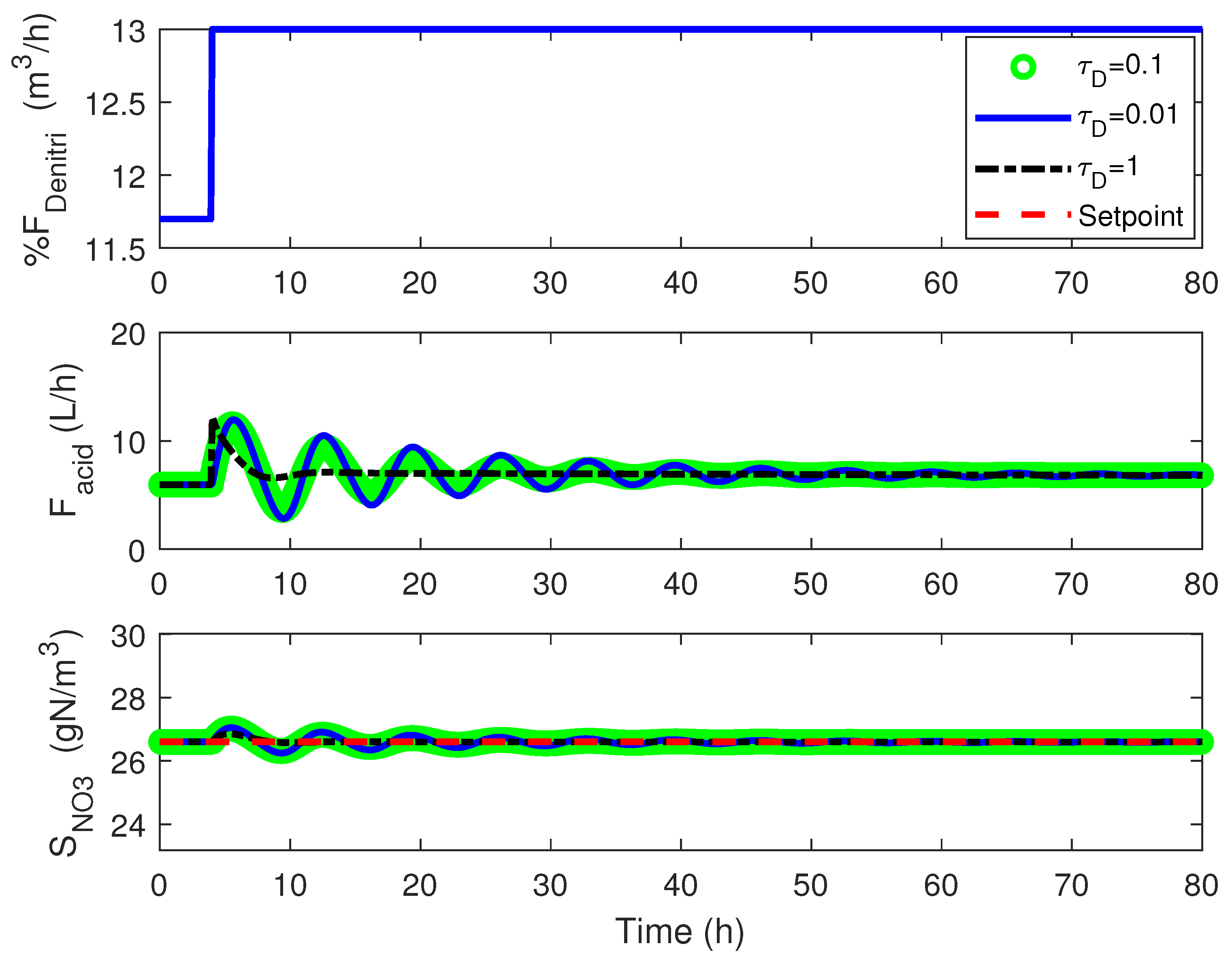
4.1. Cascade Control
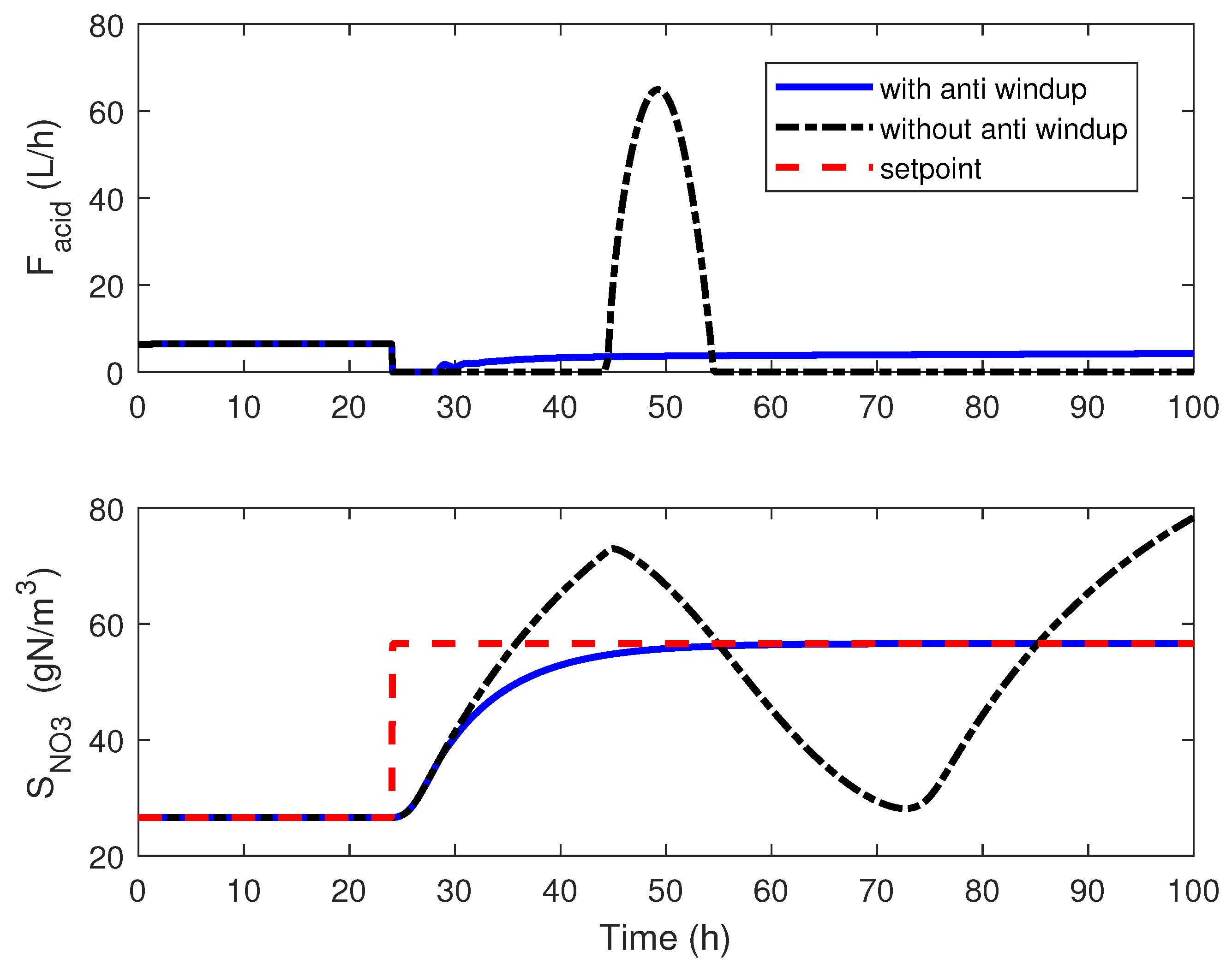
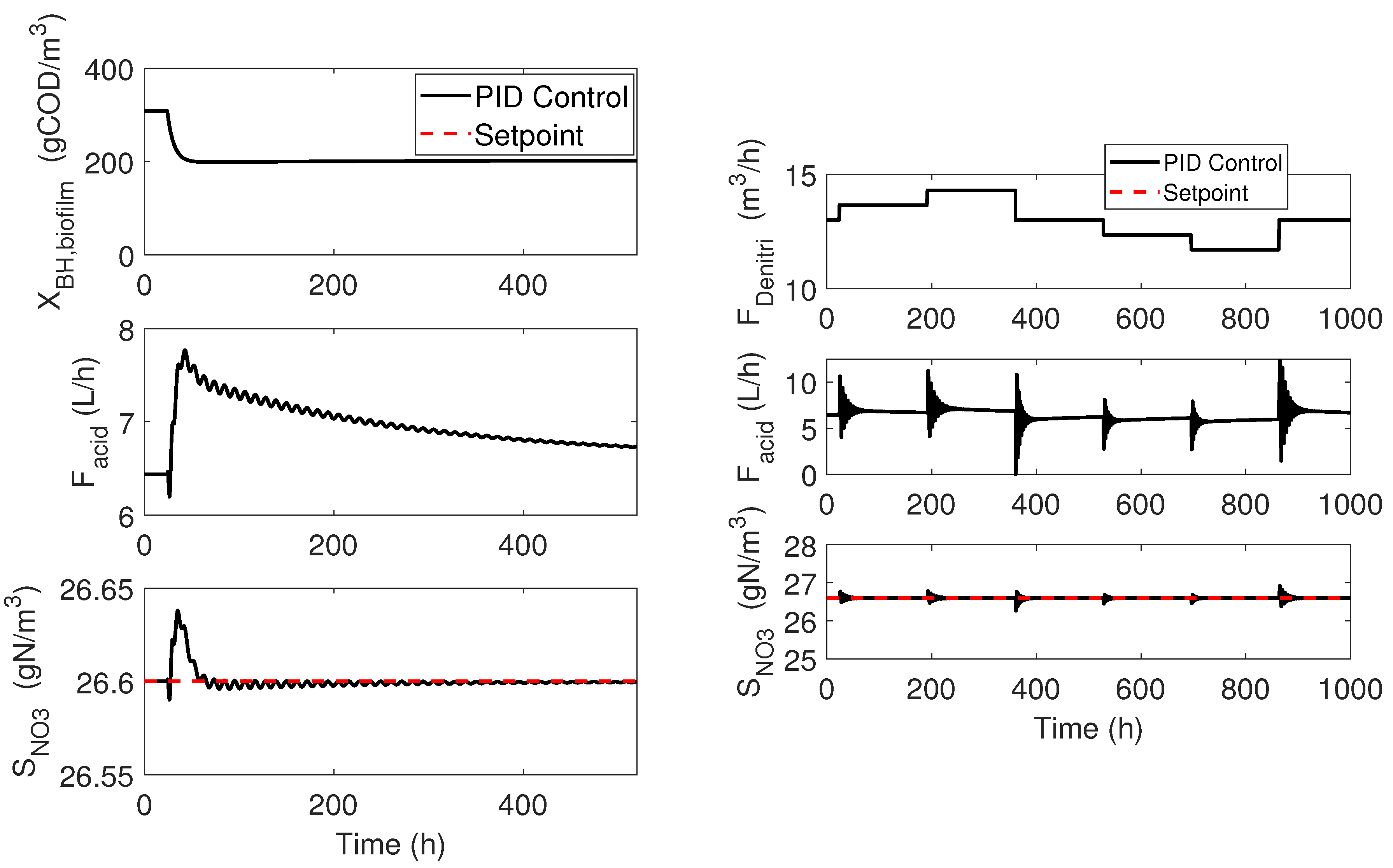
4.2. Adaptive Linearizing Control
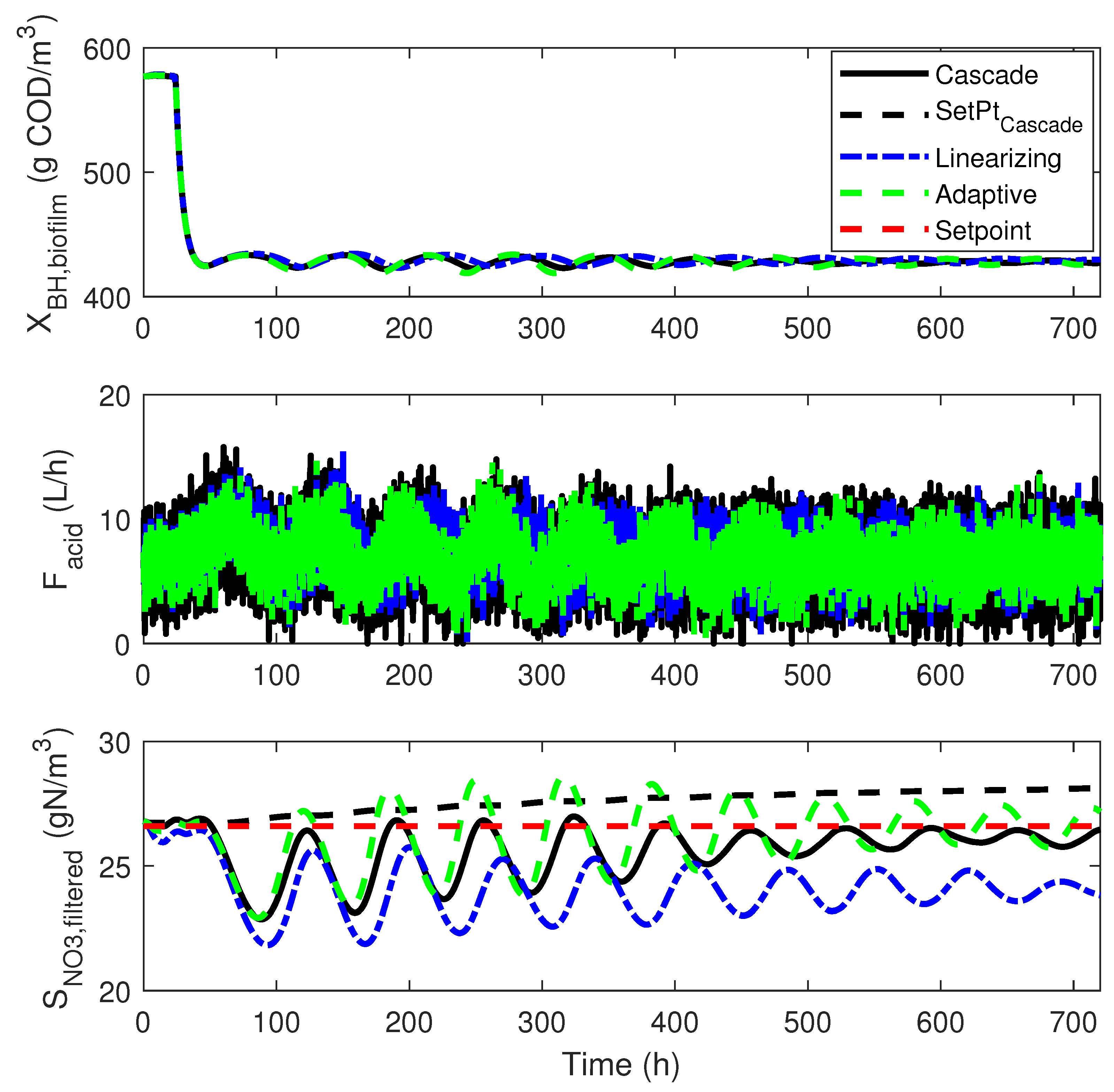
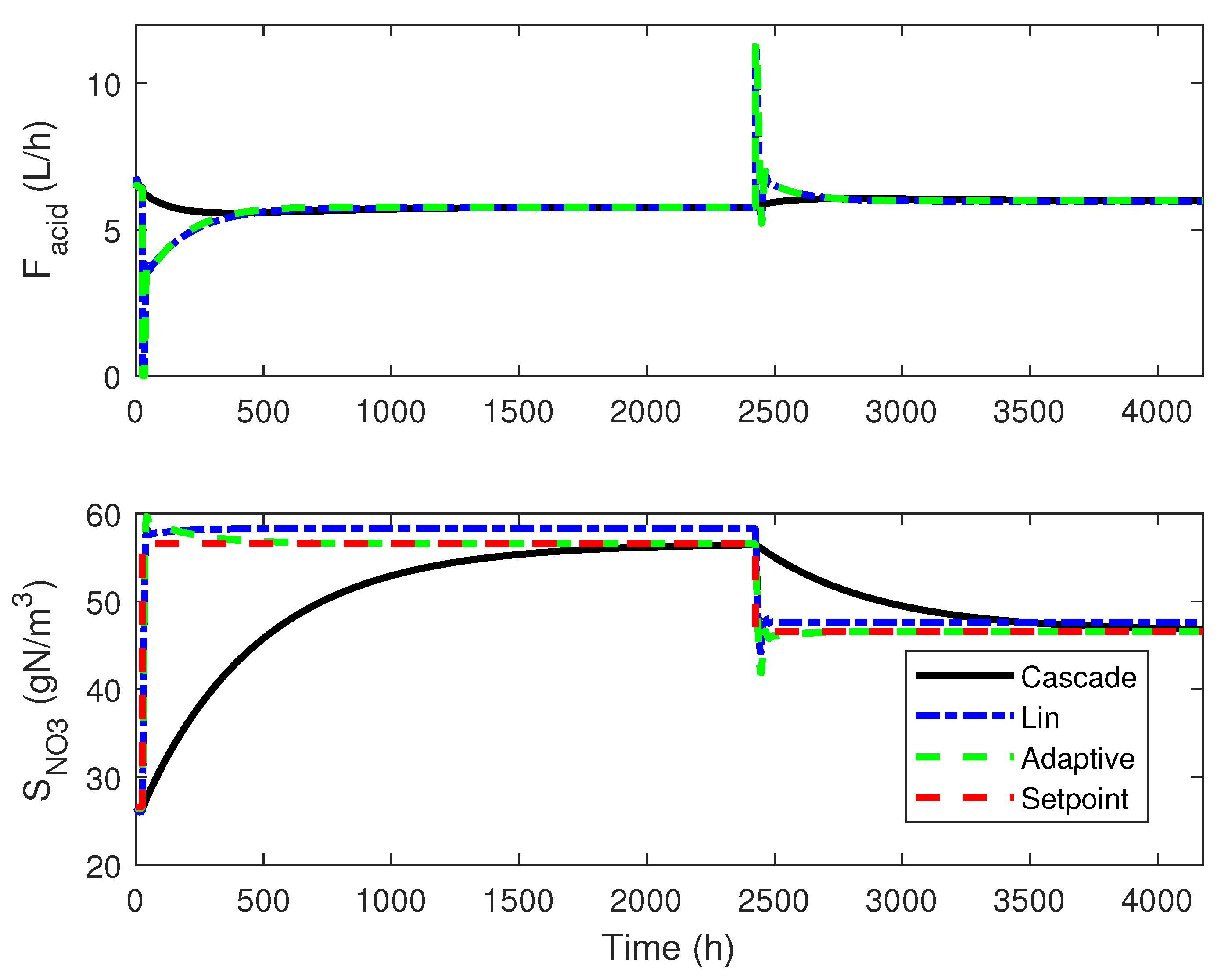
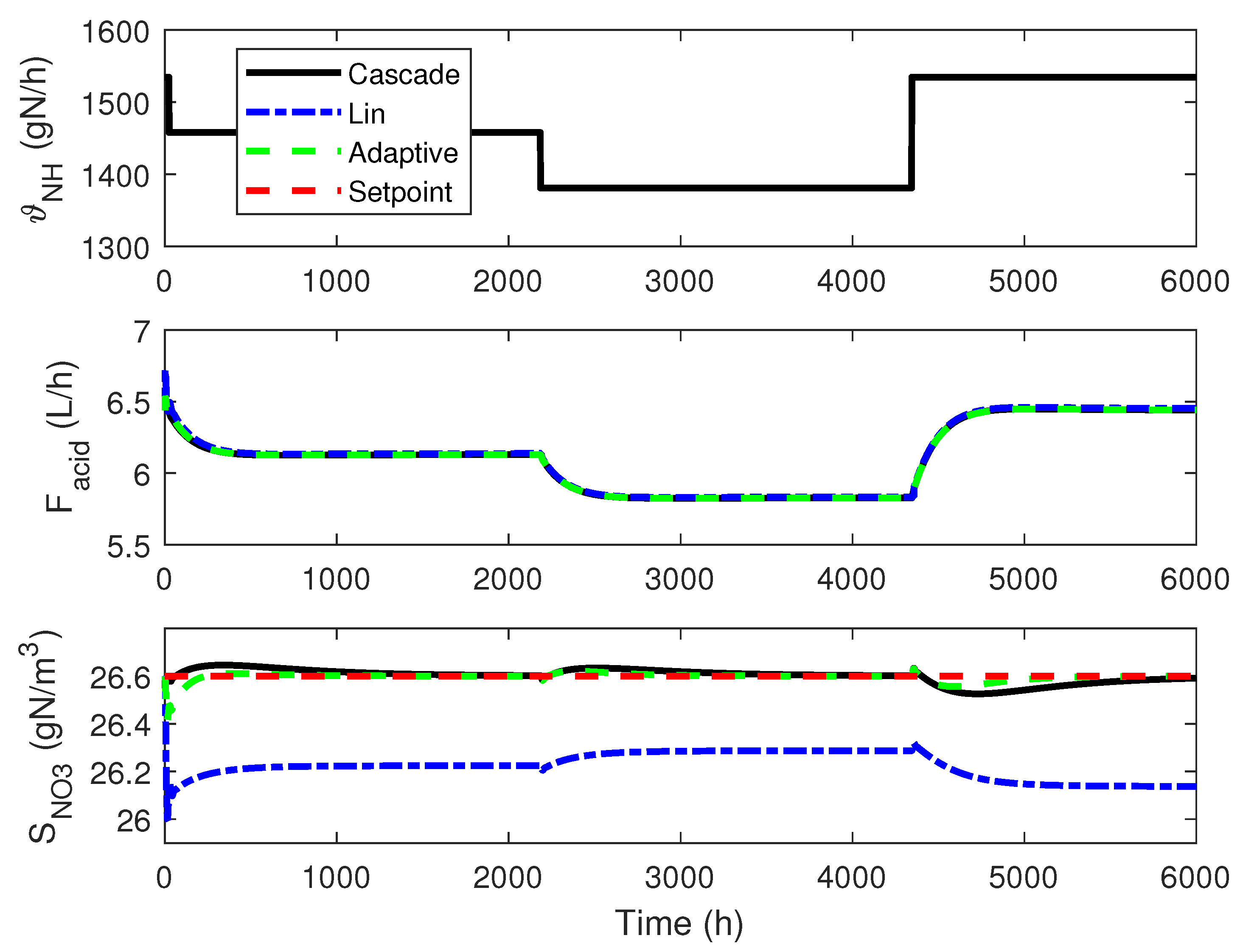
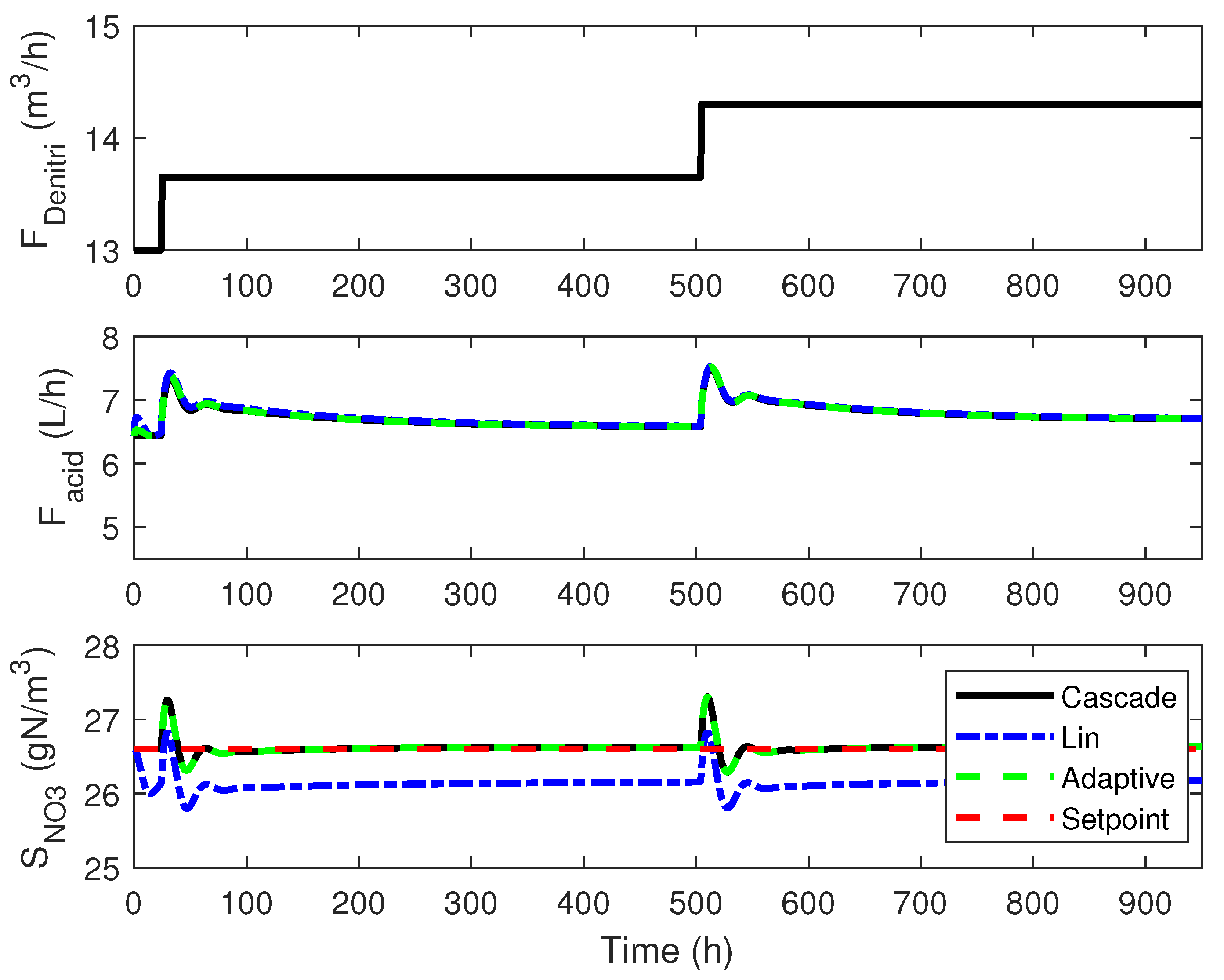
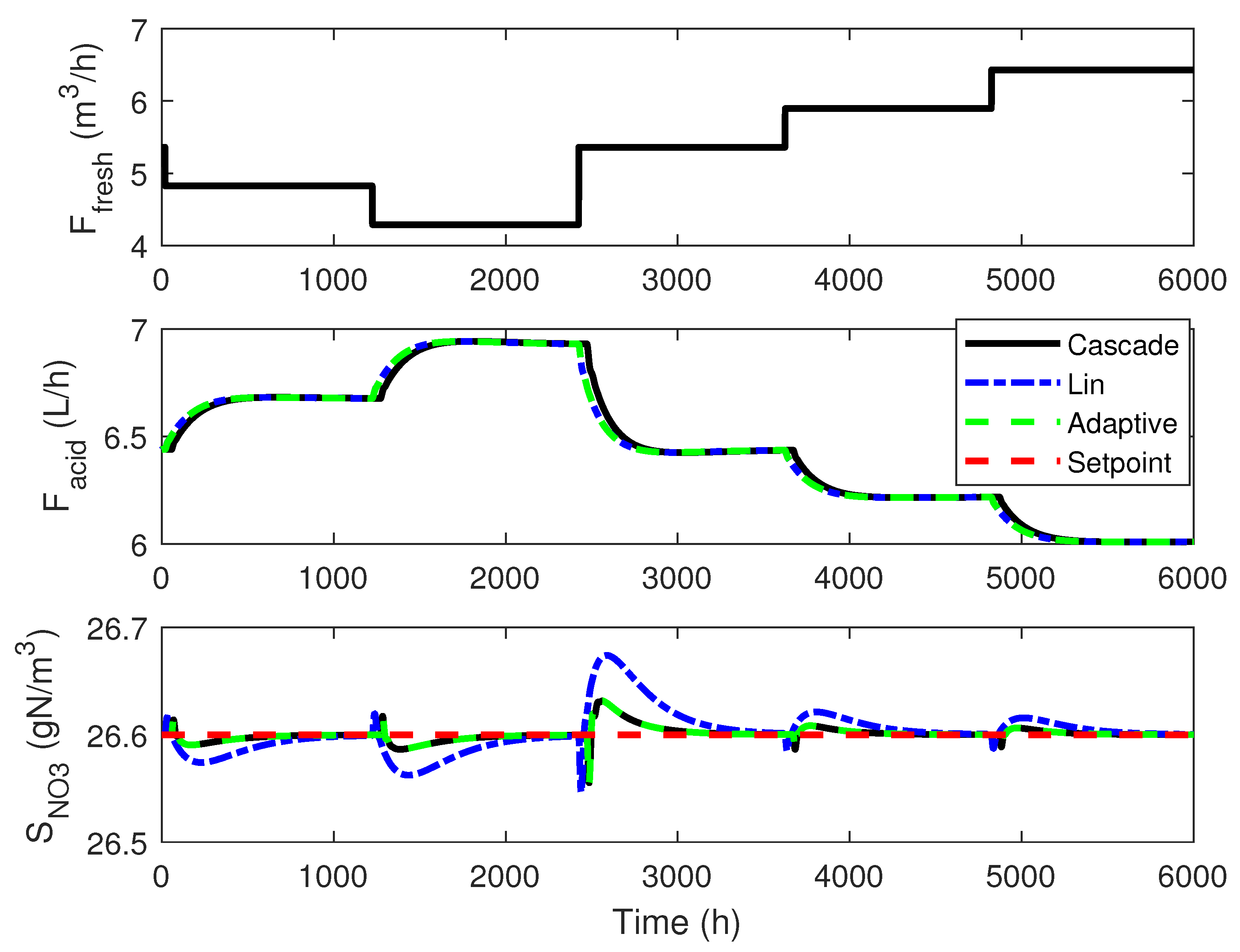
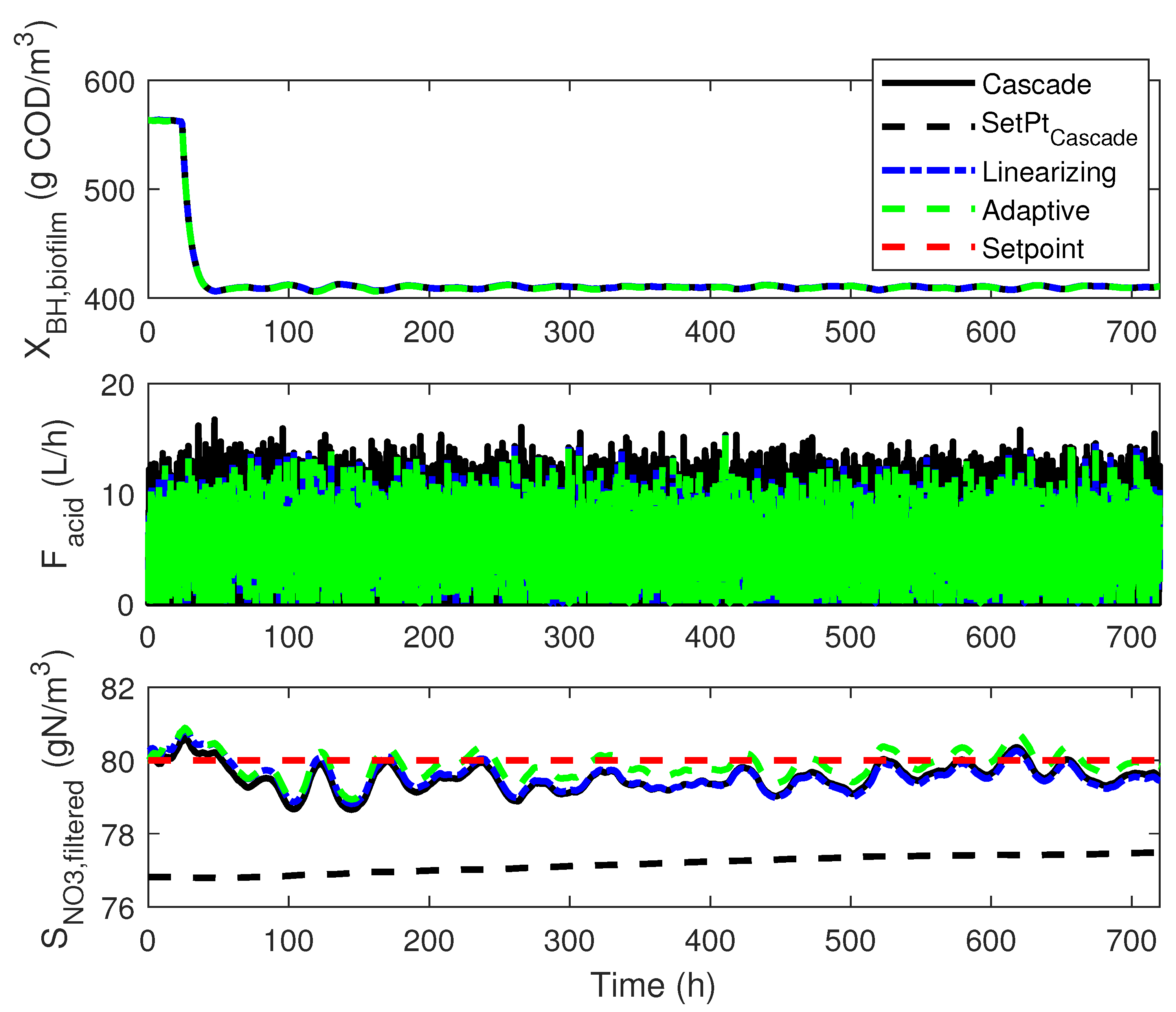
4.3. Numerical Results
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- FAO. The State of World Fisheries and Aquaculture 2018: Meeting the Sustainable Development Goals; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018; ISBN 9789251305621. [Google Scholar]
- Ruiz, P.; Vidal, J.M.; Sepúlveda, D.; Torres, C.; Villouta, G.; Carrasco, C.; Aguilera, F.; Ruiz-Tagle, N.; Urrutia, H. Overview and future perspectives of nitrifying bacteria on biofilters for recirculating aquaculture systems. Rev. Aquac. 2019, 12, 1478–1494. [Google Scholar] [CrossRef]
- Bregnballe, J. A Guide to Recirculation Aquaculture: An Introduction to the New Environmentally Friendly and Highly Productive Closed Fish Farming Systems; Food and Agriculture Organization of the United Nations: Copenhagen, Denmark, 2015. [Google Scholar]
- Gutierrez-Wing, M.T.; Malone, R.F. Biological filters in aquaculture: Trends and research directions for freshwater and marine applications. Aquac. Eng. 2006, 34, 163–171. [Google Scholar] [CrossRef]
- Pungrasmi, W.; Phinitthanaphak, P.; Powtongsook, S. Nitrogen removal from a recirculating aquaculture system using a pumice bottom substrate nitrification-denitrification tank. Ecol. Eng. 2016, 95, 357–363. [Google Scholar] [CrossRef]
- Wik, T.E.; Lindén, B.T.; Wramner, P.I. Integrated dynamic aquaculture and wastewater treatment modelling for recirculating aquaculture systems. Aquaculture 2009, 287, 361–370. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Yang, Q.; Li, J.; Zhang, Y.; Peng, Y. Online control of biofilm and reducing carbon dosage in denitrifying biofilter: Pilot and full-scale application. Front. Environ. Sci. Eng. 2017, 11, 4. [Google Scholar] [CrossRef]
- Du, R.; Peng, Y.; Cao, S.; Li, B.; Wang, S.; Niu, M. Mechanisms and microbial structure of partial denitrification with high nitrite accumulation. Appl. Microbiol. Biotechnol. 2015, 4, 2011–2021. [Google Scholar]
- Lee, P.G.; Lea, R.N.; Dohmann, E.; Prebilsky, W.; Turk, P.E.; Ying, H.; Whitson, J.L. Denitrification in aquaculture systems: An example of a fuzzy logic control problem. Aquac. Eng. 2000, 23, 37–59. [Google Scholar] [CrossRef]
- Join, C.; Bernier, J.; Mottelet, S.; Fliess, M.; Rechdaoui-Guérin, S.; Azimi, S.; Rocher, V. A simple and efficient feedback control strategy for wastewater denitrification. IFAC-PapersOnLine 2017, 50, 7657–7662. [Google Scholar] [CrossRef]
- Zúñiga, I.T.; Queinnec, I.; Vande Wouwer, A. Observer-based output feedback linearizing control strategy for a nitrification–denitrification biofilter. Chem. Eng. J. 2012, 191, 243–255. [Google Scholar] [CrossRef]
- Wahab, N.A.; Katebi, R.; Balderud, J. Multivariable PID control design for activated sludge process with nitrification and denitrification. Biochem. Eng. J. 2009, 45, 239–248. [Google Scholar] [CrossRef]
- Skogestad, S.; Grimholt, C. The SIMC method for smooth PID controller tuning. In PID Control in the Third Millennium; Springer: London, UK, 2012; pp. 147–175. [Google Scholar]
- Seborg, D.E. Process Dynamics and Control, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Dochain, D. Bioprocess Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Dewasme, L.; Coutinho, D.; Vande Wouwer, A. Adaptive and Robust Linearizing Control Strategies for Fed-Batch Cultures of Microorganisms Exhibiting Overflow Metabolism. In Informatics in Control, Automation and Robotics; Cetto, J.A., Ferrier, J.L., Filipe, J., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2011; pp. 283–305. [Google Scholar]
- Tebbani, S.; Lopes, F.; Celis, G.B. Nonlinear control of continuous cultures of Porphyridium purpureum in a photobioreactor. Chem. Eng. Sci. 2015, 123, 207–219. [Google Scholar] [CrossRef]
- Aguilar-López, R. Input-Output Linearizing-type controller design with application to continuous bioreactor. Comptes Rendus de l’Académie Bulgare des Sciences: Sciences Mathématiques et Naturelles 2016, 70. [Google Scholar]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M. Activated Sludge Models ASM1, ASM2, ASM2D and ASM3 (Scientific & Technical Reports, No. 9); IWA Publishing: London, UK, 2000. [Google Scholar]
- Thomas, S.L.; Piedrahita, R.H. Oxygen consumption rates of white sturgeon under commercial culture conditions. Aquac. Eng. 1997, 16, 227–237. [Google Scholar] [CrossRef]
- Szczepkowski, M.; Szczepkowska, B.; Kolman, R. Comparison of oxygen consumption and ammonia excretion by siberian sturgeon (acipenser baeri drandt) and its hybrid with green sturgeon (acipenser medirostris ayres). Arch. Ryb. Pol. 2000, 8, 205–211. [Google Scholar]
- Copp, J.B. The COST Simulation Benchmark: Description and Simulator Manual. COST Action 624 and COST Action 682; Office for Official Publications od the European Union: Luxembourg, 2002. [Google Scholar]
- Phillips, C.L.; Harbor, R.D. Feedback Control Systems, 4th ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Bastin, G.; Dochain, D. On-line estimation and adaptive control of bioreactors. Anal. Chim. Acta 1991, 243, 324. [Google Scholar] [CrossRef]



| Corresponding | Description | Units | |
|---|---|---|---|
| component | |||
| Inert soluble organic material | 994 | gCOD/h | |
| Readily biodegradable organic material | 0 | gCOD/h | |
| Inert particulate organic material | 994 | gCOD/h | |
| Slowly biodegradable substrate | gCOD/h | ||
| Active heterotrophic biomass | 0 | gCOD/h | |
| Active ammonia oxidizing bacteria | 0 | gCOD/h | |
| Active nitrite oxidizing bacteria | 0 | gCOD/h | |
| Part. products from biomass decay | gCOD/h | ||
| Dissolved oxygen | a | gCOD/h | |
| Nitrate nitrogen | 0 | gN/h | |
| Ammonium and ammonia nitrogen | 1.5 | gN/h | |
| Soluble biodegradable organic nitrogen | 355 | gN/h | |
| Particulate biodegradable organic nitrogen | 355 | gN/h | |
| Alkalinity (as HCO3− equivalents) | 0 | gCOD/h | |
| Dissolved carbon dioxide | 8.4 | gCO2/h | |
| Phosphorus | 497 | gP/h | |
| Nitrite concentration | 0 | gN/h |
| Process | |||||
|---|---|---|---|---|---|
| SIMC PID settings | First-order | - | |||
| Industrial-scale plant model | First-order | - |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| gNH4−N/h | h | ||
| m3 | L·m3/(h·gNO3−N) | ||
| 0.36 gNO3−N/h/m3 | h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, P.; Dewasme, L.; Vande Wouwer, A. Denitrification Control in a Recirculating Aquaculture System—A Simulation Study. Processes 2020, 8, 1306. https://doi.org/10.3390/pr8101306
Almeida P, Dewasme L, Vande Wouwer A. Denitrification Control in a Recirculating Aquaculture System—A Simulation Study. Processes. 2020; 8(10):1306. https://doi.org/10.3390/pr8101306
Chicago/Turabian StyleAlmeida, Pedro, Laurent Dewasme, and Alain Vande Wouwer. 2020. "Denitrification Control in a Recirculating Aquaculture System—A Simulation Study" Processes 8, no. 10: 1306. https://doi.org/10.3390/pr8101306
APA StyleAlmeida, P., Dewasme, L., & Vande Wouwer, A. (2020). Denitrification Control in a Recirculating Aquaculture System—A Simulation Study. Processes, 8(10), 1306. https://doi.org/10.3390/pr8101306







