Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method
Abstract
1. Introduction
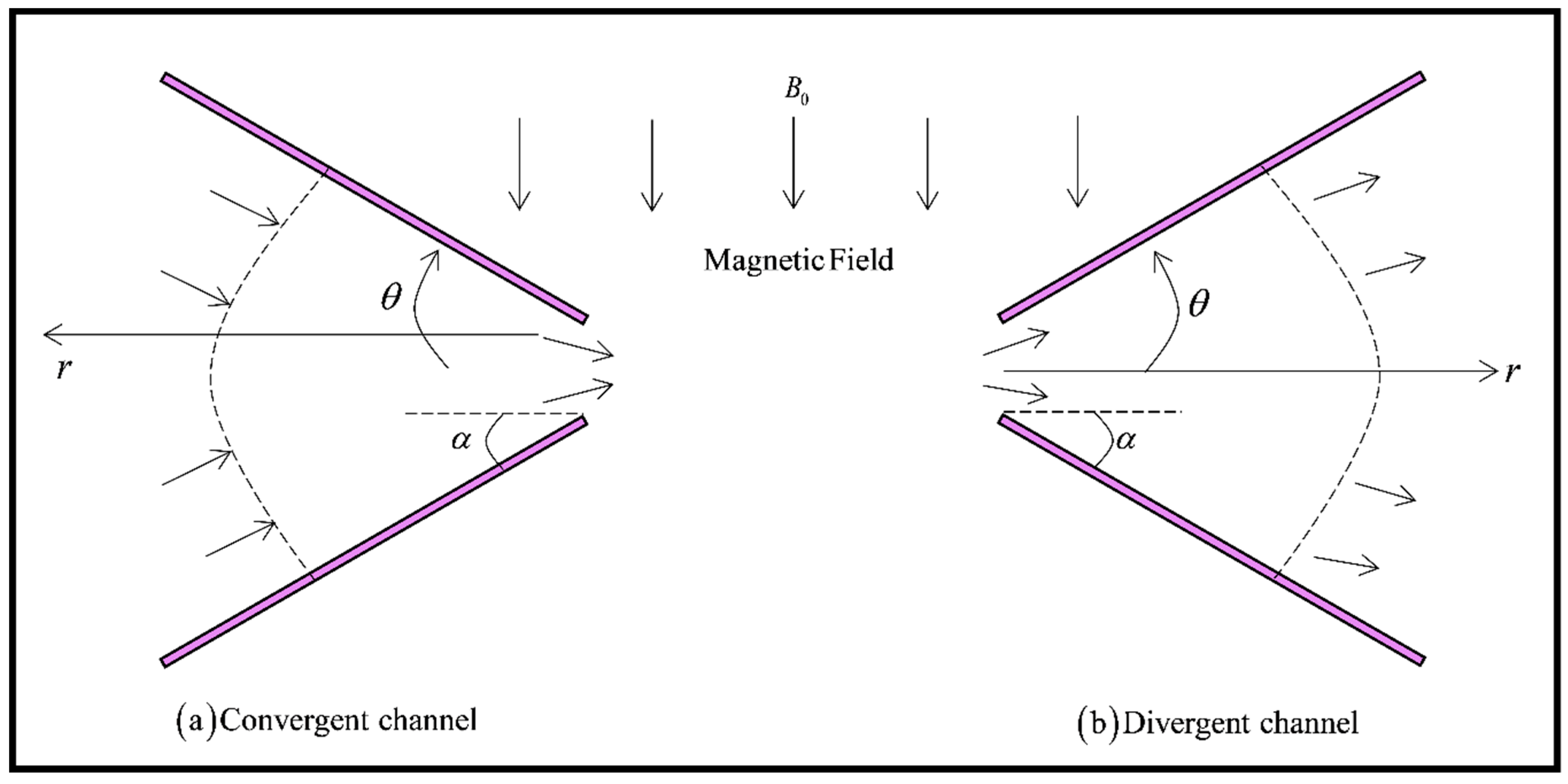
2. Mathematical Model
3. Solution by Using Spectral Homotopy Analysis Method
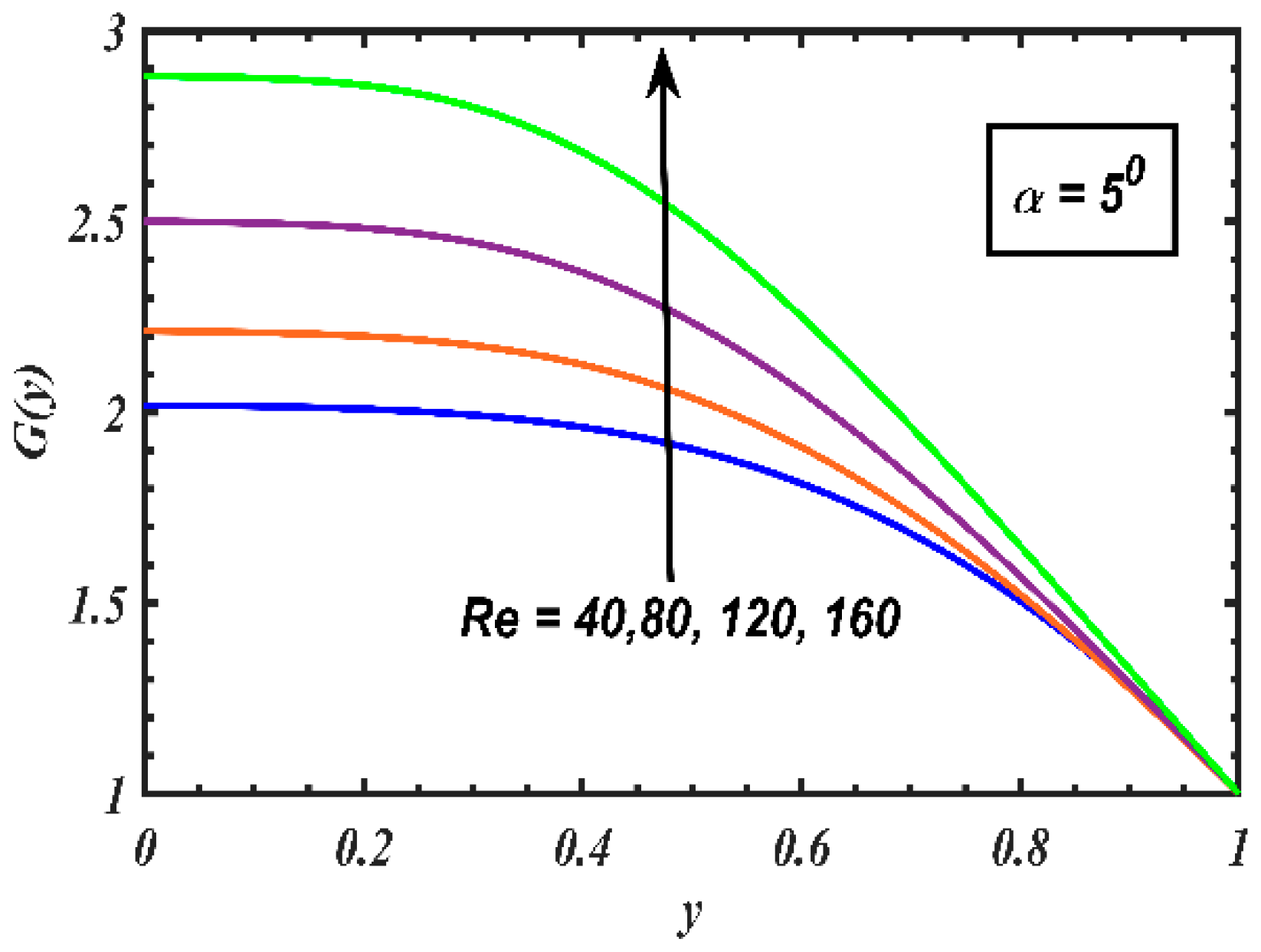
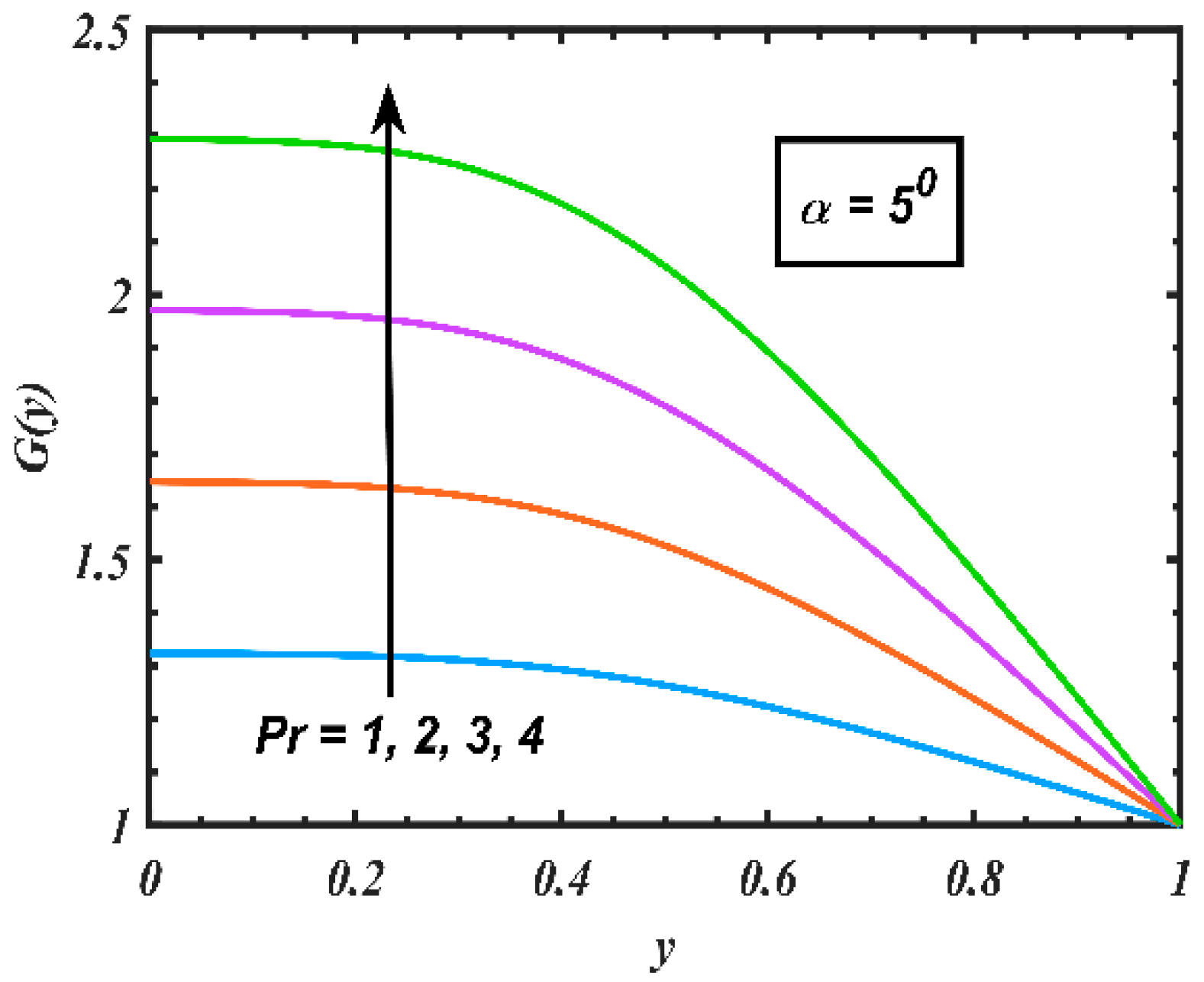
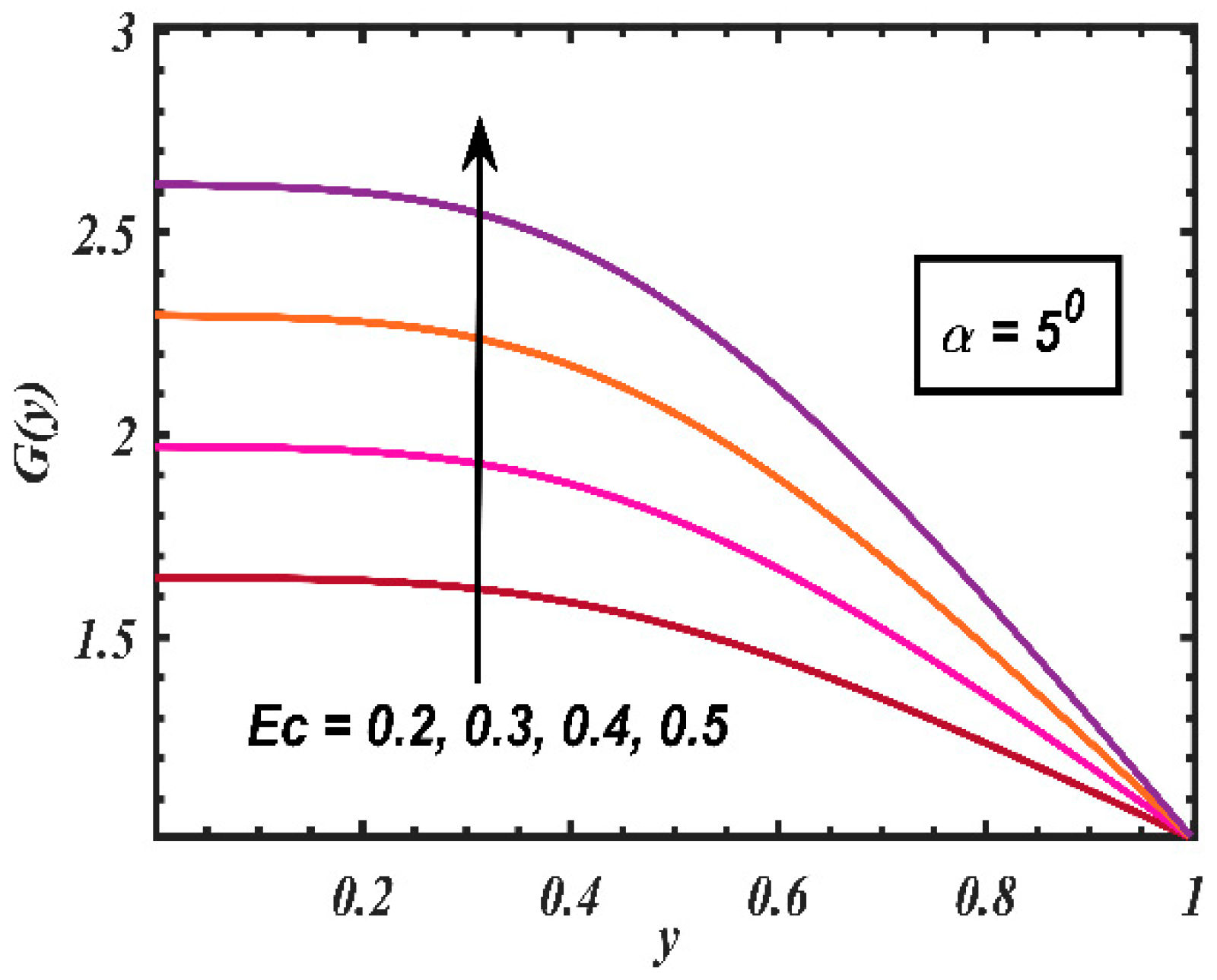
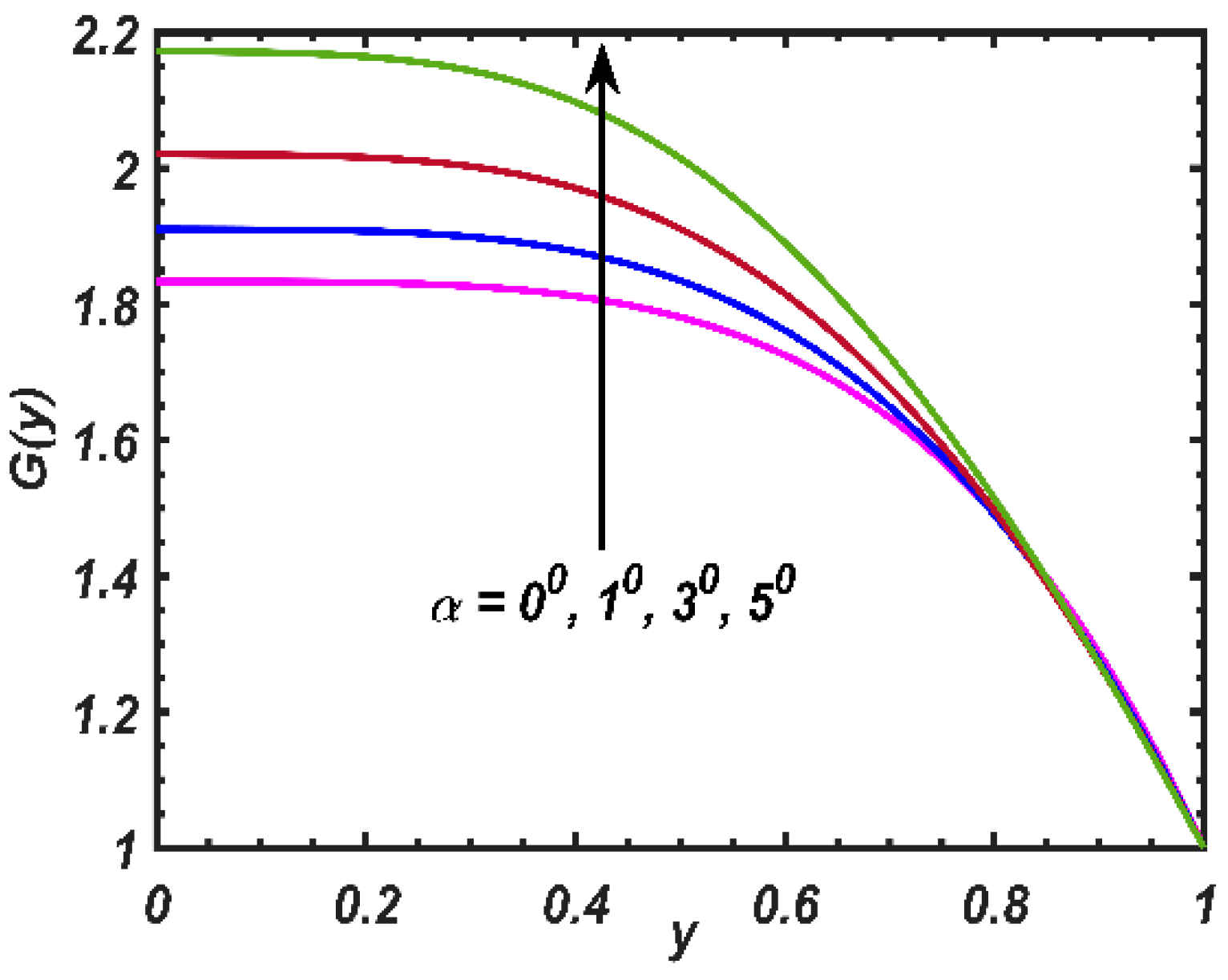
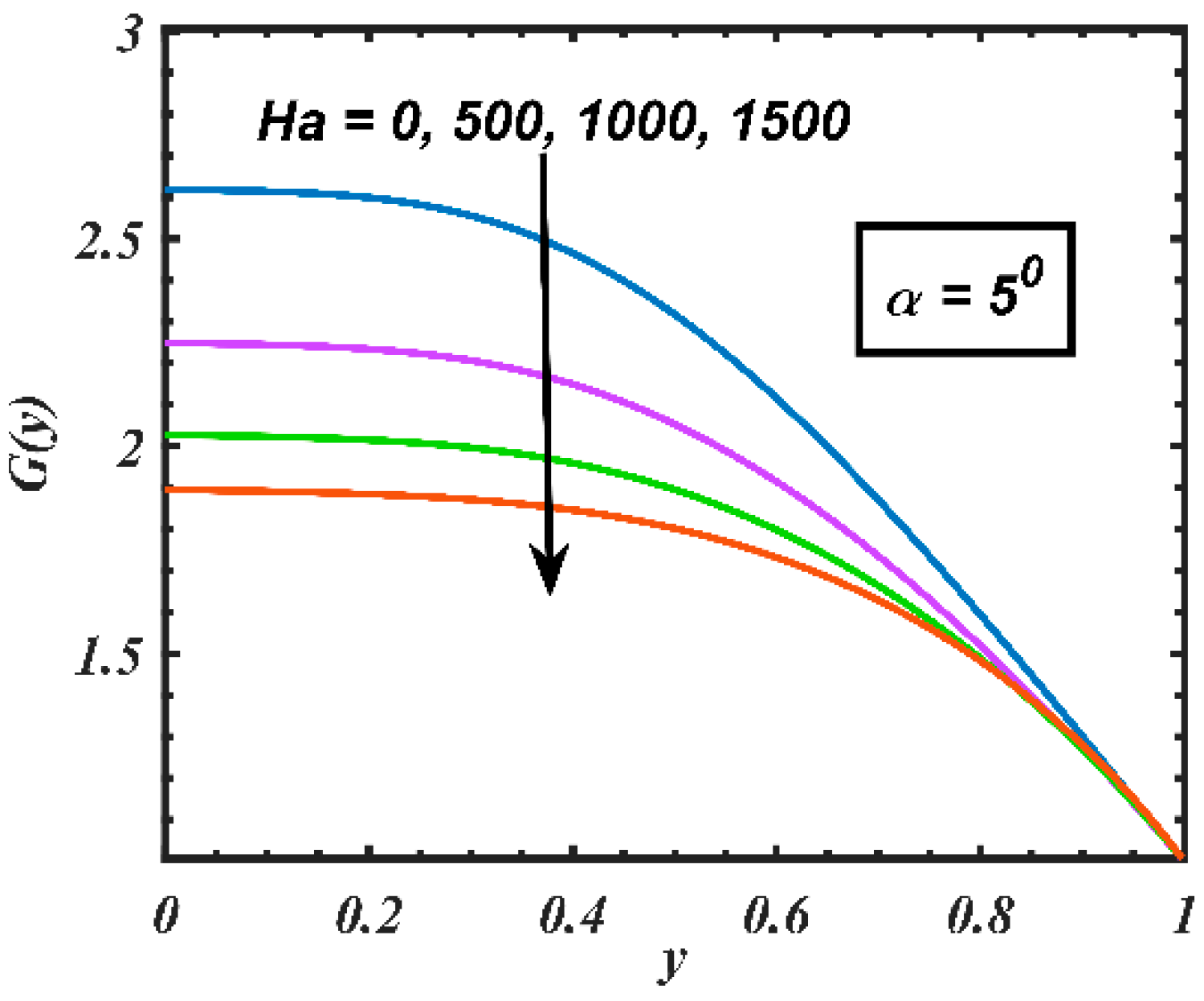
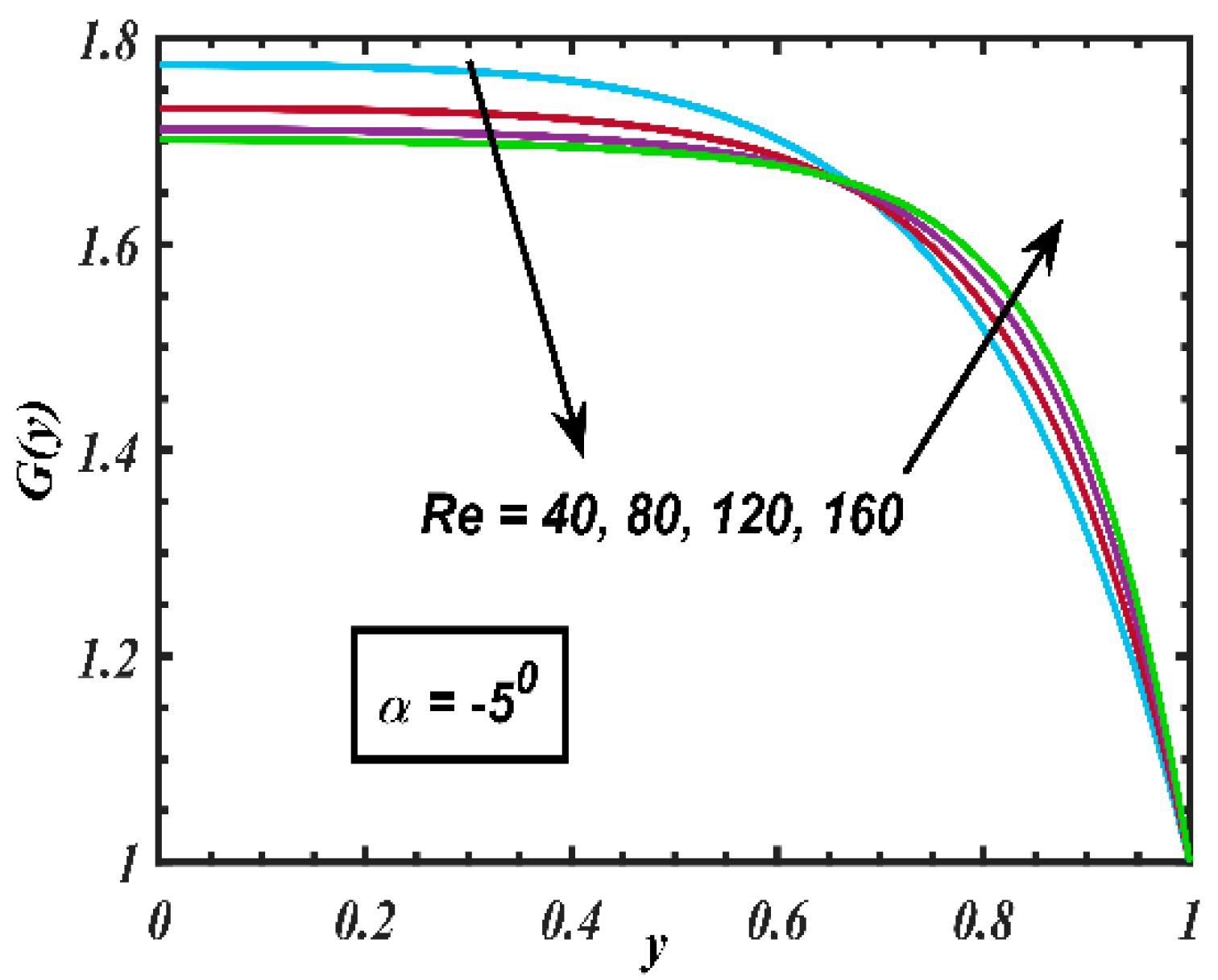
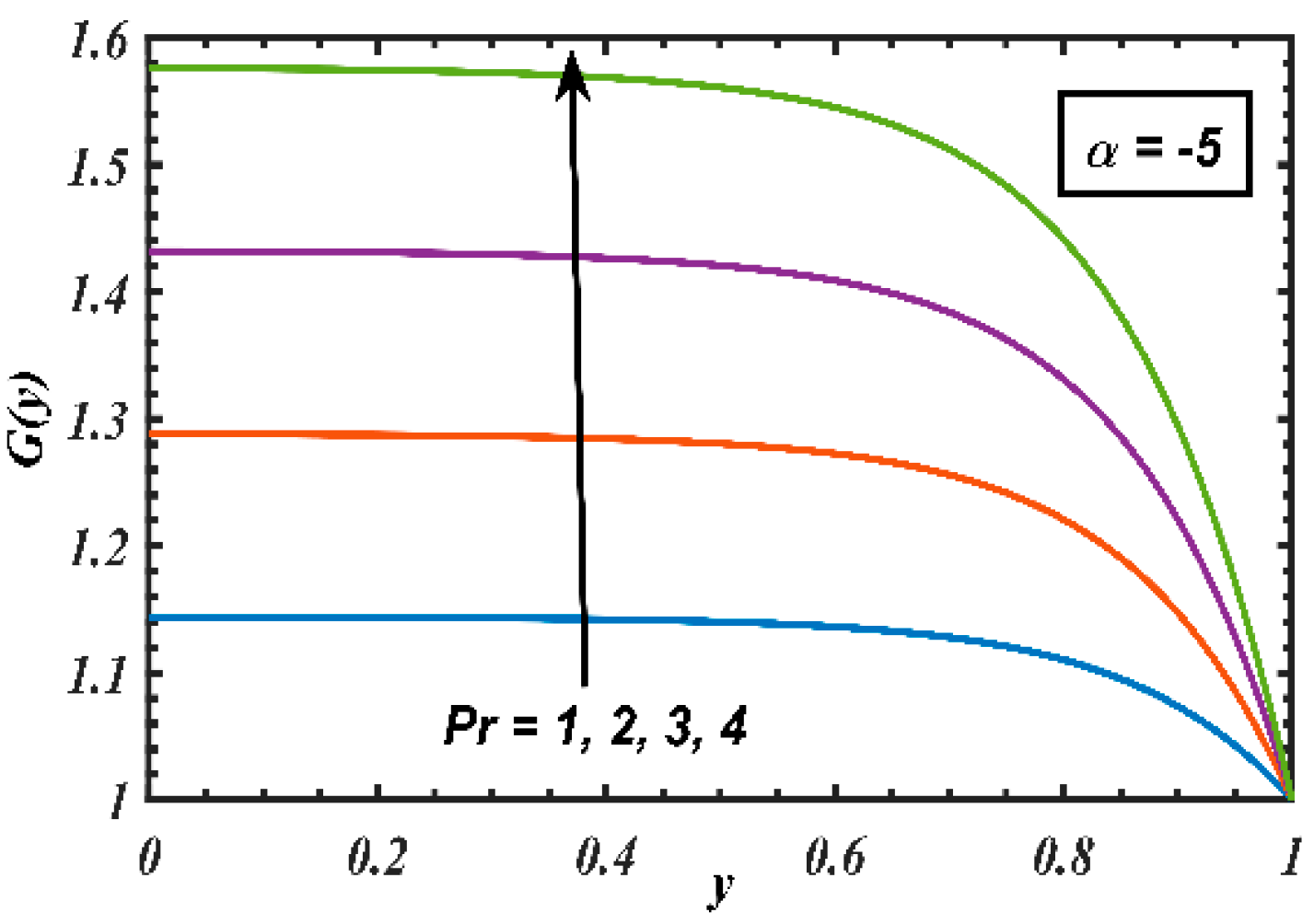
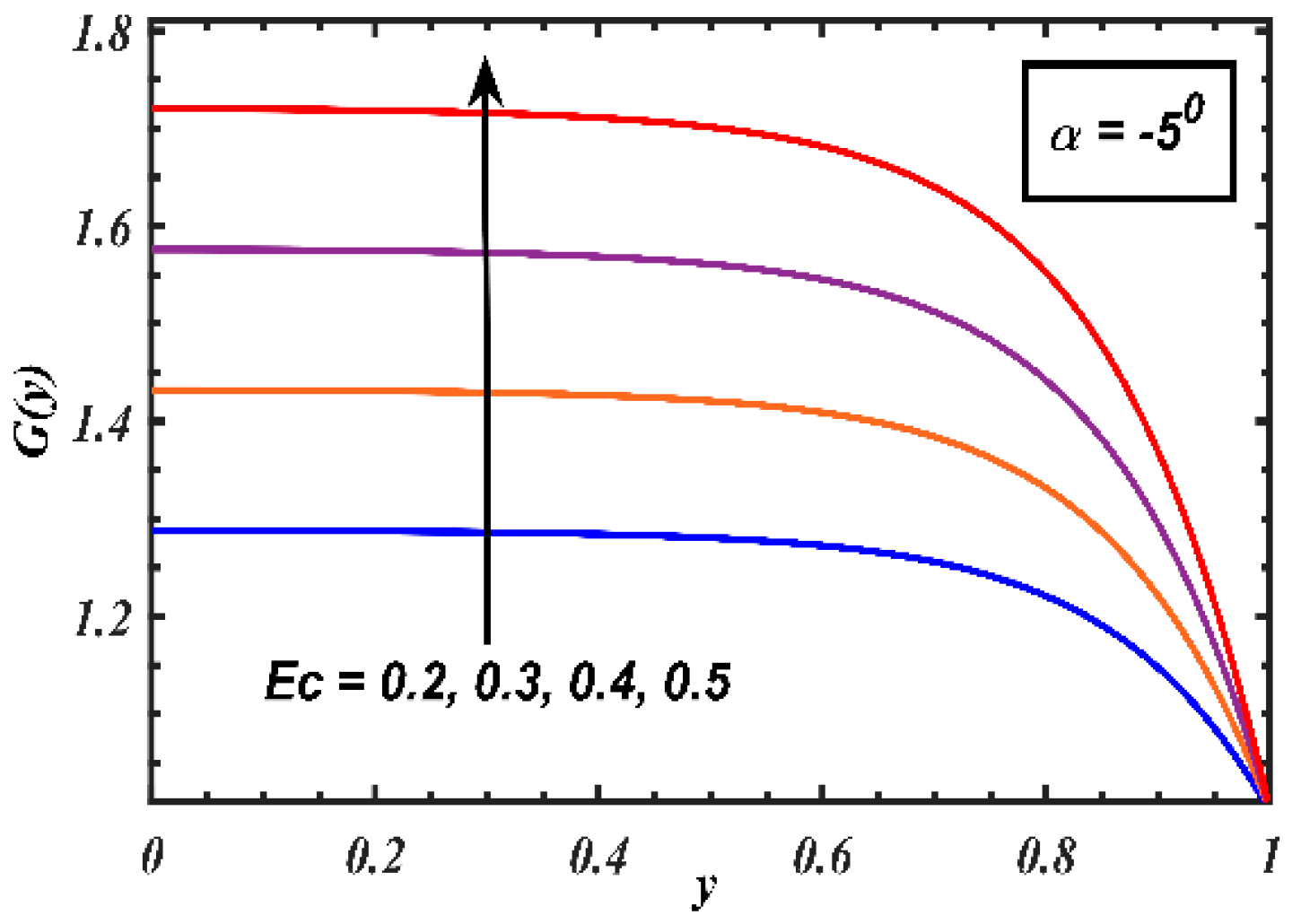
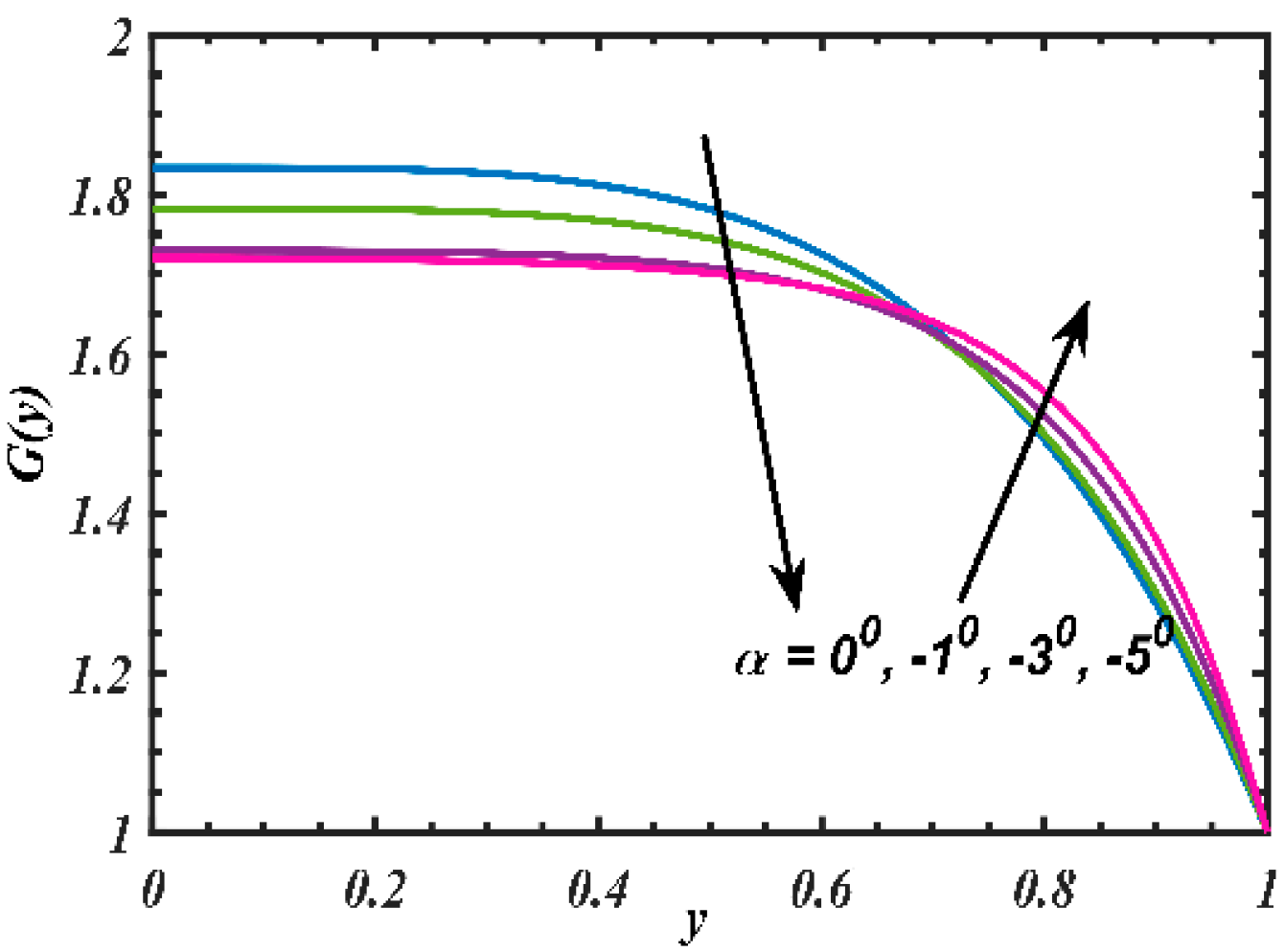
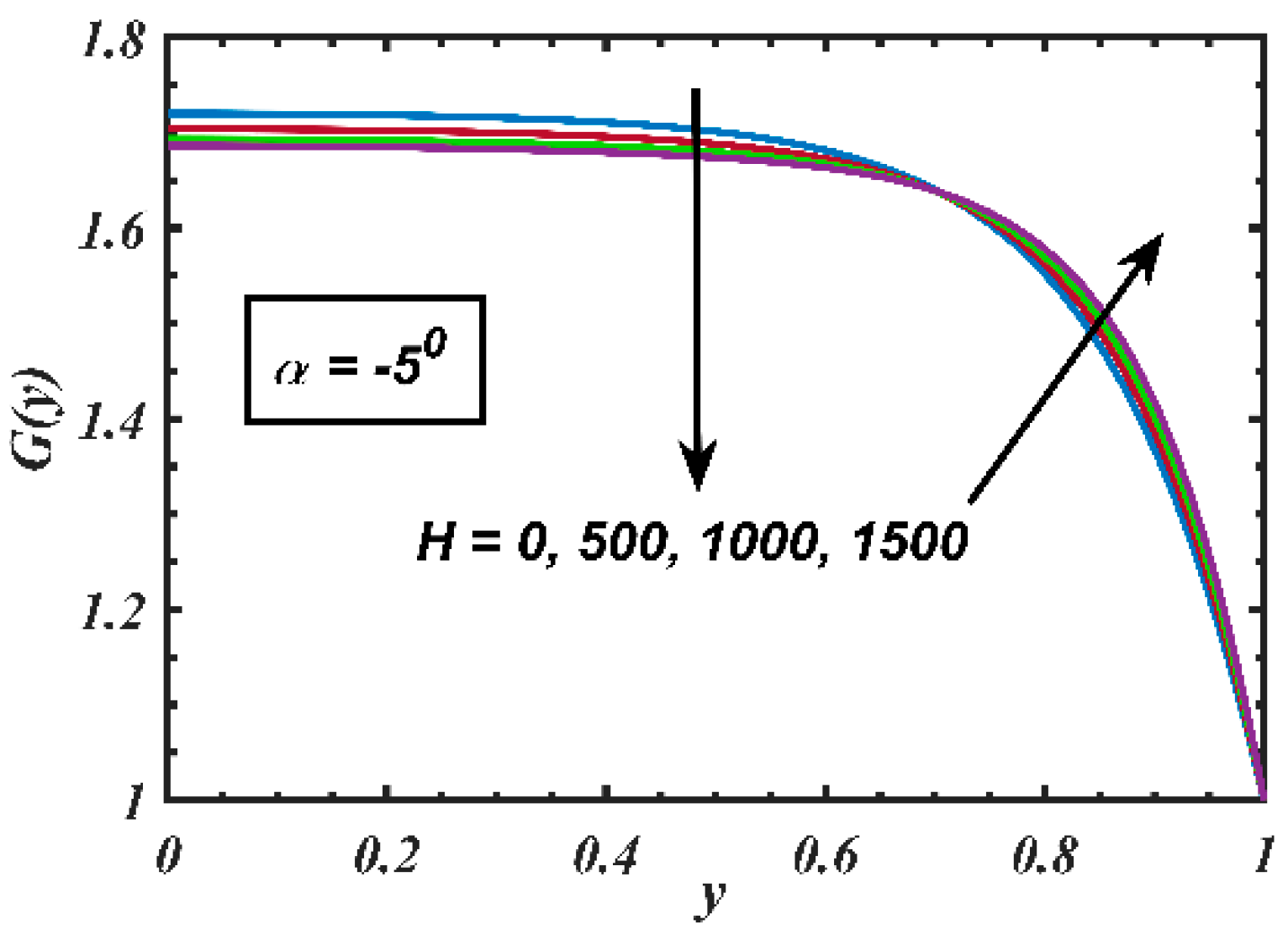
4. Results and Discussion
5. Conclusions
6. Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Sibanda, P.; Motsa, S.; Makukula, Z. A spectral-homotopy analysis method for heat transfer flow of a third-grade fluid between parallel plates. Int. J. Numer. Methods Heat 2012, 22, 4–23. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. BioScience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Ahmed, N.; Abbasi, A.; Khan, U.; Mohyud-Din, S.T. Thermal radiation effects on flow of Jeffery fluid in converging and diverging stretchable channels. Neural Comput. Appl. 2018, 30, 2371–2379. [Google Scholar] [CrossRef]
- Banks, W.; Drazin, P.; Zaturska, M. On perturbations of Jeffery-Hamel flow. J. Fluid Mech. 1988, 186, 559–581. [Google Scholar] [CrossRef]
- Domairry, D.G.; Mohsenzadeh, A.; Famouri, M. The application of homotopy analysis method to solve nonlinear differential equation governing Jeffery–Hamel flow. Commun Nonlinear Sci. 2009, 14, 85–95. [Google Scholar] [CrossRef]
- Esmaili, Q.; Ramiar, A.; Alizadeh, E.; Ganji, D. An approximation of the analytical solution of the Jeffery–Hamel flow by decomposition method. Phys Lett. A 2008, 372, 3434–3439. [Google Scholar] [CrossRef]
- Ganji, Z.; Ganji, D.D.; Esmaeilpour, M. Study on nonlinear Jeffery–Hamel flow by He’s semi-analytical methods and comparison with numerical results. Comput. Math. Appl. 2009, 58, 2107–2116. [Google Scholar] [CrossRef]
- Patel, N.; Meher, R. Analytical investigation of Jeffery-Hemal flow with magnetic field by differential transform method. Int. J. Adv. Appl. Math. Mech. 2018, 6, 1–9. [Google Scholar]
- Dey, P.K.; Zikanov, O. Turbulence and transport of passive scalar in magnetohydrodynamic channel flows with different orientations of magnetic field. Int. J. Heat Fluid Flow 2012, 36, 101–117. [Google Scholar] [CrossRef]
- Guchhait, S.K.; Jana, R. A Study of Some Magnetohydrodynamics Problems with or Without Hall Currents; Vidyasagar University: West Bengal, India, 2018. [Google Scholar]
- Hvasta, M.; Dudt, D.; Fisher, A.; Kolemen, E. Calibrationless rotating Lorentz-force flowmeters for low flow rate applications. Meas. Sci. Technol. 2018, 29, 075303. [Google Scholar] [CrossRef]
- Motsa, S.S.; Sibanda, P.; Awad, F.G.; Shateyi, S. A new spectral-homotopy analysis method for the MHD Jeffery–Hamel problem. Comput. Fluids 2010, 39, 1219–1225. [Google Scholar] [CrossRef]
- Balazadeh, N.; Sheikholeslami, M.; Ganji, D.D.; Li, Z. Semi analytical analysis for transient Eyring-Powell squeezing flow in a stretching channel due to magnetic field using DTM. J. Mol. Liq. 2018, 260, 30–36. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Khan, U.; Din, S.T.M.; Iqbal, M.A.; Wang, W. Differential transform method for unsteady nanofluid flow and heat transfer. Alex. Eng. J. 2018, 57, 1867–1875. [Google Scholar] [CrossRef]
- Ali, J. Application of New Iterative Method and Adomian Decomposition Method to Hamel’s Flow Problem. J. Adv. Civ. Eng. 2018, 4, 10–13. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. The adomian decomposition method for the slip flow and heat transfer of nanofluids over a stretching/shrinking sheet. Rom. Rep. Phys. 2018, 70, 115. [Google Scholar]
- Sobamowo, M.G.; Yinusa, A.A. Transient Combustion Analysis for Iron Micro-particles in a Gaseous Oxidizing Medium Using Adomian Decomposition Method. J. Comput. Eng. Phys. Model. 2018, 1, 1–15. [Google Scholar] [CrossRef]
- Ahmad, I.; Ilyas, H. Homotopy Perturbation Method for the nonlinear MHD Jeffery–Hamel blood flows problem. Appl. Numer. Math. 2019, 141, 124–132. [Google Scholar] [CrossRef]
- Shirkhani, M.; Hoshyar, H.; Rahimipetroudi, I.; Akhavan, H.; Ganji, D. Unsteady time-dependent incompressible Newtonian fluid flow between two parallel plates by homotopy analysis method (HAM), homotopy perturbation method (HPM) and collocation method (CM). Propul. Power Res. 2018, 7, 247–256. [Google Scholar] [CrossRef]
- Ahmad, H. Variational iteration method with an auxiliary parameter for solving differential equations of the fifth order. Nonlinear Sci. Lett. A 2018, 9, 27–35. [Google Scholar]
- Dogan, D.D.; Konuralp, A. Fractional variational iteration method for time-fractional non-linear functional partial differential equation having proportional delays. Therm. Sci. 2018, 14, 33–46. [Google Scholar] [CrossRef]
- Inc, M.; Khan, H.; Baleanu, D.; Khan, A. Modified variational iteration method for straight fins with temperature dependent thermal conductivity. Therm. Sci. 2018, 8, 229–236. [Google Scholar] [CrossRef]
- Wazwaz, A.-M.; Kaur, L. Optical solitons and Peregrine solitons for nonlinear Schrödinger equation by variational iteration method. Optik 2019, 179, 804–809. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Yan, S.; Zhang, X. Approximate solution of a piecewise linear–nonlinear oscillator using the homotopy analysis method. J. Vib. Control 2018, 24, 4551–4562. [Google Scholar] [CrossRef]
- Liu, J.; Wang, B. Solving the backward heat conduction problem by homotopy analysis method. Appl. Numer. Math. 2018, 128, 84–97. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Araghi, M.A.F.; Abbasbandy, S. Finding optimal convergence control parameter in the homotopy analysis method to solve integral equations based on the stochastic arithmetic. Numer. Algorithms 2018, 1, 237–267. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Gupta, Y.; Pop, I. Homotopy analysis method for predicting multiple solutions in the channel flow with stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 183–193. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M. A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD. Appl. Math. Comput. 2018, 316, 381–389. [Google Scholar] [CrossRef]
- Shahid, A.; Zhou, Z.; Bhatti, M.; Tripathi, D. Magnetohydrodynamics Nanofluid Flow Containing Gyrotactic Microorganisms Propagating Over a Stretching Surface by Successive Taylor Series Linearization Method. Microgravity Sci. Technol. 2018, 30, 445–455. [Google Scholar] [CrossRef]
- Shivanian, E.; Alsulami, H.; Alhuthali, M.; Abbasbandy, S. Predictor homotopy analysis method (PHAM) for nano boundary layer flows with nonlinear Navier boundary condition: Existence of four solutions. Filomat 2014, 28, 1687–1697. [Google Scholar] [CrossRef]
- Othman, M.I.; Marin, M. Effect of thermal loading due to laser pulse on thermoelastic porous medium under GN theory. Results Phys. 2017, 7, 3863–3872. [Google Scholar] [CrossRef]
- Moradi, A.; Alsaedi, A.; Hayat, T. Investigation of heat transfer and viscous dissipation effects on the Jeffery-Hamel flow of nanofluids. Therm. Sci. 2015, 19, 563–578. [Google Scholar] [CrossRef]
- Makukula, Z.G.; Sibanda, P.; Motsa, S.S. A Novel Numerical Technique for Two-Dimensional Laminar Flow between Two Moving Porous Walls. Math. Probl. Eng. 2010, 2010, 528956. [Google Scholar] [CrossRef]
- Motsa, S.S.; Shateyi, S.; Marewo, G.T.; Sibanda, P. An improved spectral homotopy analysis method for MHD flow in a semi-porous channel. Numer. Algorithms 2012, 60, 463–481. [Google Scholar] [CrossRef]
- Marin, M. Contributions on uniqueness in thermoelastodynamics on bodies with voids. Cienc. Mat. (Havana) 1998, 16, 101–109. [Google Scholar]
- Hassan, M.; Marin, M.; Ellahi, R.; Alamri, S.Z. Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids. Heat Transf. Res. 2018, 49, 1837–1848. [Google Scholar] [CrossRef]
| H | 1st Order | 2nd Order | 3rd Order | DTM | Shooting |
|---|---|---|---|---|---|
| 0 | −3.539430 | −3.539411 | −3.539415 | −3.539415 | −3.539415 |
| 100 | −3.321491 | −3.321498 | −3.321499 | −3.321499 | −3.321499 |
| 200 | −3.118488 | −3.118486 | −3.118485 | −3.118485 | −3.118485 |
| 300 | −2.929291 | −2.929295 | −2.929295 | −2.929295 | −2.929295 |
| 400 | −2.752923 | −2.752927 | −2.752927 | −2.752927 | −2.752927 |
| 500 | −2.588440 | −2.588448 | −2.588448 | −2.588448 | −2.588448 |
| 600 | −2.434932 | −2.434999 | −2.434997 | −2.434997 | −2.434997 |
| 700 | −2.291726 | −2.291771 | −2.291775 | −2.291775 | −2.291775 |
| 800 | −2.158010 | −2.158041 | −2.158042 | −2.158042 | −2.158042 |
| H | 1st Order | 2nd Order | 3rd Order | DTM | Shooting |
|---|---|---|---|---|---|
| 0 | −2.885879 | −2.885886 | −2.885885 | −2.885885 | −2.885885 |
| 100 | −2.918780 | −2.918780 | −2.918782 | −2.918782 | −2.918782 |
| 200 | −2.961804 | −2.961804 | −2.961804 | −2.961804 | −2.961804 |
| 300 | −3.013646 | −3.013659 | −3.013659 | −3.013659 | −3.013659 |
| 400 | −3.073033 | −3.073031 | −3.073035 | −3.073035 | −3.073035 |
| 500 | −3.138154 | −3.138962 | −3.138960 | −3.138960 | −3.138960 |
| 600 | −3.210500 | −3.210512 | −3.210511 | −3.210511 | −3.210511 |
| 800 | −3.367243 | −3.367331 | −3.367336 | −3.367336 | −3.367336 |
| 1000 | −3.538100 | −3.538122 | −3.538120 | −3.538120 | −3.538120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, A.; Md Basir, M.F.; Ali, U.; Mohd Kasihmuddin, M.S.; Mansor, M.A. Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes 2019, 7, 626. https://doi.org/10.3390/pr7090626
Mahmood A, Md Basir MF, Ali U, Mohd Kasihmuddin MS, Mansor MA. Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes. 2019; 7(9):626. https://doi.org/10.3390/pr7090626
Chicago/Turabian StyleMahmood, Asad, Md Faisal Md Basir, Umair Ali, Mohd Shareduwan Mohd Kasihmuddin, and Mohd. Asyraf Mansor. 2019. "Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method" Processes 7, no. 9: 626. https://doi.org/10.3390/pr7090626
APA StyleMahmood, A., Md Basir, M. F., Ali, U., Mohd Kasihmuddin, M. S., & Mansor, M. A. (2019). Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes, 7(9), 626. https://doi.org/10.3390/pr7090626







