Grouping Method of Semiconductor Bonding Equipment Based on Clustering by Fast Search and Find of Density Peaks for Dynamic Matching According to Processing Tasks
Abstract
1. Introduction
2. Semiconductor Bonding Device Grouping Method Based on Processing Task Matching
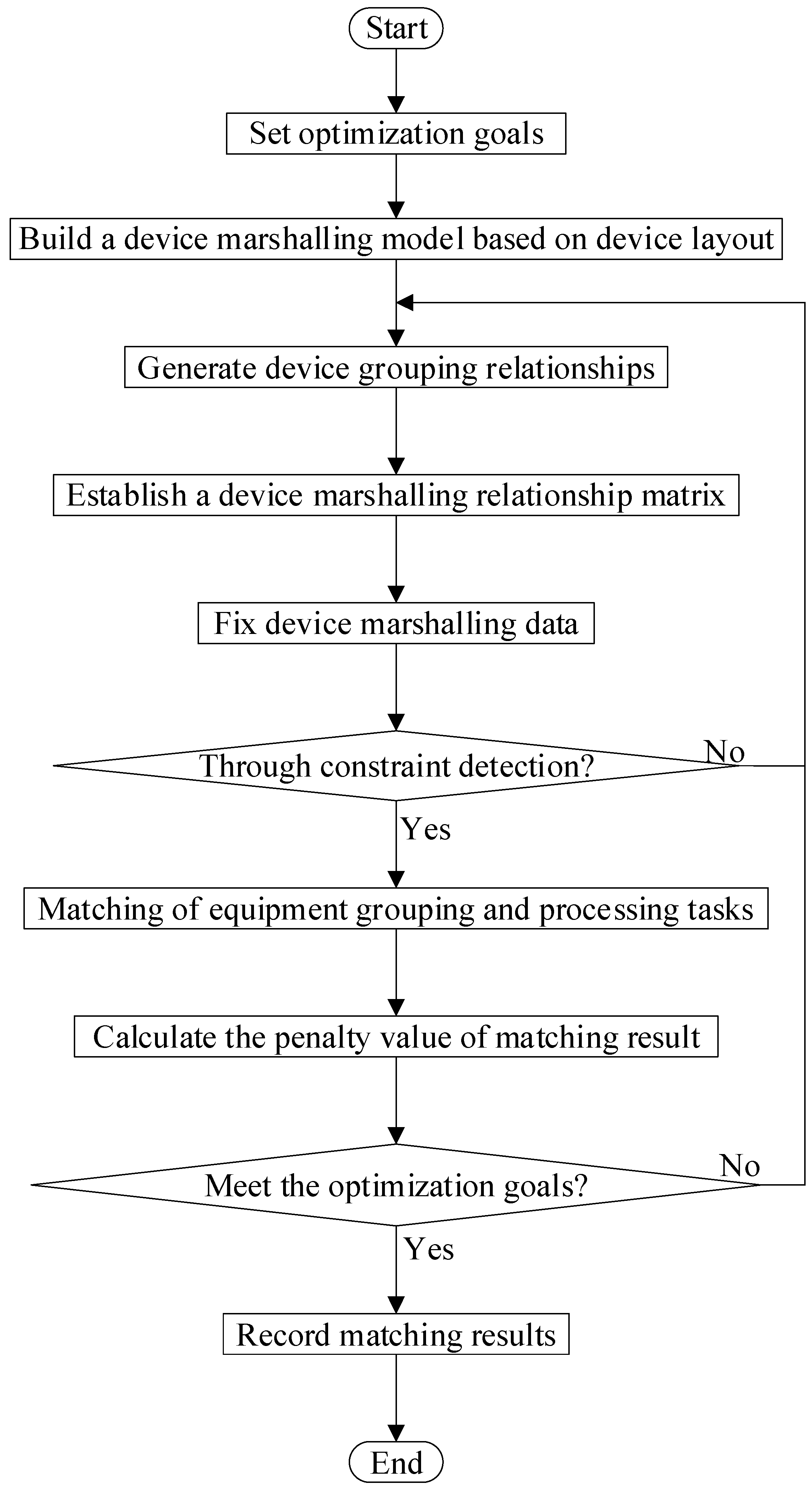
2.1. Equipment Marshalling Process
2.2. Analysis of Equipment Grouping Methods Based on Processing Task Matching
3. Grouping Method of Semiconductor Bonding Equipment Based on CFSFDP Algorithm for Dynamic Matching According to Processing Tasks
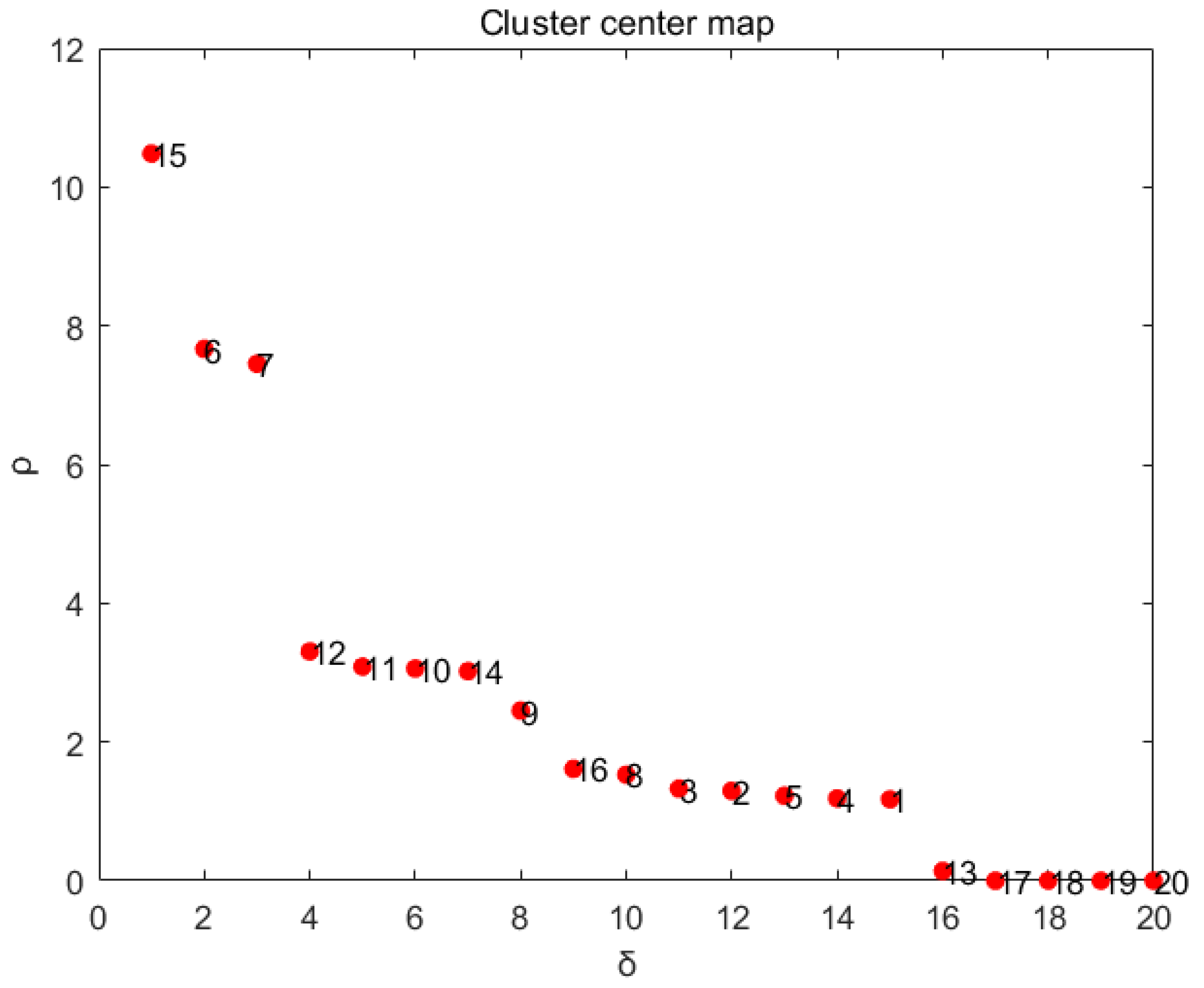
3.1. Overview of CFSFDP Clustering Algorithm
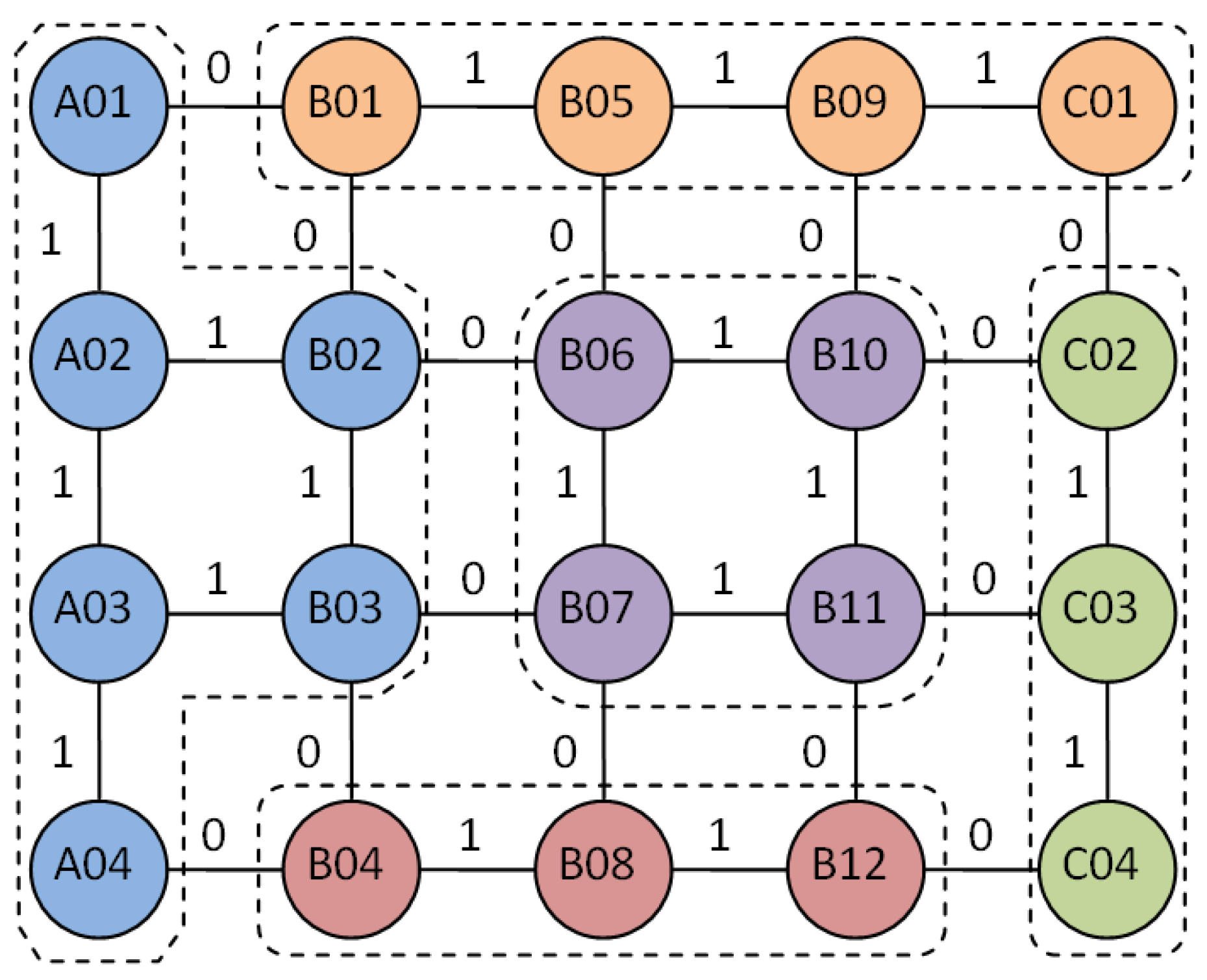
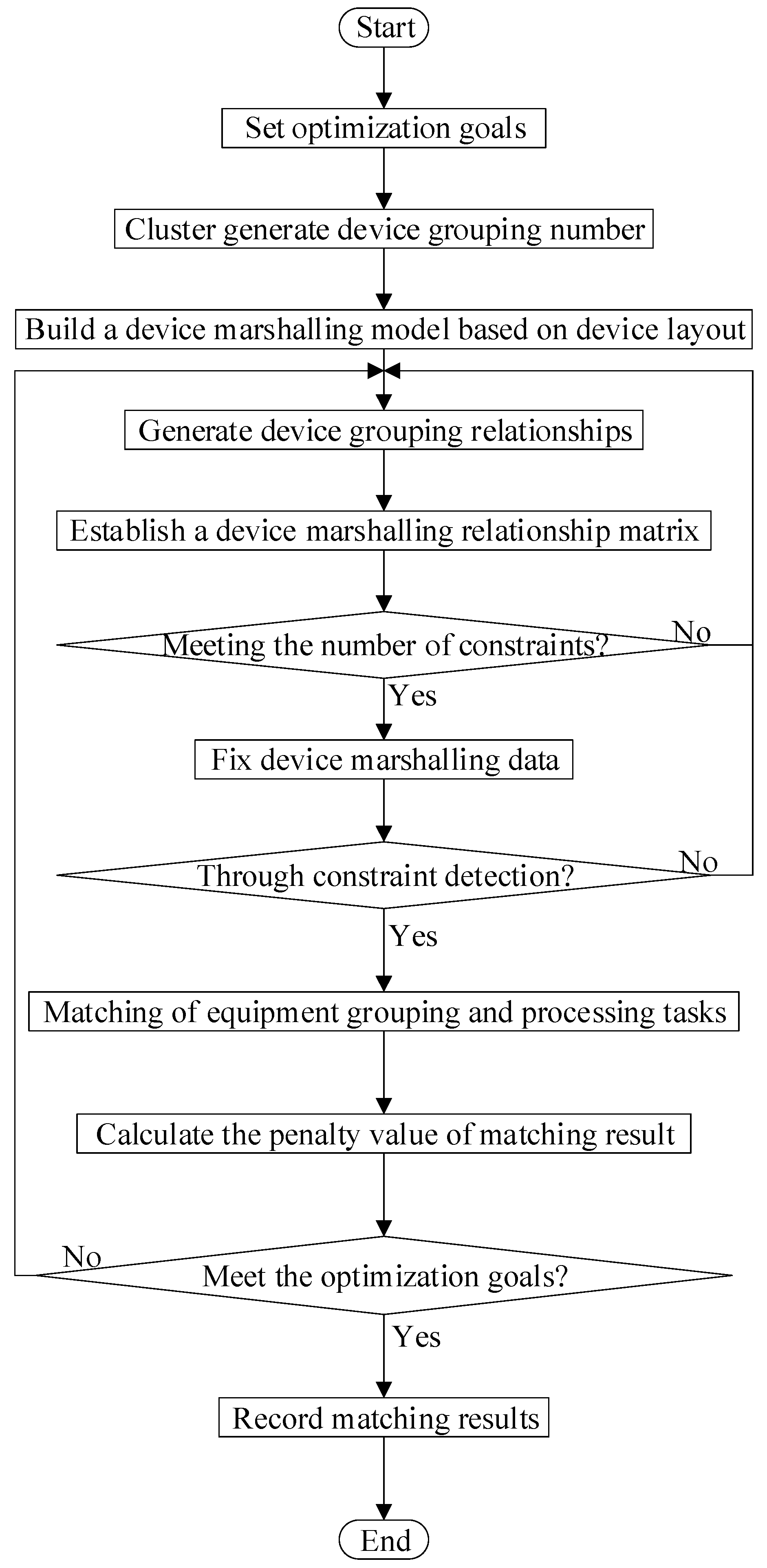
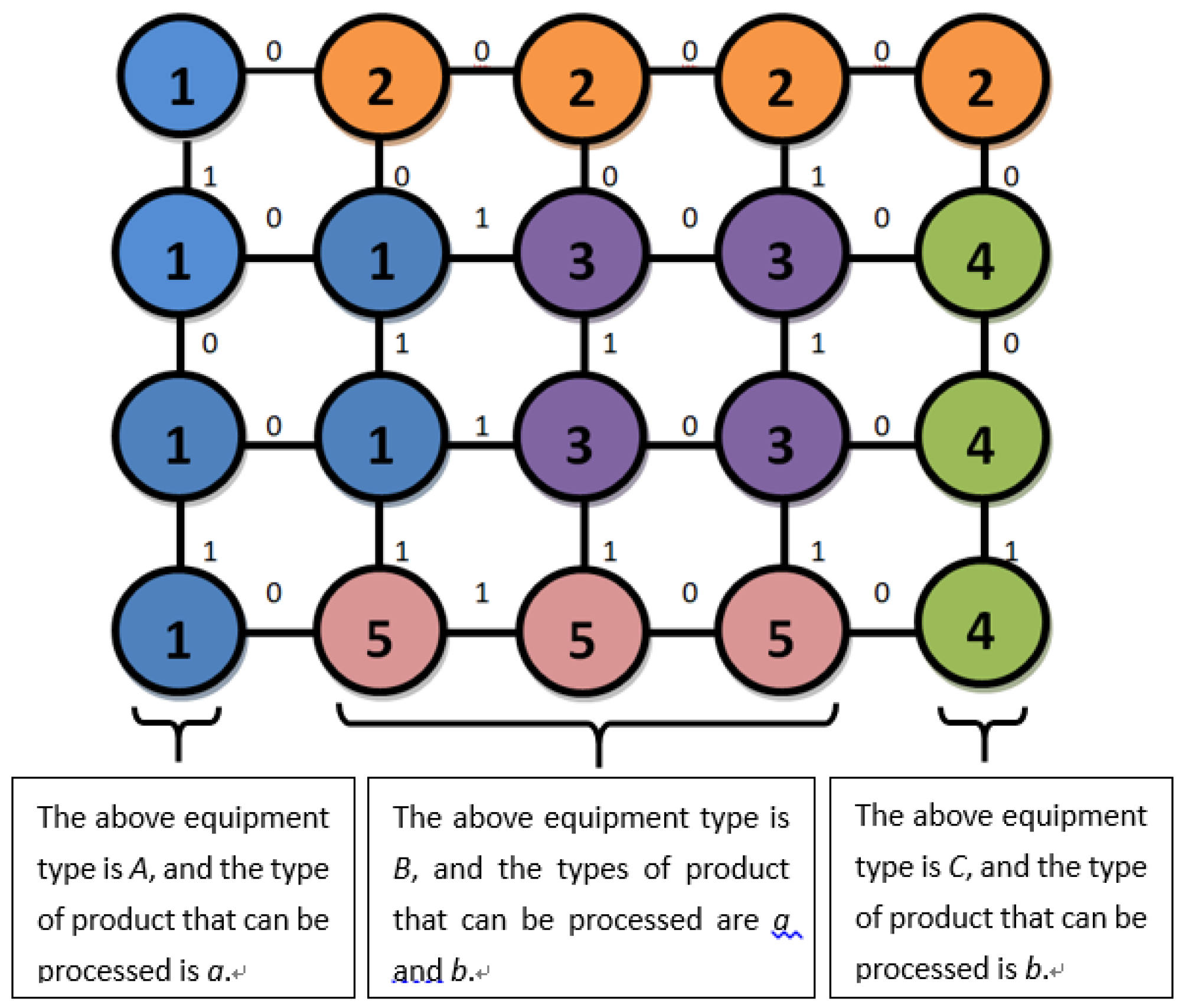
3.2. Application of CFSFDP Clustering Algorithm in Equipment Marshalling Process
4. Simulation Verification and Results Analysis
4.1. Simulation Experiment Design Related Information
4.2. Definition of Evaluation Indicators
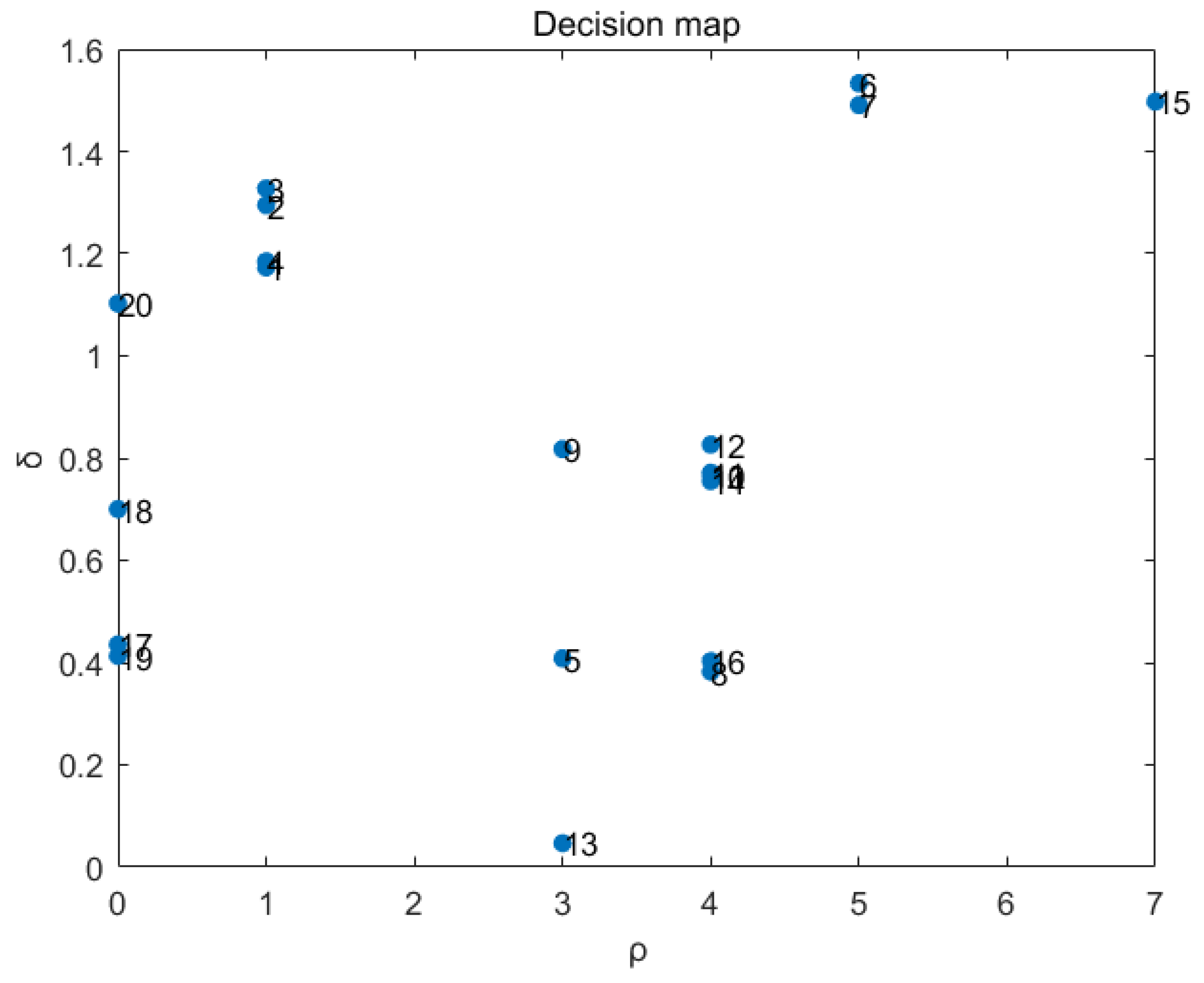
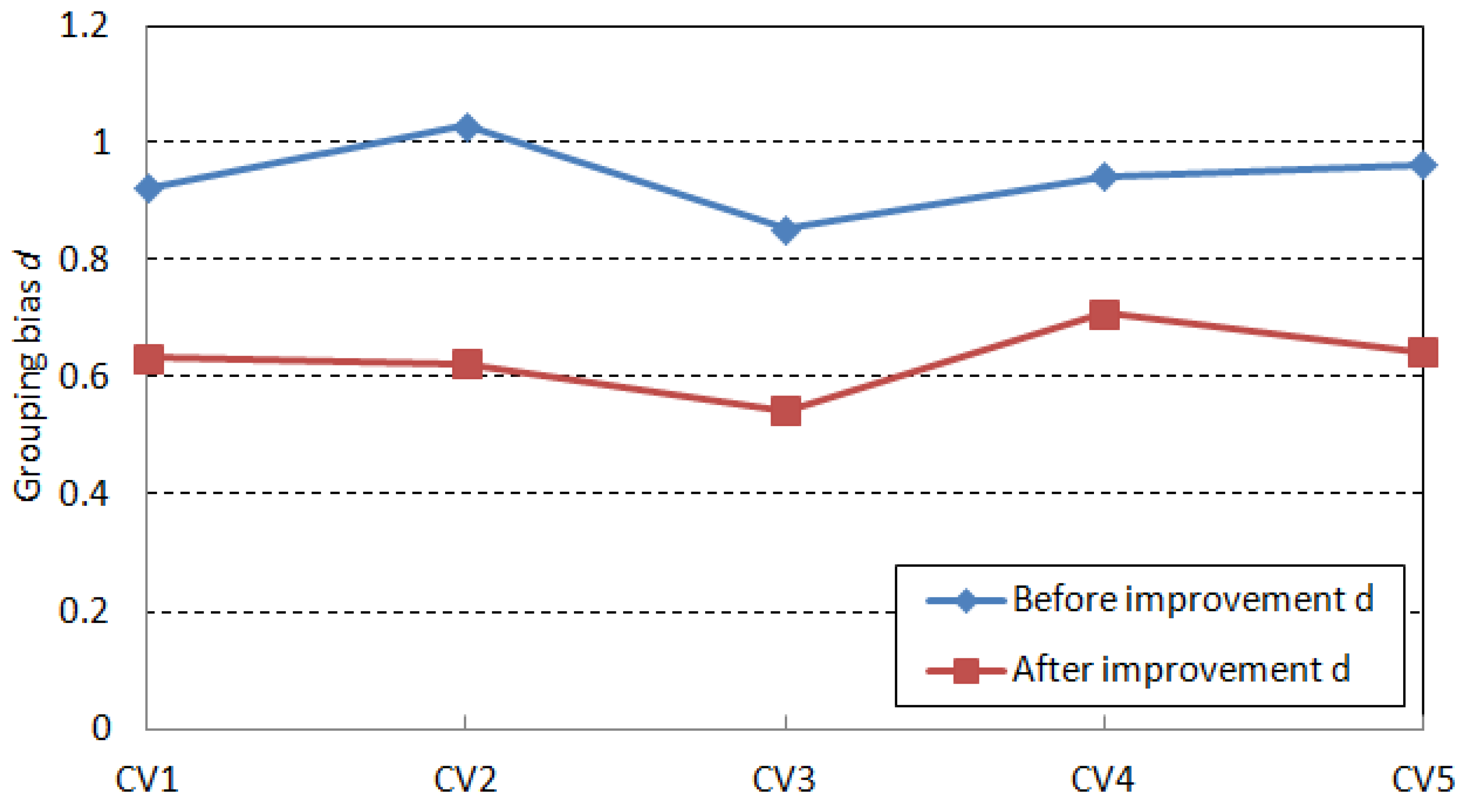
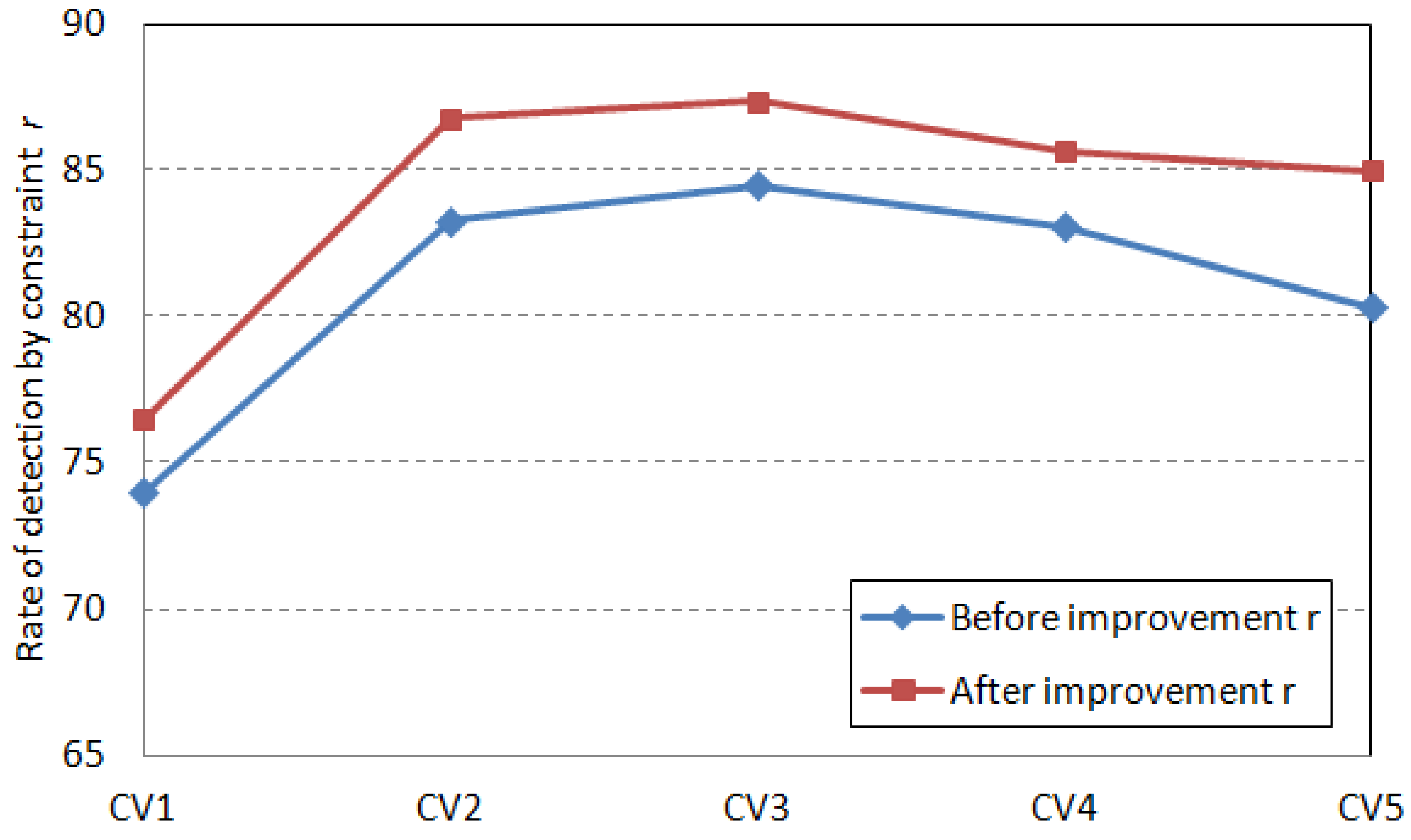
4.3. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Z.W.; Nguang, S.K.; Kong, D.X. Advances in Modelling, monitoring, and control for complex industrial systems. Complexity 2019, 2019, 2975083. [Google Scholar] [CrossRef]
- Jia, P.D.; Wu, Q.D.; Li, L. Objective-driven dynamic dispatching rule for semiconductor wafer fabrication facilities. Comput. Integr. Manuf. Syst. 2014, 20, 2808–2813. [Google Scholar]
- Zhang, G.H.; Liu, C.; Yao, L.L. A method of bottleneck detection of semiconductor assembly and test production line. Chin. J. Electron Devices 2015, 38, 44–48. [Google Scholar]
- Wu, Q.D.; Ma, Y.M.; Li, L.; Qiao, F. Data-driven dynamic scheduling method for semiconductor production line. Control Theory Appl. 2015, 32, 1233–1239. [Google Scholar]
- Wang, L.J.; Yao, P.Y. Cooperative task allocation methods in multiple groups using DLS-QGA. Control Decis. 2014, 29, 1562–1568. [Google Scholar]
- Rong, Y.P.; Zhang, X.C. Optimization for train plan of urban rail transit based on hybrid train formation. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 117–122. [Google Scholar]
- Wang, K.S.; Dong, Q.Z. An analysis on optimizing part and full routes of urban rail transit under different marshalling plans. Railw. Transp. Econ. 2018, 40, 94–99, 110. [Google Scholar]
- Jacob, R.; Márton, P.; Maue, J.; Nunkesser, M. Multistage methods for freight train classification. Networks 2011, 57, 87–105. [Google Scholar] [CrossRef]
- Hsieh, L.Y.; Hsieh, T.-J. A Throughput Management System for Semiconductor Wafer Fabrication Facilities: Design, Systems and Implementation. Processes 2018, 6, 16. [Google Scholar] [CrossRef]
- Gao, Z.W.; Saxen, H.; Gao, C.H. Data-driven approaches for complex industrial systems. IEEE Trans. Ind. Inform. 2013, 9, 2210–2212. [Google Scholar] [CrossRef]
- Gao, Z.W.; Kong, D.X.; Gao, C.H. Modeling and Control of Complex Dynamic Systems: Applied Mathematical Aspects. J. Appl. Math. 2012, 2012, 869792. [Google Scholar] [CrossRef]
- Min, Y.; Wu, N.Q. Review of operations and control of cluster tools in semiconductor wafer fabrication. Ind. Eng. J. 2012, 15, 1–15. [Google Scholar]
- Xiao, C.J.; Chen, H. Math model and scheduling method for the semiconductor assembling and testing line. Trans. Beijing Inst. Technol. 2013, 33, 1161–1164, 1170. [Google Scholar]
- Ratkiewicz, A.; Truong, T.N. Application of chemical graph theory for automated mechanism generation. J. Chem. Inf. Comput. Sci. 2003, 43, 36–44. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fu, S.P.; Li, S.B.; Luo, N. Topological Transformation and Transmission Characteristics Analysis of Vehicle Auto Transmission Based on Graph Theory. Shanghai Jiaotong Univ. Sci. 2018, 52, 348–355. [Google Scholar]
- Jayakrishna, K.; Vinodh, S.; Anish, S. A Graph Theory approach to measure the performance of sustainability enablers in a manufacturing organization. Int. J. Sustain. Eng. 2016, 9, 47–58. [Google Scholar] [CrossRef]
- Chen, H.; Gan, M.X.; Song, M.Z. An improved recommendation algorithm based on graph model. Appl. Mech. Mater. 2013, 380, 1266–1269. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, R.; Zhang, G.; Bie, R.; Dawood, H.; Ahmad, H. Clustering by fast search and find of density peaks via heat diffusion. Neurocomputing 2016, 208, 210–217. [Google Scholar] [CrossRef]
- Zhou, S.B.; Xu, W.X. A novel clustering algorithm based on relative density and decision graph. Control Decis. 2018, 33, 1921–1930. [Google Scholar]
- Calif, R.; Soubdhan, T. On the use of the coefficient of variation to measure spatial and temporal correlation of global solar radiation. Renew. Energy 2016, 88, 192–199. [Google Scholar] [CrossRef]
- Qiao, F.; Xu, X.H. Performance evaluation system for scheduling semiconductor wafer product line. J. Tongji Univ. Nat. Sci. 2007, 4, 537–542. [Google Scholar]
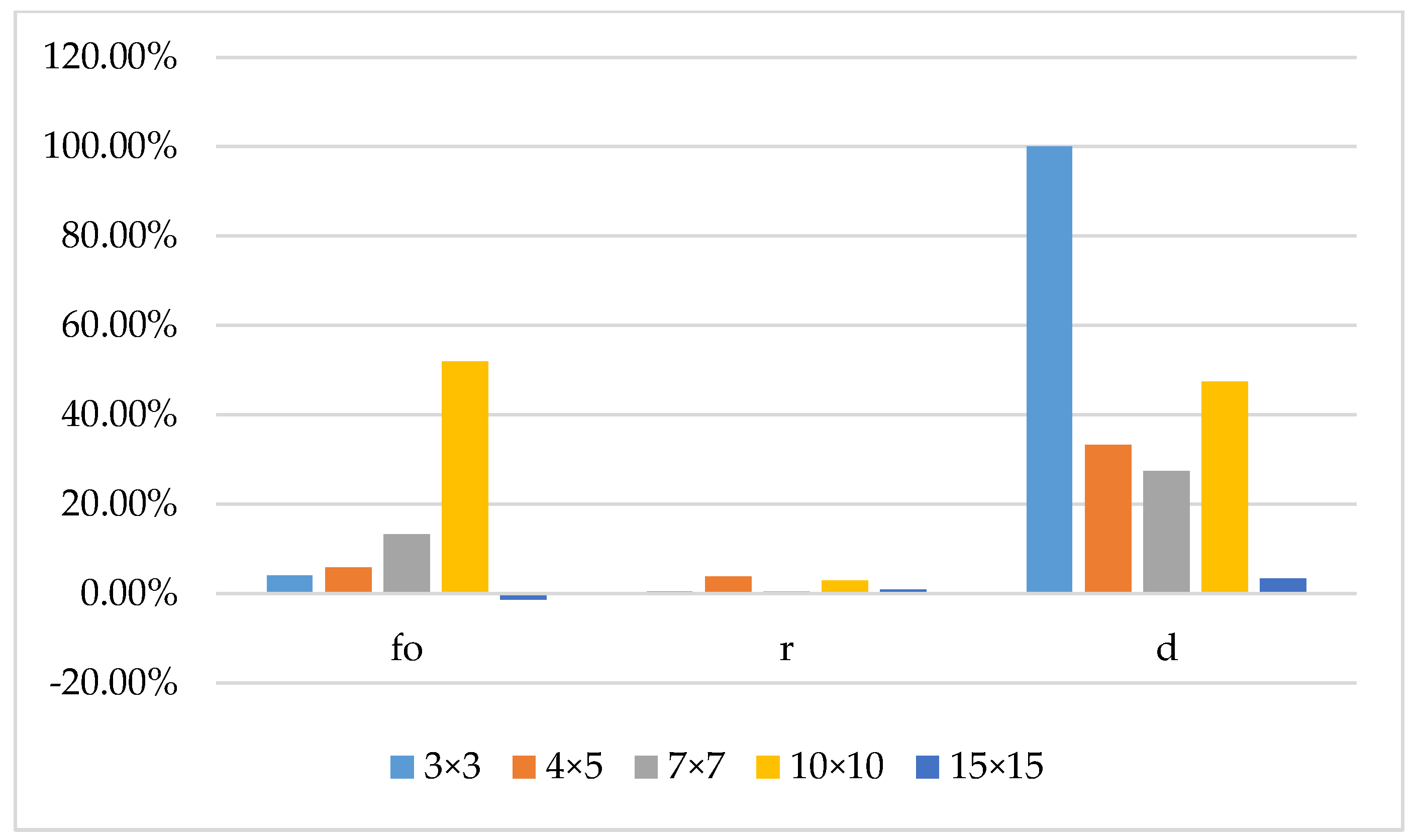
| Equipment Scale | Distance Parameter | Device Grouping Method Based on Processing Task Matching | Machining Task Matching Semiconductor Bonding Device Grouping Method Based on CFSFDP Algorithm | ||||
|---|---|---|---|---|---|---|---|
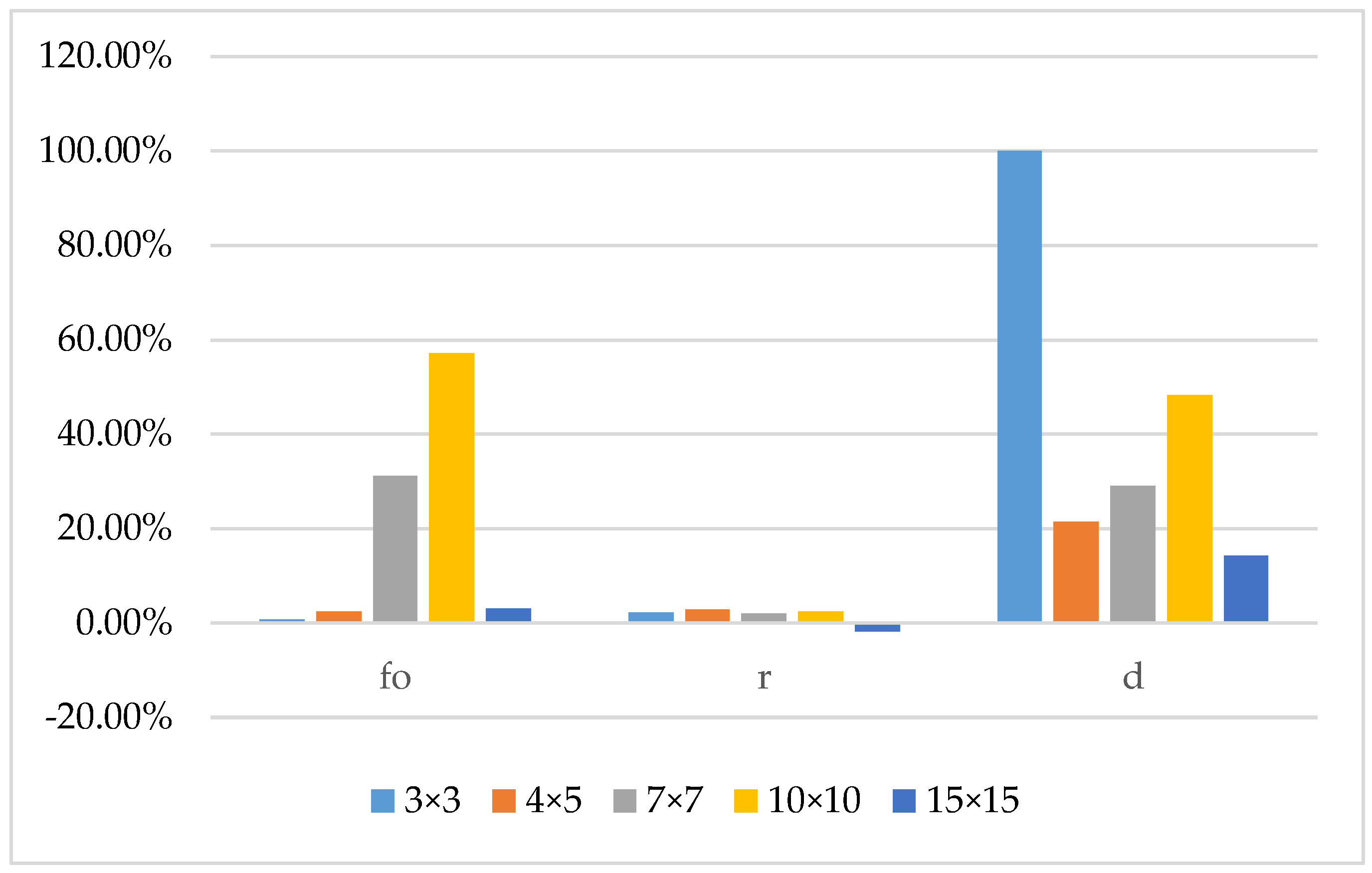
| 3 × 4 | 0.20 | 113.15 | 1.60 | 89.90 | 108.52 | 0 | 90.20 |
| 4 × 5 | 0.40 | 113.35 | 2.10 | 80.80 | 106.84 | 1.40 | 83.80 |
| 7 × 7 | 0.63 | 139.21 | 9.42 | 97.70 | 120.69 | 6.84 | 97.30 |
| 10 × 10 | 1.16 | 256.92 | 22.10 | 92.30 | 123.79 | 11.61 | 95.00 |
| 15 × 15 | 2.93 | 303.39 | 52.30 | 93.90 | 307.30 | 50.50 | 94.80 |
| Equipment Scale | Distance Parameter | Device Grouping Method Based on Processing Task Matching | Machining Task Matching Semiconductor Bonding Device Grouping Method Based on CFSFDP Algorithm | ||||
|---|---|---|---|---|---|---|---|
| 3 × 4 | 0.20 | 134.82 | 1.50 | 77.00 | 133.92 | 0 | 78.70 |
| 4 × 5 | 0.40 | 89.17 | 1.30 | 88.50 | 87.03 | 1.02 | 91.10 |
| 7 × 7 | 0.63 | 154.31 | 9.59 | 96.40 | 106.20 | 6.80 | 98.40 |
| 10 × 10 | 1.16 | 258.46 | 22.3 | 92.50 | 110.502 | 11.52 | 94.80 |
| 15 × 15 | 2.93 | 282.82 | 52.23 | 95.90 | 273.852 | 44.80 | 94.20 |
| Demand Capacity | Difference Coefficient | Device Grouping Method Based on Processing Task Matching | Machining Task Matching Semiconductor Bonding Device Grouping Method Based on CFSFDP Algorithm | ||||
|---|---|---|---|---|---|---|---|
| fo | |||||||
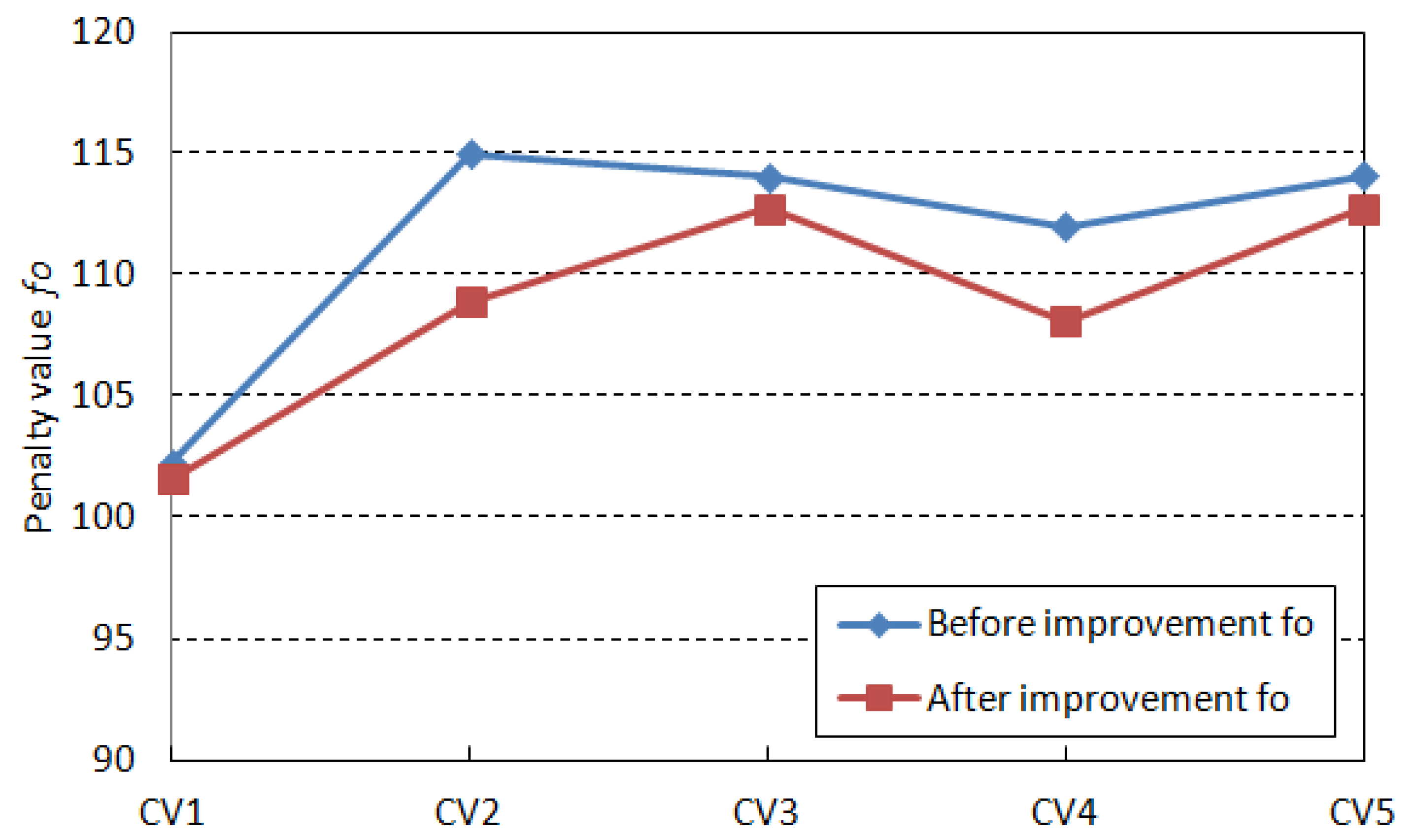
| GW1 | 0.09 | 102.24 | 0.93 | 74.00 | 101.59 | 0.64 | 76.50 |
| GW2 | 0.11 | 115.04 | 1.03 | 83.30 | 108.94 | 0.63 | 86.82 |
| GW3 | 0.28 | 114.06 | 0.86 | 84.51 | 112.77 | 0.55 | 87.40 |
| GW4 | 0.39 | 112.04 | 0.95 | 83.10 | 108.13 | 0.71 | 85.70 |
| GW5 | 0.47 | 114.14 | 0.97 | 80.35 | 112.79 | 0.65 | 85.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Si, W.; Han, Z.; Peng, J.; Qiao, F. Grouping Method of Semiconductor Bonding Equipment Based on Clustering by Fast Search and Find of Density Peaks for Dynamic Matching According to Processing Tasks. Processes 2019, 7, 566. https://doi.org/10.3390/pr7090566
Gao Z, Si W, Han Z, Peng J, Qiao F. Grouping Method of Semiconductor Bonding Equipment Based on Clustering by Fast Search and Find of Density Peaks for Dynamic Matching According to Processing Tasks. Processes. 2019; 7(9):566. https://doi.org/10.3390/pr7090566
Chicago/Turabian StyleGao, Zhijun, Wen Si, Zhonghua Han, Jiayu Peng, and Feng Qiao. 2019. "Grouping Method of Semiconductor Bonding Equipment Based on Clustering by Fast Search and Find of Density Peaks for Dynamic Matching According to Processing Tasks" Processes 7, no. 9: 566. https://doi.org/10.3390/pr7090566
APA StyleGao, Z., Si, W., Han, Z., Peng, J., & Qiao, F. (2019). Grouping Method of Semiconductor Bonding Equipment Based on Clustering by Fast Search and Find of Density Peaks for Dynamic Matching According to Processing Tasks. Processes, 7(9), 566. https://doi.org/10.3390/pr7090566





