Abstract
Metal–organic frameworks (MOFs) are the porous, crystalline structures made of metal–ligands and organic linkers that have applications in gas storage, gas separation, and catalysis. Several experimental and computational tools have been developed over the past decade to investigate the performance of MOFs for such applications. However, the experimental synthesis of MOFs is still empirical and requires trial and error to produce desired structures, which is due to a limited understanding of the mechanism and factors affecting the crystallization of MOFs. Here, we show for the first time a comprehensive kinetic model coupled with population balance model to elucidate the mechanism of MOF synthesis and to estimate size distribution of MOFs growing in a solution of metal–ligand and organic linker. The oligomerization reactions involving metal–ligand and organic linker produce secondary building units (SBUs), which then aggregate slowly to yield MOFs. The formation of secondary building units (SBUs) and their evolution into MOFs are modeled using detailed kinetic rate equations and population balance equations, respectively. The effect of rate constants, aggregation frequency, the concentration of organic linkers, and concurrent crystallization of organic linkers are studied on the dynamics of SBU and MOF formation. The results qualitatively explain the longer timescales involved in the synthesis of MOF. The fundamental insights gained from modeling and simulation analysis can be used to optimize the operating conditions for a higher yield of MOF crystals.
1. Introduction
Metal–organic frameworks (MOFs) have shown many potential applications in areas such as gas storage, capture and adsorption, and membrane separations [1,2,3]. The crystal symmetry arising due to the ordered binding of the organic linker with the metal–ligand results in highly porous structures. The synthesis of MOF was first reported with a solvothermal process which is a solution crystallization method at elevated temperatures [4]. Since then the synthesis methods have evolved into techniques such as electrochemical synthesis, microwave-assisted synthesis, template crystallization, and atomic layer deposition, where temperature and concentration of secondary building units (SBUs) play a vital role in the yield and growth of MOF [5]. SBU is an intermediate oligomer formed by the reaction of organic linkers and metal–ligands which repeats itself to form a MOF-like structure.
The complex reaction scheme of SBU synthesis and their aggregation during the crystallization process makes mechanistic understanding of the MOF synthesis a challenging task [6]. The approaches to understanding the mechanism of MOF synthesis are mostly limited to experimental studies [7,8,9,10]. The computational approaches are aimed primarily towards the understanding of processes involving MOFs such as gas adsorption and catalytic reactions [11,12,13,14]. Very few computational studies focus on kinetic modeling of MOF synthesis, which do not consider key physical processes such as oligomerization reaction and aggregation of SBUs in the models [15]. Here, we model the formation of SBUs using the detailed rate expressions similar to those used for chain polymerization reactions [16] and model the aggregation of SBUs using population balance models [17]. Further, the concurrent crystallization of organic linker during the formation of SBUs is also taken into consideration which affects the amount of linker in the solution. Since the organic linkers usually have very low solubilities in aqueous solvents, their concentration is typically maintained below the saturation limit during MOF synthesis to avoid concurrent crystallization of linkers. Such limitations on the concentration of organic linker result in a lower yield of MOF. In general, the experimental studies have shown that the yield of MOF increases at higher concentration of organic linkers and temperatures [9]. To further reveal the effect of higher concentration of organic linkers, we allow the concurrent crystallization of organic linkers during MOF synthesis. We also sweep the rate parameters of oligomerization and crystallization kinetics to quantify their effect on the yield of MOFs under different possible temperatures and operating conditions.
Figure 1 shows a possible mechanism of the synthesis of copper trimesate (HKUST-1) MOF. The SBU of HKUST-1 is made of benzene-1,3,5-tricarboxylic acid (BTC) and copper ions. HKUST-1 was considered as a model material in this study because of the availability of extensive experimental data for the synthesis of HKUST-1 [7,15,18]. It is commonly synthesized at elevated temperatures in ethanol/water solutions containing metal salts, such as copper nitrate, and organic linkers, such as BTC. Section 2 describes the models and assumptions used to study the formation of SBUs, with and without concurrent crystallization of organic linker, and evolution of SBUs into MOF-like structures. The section also includes the ranges of parameters evaluated. In Section 3, we present and discuss the effect of different sets of parameters on the yield of MOF in terms of average molecular weight over a period of time. Section 4 provides conclusions and insights obtained from the analysis as well as guidelines to improve the yield of MOFs.

Figure 1.
Schematic describing the mechanism and modeling approach for the synthesis of metal–organic frameworks (MOFs). In the case of copper trimesate (HKUST-1) MOF, the formation of secondary building units (SBUs) is modeled using kinetic rate equations and the resulting steady-state distribution is supplied as an initial condition to the aggregation-based population balance equations to obtain the distribution of MOFs.
2. Methods
A constant-volume batch crystallizer for the synthesis of MOFs is simulated by considering three simultaneous physical processes, namely oligomerization reaction for the synthesis of SBUs, concurrent crystallization of BTC, and aggregation of SBUs to produce MOFs. The solution inside the batch crystallizer initially consists of 1,3,5-benzene tricarboxylic acid (BTC), copper nitrate (Cu(NO3)2) and water. The solubilities of BTC (0.0084 mol L−1) and copper nitrate (7.2348 mol L−1) at 298.15 K are obtained from published experimental studies [19]. Since the solubility of copper nitrate is significantly higher than BTC, the concentration of BTC governs the yield of MOFs and the copper ions can be assumed as an excess reagent.
2.1. Formation of Secondary Building Units for MOF Production
The initial stage of MOF synthesis is the formation of SBUs and is studied with the following system of reactions [15].
where [unit: ] denotes the number of SBUs in the oligomer , and [units: ] is the reaction rate constant. This reaction scheme is similar to chain polymerization where the rate constant for the addition of new repeating unit is assumed to be independent of the number of repeating units in and hence the rate constant of each reaction is identical [20]. The continuity equations for constant volume reactor are given below.
The coupled ordinary differential equations are solved for unknowns as follows.
where [units: ] is the concentration of oligomer and [units: ] is the concentration of BTC. The system was solved for , as the concentrations of SBUs for n > 20 was negligible for the range of parameters studied. The solution of continuity equations provides the molar concentration of oligomers of SBU which are structurally similar and have different molecular weights. The number of repeating units is converted to the molecular weight [units: ] of oligomer which is obtained by summing the molecular weights of all BTC molecules and copper atoms in the oligomer. The concentration distribution is then converted into a density distribution [units: ] using a smoothened cumulative concentration distribution as follows:
Here, the molecular weight of the SBU oligomer is directly proportional to its size. The density distribution can be normalized using the total concentration of SBUs [units: ] such that
The average molecular weight of MOFs can be now obtained as
Equation (4) gives the size distribution of SBUs as a function of molecular weight of SBUs. Equation (5) normalizes the size distribution [units: ] and Equation (6) gives , the average molecular weight as a function of time. The average molecular weight of HKUST-1 MOFs can also be related to the size, as they have octahedron morphology.
2.2. Concurrent Crystallization of BTC
The organic linker-BTC can also crystallize to form a needle-like (parallelepiped) crystals when the solution is supersaturated [21]. This size and morphology evolution of BTC crystals can be modeled using population balances [22,23,24,25,26] and measured using experimental tools [27,28]. The morphology of BTC can be described using -vectors (see Supplementary Information) assuming a constant aspect ratio of 10 between [units: ] and [units: ]. The one-dimensional population balance equation for number density, written in terms of the longest length of needle-like morphology, is given as [29]
subject to the initial condition
and boundary condition corresponding to nucleation and growth of zero size nucleus.
The solution can be obtained using the method of characteristics.
where [units: ] is the number density, [units: ] is the growth rate, and [units: ] is the nucleation rate.
Equation (8) is evaluated only at supersaturated conditions. For undersaturated conditions, the BTC crystals dissolve and the dissolution rate is assumed to have the same functional dependence on undersaturation as of growth rate on supersaturation. The nucleation and growth rates kernels are provided in Table 1.

Table 1.
Processes affecting the kinetics of MOF synthesis, their constitutive equations, list of parameters involved, and the ranges of the parameters evaluated in this study.
2.3. Effect of Parameters
The change in the average molecular weight of SBU oligomers is studied with and without concurrent crystallization of BTC. The formation of SBU oligomers is influenced by the concentration of BTC, which in turn is affected by concurrent crystallization of BTC. The kinetics of these simultaneous processes are studied by varying the parameters given below in Table 1. The ranges of parameters were chosen to keep the values relevant to the corresponding experimental studies [15].
The vector and matrix are as shown in Equation (3). The BTC is depleted from solution due to concurrent crystallization and the formation of SBU oligomers. The BTC consumed due to oligomerization is calculated by rate equation as depicted in Equation (2). The BTC consumed due to crystallization is calculated as
where is the initial concentration of BTC, [units: ] is the density of BTC crystal, and [units: ] is the molecular weight of BTC, is the length of second h-vector at the time , and is the volume [units: ] of crystal at a time . The integral term in the RHS of Equation (10) becomes positive for an undersaturated solution until all of the BTC in the crystal is dissolved. For the sake of completeness, the modified rate equation considering the crystallization or dissolution of BTC as well as oligomerization reaction is given below.
Equation (3) was solved at each time-step with built-in ODE solver (ode45) of MATLAB software and Equation (8) was evaluated simultaneously. At the time , the system of equations described in Equation (3) was solved with an initial concentration of BTC in the system. The BTC concentration at following time-steps is guessed based on the BTC depleted due to reaction and crystallization at previous times and the new solution was allowed to converge until the relative error between the previous and new concentration of BTC achieved a threshold of .
2.4. Modeling of MOF Synthesis Using Aggregation-Based Population Balance Equation
Since the aggregation of SBUs is much slower than the synthesis step, a steady-state distribution of SBUs can be assumed before the initiation of aggregation that is captured using aggregation-based population balance model. The frequency of attachment is assumed to be constant and hence independent of size. A generalized model is provided in the Supporting Information that includes simultaneous oligomerization, crystallization, and aggregation with the most general form of rate kernels. The population balance equations are described below.
Subject to the initial condition,
where is the attachment frequency of particles of size at the time . Here, we assume . Normalizing with , and using dimensionless time , followed by taking Laplace transform of Equation (12), results in the non-linear ordinary differential equation.
Subject to the initial condition
where is the solution of the differential equation
with the initial condition,
The inverse Laplace transform of the solution of Equation (13) provides the time-dependent distribution of MOF-like structure obtained from the aggregation of the initial distribution of SBUs. Equation (13) is solved until the peak value of the average molecular weight is achieved. When the normalized size distributions of the SBUs has an exponential form, the inverse Laplace transform is given as,
where and are the fitting parameters of the initial exponential distribution of SBUs
3. Results and Discussion
Figure 2 shows the change in the average molecular weight of oligomers for different values of rate constants in the absence of BTC crystallization as the initial concentrations are below the saturation limit. The steady-state concentration of oligomers of SBUs at the moderate value of the rate constant of and at high initial saturation of is shown in Figure 2a. The steady-state distribution of SBU oligomers follows an exponential distribution, where the majority of oligomers are of size n < 10. Figure 2b–d show the transient evolution of the average molecular weight of SBU oligomers for the reaction rate constants of = , , , and , and the initial saturation ratios of 0.2, 0.5, and 1. The time required to reach the steady-state increases with decreasing the rate constants or decreasing temperature. The yield of oligomers of SBUs increases with increasing the saturation ratios of BTC. Since the metal–ligand is in excess, the yield of SBUs is primarily affected by the concentration of BTC.
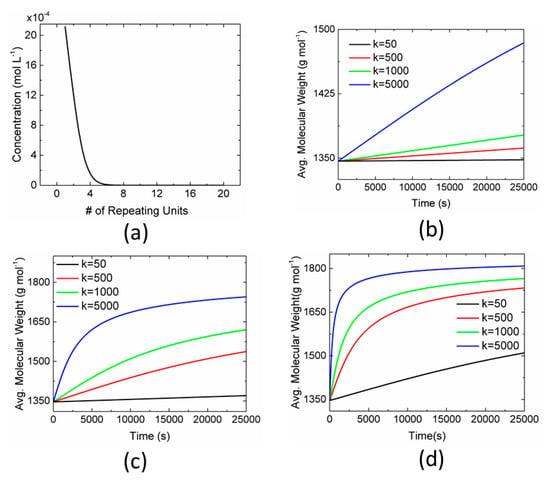
Figure 2.
Change in average molecular weight of SBU oligomers as a function of time for different values of oligomerization rate constants. (a) Steady-state distribution of oligomers of SBUs at and initial saturation ratio of 1. The transient evolution of average molecular weight for initial saturation ratios of (b) 0.2, (c) 0.5, and (d) 1.
Figure 3 shows the effect of reaction rate constants on the simultaneous synthesis of SBU oligomers and BTC crystals when initial saturation ratios are >1. The lower portions of Figure 3a (σ = 1.2) and Figure 3b (σ = 1.5) show that the concentration of BTC crystals increases initially due to nucleation and growth and then decreases due to dissolution, whereas the upper portions show a continuous increase in the average molecular weight of SBU oligomers. The supersaturation of BTC in solution decreases as BTCs are consumed via the reaction to produce SBU oligomers and crystallization to produce BTC crystals. The rate of BTC crystallization decreases with decreasing supersaturation and reaches a plateau when the saturation ratio is 1. The continuous reaction of BTC to produce SBU oligomers causes saturation ratio to decrease below 1, which create undersaturation for BTC crystals to dissolve. The rate of synthesis of SBU oligomers depends on the available concentration of BTC in the solution, which decreases with the increasing rate of crystallization. Increasing the initial supersaturation from 1.2 to 1.5 increases the BTC crystallization by almost an order of magnitude, which reduces the initial rates of synthesis of SBU oligomers while the total yield of oligomers increases. Moreover, the time required to produce SBUs increases with increasing the initial supersaturation. Therefore, the initial supersaturation can be controlled to optimize the rate of formation of SBU oligomers and thereby yield of MOFs. Furthermore, it can be noted that the kinetics of crystallization does not significantly affect the yield of SBU oligomers but only affect the available concentration of BTC at initial times. Hence, the effect of varying crystallization parameters is not shown here. Increasing the reaction rate constant increases the rate of depletion of supersaturation and hence decreases the rate of BTC crystallization. The time required to attain steady-state decreases with increasing the reaction rate constant. The reaction rate constants can be controlled by varying temperature to improve the rate of SBU oligomer synthesis.
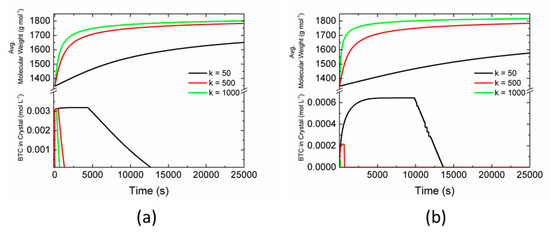
Figure 3.
Effect of concurrent crystallization of benzene-1,3,5-tricarboxylic acid (BTC) on the formation of SBU oligomers as a function of time for initial supersaturation ratios of (a) 1.2 and (b) 1.5. The lower portion in both figures shows the concentration of BTC in the crystal phase. The upper portion shows the average molecular weight of SBU oligomers.
Figure 4 shows the steady-state average molecular weight of SBU oligomers as a function of initial supersaturation and oligomerization rate constants. The yield of SBU oligomers increases linearly with increasing initial supersaturations, whereas it increases rapidly with increasing the reaction rate constant. The steady-state values of the average molecular weight of SBU oligomers with concurrent crystallization of BTC are significantly higher than in the case without concurrent crystallization depicted in Figure 2. Conversely, the concurrent crystallization of BTC delays the synthesis of SBUs and might pose an issue in the downstream separation of MOFs from BTC crystal suspension.
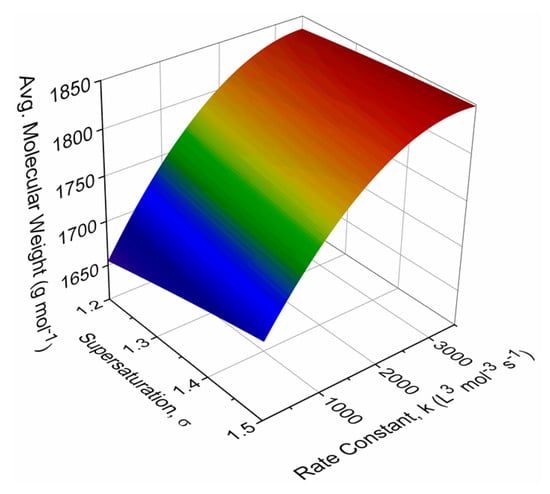
Figure 4.
Steady-state distribution of the average molecular weight of SBU oligomers as a function of initial supersaturation ratio and oligomerization rate constant.
Figure 5 shows the evolution of the average molecular weight of HKUST-1 MOF due to the aggregation of SBUs at a constant frequency. Figure 5a shows the distribution of molecular weights of MOFs at different dimensionless times. It can be seen that the SBUs of lower molecular weights is aggregating to produce MOFs of higher molecular weights as time increases. In this case, the aggregation frequency is assumed to be constant for attachment which results in the decaying exponential distribution with increasing dimensionless time. The size-dependent aggregation frequency will result in more realistic Gaussian-like distribution at higher times. Figure 5b shows the change in average molecular weight as a function of dimensionless time. The effect of aggregation kinetics on the average molecular weight can also be obtained from the dimensionless time in Figure 5b.
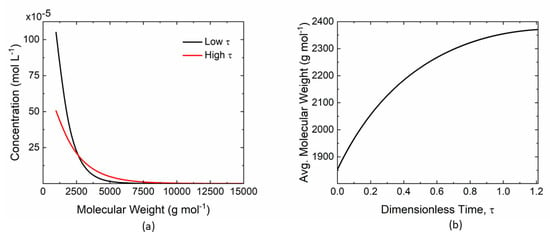
Figure 5.
Evolution of the molecular weight of HKUST-1 MOF due to the aggregation of SBU oligomers at a constant frequency of attachment. (a) Concentration distribution of the molecular weight of MOF at low and high dimensionless times. (b) Transient evolution of the average molecular weight of MOFs.
4. Conclusions
A comprehensive model is developed to simulate the synthesis of SBU oligomers and growth of MOFs while accounting for concurrent crystallization of organic linker. The model provides insights into the mechanism of MOF crystallization which involves the synthesis of SBU oligomers of lower molecular weights followed by their aggregation to produce MOFs of higher molecular weight. While the kinetics of oligomerization and aggregation have the highest impact on the rate of MOF synthesis, the initial supersaturation of organic linkers affected the yield of MOFs. The SBU oligomers are the precursors to MOF synthesis, which can be increased by using a higher initial concentration of BTC. When the initial concentration is higher than the saturation limit, the BTC crystallization can cause an initial lag in the growth of SBU oligomers delaying the steady-state. However, as the supersaturation depletes, the dissolution of BTC crystals can boost the overall yield of SBU oligomers and hence the yield of MOF. Since the solubility of metal–ligands is much higher than the organic linkers, the concentration of organic linkers often limits the yield of MOFs. The effect of higher rate constants is to reduce the time required to produce MOFs; however, the higher BTC concentration increases the concentration of SBUs available for the synthesis of MOFs. Sweeping the values of reaction rate constant also provides an insight into how temperature can affect the overall synthesis of MOFs. It can be inferred that temperature determines how fast the production of MOF occurs while the saturation ratio determines the yield of MOF. The aggregation kinetics even with the assumption of the constant frequency of attachment captures the physics of aggregation of SBUs to form MOF-like structures. A generalized comprehensive model is also developed that accounts for different oligomerization mechanisms, simultaneous oligomerization, and aggregation, and general rate kernels to facilitate mechanistic understanding of the synthesis of different MOFs.
The timescale of crystallization is much smaller than the production of MOF and hence experimental approaches can be designed to operate at a supersaturated concentration of organic linkers and increased residence time to obtain the highest possible yield of MOF, unlike traditional solvothermal approaches. At the same time, an increase in the temperature would reduce the time for the formation of SBUs leading to the faster synthesis of MOFs.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-9717/7/8/527/s1, Figure S1: Supersaturation depletion as a function of time for different rate constants and different initial saturation ratios in case of no concurrent crystallization. Figure S2: Supersaturation depletion as a function of time for different rate constants and different initial saturation ratios in case of concurrent crystallization. Figure S3: Needle-like morphology of BTC crystals with h-vectors. Section S3: General model considering simultaneous oligomerization, crystallization of linkers, and aggregation of oligomers.
Author Contributions
Investigation, software, and writing—original draft preparation, A.V.D. and R.Y.N.; conceptualization, methodology, and writing—review and editing, M.R.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sumida, K.; Rogow, D.L.; Mason, J.A.; McDonald, T.M.; Bloch, E.D.; Herm, Z.R.; Bae, T.-H.; Long, J.R. Carbon Dioxide Capture in Metal–Organic Frameworks. Chem. Rev. 2012, 112, 724–781. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Sculley, J.; Zhou, H. Metal–Organic Frameworks for Separations. Chem. Rev. 2012, 112, 869–932. [Google Scholar] [CrossRef] [PubMed]
- Mason, J.A.; Veenstra, M.; Long, J.R. Evaluating metal–organic frameworks for natural gas storage. Chem. Sci. 2014, 5, 32–51. [Google Scholar] [CrossRef]
- Yaghi, O.M. Crystalline Metal-Organic Microporous Materials. U.S. Patent No. 5,648,508, 15 July 1997. [Google Scholar]
- Rubio-Martinez, M.; Avci-Camur, C.; Thornton, A.W.; Imaz, I.; Maspoch, D.; Hill, M.R. New synthetic routes towards MOF production at scale. Chem. Soc. Rev. 2017, 46, 3453–3480. [Google Scholar] [CrossRef] [PubMed]
- Kalmutzki, M.J.; Hanikel, N.; Yaghi, O.M. Secondary building units as the turning point in the development of the reticular chemistry of MOFs. Sci. Adv. 2018, 4, eaat9180. [Google Scholar] [CrossRef]
- Shoaee, M.; Anderson, M.W.; Attfield, M.P. Crystal Growth of the Nanoporous Metal-Organic Framework HKUST-1 Revealed by In Situ Atomic Force Microscopy. Angew. Chem. Int. Ed. 2008, 47, 8525–8528. [Google Scholar] [CrossRef]
- Laybourn, A.; López-Fernández, A.M.; Thomas-Hillman, I.; Katrib, J.; Lewis, W.; Dodds, C.; Harvey, A.P.; Kingman, S.W. Combining continuous flow oscillatory baffled reactors and microwave heating: Process intensification and accelerated synthesis of metal-organic frameworks. Chem. Eng. J. 2019, 356, 170–177. [Google Scholar] [CrossRef]
- Shekhah, O.; Wang, H.; Zacher, D.; Fischer, R.A.; Wöll, C. Growth Mechanism of Metal-Organic Frameworks: Insights into the Nucleation by Employing a Step-by-Step Route. Angew. Chemie Int. Ed. 2009, 48, 5038–5041. [Google Scholar] [CrossRef]
- Millange, F.; El Osta, R.; Medina, M.E.; Walton, R.I. A time-resolved diffraction study of a window of stability in the synthesis of a copper carboxylate metal–organic framework. CrystEngComm 2011, 13, 103–108. [Google Scholar] [CrossRef]
- Colón, Y.J.; Snurr, R.Q. High-throughput computational screening of metal–organic frameworks. Chem. Soc. Rev. 2014, 43, 5735–5749. [Google Scholar] [CrossRef]
- Bernales, V.; Ortuño, M.A.; Truhlar, D.G.; Cramer, C.J.; Gagliardi, L. Computational Design of Functionalized Metal–Organic Framework Nodes for Catalysis. ACS Cent. Sci. 2018, 4, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Haldoupis, E.; Nair, S.; Sholl, D.S. Finding MOFs for Highly Selective CO2/N2 Adsorption Using Materials Screening Based on Efficient Assignment of Atomic Point Charges. J. Am. Chem. Soc. 2012, 134, 4313–4323. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Xie, L.-H.H.; Li, J.-R.R.; Ma, Y.; Seminario, J.M.; Balbuena, P.B. CO2 Capture and Separations Using MOFs: Computational and Experimental Studies. Chem. Rev. 2017, 117, 9674–9754. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, P.; Kapteijn, F.; van der Veen, M.A.; Domke, K.F. Understanding the Inhibiting Effect of BTC on CuBTC Growth through Experiment and Modeling. Cryst. Growth Des. 2017, 17, 5603–5607. [Google Scholar] [CrossRef]
- Ray, W.H.; Laurence, R.L. Polymerization reaction engineering. In Chemical Reactor Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1977; pp. 532–582. [Google Scholar]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Van Assche, T.R.C.; Desmet, G.; Ameloot, R.; De Vos, D.E.; Terryn, H.; Denayer, J.F.M. Electrochemical synthesis of thin HKUST-1 layers on copper mesh. Microporous Mesoporous Mater. 2012, 158, 209–213. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E.; Abo Balal, N. The solubilities of benzene polycarboxylic acids in water. J. Chem. Thermodyn. 2006, 38, 565–571. [Google Scholar] [CrossRef]
- Huggins, M.L. Principles of Polymer Chemistry. J. Am. Chem. Soc. 1954, 76, 2854. [Google Scholar] [CrossRef]
- Varga, J.; Stoll, K.; Menyhárd, A.; Horváth, Z. Crystallization of isotactic polypropylene in the presence of a β-nucleating agent based on a trisamide of trimesic acid. J. Appl. Polym. Sci. 2011, 121, 1469–1480. [Google Scholar] [CrossRef]
- Singh, M.R.; Nere, N.; Tung, H.-H.; Mukherjee, S.; Bordawekar, S.; Ramkrishna, D. Measurement of Polar Plots of Crystal Dissolution Rates Using Hot-Stage Microscopy. Some Further Insights into Dissolution Morphologies. Cryst. Growth Des. 2014, 14, 5647–5661. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Singh, M.R. Population Balance Modeling: Current Status and Future Prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.R.; Ramkrishna, D. A Comprehensive Approach to Predicting Crystal Morphology Distributions with Population Balances. Cryst. Growth Des. 2013, 13, 1397–1411. [Google Scholar] [CrossRef]
- Singh, M.R.; Ramkrishna, D. Dispersions in crystal nucleation and growth rates: Implications of fluctuation in supersaturation. Chem. Eng. Sci. 2014, 107, 102–113. [Google Scholar] [CrossRef]
- Singh, M.R.; Verma, P.; Tung, H.-H.; Bordawekar, S.; Ramkrishna, D. Screening Crystal Morphologies from Crystal Structure. Cryst. Growth Des. 2013, 13, 1390–1396. [Google Scholar] [CrossRef]
- Singh, M.R.; Chakraborty, J.; Nere, N.; Tung, H.-H.; Bordawekar, S.; Ramkrishna, D. Image-Analysis-Based Method for 3D Crystal Morphology Measurement and Polymorph Identification Using Confocal Microscopy. Cryst. Growth Des. 2012, 12, 3735–3748. [Google Scholar] [CrossRef]
- Coliaie, P.; Kelkar, M.S.; Nere, N.K.; Singh, M.R. Continuous-flow, well-mixed, microfluidic crystallization device for screening of polymorphs, morphology, and crystallization kinetics at controlled supersaturation. Lab Chip 2019, 19, 2373–2382. [Google Scholar] [CrossRef] [PubMed]
- Ramkrishna, D. Population Balances. Chem. Eng. 2000, 1, 355. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).