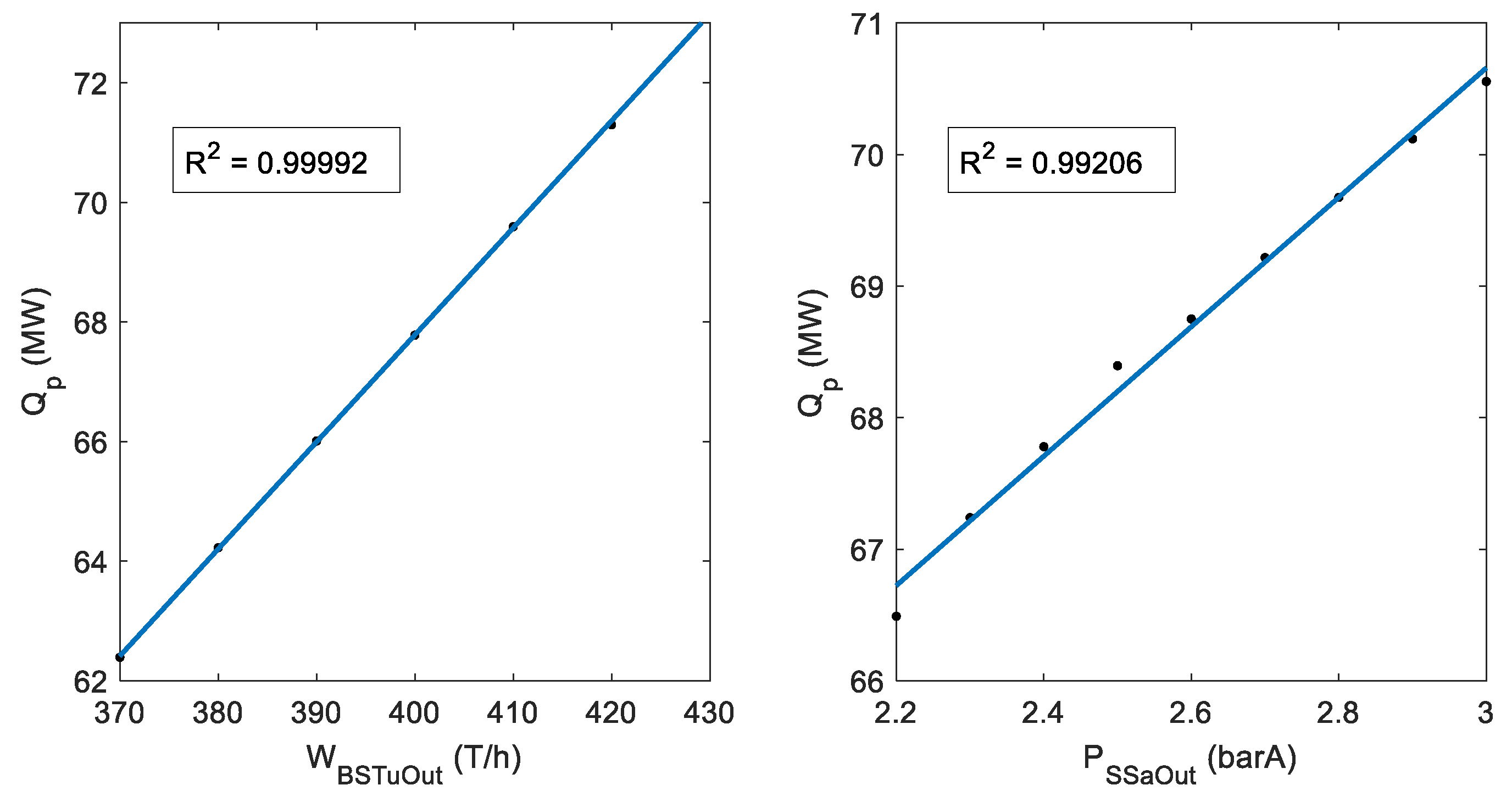Modeling On-Site Combined Heat and Power Systems Coupled to Main Process Operation

Abstract

Many production processes work with on-site Combined Heat and Power (CHP) systems to reduce their operational cost and improve their incomes by selling electricity to the external grid. Optimal management of these plants is key in order to take full advantage of the possibilities offered by the different electricity purchase or selling options. Traditionally, this problem is not considered for small cogeneration systems whose electricity generation cannot be decided independently from the main process production rate. In this work, a non-linear gray-box model is proposed in order to deal with this dynamic optimization problem in a simulated sugar factory. The validation shows that with only 52 equations, the whole system behavior is represented correctly and, due to its structure and small size, it can be adapted to any other production process working along a CHP with the same plant configuration.

1. Introduction

In a world facing continuous challenges from an economic and environmental point of view, a lot of industrial processes rely on on-site Combined Heat and Power (CHP) systems to increase their global energy efficiency. The main feature of CHP is the possibility of obtaining heat and electricity simultaneously, from a single power source. This has many advantages, such as an increased reliability, fewer energy generation related costs, a reduction in the amount of emissions and, of course, an improvement in the energy efficiency of the process. More information about CHP systems and their operation can be found in [1].

When it comes to the management of industrial CHP plants, the idea is to exploit them in such a way that the operational costs related to heat and power generation are reduced to a minimum. This is a difficult problem due to the number of things that must be considered at the same time. Among others, the electricity purchase and selling options, the legislation related to cogeneration systems, and the uncertainty inherent to industrial processes, make essential the use of advanced decision-making tools, to help industry managers and operators to manage this kind of systems in the best possible way.

From the literature, it is clear that the traditional way to deal with this problem is to apply a sequential approach, where the main process operation is decided first, then the energy needs are estimated, and finally the CHP plant management is optimized. Thus, the main process and cogeneration are treated independently. This problem is known as the short-term operation planning on CHP systems. Some examples are [2,3,4,5,6]. For these problems, decisions can be taken at two different levels:

• At the plant level, decisions are related to the quantity of electricity that must be bought from the external grid, or generated on site in order to sell a surplus if possible. Here, different contracts (Base load, Tarif of Use (TOU)), and electricity markets (Day-ahead market, intra-day market) are usually considered, and the price of the electricity takes on a special relevance.
• At the equipment level, once the quantity of electricity to be generated has been decided, the next step is to decide what equipment is going to be used; this is known as the Unit-Commitment (UC) problem. Then, the load generation of each of the selected pieces of equipment is decided. This is the Economic Dispatch (ED) problem.

In [7], the main research lines related to the short-term operation planning problem are set out. One of the most important branches focuses on the formulation of the model used to later carry out the optimization. This is a critical step in obtaining a good solution with the least computational effort possible. This way, although CHP plants are typically non-linear, they are usually linearized due to the computational advantages involved, being Mixed Integer Linear Programming (MILP) models the approach traditionally selected to solve this problem [5,8,9]. However, works such as [4] and [3] claim that sometimes this kind of model leads the optimization to suboptimal or infeasible solutions, and non-linearities should be considered, turning the problem into Mixed Integer Non-Linear Programing (MINLP).

If the main process and the CHP plant are part of the same company, instead of following the sequential approach, an integrated one could be taken, where the operational planning of the CHP is obtained along with the best process operation strategy. Here, the main idea is to simultaneously adapt the way energy is produced and how production is carried out, according to such external factors as the electricity prices. This approach is taken in [10], leading to a bigger optimization model than if a sequential approach were considered, but obtaining better optimization results.

Although this approach is not so well studied as the sequential one, it is very close to the one proposed for solving the industrial Demand-Side Management problem (iDSM) [11]. There, industrial processes try to adapt the load profile, and therefore the production, according to some financial incentives given by the grid operator, in order to maintain grid stability if emergencies occur. These incentives can be in many forms, one of them being in the electricity prices, encouraging facilities to adapt their production schedule to them. Therefore, in this problem, the decisions taken, as in the integrated approach, affect the production strategy and energy management.

In spite of the fact that, in iDSM problems, only the way electricity is consumed and bought is usually considered, some studies have also explored the possibility of selling electricity to the external grid. This is the case in [12], where the authors developed an MILP model to optimize the production scheduling of an energy-intensive part of the steel production process with energy awareness. Thus, the optimization problem was able to decide whether it was convenient to buy electricity, or generate it in an on-site plant in order to reduce electricity demand at peak time, or even sell it to the external grid. However, the nature of the on-site generation plant was not given, and in this case the load-commitment curve with the grid operator had previously been fixed. In [13], the authors went one step further, developing a stochastic mixed-integer linear programming model capable of obtaining at the same time, the scheduling of a continuous energy-intensive process and its load-commitment curve, considering two different sources of uncertainty.

As can be seen in the literature regarding the kind of models used, in both the sequential and integrated approach, the mixed-integer formulation of the problems come from the possibility of deciding between different equipment, either in the main process or in the CHP plant. On the other hand, the assumptions made concerning the equipment make the problem linear or non-linear, and with respect to dynamics, they are usually neglected. This is due to the fact that changes in the operation are usually caused by changes in the electricity prices, and the latter typically have a much slower dynamic.

Regarding the case studies considered, in the sequential approach bibliography, the CHP plants present different configurations, where energy can be obtained using different equipment and heat can sometimes be stored. However, they do not cover all the possible cases. There are many small or medium sized industries that work with simple CHP units, made up of a small number of boilers and turbines designed to fill the main process energy demands. In these cases, if the sequential approach is used to optimize the CHP management, it is found that neither the equipment nor the plant level decisions can be modified. This is due to the fact that, typically, all the equipment (boilers and turbines) that forms the cogeneration unit is the same, and is being used at the same capacity level, without any spare, so the choice of equipment is not necessary. On the other hand, since these CHP systems are designed to fill the heat demand of the main process they are attached to, and with the heat generated, produce the electricity needed by the main process with a small surplus, buying electricity from the external grid usually makes no sense. Furthermore, the fact that, typically, the excess of power generated is not very big, and that it can vary sharply depending on the main process operation, means that the possibility of selling electricity to the external grid is seldom considered.

Now, if the integrated approach is considered for these cases, two different scenarios may appear, depending on how the main process energy demand can be modified. If it can be adapted without changing the production rate, then a close problem to the one presented by [10] or by the iDSM community could be proposed. Thus, the production would be adapted to generate a bigger electricity surplus when electricity prices are more convenient. However, if this is not the case, the only way to change the energy demanded is by changing the production rate. If this way of working is considered, the fact that it is still an open issue in the literature must be taken into account. Here, the dynamic of the CHP plant is determined by the dynamic of the main process, so it could be said that the generation of electricity is coupled to the production rate. If the main process dynamic is close to that of the electricity prices, the problem can no longer be static, and dynamics will have to be considered explicitly in the optimization model.

This work focuses on this last scenario, where the production rate is adapted in order to operate the whole system (main process and CHP plant) in the best possible way, from an economic point of view. Considering the importance of the dynamics of the main process, and the absence of scheduling decisions, dynamic optimization will be the approach selected to solve this problem. With this technique, a dynamic model of the system is used to find the best control action sequence over time. Typically, depending on how the dynamic model is used during the optimization, two methods can be found to solve these problems: sequential or simultaneous approach. In the sequential approach, the control variables are discretized over time, and an external simulation of the model is used to evaluate the performance of the solution given by the optimizer each iteration. This way of working brings some advantages, like a good accuracy when solving the model. However, there are also some disadvantages, like difficulties when calculating the gradients needed for gradient based optimization solvers, or a high time spent for evaluating each solution in the simulator if the model is too complex. These facts often make the use of this approach infeasible. In the simultaneous method, the whole model is discretized and incorporated to optimization problem as a set of constraints. With this method, the optimization problem increases its size, but if the discretization is done in an appropriate way, it is usually solved faster than the sequential approach. Furthermore, convergence problems in the simulation are avoided as no simulator is being used, and path constraints can be more easily added to the optimization problem [14].

Since it has been explained, models in dynamic optimization are a key part of the problem. Concerning the modeling of energy generation systems, many references can be found. A good review on the modeling of energy generation can be found in [15]. On the other hand, many tools, designed for modeling and simulating different energy simulation systems are available in the market; in [16], an extensive review of the available tools can be found. Some of the developed models found in the literature are built based on model libraries offered by third parties, such is the case for Modelica [17], EcosimPro [18] or Aspenplus [19]. In addition, detailed models for the individual components constituting CHP plants such as boilers [20,21,22] or steam turbines [23] can be found.

The models presented so far are in general complex models comprised by many equations which represent the behavior of the system with great accuracy. The objective of these models is usually to test different operating policies in simulation, training or control design, but in general are not useful for optimization. This is because its complexity makes it hard to find the solution of the optimization problem. Therefore, simpler models are usually searched for optimization, trying at the same time, to represent the main behavior of the system in the best possible way. In this work, a dynamic gray-box model is proposed for one of the most commonly used CHP configurations in industry, able to be adapted to any main process that uses it. In order to be as accurate as possible, the model will be non-linear where the complexity of the process is too high. However, in order to make it computationally tractable, it will have linear equations based on experimental data where linearity is demonstrated. As a case study, a simulated sugar plant is used as the real plant to obtain experimental data and validate the model proposed. It is based on the experience of the working team in the sugar factory process and previous works in sugar factory simulators [18,24,25], and has been thoroughly validated [26].

The rest of this paper is organized as follows. In the next section, a brief description of the sugar factory problem is given. The third section presents obtaining the gray-box model for the case study considered. The fourth section examines the validity of the model and a discussion about the results. The fifth section explains how to extend the model for other case studies. Lastly, the paper finishes with some conclusions, limitations and future work with the model developed.

2. Case Study

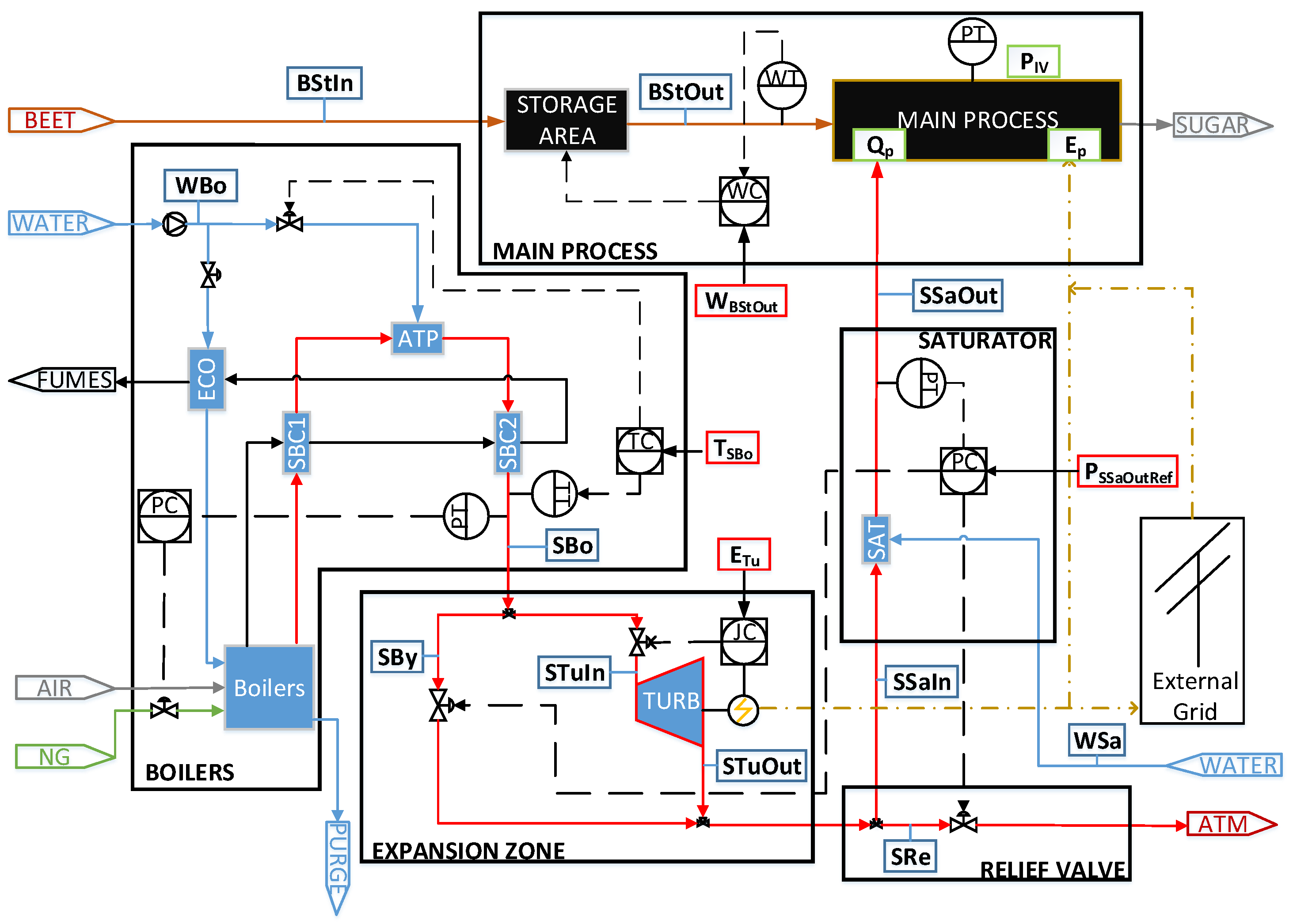
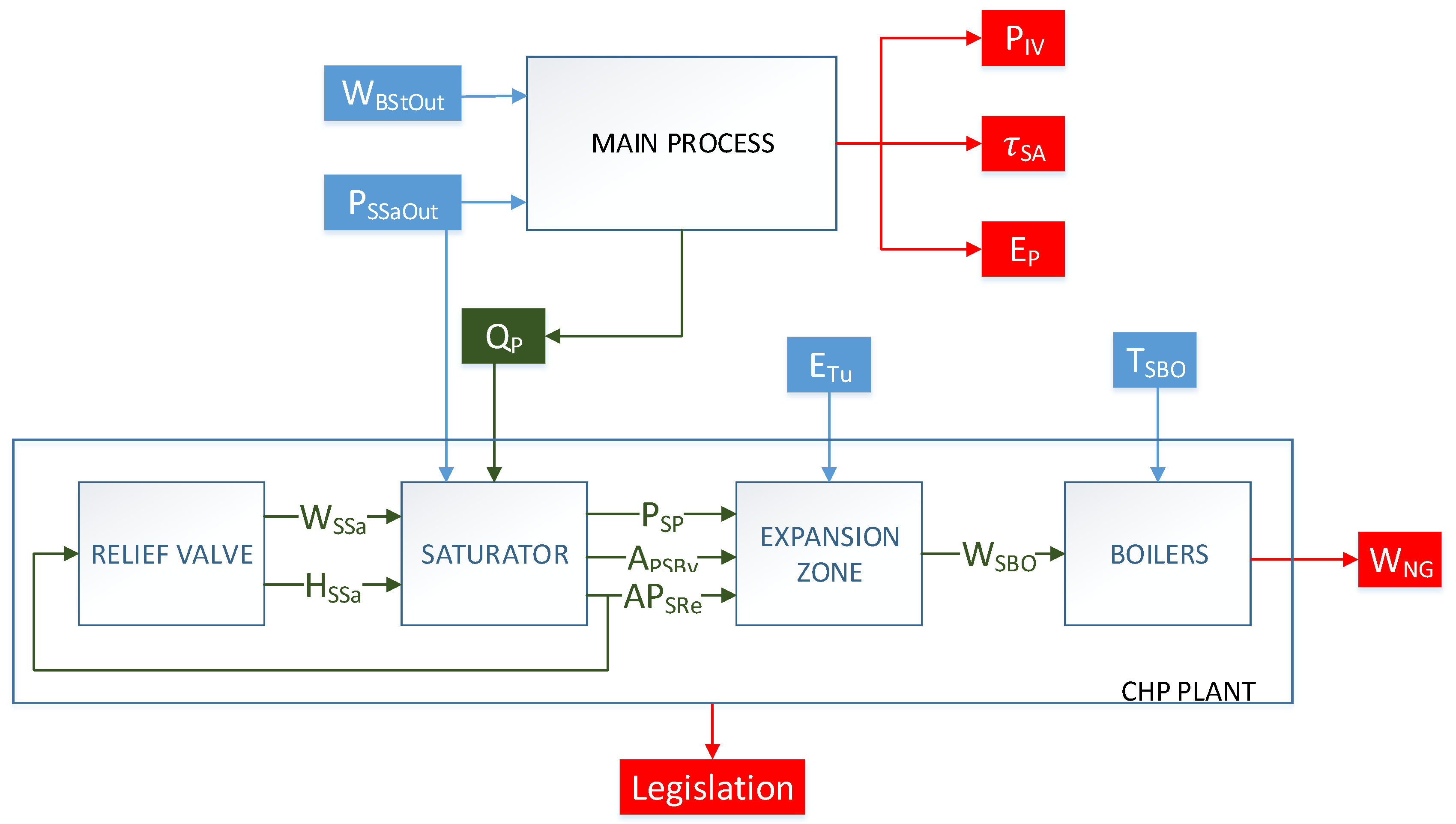
A sugar factory with a CHP configuration like the one shown in Figure 1, is to be operated according to the Day-Ahead electricity market, so as to improve its competitiveness in the sugar market. Currently, due to the complexity of the electricity market considered and the small surplus of power generated in turbines, no electricity is being sold and the plant is operating isolated from the external grid. To benefit from some advantages set by European legislation [27,28], rewarding efficient cogeneration processes, some energy indexes must be considered during CHP operation.

In the factory considered, there are three steam boilers working in parallel to produce the amount of heat needed by the main process. These boilers burn natural gas to obtain heat from boiling water. As a result, superheated high pressure (HP) steam is obtained in this process. In the boilers, there is a control system that allows operators to select the desired steam pressure and temperature. The steam needed by the process must have low pressure (LP) and be saturated, so the expansion of the obtained steam must be carried out. To do so, there are two different possibilities: passing it through three similar steam turbines, or through a bypass. During normal process operation, almost all the steam is passed through the steam turbines to obtain the electricity needed by the main process, which is able to obtain a maximum of 11 MW. However, the process usually needs less electricity than that which can be generated with the steam required, so an electricity surplus can be sold to the external grid. If the possibility of selling electricity is not considered, steam is recirculated through the bypass valve, where its expansion takes place using the valve pressure drop. Once the LP steam leaves the expansion zone, it must be saturated. For that purpose, a saturator, where water absorbs steam energy, is used, and the saturated LP steam is sent to the process.

Regarding the sugar process, it is a continuous process that uses sugar beet to obtain white sugar using the heat and power provided by the CHP system. Before being processed, beet is stored in big piles outside the factory. The storage time is crucial, as the quality of the sugar decreases because of rotting. Inside the factory, sucrose is extracted from the sugar beet, obtaining a juice that has to be purified and then concentrated in an evaporation section. Finally, sucrose is crystallized obtaining sugar crystals. Each of these processes needs heat and power to operate; however, one of the main features of the sugar industry is its energy integration. Evaporation needs LP steam obtained directly from the CHP system to remove water from the sugar solution. This stage is carried out concurrently by different evaporation effects, six in the case study considered. In this process, vapor is obtained as a byproduct, and it is used by the rest of the consumers of the plant to obtain the heat they need. To ensure its availability, the pressure inside the evaporators must be monitored and maintained between bounds.

The pressure of the steam that leaves the cogeneration is one of the most important variables of the CHP system, and it must be maintained between limits. If the pressure were higher than expected it could caramelize the sugar in the evaporation stage, and if it were lower, evaporation could not take place, compromising the rest of the process. To control the LP steam pressure, a split range controller is used. The manipulated variables are the openings of the bypass valve and the relief valve located between the expansion zone and the saturator. Thus, if the pressure is too low, the bypass valve will open and let live steam mix with the steam expanded in the turbines; and if it is too high, the relief valve will let it escape to the atmosphere. More information about the sugar industry can be found in [29] or [30].

Following the discussion set out in the first section, in this case study, the management optimization of the CHP system cannot be treated independently from the main process operation. Therefore, an integrated approach must be considered. If the modeling literature is reviewed, some approaches have been found that deal with sugar plants working with CHP systems [31,32,33]. However, the purpose is to study different aspects of process operation, without solving an optimization problem. Furthermore, they are focused on sugar cane factories, where bagasse, the residue of juice extraction from sugar cane, is used as fuel in the boilers, changing considerably the energy problem. In our case, since no process scheduling can be done to modify the energy consumption of the factory, the production rate must be changed to optimize the whole system operation. Due to the inherent complexity to the explained process, the setting time when changes are made in the production rate is around three hours. This contrasts with the quick response of the CHP plant, where changes in the electricity generation, can be done in less than 10 min. Since the Day-Ahead electricity market is considered, and prices there change hourly, in this case the dynamics of the main process must be considered explicitly.

In the next section, the process to obtain the dynamic model, and how it can be extended to other processes with the same CHP configuration, is shown.

3. Obtaining the Model

The first step to obtaining a model, is to make clear its objectives. In our case, a dynamic model is sought to optimize the sugar production process and CHP management according to electricity prices. To do so, an index that evaluates the cost of the energy needed to process a determined amount of beet, will be optimized.

$$Cost\left(t\right)={\int }_0^{T_N}{\displaystyle \frac{{\displaystyle \frac{W_G\left(t\right)}{{\rho }_G}}·HC{V}_G·P{r}_G-{\displaystyle \frac{(E_{Tu}\left(t\right)-E_P\left(t\right))·P{r}_E}{3600}}}{W_{BStOut}\left(t\right)}}\delta t$$

(1)

In (1), the numerator presents the difference between the cost of natural gas used in boilers and the incomes obtained by selling electricity to the external grid. In the denominator, the beet process rate is found. The function can be interpreted as the integral of the specific energy cost of the process. A full description of the model variables and parameters can be found in Appendix A.

Next, the inputs and outputs of the model can be set. Regarding the inputs, since the aim is to adjust the production rate to electricity generation, both must be considered. On the other hand, manipulating the thermodynamic conditions of the steam generated in the boilers can greatly modify the steam consumption of the whole system and, therefore, its manipulation will be indispensable to achieve the objectives marked by the European legislation mentioned in the previous section. To do so, the temperature of the superheated steam obtained in the boilers and the pressure of the saturated steam delivered to evaporation are the two most influential variables. With that in mind, a list of the model inputs and its working range, is shown below:

• Beet production rate ($W_{BStOut}$) [370–430 T/h].
• Electricity power generation ($E_{Tu}$) [5000–11,000 kW].
• Evaporation working pressure ($P_{SSaOut}$) [2.2–3.0 barA].
• Superheated steam temperature obtained in boilers ($T_{SBo}$) [360– 420 ${}^{\circ }\mathrm{C}$].

Regarding the outputs of the model, the natural gas used in the boilers and the electricity power consumption of the process are essential for computing an operation policy. On the other hand, according to the description of the process, the beet accumulation, the pressure inside the evaporators and the legislation indexes will be needed to assure its feasibility.

With respect to beet accumulation, this can be measured in two different ways. One is measuring the remaining beet in the storage zone, and the other is computing the average residence time the beet spends inside the storage zone. The last is defined as the accumulated beet over the beet production rate, and if this is too high, the beet can rot. On the other hand, it shows how long the process can be operated at a specified production rate without running out of beet, if the beet input drops to zero. Since the residence time gives more information about the beet storage, and it is easier to constrain, this is used in the optimization problem and will therefore be an output of the model.

Concerning the pressure inside the evaporators, as mentioned in the previous section, in the evaporation stage, the pressures are variables that must be monitored continuously during the sugar process operation. Since the crystallization section demands a great part of the steam generated, it is considered the most important steam consumer. Given that the quality of the sugar obtained depends greatly on this last stage, sufficient steam for its operation must be guaranteed. The evaporation effect that feeds the crystallization section with steam may vary for different factories. In the one considered, crystallization is fed by the fourth evaporation effect, so in order to ensure that there will be enough steam to operate that section, the steam pressure of this stage must be maintained above a specified minimum. Having controlled the pressure of the steam that goes into the evaporation and monitored and maintained the pressure of the fourth effect between bounds, it is enough to ensure that the evaporation is running smoothly, so the pressure from other evaporators is not needed.

In relation to the calculation of the European legislation indexes, they have to be measured once per year. However, to introduce them into the optimization problem, they are computed for each instant. Thus, if they are always above the limits, it will be considered that they are respected.

On the other hand, since one of the objectives of any CHP system is to generate the amount of heat energy demanded by the main process, the heat energy consumed by the sugar factory will also be considered as an output of the model.

To sum up, a list of the desired output variables is shown below:

• Electricity consumption of the sugar factory ($E_p$).
• Natural gas mass flow needed to operate the whole process ($W_G$).
• Average time beet spends in the storage zone (${\tau }_{St}$).
• Steam pressure inside the fourth effect of the evaporation ($P_{IV}$).
• European legislation Indexes.
• Heat energy consumption of the sugar factory ($Q_p$).

Once the input and outputs of the model have been specified, the relationships between them are sought. As direct relations are sometimes very difficult or even impossible to find, the whole process is divided into different control volumes in order to make the modeling process easier. The division taken is shown in Figure 1, where the control volumes are emphasized with black lines. They have been selected from knowledge of the process behavior. However, this is not the only possibility, and other control volumes could have been chosen. With the division made, the equations and experimental relationships that represent the behavior of each control volume must be found.

System identification is the technique that has been selected to obtain the experimental relationships [34,35]. This is due to the fact that it is quite a common technique in the process industry and makes the extension to other case studies easier. Thus, since it is explained in Section 5, for other plants with cogeneration systems, if the structure of the CHP is the same, simply identifying the relation between some variables, and using its own parameters, the model proposed can easily be extended. Otherwise, for cases where the structure of the CHP is different and the model developed cannot be used directly, the work described in this paper will serve as a guide for building models for other CHP configurations.

In order to make the optimization model simpler, the possibility of using linear identification is studied first and applied for each case if possible. Among the different types of models available for linear identification, state-space is selected. This is because relationships in this form are written as a system of first-order differential equations depending on time, and this is very convenient for incorporating them later in any simulation or optimization environment. Furthermore, they can deal with Multiple-Input Multiple-Output (MIMO) systems and delays can easily be incorporated, which in our case will be very useful.

3.1. Main Process

The beet sugar plant is understood as a black box system, where beet is transformed into white sugar using a determined amount of heat and electricity power. From this control volume, heat and power energy consumption, pressure inside the fourth evaporation effect, and available beet in the storage zone are sought.

3.2. Heat Consumption

Although the main process heat consumption depends on many variables, it has been assumed that the most influential ones are the specified production rate ($W_{BStOut}$), and the evaporation working pressure ($P_{SSaOut}$) due to modifications in the performance of the evaporators [36]. To avoid modeling the whole process, a direct relationship between the heat consumption of the main process and the pressure and production described above, is searched.

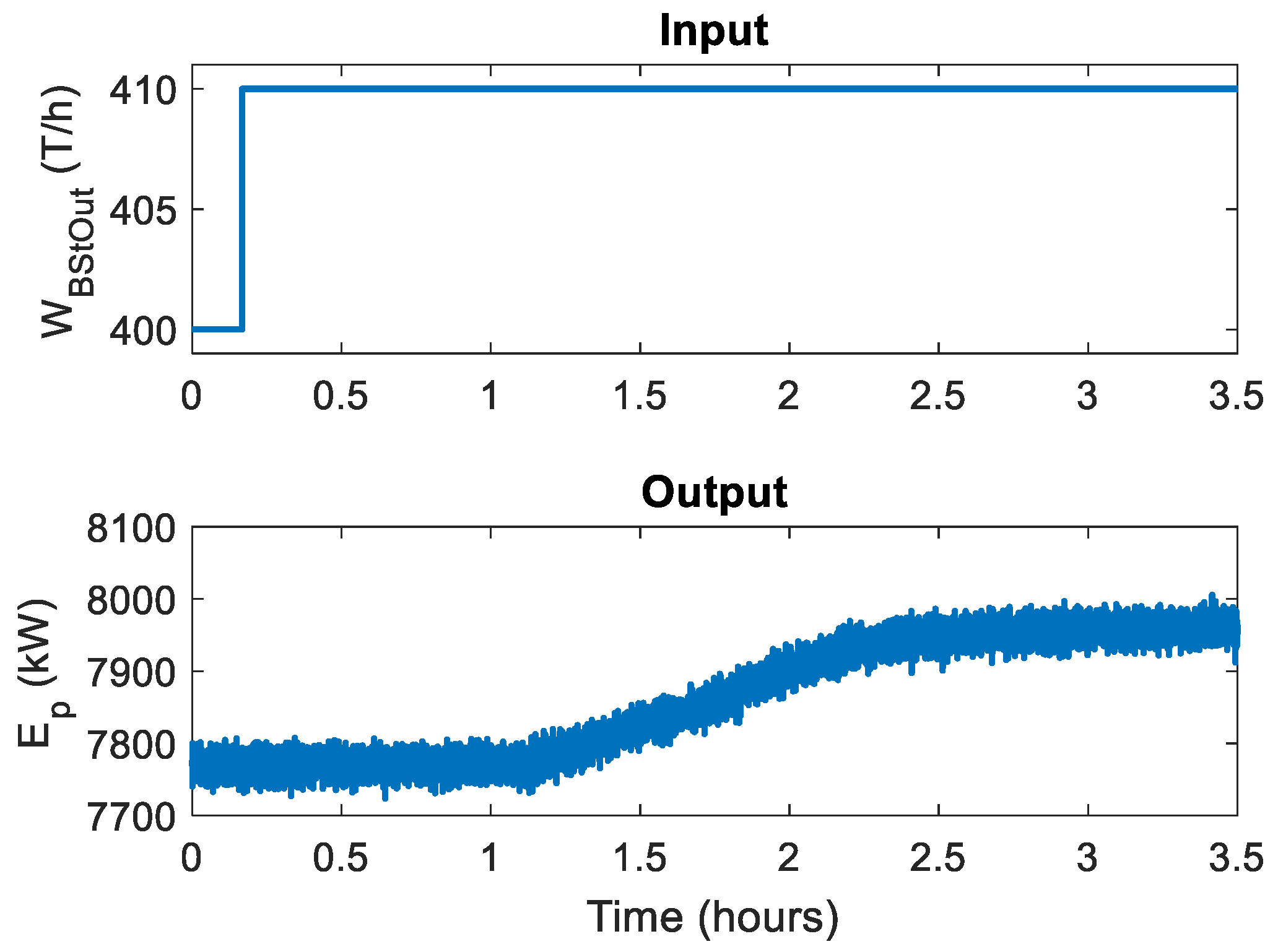
To do so, the step response for both inputs, shown in Figure 2, must first be analyzed. A second order dynamic response, with a delay of almost one hour and a settling time of three hours, can be discerned for $W_{BStOut}$. Regarding $P_{SSaOut}$, things are more complicated to deduct, due to the step response during the first instants of the transitory period. This behavior is due to the aggressive tuning of the split range pressure controller, which tries to take the pressure to the new set point in the less possible time. This is done in order to send steam to the system as quickly as possible if required. A settling time of one hour can be observed, and there is no delay in the response. If the first part of the transient is ignored, the step response behavior is close to a typical linear first order system, with no delay and a settling time of one hour.

Once the dynamic response for both inputs has been studied, steady state linearity between inputs and outputs is considered. With this in mind, some experiments are carried out trying different scenarios for both variables throughout its working range, and measuring the heat demand for each case in the stationary state. The experiments have been carried out independently for each input variable, maintaining the other one constant. Therefore, it is assumed that the superposition principle is valid for all the operational range of the variables, and this will be checked in the validation section. This has been done for any identification model where more than one input is involved. The results of these experiments are shown in Figure 3.

As can be seen, for the range of operation considered, the relationship of pressure and production with heat consumption can be assumed to be linear in the steady state. For the optimization problem considered, capturing the steady state is essential, but transients are also important if they expand in time. In the case of the heat energy consumption with respect to the evaporation working pressure, the transient overshoot is damped relatively quickly, so the model proposed for its identification should not be focused on this short response.

Therefore, a second order state-space model is proposed for identification in order to capture the stationary and essential response of the transient. To obtain it, the MATLAB^® system identification toolbox [37] is used, and the model obtained is shown in Equation (2). The validity of this model is shown in the next section along with the rest of the model.

$$\begin{array}{c}{Q}_p\left(t\right)=Q_{p_{eq}}+\Delta Q_p\left(t\right)\hfill \\ \Delta Q_p\left(t\right)=172.400·Q_{p_{x1}}\left(t\right)+1.744·Q_{p_{x2}}\left(t\right)+5.629\times {10}^{-5}·Q_{p_{x3}}(t-3312)+1.744·Q_{p_{x4}}(t-3312)\hfill \\ {\dot{Q}}_{p_{x1}}\left(t\right)=-1.077·Q_{p_{x1}}\left(t\right)-8.815\times {10}^{-2}·Q_{p_{x2}}\left(t\right)+256·(P_{SSaOut}\left(t\right)-P_{SSaOu{t}_{eq}})\hfill \\ {\dot{Q}}_{p_{x2}}\left(t\right)=6.25\times {10}^{-2}·Q_{p_{x1}}\left(t\right)\hfill \\ {\dot{Q}}_{p_{x3}}\left(t\right)=-5.521\times {10}^{-4}·Q_{p_{x3}}\left(t\right)-3.252\times {10}^{-4}·Q_{p_{x4}}\left(t\right)+0.250·(W_{BStOut}\left(t\right)-W_{BStOu{t}_{eq}})\hfill \\ {\dot{Q}}_{p_{x4}}\left(t\right)=4.883\times {10}^{-4}·Q_{p_{x3}}\left(t\right)\hfill \end{array}$$

(2)

3.3. Electricity Power Consumption

According to [36,38], it has been assumed that for the operational range considered, among all the process variables, electricity power consumption depends mainly on the beet processing rate in a linear way. The step response of $E_p$ with respect to $W_{BStOut}$ is shown in Figure 4.

From Figure 4, a second order dynamic response can be inferred. Again, a delay of almost one hour appears between the input and the output, and a settling time of approximately three hours can be discerned. A state-space second order dynamic system is obtained and shown in Equation (3).

$$\begin{array}{c}{E}_p\left(t\right)=E_{p_{eq}}+\Delta E_p\left(t\right)\hfill \\ \Delta E_p\left(t\right)=2.423\times {10}^{-2}·E_{p_{x1}}(t-3312)+0.1273·E_{p_{x2}}(t-3312)\hfill \\ {\dot{E}}_{p_{x1}}\left(t\right)=-1.021\times {10}^{-3}·E_{p_{x1}}\left(t\right)-8.359\times {10}^{-4}·E_{p_{x2}}\left(t\right)+0.125·(W_{BStOut}\left(t\right)-W_{BStOu{t}_{eq}})\hfill \\ {\dot{E}}_{p_{x2}}\left(t\right)=4.883\times {10}^{-4}·E_{p_{x1}}\left(t\right)\hfill \end{array}$$

(3)

3.4. Pressure Inside Fourth Effect

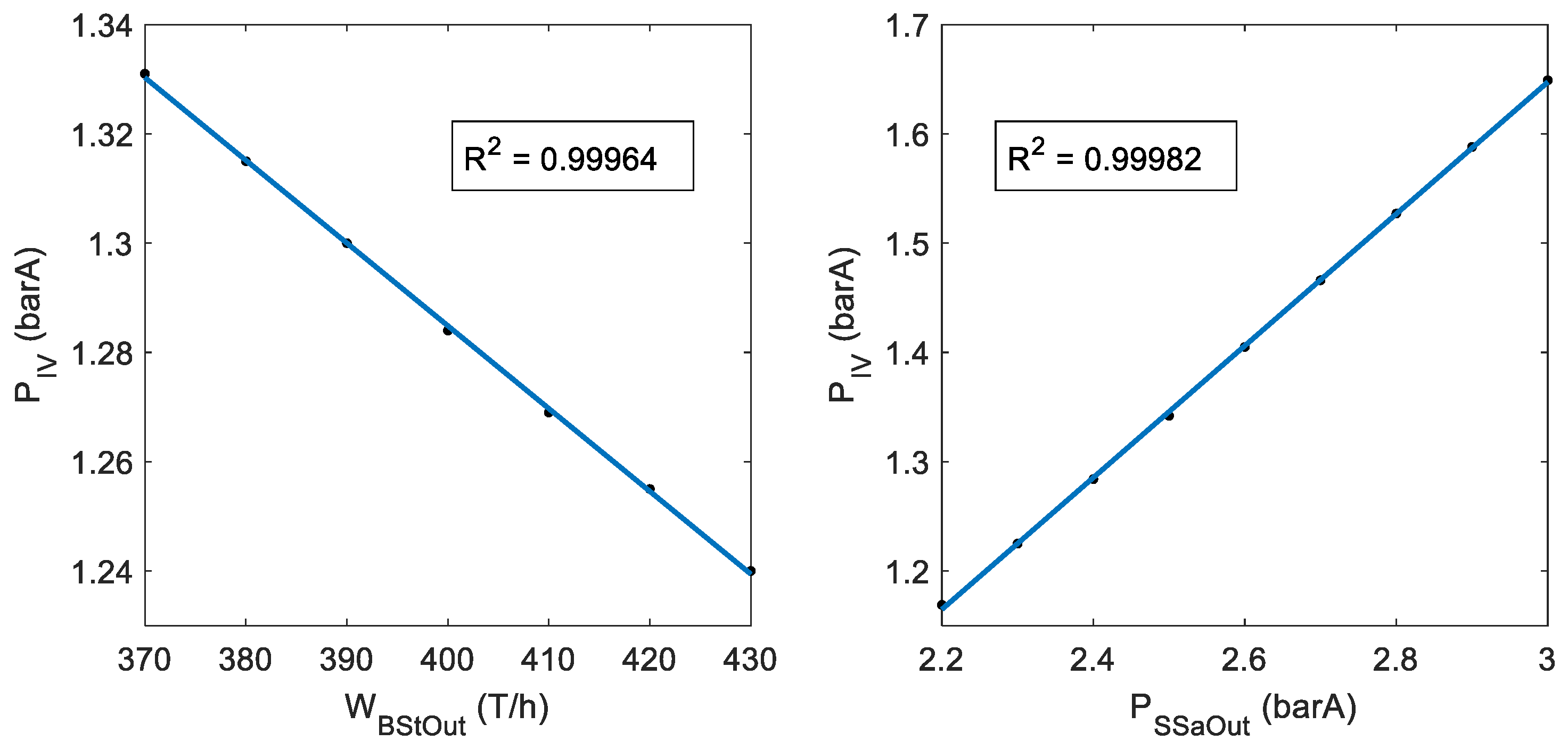
Regarding pressure inside the fourth evaporation effect, since modeling the whole evaporation section would be inefficient for the purpose described, a simple expression is sought based on experimental data that represents how pressure inside this effect varies during the process operation. Firstly, the causes that affect its value are identified. In the factory studied, these are essentially the beet production rate and the evaporation working pressure. If production is increased and the evaporation working pressure is maintained constant, the water removed from the juice will not be enough to cope with the process steam demand, and eventually the pressure of every evaporation effect will drop. Instead, if the working pressure is increased, but the evaporation input juice flow remains constant, more water than necessary will be removed and the pressure of the evaporators will increase. Other variables may affect pressure inside the evaporators, but they are rarely changed during normal process operation and its effect is not very significant, so they will not be considered.

In Figure 5, the step responses of $P_{IV}$ when changes are introduced in $W_{BStOut}$ and $P_{SSaOut}$ are shown. Regarding the beet production rate, when it is increased, the pressure inside the fourth effect rises following a typical linear second order response. The delay and settling time are the same as before with $Q_p$ and $E_p$. With respect to $P_{SSaOut}$, a very similar response to the one seen for $Q_p$ is found. Again, if the first part of the transient state is ignored, the response of the system is close to a first order dynamic. There is no delay and the settling time is one hour.

In order to find the linearity of $P_{IV}$ with both inputs, different experiments are carried out with several values of $W_{BStOut}$ and $P_{SSaOut}$. Again the superposition principle has been assumed as valid. The results of these experiments are shown in Figure 6.

Figure 6 shows that, for the operational range considered, it can be assumed that both inputs are related to the fourth effect pressure in a linear way. With the same reasoning as that used for the identification of $Q_p$, a MIMO second order space-estate model is searched using identification techniques. The model obtained can be seen in Equation (4).

$$\begin{array}{c}{P}_{IV}\left(t\right)=P_{I{V}_{eq}}+\Delta P_{IV}\left(t\right)\hfill \\ \Delta P_{IV}\left(t\right)=9.397\times {10}^{-2}·P_{I{V}_{x1}}\left(t\right)+0.122·P_{I{V}_{x2}}\left(t\right)-1.449\times {10}^{-7}·P_{I{V}_{x3}}(t-3312)-5.935\times {10}^{-4}·P_{I{V}_{x4}}(t-3312)\hfill \\ {\dot{P}}_{I{V}_{x1}}\left(t\right)=-0.309·P_{I{V}_{x1}}\left(t\right)-5.434\times {10}^{-2}·P_{I{V}_{x2}}\left(t\right)+0.25·(P_{SSaOut}\left(t\right)-P_{SSaOu{t}_{eq}})\hfill \\ {\dot{P}}_{I{V}_{x2}}\left(t\right)=6.25\times {10}^{-2}·P_{I{V}_{x1}}\left(t\right)\hfill \\ {\dot{P}}_{I{V}_{x3}}\left(t\right)=-7.163\times {10}^{-4}·P_{I{V}_{x3}}\left(t\right)-3.915\times {10}^{-4}·P_{I{V}_{x4}}\left(t\right)+9.766\times {10}^{-4}·(W_{BStOut}\left(t\right)-W_{BStOu{t}_{eq}})\hfill \\ {\dot{P}}_{I{V}_{x4}}\left(t\right)=4.883\times {10}^{-4}·P_{I{V}_{x3}}\left(t\right)\hfill \end{array}$$

(4)

3.5. Storage Zone

The storage area, where beet is accumulated until it can be processed, has also been incorporated into this control volume. The calculation of the remaining beet is necessary to know if a determined control sequence leads to a situation where the beet is completely used up, or on the contrary, the storage zone is overflowing. To model it, a mass balance is considered between its input and output. Since the beet input and output flow are measured in [T/h] and the rest of the model variables are in seconds, a change of units must be done, dividing the difference by 3600.

$${\dot{m}}_{St}\left(t\right)={\displaystyle \frac{W_{BStIn}\left(t\right)-W_{BStOut}\left(t\right)}{3600}}$$

(5)

To calculate the output of this mass balance, the beet input must be known or predicted beforehand. As mentioned before, instead of the accumulated beet in the storage zone, the average residence time beet spends there is the desired output. It is defined as follows:

$${\tau }_{St}\left(t\right)={\displaystyle \frac{m_{St}\left(t\right)}{W_{BStOut}\left(t\right)}}$$

(6)

With the equations described so far, outputs number one, three, four and six from the list enumerated previously in this section are accomplished. The others are related to the CHP plant. Output number two concerns the quantity of natural gas needed during normal process operation that will be used to generate a determined amount of steam demanded by the main process or by the expansion turbines.

To calculate it, an experimental relationship between the natural gas consumed, and the steam used by the main process and turbines is necessary. A priori, it could be thought that both steam mass flows should be close or the same; however, due to the use of the split range controller, this does not always have to be true, and its presence makes the system complex and highly nonlinear. On the other hand, using a first principles model to describe the behavior of the whole CHP plant does not seem wise, since it would yield a large model not suitable for optimization. These problems make use of a different approach advisable, where the natural gas is obtained using a combination of first principle equations and experimental direct relationships, taking advantage of both methods. To do so, the other control volumes depicted in Figure 1 will be used.

3.6. Boilers

Within this control volume, a relationship is sought between the natural gas used in boilers and the superheated steam obtained. In this way, the amount of natural gas needed to generate the steam demanded by both the main process and the turbines could be known. However, it would still be necessary to determine the individual steam consumption of each one. This control volume includes the preheating water system, the boilers themselves, and the overheating of the saturated steam obtained. Modeling the system in detail makes no sense if the aim is to make this model useful for other industries with other types of boiler. Thus, an experimental relation between natural gas and steam must be found.

When some experiments were carried out, we found that, in most of the cases, the relationship between their mass flows is almost linear. However, this is only true if the temperature of the superheated steam remains constant. For example, more natural gas will sometimes be needed to obtain less superheated steam, but with a higher temperature. Therefore, a variable that includes both mass flow and temperature information for the superheated steam is needed. That variable is the energy heat of the current $Q_{SBo}$.

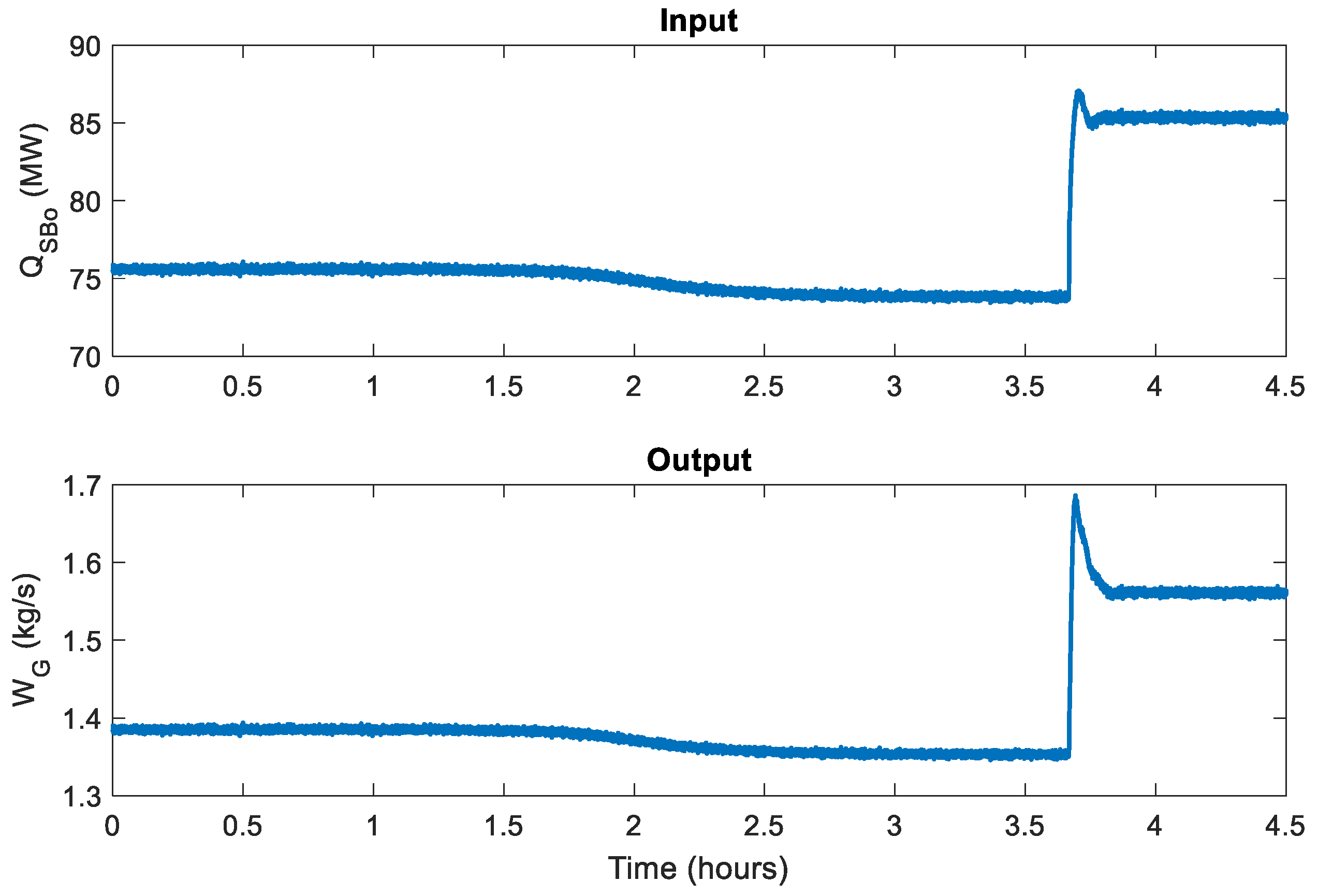
The dynamic relation between $Q_{SBo}$ and $W_G$ is studied. Since the heat of a current cannot be manipulated directly, a negative step change has been made in $W_{BStOut}$ and a positive one in the power energy generated in the turbine ($E_{Tu}$) to move it. They are the most influential input variables.

Figure 7 shows the similar behavior presented by both variables. Since a proper step cannot be carried out in this case, apart from the lack of delay between them, little information can be gathered from the dynamic behavior of $W_G$.

To study the linearity between both variables, several experiments were carried out using the simulator. Different combinations of the input variables, $W_{BStOut}$ and $E_{Tu}$, were tested to determine if linearity remains for all the operational range considered. The outcome of the experiments is shown in Figure 8.

From these results, it can be inferred that the relation between the superheated steam heat and the natural gas flow is almost linear in a stationary state. Hence, a second order state-space model is identified and the result is shown in Equation (7).

$$\begin{array}{c}{W}_G\left(t\right)=W_{N{G}_{eq}}+\Delta W_G\left(t\right)\hfill \\ \Delta W_G\left(t\right)=1.038\times {10}^{-3}·W_{N{G}_{x1}}\left(t\right)+2.308\times {10}^{-4}·W_{N{G}_{x2}}\left(t\right)+2.101\times {10}^{-6}·(Q_{SBo}\left(t\right)-Q_{SB{o}_{eq}})\hfill \\ {\dot{W}}_{N{G}_{x1}}\left(t\right)=-7.528\times {10}^{-2}·W_{N{G}_{x1}}\left(t\right)-2.828\times {10}^{-2}·W_{N{G}_{x2}}\left(t\right)+1.953\times {10}^{-3}·(Q_{SBo}\left(t\right)-Q_{SB{o}_{eq}})\hfill \\ {\dot{W}}_{N{G}_{x2}}\left(t\right)=-1.563\times {10}^{-2}·W_{N{G}_{x1}}\left(t\right)\hfill \end{array}$$

(7)

Since the heat energy of a current is a variable that it is not measured in process industry, it must be calculated using Equation (8).

$$Q_{SBo}\left(t\right)=W_{SBo}\left(t\right)·H_{SBo}\left(t\right)$$

(8)

To solve Equation (8), both the mass flow and the specific enthalpy of the superheated steam obtained in the boilers are needed. The enthalpy can be calculated using steam property tables [39], but to incorporate its calculation within the model, a linear function interpolating the data from the table is used instead. The obtained function (Equation (9)) is valid for every pressure, when the temperature is higher than 283 ${}^{\circ }\mathrm{C}$.

$$H_{SBo}\left(t\right)=2355-1.490·P_{SBo}+2.291·T_{SBo}\left(t\right)$$

(9)

In Equation (9), both the pressure and temperature of the overheated steam are required. The first can be chosen freely thanks to the pressure control system, but as it has almost no effect on any of the desired outputs, it will remain constant. On the other hand, the temperature will be a decision variable of the optimization problem, and hence it will also be known.

Since the boilers model should be as simple as possible, no more equations are added to this control volume. The steam mass flow generated in the boilers ($W_{SBo}$) is still needed to obtain the natural gas flow consumed. Therefore, other control volumes must be used.

3.7. Expansion Zone

The steam expansion control volume contains three identical turbines working in parallel and a bypass recirculation for steam. To simplify the problem, only one large steam turbine has been modeled, in such a way that it will consume the same amount of steam to generate the same amount of power as the sum of the other three. The first equation considered in this control volume is a mass balance, where the steam mass flow generated in the boilers must be equal to the steam mass flow that goes through the turbine and the bypass valve.

$$W_{SBo}\left(t\right)=W_{SBy}\left(t\right)+W_{STuIn}\left(t\right)$$

(10)

The objective now is to find both mass flows in order to calculate $W_{SBo}$. The amount of steam used by the turbine can be calculated using the following expression obtained from [40], where $K_{Tu}$ is a parameter that must be adjusted from experimental data.

$$W_{STuIn}\left(t\right)={\displaystyle \frac{K_{Tu}}{\sqrt{T_{STuIn}\left(t\right)}}}·\sqrt{P_{STuIn}{\left(t\right)}^2-P_{STuOut}{\left(t\right)}^2}$$

(11)

It has been assumed that the pressure drop due to the pipes and the saturator is negligible, so the steam pressure at the output of the turbines is assumed to be equal to the evaporation working pressure.

$$P_{STuOut}\left(t\right)=P_{SSaOut}\left(t\right)$$

(12)

To obtain the steam pressure at the input of the turbines, $P_{STuIn}$, a relation between the enthalpy of this current and its pressure and temperature can be found using the relation shown in Equation (9), but applied to this current.

$$H_{STuIn}\left(t\right)=2355-1.49·P_{STuIn}\left(t\right)+2.291·T_{STuIn}\left(t\right)$$

(13)

Valves have been assumed to be completely insulated, so they can be considered as adiabatic. If so, the enthalpy before and after them must remain constant. This property can be used to obtain the steam specific enthalpy at the input of the turbine, which must be equal to that of the overheated steam obtained from the boilers, which was calculated using Equation (9).

$$H_{STuIn}\left(t\right)=H_{SBo}\left(t\right)$$

(14)

Regarding the temperature at the input of the turbine ($T_{STuIn}$), assuming that the steam expansion through a turbine is isentropic and adiabatic, the following expression is used to obtain the steam temperature at the input of the turbines, where k is the polytrophic expansion factor for steam.

$${\displaystyle \frac{T_{STuOut}\left(t\right)+273.15}{T_{STuIn}\left(t\right)+273.15}}={{\displaystyle \frac{P_{STuOut}\left(t\right)}{P_{STuIn}\left(t\right)}}}^{({\displaystyle \frac{k-1}{k}})}$$

(15)

At this point, since $T_{STuIn}$ is needed to calculate $P_{STuIn}$ and vice versa, a nonlinear algebraic loop appears affecting Equations (13) and (15). To solve Equation (15), the temperature at the output of the turbine is needed ($T_{STuOut}$). This can be obtained using the relation between the specific enthalpy of this current and its pressure and temperature.

$$H_{STuOut}\left(t\right)=2355-1.49·P_{STuOut}\left(t\right)+2.291·T_{STuOut}\left(t\right)$$

(16)

However, as $H_{STuOut}$ is still unknown, more equations must be added to find it. For example, the electricity generated in the turbines, which can be expressed as a relationship between the specific enthalpy of its input and output current.

$$E_{Tu}\left(t\right)={\mu }_{Tu}·W_{STuIn}\left(t\right)·(H_{STuIn}\left(t\right)-H_{STuOut}\left(t\right))$$

(17)

In Equation (17), ${\mu }_{Tu}$ is the efficiency of the steam turbine, which must be known beforehand, and $E_{Tu}$ is the electricity generated in the turbine. It has been assumed that changes in the power generated by the turbines are very quick compared to the dynamic of the main process, so the equation used to represent the electricity generation is static. For the same reason, the dynamic of the power controller has also been ignored. Thus, changes in the set-point of the power controller are considered to be direct changes to the generated power.

With Equations (11) to (17), the full behavior of the large turbine can be explained, and only the pressure at the output of the saturator ($P_{SSaOut}$) is needed to obtain the mass flow of steam at the input of the turbines ($W_{STuIn}$). If these equations are analyzed carefully, it can be seen how a new nonlinear algebraic loop appears affecting all of them.

On the other hand, to solve Equation (10), the steam mass flow passing through the bypass valve must also be calculated. To do so, the following expression is used, where the rated valve coefficient ($K{v}_{By}$) of the bypass valve must be known beforehand.

$$W_{SBy}\left(t\right)=K{v}_{By}·{\displaystyle \frac{A{p}_{By}\left(t\right)}{100}}·\sqrt{P_{SBo}{\left(t\right)}^2-P_{SSaOut}{\left(t\right)}^2}$$

(18)

In Equation (18), everything is known except the opening of the bypass valve ($A{p}_{By}$) and $P_{SSaOut}$. In Figure 1, it can be seen that this valve is an actuator of the split range controller used to control the evaporation working pressure. In order to obtain the opening of this valve, the output signal of that controller needs to be calculated. In conclusion, to obtain $W_{SBo}$, there are now two unknown variables, so more equations must be used.

3.8. Saturator

The two variables needed are related to the steam used in the evaporation section, so the saturator control volume is used to find relationships between these two variables and the ones calculated before. This contains the split-range pressure controller and the piece of equipment known as the saturator, where the exhausted steam obtained from the expansion zone is saturated with a water flow before using it in the evaporation section.

In order to calculate the opening of the bypass valve, the entire PI controller has been modeled with the same equations and parameters used in the simulated plant. As the parameters of the controller should always be known, the same approach could be extended to any real factory, using its own equations.

$$\begin{array}{c}A{p}_{By}\left(t\right)=max(0,min(100,{\displaystyle \frac{v_{max}}{v_{max}-45}}·(v\left(t\right)-45)))\\ A{p}_{Re}\left(t\right)=max(0,min(100,{\displaystyle \frac{-v_{max}}{45}}·(v\left(t\right)-45)))\\ v\left(t\right)=kp·e\left(t\right)+v_i\left(t\right)\\ \dot{v_i}\left(t\right)={\displaystyle \frac{kp}{Ti}}·e\left(t\right)\\ e\left(t\right)=P_{SSaOutRef}\left(t\right)-P_{SSaOut}\left(t\right)\end{array}$$

(19)

As can be seen in Equation (19), the opening of the bypass valve depends on the control signal calculated by the split range controller, which in turn also depends on $P_{SSaOut}$. So if this pressure is obtained, the whole model could be solved.

To do so, the relation between the saturated steam pressure and its specific enthalpy is used. Since it is saturated, the specific enthalpy can be computed using only one thermodynamic property. As mentioned for Equation (9), the specific enthalpy can be computed using thermodynamic tables, but as the operation range is not going to change greatly, an interpolation linear function that works in a pressure interval from 1 to 3 bar, is used instead.

$$H_{SSaOut}\left(t\right)=24.35·P_{SSaOut}\left(t\right)+2656$$

(20)

To obtain the specific enthalpy of the saturated steam at the output of the saturator ($H_{SSaOut}$), an energy balance is used.

$$W_{SSaOut}\left(t\right)·H_{SSaOut}\left(t\right)=W_{SSaIn}\left(t\right)·H_{SSaIn}\left(t\right)+W_{WSa}\left(t\right)·H_{WSa}$$

(21)

In Equation (21), $H_{WSa}$ is the specific enthalpy of the water used to saturate the steam, which is assumed to have atmospheric conditions, and can therefore be easily computed. However, the steam mass flow that leaves the saturator ($W_{SSaOut}$), the one that enters ($W_{SSaIn}$), its specific enthalpy ($H_{SSaIn}$) and the mass flow of water needed to saturate the steam ($W_{WSa}$), are unknown variables which must be calculated. One relation between them can easily be found by using a mass balance in the saturator.

$$W_{WSa}\left(t\right)=W_{SSaOut}\left(t\right)-W_{SSaIn}\left(t\right)$$

(22)

$W_{WSa}$ can be computed with Equation (22), while a relationship between $W_{SSaOut}$ and the process heat energy consumed can be obtained with Equation (2), so the following expression can be found.

$$Q_P\left(t\right)=W_{SSaOut}\left(t\right)·H_{SSaOut}\left(t\right)$$

(23)

With all the equations expressed above, there are still two unknown variables, $W_{SSaIn}$ and $H_{SSaIn}$, so the last control volume related to the relief valve, must be used.

3.9. Relief Valve

This control volume includes the bifurcation that leads the expanded steam to the saturator or to the reflief valve, which is used for reducing an excess of pressure in the system, if necessary. The first equation considered to find the unknown variables is a mass balance between the steam mass flow through the bypass, the steam turbine, the relief valve and the saturator.

$$W_{SSaIn}\left(t\right)=W_{SBy}\left(t\right)+W_{STuIn}\left(t\right)-W_{SRe}\left(t\right)$$

(24)

In this equation, the mass flow that goes through the relief valve appears, and it will be calculated using a similar expression to (18).

$$W_{SRe}\left(t\right)=K{v}_{Re}·{\displaystyle \frac{A{p}_{Re}\left(t\right)}{100}}·\sqrt{P_{SSaOut}{\left(t\right)}^2-P_{atm}{\left(t\right)}^2}$$

(25)

The $Kv$ of the valve and the atmospheric pressure are known parameters, so the opening of the relief valve is the only unknown variable, which can be computed using Equation (19). Therefore, at this point, only the specific enthalpy of the team that goes into the saturator ($H_{SSaIn}$) is required to solve the entire model.

To obtain this, an energy balance is used with the same streams as in Equation (24). As a disjunction occurs, the specific steam enthalpy at the input of the relief valve is the same as at the input of the saturator. Furthermore, the bypass valve is considered to be isenthalpic, so the specific enthalpy of this current can be assumed to be the same as that of the superheated steam that leaves the boilers.

$$\begin{array}{c}{H}_{SRe}\left(t\right)=H_{SSaIn}\left(t\right)\\ H_{SBy}\left(t\right)=H_{SBo}\left(t\right)\\ W_{SBy}\left(t\right)·H_{SBo}\left(t\right)+W_{STuIn}\left(t\right)·H_{STuOut}\left(t\right)=W_{SRe}\left(t\right)·H_{SSaIn}\left(t\right)+W_{SSaIn}\left(t\right)·H_{SSaIn}\left(t\right)\end{array}$$

(26)

With Equations (7) to (26), the consumption of natural gas can be computed and, since the behavior of the CHP has been explained, the European indexes can also be computed in the next subsection. In Figure 9, a scheme of the inputs and outputs of the different control volumes used to obtain the model can be found. As it can be observed, a new nonlinear algebraic loop appears for calculating the opening of the relief valve.

3.10. European Legislation

Following Directive 2012/27/UE [27], in order to consider the cogeneration system as efficient, an index called Primary Energy Savings (PES) is defined. This compares the performance of the CHP plant studied to some expected heat and power efficiency references given for each type of cogeneration system. Cogeneration systems like the one treated in this work, which has a capacity of more than 1 MWe, will be considered efficient if its PES index is greater than 0.10.

$$PES\left(t\right)=1-{\displaystyle \frac{1}{{\displaystyle \frac{\mu Q_{CHP}\left(t\right)}{\mu Q_{Ref}}}+{\displaystyle \frac{\mu E_{CHP}\left(t\right)}{\mu E_{Ref}}}}}$$

(27)

In order to obtain the efficiency reference values, the European regulation 2015/2402 must be consulted [28]. The actual heat and power efficiencies are defined, respectively, as the useful heat and power energy obtained divided by the energy obtained from fuel combustion:

$$\begin{array}{cc}\hfill \mu Q_{CHP}\left(t\right)& ={\displaystyle \frac{Q_{CHP}\left(t\right)}{F_{CHP}\left(t\right)}}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \mu E_{CHP}\left(t\right)& ={\displaystyle \frac{E_{CHP}\left(t\right)}{F_{CHP}\left(t\right)}}\hfill \end{array}$$

(29)

Useful heat in this problem has been obtained as the difference between the steam enthalpy at the input of the saturator, and the water enthalpy at the input of the boiler. This difference is the energy given by the fuel. The heat lost in purging the boilers has been neglected.

$$Q_{CHP}\left(t\right)=W_{SSAT}\left(t\right)·(H_{SSAT}\left(t\right)-H_{WBo})$$

(30)

According to the European law, energy can be generated in “cogeneration mode” or not. While the useful heat generated in cogeneration systems is always considered as generated in cogeneration mode, the same cannot be applied to the useful electricity ($E_{CHP}$) and the fuel used ($F_{CHP}$). This is done to avoid trickery, as electricity may be generated only for selling it to the external grid, and not for the main process operation. These variables will be considered the same if and only if the global efficiency of the plant for one year is considered greater than or equal to 0.75. This limit has been obtained from Directive 2012/27/UE, considering a cogeneration system with counter pressure turbines and without condensation. The global efficiency is a percentage of how much of the energy generated from burning fuel in the boilers has been used and not wasted.

$${\mu }_G\left(t\right)={\displaystyle \frac{E_{Plant}\left(t\right)+Q_{CHP}\left(t\right)}{F_{Plant}}}$$

(31)

In this expression, $E_{plant}$ is the actual electricity being generated in the turbines at instant t $\left(E_{Tu}\left(t\right)\right)$, while $F_{plant}$ is the energy contained in the fuel being burned at instant t. For the process considered, the fuel used to obtained steam is natural gas.

$$F_{plant}\left(t\right)=W_G\left(t\right)·PC{I}_{NG}$$

(32)

Should the global efficiency of the plant be below 0.75, the useful electricity and the fuel energy would have to be divided into two different parts, cogeneration and non-cogeneration mode. For the case study considered, the global efficiency is always above 0.75, using restrictions in the optimization problem. Therefore, more equations are not necessary to compute the PES of the system.

Table 1. Comparison between the model used for simulation and the model obtained for optimization.

	Simulator	Optimization Model
Number of equations	6485	52
- Static	6036	38
- Dynamic	449	14
Parameters	2131	23
Variables	6456	48
Input variables	29	4
Non-linear algebraic loops	8	3

shows the principal features of the model developed and compares them with the model used for simulation.

4. Validation

In this section, the validity of the model developed in the previous section is analyzed. In order to do so, the model will be simulated in EcosimPro^® [41], an object oriented modeling and simulation software. Several experiments, which are shown in Figure 10, have been carried out to test the response of the model. These tests correspond to different typical operational points.

As the methodology for validation, the same inputs have been introduced to both the simulator and the optimization model. Their response is analyzed in two different ways: on the one hand, both responses can be compared graphically in Figure 11; while on the other, the Root Mean Squared Error (RMSE) has been computed to show the error of the model numerically. This index is one of the most used in the literature and calculates the error of the model with respect to the measurements, weighing the farthest predictions.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(y_i-\widehat{y_i})}^2}$$

(33)

Discussion of the Results

In this subsection, the accuracy of the model is discussed. This is a highly relevant topic in optimization problems, since a bad model may lead the optimization to suboptimal or even infeasible results when the responses are sent to the plant. If the accuracy of the model is not good enough, caused for example by uncertainty in process measurements, this will have to be considered explicitly in the optimization problem. The way to do it is using a different approach that considers this kind of uncertainty explicitly. Several methodologies can be applied for this topic, like the two-step approach [42], modifier adaptation [43], or extremum seeking control [44], among others [45].

Looking at Figure 10 three typical operational points, corresponding to three different beet production rates, can be discerned. The energy generated in turbines is moved in order to sell more or less electricity and the steam boilers temperature and evaporation working pressure are modified to try to maintain the $P_{IV}$ and PES between limits.

Figure 11 shows that, for almost all the time, the output of the optimization model follows the shape of the output of the simulator. For every output variable, it can be seen how the stationary state is captured reasonably well. The transient state is clearly affected by the linear assumptions made when obtaining the model. Here, the behaviour of the model during slow and quick transients can be differentiated. For slow transients, caused by changes in production, the dynamic of the real plant is approximated by a straight line. This can be observed, for example, in $W_G$ from 10 to 13 h approximately. Although this response is not perfect, for the purpose of the model, it is sufficiently close to the real value of the plant. On the other hand, when quick transients are considered, in most cases, it can be seen that the model is able to predict these changes, but that fails when computing the amplitude. This is especially relevant in the prediction of the PES. However, since those transients are too short and this index is evaluated yearly, it is enough for the desired purpose.

The graphic results can be corroborated in

Table 2. Indexes for the output variables of the model.

Output Variable	RMSE [Ud]	Output Mean [Ud]	Relative Error [%]
$Q_p$	566.03 kW	67,614.00 kW	0.84
$E_p$	36.72 kW	7793.89 kW	0.47
$W_G$	0.018 kg/s	1.47 kg/s	1.24
${\tau }_{St}$	0.52 h	45.96 h	1.12
PES	0.01	0.13	6.31
$P_{IV}$	0.01 barA	1.22 barA	0.52

. Here, for every variable except PES, the relative error is below 2%. This means that the response of the model is very close to the response of the plant. In the case of the PES, the quick transients, and a bias from hour 3 to hour 7, make the relative error move to 6.31. Traditionally, an error below 5% is considered sufficiently good. In our case, this value is slightly exceeded because of the reasons stated above, so it can be concluded that it is acceptable, but additional caution will have to be taken during optimization.

With these results, it can be concluded that the model accuracy is good enough for the operational range considered, and therefore an optimization approach that deals with model mismatch will not be needed.

5. Extension to Other Case Studies

In this section, the methodology used for obtaining the model is presented in a schematic way. Thus, it can be used for other case studies.

• Establishment of the simulation objectives.
• Set model inputs and outputs.
• Search for relations between the inputs and outputs.

  3.1.

  Look for control volumes to disaggregate the model.

  3.2.

  Select where to apply first principles or experimental models.

• Experimental modeling.

  4.1.

  Analyze the response of the selected outputs, when steps are performed in the inputs.

  4.2.

  Check linearity between the inputs and outputs selected.

  4.3.

  If the relation is linear, apply linear identification techniques. Otherwise, look for another approach like symbolic regression [46], Neural Networks or Fuzzy models [47].

• Parametrization of the model.
• Symbolic manipulation of the gray-box model obtained. To do so, we recommend the use of a software like EcosimPro [41] as modeling and simulation environment.

  6.1.

  Perform a degree of freedom analysis.

  6.2.

  Look for algebraic loops.

  6.3.

  Check the existence of high-index problems.

• Initialization of the model. Use a stationary point obtained by the real system.
• Validation of the model.

  8.1.

  Qualitative validation. Check the transient response and robustness of the model for different inputs.

  8.2.

  Quantitative validation. Compare the output of the obtained model with the real process. This has been done in a graphical and analytical way.

If the CHP scheme is different from the one proposed, all this steps must be performed in order to obtain a new model. However, if it is maintained, several points can be avoided. This way, the first step would be to change the inputs and outputs of the model, since they are process dependent (point 2). Next, the control volumes could be kept, and the experimental models would have to be obtained for the new process (Point 4). The parametrization of the system is also required (point 5), but the model would not need to be manipulated again. Finally, the initialization and validation of the model would be required for the specific case study (points 7 and 8).

6. Conclusions

In this paper, the methodology to obtain a gray-box model for optimizing the production rate of an industrial process, along with the management of an on-site CHP plant, has been reported. This model is especially designed for cases where cogeneration is coupled to the main process and electricity generation depends on the production rate. This is the case of the sugar factory presented as case study. A model of this process was obtained in a previous work; however, due to its size, it cannot be used for optimization. Nevertheless, thanks to its performance and response, which has already been validated, it has been used as a real plant, making the development of the optimization model faster. The resulting model is dynamic and non-linear, mixing first principle equations with linear identification. Thus, if the CHP structure is maintained, it can be extended to other industries simply by identifying their own response, and using their own parameters, which are easy to obtain. It has been shown to be able to predict the behavior of the system reasonably well, simultaneously computing the European legislation indexes for CHP efficiency with only 52 equations, which makes it suitable for optimization.

In future work, this model will be used in the optimization, according to the electricity Day-Ahead market, of the process and CHP management of the simulated sugar factory.