Energy Saving and Low-Cost-Oriented Design Processes of Blank’s Dimensions Based on Multi-Objective Optimization Model

Abstract

The blank’s dimensions are an important focus of blank design as they largely determine the energy consumption and cost of manufacturing and further processing the blank. To achieve energy saving and low cost during the optimization of blank dimensions design, we established energy consumption and cost objectives in the manufacturing and further processing of blanks by optimizing the parameters. As objectives, we selected the blank’s production and further processing parameters as optimization variables to minimize energy consumption and cost, then set up a multi-objective optimization model. The optimal blank dimension was back calculated using the parameters of the minimum processing energy consumption and minimum cost state, and the model was optimized using the non-dominated genetic algorithm-II (NSGA-II). The effect of designing blank dimension in saving energy and costs is obvious compared with the existing methods.

1. Introduction

The manufacturing industry plays an important role in China’s national economy. The manufacturing industry consumes an enormous amount of energy while promoting rapid development of the economy. About 70% of China’s primary energy consumption is provided by industrial energy consumption, and about 60% of China’s total energy consumption is consumed by manufacturing [1]. Liu et al. studied the complex energy consumption features of discrete manufacturing systems, as well as the research status of energy efficiency, summarizing several difficulties with energy efficiency for discrete manufacturing systems [2].

The blank is a production object used for further processing according to the shape, process size, etc. required by the work [3]. The process from the blank to work is the source of energy consumption in the manufacturing industry. The blank design stage determines the resource consumption and cost generation of more than 80% of blank production and processing. Given the importance of optimum blank dimension design, it has been studied by many scholars from different perspectives. Hou et al. constructed a set of indicators of energy, gross domestic product (GDP) productivity, carbon index and so on, and proposed a policy to increase the cross-border renewable energy trade [4]. Kuwabara et al. optimized the shape of a drawing blank based on a finite element computer program [5]. Lee used the three-dimensional (3D) multi-step backward analysis finite element method (FEM) to analyze the sheet metal forming process, and optimized the design of the blank’s shape [6]. Qian proposed four blank designs and validated the rectangular cross-section design through experiments [7]. In another study, to improve product quality, response surface methodology (RSM) and radial basis function (RBF) were applied to optimize the shape of the blank [8]. Padmanabhan et al. used FEM to predict deformation behavior and simulate the features of Non-Uniform Rational B-Splines surface to design the blank’s shape for deep drawing parts [9]. Ku et al. used the FEM of a reverse tracking scheme to design the blank’s shape for sheet metal forming [10]. Shim developed a design method to ascertain the best blank shape by iteratively executing the test blank shape corresponding to the required deformation by changing the required deformation shape [11]. Chamekh et al. used an artificial neural network (ANN) to forecast the optimal blank shape, and then provided suggestions for the shape design of the blank [12]. Liu et al. proposed an RSM based on support vector regression to optimize a polygon blank shape [13]. The different blank structure design methods have different advantages.

In terms of research on energy and cost savings based on designed blank dimension, Cai et al. presented a set of strategies and criteria through lean energy savings and sustainable development, and also made a comparison [14,15,16]. A multi-objective optimization model for high-speed and energy-saving numerical control of hobbing processing parameters was presented, which significantly reduced the processing energy consumption and time [17]. Li et al. presented a new short casting-rolling compound forming process for ring parts, which produced energy savings [18]. Wang et al. established an optimization model for a cutting process with the goals of low cost, low energy consumption, and high quality, and solved the model using the non-dominated genetic algorithm-II (NSGA-II) [19]. Li et al. established an optimization model to minimize the energy consumption of workshop operation, and solved the optimization model using the simulated annealing algorithm [20]. Wei et al. used the fitness sharing genetic algorithm (FSGA) to minimize welding energy consumption and maximize thermal efficiency. The FSGA was used to optimize the solution, and the effect was compared with the general genetic algorithm solution [21]. To lower energy consumption, Albertelli et al. verified the effectiveness of the proposed energy consumption optimization method for an absorbing and milling plane through experimental research [22]. Lu et al. aimed to decrease energy consumption while maintaining high processing quality, and achieved optimization using a multi-objective backtracking search algorithm [23]. Kant et al. aimed to lower energy consumption and maintain high surface quality, and used grey correlation analysis, principal component analysis (PCA), and RSM to optimize the solution [24].

To summarize, to increase energy savings and reduce the cost of blank production and processing, many scholars have analyzed blank dimension design via the optimization of process factors during the production stage of the blank and selected the blank’s dimensions based on experience. Considerable research has been conducted on the optimization of processing parameters during further processing of the blank. However, at present, the traditional blank dimensions determination method only considers the factors of the blank production stage in the design process, and the appropriate blank dimensions are selected for further blank processing after blank design and production. The blank dimensions optimized by single production process factors can guarantee optimization of the objectives during production stage, but cannot guarantee the optimization of the comprehensive objectives during the production and further processing of the blank. Few studies have considered the influence of different factors of blank production and further processing on the total process energy consumption and cost during the blank design process.

Based on the above review, we propose an optimum design method for the blank’s dimension based on a model of energy and cost savings during blank production and further processing. In this method, energy consumption and cost are set as optimization objectives. The blank rolling mill pass parameters include width, height, arc radius, corner radius; the blank turning parameters include cutting speed, feed, and back feed as independent variables; and the constraints include the limits of the rolling machine and the turning machine, and product specifications. NSGA-II was applied to optimize model. The blank’s dimensions can be calculated using minimum energy consumption and cost state parameters.

2. Establishment of Blank Dimension Design Using Multi-Objective Optimization Model

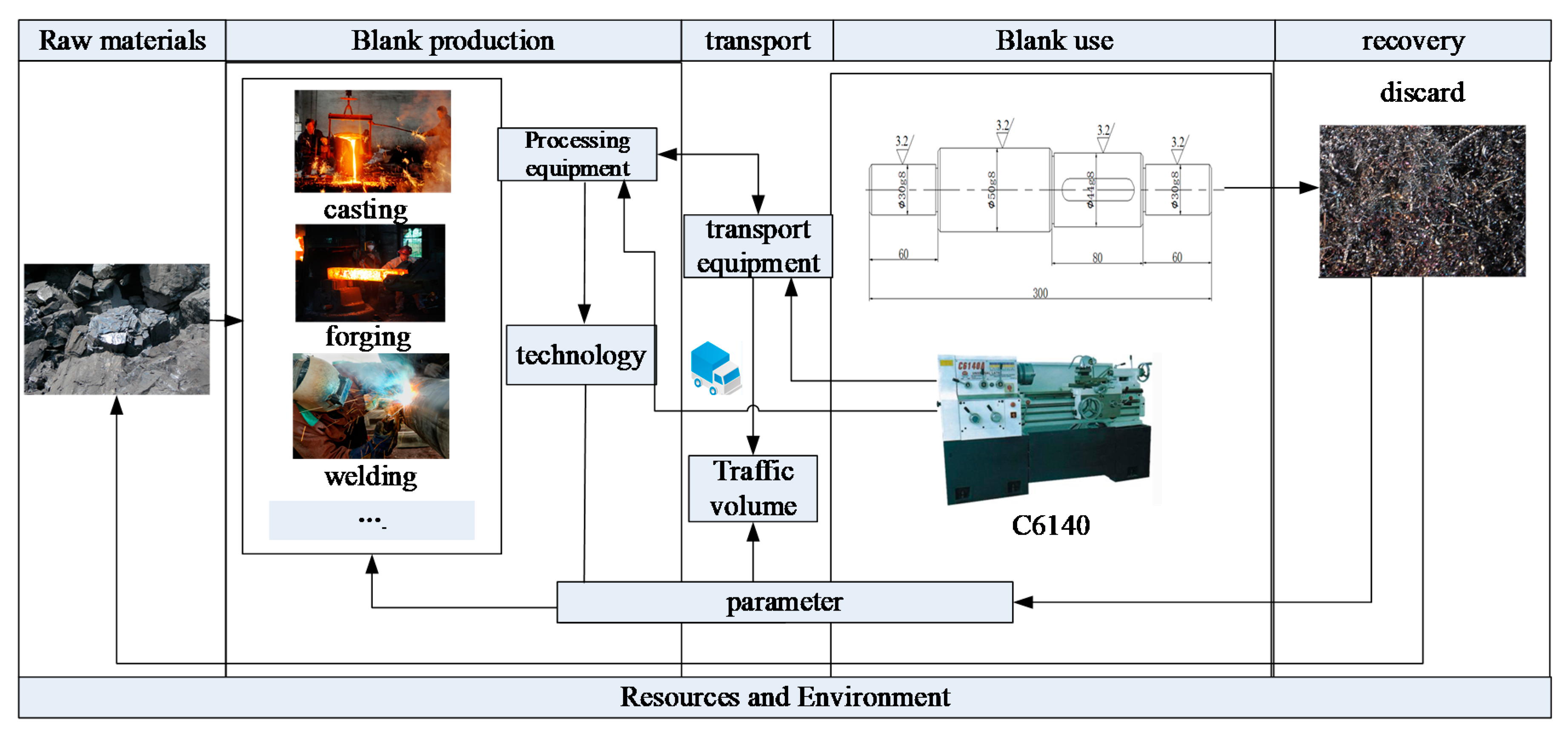
2.1. Impacts of Blank Dimension Design on Energy Consumption and Cost

The blank’s dimensions are the basis for determining the process plan. The features and characteristics of the work form the implementation of the processing plan. Manufacturing requirements, including manufacturing equipment, tools, and operating conditions for each process, usually depend on process planning. Taking energy consumption and cost as additional objectives in process planning may result in a different outcome than that based on traditional objectives. In the planning process from raw materials to manufacturing, the specific operations and blank dimensions impact the total energy consumption and cost.

2.2. Energy Objective

Blank production and further processing are optimized with the goal of reducing energy consumption. So, Equation (1) can be used to determine the total energy consumption:

$$E=E_Z+E_U$$

(1)

where $E_Z$ and $E_U$ represent the rolling energy consumption in the blank production stage and turning energy consumption in the blank further processing stage, respectively; and E represents the total energy consumption.

According to Zhang et al. [25], rolling energy consumption $E_Z$ can be expressed as

$$E_Z={\displaystyle \sum _{t=1}^n}{q}_t={\displaystyle \sum _{t=1}^n}{M}_t{v}_t{\tau }_t/D_t$$

(2)

where $M_t$ is the rolling moment of the t pass, $v_t$ is the rolling speed of the t pass, ${\tau }_t$ is the rolling time of the t pass, $D_t$ is the working diameter of the $t$ roll, $a$ is the coefficient, $q_t$ denotes the rolling energy consumption of the $t$ pass, and $n$ denotes the rolling pass. Rolling pass $n$ is a variable related to the total elongation coefficient and the average elongation coefficient, in which $u_z$ is the total elongation coefficient and $u_p$ is the average elongation coefficient. n and $u_z$ can be expressed as shown in Equations (3) and (4), respectively:

$$n=\frac{\log \left(u_z\right)}{\log \left(u_p\right)}$$

(3)

$$u_z=\frac{F_0}{F_n}=\frac{{\left(a_t{A}_t\right)}^2-0.86\times {\left(0.1\times a_t{A}_t\right)}^2}{\pi \times {\left(D{a}_t\right)}^2/4}$$

(4)

where $a_t$ is the thermal expansion coefficient, $A_t$ is the billet side length, D is the blank diameter, $F_0$ is the section area of the red billet, and $F_n$ is the section area of the finished product and thermal state.

In general, Equation (5) can be used to indicate the energy consumption of the turning operation [26]:

$$E_U=E_S+E_K+E_M$$

(5)

where $E_S,E_K,\mathrm{and}{E}_M$ represent the startup energy consumption, no-load energy consumption, and processing energy consumption of machine tools, respectively.

Reference [27] provided another form of energy consumption for turning operations, as shown in Equation (6):

$$E_U={\mathrm{p}}_0{t}_1+\left({\mathrm{p}}_0+(1+a_1)\frac{C_{Fc}(\frac{D-d}{2}){}^{x_{Fc}}{f}^{y_{Fc}}{v}_c^{n_{Fc}}{K}_{Fc}{v}_c}{6\times {10}^4}+a_2{(\frac{C_{Fc}(\frac{D-d}{2}){}^{x_{Fc}}{f}^{y_{Fc}}{v}_c^{n_{Fc}}{K}_{Fc}{v}_c}{6\times {10}^4})}^2\right)t_2+{\mathrm{p}}_0{t}_3(\frac{t_2}{T})+y_E(\frac{t_2}{T})$$

(6)

where, ${\mathrm{p}}_0$ is the cutting power, $t_1$ is the no-load time, $t_2$ is the cutting time, $a_1$, $a_2$ is the additional load loss factor, $C_{Fc},x_{Fc},y_{Fc},n_{Fc}$ is represent the coefficient related to the material and cutting conditions of the workpiece, $y_E$ is the average energy of each cutting edge, T represents the tool life, and d represents the dimension of d-blank after use.

Equation (7) can be used to express the total energy consumption of processes.

$$E={\displaystyle \sum _{t=1}^n}\frac{M_t{v}_t{\tau }_t}{D_t}+E_U$$

(7)

2.3. Cost Objective

The cost objective is calculated according to the processing conditions; cost can be expressed as

$$C=C_Z+C_U$$

(8)

where $C$ is the total cost objectives during the production and further processing of the blank; $C_Z$ is the cost objective of the blank production stage, which is expressed by Equation (9); and $C_U$ is the cost objective of further blank processing, which is expressed by Equation (10) [28]:

$$C_Z={\displaystyle \sum _{i=1}^n}{c}_i$$

(9)

$$C_U=x\times \left(t_1+t_2+t_3\times \frac{t_2}{T}\right)+\frac{t_3}{T}\times y_c$$

(10)

where x is the equipment cost rate, $t_3$ is the tool changing time, and $y_c$ is the average cost per cutting edge.

From the above discussion, the total cost of blank production and further processing can be represented by

$$C={\displaystyle \sum _{i=1}^n}{c}_i+x\times \left(t_1+t_2+t_3\times \frac{t_2}{T}\right)+\frac{t_3}{T}\times y_c$$

(11)

3. Constraints

The optimization of the design of a blank’s dimension is limited by production process equipment, further processing equipment, and related requirements, so the value within the limited conditions must be selected:

$$\mathsf{\alpha }\le {\mathsf{\alpha }}_{max}$$

(12)

where $\mathsf{\alpha }$ is the actual bite angle and ${\mathsf{\alpha }}_{max}$ is the maximum bite angle.

$${\mathsf{\beta }}_{\min }<\beta <{\mathsf{\beta }}_{\max }$$

(13)

$$\frac{\pi \times d_0\times n_{min}}{1000}\le v\le \frac{\pi \times d_0\times n_{max}}{1000}$$

(14)

where $n_{min}$ and $n_{max}$ represent the minimum and maximum speed of the machine tool spindle, respectively.

$$f_{\min }<f<f_{\max }$$

(15)

where $f_{\min }$ and $f_{\max }$ represent the minimum and maximum feed of the machine tool, respectively.

$$F<F_{\max }$$

(16)

where $F_{\max }$ is the maximum cutting force.

$$P\le \mu P_{\max }$$

(17)

where $\mu$ is the power effective coefficient and $P_{\max }$ is the maximum effective cutting power.

$$R\le R_{\max }$$

(18)

where $R$ represents the actual surface roughness and $R_{\max }$ represents the maximum allowable surface roughness.

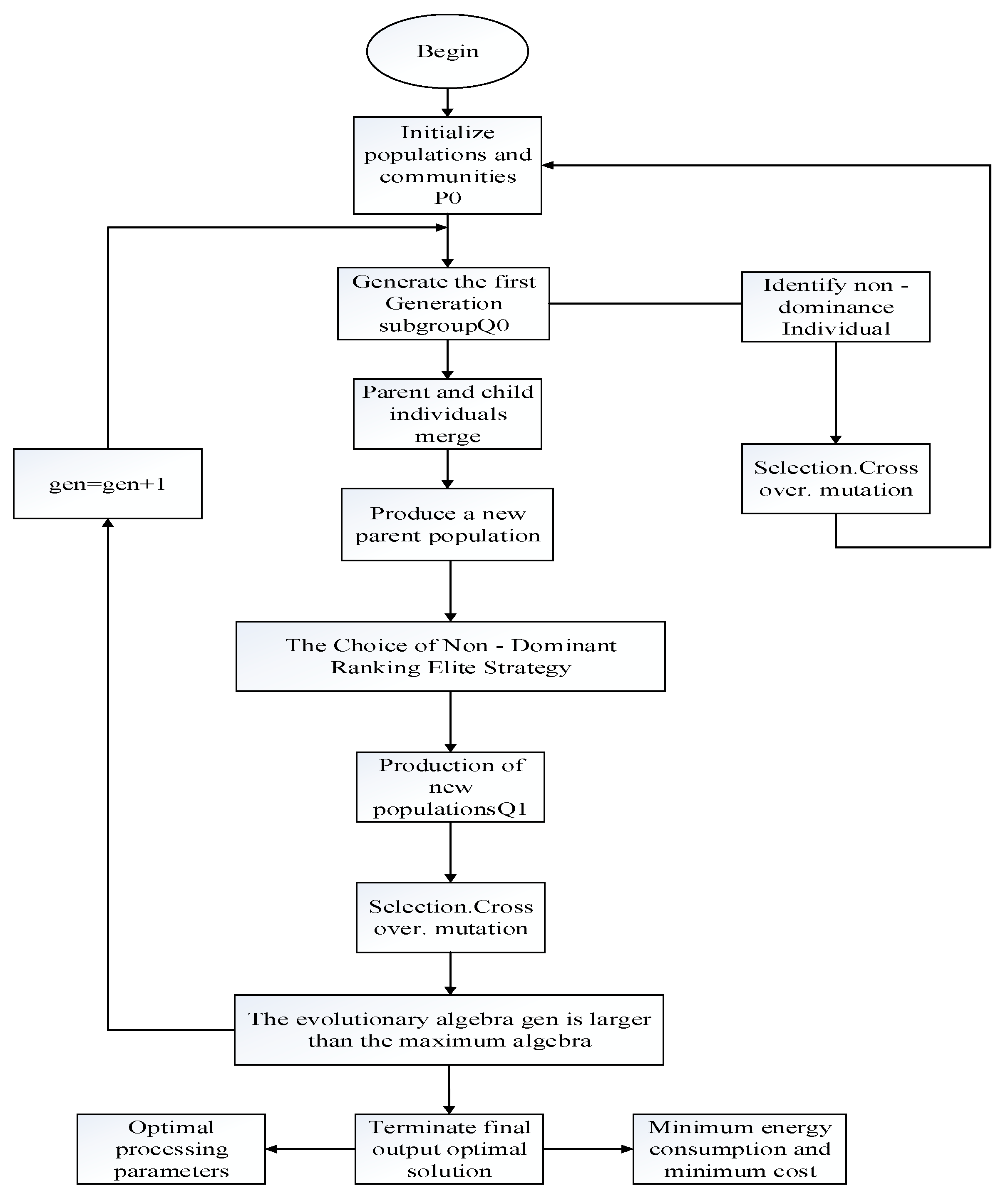
4. Solving Optimization Model Based on NSGA-II

4.1. Analysis of NSGA-II Algorithm

In practical engineering applications, multiple items are often needed. Decision-making problems are marked as optimal in a given feasible region. At present, many scholars have studied the multi-objective optimization method. However, among these methods, NSGA-II is commonly used to obtain the best processing parameters [29,30]. The fast non-dominated sorting in NSGA-II stratifies the population according to the individual’s non-inferior solution level and then guides the search to the Pareto optimal solution set. NSGA-II incorporates the concept of individual crowding distance to selectively rank individuals with the same non-dominant ordering value. To distribute the calculation results more evenly in the target space and maintain the diversity of the population, individuals with larger crowding distance are preferred. To prevent the Pareto optimal solution from losing, the best individuals in the parent generation are reserved to directly enter the next generation. NSGA-II in MATLAB (MathWorks, Natick, MA, USA, 2009) was used to solve the multi-objective optimization problems in this study. Considering the above, the specific implementation steps of NSGA-II are shown in Figure 1.

4.2. Basic Parameter Setting of NSGA-II

Generally, no standard calculation method exists for population size and genetic algebra. The calculation method is based on experiments. The standard population range is generally 10 to 100. After many experiments, a population size of 100 was selected. The range of genetic algebra is generally 100 to 1000. After many experiments, the maximum genetic algebra of 100 was, and we found 100 was appropriate in actual operation. The crossover method was analog binary crossover, and the crossover coefficient was 20. The variation method was polynomial variation with a variation distribution coefficient of 20. The crossover probability was 1 and the mutation probability was 1/2.

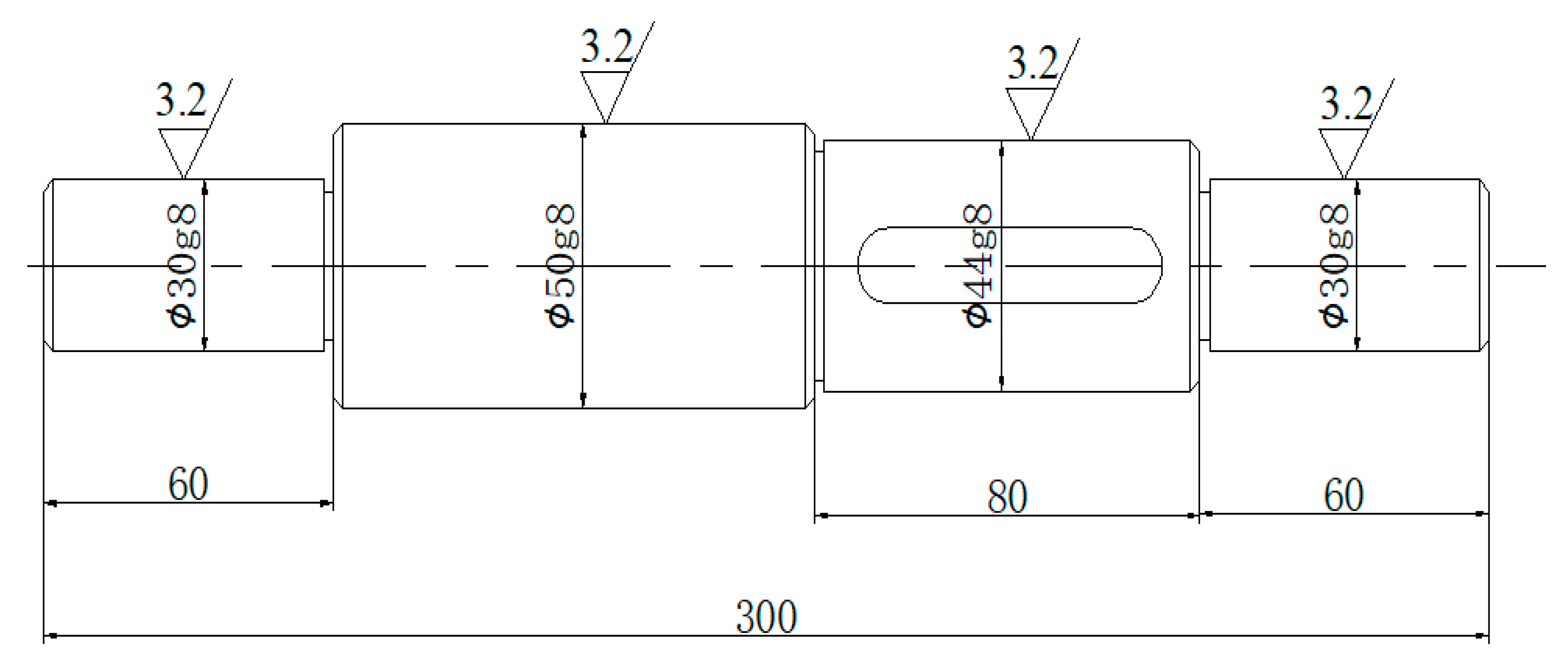
4.3. Background of the Optimization Problem

A factory receives the blank dimension design of the axle, as shown in Figure 2. The axle mainly bears torsion, hardly bears any bending moment, and the number is 10,000. These dimensions are the dimension after the use of the blank, as shown in Figure 2.

4.4. Experimental Conditions

The blank’s designed dimensions must be based on actual factory conditions. The equipment used for the blank is the machine tool. According to the actual factory, the machine tool CJK6140 (Huazhong CNC Co., Ltd., Wuhan, China, 2015) was selected as the tool to further process the blank. The experimental conditions for the design of the blank’s dimensions are shown in Figure 3.

The blank production equipment was as follows: A continuous rolling mill from a wire rod plant of a steel company is equipped with 22 rolling mills, which are divided into rough rolling, medium rolling, and finishing rolling mills. Each rolling mill is driven separately by a direct current (DC) motor, and the rolling mill is arranged in alternating horizontal and vertical directions with 45 steel with 165 × 165 mm billet. The rolling mill consists of roughing mill, intermediate mill, first finishing mill and second finishing mill, which are respectively 4–6–6–6 stand mill.

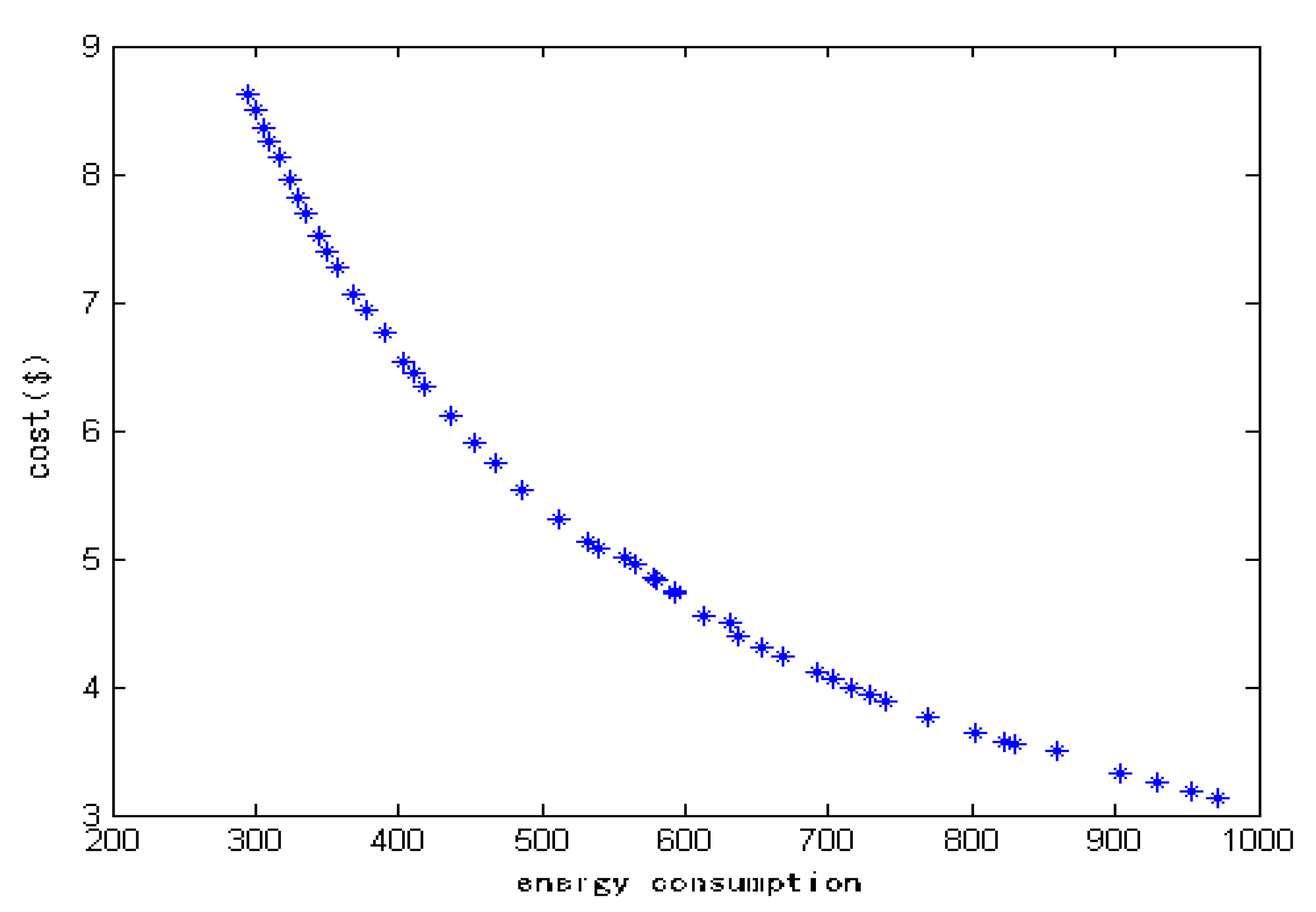
4.5. Simulation Results

The two-dimensional view (Figure 4) obtained by optimizing the processing parameters using NSGA-II is parabola-shaped. From the simulation, the corresponding process parameters were determined using a background program, and the optimized objective function values were 460.82 and 5.52, respectively. The blank dimension was 53.7.

4.6. Discussion and Practical Implications

Compared with traditional blank design dimensions of 53 and 55, the optimal functions values are 487.7 and 6.56, and 511.5 and 7.11, which shows that the proposed optimization method results in energy and cost savings. Compared with the existing standard blank dimensions of 53 and 55, the energy consumption of the designed blank dimension is 94.5% and 90.1% of the original marked dimension, and the cost is 84.1% and 77.6% of the standard dimension. Therefore, the dimensions of the blank designed using this method can reduce the process energy consumption and the process costs.

This method provides new ideas for scholars and enterprise managers when designing the blank’s dimensions and indicates the required direction for the manufacturing industry to improve the use rate of raw materials and energy. In particular, we considered the influence of further blank processing factors in the multi-objective optimization design process of the blank’s dimensions. Therefore, both in theory and in practice, we created a design method that can ensure the optimal target value in the production and further processing of the blank.

4.7. Comparison of the Proposed Method and Methods in the Literature

Various studies [14,15,16,17,18,19,20,21,22,23,24] have reported many methods to optimize processing parameters using different algorithms to reduce further blank processing energy consumption and costs. These methods and algorithms effectively achieve those goals. However, these methods only start from the further processing of the blank. As such, guaranteeing the lowest energy consumption and cost during the production process and the further processing is difficult due to the previously produced blank dimensions. Whether the blank dimensions are suitable depends on the blank design process to a large extent. In this study, the influence of the production and additional processes was considered during the design of the blank’s dimensions.

5. Conclusions

An optimization design approach of the blank’s dimensions to reduce energy consumption and costs during the blank’s manufacturing and further processing was proposed in this paper. With this method, total energy consumption and cost are set as the objective functions, considering the width, height, arc radius, and corner radius of each pass in bar rolling. Bar turning parameters, including cutting speed, feed, and back feed, were set as independent variables, then NSGA-II was used to optimize the solution Finally, the effectiveness of the proposed method was verified by case analysis.

Optimizing the design of the blank’s dimensions is an important basis for the sustainable development of the manufacturing industry. We designed the blank’s dimensions from the perspective of energy consumption and cost optimization, and enriched the research on blank dimensions design to a certain extent, providing a theoretical reference for enterprises to achieve energy savings and emissions reduction. However, we only verified the influence of radial dimension optimization design on energy consumption and cost. Future research should comprehensively and deeply evaluate the influence of the blank’s diameters and length on energy consumption, cost, other objectives, and the use of the new parameter optimization calculation method.