Adaptive Control of Biomass Specific Growth Rate in Fed-Batch Biotechnological Processes. A Comparative Study
Abstract
1. Introduction
2. Materials and Methods
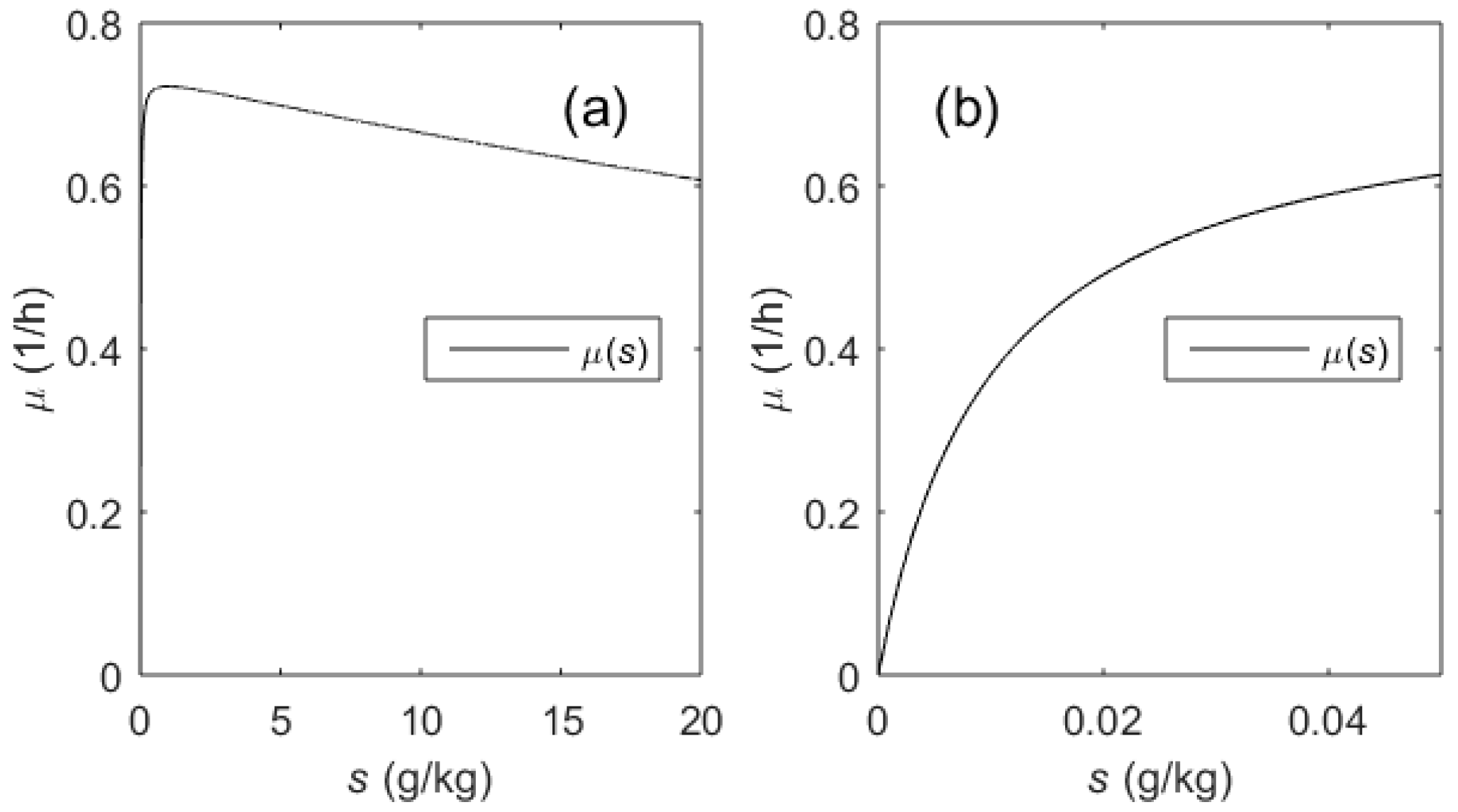
2.1. Biotechnological Process and Its Mathematical Model
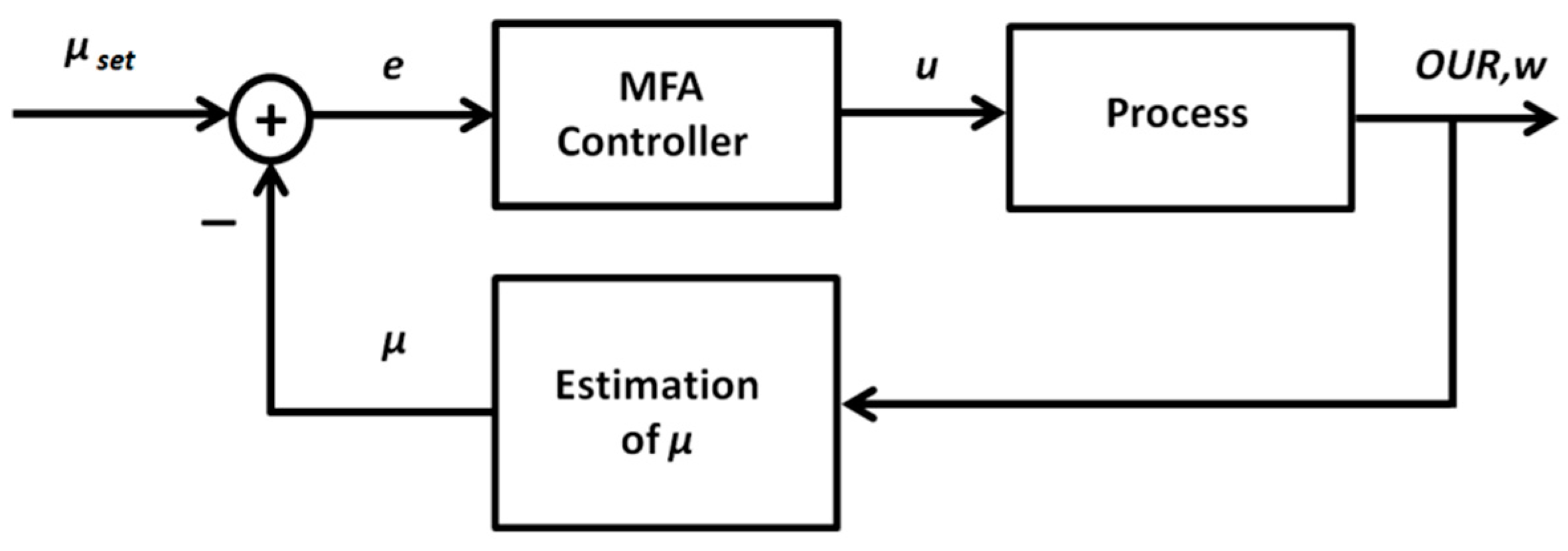
2.2. Adaptive Control Algorithms
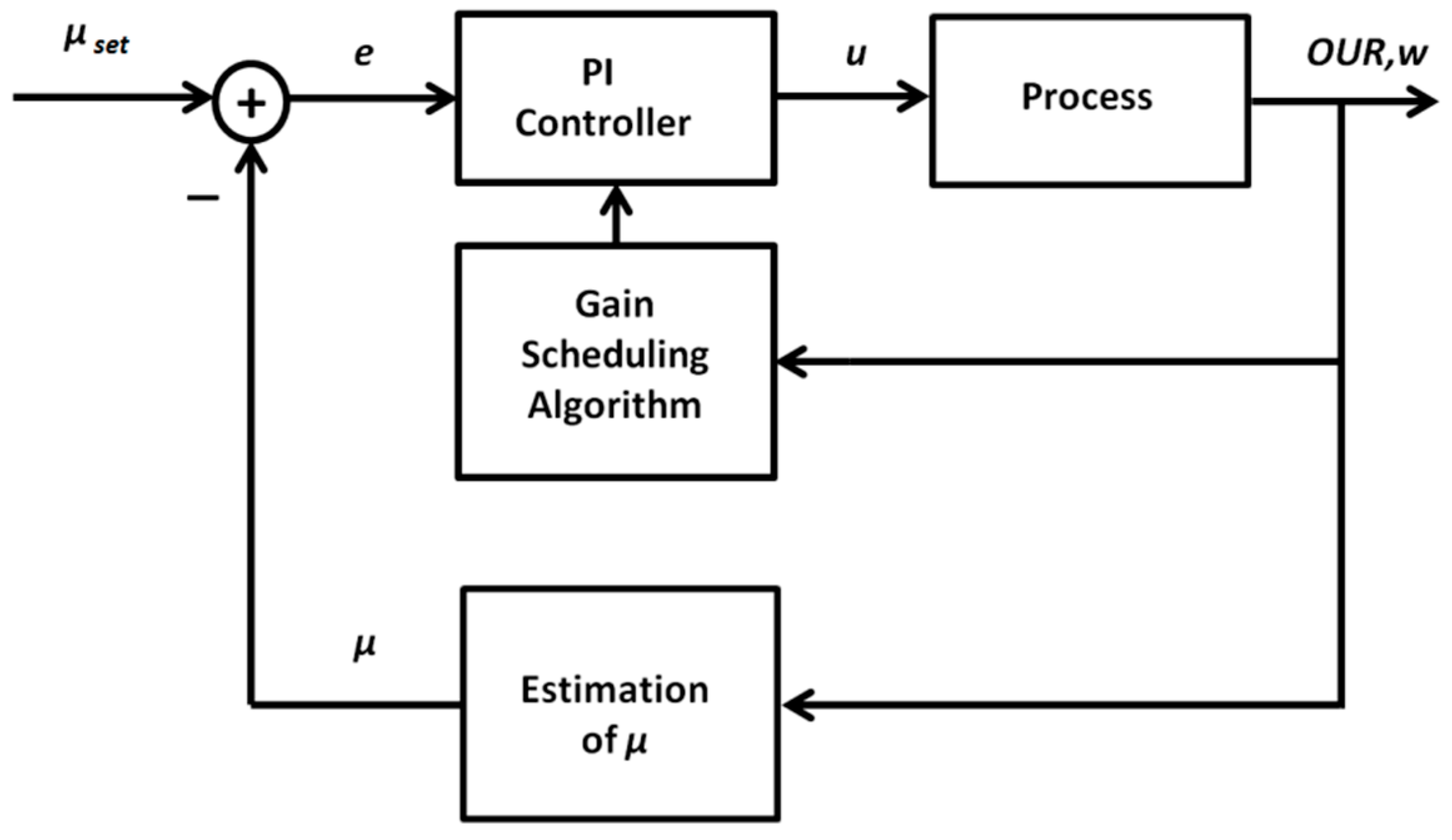
2.2.1. Adaptive PID Control Based on the Gain Scheduling Technique
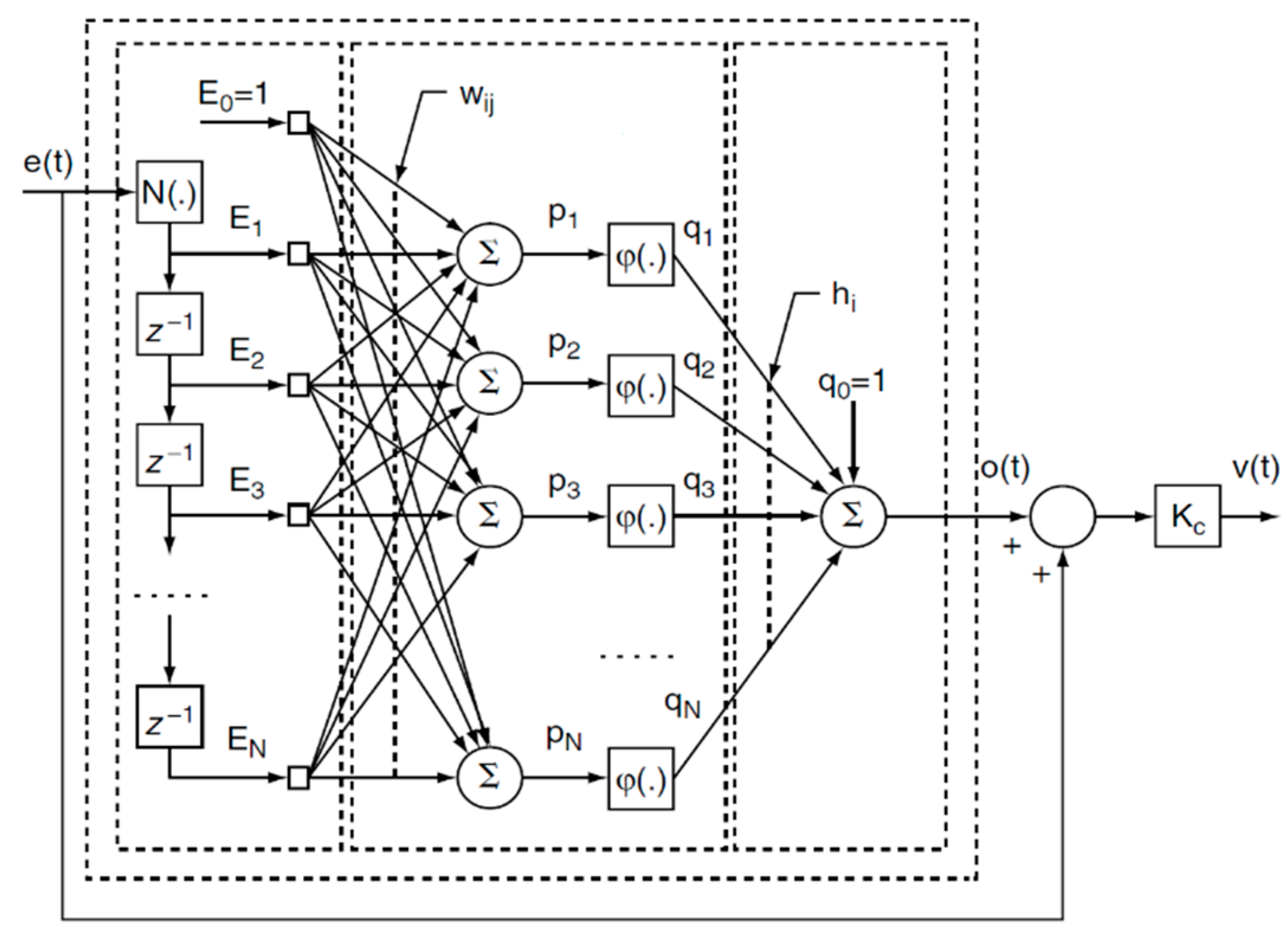
2.2.2. Model-Free Adaptive ANN-Based Control
2.3. Numerical Simulation Techniques
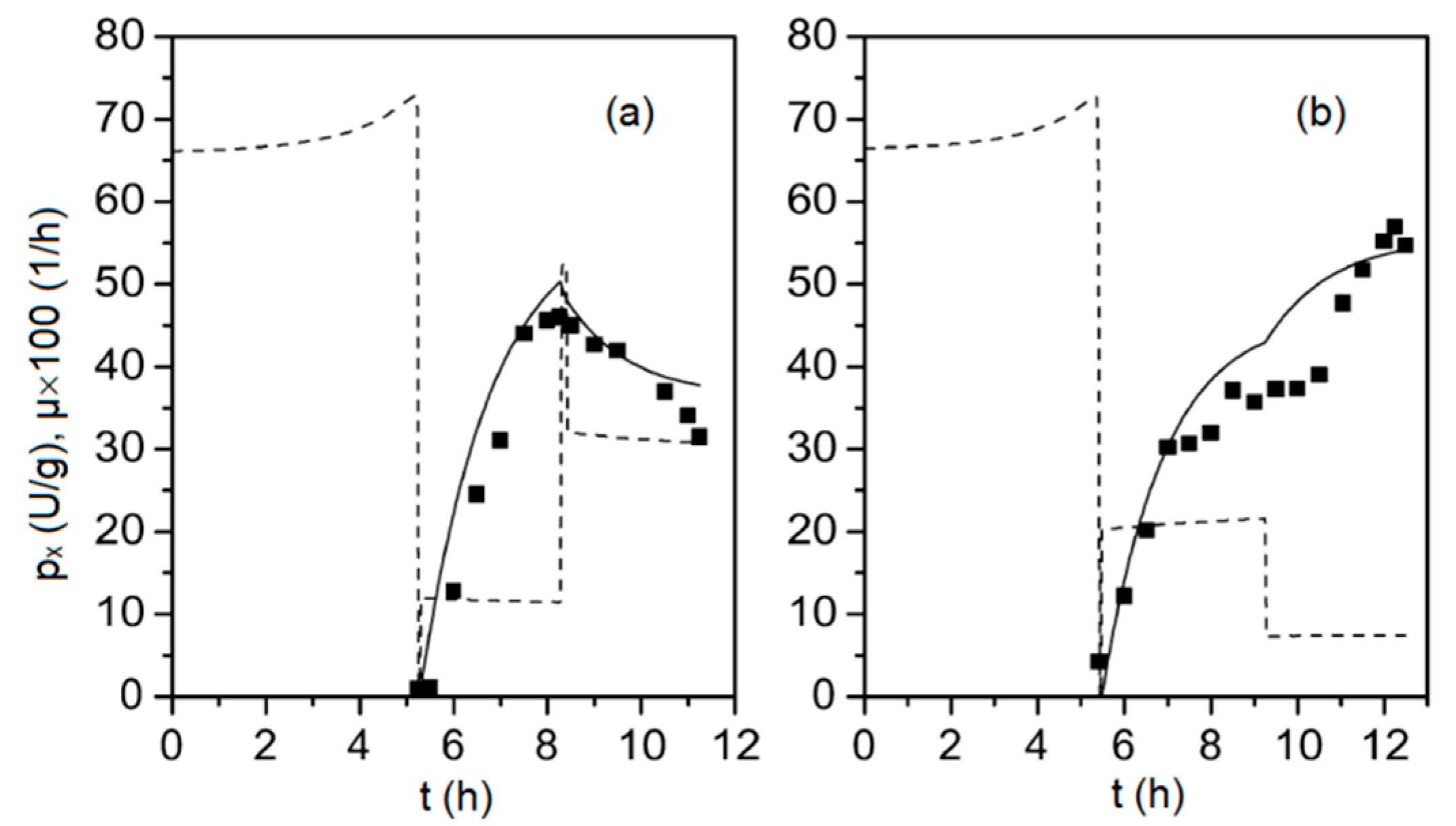
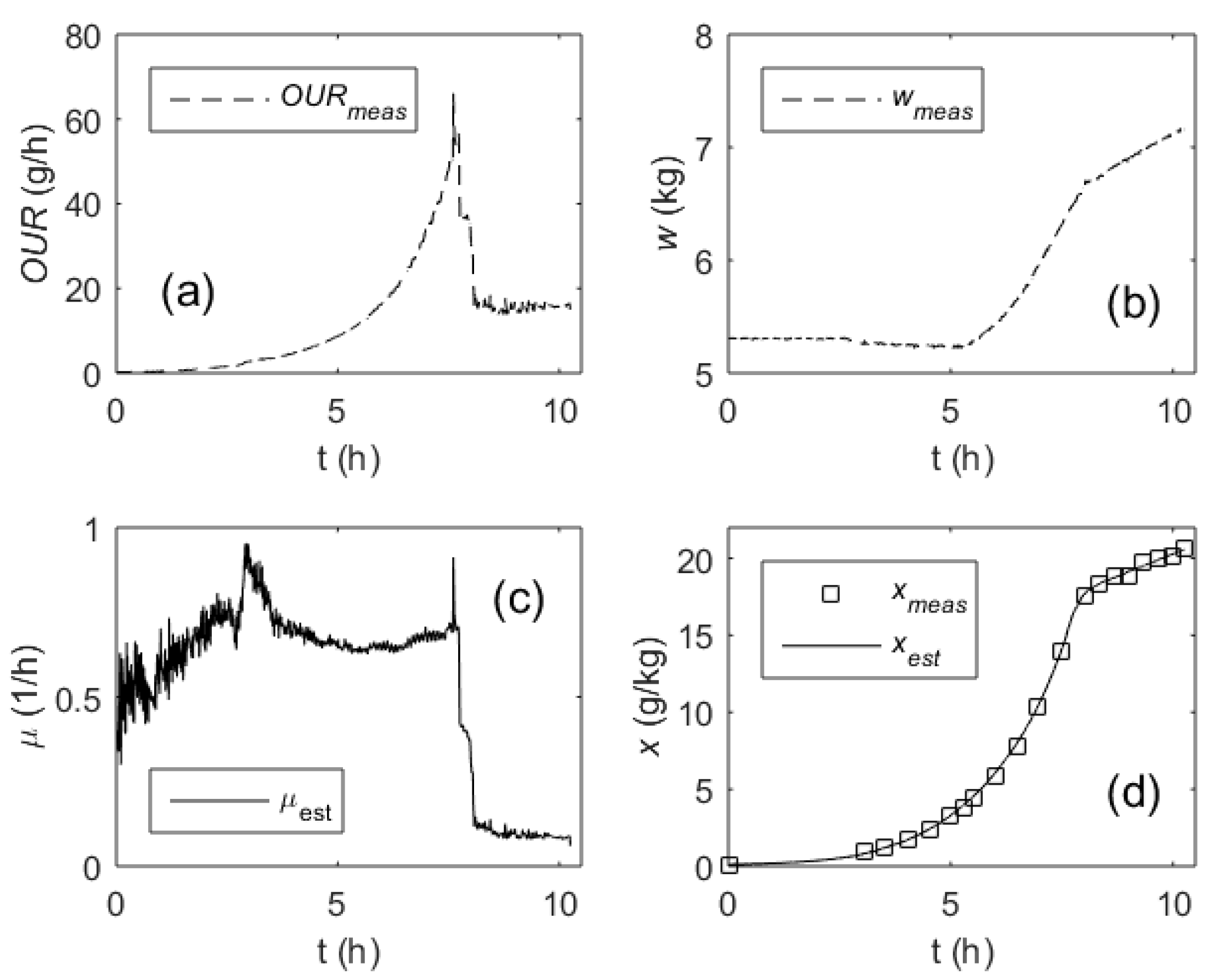
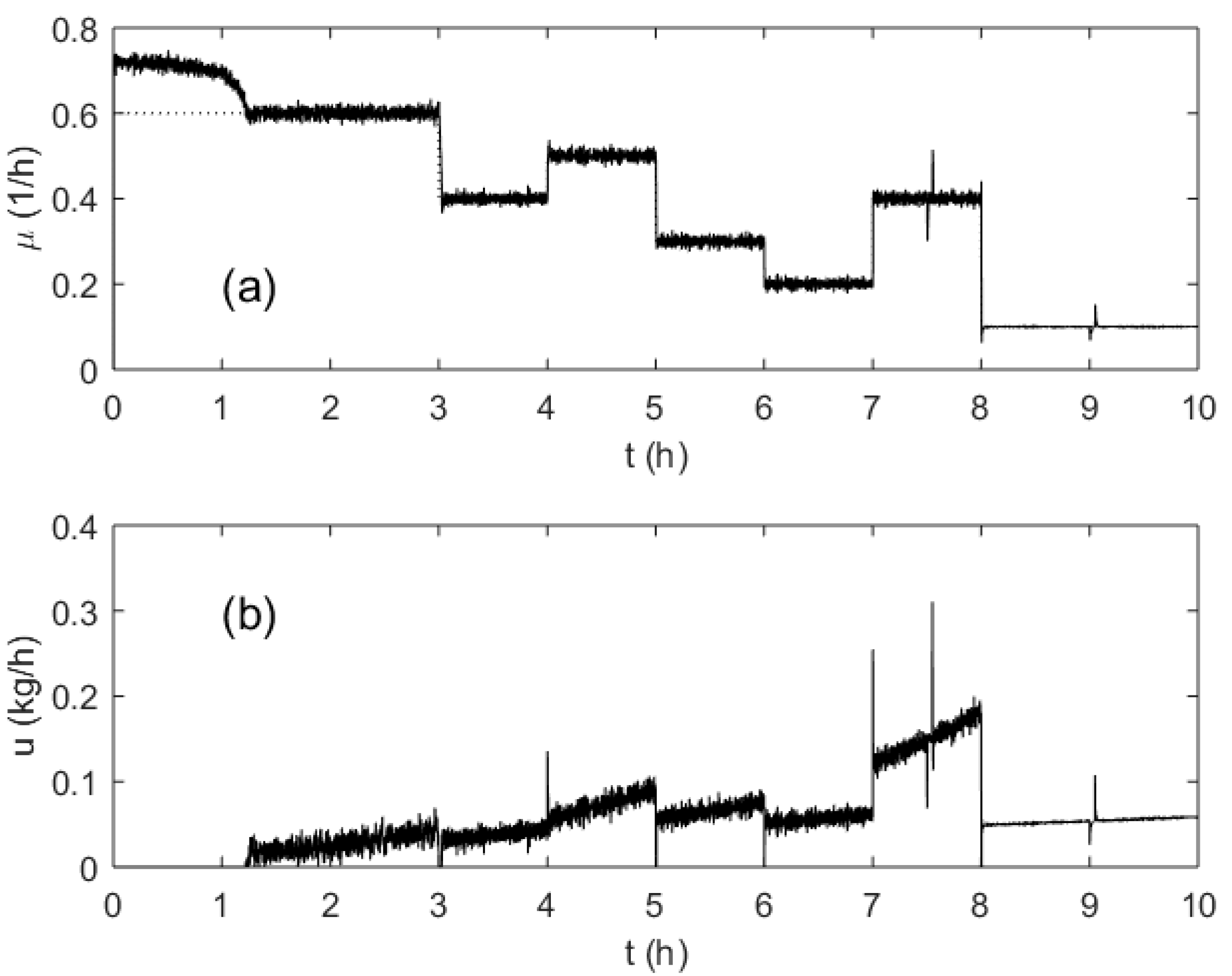
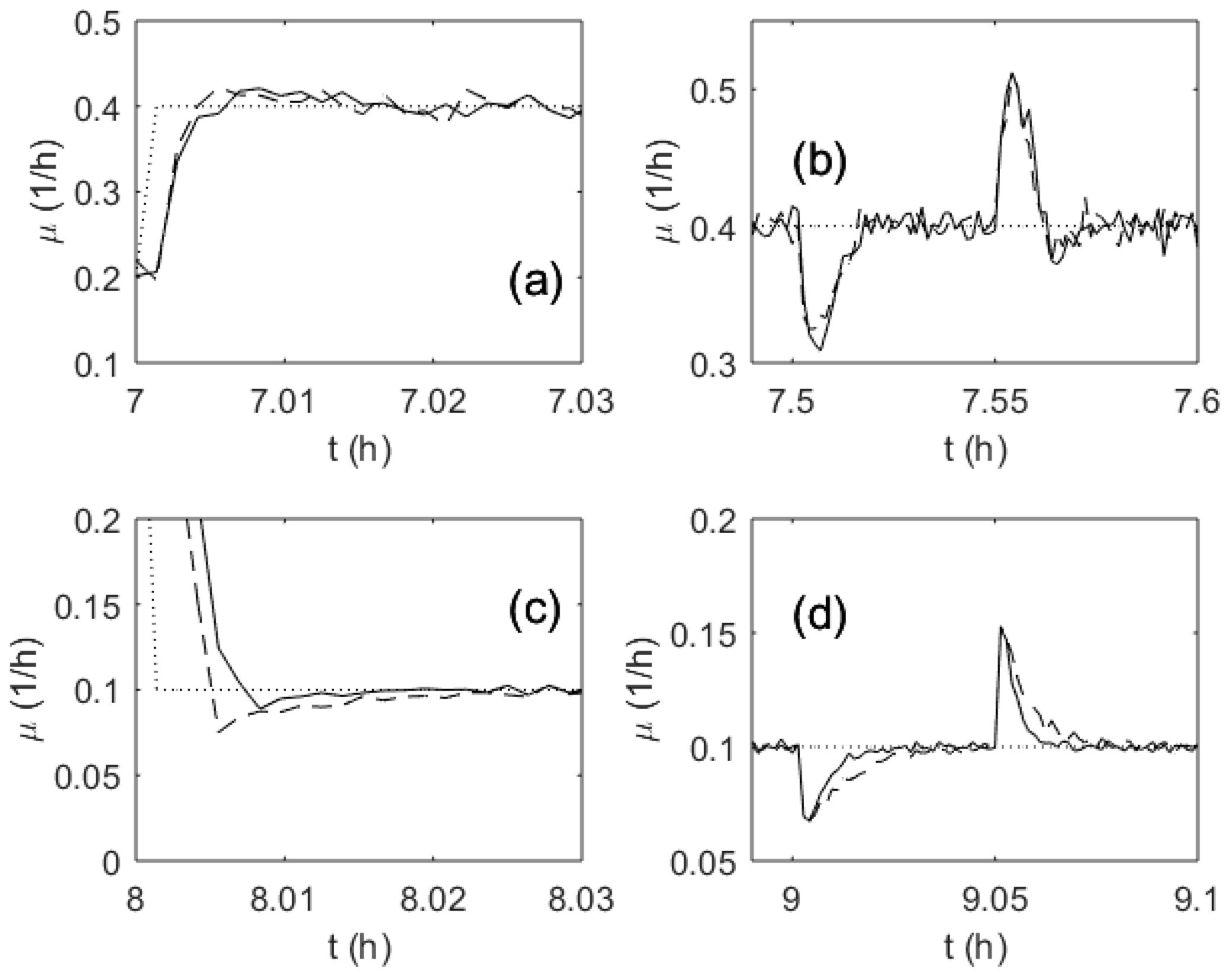
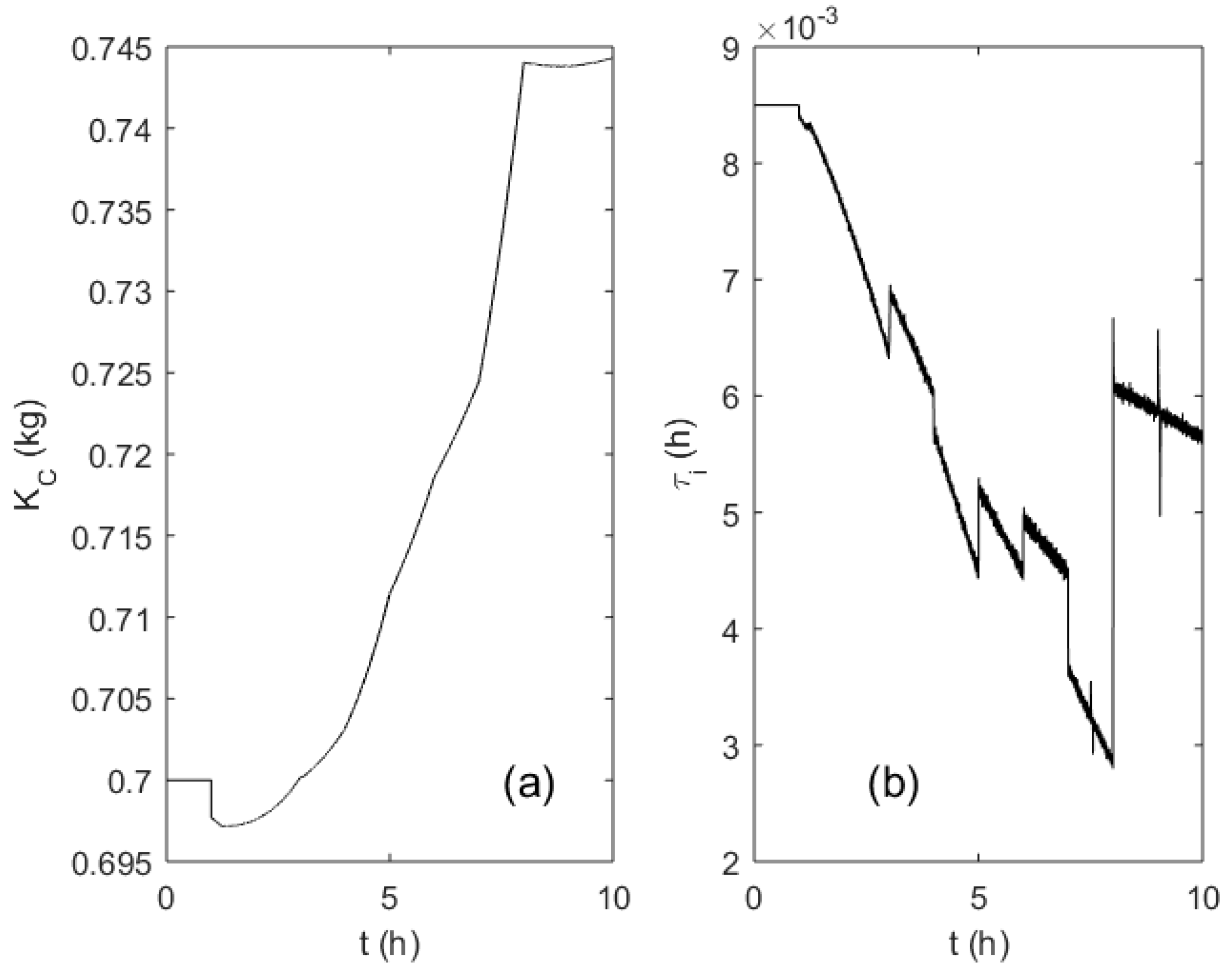
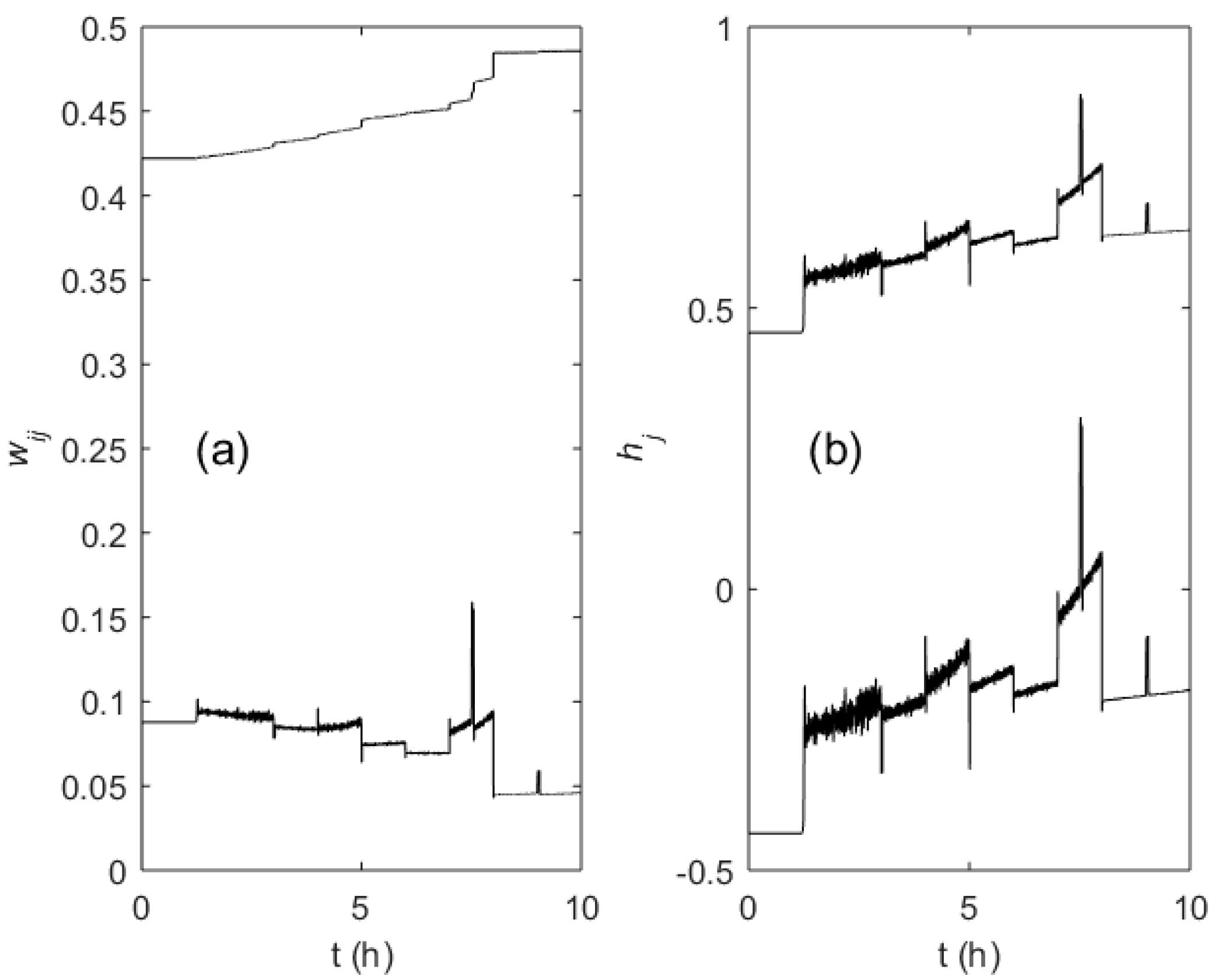
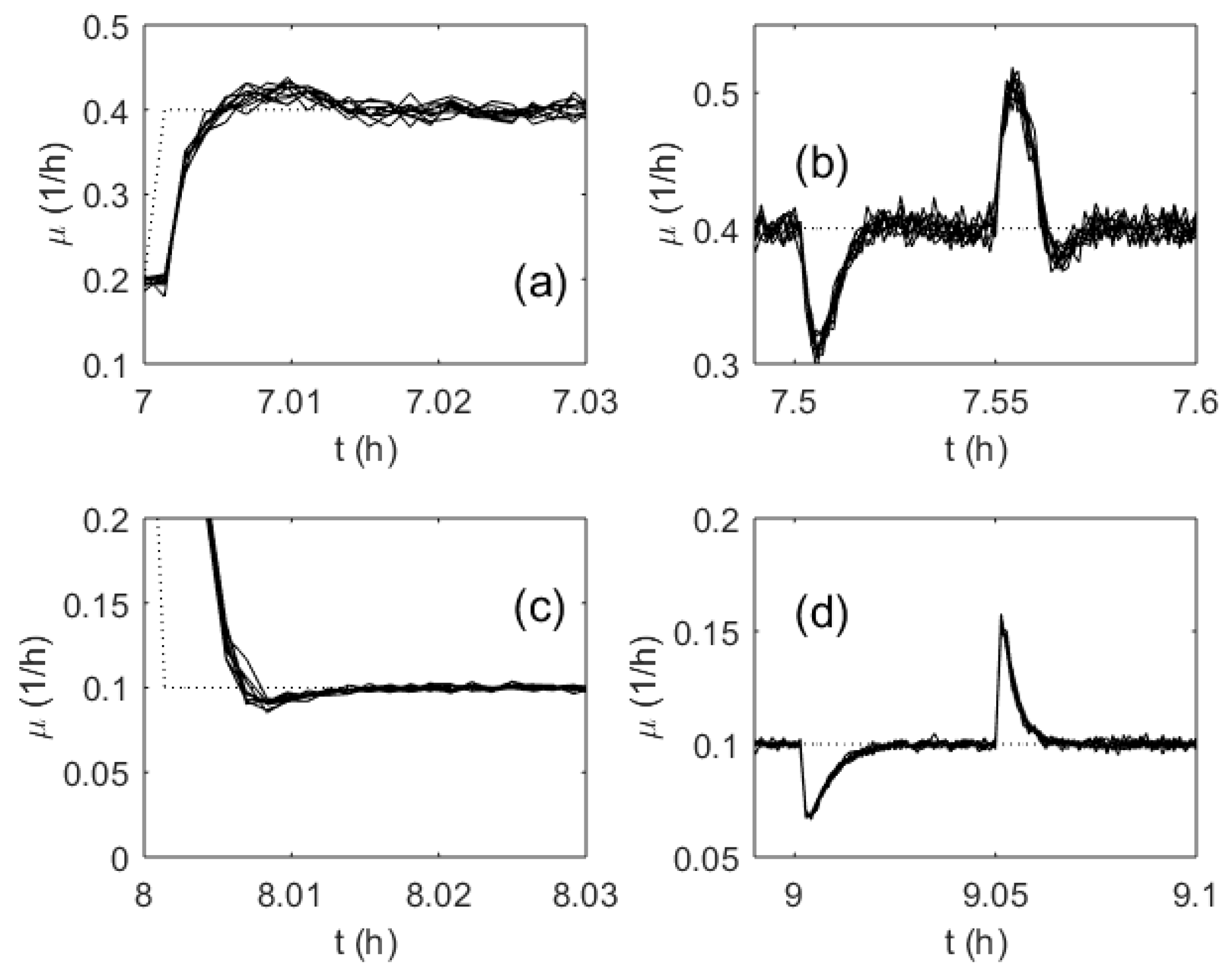
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Boudreau, M.A.; McMillan, G.K. New Directions in Bioprocess Modelling and Control: Maximizing Process Analytical Technology Benefits; ISA: Durham, NC, USA, 2006; ISBN 978-1-556-17905-1. [Google Scholar]
- Dochain, D. Bioprocess Control; ISTE: London, UK, 2008; ISBN 978-0-470-61112-8. [Google Scholar]
- Food and Drug Administration. Guidance for Industry. PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance. 2004. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/pat-framework-innovative-pharmaceutical-development-manufacturing-and-quality-assurance (accessed on 1 October 2019).
- Simutis, R.; Lübbert, A. Bioreactor control improves bioprocess performance. Biotechnol. J. 2015, 10, 1115–1130. [Google Scholar] [CrossRef] [PubMed]
- Galvanauskas, V.; Simutis, R.; Levišauskas, D.; Urniežius, R. Practical solutions for specific growth rate control systems in industrial bioreactors. Processes 2019, 7, 693. [Google Scholar] [CrossRef]
- Schuler, M.M.; Marison, I.W. Real-time monitoring and control of microbial bioprocesses with focus on the specific growth rate: Current state and perspectives. Appl. Microbiol. Biotechnol. 2012, 94, 1469–1482. [Google Scholar] [CrossRef] [PubMed]
- Rocha, I.; Veloso, A.; Carneiro, S.; Costa, R.; Ferreira, E. Implementation of a specific rate controller in a fed-batch E. coli fermentation. IFAC Proc. Vol. 2008, 41, 15565–15570. [Google Scholar] [CrossRef]
- Puertas, J.; Ruiz, J.; Vega, M.R.; Lorenzo, J.; Caminal, G.; González, G. Influence of specific growth rate over the secretory expression of recombinant potato carboxypeptidase inhibitor in fed-batch cultures of Escherichia coli. Process. Biochem. 2010, 45, 1334–1341. [Google Scholar] [CrossRef]
- Lim, H.C.; Shin, H.S. Fed-batch Cultures: Principles and Applications of Semi-Batch Bioreactors; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-0-521-51336-4. [Google Scholar] [CrossRef]
- Mears, L.; Stocks, S.M.; Sin, G.; Gernaey, K.V. A review of control strategies for manipulating the feed rate in fed-batch fermentation processes. J. Biotechnol. 2017, 245, 34–46. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.Y.; Park, S.; Middelberg, A.P.J. Control of fed-batch fermentations. Biotechnol. Adv. 1999, 17, 29–48. [Google Scholar] [CrossRef]
- Åkesson, M.; Hagander, P. A gain-scheduling approach for control of dissolved oxygen in stirred bioreactors. IFAC Proc. Vol. 1999, 32, 7608–7613. [Google Scholar] [CrossRef]
- Kuprijanov, A.; Gnoth, S.; Simutis, R.; Lübbert, A. Advanced control of dissolved oxygen concentration in fed batch cultures during recombinant protein production. Appl. Microbiol. Biotechnol. 2009, 82, 221–229. [Google Scholar] [CrossRef]
- Gnoth, S.; Kuprijanov, A.; Simutis, R.; Lübbert, A. Simple adaptive pH control in bioreactors using gain-scheduling methods. Appl. Microbiol. Biotechnol. 2009, 85, 955–964. [Google Scholar] [CrossRef]
- Levišauskas, D. An algorithm for adaptive control of dissolved oxygen concentration in batch culture. Biotechnol. Tech. 1995, 9, 85–90. [Google Scholar] [CrossRef]
- Levišauskas, D.; Simutis, R.; Galvanauskas, V. Adaptive set-point control system for microbial cultivation processes. Nonlinear Anal. Model. Control. 2016, 21, 153–165. [Google Scholar] [CrossRef]
- Babuška, R.; Damen, M.R.; Hellinga, C.; Maarleveld, H. Intelligent adaptive control of bioreactors. J. Intell. Manuf. 2003, 14, 255–265. [Google Scholar] [CrossRef]
- Smets, I.Y.; Claes, J.E.; November, E.J.; Bastin, G.P.; Impe, J.F. Optimal adaptive control of (bio) chemical reactors: Past, present and future. J. Process. Contr. 2004, 14, 795–805. [Google Scholar] [CrossRef]
- Bastin, G.; Impe, J.F. Nonlinear and adaptive control in biotechnology: A tutorial. Eur. J. Contr. 1995, 1, 37–53. [Google Scholar] [CrossRef]
- Ginkel, S.Z.; Dooley, T.P.; Suling, W.J.; Barrow, W.W. Identification and cloning of the Mycobacterium avium folA gene, required for dihydrofolate reductase activity. FEMS Microbiol. Lett. 2006, 156, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Levišauskas, D.; Galvanauskas, V.; Henrich, S.; Wilhelm, K.; Volk, N.; Lübbert, A. Model-based optimization of viral capsid protein production in fed-batch culture of recombinant Escherichia coli. Bioproc. Biosyst. Eng. 2003, 25, 255–262. [Google Scholar] [CrossRef]
- Galvanauskas, V.; Volk, N.; Simutis, R.; Lübbert, A. Design of recombinant protein production processes. Chem. Eng. Comm. 2004, 191, 732–748. [Google Scholar] [CrossRef]
- Gasser, B.; Saloheimo, M.; Rinas, U.; Dragosits, M.; Rodríguez-Carmona, E.; Baumann, K.; Villaverde, A. Protein folding and conformational stress in microbial cells producing recombinant proteins: A host comparative overview. Microb. Cell. Fact. 2008, 7, 11. [Google Scholar] [CrossRef]
- Gnoth, S.; Jenzsch, M.; Simutis, R.; Lübbert, A. Product formation kinetics in genetically modified E. coli bacteria: Inclusion body formation. Bioproc. Biosyst. Eng. 2007, 31, 41–46. [Google Scholar] [CrossRef]
- Gnoth, S.; Simutis, R.; Lübbert, A. Selective expression of the soluble product fraction in Escherichia coli cultures employed in recombinant protein production processes. Appl. Microbiol. Biotechnol. 2010, 87, 2047–2058. [Google Scholar] [CrossRef] [PubMed]
- Luedeking, R.; Piret, E.L. A kinetic study of the lactic acid fermentation. Batch process at controlled pH. Biotechnol. Bioeng. 2000, 67, 636–644. [Google Scholar] [CrossRef]
- Pirt, S.J. Principles of Microbe and Cell Cultivation; Blackwell Scientific Publications: Oxford, UK, 1985; ISBN 978-0-632-01455-2. [Google Scholar]
- Rivera, D.E.; Morari, M.; Skogestad, S. Internal model control: PID controller design. Ind. Eng. Chem. Process. Des. Dev. 1986, 25, 252–265. [Google Scholar] [CrossRef]
- Simutis, R.; Lübbert, A. Hybrid approach to state estimation for bioprocess control. Bioengineering 2017, 4, 21. [Google Scholar] [CrossRef] [PubMed]
- Urniezius, R.; Survyla, A.; Paulauskas, D.; Bumelis, V.A.; Galvanauskas, V. Generic estimator of biomass concentration for Escherichia coli and Saccharomyces cerevisiae fed-batch cultures based on cumulative oxygen consumption rate. Microb. Cell Factories 2019, in press. [Google Scholar] [CrossRef]
- Cheng, G.S. Model Free Adaptive control with CYBOCON. In Techniques for Adaptive Control; VanDoren, V.J., Ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2003; pp. 145–202. [Google Scholar]
- Press, W.H.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fogel, D.B. Evolutionary Computation toward a New Philosophy of Machine Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]

| Model Parameter | Value | Units |
|---|---|---|
| Ki | 93.8 ± 12.7 | g/kg |
| Kiµ | 0.0174 ± 0.0012 | 1/h |
| Km | 751 ± 27 | U/g |
| Ks | 0.01 ± 0.005 | g/kg |
| Kµ | 0.61 ± 0.03 | 1/h |
| m | 0.0242 ± 0.004 | g/(gh) |
| mox | 0.05 ± 0.0025 | g/(gh) |
| sf | 151 | g/kg |
| Tpx | 1.5 ± 0.1 | h |
| Tref | 37 | °C |
| Yox | 0.7 ± 0.01 | g/g |
| Yxs | 0.46 ± 0.01 | g/g |
| α | 0.0495 ± 0.0025 | 1/°C |
| µmax | 0.737 ± 0.01 | 1/h |
| Model Parameter | Value | Units |
|---|---|---|
| KC | 0.4 | kg |
| η | 1.5 | – |
| κ0 | 0.14 | kg |
| κ1 | 0.008 | g/kg |
| κ2 | 0.8 | g/(kg h) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galvanauskas, V.; Simutis, R.; Vaitkus, V. Adaptive Control of Biomass Specific Growth Rate in Fed-Batch Biotechnological Processes. A Comparative Study. Processes 2019, 7, 810. https://doi.org/10.3390/pr7110810
Galvanauskas V, Simutis R, Vaitkus V. Adaptive Control of Biomass Specific Growth Rate in Fed-Batch Biotechnological Processes. A Comparative Study. Processes. 2019; 7(11):810. https://doi.org/10.3390/pr7110810
Chicago/Turabian StyleGalvanauskas, Vytautas, Rimvydas Simutis, and Vygandas Vaitkus. 2019. "Adaptive Control of Biomass Specific Growth Rate in Fed-Batch Biotechnological Processes. A Comparative Study" Processes 7, no. 11: 810. https://doi.org/10.3390/pr7110810
APA StyleGalvanauskas, V., Simutis, R., & Vaitkus, V. (2019). Adaptive Control of Biomass Specific Growth Rate in Fed-Batch Biotechnological Processes. A Comparative Study. Processes, 7(11), 810. https://doi.org/10.3390/pr7110810





