Flow Characteristics and Stress Analysis of a Parallel Gate Valve
Abstract
:1. Introduction
2. Model Description
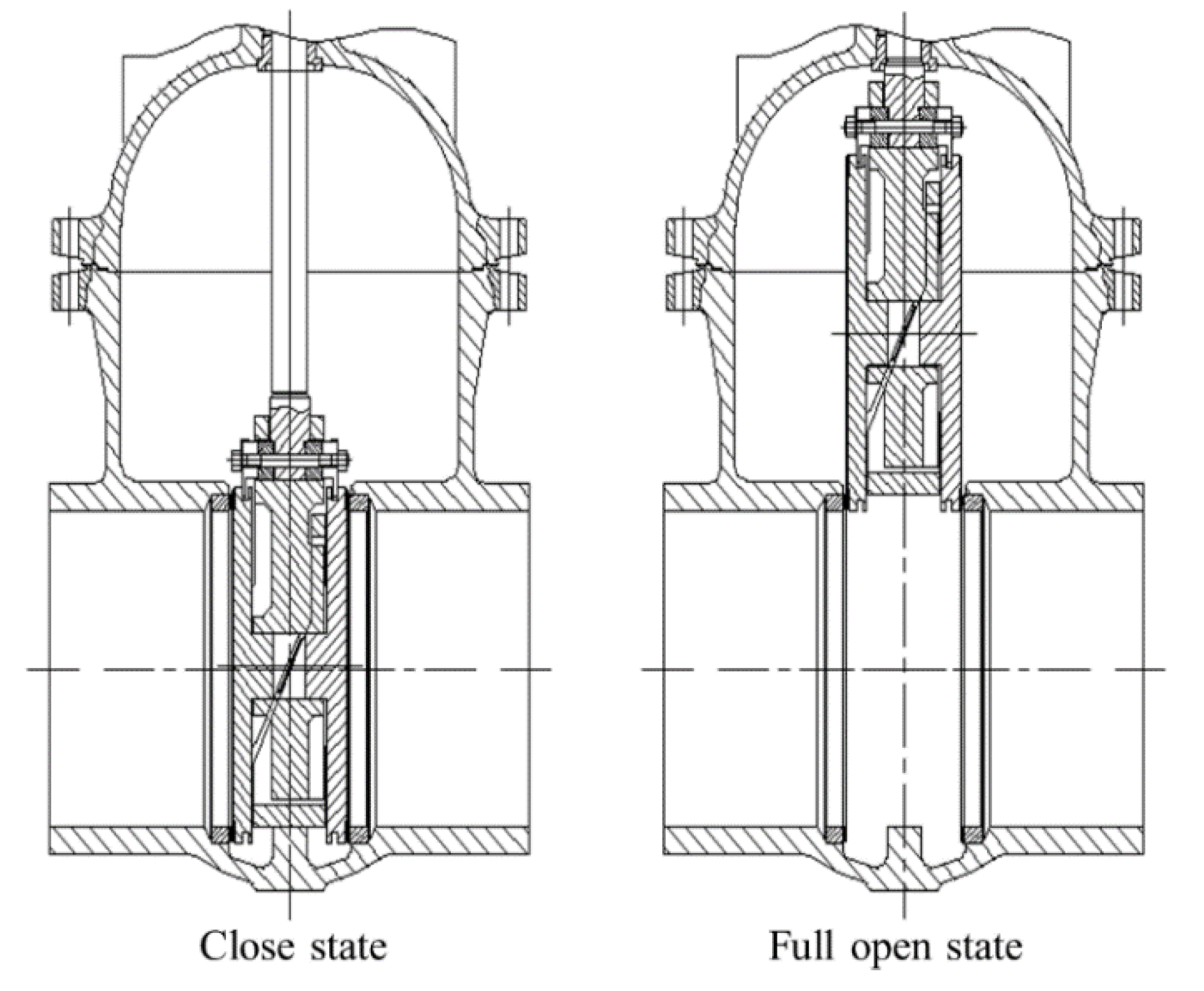
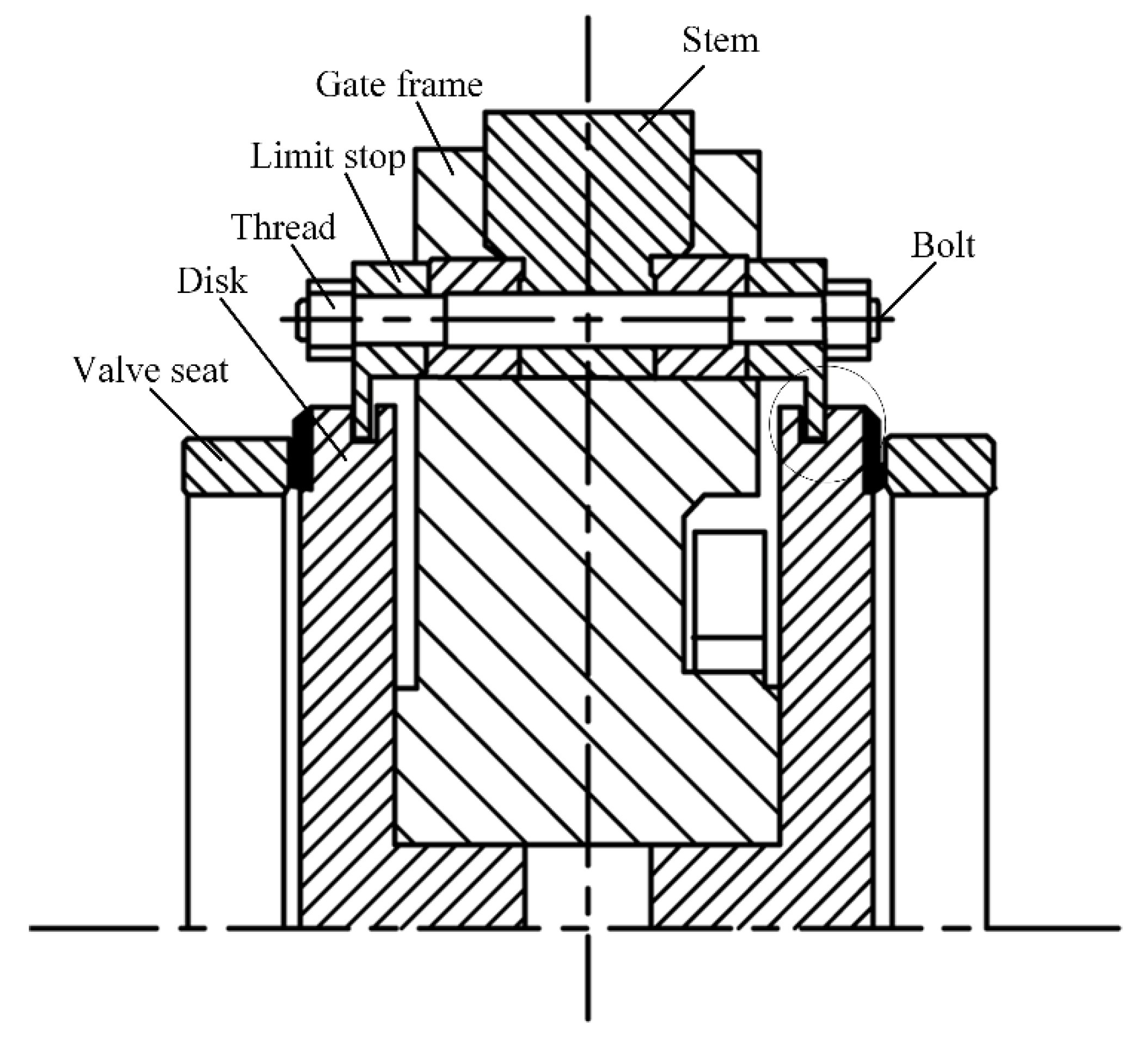
2.1. Physic Model
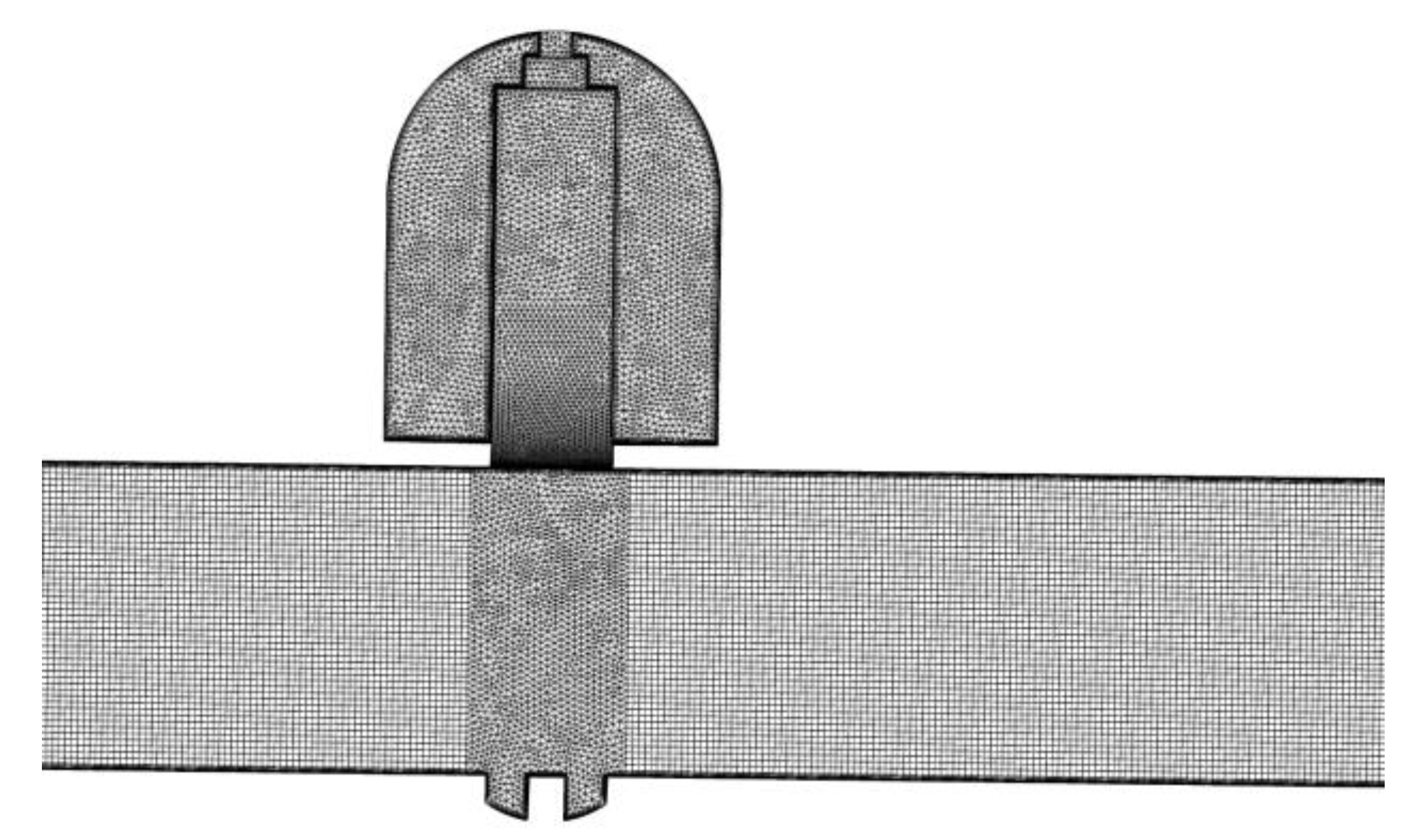
2.2. Numerical Model
2.3. Model Validation
3. Results and Discussion
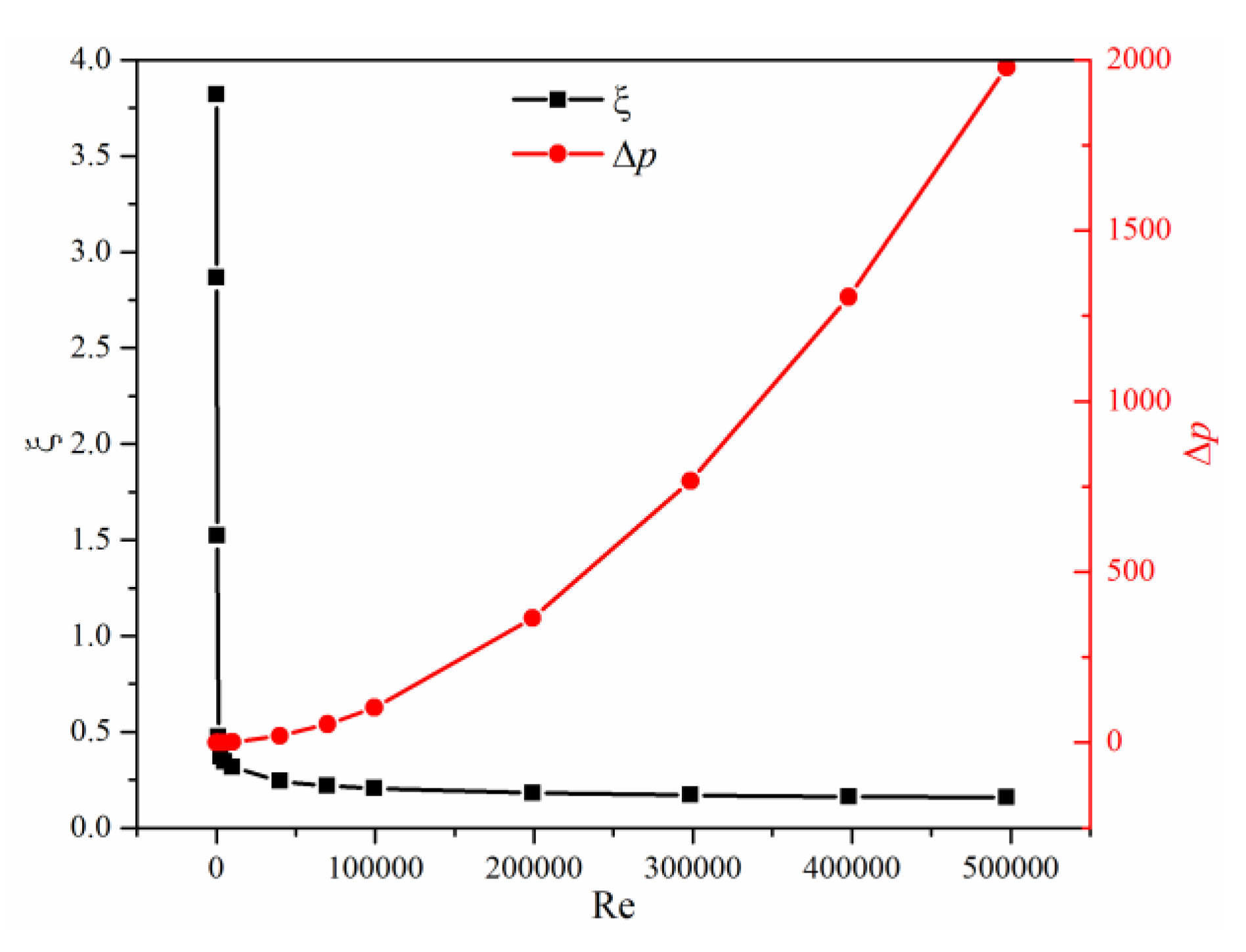
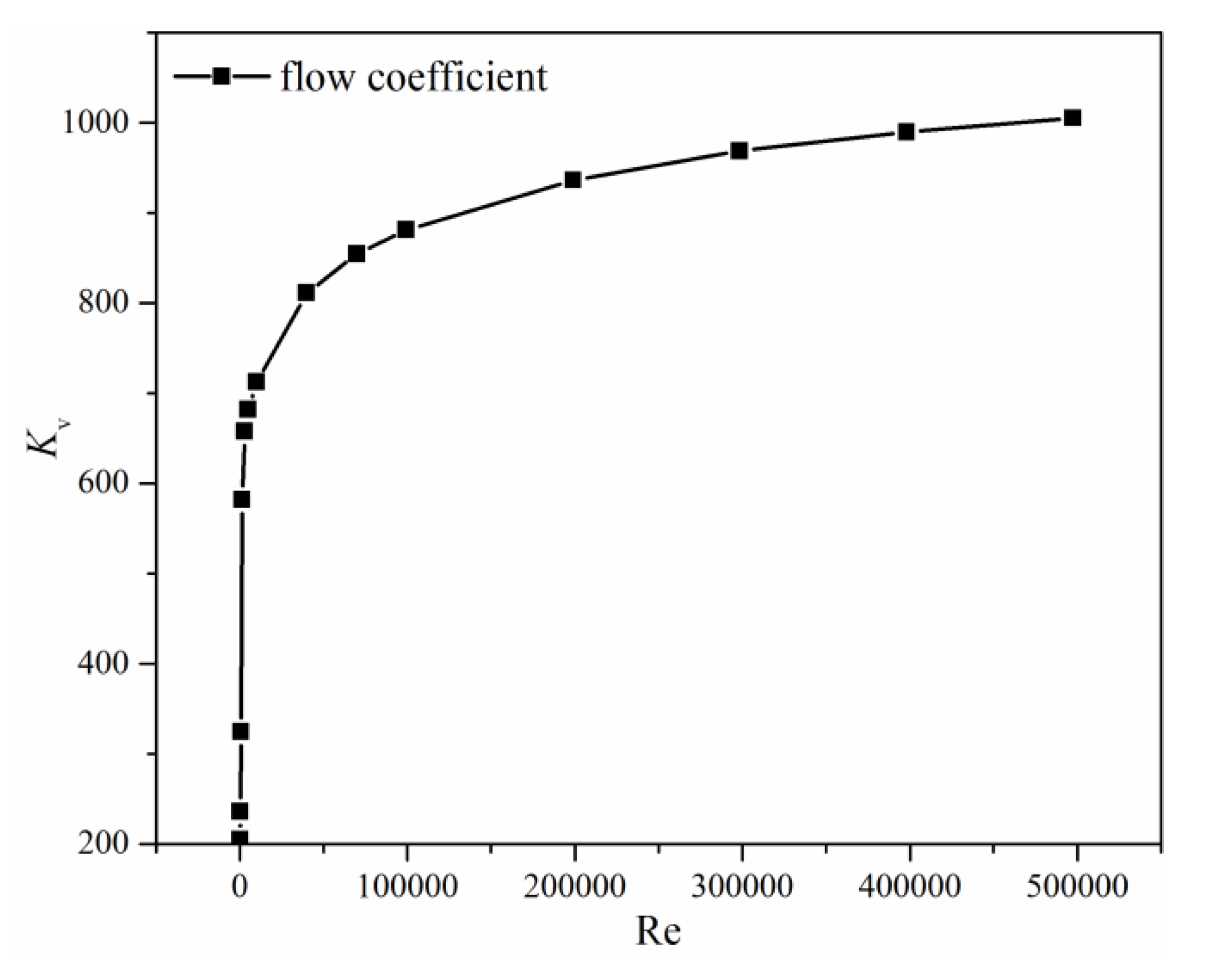
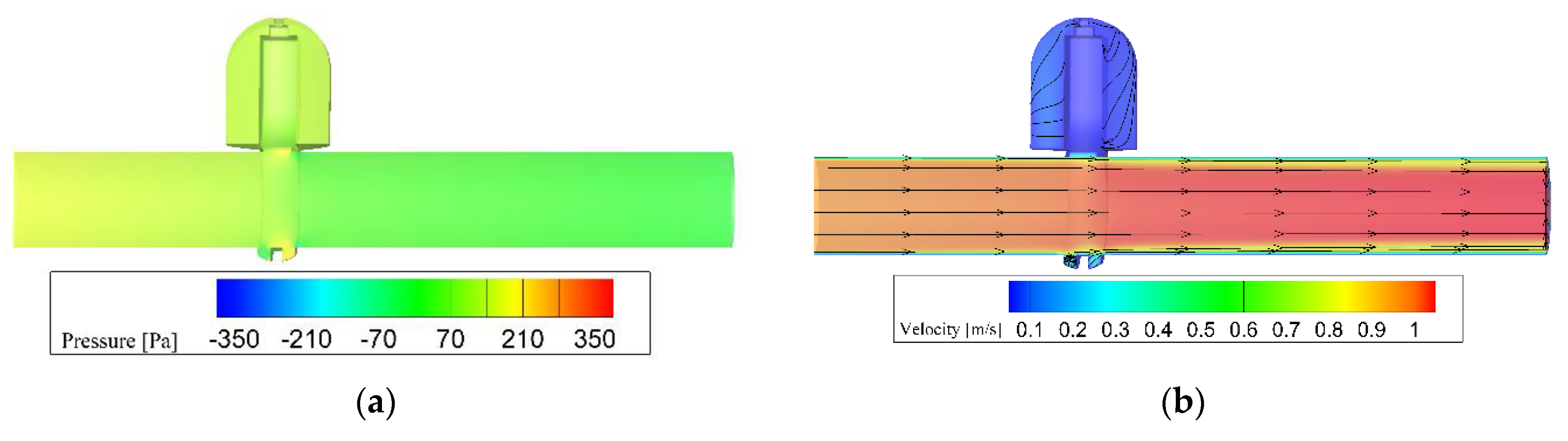
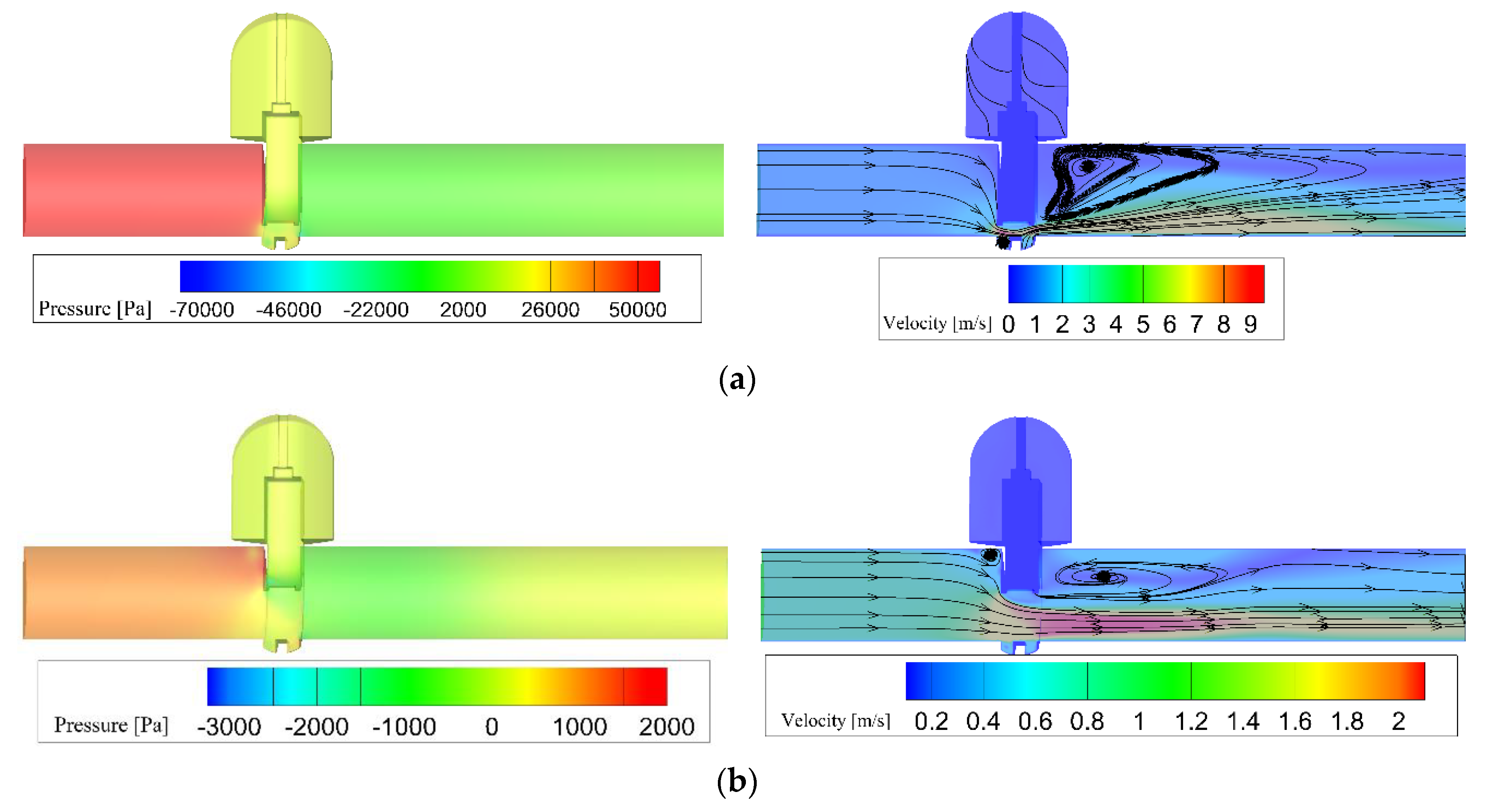
3.1. Flow and Loss Characteristics
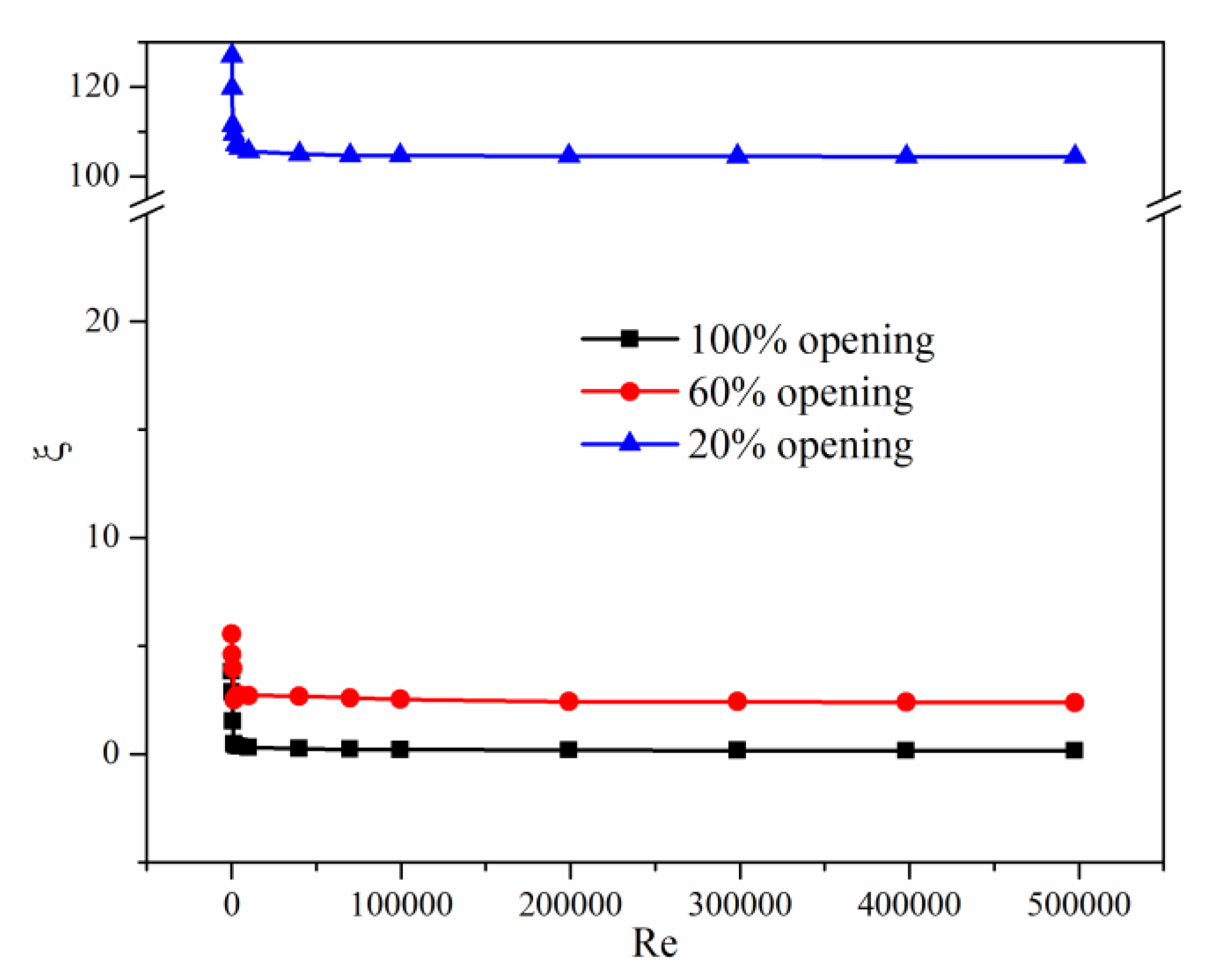
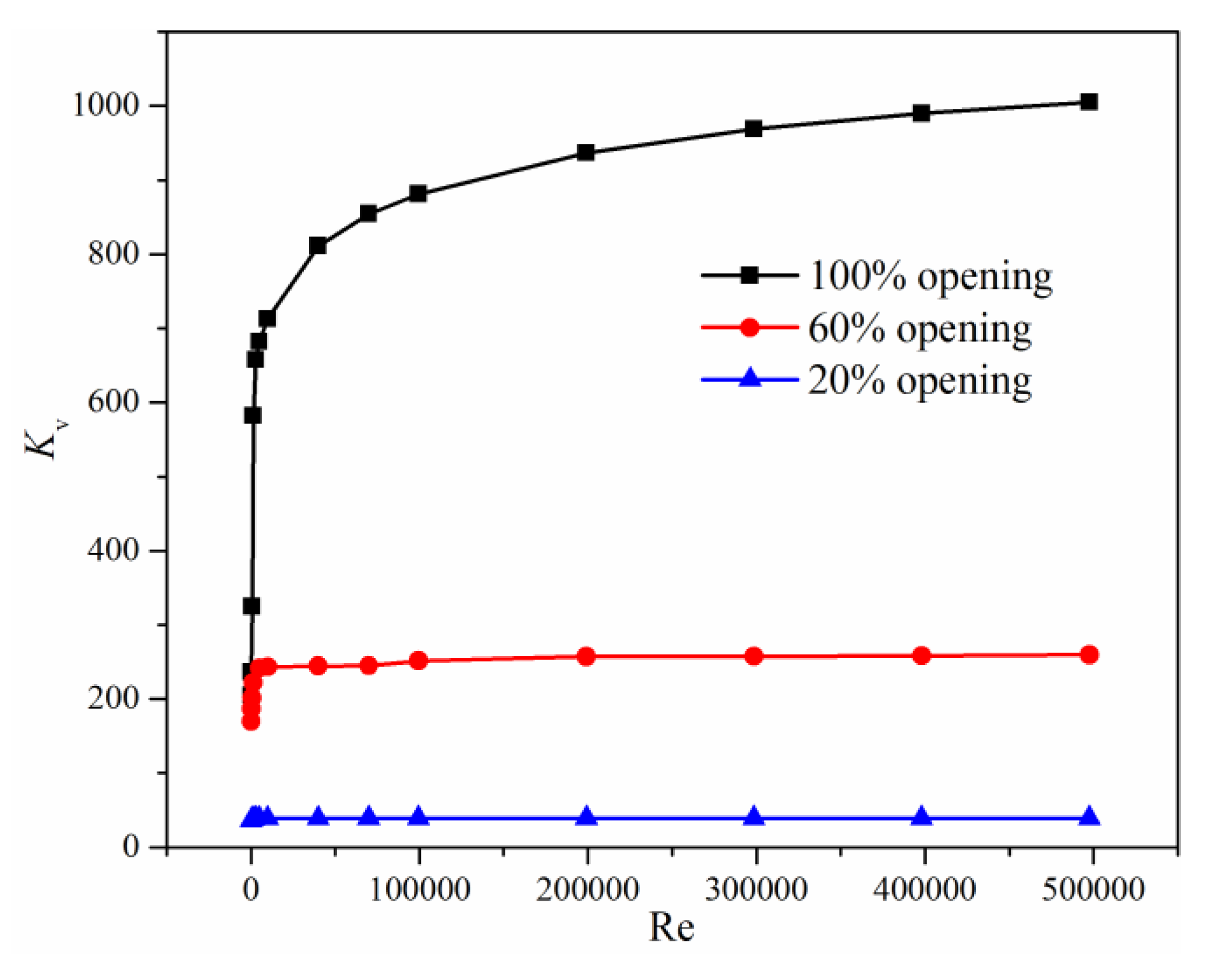
3.2. Effects of Valve Opening Degree
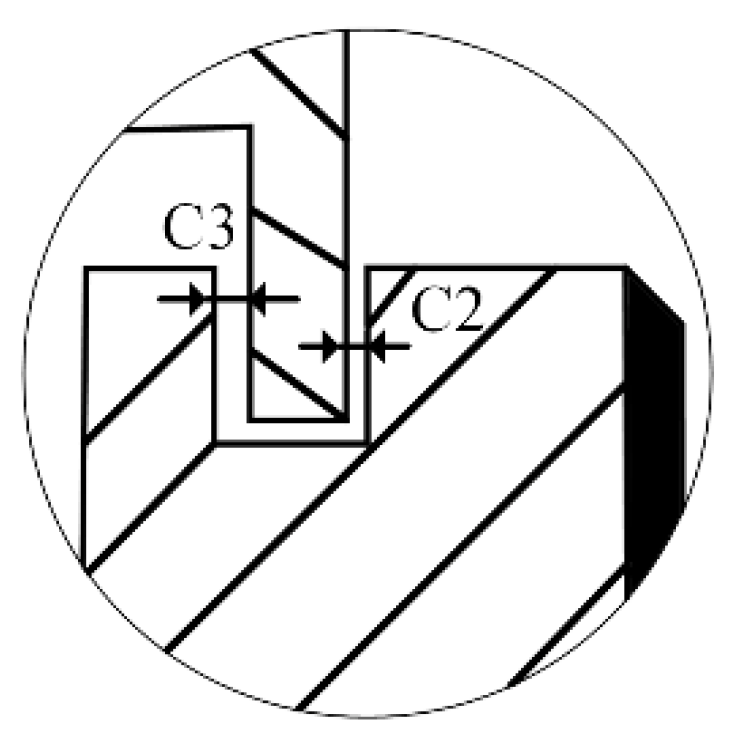
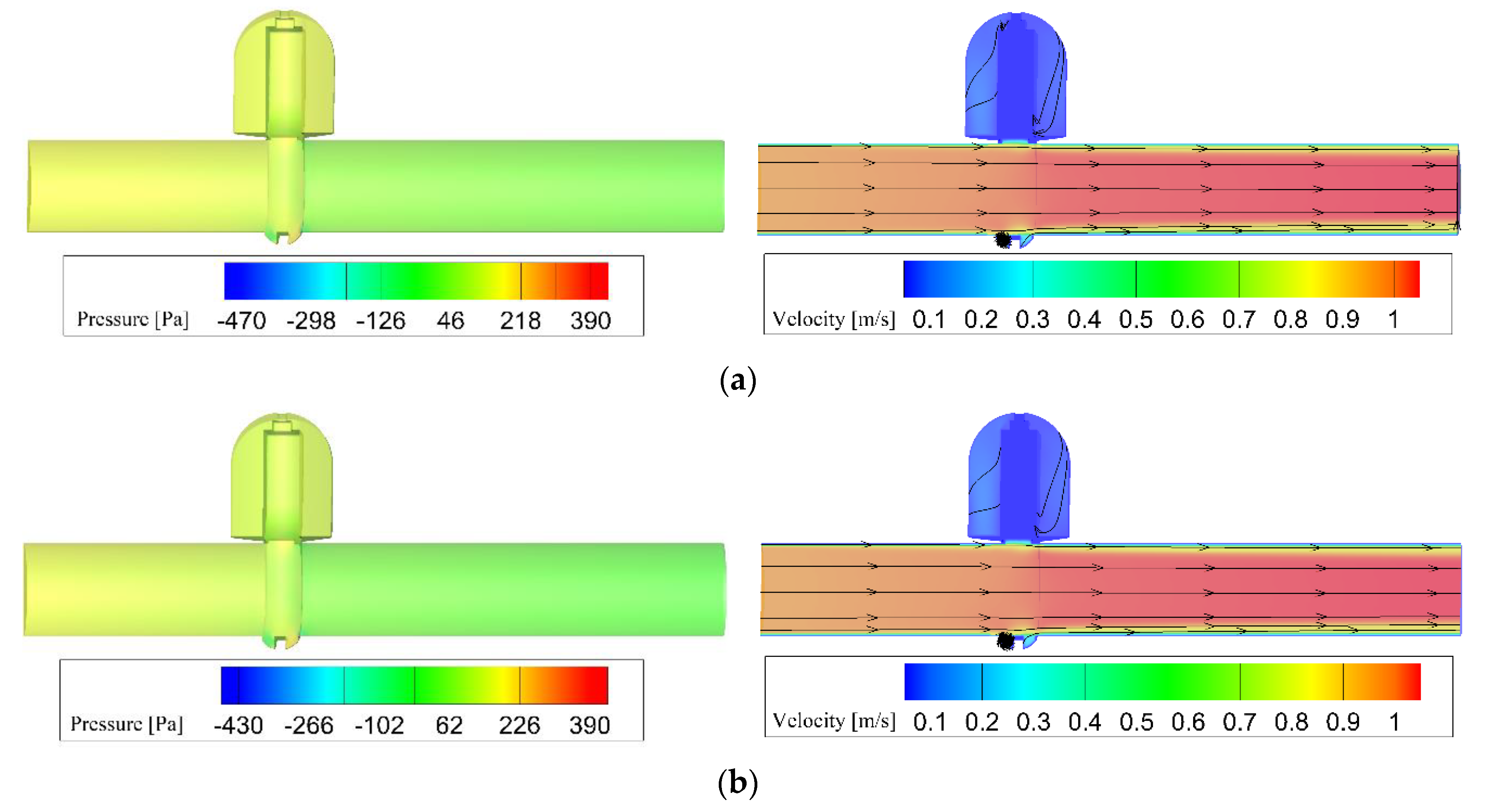
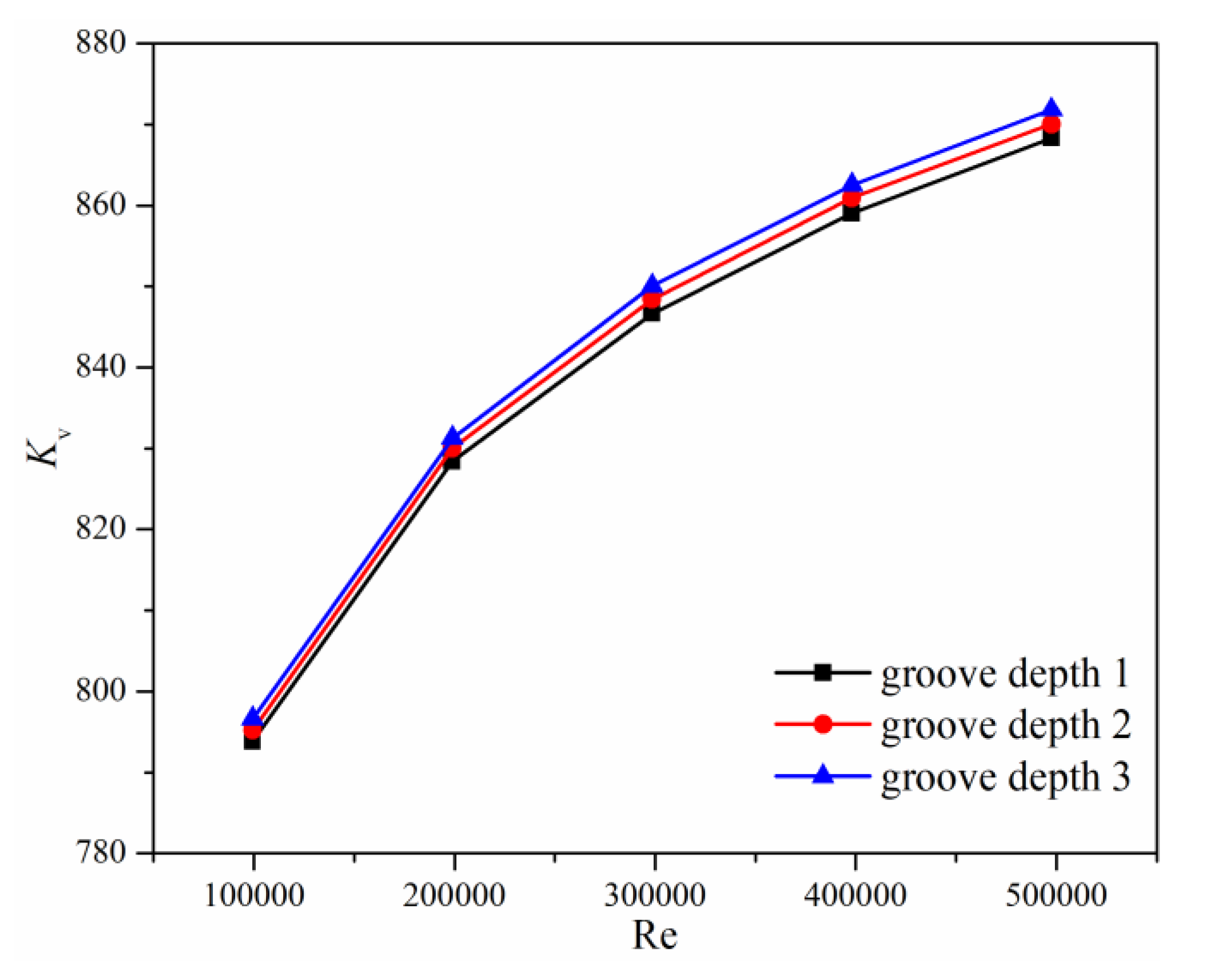
3.3. Effects of the Groove Depth
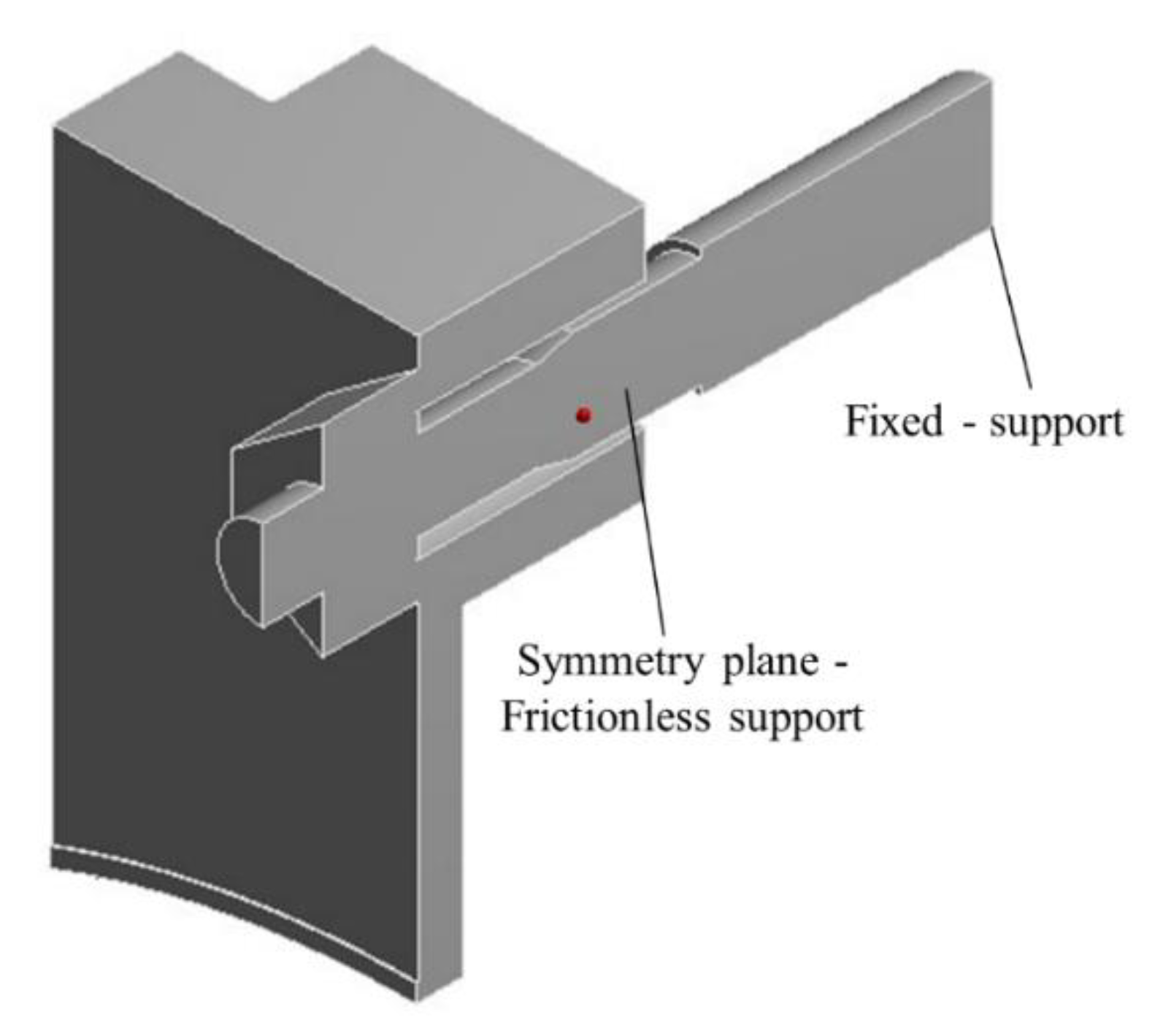
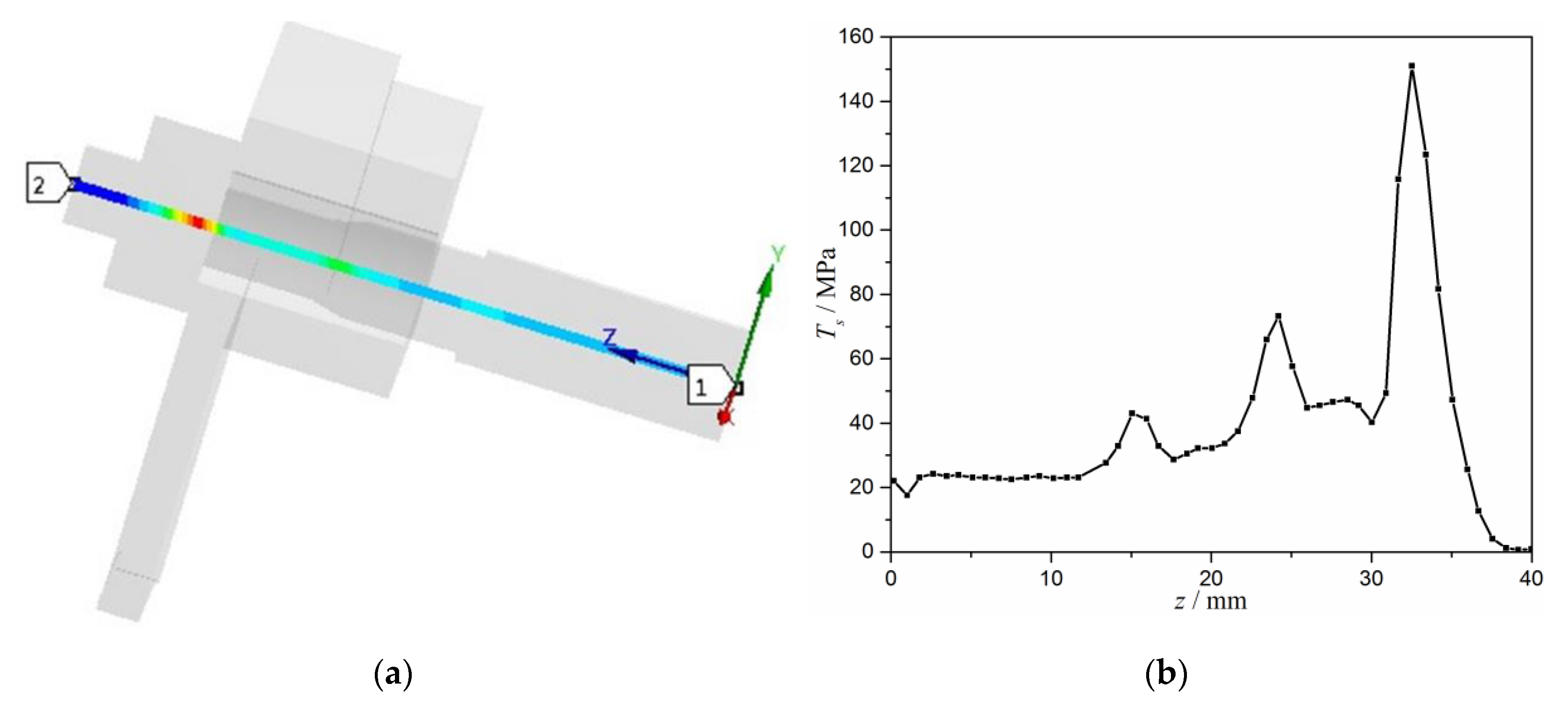
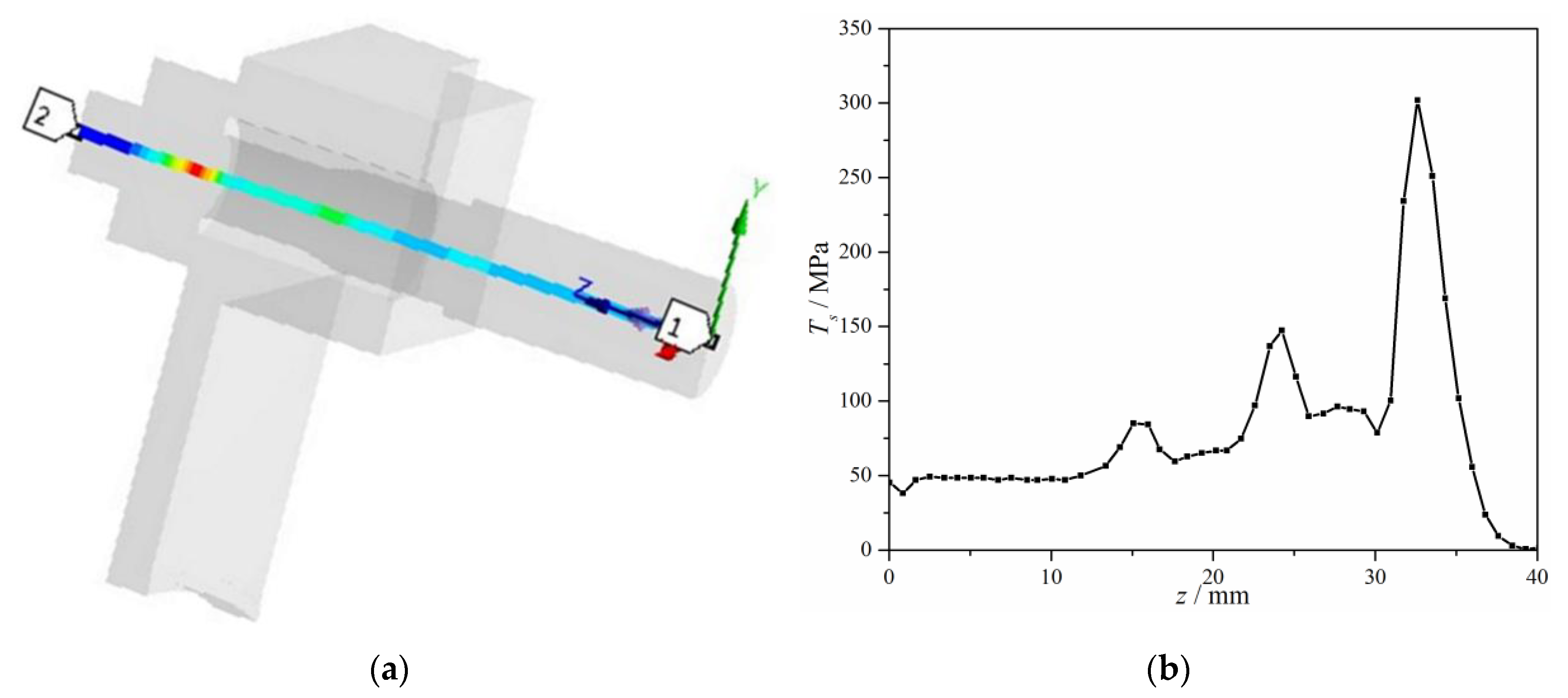
3.4. Stress Analysis of the Bolt
3.4.1. Effects of the Gap C2
3.4.2. Effects of the Gap C3
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barsoum, I.; Muñoz, A. Failure Analysis of a Large Knife Gate Valve Subjected to Multiaxial Loading. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2017. [Google Scholar]
- Owen, D.M.; Beavers, J.A. Investigation of Bolt Failures on a Gate Valve from a Natural Gas Pipeline. In Proceedings of the 4th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2002; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2002. [Google Scholar]
- Ifezue, D.; Tobins, F. Failure Investigation of a Gate Valve Eye Bolt Fracture During Hydrotesting. J. Fail. Anal. Prev. 2013, 13, 249–256. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Gao, Z.X.; Jin, Z.J. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Qian, J.Y.; Wu, J.Y.; Gao, Z.X.; Wu, A.; Jin, Z.J. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrogen Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Yuan, C.; Song, J.; Zhu, L.; Liu, M. Numerical investigation on cavitating jet inside a poppet valve with special emphasis on cavitation-vortex interaction. Int. J. Heat Mass Transfer 2019, 141, 1009–1024. [Google Scholar] [CrossRef]
- Jin, Z.J.; Gao, Z.X.; Qian, J.Y.; Wu, Z.; Sunden, B. A parametric study of hydrodynamic cavitation inside globe valves. ASME J. Fluids Eng. 2018, 140, 031208. [Google Scholar] [CrossRef]
- Dasgupta, K.; Ghoshal, S.K.; Kumar, S.; Das, J. Dynamic analysis of an open-loop proportional valve controlled hydrostatic drive. Proc. Inst. Mech. Eng. Part E 2019, 0954408919861247. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, L.; Yang, L. Numerical simulation study on the opening process of the atmospheric relief valve. Nucl. Eng. Des. 2019, 351, 106–115. [Google Scholar] [CrossRef]
- Qian, J.Y.; Wei, L.; Jin, Z.J.; Wang, J.K.; Zhang, H. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve. Energy Convers. Manage. 2014, 87, 220–226. [Google Scholar] [CrossRef]
- Jin, Z.J.; Gao, Z.X.; Zhang, M.; Liu, B.Z.; Qian, J.Y. Computational fluid dynamics analysis on orifice structure inside valve core of pilot-control angle globe valve. Proc. Inst. Mech. Eng. Part C 2018, 232, 2419–2429. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.Y.; Gao, Z.X.; Liu, B.Z.; Jin, Z.J. Parametric study on fluid dynamics of pilot-control angle globe valve. ASME J. Fluids Eng. 2018, 140, 111103. [Google Scholar] [CrossRef]
- Xu, X.G.; Liu, T.Y.; Li, C.; Zhu, L.; Li, S.X. A Numerical Analysis of Pressure Pulsation Characteristics Induced by Unsteady Blood Flow in a Bileaflet Mechanical Heart Valve. Processes 2019, 7, 232. [Google Scholar] [CrossRef]
- Chen, F.Q.; Zhang, M.; Qian, J.Y.; Fei, Y.; Chen, L.L.; Jin, Z.J. Thermo-mechanical stress and fatigue damage analysis on multi-stage high pressure reducing valve. Ann. Nucl. Energy 2017, 110, 753–767. [Google Scholar] [CrossRef]
- Qian, J.Y.; Hou, C.W.; Wu, J.Y.; Gao, Z.X.; Jin, Z.J. Aerodynamics analysis of superheated steam flow through multi-stage perforated plates. Int. J. Heat Mass Transfer 2019, 141, 48–57. [Google Scholar] [CrossRef]
- Solek, M.; Mika, L. Ice slurry flow through gate valves—Local pressure loss coefficient. In Proceedings of the 2nd International Conference on the Sustainable Energy and Environmental Development, Beijing, China, 24–25 March 2019. [Google Scholar]
- Alimonti, C. Experimental characterization of globe and gate valves in vertical gas–liquid flows. Exp. Therm. Fluid Sci. 2014, 54, 259–266. [Google Scholar] [CrossRef]
- Lin, Z.; Ma, G.; Cui, B.; Li, Y.; Zhu, Z.; Tong, N. Influence of flashboard location on flow resistance properties and internal features of gate valve under the variable condition. J. Nat. Gas Sci. Eng. 2016, 33, 108–117. [Google Scholar] [CrossRef]
- Yu, L.; Yu, S. High Temperature Flow Characteristics in Non-Full Opening Steam Gate Valve for Thermal Power Plant. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Hu, B.; Zhu, H.; Ding, K.; Zhang, Y.; Yin, B. Numerical investigation of conjugate heat transfer of an underwater gate valve assembly. Appl Ocean Res. 2016, 56, 1–11. [Google Scholar] [CrossRef]
- Kolesnikov, G.N.; Tikhonov, E.A. Influence of the Angle of Taper of Output Channel of Wedge Gate Valve on the Movement of a Liquid. Chem. Pet. Eng. 2017, 52, 707–709. [Google Scholar] [CrossRef]
- Xu, X.; Li, S.; Gong, L.; Wang, H.; Wang, Y. Study on seals of subsea production gate valves. Int. J. Comput. Appl. Technol. 2018, 58, 29–36. [Google Scholar] [CrossRef]
- Babaev, S.G.; Kerimov, V.I. Increase in the Working Capacity of Christmas-Tree Gate Valves Based on Studying the Wear Mechanism of a Gate and Seat Pair. Chem. Pet. Eng. 2015, 51, 526–529. [Google Scholar] [CrossRef]
- Lin, Z.; Ruan, X.D.; Zhu, Z.C.; Fu, X. Three-dimensional numerical investigation of solid particle erosion in gate valves. Proc. Inst. Mech. Eng. Part C 2014, 228, 1670–1679. [Google Scholar] [CrossRef]
- Lin, Z.; Zhu, L.; Cui, B.; Li, Y.; Ruan, X. Effect of placements (horizontal with vertical) on gas-solid flow and particle impact erosion in gate valve. J. Therm. Sci. 2014, 23, 558–563. [Google Scholar] [CrossRef]
- Liao, Y.; Lian, Z.; Long, R.; Yuan, H. Effects of multiple factors on the stress of the electro-hydraulic directional valve used on the hydraulic roof supports. Int. J. Appl. Electrom. 2015, 47, 199–209. [Google Scholar] [CrossRef]
- Zakirnichnaya, M.M.; Kulsharipov, I.M. Wedge gate valves selected during technological pipeline systems designing service life assessment. Procedia Eng. 2017, 206, 1831–1838. [Google Scholar] [CrossRef]
- Punitharani, K.; Murugan, N.; Sivagami, S.M. Finite element analysis of residual stresses and distortion in hard faced gate valve. J. Sci. Ind. Res. 2010, 69, 129–134. [Google Scholar]
- Zhang, C.; Yu, L.; Feng, R.; Zhang, Y.; Zhang, G. A numerical study of stress distribution and fracture development above a protective coal seam in longwall mining. Processes 2018, 6, 146. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Li, D. Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks. Processes 2018, 6, 113. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-e eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
| Grid 1 | Grid 2 | Grid 3 | |
|---|---|---|---|
| N × 105 | 6.7 | 13.3 | 25.3 |
| ∆p (pa) | 104.54 | 102.95 | 102.08 |
| Valve Opening Degree | 3/8 | 5/8 | 1 |
|---|---|---|---|
| ξE [17] | 10.82 | 3.69 | 2.03 |
| ξN | 11.03 | 3.74 | 1.98 |
| Error (%) | 1.9 | 1.3 | −2.5 |
| Re | Groove Depth 1 | Groove Depth 2 | Groove Depth 3 |
|---|---|---|---|
| 200 | 3.763 | 3.763 | 3.763 |
| 800 | 1.570 | 1.569 | 1.570 |
| 5000 | 0.429 | 0.428 | 0.425 |
| 40,000 | 0.293 | 0.293 | 0.292 |
| 100,000 | 0.254 | 0.253 | 0.252 |
| 200,000 | 0.233 | 0.233 | 0.232 |
| 300,000 | 0.223 | 0.223 | 0.222 |
| 400,000 | 0.217 | 0.216 | 0.215 |
| 500,000 | 0.212 | 0.212 | 0.211 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Li, J.-y.; Gao, Z.-x. Flow Characteristics and Stress Analysis of a Parallel Gate Valve. Processes 2019, 7, 803. https://doi.org/10.3390/pr7110803
Wu H, Li J-y, Gao Z-x. Flow Characteristics and Stress Analysis of a Parallel Gate Valve. Processes. 2019; 7(11):803. https://doi.org/10.3390/pr7110803
Chicago/Turabian StyleWu, Hui, Jun-ye Li, and Zhi-xin Gao. 2019. "Flow Characteristics and Stress Analysis of a Parallel Gate Valve" Processes 7, no. 11: 803. https://doi.org/10.3390/pr7110803
APA StyleWu, H., Li, J.-y., & Gao, Z.-x. (2019). Flow Characteristics and Stress Analysis of a Parallel Gate Valve. Processes, 7(11), 803. https://doi.org/10.3390/pr7110803




