Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head
Abstract
1. Introduction
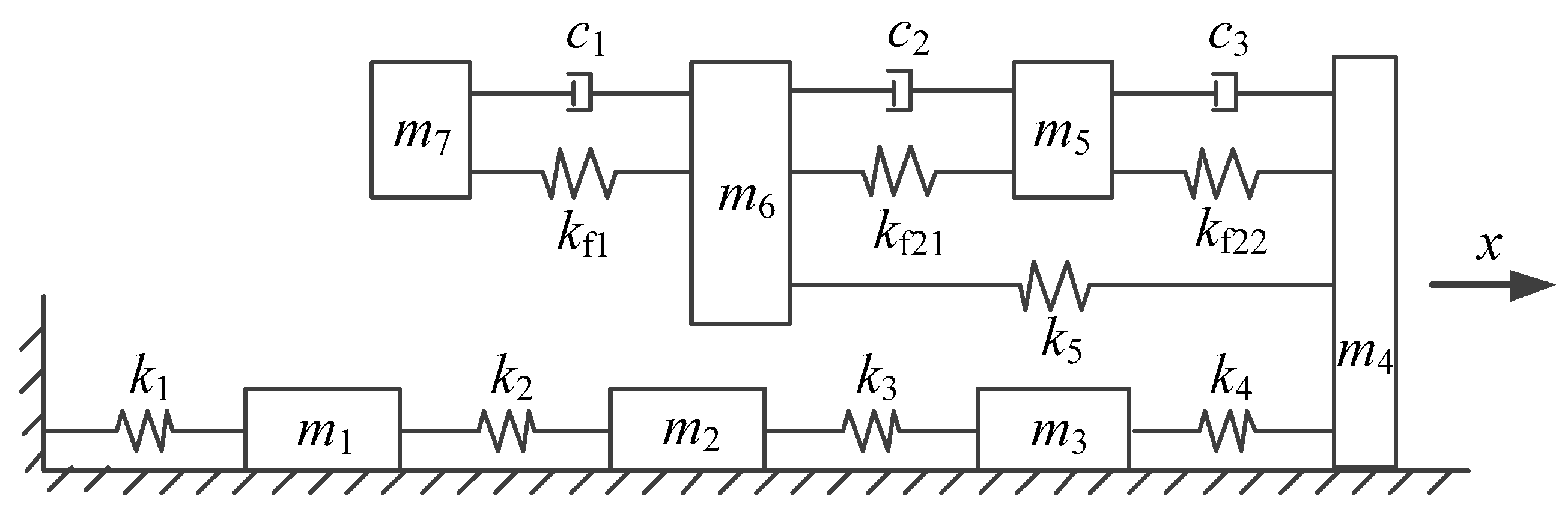
2. Establishment of the Dynamic Model and Equations of the Jet System
- (1)
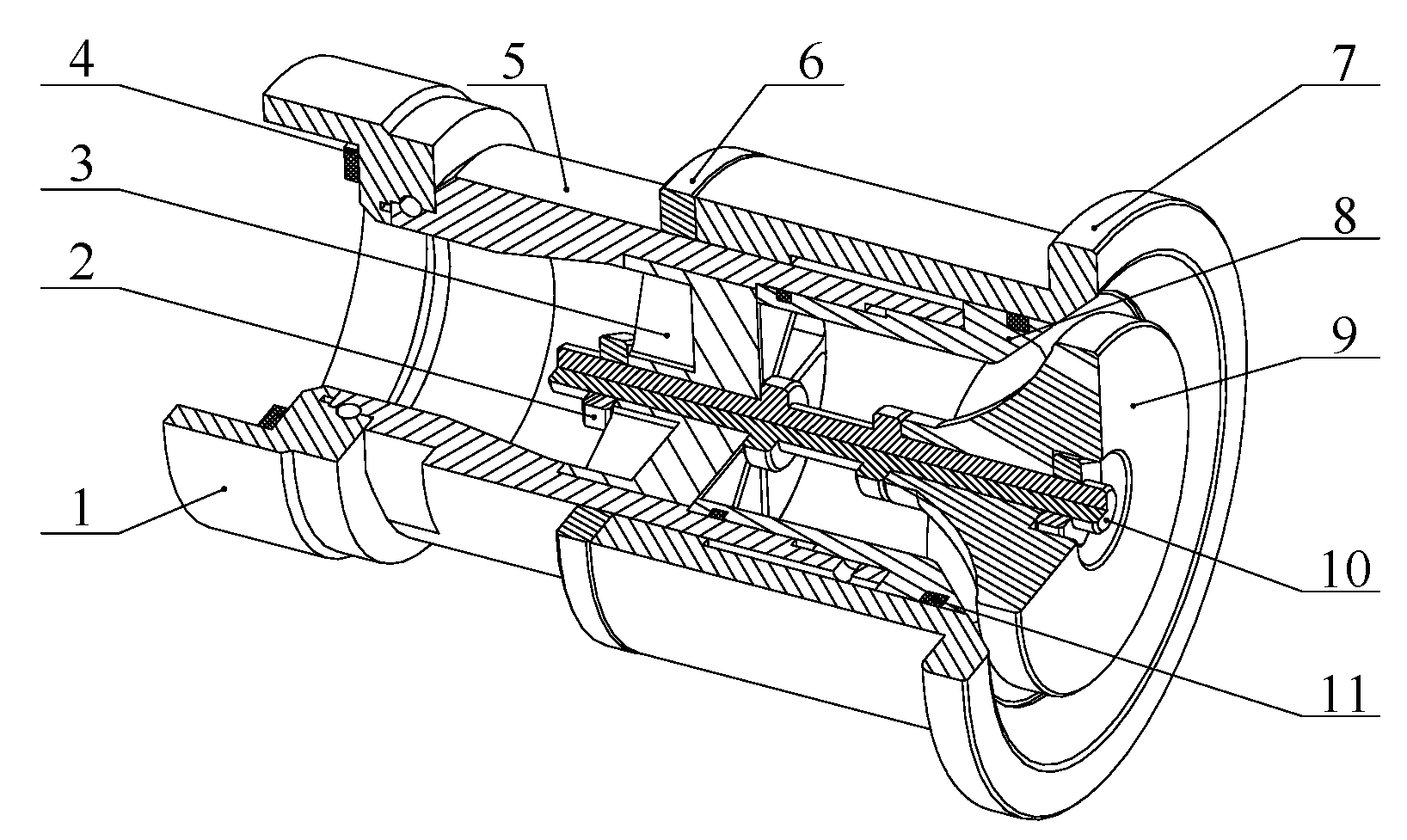
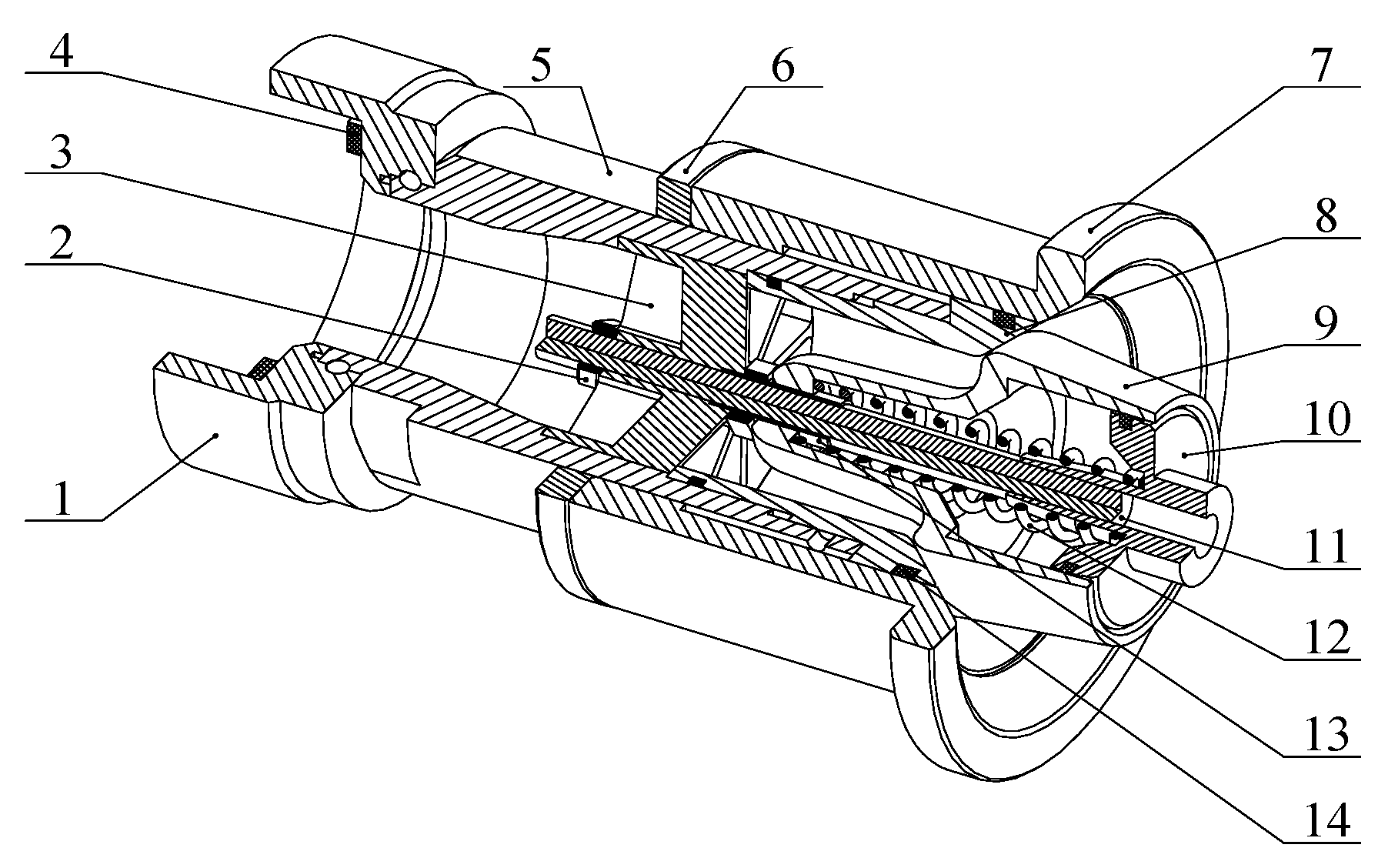
- The jet system is modeled based on the lumped parameter method. It is considered that the density, stiffness, pressure, and other attribute parameters of each fluid unit in the jet system are evenly distributed in the control volume and equal everywhere;
- (2)
- Except for the fluid units and the spring, it is considered that the parts such as the spray core, the gun head enclosure, the barrel, and the outer wall of the pipe are rigid bodies, regardless of their deformation;
- (3)
- The spray core, the core rod-end cap structure, and each fluid unit are only affected by the axial force, and the force of the fluid units on the solid units is equivalent to the axial linear spring force;
- (4)
- The damping between the fluid units and the solid units is equivalent to axial linear damping;
- (5)
- Ignore the processing and installation errors of each component.
3. Derivation of the Sensitivity Formula of the Jet System
3.1. Sensitivity of the Natural Frequency of the Jet System to the Mass of Fluid Unit 1
3.2. Sensitivity of the Natural Frequency of the Jet System to the Stiffness of Fluid Unit 1
3.3. Sensitivity of the Natural Frequency of the Jet System to the Mass of Fluid Unit 2
3.4. Sensitivity of the Natural Frequency of the Jet System to the Stiffness of Fluid Unit 2
3.5. Sensitivity of the Natural Frequency of the Jet System to the Mass of the Spray Core
3.6. Sensitivity of the Natural Frequency of the Jet System to the Stiffness of the Spring in the Gun Head
4. Sensitivity Analysis of the Jet System
4.1. Modal Analysis of the Jet System
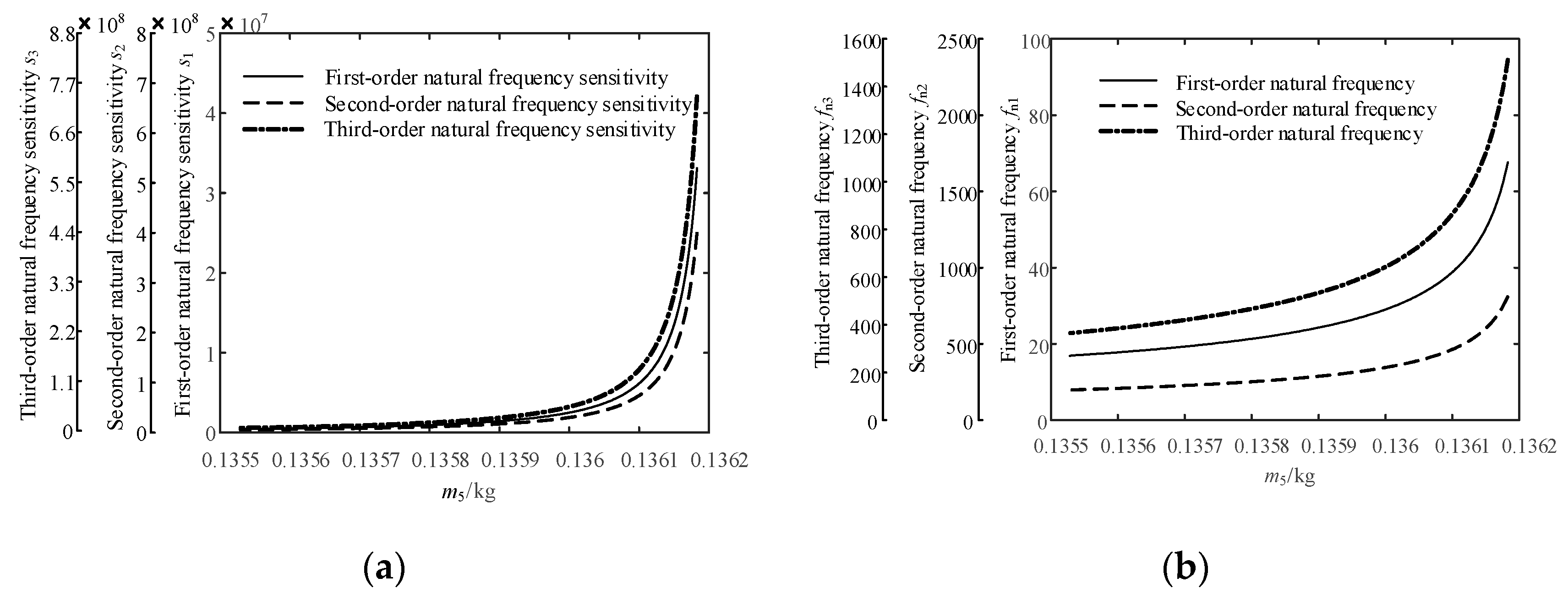
4.2. Sensitivity Analysis of the Natural Frequency of the Jet System to the Mass of Fluid Unit 1
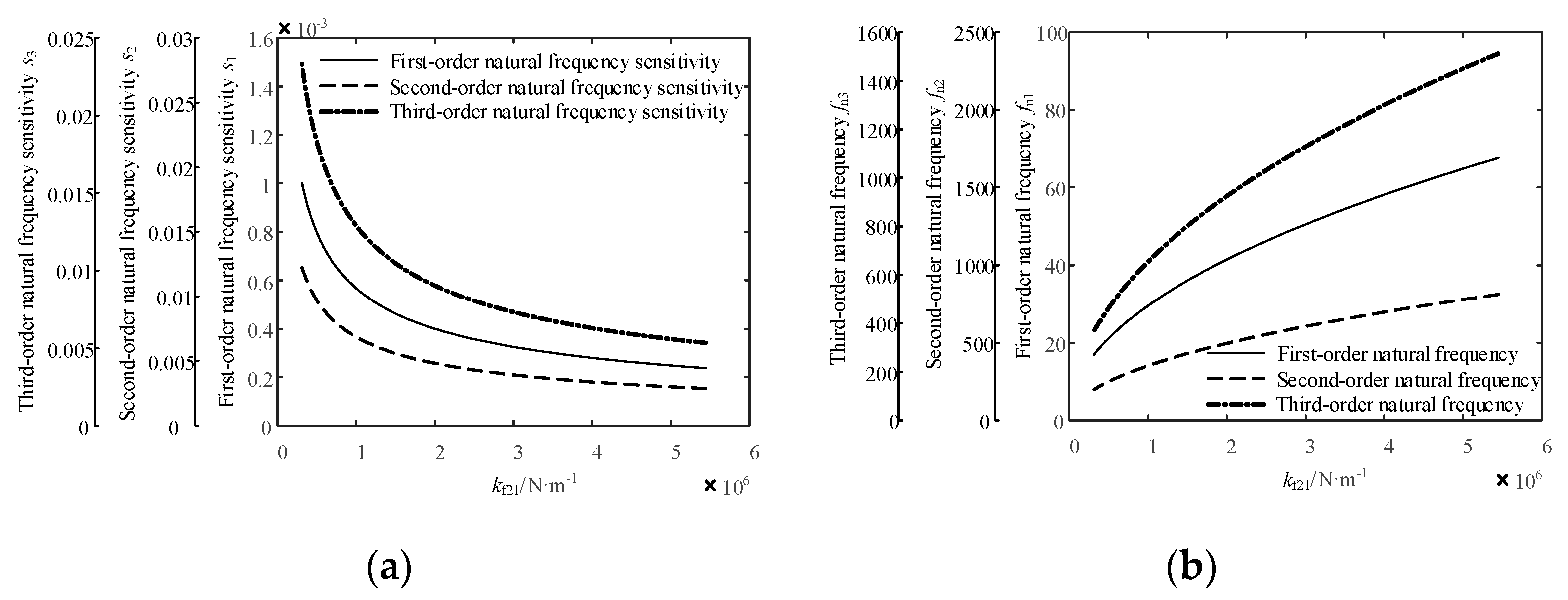
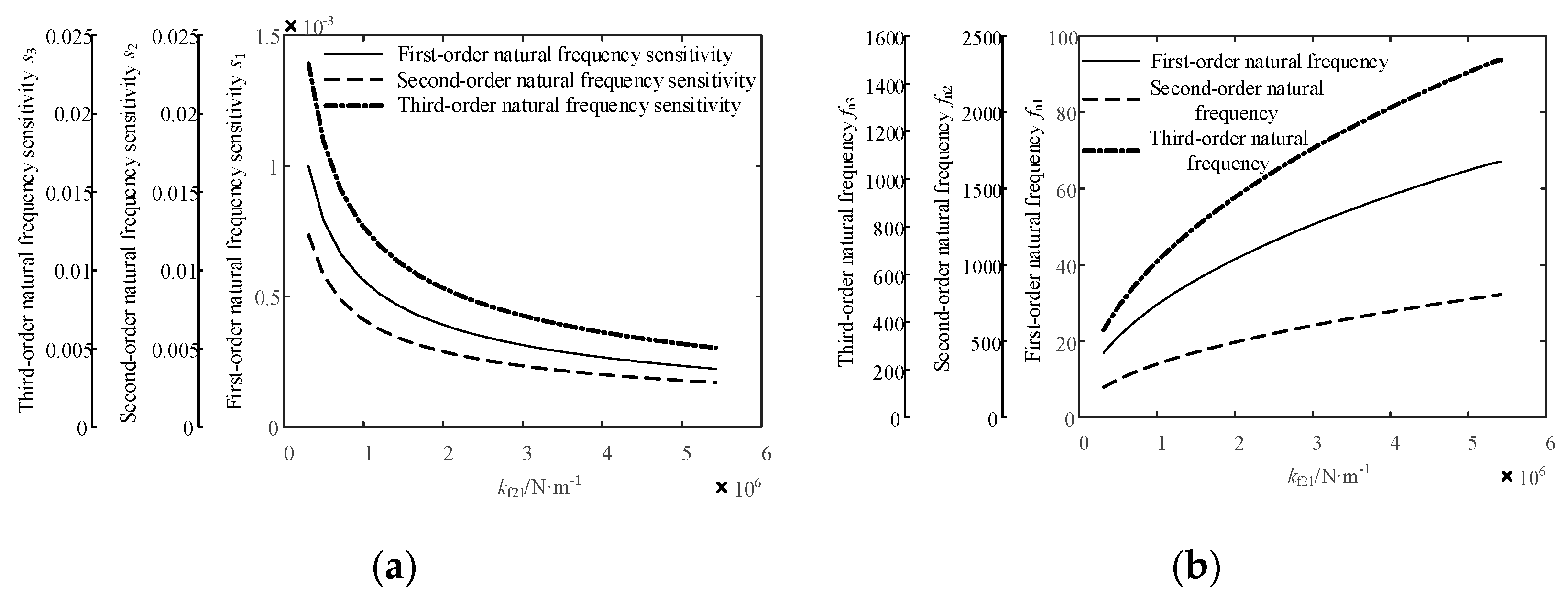
4.3. Sensitivity Analysis of the Natural Frequency of the Jet System to the Stiffness of Fluid Unit 1
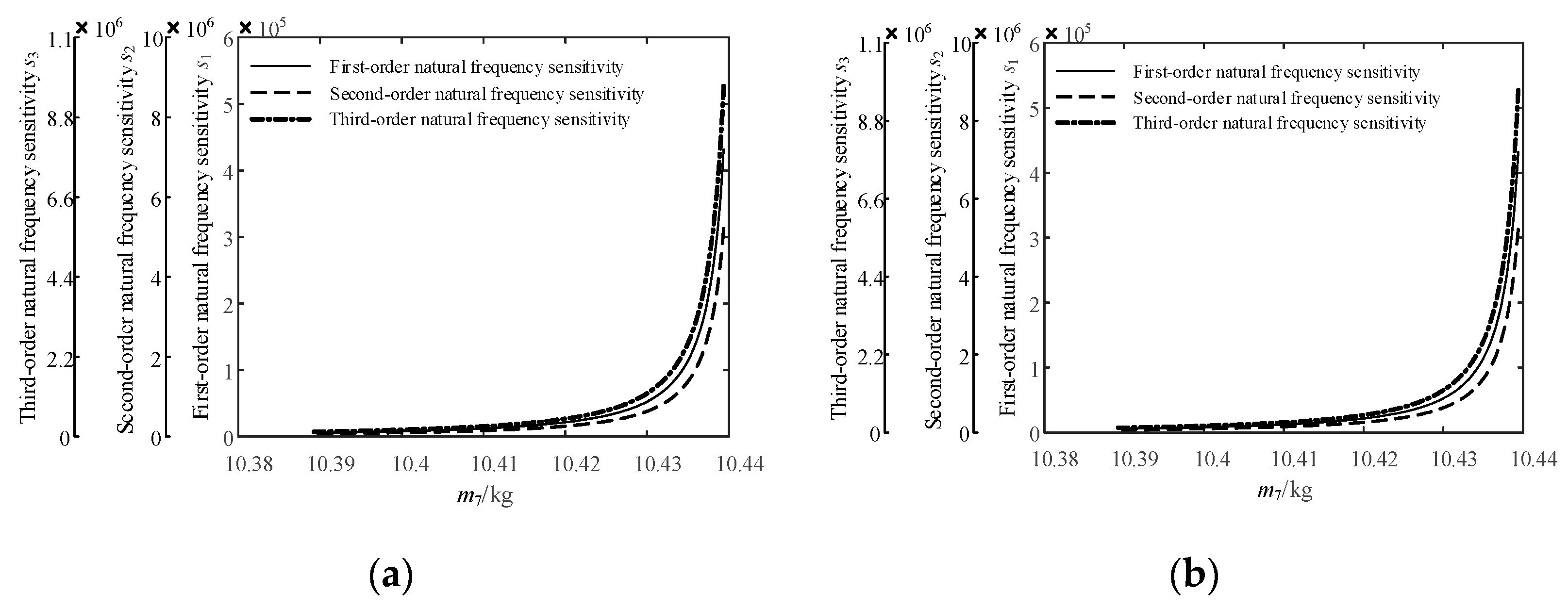
4.4. Sensitivity Analysis of the Natural Frequency of the Jet System to the Mass of Fluid Unit 2
4.5. Sensitivity Analysis of the Natural Frequency of the Jet System to the Stiffness of Fluid Unit 2
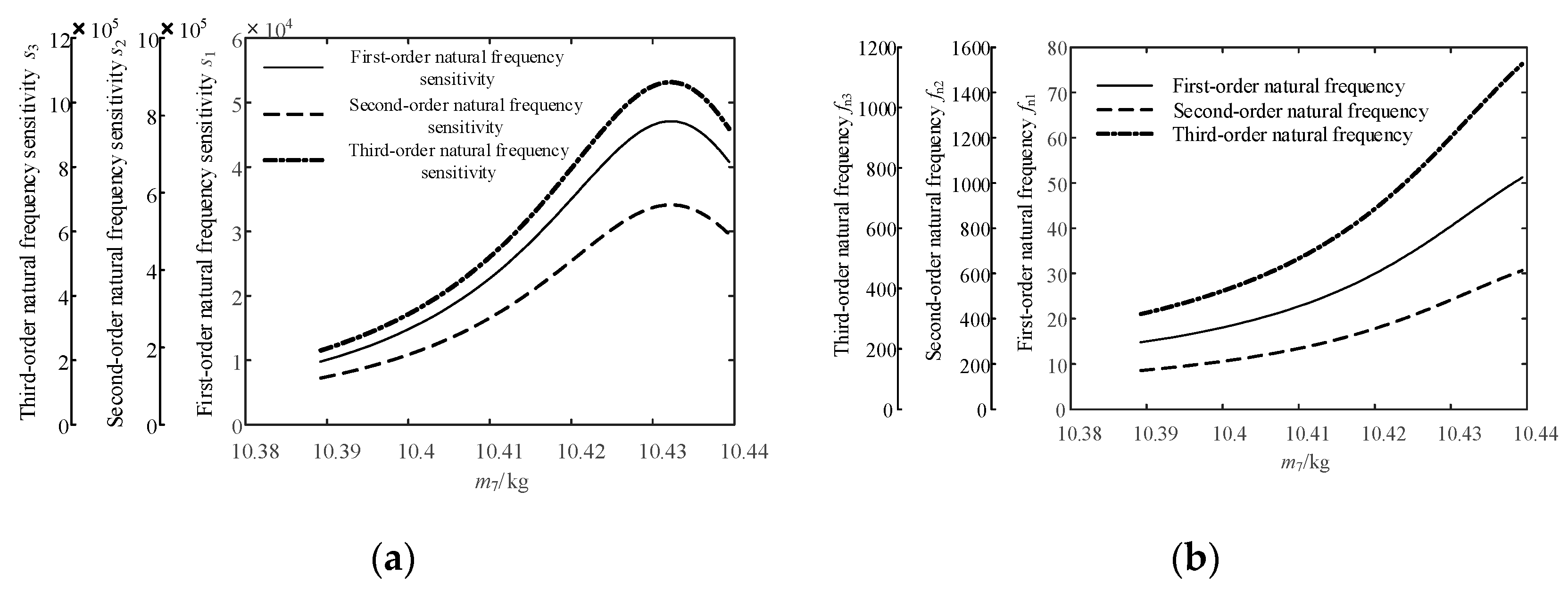
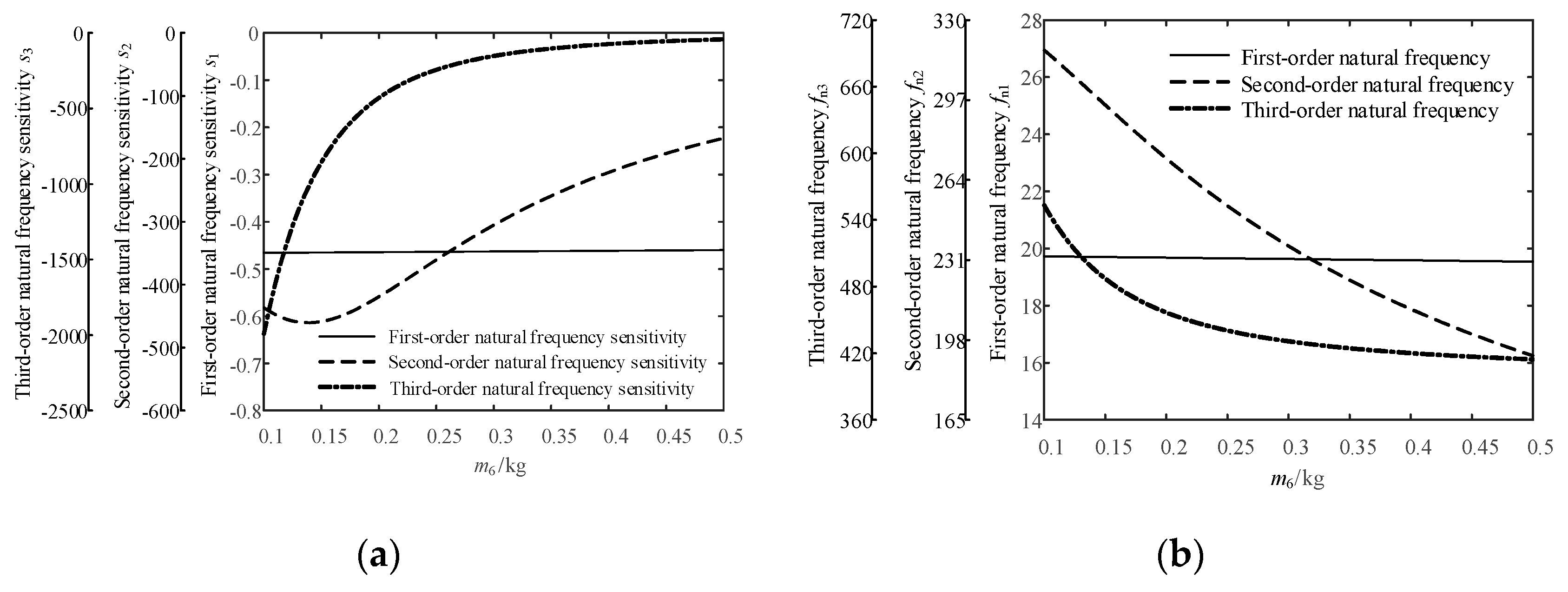
4.6. Sensitivity Analysis of the Natural Frequency of the Jet System to the Mass of the Spray Core
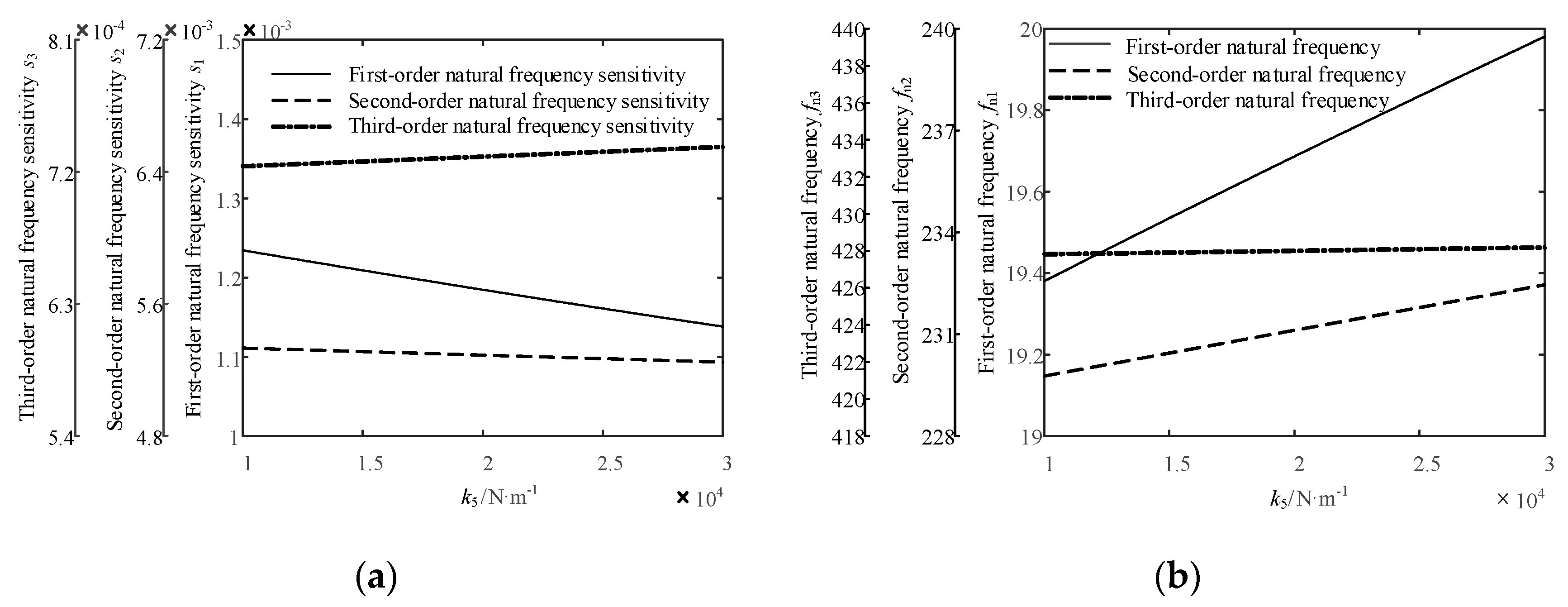
- (1)
- With the increase in the mass of the spray core, the first-order natural frequency sensitivity of the jet system increases slightly in the process, but it can be regarded as basically unchanged due to the small increase. The absolute value of the sensitivity is small and negative. In the variation of the natural frequency, the first-order natural frequency decreases slightly from 19.73 Hz to 19.54 Hz with the increase in the mass of the spray core.
- (2)
- With the increase in the mass of the spray core, the second-order natural frequency sensitivity of the jet system is negative, and its absolute value increases first and then decreases. Therefore, the second-order natural frequency of the jet system appears to decrease monotonically with the increase in the mass of the spray core, and the rate of decline increases slightly first and then decreases gradually.
- (3)
- With the increase in the mass of the spray core, the third-order natural frequency sensitivity of the jet system is negative, and its absolute value decreases gradually. Therefore, the third-order natural frequency of the jet system decreases with the increase in the mass of the spray core. The rate of decline decreases gradually and tends to zero eventually.
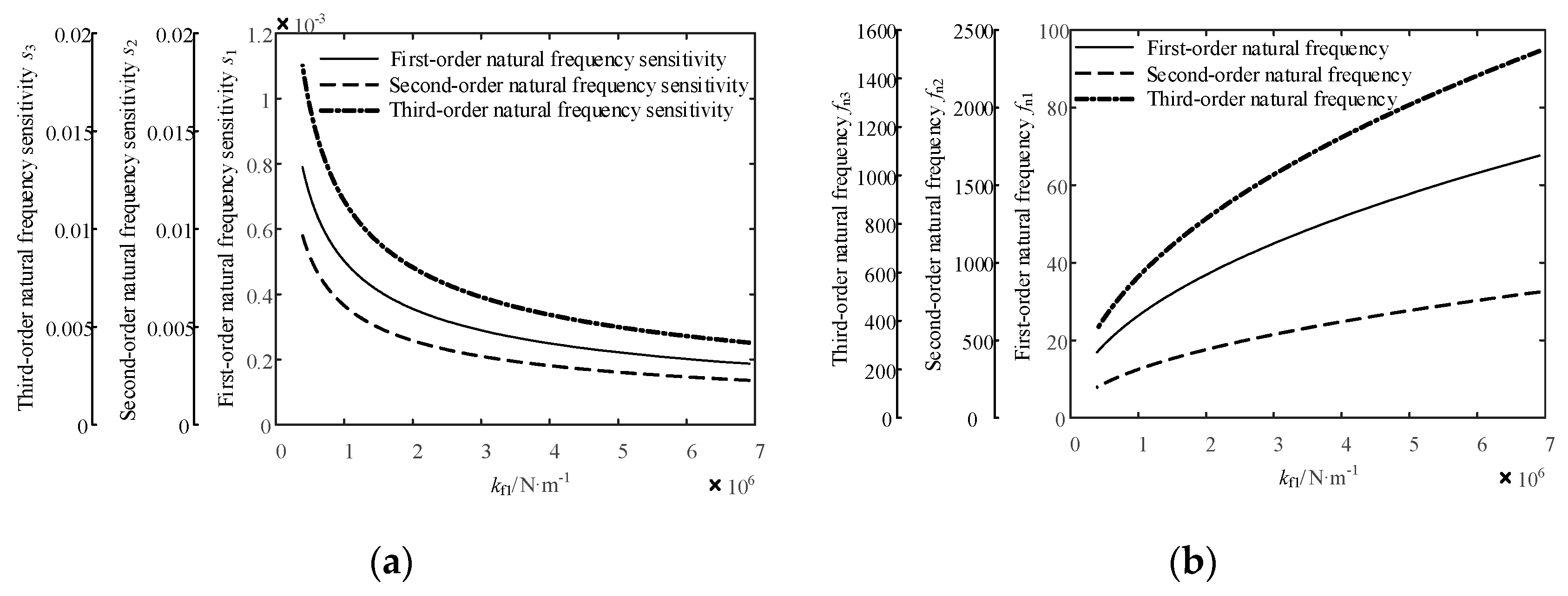
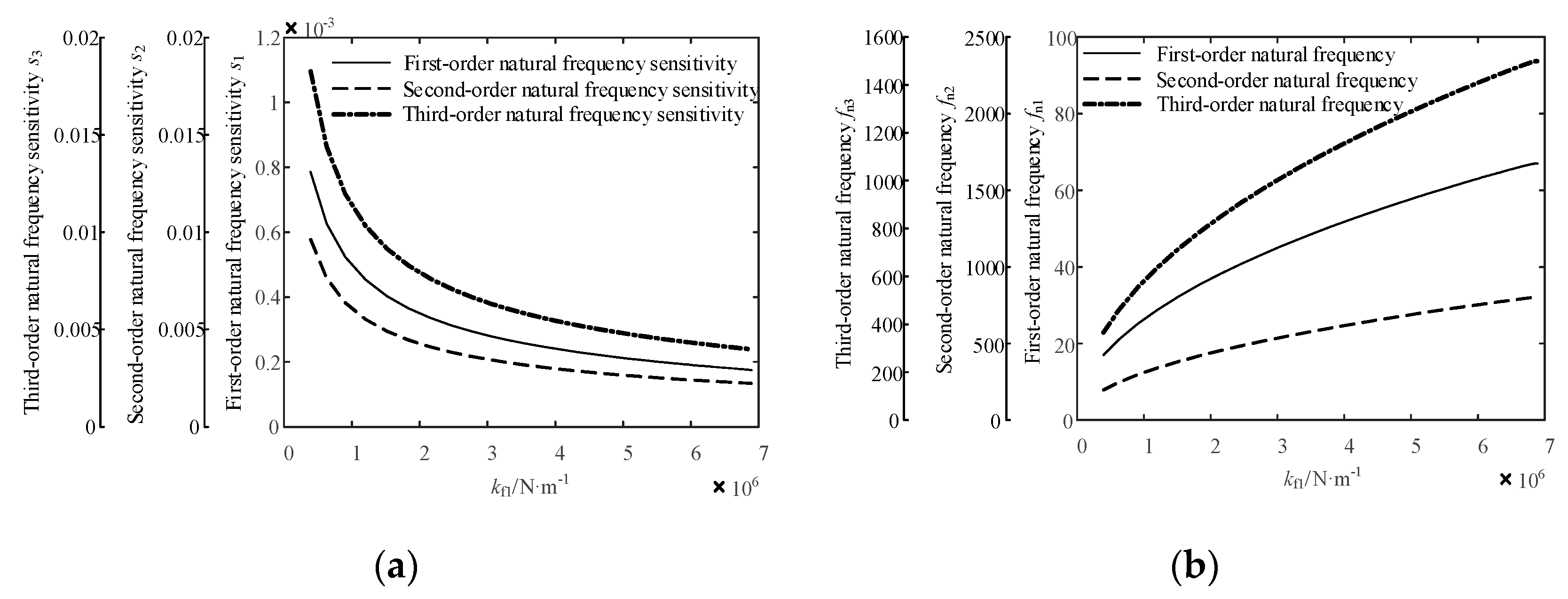
4.7. Sensitivity Analysis of the Natural Frequency of the Jet System to the Stiffness of the Spring in the Gun Head
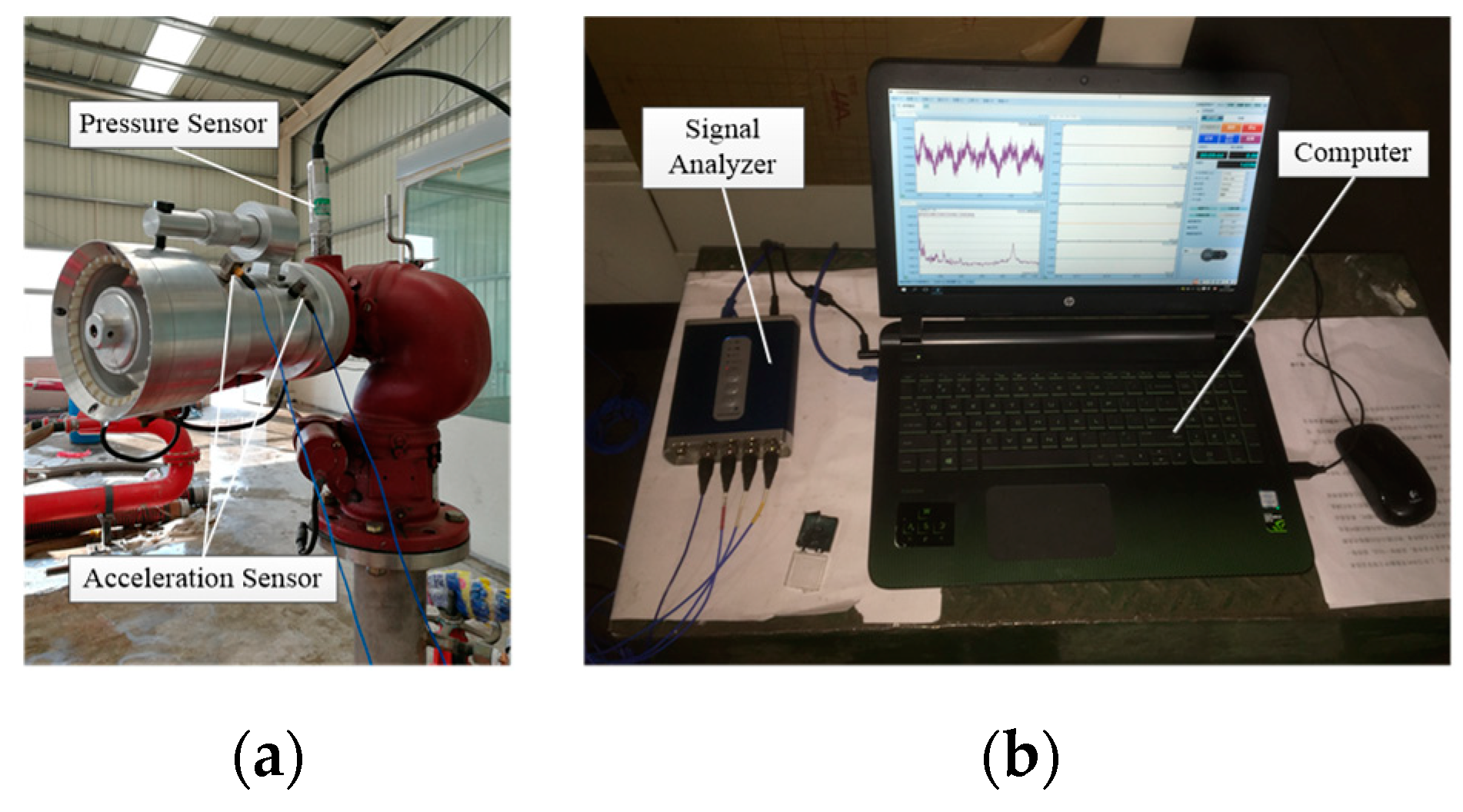
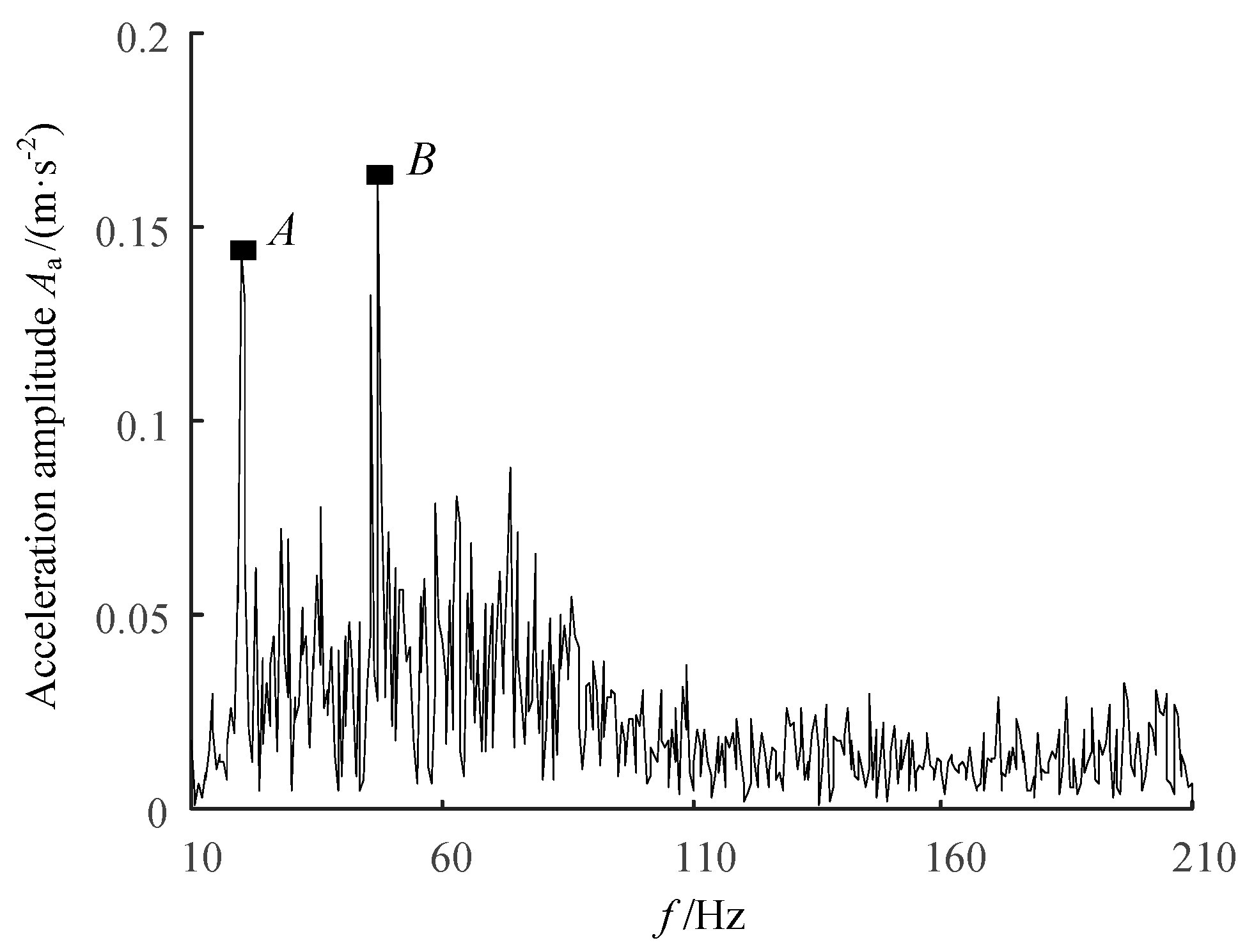
5. Experimental Verification
6. Conclusions
- (1)
- Considering the fluid-structure interaction and discrete-continuous coupling characteristics of the fire-fighting jet system with the adaptive gun head, the dynamic model and equations of the fire-fighting jet system with adaptive gun head were established based on the lumped parameter method. The sensitivity calculation formulas of the natural frequency of the jet system to typical design parameters were derived.
- (2)
- The modal analysis of the jet system was carried out, and the natural frequencies of the orders and the corresponding modal vectors under given conditions were obtained. The sensitivity analysis of the jet system was carried out, and the variation law of the first three natural frequencies and their sensitivities of the jet system to typical design parameters was revealed. Among the parameters involved, the first three natural frequencies of the jet system were the most sensitive to the change in the mass of fluid unit 2 in the range of a certain initial gas content.
- (3)
- The platform for the dynamic experiment of the fire-fighting jet system with the adaptive gun head was built, and the modal experiment of the jet system was carried out. There was only a 0.51% error between the value of the first-order natural frequency of the jet system determined by the modal experiment and the theoretical one determined by the analytical method, showing that good agreement with the first-order natural frequency of the jet system was found.
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, J.; Li, W.; Lin, D.; Zhao, G. Study on water jet trajectory model of fire monitor based on simulation and experiment. Fire Technol. 2018, 55, 773–787. [Google Scholar] [CrossRef]
- Hu, G.L.; Chen, W.G.; Gao, Z.G. Flow analysis of spray jet and direct jet nozzle for fire water monitor. Adv. Mater. Res. 2010, 139–141, 913–916. [Google Scholar] [CrossRef]
- Bhende, A.R.; Kadu, P.S. Behavioral analysis of hydraulically driven fire fighting water monitor trailer subjected to type of fire & ways of its fire protection. In Proceedings of the 2009 Second International Conference on Emerging Trends in Engineering & Technology, Nagpur, India, 16–18 December 2009. [Google Scholar]
- Berner, O. A volume and pressure controlling spill valve equipped for removal of excess aesthetic gas. Acta Anaesthesiol. Scand. 2010, 16, 252–258. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.Y.; Gao, Z.X.; Liu, B.Z.; Jin, Z.J. Parametric study on fluid dynamics of pilot-control angle globe valve. ASME J. Fluids Eng. 2018, 140, 111103. [Google Scholar] [CrossRef]
- Salacinska, K.; El Serafy, G.Y.; Los, F.J.; Blauw, A. Sensitivity analysis of the two dimensional application of the Generic Ecological Model (GEM) to algal bloom prediction in the North Sea. Ecol. Model. 2010, 221, 178–190. [Google Scholar] [CrossRef]
- Gallivan, S. Challenging the role of calibration, validation and sensitivity analysis in relation to models of health care processes. Health Care Manag. Sci. 2008, 11, 208–213. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Qian, P.; Tang, S.; Jiang, W.; Li, W.; Zhao, J. Amplitude-frequency characteristics analysis for vertical vibration of hydraulic AGC system under nonlinear action. AIP Adv. 2019, 9, 035019. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation characteristic research on the load vertical vibration of a hydraulic automatic gauge control system. Processes 2019, 7, 718. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Quan, L.; Jiang, W.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Félix, G.; Ancheyta, J.; Trejo, F. Sensitivity analysis of kinetic parameters for heavy oil hydrocracking. Fuel 2019, 241, 836–844. [Google Scholar] [CrossRef]
- Prieur, C.; Viry, L.; Blayo, E.; Brankart, J.-M. A global sensitivity analysis approach for marine biogeochemical modeling. Ocean Model. 2019, 139, 101402. [Google Scholar] [CrossRef]
- Guo, R.; Hu, Y.; Liu, M.Z.; Heiselberg, P. Influence of design parameters on the night ventilation performance in office buildings based on sensitivity analysis. Sustain. Cities Soc. 2019, 50, 101661. [Google Scholar] [CrossRef]
- Gunay, H.B.; Ouf, M.; Newsham, G.; O’Brien, W. Sensitivity analysis and optimization of building operations. Energy Build. 2019, 199, 164–175. [Google Scholar] [CrossRef]
- Dong, F.; Li, J.Y.; Zhang, S.N.; Wang, Y.; Sun, Z.Y. Sensitivity analysis and spatial-temporal heterogeneity of CO2 emission intensity: Evidence from China. Resour. Conserv. Recycl. 2019, 150, 104398. [Google Scholar] [CrossRef]
- Rezaie, F.; Bayat, M.A.; Farnam, S.M. Sensitivity analysis of pre-stressed concrete sleepers for longitudinal crack prorogation effective factors. Eng. Fail. Anal. 2016, 66, 385–397. [Google Scholar] [CrossRef]
- Tashakor, S.; Afsari, A.; Hashemi-Tilehnoee, M. Sensitivity analysis of thermal-hydraulic parameters to study the corrosion intensity in nuclear power plant steam generators. Nucl. Eng. Technol. 2019, 51, 394–401. [Google Scholar] [CrossRef]
- Cao, J.K.; Ding, S.T. Sensitivity analysis for safety design verification of general aviation reciprocating aircraft engine. Chin. J. Aeronaut. 2012, 25, 675–680. [Google Scholar] [CrossRef]
- He, X.; Jiao, W.; Wang, C.; Cao, W. Influence of surface roughness on the pump performance based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Jia, W.H.; Yin, C.B.; Hao, F.; Li, G.; Fan, X.Z. Dynamic characteristics and stability analysis of conical relief valve. Mechanika 2019, 25, 25–31. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Karney, B.W.; Mcpherson, D.L. Pressure-relief valve selection and transient pressure control. Am. Water Works Assoc. 2008, 100, 62–69. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018, 139, 1–7. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, J.; Xu, B.; Zhu, S. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Process. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute stability condition derivation for position closed-loop system in hydraulic automatic gauge control. Processes 2019, 7, 766. [Google Scholar] [CrossRef]
- Imagine, S.A. HYD advanced fluid properties. Technical Bulletin. 2007, 117, 7. [Google Scholar]
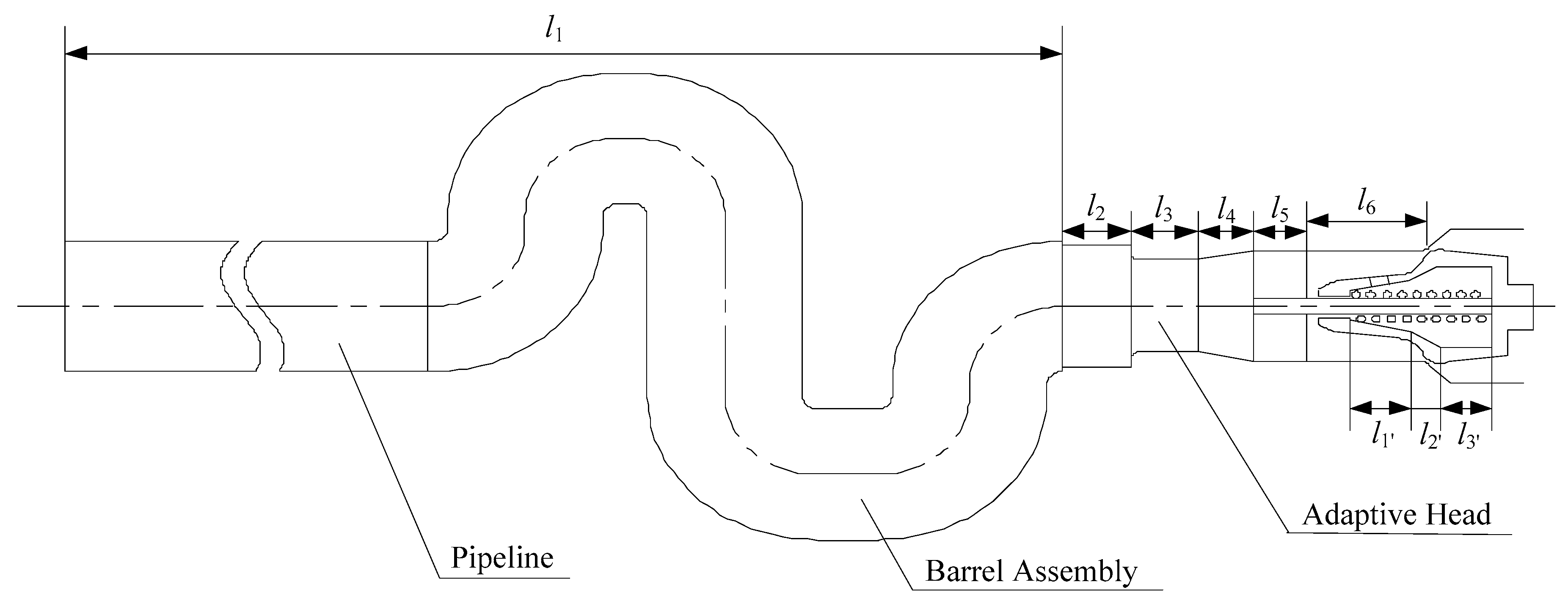


| Fluid Unit | Segmentation | Equivalent Stiffness of Fluid Unit Subsection | Average Area of Flow Cross Section Sai/(mm2) | Axial Length of the Fluid Domain Li/(mm) |
|---|---|---|---|---|
| Fluid unit 1 | l1 | kf11 | 6221 | 1534.6 |
| l2 | kf12 | 6200 | 38 | |
| l3 | kf13 | 3200 | 39 | |
| l4 | kf14 | 3800 | 35.5 | |
| l5 | kf15 | 4400 | 38 | |
| l6 | kf16 | 3700 | 64 | |
| Fluid unit 2 | l1’ | kf21’ | 300 | 46.1 |
| l2’ | kf22’ | 800 | 11 | |
| l3’ | kf23’ | 2800 | 40.5 |
| Parameter Name | Parameter Symbol | Unit | Value |
|---|---|---|---|
| Mass of core rod | m | kg | 0.0354 |
| Mass of end cap | md | kg | 0.1177 |
| Mass of spray core | m6 | kg | 0.3163 |
| Mass of Fluid unit 1 | m7 | kg | 16.4593 |
| Mass of Fluid unit 2 | m5 | kg | 0.1362 |
| Stiffness of discrete unit of the core rod | k1 | kN/m | 333,460 |
| Equivalent stiffness 1 of fluid | kf1 | kN/m | 354.05 |
| Equivalent stiffness 2 of fluid | kf2 | kN/m | 424.07 |
| Equivalent stiffness 3 of fluid | kf3 | kN/m | 424.07 |
| Stiffness of the spring in the gun head | k5 | kN/m | 18 |
| Fluid pressure | p | MPa | 0.6 |
| Initial gas content of fluid | x | % | 2 |
| Bulk elastic modulus of fluid | Bf | MPa | 161.1432 |
| Temperature | T | K | 293 |
| Order | First-Order | Second-Order | Third-Order | Fourth-Order | Fifth-Order | Sixth-Order | Seventh-Order |
|---|---|---|---|---|---|---|---|
| Natural frequency fni/Hz | fn1 | fn2 | fn3 | fn4 | fn5 | fn6 | fn7 |
| 19.6 | 230.8 | 427.4 | 4040 | 24,276.9 | 43,906 | 57,146.6 | |
| Principal mode of each mode Φni | 0.0004 | 0.001 | 0.0013 | 0.261 | 0.7231 | 1 | −0.7044 |
| 0.0009 | 0.002 | 0.0025 | 0.5176 | 1 | −0.0186 | 1 | |
| 0.0015 | 0.003 | 0.0038 | 0.7653 | 0.6597 | −0.9997 | −0.7153 | |
| 0.0019 | 0.0041 | 0.005 | 1 | −0.0877 | 0.0372 | 0.0155 | |
| 0.3549 | 0.7578 | 1 | −0.0049 | 0 | 0 | 0 | |
| 0.7062 | 1 | −0.3205 | 0.0001 | 0 | 0 | 0 | |
| 1 | −0.0252 | 0.0023 | 0 | 0 | 0 | 0 |
| Natural Frequency | Experimental Data | Theoretical Value | Error |
|---|---|---|---|
| The first-order natural frequency | 19.5 Hz | 19.6 Hz | 0.51% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Zhu, X.; Wang, C.; Zhang, L.; Zhu, Y. Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head. Processes 2019, 7, 808. https://doi.org/10.3390/pr7110808
Yuan X, Zhu X, Wang C, Zhang L, Zhu Y. Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head. Processes. 2019; 7(11):808. https://doi.org/10.3390/pr7110808
Chicago/Turabian StyleYuan, Xiaoming, Xuan Zhu, Chu Wang, Lijie Zhang, and Yong Zhu. 2019. "Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head" Processes 7, no. 11: 808. https://doi.org/10.3390/pr7110808
APA StyleYuan, X., Zhu, X., Wang, C., Zhang, L., & Zhu, Y. (2019). Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head. Processes, 7(11), 808. https://doi.org/10.3390/pr7110808







