DynamFluid: Development and Validation of a New GUI-Based CFD Tool for the Analysis of Incompressible Non-Isothermal Flows
Abstract
1. Introduction
- Windows-based software, which can be run in any Windows Operating System: both 32- and 64-bit architectures are supported. When run in a 64-bit architecture, the software leverages on the larger word-size when performing computations.
- Graphical user interface for defining the geometric domain, physical model, boundary conditions, and displaying the results obtained in any simulation.
- Custom database for storing both the project domain definition and all the information generated during the simulation. The database provides the user with ODBC (Open DataBase Connectivity) interface for interacting with any ODBC client.
- Support for NASTRAN format file importing, which allows the user to import any geometry and physical definition in DMAP (Direct Matrix Abstraction Programming) language.
- Vtk file format capabilities, to export generated simulations into ASCII text Vtk files that can be visualized using Paraview [20].
- Basic meshing capabilities to sample the geometric domain. Two methods have been implemented: (a) structured meshing (linear, logarithmic) using both quadrangular elements (QUAD) and triangular elements (TRIA) for regular geometric domains, and (b) Delaunay–Voronoi meshing for irregular geometric domains.
- Software designed to run in a computer with a motherboard that may have one or several multi-core processors. This includes parallel computation of the finite element matrices, parallel assembly of the global matrices and parallel computation of the right hand side of each step of the algorithm. The software uses the conjugate gradient stabilized algorithm provided by the Eigen library [21] to solve the linear systems, and it has been compiled with the openmp compiler flag so that the Eigen library exploits the multiple cores available in the hardware.
- Custom user language for post-processing the results (velocity, pressure and temperature), with basic algebra functions and support for different coordinate reference systems. Internal compiler for translating this user language into machine code that can be applied in parallel to every node and/or finite element.
- Support for different types of finite elements (both Lagrangian and Serendipity): (a) linear TRIA elements and (b) linear and quadratic QUAD elements.
- DynamFluid is a freeware CFD tool available at https://sites.google.com/view/dynamfluid.
- (i)
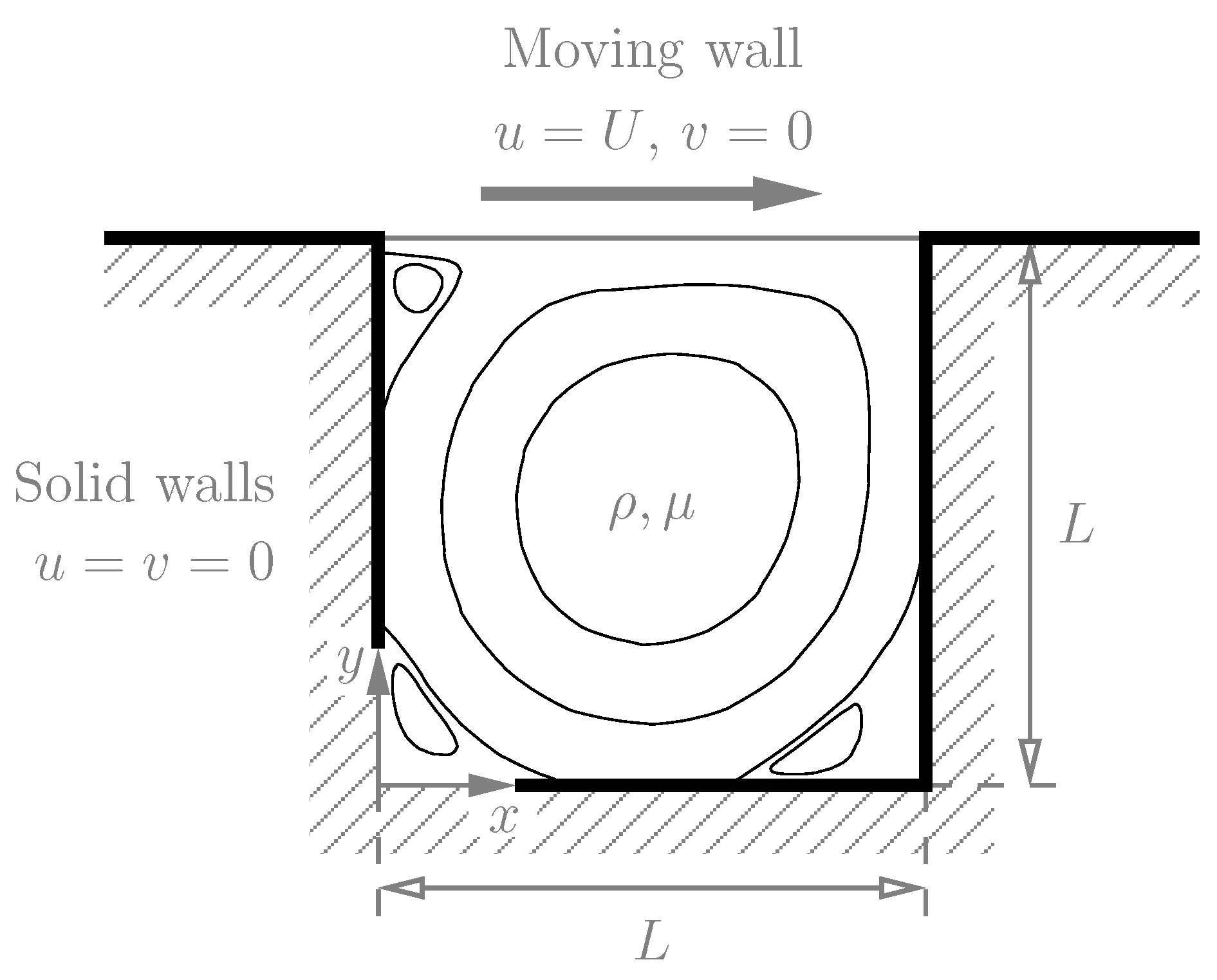
- The lid-driven cavity flow.This is a classical benchmark problem that has been widely used since the early days of CFD to assess and validate new techniques and methods. This test case is easy to set and simulate because its boundary conditions are particularly simple. However, the fully developed flow displays almost all fluid mechanical phenomena, with increasingly complex aspects emerging as the Reynolds number is increased, such as corner eddies, laminar to turbulence regime transition, and even turbulence at high Reynolds number. A recent comprehensive review of the literature on the subject can be found in [22], where the work of several authors is presented and discussed [23,24,25,26,27,28]. Available benchmark results have been tabulated to provide a comprehensive source of validation data [29].
- (ii)
- Mixed convection flow in a vertical channel with asymmetric wall temperatures. In this mixed convection heat transfer problem, an initially uniform flow develops in a slender vertical channel whose walls are at different temperatures. The cold and hot wall temperatures may also differ from the incoming flow temperature. As a result of the upward buoyancy force that appears near the hot wall, the velocity increases in the near-wall region. As the fluid accelerates downstream, the fluid near the cold wall may suffer flow reversal so as to maintain the imposed fixed flow rate. One of the most interesting features exhibited by this flow is thus the possibility of flow reversal at the cold wall as the flow develops. The occurrence (or not) of flow reversal depends on the length of the vertical channel and the buoyancy effect induced by the temperature difference between the hot and cold walls. Previous studies have shown that for the flow reversal to occur, in high Reynolds number flows the ratio of the Grashof number to the Reynolds number must be higher than a critical value that depends on the wall temperature difference ratio [30,31,32,33,34,35,36,37,38,39,40,41,42,43].
- (iii)
- Unsteady incompressible flow past a circular cylinder. The flow of a constant density fluid past a bluff body is another classical problem that has been widely studied in the literature. Understanding the flow regimes past bluff bodies poses a daunting challenge, so that 2D and 3D vortical structures in wakes of different bodies have been analyzed by scientists and engineers for decades. The reason for this interest is the vast range of applications of external flow past round bluff bodies: aerodynamics (planes, rockets, ground vehicles), hydrodynamics (ships, submarines) or wind energy (wind turbines), to name the few. At very low Reynolds numbers (creeping flow) the flow past a non-heated circular cylinder is symmetric in the streamwise direction [44,45,46,47]. As the Reynolds number grows to values of order unity the symmetry is lost, and when it exceeds a critical value the non-linear convective effects trigger the onset of steady flow separation, accompanied by the appearance of steady recirculation bubbles behind the cylinder. One important aspect of these flows is the so-called vortex shedding, which is an oscillating flow pattern that emerges for even larger Reynolds numbers. This regime has been thoroughly studied experimentally [48,49,50,51,52] and numerically [53,54,55,56,57]. The alternate shedding of vortices in the wake leads to the well known Kármán vortex street, which originates large fluctuating pressure forces in the direction transverse to the flow and may cause structural vibrations, acoustic noise, or resonance, which in some cases may lead to structural damage or even collapse.
- (iv)
- Steady non-isothermal flow past a circular cylinder with negligible buoyancy effects. This case is similar to the previous one but with the particularity that the temperature of the cylinder differs from the temperature of the incoming fluid, which causes the flow past a circular cylinder to exhibit interesting heat transfer features. This problem is of interest for the design of cylinder-shaped sensors located in fluid streams, hot-wire anemometers, tube heat exchangers, nuclear reactor fuel rods and chimneys. In this work, attention will be restricted to steady flow with negligible buoyancy effects, with the aim of characterizing the local Nusselt number at the cylinder wall for different Reynolds numbers [44,54,58,59].
2. Governing Equations
3. Numerical Method
3.1. Temporal Discretization: The Characteristics-Based-Split Algorithm
- Calculate from Equation (19).
- Calculate or from Equation (21).
- Calculate from Equation (20), which yields the velocity at time .
- Calculate from Equation (22), which can be calculated in parallel with the other steps since the right hand side of Equation (22) does not depend on the variables at time . Step 4 allows obtaining the value of the energy at time .
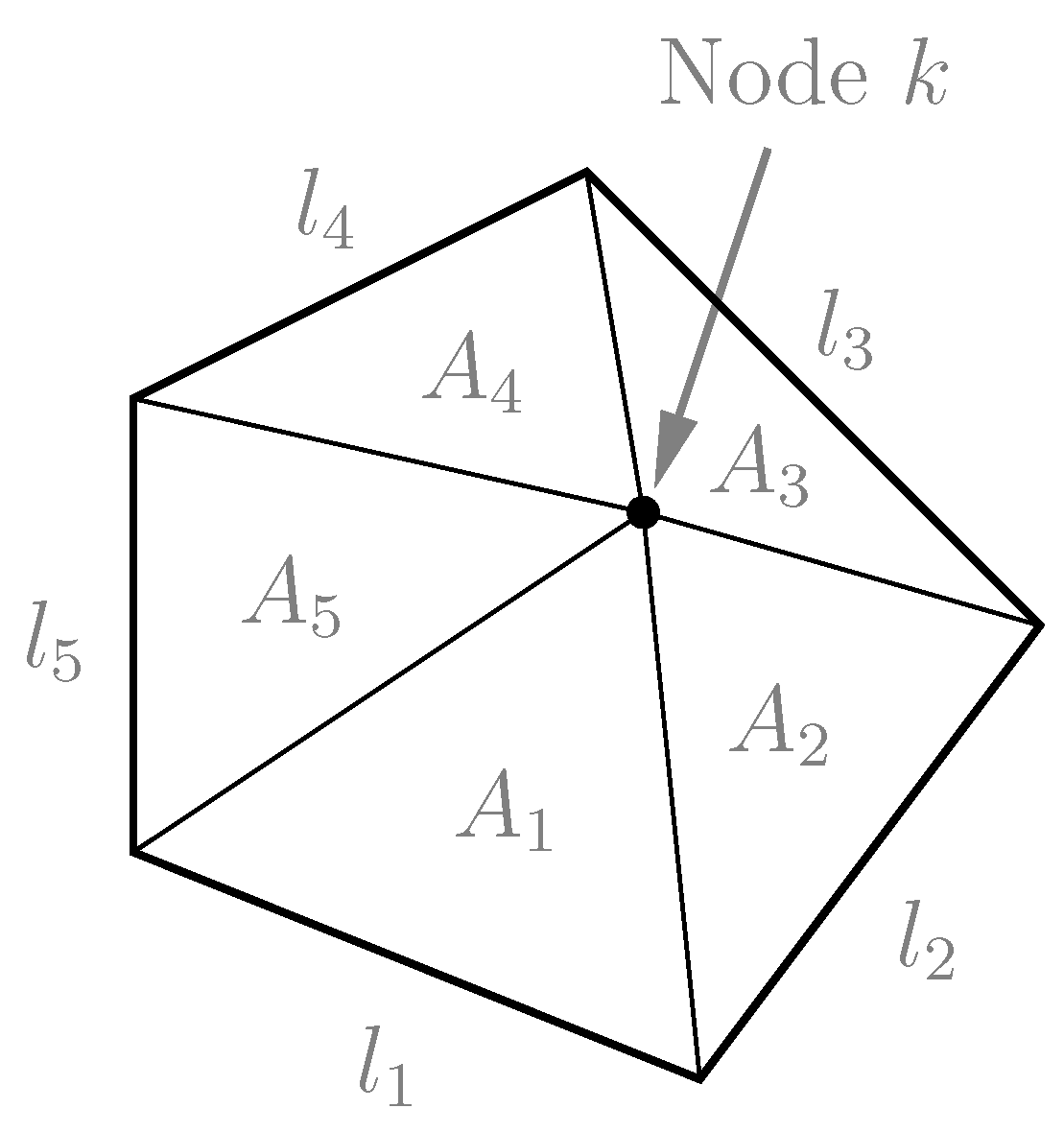
3.2. Spatial Discretization
4. Software Validation
4.1. Lid-Driven Cavity Flow
4.1.1. Literature Review
4.1.2. Boundary and Initial Conditions
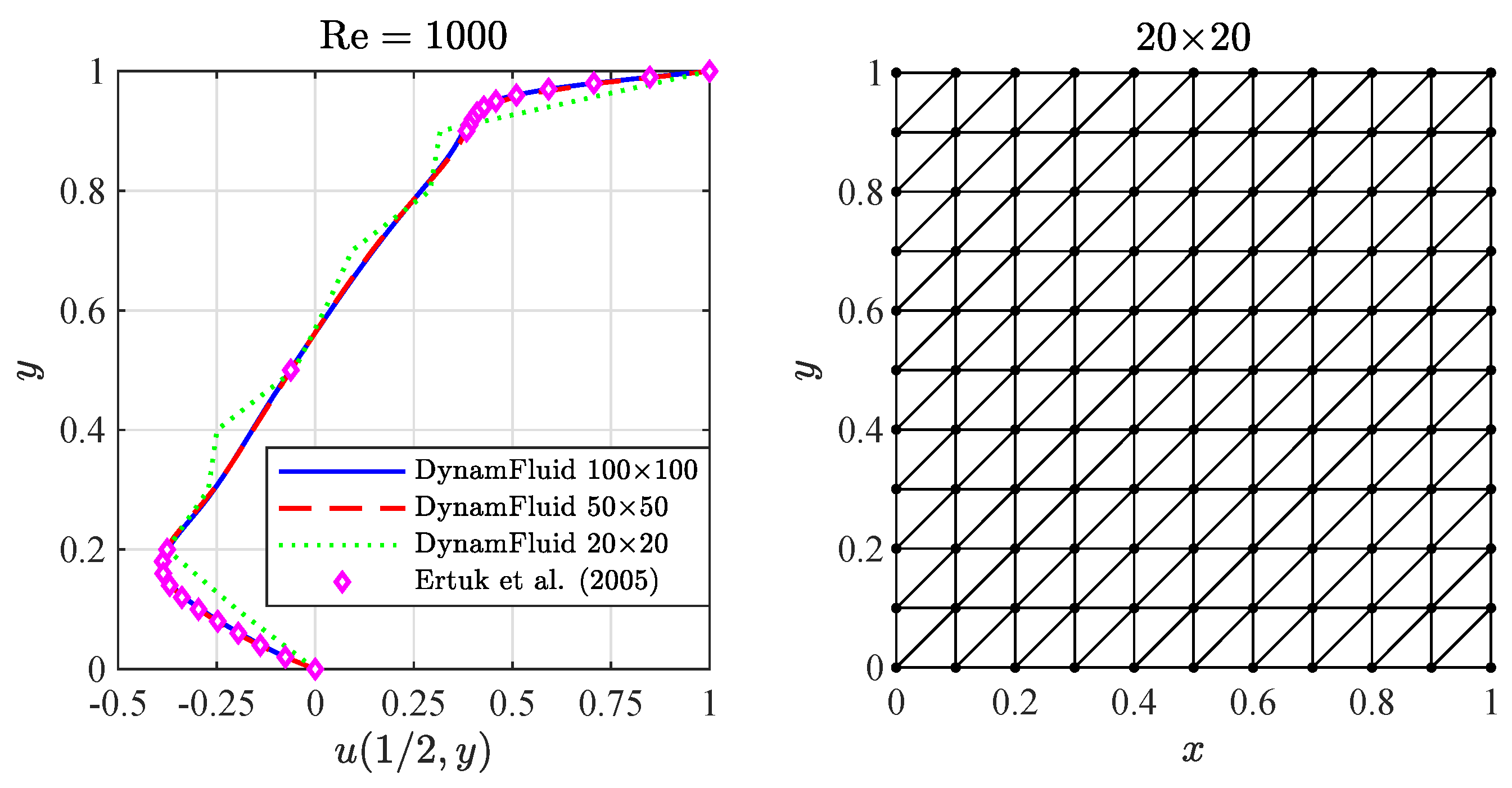
4.1.3. Convergence Analysis
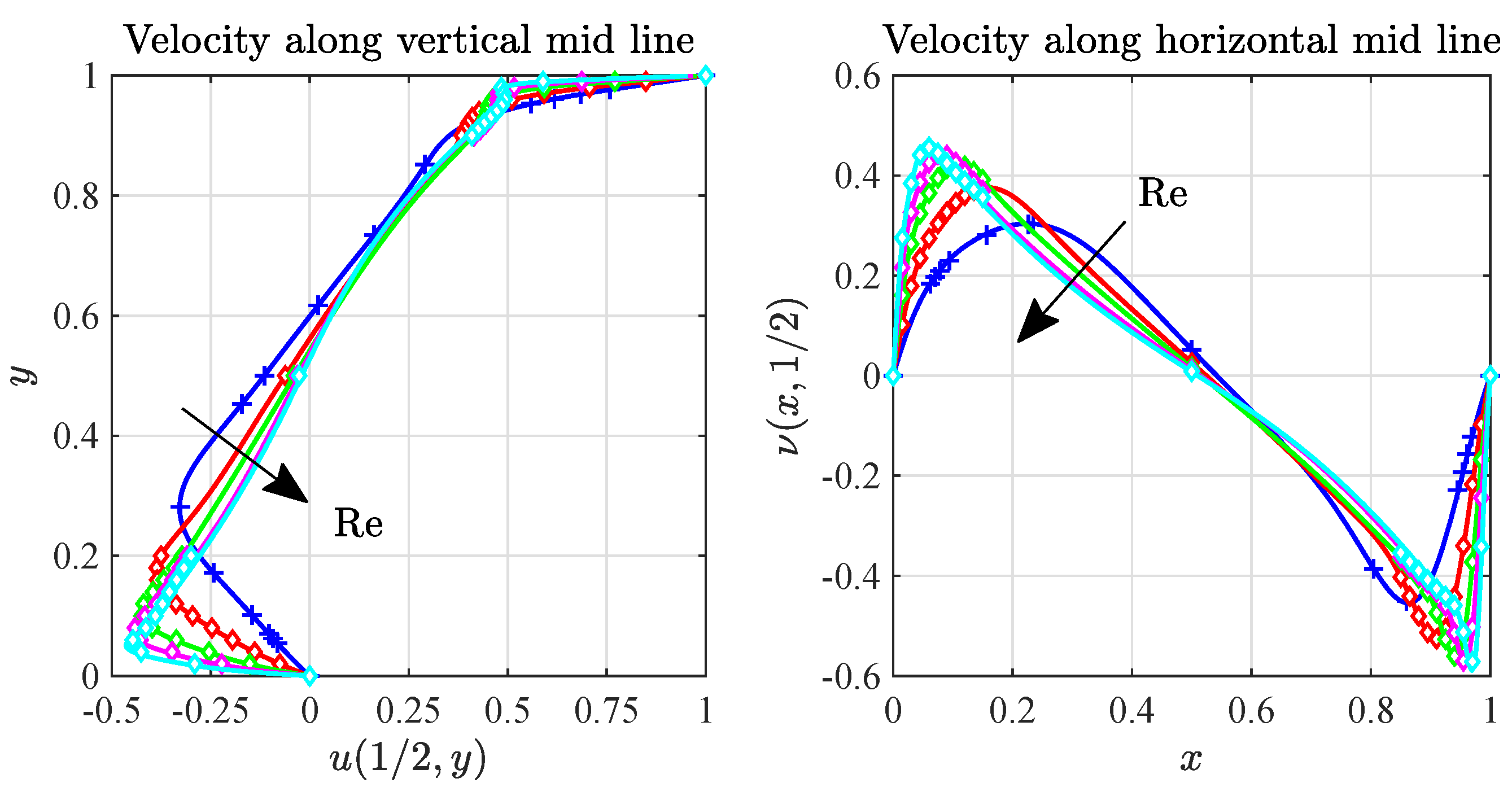
4.1.4. Results for up to 10,000
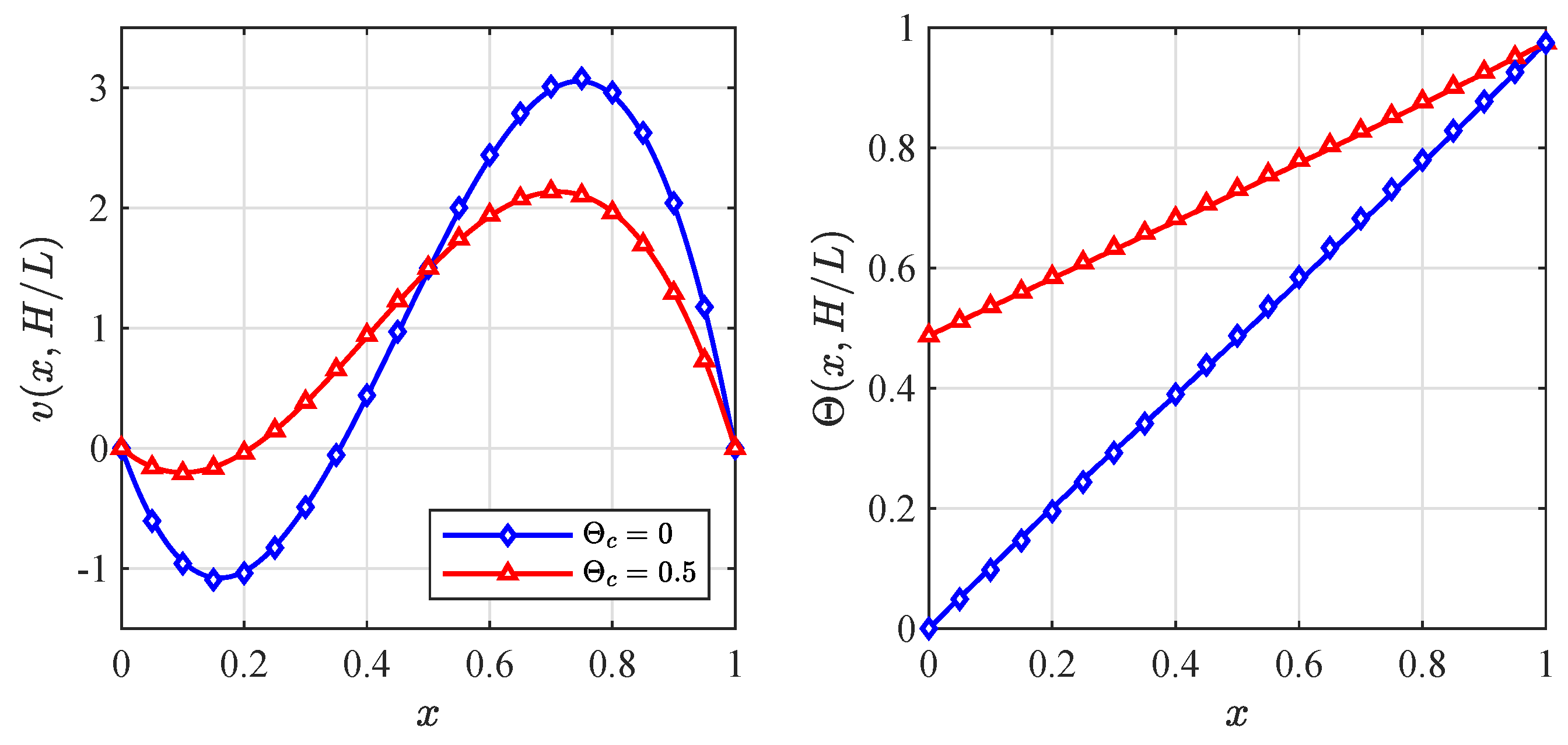
4.2. Mixed Convection Flow in a Vertical Channel with Asymmetric Wall Temperatures
4.2.1. Literature Review
4.2.2. Boundary and Initial Conditions
- Left, cold non-slip wall: .
- Right, hot non-slip wall: .
- Bottom side, incoming flow: .
- Top side, outgoing flow: .
4.2.3. Discussion of Results
4.3. Isothermal Flow Past a Circular Cylinder
4.3.1. Literature Review
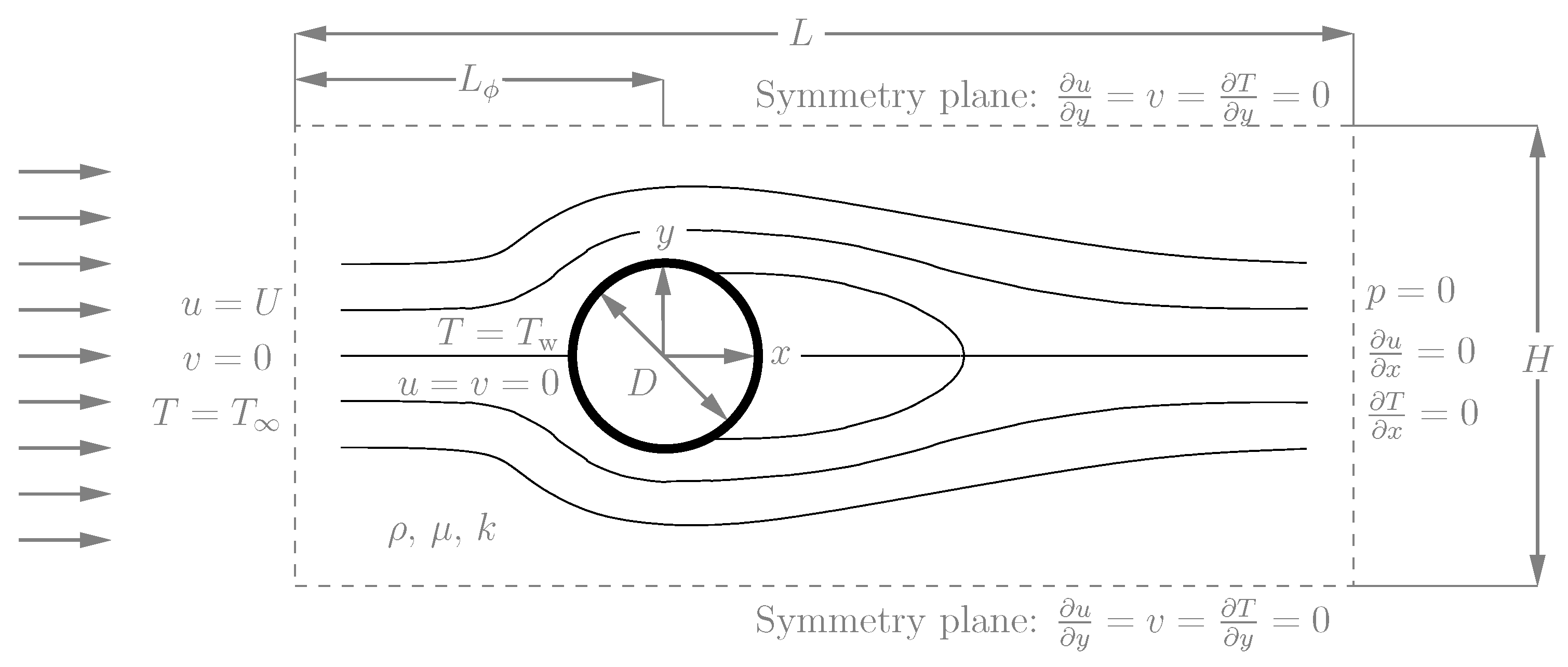
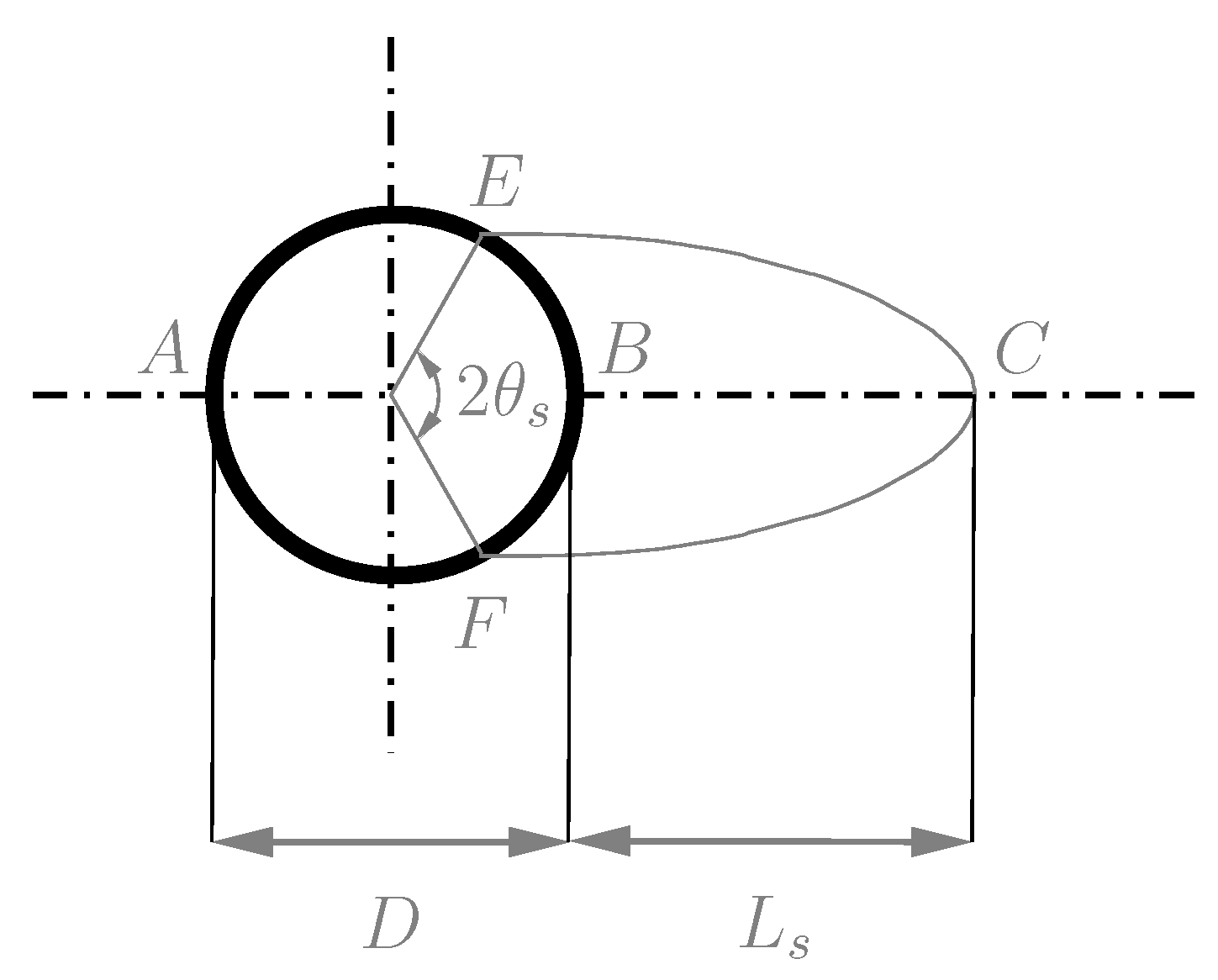
4.3.2. Computational Domain, Boundary and Initial Conditions and Mesh Generation
- Left boundary, uniform incoming flow: .
- Right boundary, outflow boundary condition: .
- Top and bottom boundaries, symmetry boundary condition: .
- Cylinder wall, non-slip condition: .
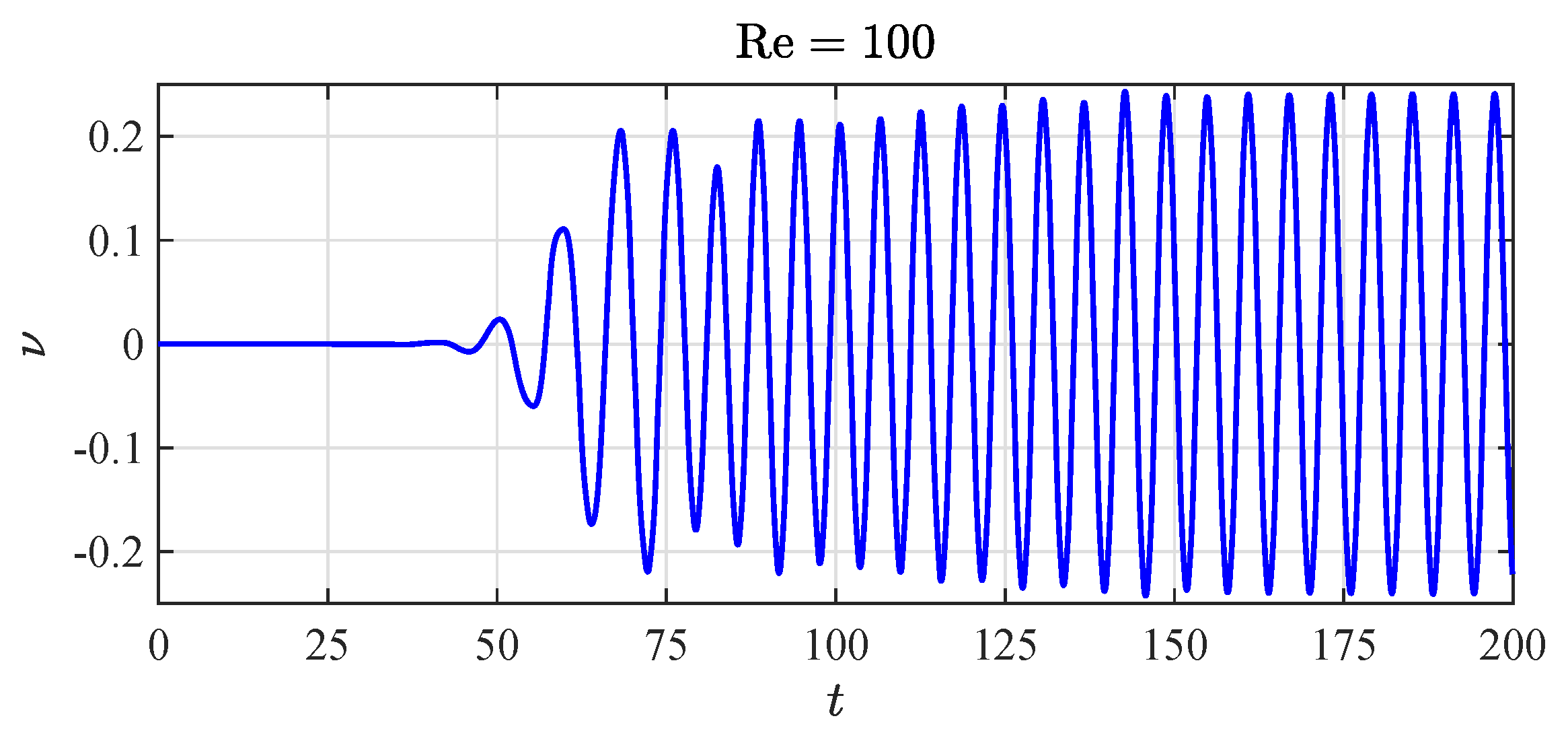
4.3.3. Discussion of Results
4.4. Flow Past a Heated Circular Cylinder with Forced Convection
4.4.1. Literature Review
4.4.2. Computational Domain and Boundary Conditions
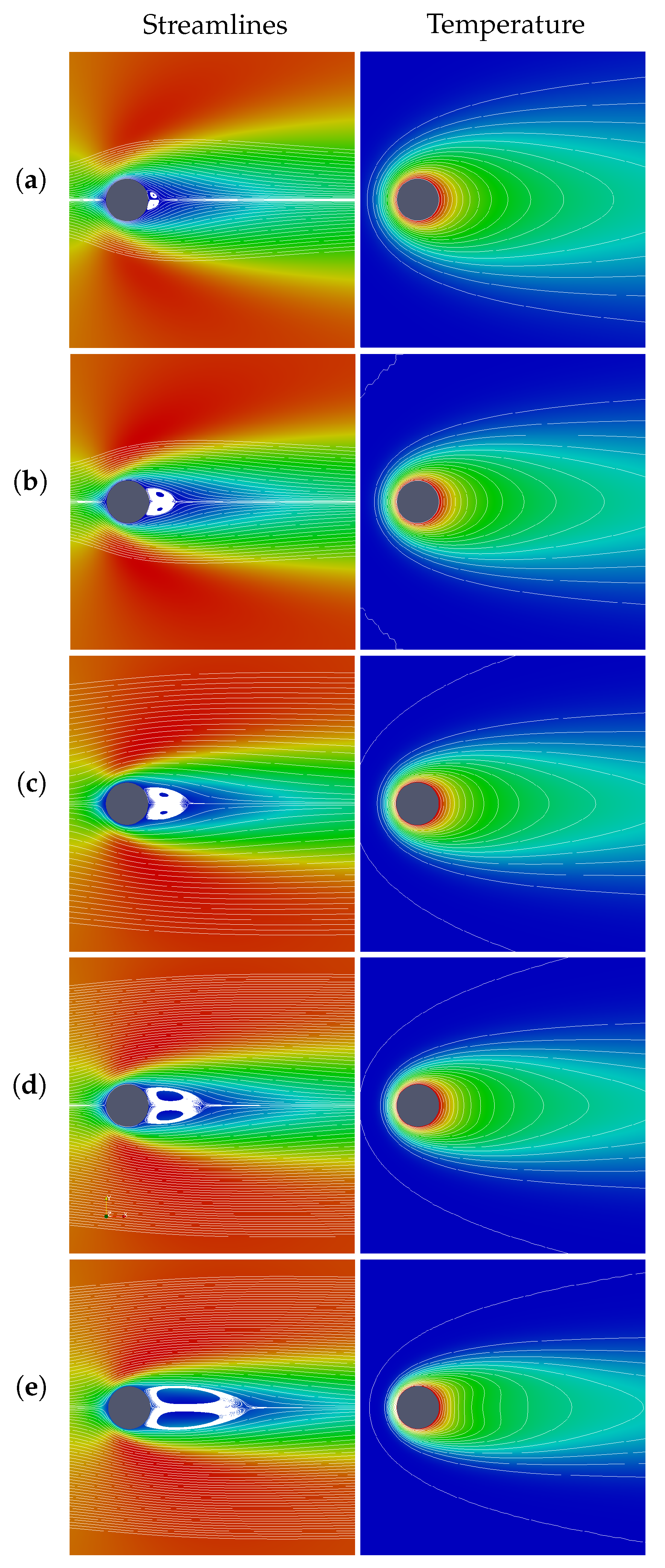
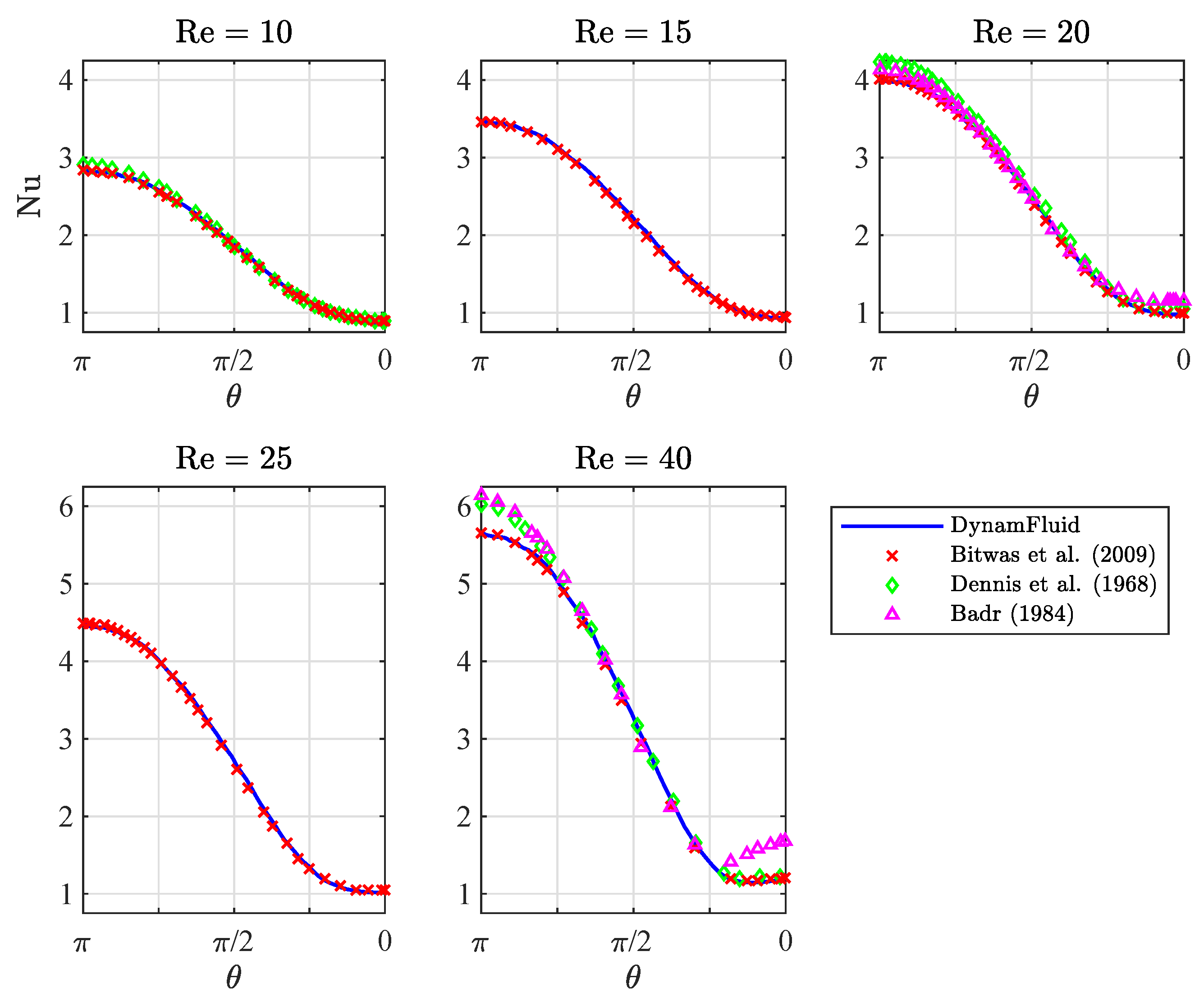
4.4.3. Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | Speed of sound |
| B | Blockage ratio () |
| Specific heat at constant pressure | |
| Specific heat at constant volume | |
| D | Cylinder diameter |
| e | Internal energy per unit mass, |
| Total energy per unit mass, | |
| Energy tensor containing the values of in every node of the mesh | |
| Difference in the estimating function between mesh #i and mesh #j | |
| f | Frequency |
| g | Acceleration of gravity |
| Gr | Grashof number |
| h | element size |
| H | Characteristic height of the problem |
| Identity tensor | |
| k | Thermal conductivity |
| L | Characteristic length of the problem |
| Distance from the inlet to the center of the cylinder | |
| Eddy length | |
| n | outward normal coordinate |
| Shape functions | |
| Nu | Local Nusselt number |
| p | Pressure |
| Pressure tensor containing the values of p in every node of the mesh | |
| Pr | Prandtl number, |
| Re | Reynolds number |
| Ri | Richardson number, Gr/Re |
| St | Strouhal number |
| t | Time |
| i-th component of the prescribed stress | |
| T | Temperature |
| Prescribed Temperature | |
| Temperature tensor containing the values of T in every node of the mesh | |
| i-th component of the prescribed temperature gradient | |
| i-th component of the velocity vector, | |
| Velocity tensor containing the i-th component of the velocity vector in every node of the mesh | |
| i-th component of the prescribed velocity | |
| i-th Cartesian coordinate, | |
| Greek letters | |
| Thermal diffusivity, | |
| Thermal expansion coefficient, | |
| Dynamic viscosity | |
| Variable to approximate using the finite element method | |
| Angle of detachment | |
| Density | |
| Kinematic viscosity, | |
| deviatoric viscous stress tensor | |
| velocity relaxation factor | |
| pressure relaxation factor | |
| the wall temperature difference ratio, | |
| unstructured triangulation composed by non-overlapping elements | |
| Subscripts | |
| c | Cold boundary |
| h | Hot boundary |
| w | Wall |
| ∞ | Reference value |
References
- Batchelor, C.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; ISBN 0-521-66396-2. [Google Scholar]
- Van Dyke, M. An Album of Fluid Motion; The Parabolic Press: Stanford, CA, USA, 1982; ISBN 978-0915760022. [Google Scholar]
- Barenblatt, G.I. Dimensional Analysis; CRC Press: Amsterdam, The Netherlands, 1987; ISBN 3-7186-0438-8. [Google Scholar]
- Bridgman, P.W. Dimensional Analysis; Yale University Press: New Haven, CT, USA, 1922. [Google Scholar]
- Anderson, J.D.; Wendt, J. Computational Fluid Ddynamics; McGraw-Hill: New York, NY, USA, 1995; Volume 206. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer Science Business Media: New York, NY, USA, 2012; ISBN 978-540-42074-3. [Google Scholar]
- Fletcher, C. Computational Techniques for Fluid Dynamics 1. Fundamental and General Techniques; Springer Science Business Media: New York, NY, USA, 1998; ISBN 978-3-642-97037-5. [Google Scholar]
- Fletcher, C.A. Computational Techniques for Fluid Dynamics 2: Specific Techniques for Different Flow Categories; Springer Science Business Media: New York, NY, USA, 2012; ISBN 978-3-642-97073-3. [Google Scholar]
- Pironneau, O. Finite Element Methods for Fluids; John Wiley & Sons: New York, NY, USA, 1989; ISBN 0-471-92255-2. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: the Finite Volume Method; Pearson Education: Harlow, UK, 2007; ISBN 978-0-13-127498-3. [Google Scholar]
- ANSYS Fluent: 2019 ANSYS, Inc. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 9 October 2019).
- Star-CCM+: 2019 Siemens Product Lifecycle Management Software Inc., All Rights Reserved. Available online: https://mdx.plm.automation.siemens.com/star-ccm-plus (accessed on 9 October 2019).
- COMSOL Multiphysics® v.5.4. Available online: https://www.comsol.com (accessed on 9 October 2019).
- Altair AcuSolve™ ©: 2019 Altair Engineering, Inc. Available online: https://altairhyperworks.com/product/AcuSolve (accessed on 9 October 2019).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, IUC, Dubrovnik, Croatia, 19–21 September 2007. [Google Scholar]
- OpenFOAM: OpenCFD Ltd (ESI Group). Available online: https://www.openfoam.com (accessed on 9 October 2019).
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Alnaes, M.S.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS Project Version 1.5. Arch. Numer. Soft. 2015, 3, 9–23. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large-Data Visualization. In The Visualization Handbook; Hansen, C.D., Johnson, C.R., Eds.; Elsevier Butterworth-Heinemann: Amsterdam, The Netherlands, 2005; pp. 717–731. ISBN 978-0-12-387582-2. [Google Scholar]
- Eigen: GNU Free Documentation License 1.2. Available online: http://eigen.tuxfamily.org (accessed on 9 October 2019).
- AbdelMigid, T.A.; Saqr, K.M.; Kotb, M.A.; Aboelfarag, A.A. Revisiting the lid-driven cavity flow problem: Review and new steady state benchmarking results using GPU accelerated code. Alex. Eng. J. 2017, 56, 123–135. [Google Scholar] [CrossRef]
- Erturk, E.; Corke, T.C.; Gökçöl, C. Numerical solutions of 2D steady incompressible driven cavity flow at high Reynolds numbers. Int. J. Numer. Methods Fluids 2005, 48, 747–774. [Google Scholar] [CrossRef]
- Erturk, E. Discussions on driven cavity flow. Int. J. Numer. Methods Fluids 2009, 60, 275–294. [Google Scholar] [CrossRef]
- Yapici, K.; Uludag, Y. Finite volume simulation of 2-D steady square lid-driven cavity flow at high reynolds numbers. Braz. J. Chem. Eng. 2013, 30, 923–937. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re Solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Marchi, C.H.; Suero, R.; Araki, L.K. The lid-driven square cavity flow: Numerical solution with a 1024 x 1024 grid. J. Braz. Soc. Mech. Sci. 2009, 31, 186–198. [Google Scholar] [CrossRef]
- Zhen-Hua, C.; Bao-Chang, S.; Lin, Z. Simulating high Reynolds number flow in two-dimensional lid-driven cavity by multi-relaxation-time lattice Boltzmann method. Chin. Phys. 2006, 15, 1855. [Google Scholar] [CrossRef]
- Erturk, E.; Dursun, B. Numerical solutions of 2-D steady incompressible flow in a driven skewed cavity. ZAMM Z. Angew. Math. Mech. 2007, 87, 377–392. [Google Scholar] [CrossRef]
- Aung, W.; Worku, G. Developing flow and flow reversal in a vertical channel with asymmetric wall temperatures. J. Heat Transf. 1986, 108, 299–304. [Google Scholar] [CrossRef]
- Aung, W.; Worku, G. Mixed convection in ducts with asymmetric wall heat fluxes. J. Heat Transf. 1987, 109, 947–951. [Google Scholar] [CrossRef]
- Aung, W.; Worku, G. Theory of fully developed, combined convection including flow reversal. J. Heat Transf. 1986, 108, 485–488. [Google Scholar] [CrossRef]
- Barletta, A. Analysis of flow reversal for laminar mixed convection in a vertical rectangular duct with one or more isothermal walls. Int. J. Heat Mass Transf. 2001, 44, 3481–3497. [Google Scholar] [CrossRef]
- Barletta, A.; Magyari, E.; Keller, B. Dual mixed convection flows in a vertical channel. Int. J. Heat Mass Transf. 2005, 48, 4835–4845. [Google Scholar] [CrossRef]
- Boulama, K.; Galanis, N. Analytical solution for fully developed mixed convection between parallel vertical plates with heat and mass transfer. J. Heat Transf. 2004, 126, 381–388. [Google Scholar] [CrossRef]
- Cheng, C.H.; Kou, H.S.; Huang, W.H. Flow reversal and heat transfer of fully developed mixed convection in vertical channels. J. Thermophys. Heat Transf. 1990, 4, 375–383. [Google Scholar] [CrossRef]
- El-Din, M.S. Effect of thermal and mass buoyancy forces on the development of laminar mixed convection between vertical parallel plates with uniform wall heat and mass fluxes. Int. J. Therm. Sci. 2003, 42, 447–453. [Google Scholar] [CrossRef]
- Gau, C.; Yih, K.A.; Aung, W. Reversed flow structure and heat transfer measurements for buoyancy-assisted convection in a heated vertical duct. J. Heat Transf. 1992, 114, 928–935. [Google Scholar] [CrossRef]
- Hamadah, T.T.; Wirtz, R.A. Analysis of laminar fully developed mixed convection in a vertical channel with opposing buoyancy. J. Heat Transf. 1991, 113, 507–510. [Google Scholar] [CrossRef]
- Ingham, D.B.; Keen, D.J.; Heggs, P.J. Flows in vertical channels with asymmetric wall temperatures and including situations where reverse flows occur. J. Heat Transf. 1988, 110, 910–917. [Google Scholar] [CrossRef]
- Ingham, D.B.; Keen, D.J.; Heggs, P.J. Two dimensional combined convection in vertical parallel plate ducts, including situations of flow reversal. Int. J. Numer. Methods Eng. 1988, 26, 1645–1664. [Google Scholar] [CrossRef]
- Jeng, Y.N.; Chen, J.L.; Aung, W. On the Reynolds-number independence of mixed convection in a vertical channel subjected to asymmetric wall temperatures with and without flow reversal. Int. J. Heat Fluid Flow 1992, 13, 329–339. [Google Scholar] [CrossRef]
- Kim, S.H.; Anand, N.K.; Aung, W. Effect of wall conduction on free convection between asymmetrically heated vertical plates: Uniform wall heat flux. Int. J. Heat Mass Transf. 1990, 33, 1013–1023. [Google Scholar] [CrossRef]
- Dennis, S.C.R.; Chang, G.-Z. Numerical solutions for steady flow past a circular cylinder at Reynolds number up to 100. J. Fluid Mech. 1970, 42, 471–489. [Google Scholar] [CrossRef]
- Dennis, S.C.R.; Hudson, J.D. An h4 accurate vorticity-velocity formulation for calculating flow past circular cylinder. Int J. Numer. Methods Fluids 1995, 21, 489–497. [Google Scholar] [CrossRef]
- Dennis, S.C.R.; Hudson, J.D.; Smith, N. Steady laminar forced convection from a circular cylinder at low Reynolds numbers. Phys. Fluids 1968, 11, 933–940. [Google Scholar] [CrossRef]
- Grove, A.S.; Shair, F.H.; Petersen, E.E. An experimental investigation of the steady separated flow past a circular cylinder. J. Fluid Mech. 1964, 19, 60–80. [Google Scholar] [CrossRef]
- Norberg, C. Pressure forces on a circular cylinder in cross flow. In Bluff-Body Wakes, Dynamics and Instabilities; Eckelmann, H., Graham, J.M.R., Huerre, P., Monkewitz, P.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 275–278. ISBN 978-3-662-00414-2. [Google Scholar]
- Norberg, C. An experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J. Fluid Mech. 1994, 258, 287–316. [Google Scholar] [CrossRef]
- Norberg, C. Flow around a circular cylinder: Aspects of fluctuating lift. J. Fluid Struct. 2001, 15, 459–469. [Google Scholar] [CrossRef]
- Norberg, C. Fluctuating lift on a circular cylinder: Review and new measurements. J. Fluid Struct. 2003, 17, 57–96. [Google Scholar] [CrossRef]
- Triton, D.J. Experiments on the flow past a circular cylinder at low Reynolds number. J. Fluid Mech. 1959, 6, 547–567. [Google Scholar] [CrossRef]
- Chakraborty, J.; Verma, N.; Chhabra, R.P. Wall effects in the flow past a circular cylinder in a plane channel: A numerical study. Chem. Eng. Process. 2004, 43, 1529–1537. [Google Scholar] [CrossRef]
- Ding, H.; Shu, C.; Yeo, K.S.; Xu, D. Simulation of incompressible viscous flows past a circular cylinder by hybrid FD scheme and meshless least square-based finite difference scheme. Comput. Methods Appl. Mech. 2004, 193, 727–744. [Google Scholar] [CrossRef]
- Park, J.; Kwon, K.; Choi, H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160. KSME Int. J. 1998, 12, 1200–1205. [Google Scholar] [CrossRef]
- De Sampaio, P.A.B.; Lyra, P.R.M.; Morgan, K.; Weatherill, N.P. Petrov-Galerkin solutions of the incompressible Navier-Stokes equations in primitive variables with adaptative remeshing. Comput. Methods Appl. Mech. 1993, 106, 143–178. [Google Scholar] [CrossRef]
- Subhankar, S.; Sanjay, M.; Gautam, B. Numerical Simulation of Steady Flow Past a Circular Cylinder. In Proceedings of the 37th National and 4th International Conference on Fluid Mechanics and Fluid Power, IIT Madras, Chennai, India, 16–18 December 2010. [Google Scholar]
- Bitwas, G.; Sarkar, S. Effect of thermal buoyancy on vortex shedding past a circular cylinder in cross-flow at low Reynolds numbers. Int J. Heat Mass Transf. 2009, 52, 1897–1912. [Google Scholar] [CrossRef]
- Takami, H.; Keller, H.B. Steady two-dimensional viscous flow of an incompressible fluid past a circular cylinder. Phys. Fluids 1969, 12, II-51–II-56. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Morgan, K.; Satya Sai, B.V.K.; Codina, R.; Vazquez, M. A general algorithm for compressible and incompressible flow—Part II. Tests on the explicit form. Int. J. Numer. Methods Fluids 1995, 20, 887–913. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Codina, R. A general algorithm for compressible and incompresible flow - Part I. The split, characteristic based scheme. Int. J. Numer. Methods Fluids 1996, 20, 869–885. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Nithiarasu, P.; Codina, R.; Vazquez, M.; Ortiz, P. The characteristic-based-split procedure: An efficient and accurate algorithm for fluid problems. Int. J. Numer. Methods Fluids 1999, 31, 359–392. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method. Volume 3: Fluid Dynamics, 6th ed.; Elsevier Butterworth-Heinemann: Amsterdam, The Netherlands, 2005; ISBN 0-7506-6322-7. [Google Scholar]
- Nithiarasu, P.; Codina, R.; Zienkiewicz, O.C. The Characteristic-Based Split (CBS) scheme—A unified approach to fluid dynamics. Int. J. Numer. Methods Eng. 2006, 66, 1514–1546. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Codina, R.; Vazquez, M.; Zienkiewicz, O.C. A general algorithm for compressible and incompressible flows. Part III: The semi-implicit form. Int. J. Numer. Methods Fluids 1998, 27, 13–32. [Google Scholar] [CrossRef]
- Editorial Board. Georgii Ivanovich Petrov (on his 100th birthday). Fluid Dyn. 2012, 47, 289–291. [Google Scholar] [CrossRef]
- Ern, A.; Guermond, J.L. Theory and Practice of Finite Elements; Springer: New York, NY, USA, 2004; ISBN 9780387205748. [Google Scholar]
- Mikhlin, S.G. Variational Methods in Mathematical Physics; Pergamon Press: New York, NY, USA, 1964. [Google Scholar]
- Carpio, J.; Prieto, J.L.; Vera, M. A local anisotropic adaptive algorithm for the solution of low-Mach transient combustion problems. J. Comput. Phys. 2016, 306, 19–42. [Google Scholar] [CrossRef]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; Wiley: West Sussex, UK, 2004; ISBN 978-0-470-02081-4. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Desrayaud, G.; Lauriat, G. Flow reversal of laminar mixed convection in the entry region of symmetrically heated, vertical plate channels. Int. J. Therm. Sci. 2009, 48, 2036–2045. [Google Scholar] [CrossRef]
- Nithiarasu, P. An efficient artificial compressibility (AC) scheme based on the characteristic based split (CBS) method for incompressible flows. Int. J. Numer. Methods Eng. 2003, 5, 1815–1845. [Google Scholar] [CrossRef]
- Massarotti, N.; Arpino, F.; Lewis, R.W.; Nithiarasu, P. Explicit and semi-implicit CBS procedures for incompressible viscous flows. Int. J. Numer. Methods Eng. 2006, 66, 1618–1640. [Google Scholar] [CrossRef]
- Selvam, R.P. Finite element modelling of flow around a circular cylinder using LES. J. Wind Eng. Ind. Aerod. 1997, 67, 129–139. [Google Scholar] [CrossRef]
- Qu, L.; Norgerg, C.; Davidson, L.; Peng, S.; Wang, F. Quantitive numerical analysis of flow past a circular cylinder at Reynolds number between 50 and 200. J. Fluid Struct. 2013, 39, 347–370. [Google Scholar] [CrossRef]
- Sahin, M.; Owens, R.G. A numerical investigation of wall effects up to high blockage ratios on two-dimensional flow past a confined circular cylinder. Phys. Fluids 2004, 16, 1305–1320. [Google Scholar] [CrossRef]
- Posdziech, O.; Grundmann, R. A systematic approach to the numerical calculation of fundamental quantities of the two-dimensional flow over a circular cylinder. J. Fluid Struct. 2007, 23, 479–499. [Google Scholar] [CrossRef]
- Mittal, S.; Raghuvanshi, A. Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Int. J. Numer. Methods Fluids 2001, 35, 421–447. [Google Scholar] [CrossRef]
- Mittal, S.; Kumar, V. Finite element study of vortex-induced cross-flow and in-line oscillations of a circular cylinder at low Reynolds numbers. Int. J. Numer. Methods Fluids 1999, 31, 1087–1120. [Google Scholar] [CrossRef]
- Kieft, R.; Rindt, C.C.M.; van Steenhoven, A.A. Near-weak effects of a heat input on the vortex-shedding mechanism. Int. J. Heat Fluid Flow 2007, 28, 938–947. [Google Scholar] [CrossRef]
- Jordan, S.A.; Ragab, S.A. A large-eddy simulation of the near wake of a circular cylinder. J. Fluid Eng. 1998, 120, 243–252. [Google Scholar] [CrossRef]
- Behr, M.; Hastreiter, D.; Mittal, S.; Tezduyar, T.E. Incompressible flow past a circular cylinder: Dependence of the computed flow field on the location of the lateral boundaries. Comput. Methods Appl. Mech. 1995, 123, 309–316. [Google Scholar] [CrossRef]
- Rahman, M.; Karim, M.; Alim, A. Numerical investigation of unsteady flow past a circular cylinder using 2-D Finite Volume Method. JNAME 2007, 4, 27–42. [Google Scholar] [CrossRef]
- Rajani, B.N.; Kandasamy, A.; Majumdar, S. Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model. 2009, 33, 1228–1247. [Google Scholar] [CrossRef]
- Apelt, C.J.; Ledwich, M.A. Heat transfer in transient and unsteady flows past a circular cylinder in the range 1 < R < 40. J. Fluid Mech. 1979, 95, 761–777. [Google Scholar] [CrossRef]
- Rashid, A.; Ahmad, P.H. Steady-State Numerical Solution of the Navier-Stokes and Energy Equations around a Horizontal Cylinder at Moderate Reynolds Numbers from 100 to 500. Heat Transf. Eng. 1996, 17, 31–81. [Google Scholar] [CrossRef]
- Badr, H.M. Laminar combined convection from a horizontal cylinder—Parallel and contra flow regimes. Int. J. Heat Mass Transf. 1984, 27, 15–27. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]



| Grid Comparison | |||
|---|---|---|---|
| vs. | |||
| vs. |
| [56] | [77] | [86] | [85] | [54] | Present Work | |
|---|---|---|---|---|---|---|
| 100 | 0.164 | |||||
| 200 | − | − | 0.196 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Redal, H.; Carpio, J.; García-Salaberri, P.A.; Vera, M. DynamFluid: Development and Validation of a New GUI-Based CFD Tool for the Analysis of Incompressible Non-Isothermal Flows. Processes 2019, 7, 777. https://doi.org/10.3390/pr7110777
Redal H, Carpio J, García-Salaberri PA, Vera M. DynamFluid: Development and Validation of a New GUI-Based CFD Tool for the Analysis of Incompressible Non-Isothermal Flows. Processes. 2019; 7(11):777. https://doi.org/10.3390/pr7110777
Chicago/Turabian StyleRedal, Héctor, Jaime Carpio, Pablo A. García-Salaberri, and Marcos Vera. 2019. "DynamFluid: Development and Validation of a New GUI-Based CFD Tool for the Analysis of Incompressible Non-Isothermal Flows" Processes 7, no. 11: 777. https://doi.org/10.3390/pr7110777
APA StyleRedal, H., Carpio, J., García-Salaberri, P. A., & Vera, M. (2019). DynamFluid: Development and Validation of a New GUI-Based CFD Tool for the Analysis of Incompressible Non-Isothermal Flows. Processes, 7(11), 777. https://doi.org/10.3390/pr7110777






