Numerical Study of the Unsteady Flow Characteristics of a Jet Centrifugal Pump under Multiple Conditions
Abstract
:1. Introduction
2. Research Method and Model
2.1. The Model Pump
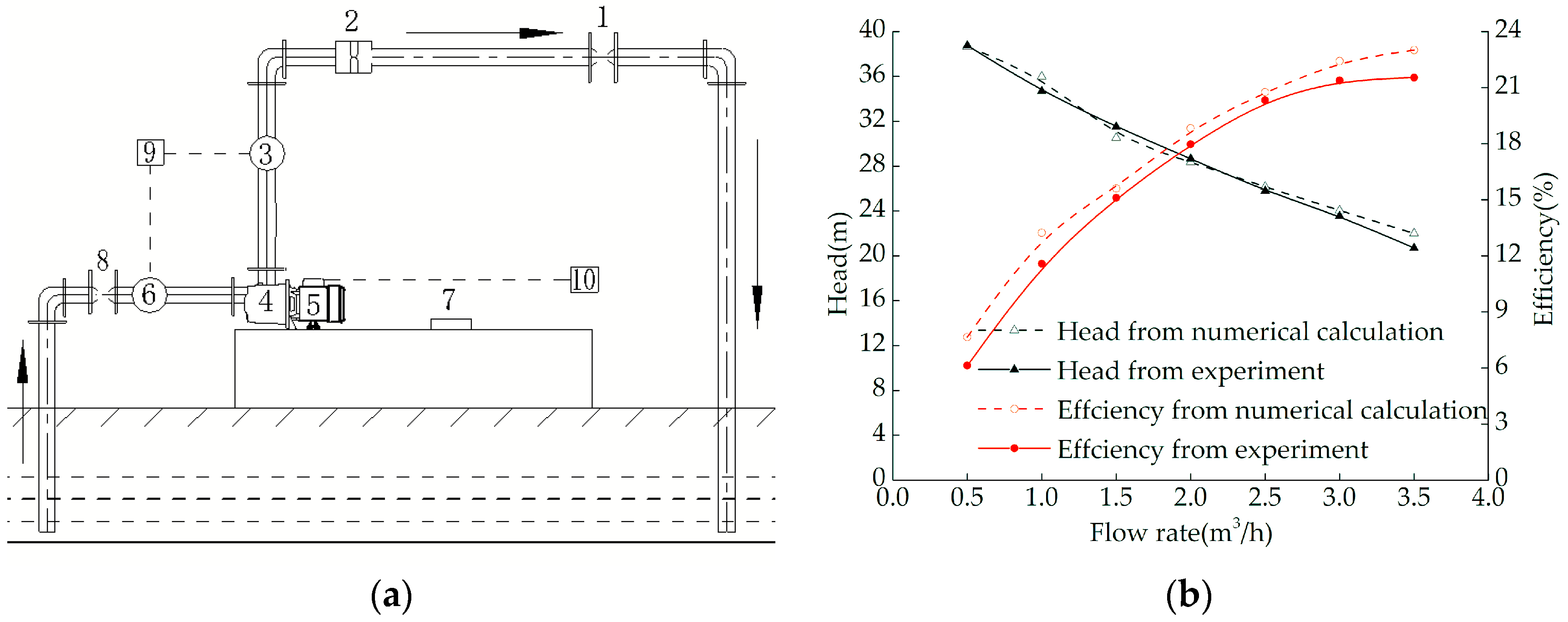
2.2. Numerical Method
2.3. Numerical Validation
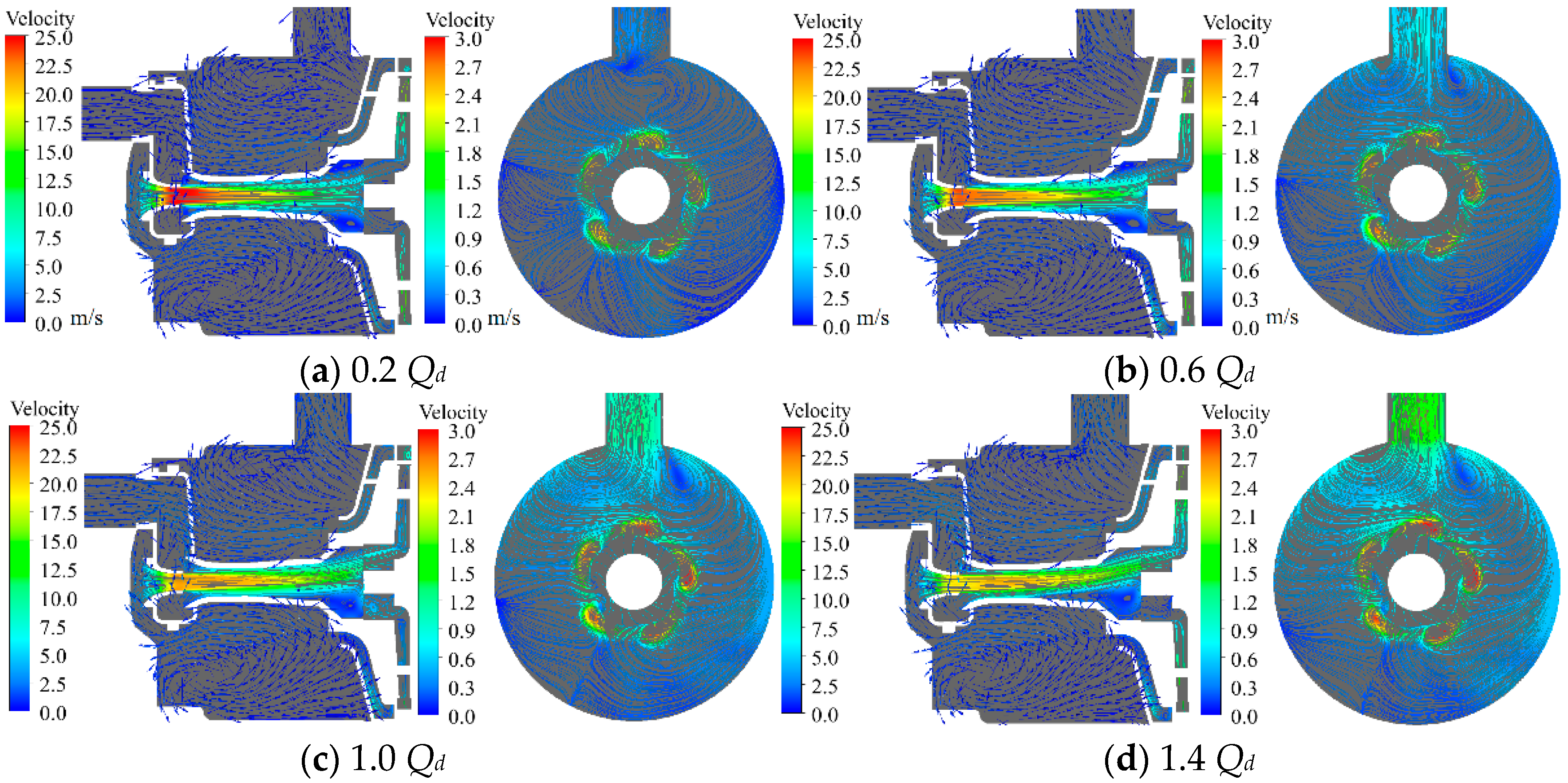
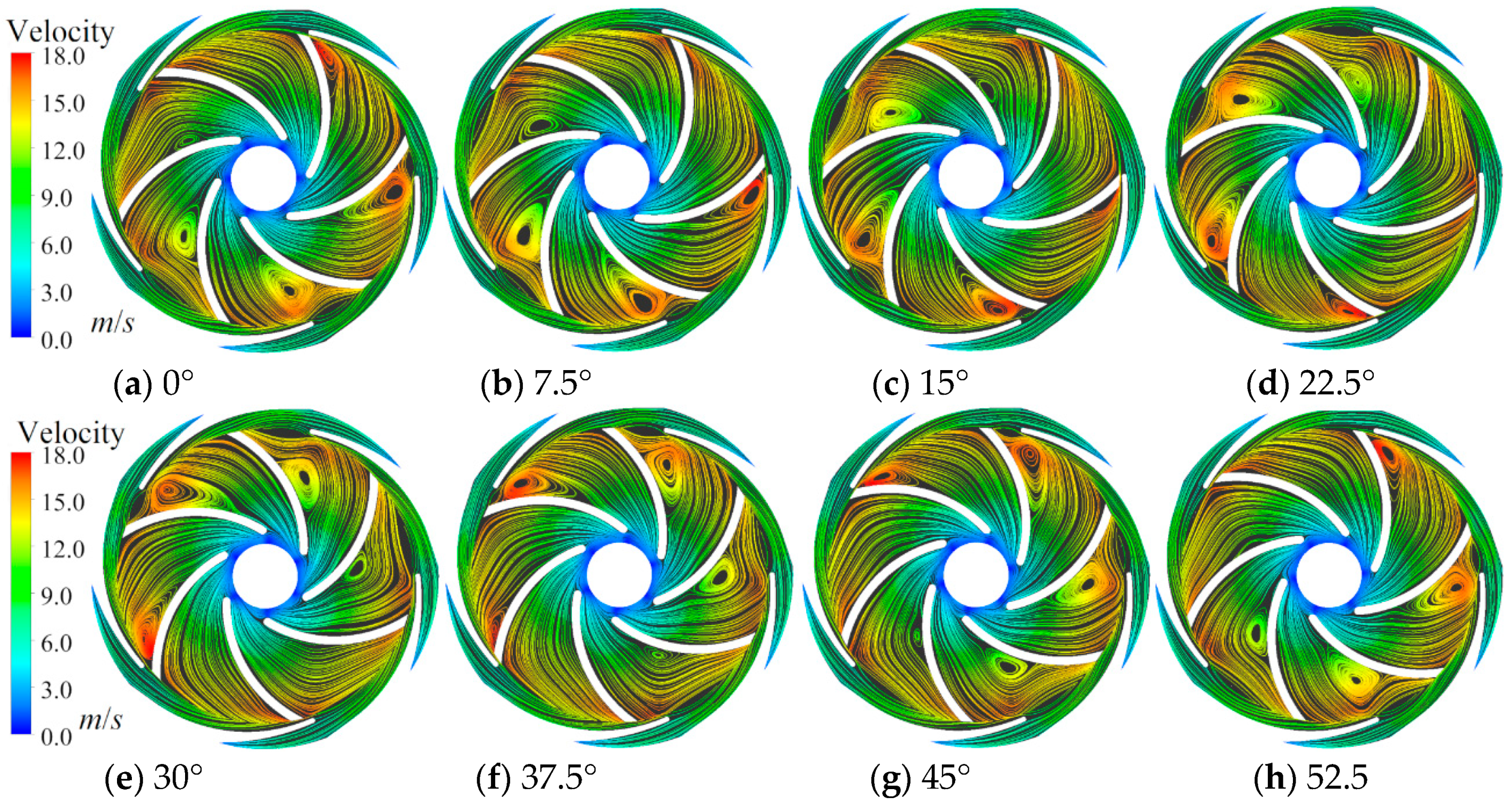
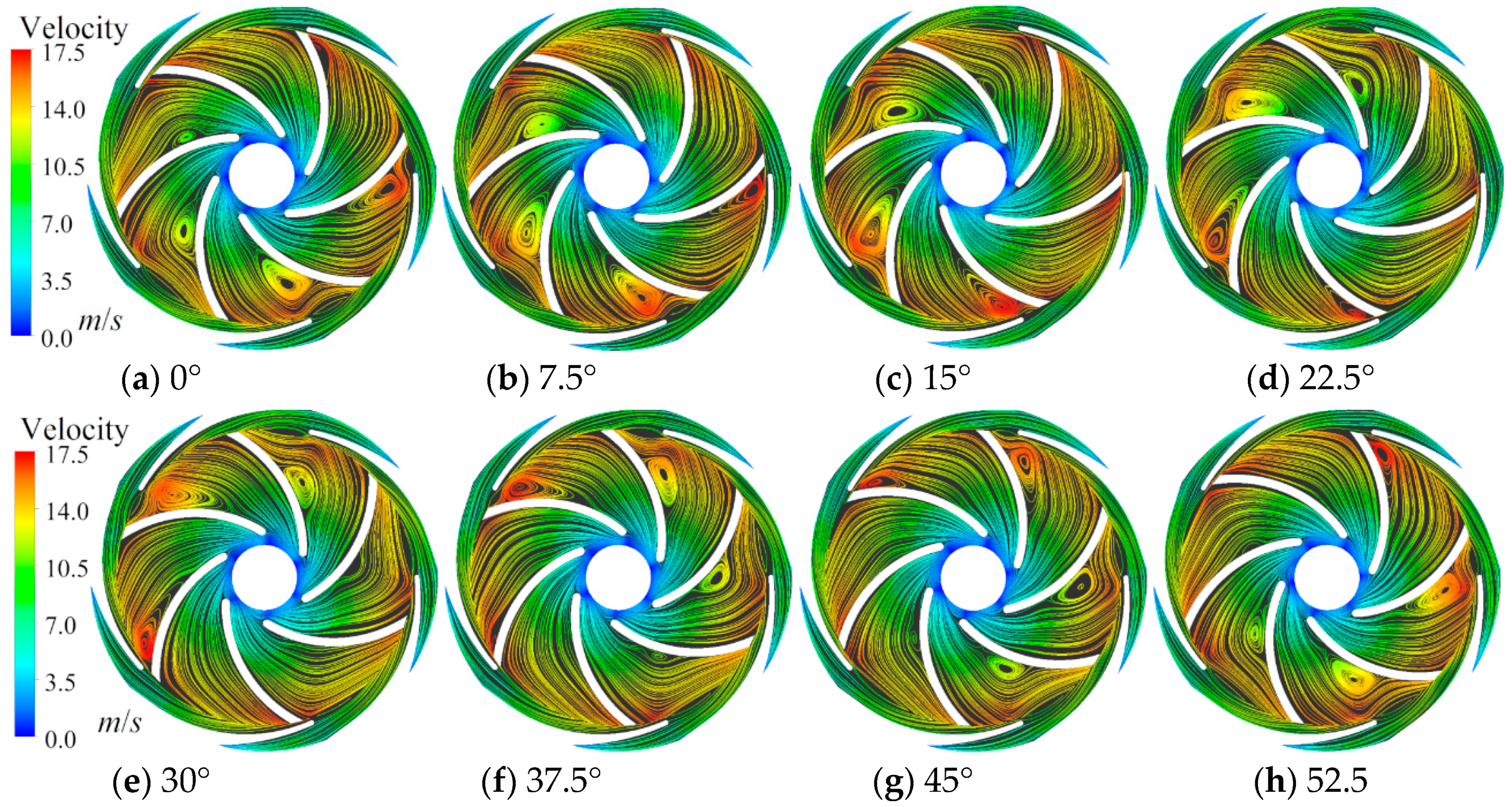
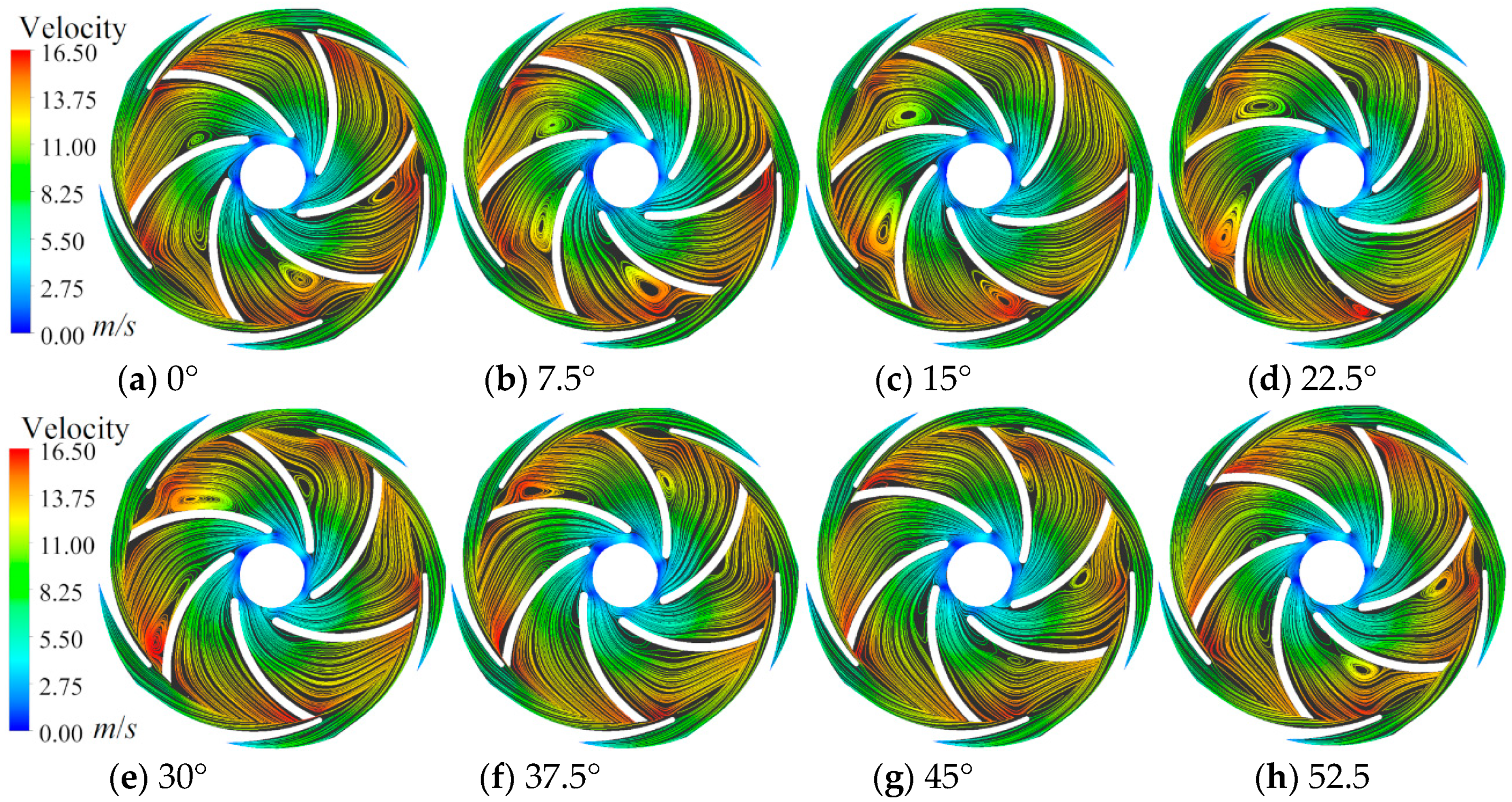
3. Analysis of the Velocity Vector and Streamline
4. Analysis of Unsteady Flow Field Characteristics Based on a Statistical Method
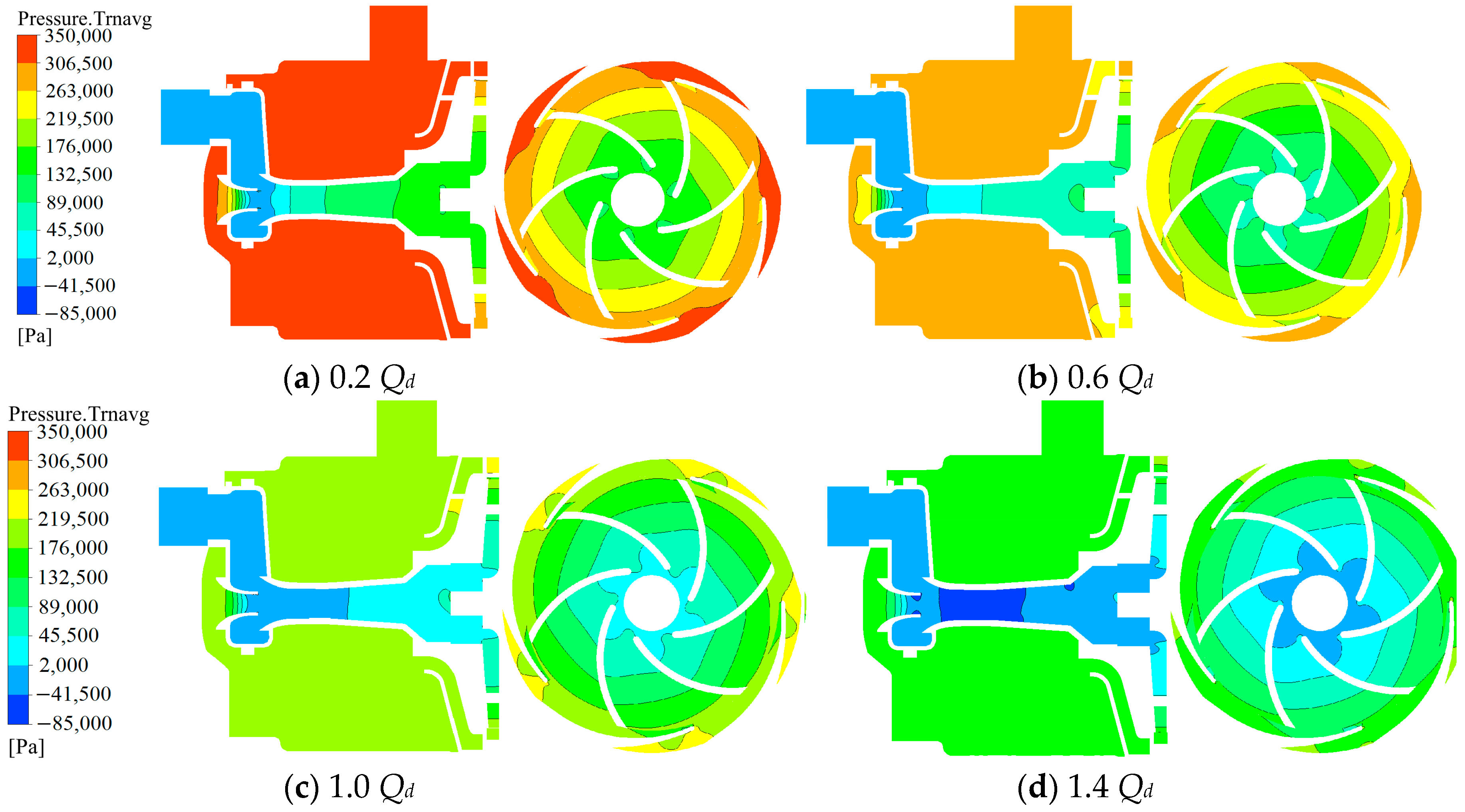
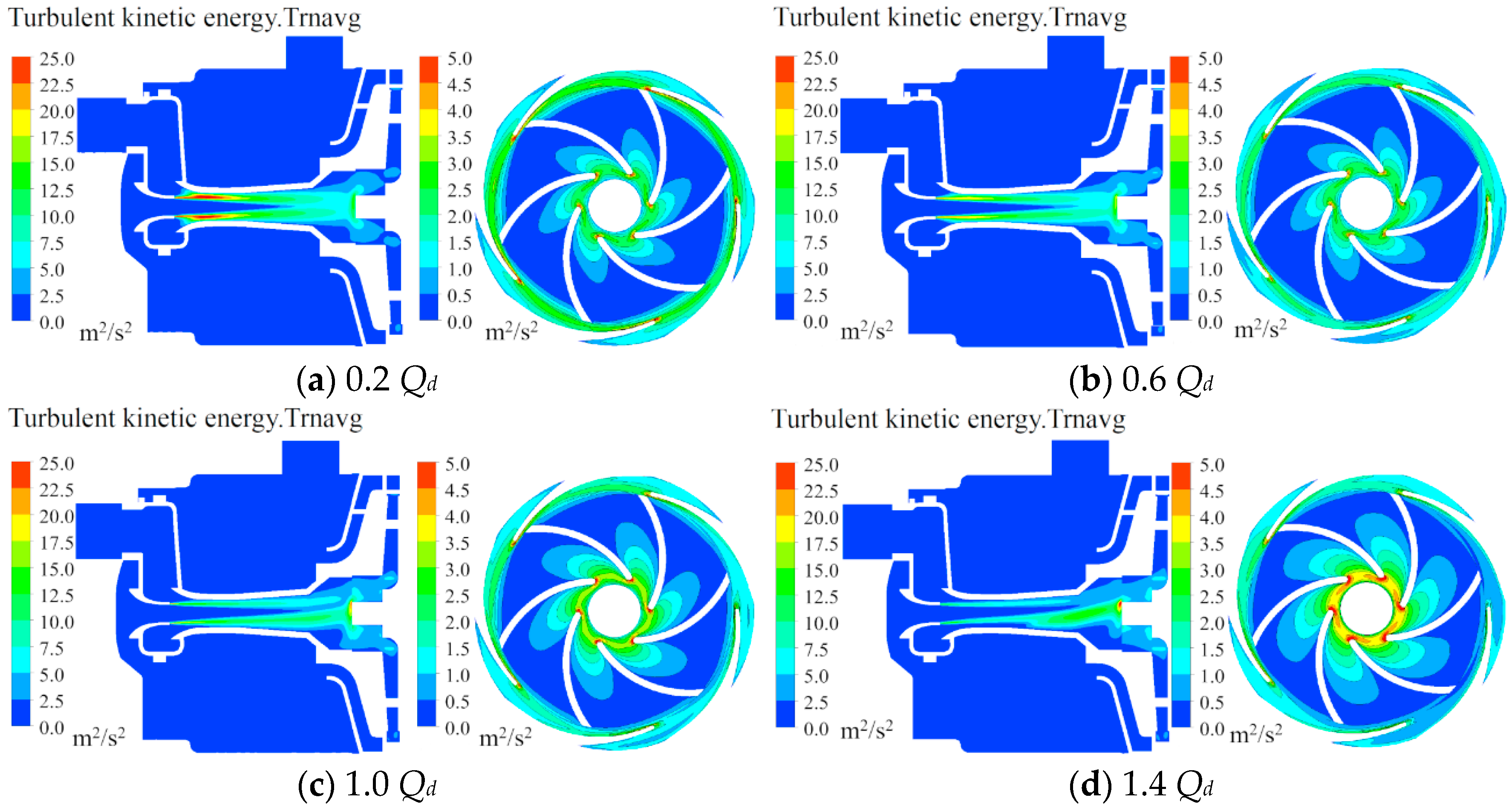
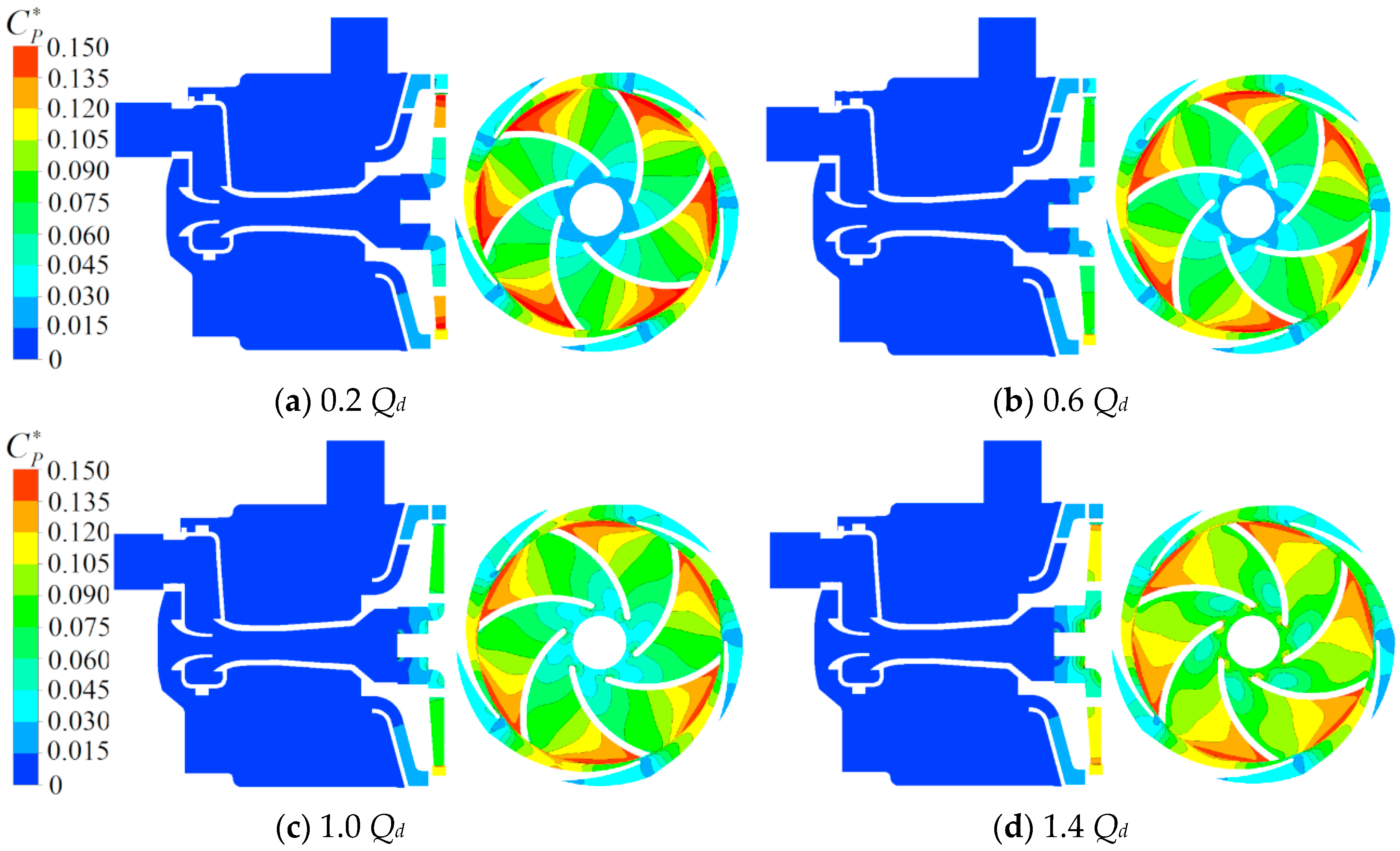
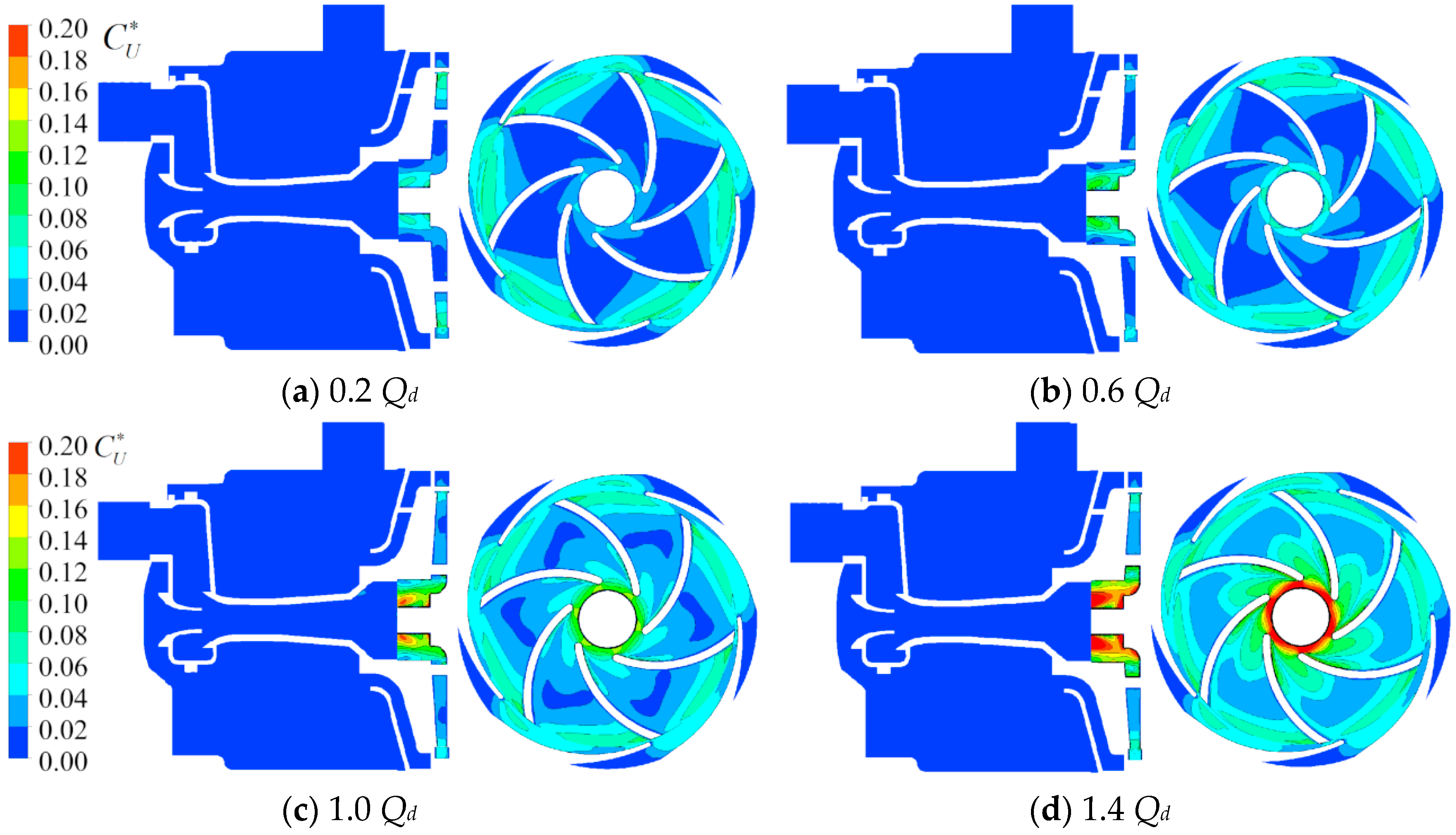
4.1. Time-Averaged Distribution Characteristics of the Flow Field
4.2. Distribution Characteristics of the Fluctuation Intensity of the Flow Field
5. Analysis of Spatial–Temporal Evolution of Vortices in the Rotor–Stator Cascades
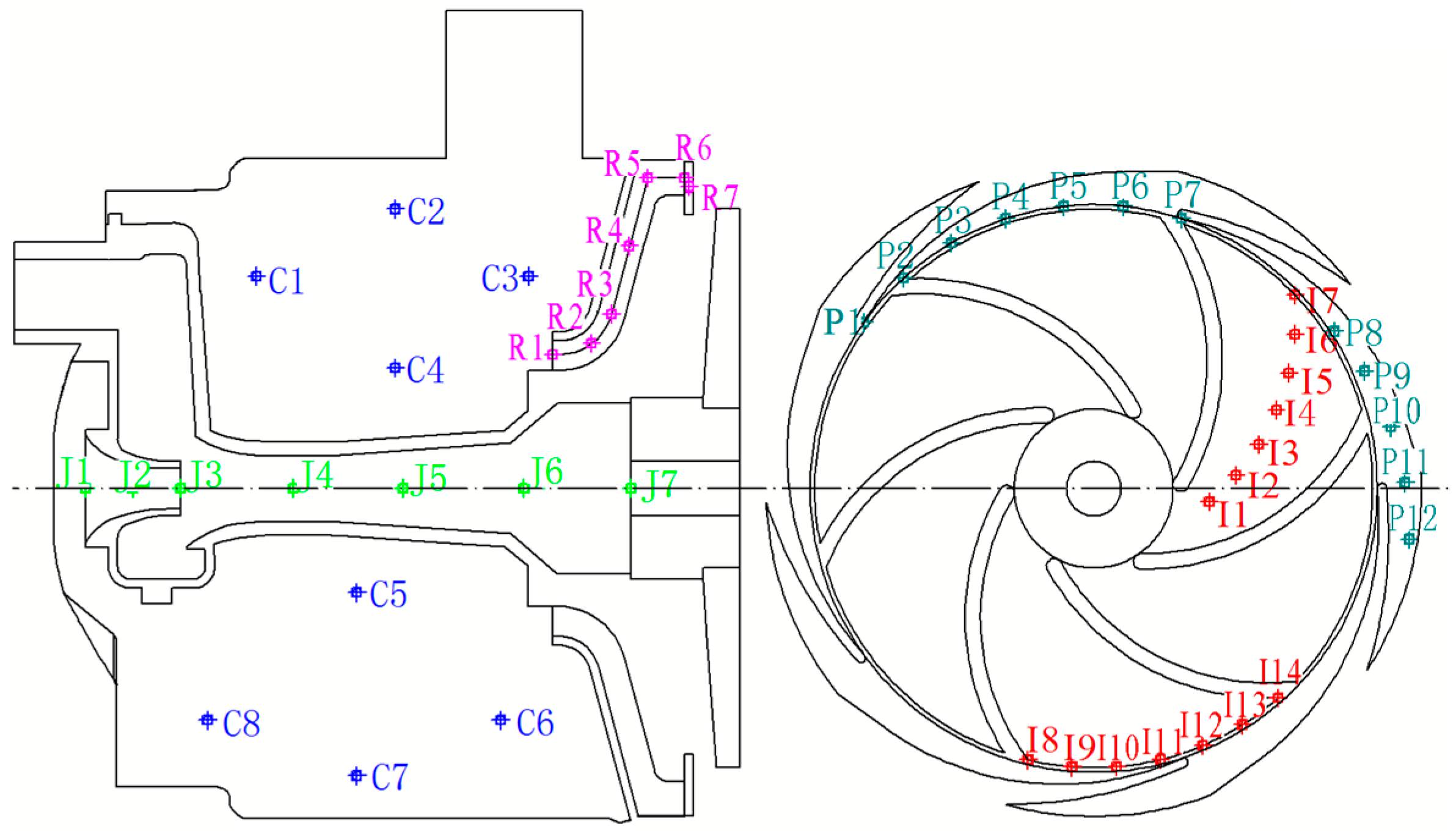
6. Pressure Fluctuation Characteristics of the Main Flow Passage Components
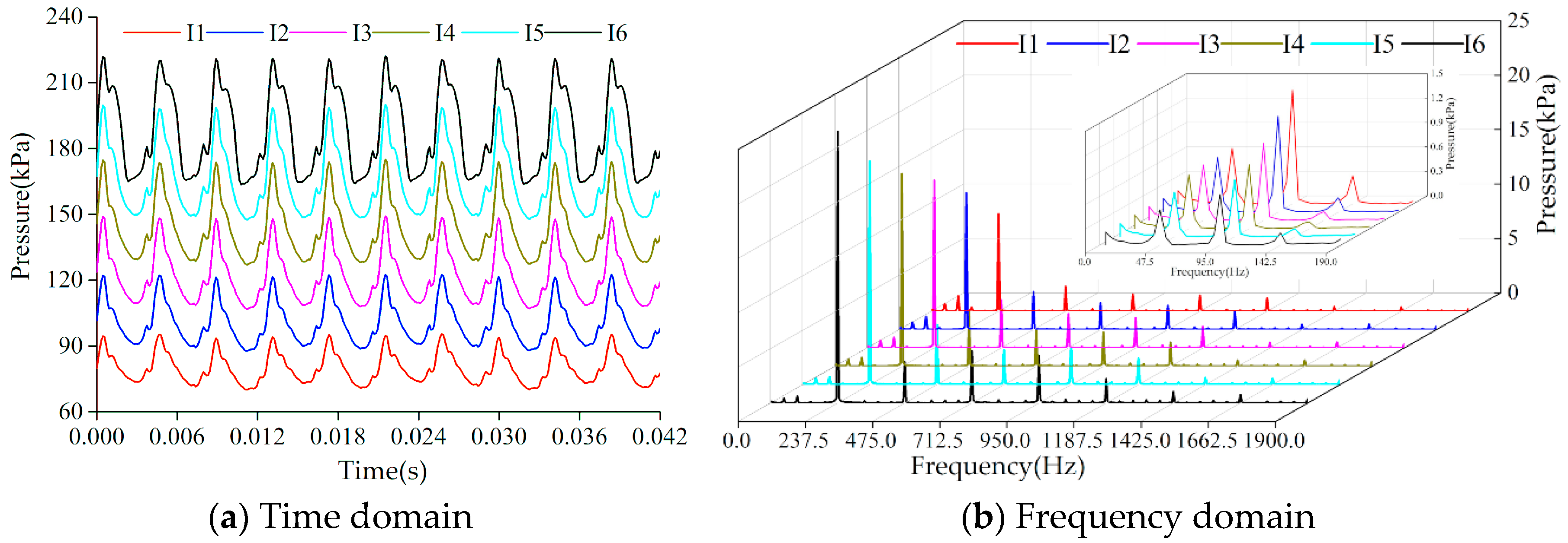
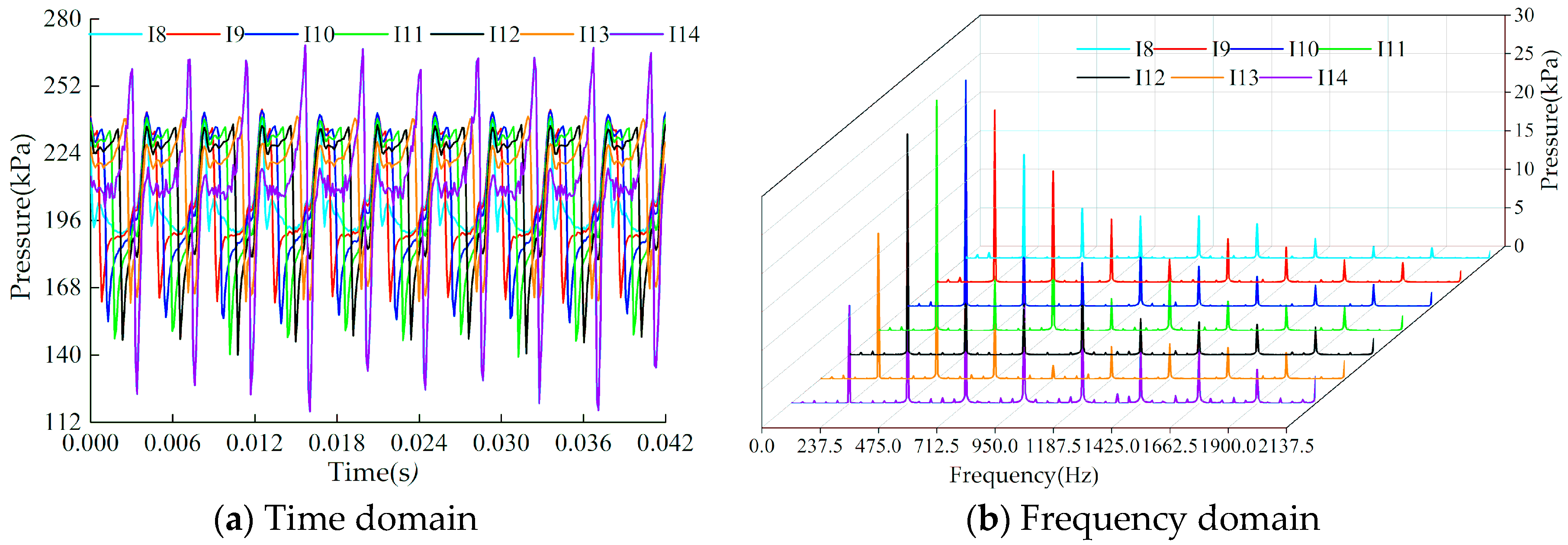
6.1. Impeller
6.1.1. Monitoring Points Stationary Relative to the Fixed Coordinate System
6.1.2. Monitoring Points Stationary Relative to the Rotating Coordinate System
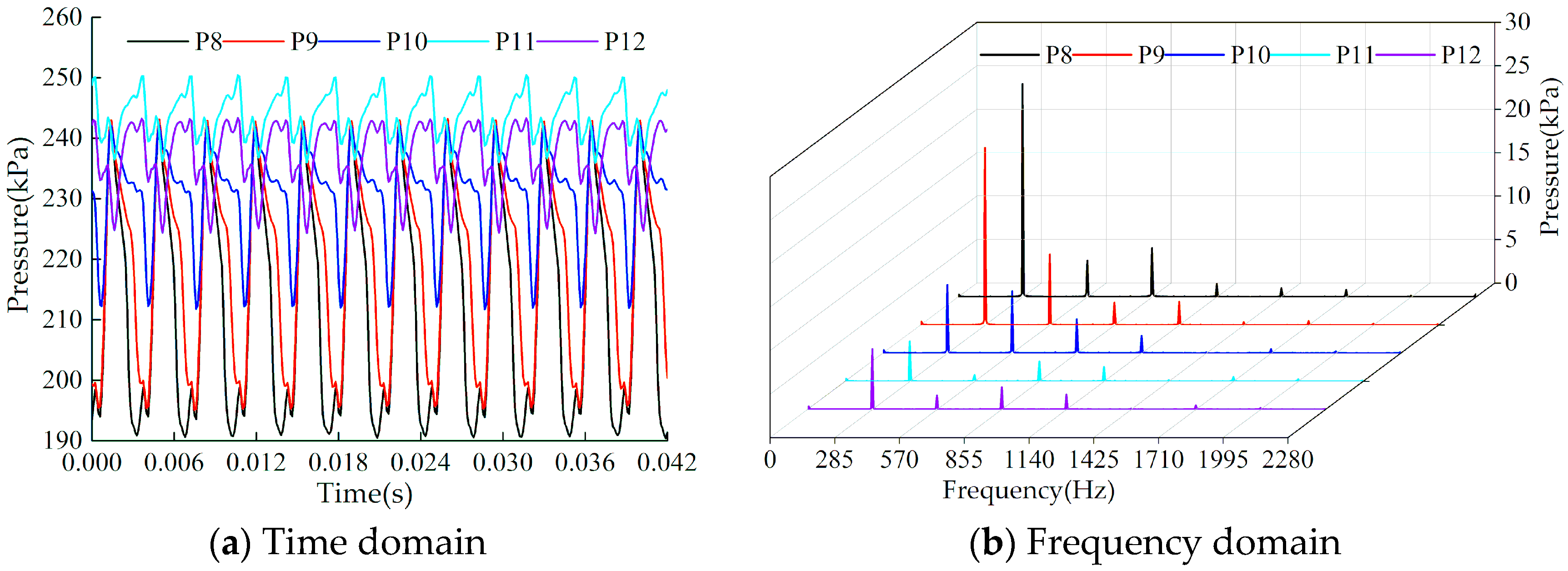
6.2. Guide Vane
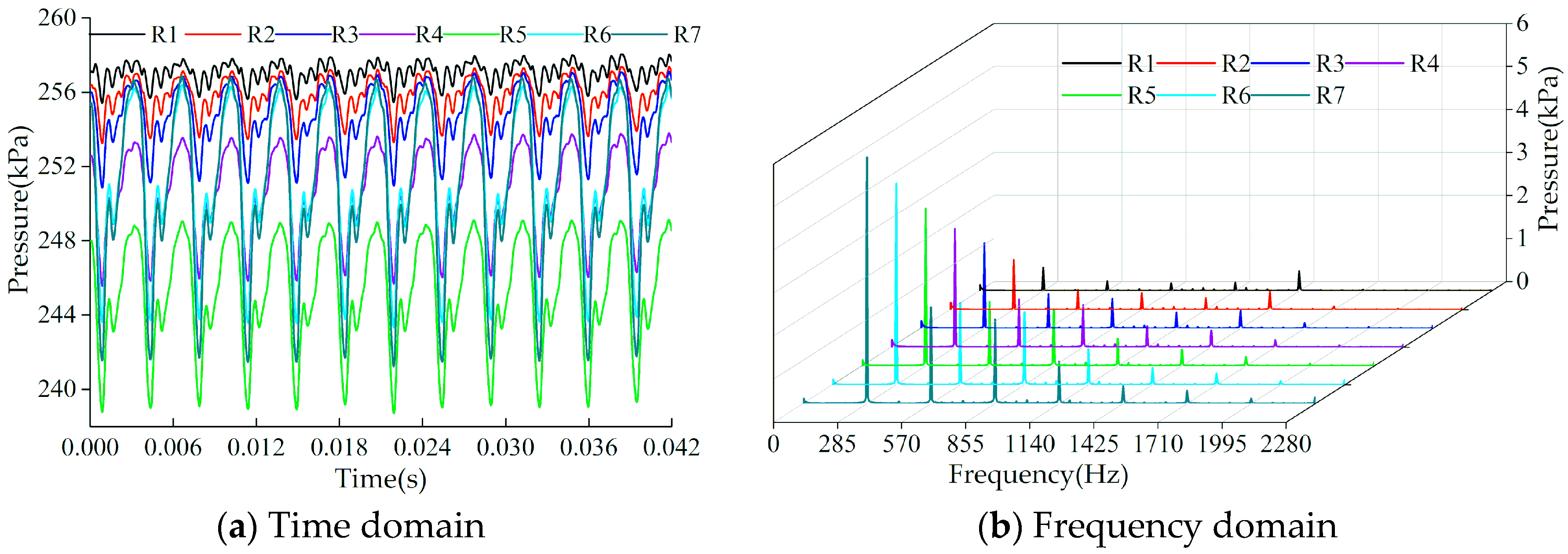
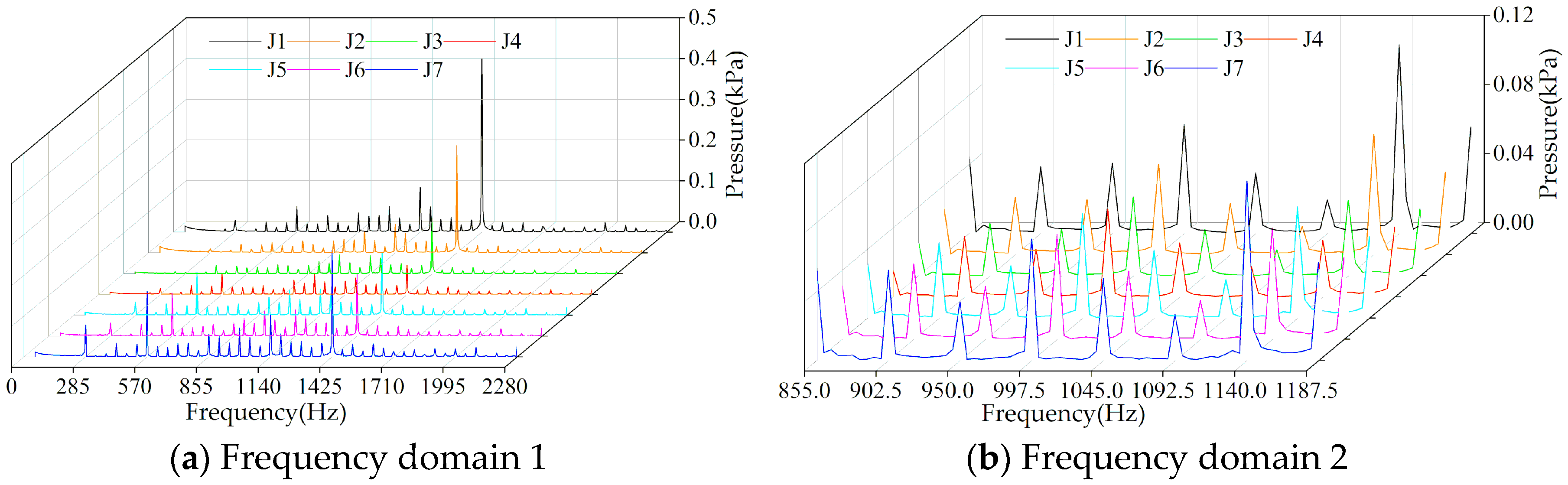
6.3. Pump Chamber and Ejector
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Qd | Rated volume flow m3/h |
| Hd | Rated water head m |
| ηd | Rated efficiency % |
| n | Rotational speed r/min |
| SPF | Shaft passing frequency Hz |
| BPFI | Blade passing frequency of impeller Hz |
| BPFG | Blade passing frequency of guide vane Hz |
| Dj | Inlet diameter of impeller mm |
| D2 | Outlet diameter of impeller mm |
| Z1 | Blade number of impeller |
| φ1 | Blade wrap angle of impeller ° |
| b2 | Blade outlet width of impeller mm |
| D3 | Base diameter of guide vane mm |
| D4 | Outlet diameter of guide vane mm |
| Z2 | Blade number of guide vane |
| GGI | General grid interface |
| Time-averaged components | |
| Periodic components | |
| n | Grid nodes |
| N | Number of samples in an impeller rotating period |
| t | Total time |
| t0 | Starting time of the rotation cycle |
| Non-dimensional pressure fluctuation intensity | |
| Non-dimensional velocity fluctuation intensity | |
| Non-dimensional turbulence energy fluctuation intensity | |
| Pressure fluctuation intensity | |
| Velocity fluctuation intensity | |
| Turbulence energy fluctuation intensity |
References
- Liu, J.R.; Zhou, G.P. Research and prospects for the self-priming irrigation pumps. Trans. Chin. Soc. Agric. Mach. 2007, 8, 177–180. [Google Scholar] [CrossRef]
- Wang, W.J.; Tang, Y.; Ma, H.; Yang, Z. Design and research of jet self-priming centrifugal pump. Equip. Manuf. Technol. 2017, 5, 32–34. [Google Scholar]
- Li, W.; Chang, H.; Liu, J.R.; Zhou, L.; Wang, C. Research situation and prospect of jet type self-priming centrifugal pump. Drain. Irrig. Mach. Eng. 2016, 34, 947–952. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.L.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.D.; Cao, P.Y.; Yin, G.; Cui, Y.R.; Li, Y.C. Effects of internal circulation flow on self-priming performance of flow-ejecting self-priming pump. Trans. Chin. Soc. Agric. Mach. 2014, 45, 129–133. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.W.; Zhu, X.X.; Sun, W.; Cao, P.Y.; Wu, W. Optimization and experiment on performance of flow-ejecting self-priming pump based on CFD. Trans. Chin. Soc. Agric. Eng. 2016, 32, 16–21. [Google Scholar] [CrossRef]
- Liu, J.R.; Wen, H.G.; Gao, Z.J.; Guo, C.X.; Wang, P. Effects of geometric parameters for jet nozzle on self-priming performance of spray pump. Trans. Chin. Soc. Agric. Eng. 2012, 28, 47–54. [Google Scholar] [CrossRef]
- Liu, J.R.; Wen, H.G.; Xiang, H.J.; Guo, C.X.; Gao, Z.J. Effects of diffuser on self-priming performance of flow-ejecting self-priming centrifugal pump. Trans. Chin. Soc. Agric. Mach. 2013, 44, 43–47. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.D.; Li, W.; Zhang, D.S.; Jiang, X.P. Unsteady numerical calculation and validation on self-priming process of self-priming spray irrigation pump. Trans. Chin. Soc. Agric. Eng. 2016, 32, 65–72. [Google Scholar] [CrossRef]
- Zhang, R.H.; Zhang, S.D.; Tian, L.; Chen, X.B. Research on performance and inner flow characteristics of jet centrifugal pump. J. Drain. Irrig. Mach. Eng. 2019, 37, 763–768+775. [Google Scholar] [CrossRef]
- Chen, N.; Liu, W.H.; Lai, H.Q. Numerical analysis of flow field inside injection pump by CFD. Ship Sci. Technol. 2016, 38, 53–56. [Google Scholar] [CrossRef]
- Li, G.D.; Wang, Y.; Yang, X.M.; Zhao, L.F.; Wu, W.; Hu, R.X. Features of internal flow in jet nozzle of self-priming centrifugal pump based on large eddy simulation. J. Drain. Irrig. Mach. Eng. 2017, 35, 369–374. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Y.R.; Wang, K.; Wang, W.J.; Li, G.D.; Yin, G. Analysis of unsteady flow in flow-ejecting self-priming centrifugal pump based on LES. J. Drain. Irrig. Mach. Eng. 2015, 33, 481–487. [Google Scholar] [CrossRef]
- Wang, W.J.; Wang, Y.; Li, G.D.; Yin, G.; Cao, P.Y. Numerical simulation and testing analysis of three dimensional turbulence flow in flow-ejecting self-priming centrifugal pump. Trans. Chin. Soc. Agric. Mach. 2014, 45, 54–60. [Google Scholar] [CrossRef]
- Li, G.D.; Wang, Y.; Cao, P.Y.; Zhou, G.H.; Wu, W.; Han, Y.W. Internal flow of flow-ejecting centrifugal pump under off-design conditions. Trans. Chin. Soc. Agric. Mach. 2015, 46, 48–53. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Pei, J.; Yuan, S.Q.; Yuan, J.P.; Wang, W.J. Comparative study of pressure fluctuation intensity for a single blade pump under multiple operating conditions. J. Huazhong Univ. Sci. Technol. 2013, 41, 29–33. [Google Scholar] [CrossRef]
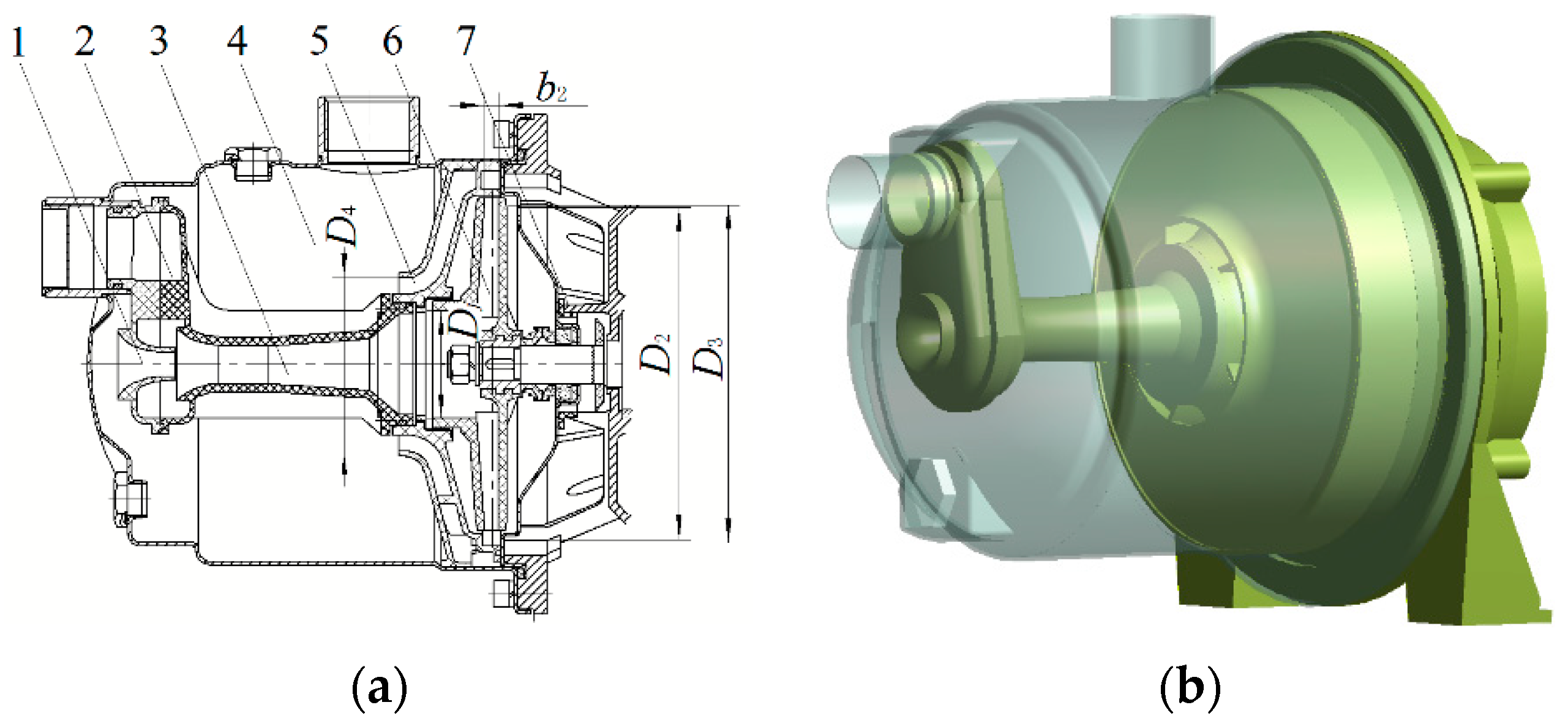








| Parameter | Value | |
|---|---|---|
| Impeller | Inlet Diameter Dj (mm) | 40 |
| Outlet Diameter D2 (mm) | 123 | |
| Blade Number Z1 | 6 | |
| Blade Wrap Angle φ (°) | 76 | |
| Blade Outlet Width b2 (mm) | 5.3 | |
| Guide Vane | Base Diameter (mm) | 125 |
| Outlet Diameter D3 (mm) | 64 | |
| Blade Number Z2 | 5 |
| Schemes | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | Scheme 5 | Scheme 6 |
|---|---|---|---|---|---|---|
| Number of the grid | 1,483,718 | 1,975,598 | 2,526,764 | 3,030,389 | 3,494,674 | 4,046,652 |
| Head (m) | 23.97 | 24.22 | 25.43 | 26.15 | 26.17 | 26.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Li, R.; Zhang, R.; Han, W. Numerical Study of the Unsteady Flow Characteristics of a Jet Centrifugal Pump under Multiple Conditions. Processes 2019, 7, 786. https://doi.org/10.3390/pr7110786
Guo R, Li R, Zhang R, Han W. Numerical Study of the Unsteady Flow Characteristics of a Jet Centrifugal Pump under Multiple Conditions. Processes. 2019; 7(11):786. https://doi.org/10.3390/pr7110786
Chicago/Turabian StyleGuo, Rong, Rennian Li, Renhui Zhang, and Wei Han. 2019. "Numerical Study of the Unsteady Flow Characteristics of a Jet Centrifugal Pump under Multiple Conditions" Processes 7, no. 11: 786. https://doi.org/10.3390/pr7110786
APA StyleGuo, R., Li, R., Zhang, R., & Han, W. (2019). Numerical Study of the Unsteady Flow Characteristics of a Jet Centrifugal Pump under Multiple Conditions. Processes, 7(11), 786. https://doi.org/10.3390/pr7110786





