Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study
Abstract
1. Introduction
2. Materials and Methods
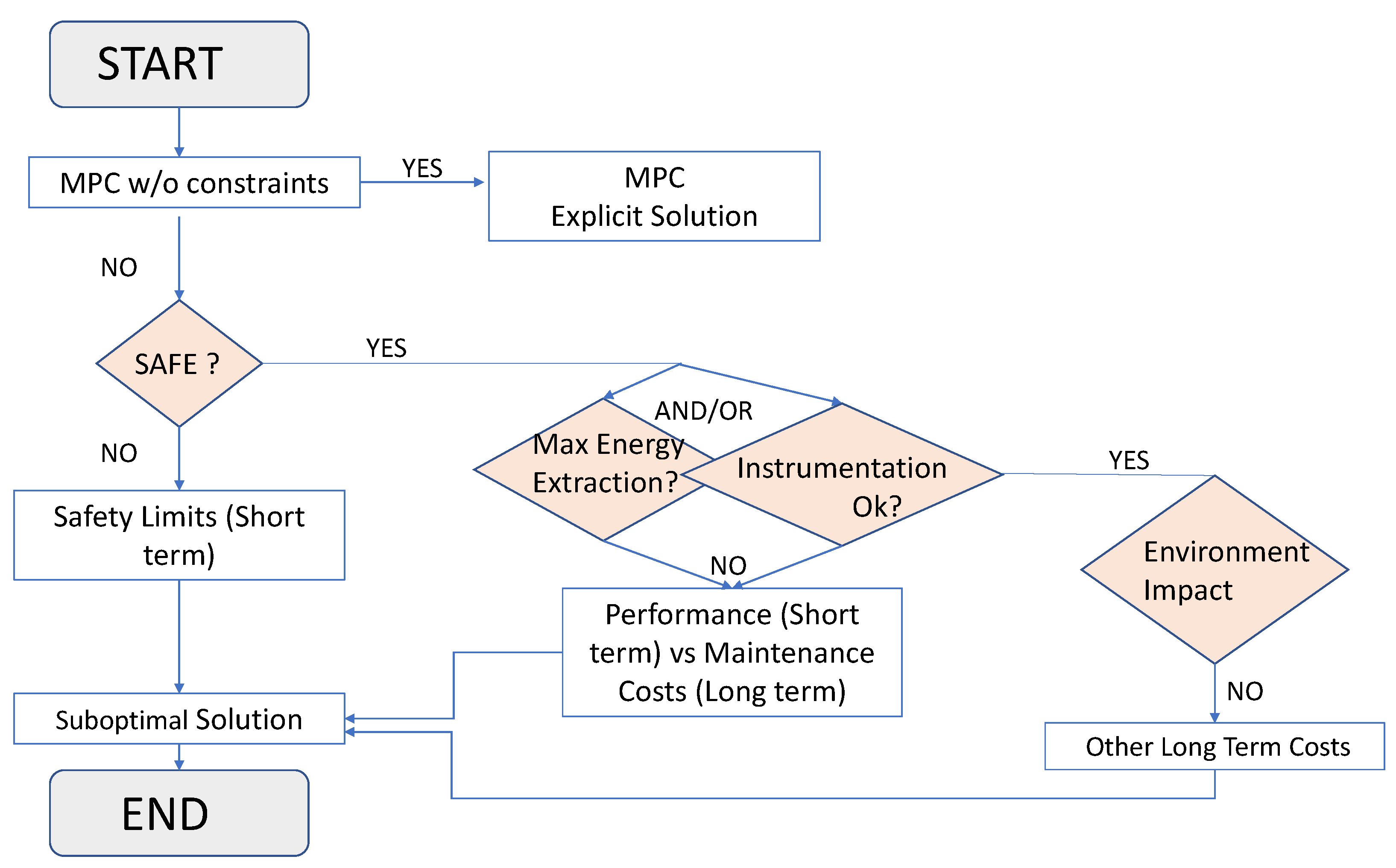
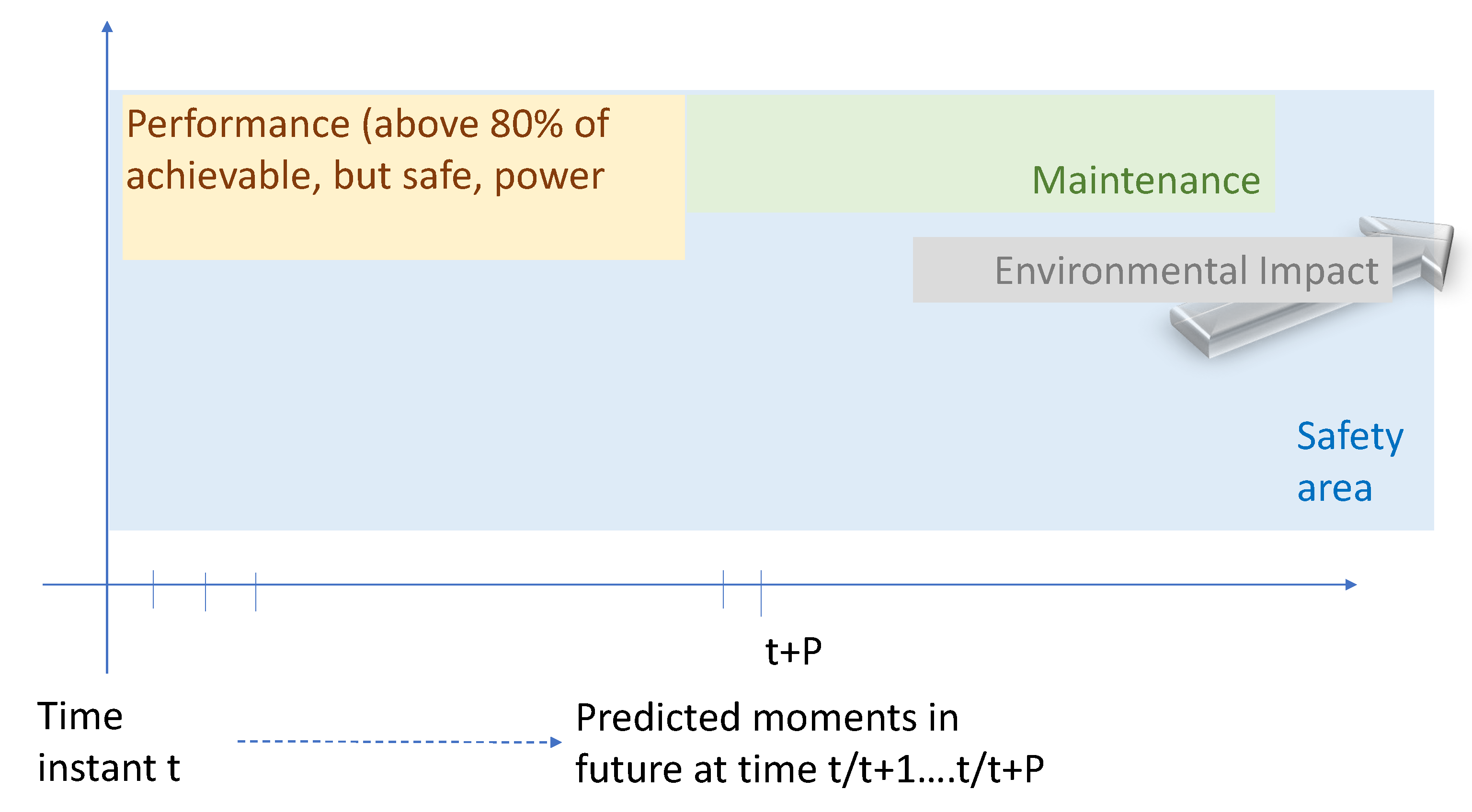
2.1. Multi Objective Optimization with Priorities
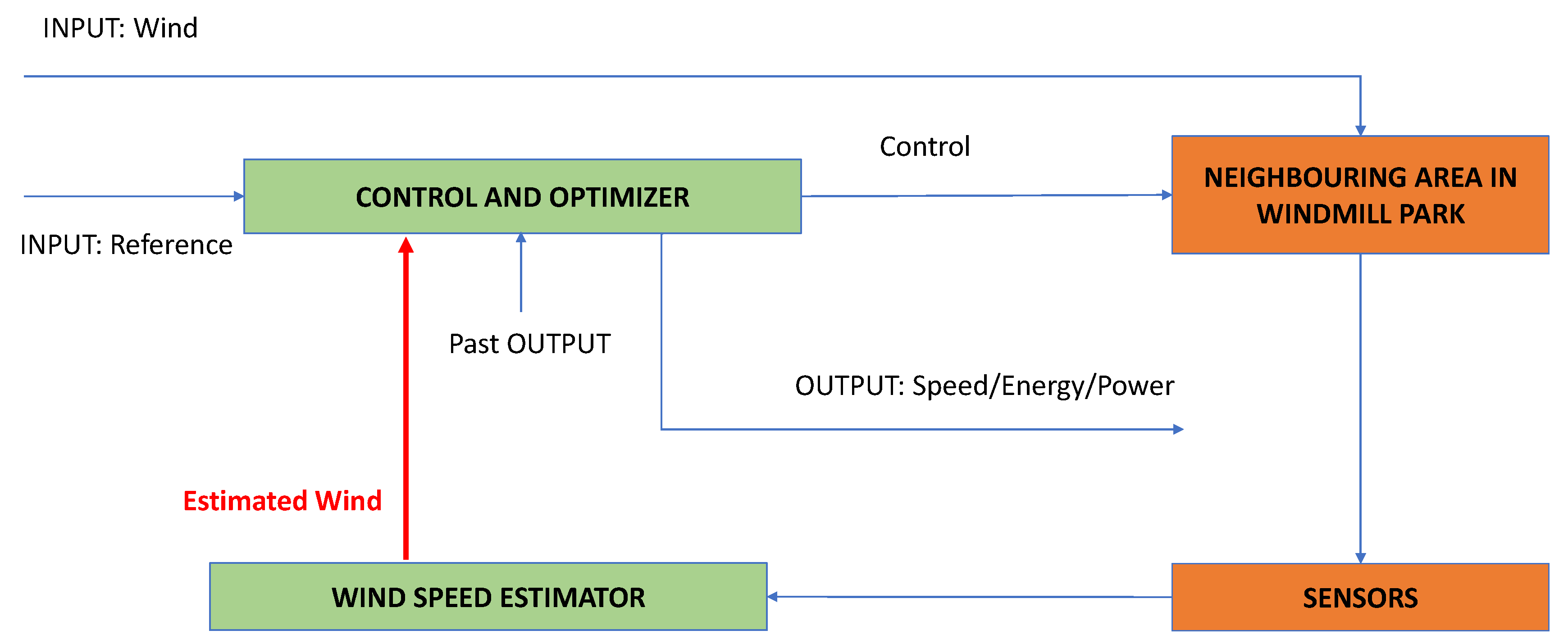
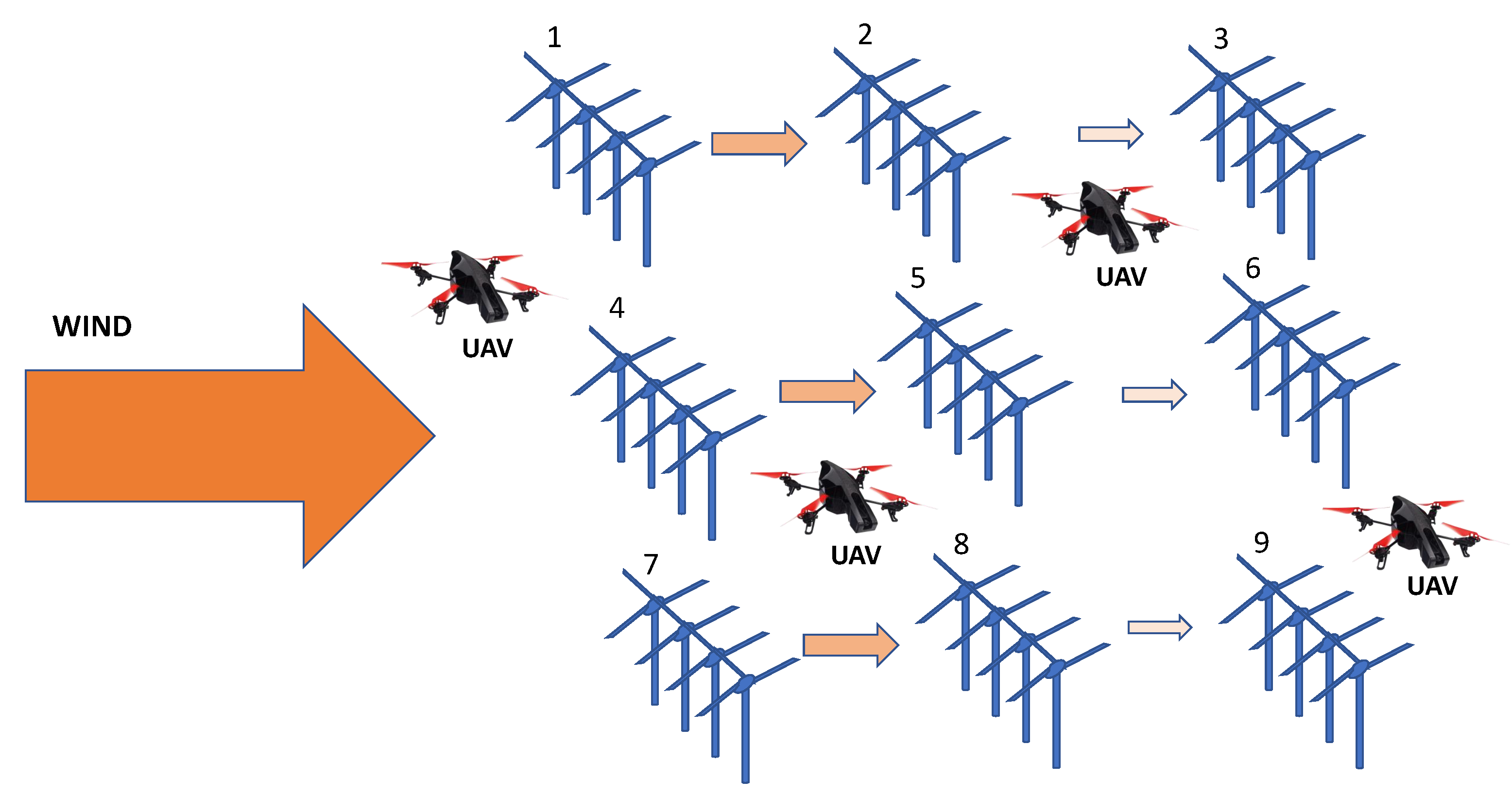
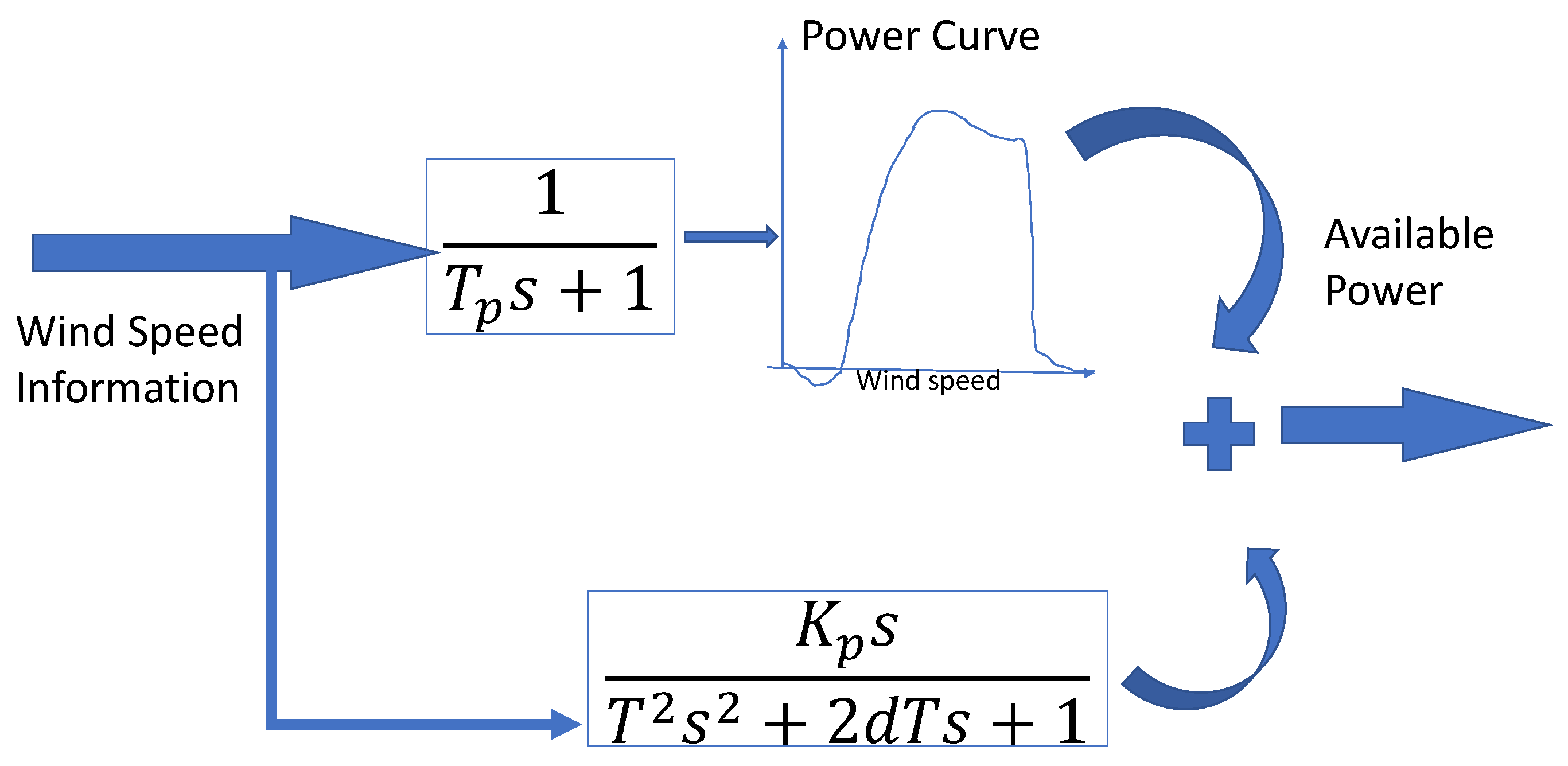
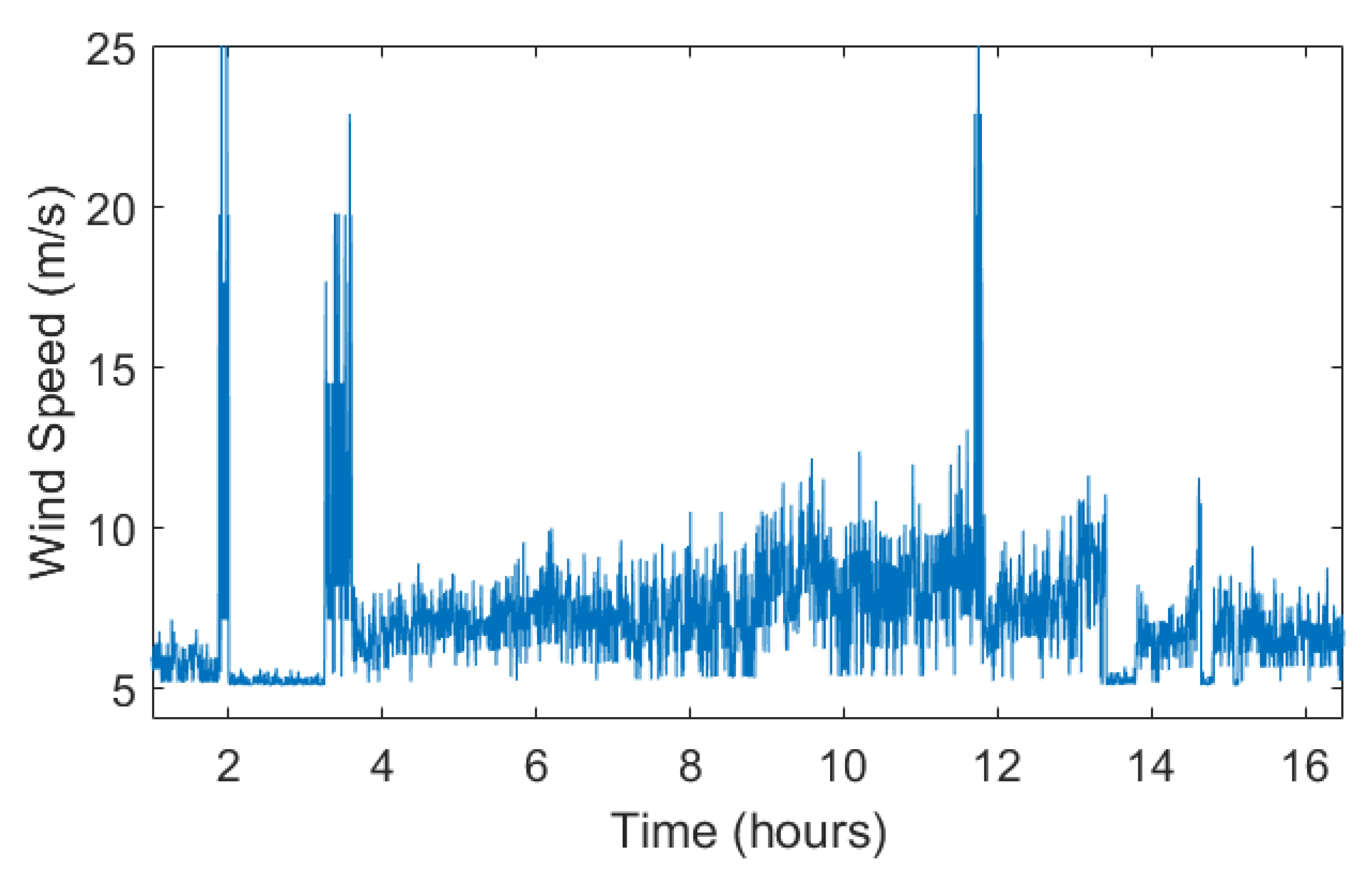
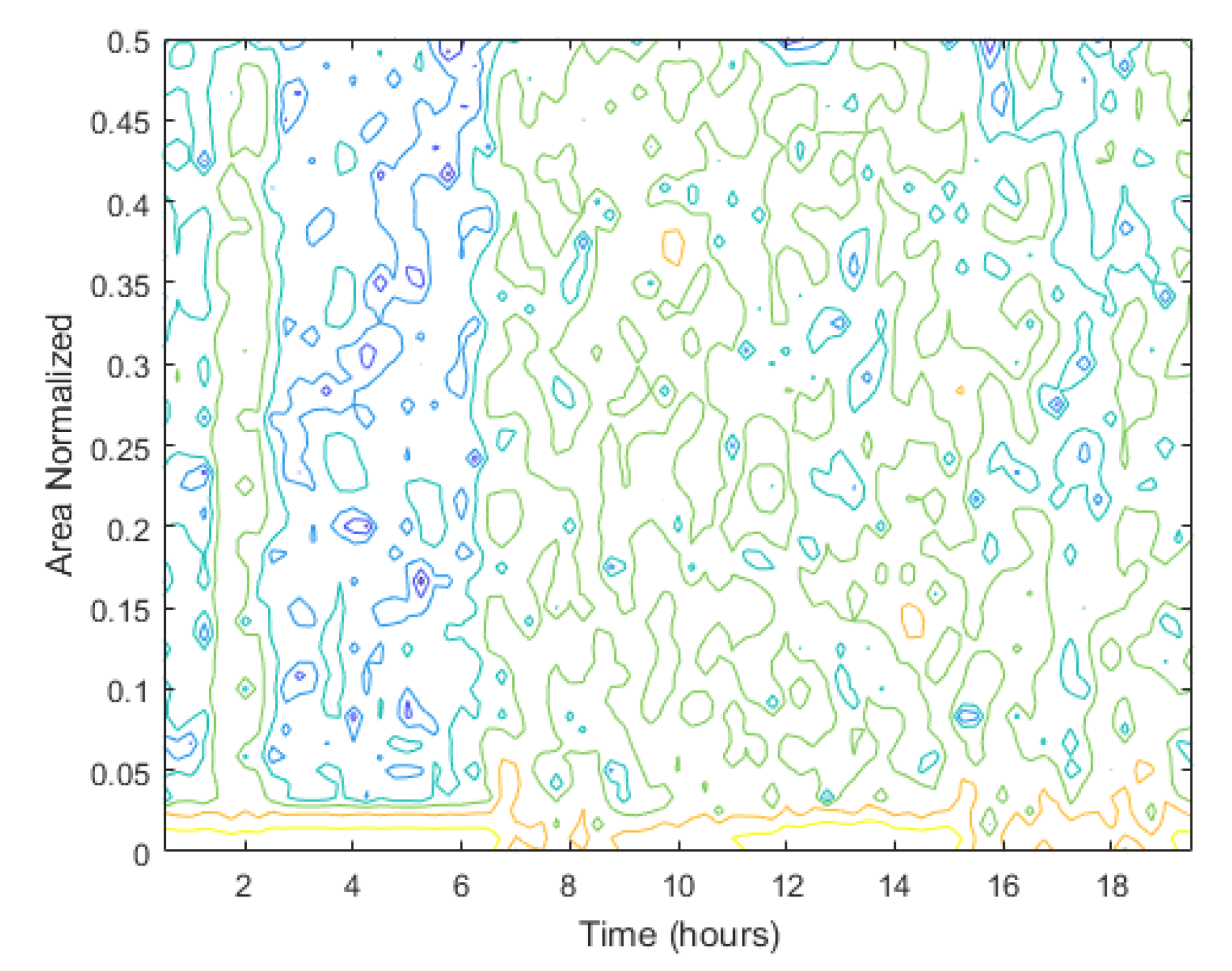
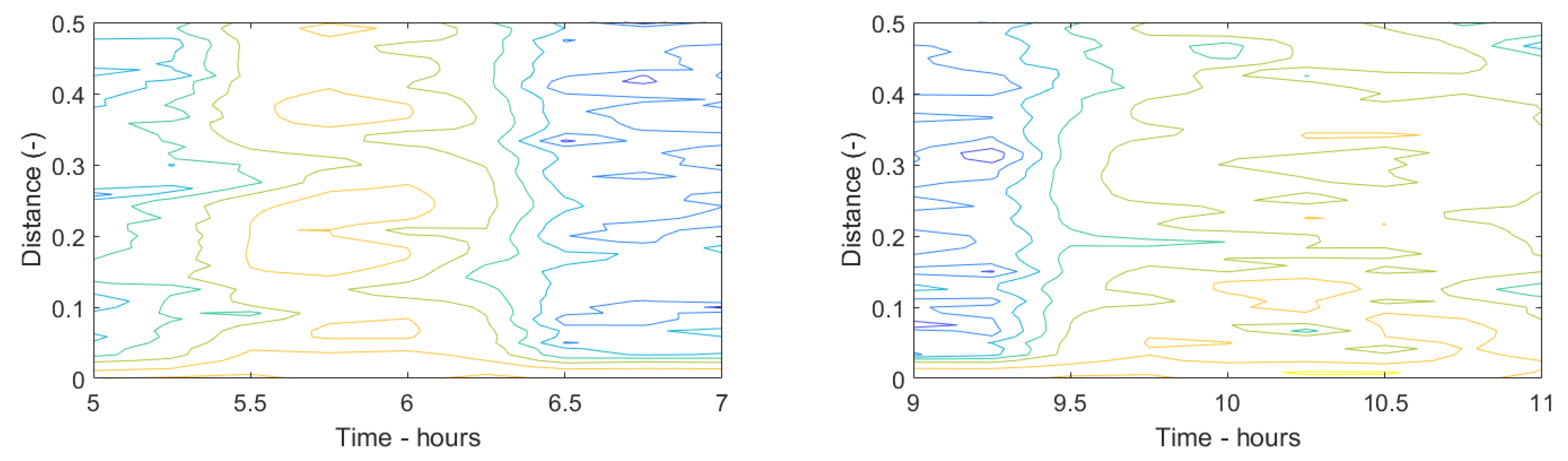
2.2. Area-Wise Wind Speed Estimation
2.3. Windmill Park Simulator
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| dMPC | distributed Model Predicitve Control |
| MOOP | Multi Objective Optimization Procedure |
| UAV | Unmanned Aerial Vehicle |
References
- Samad, T. A survey on industry impact and challenges thereof. IEEE Control Syst. Mag. 2017, 37, 17–18. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D.; Copot, C.; Ionescu, C.M. The 5Ws for control as part of Industry 4.0: Why, what, where, who and when—A PID and MPC control perspective. Inventions 2016, 4, 10. [Google Scholar] [CrossRef]
- Zhao, S.; Cajo, R.; De Keyser, R.; Liu, S.; Ionescu, C.M. Nonlinear predictive control applied to steam/water loop in large scale ships. In Proceedings of the 12th IFAC Symposium on Dynamics and Control of Process Systems, Including Biosystems, Florianopolis, Brazil, 23–26 April 2019; pp. 868–873. [Google Scholar] [CrossRef]
- Zhao, S.; Maxim, A.; Liu, S.; De Keyser, R.; Ionescu, C.M. Distributed model predictive control of steam/water loop in large scale ships. Processes 2019, 7, 442. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D.; De Keyser, R.; Ionescu, C.M. An industrially relevant formulation of a distributed model predictive control algorithm based on minimal process information. J. Process Control 2018, 68, 240–253. [Google Scholar] [CrossRef]
- Fu, D.; Zhang, H.-T.; Yu, Y.; Ionescu, C.M.; Aghezzaf, E.-H.; De Keyser, R. A distributed model predictive control strategy for the bullwhip reducing inventory management policy. IEEE Trans. Ind. Inf. 2019, 15, 932–941. [Google Scholar] [CrossRef]
- Fu, D.; Ionescu, C.M.; Aghezzaf, E.-H.; De Keyser, R. Quantifying and mitigating the bullwhip effect in a benchmark supply chain system by an extended prediction self-adaptive control ordering policy. Comput. Ind. Eng. 2015, 81, 46–57. [Google Scholar] [CrossRef]
- Wang, S.; Meng, X.; Chen, T. Wide-area control of power systems through delayed network communication. IEEE Trans. Control Syst. Technol. 2012, 20, 495–503. [Google Scholar] [CrossRef]
- Allen, W. Effects of wide-area control on the protection and operation of distribution networks. In Proceedings of the 2009 Power Systems Conference, Clemson, SC, USA, 10–13 March 2009. [Google Scholar] [CrossRef]
- Sadamoto, T.; Chakrabortty, A.; Ishizaki, T.; Imura, J.-C. Dynamic modelling, stability, and control of power systems with distributed energy resources. IEEE Control Syst. Mag. 2019, 39, 34–65. [Google Scholar] [CrossRef]
- MacNaughton, P.; Pegues, J.; Satish, U.; Santanam, S.; Spengler, J.; Allen, J. Economic, environmental and health implications of enhanced ventilation in office buildings. Int. J. Environ. Res. Public Health 2015, 12, 14709–14722. [Google Scholar] [CrossRef]
- Sutandi, C. Advanced traffic control system impacts on environmental quality in a large city in a developing country. J. East. Asia Soc. Transp. Stud. 2007, 7, 1169–1179. [Google Scholar]
- Caputo, F.; Veltri, S.; Venturelli, A. Sustainability strategy and management control systems in family firms. Evidence from a case study. Sustainability 2017, 9, 977. [Google Scholar] [CrossRef]
- De Koker, K.; Crevecoeur, G.; Meersman, B.; Vantorre, M.; Vandevelde, L. A wave emulator for ocean wave energy, a Froude-scaled dry power take-off test setup. Renew. Energy 2017, 105, 712–721. [Google Scholar] [CrossRef]
- Klaeboe, R.; Sundfor, H.B. Windmill noise annoyance, visual aesthetics, and attitudes towards renewable energy sources. Int. J. Environ. Res. Public Health 2016, 13, 746. [Google Scholar] [CrossRef] [PubMed]
- Johannessen, O.M.; Korsbakken, E. Determination of wind energy from SAR images for siting windmill locations. Earth Obs. Q. 1998, 1. Available online: http://www.esa.int/esapub/eoq/eoq59/JOHANNESSEN.pdf (accessed on 12 September 2019).
- Stevens, R.J.A.M.; Gayme, D.F.; Meneveau, C. Effects of turbine spacing on the power output of extended wind-farms. Wind Energy 2015, 19, 359–370. [Google Scholar] [CrossRef]
- Bailey, H.; Brookes, K.L.; Thompson, P.M. Assessing environmental impacts of offshore wind farms: Lessons learned and recommendations for the future. Aquat. Biosyst. 2014, 10. [Google Scholar] [CrossRef]
- Anaya-Lara, O.; Campos-Gaona, D.; Moreno-Goytia, E.; Adam, G. Offshore Wind Energy Generation: Control, Protection and Integration to Electrical Systems; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- European Wind Power Association. Operation and Maintenance Costs of Wind Generated Power. Available online: https://www.wind-energy-the-facts.org/operation-and-maintenance-costs-of-wind-generated-power.html (accessed on 12 September 2019).
- IRENA—International Renewable Energy Agency. Renewable Power Generation Costs in 2017. Abu Dhabi, 2018. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018 (accessed on 12 September 2019).
- Muljadi, E.; Butterfield, C.; Parsons, B.; Ellis, A. Effect of variable speed wind turbine generator on stability of a weak grid. IEEE Trans. Energy Convers. 2007, 22, 29–36. [Google Scholar] [CrossRef]
- Feltes, J.W.; Fernandes, B.S. Wind turbine generator dynamic performance with weak transmission grids. In Proceedings of the IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; 7p. [Google Scholar] [CrossRef]
- Kadar, P. Pros and Cons of the renewable energy application. Acta Polytech. Hung. 2014, 11, 211–224. [Google Scholar]
- Tudorache, T.; Popescu, M. FEM optimal design of wind energy based heater. Acta Polytech. Hung. 2009, 6, 55–70. [Google Scholar]
- Bindner, H. Power Control for Wind Turbines in Weak Grids: Concepts Development. Denmark. Forskningscenter Risoe, 1999, Risoe-R, No. 1118 (EN). Available online: https://orbit.dtu.dk/files/7729819/ris_r_1118.pdf (accessed on 12 September 2019).
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Dynamic load stress analysis of a large horizontal axis wind turbine using full scale fluid-structure interaction simulation. Renew. Energy 2019, 140, 212–226. [Google Scholar] [CrossRef]
- Rossiter, J.A. A First Course in Predictive Control, 2nd ed.; Textbook; CRC Press, Taylor and Francis Group: London, UK, 2018; ISBN 9781138099340. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Advances in Industrial Control Series; Springer: London, UK, 2009; ISBN 9781848823303. [Google Scholar]
- Kouvaritakis, B.; Cannon, M. Model Predictive Control, Advanced Textbooks in Control and Signal Processing; Springer International Publishing: Cham, Switzerland, 2016; ISBN 9783319248516. [Google Scholar]
- De Keyser, R.; Van Cauwenberghe, A. A self-tuning multistep predictor application. Automatica 1981, 17, 167–174. [Google Scholar] [CrossRef]
- De Keyser, R. Model Based Predictive Control for Linear Systems. In UNESCO Encyclopaedia of Life Support Systems; Series on Control Systems, Robotics and Automation; Eolss Publishers Co. Ltd.: Oxford, UK, 2003; Volume XI, 30p, Article Contribution 6.43.16.1; Available online: http://www.eolss.net/ebooklib/cart.aspx (accessed on 10 September 2019).
- Ishizaki, T.; Sadamoto, T.; Imura, J.-C.; Sandberg, H.; Johansson, K.H. Retrofit control: Localization of controller design and implementation. Automatica 2018, 95, 336–346. [Google Scholar] [CrossRef]
- Lesser, K.; Abate, A. Multi-objective optimal control with safety as a priority. In Proceedings of the 2017 International Conference on Cyber-Physical Systems (ICCPS), Pittsburgh, PA, USA, 18–21 April 2017; pp. 25–36. [Google Scholar]
- Maree, J.; Imsland, L. On multi-objective economic predictive control for cyclic process operation. J. Process Control 2014, 24, 1328–1336. [Google Scholar] [CrossRef]
- Bemporad, A.; de la Pena, D. Multiobjective model predictive control. Automatica 2009, 45, 2823–2830. [Google Scholar] [CrossRef]
- Yamashita, A.; Zanin, A.; Odloak, D. Tuning of model predictive control with multi-objective optimization. Braz. J. Chem. Eng. 2016, 33, 333–346. [Google Scholar] [CrossRef]
- Tan, K.; Khor, E.; Lee, T.; Sathikannan, R. An evolutionary algorithm with advanced goal and priority specification for multi-objective optimization. J. Artif. Intell. Res. 2003, 18, 183–215. [Google Scholar] [CrossRef]
- Wojsznis, W.; Mehta, A.; Wojsznis, P.; Thiele, D.; Blevins, T. Multiobjective optimization for model predictive control. ISA Trans. 2007, 46, 351–361. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Liu, Y. Implementation of maximum power point tracking based on variable speed forecasting for wind energy systems. Processes 2019, 7, 158. [Google Scholar] [CrossRef]
- Prudden, S.; Fisher, A.; Marino, M.; Mohamed, A.; Watkins, S.; Wild, G. Measuring wind with Small Unmanned Aircraft Systems. J. Wind Eng. Ind. Aerodyn. 2018, 176, 197–210. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F.J. Wind Estimation in the Lower Atmosphere Using Multirotor Aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Qu, Y.; Duan, J.; Zhang, Y. An algorithm of online wind field estimation for small fixed-wing UAVs. In Proceedings of the 2016 Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 10645–10650. [Google Scholar] [CrossRef]
- Rhudy, M.B.; Fravolini, M.L.; Gu, Y.; Napolitano, M.R.; Gururajan, S.; Chao, H. Aircraft model-independent airspeed estimation without pitot tube measurements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1980–1995. [Google Scholar] [CrossRef]
- Xing, Z.; Qu, Q.; Zhang, Y. Shear wind estimation with quadrotor UAVs using filtering regressing method. In Proceedings of the 2017 International Conference on Advanced Mechatronic (ICAMechS), Xiamen, China, 6–9 December 2017; pp. 196–201. [Google Scholar] [CrossRef]
- Pappu, V.S.R.; Liu, Y.; Horn, J.F.; Cooper, J. Wind gust estimation on a small VTOL UAV. In Proceedings of the 7th AHS Technical Meeting on VTOL Unmanned Aircraft Systems and Autonomy, Mesa, AZ, USA, 24–26 January 2017. [Google Scholar]
- Rios, H.; Efimov, D.; Moreno, J.A.; Perruquetti, W.; Rueda-Escobedo, J.G. Time-Varying Parameter Identification Algorithms: Finite and Fixed-Time Convergence. IEEE Trans. Autom. Control 2017, 62, 3671–3678. [Google Scholar] [CrossRef]
- Perozzi, G.; Efimov, D.; Biannic, J.-M.; Planckaert, L. Trajectory tracking for a quadrotor under wind perturbations: Sliding mode control with state-dependent gains. J. Frankl. Inst. 2018, 355, 4809–4838. [Google Scholar] [CrossRef]
- Suvire, G.O.; Mercado, P.E. Wind farm: Dynamic model and impact on a weak power system. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America, Bogota, Colombia, 13–15 August 2008; 8p. [Google Scholar] [CrossRef]
- Caruntu, C.F. Distributed predictive control for wind farms efficiency maximization: Challenges and opportunities. In Proceedings of the 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 452–457. [Google Scholar] [CrossRef]
- Ugalde-Loo, C.E.; Ekanayake, J.B.; Jenkins, N. State-space modeling of wind turbine generators for power system studies. IEEE Trans. Ind. Appl. 2013, 49, 223–232. [Google Scholar] [CrossRef]
- Sadamoto, T. CSM2018 Matlab Codes. Available online: https://github.com/TSadamoto/CSM2018 (accessed on 10 September 2019).
- Degraer, S.; Brabant, R.; Rumes, B.; Vigin, L. (Eds.) Environmental Impacts of Offshore Wind Farms in the Belgian Part of the North Sea; Scientific Reports Series: Memoirs on the Marine Environment; 2018; 136p, Available online: https://odnature.naturalsciences.be/downloads/mumm/windfarms/winmon_report_2018_final.pdf (accessed on 12 September 2019).
- Ionescu, C.; Copot, D. Hands-on MPC tuning for industrial applications. Bull. Pol. Acad. Sci. Tech. Sci. 2019. accepted. [Google Scholar]
- Hernandez, J.A.; Murcia, H.; Copot, C.; De Keyser, R. Towards the development of a smart flying sensor: Illustration in the field of precision agriculture. IEEE Sens. J. 2015, 15, 16688–16709. [Google Scholar] [CrossRef]
- Van de Voorde, P.; Gautama, S.; Momont, A.; Ionescu, C.M.; De Paepe, P.; Fraeyman, N. The drone ambulance [A-UAS]: Golden bullet or just a blank? Resuscitation 2017, 116, 46–48. [Google Scholar] [CrossRef]
- Mian Ab, M.S.; De Kooning, J.; Vandevelde, L.; Crevecoeur, G. Harvesting wind gust energy with small and medium wind turbines using a bidirectional control strategy. J. Eng. 2019, 2019, 4261–4266. [Google Scholar]
- Papadopoulos, V.; Knockaert, J.; Develder, C.; Desmet, J. Investigating the need for real time measurements in industrial wind power systems combined with battery storage. Appl. Energy 2019, 247, 559–571. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Analysis of the aerodynamic loads on a wind turbine in off-design conditions. In Recent Advances in CFD for Wind and Tidal Offshore Turbines; Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2019; pp. 51–59. [Google Scholar]
| Method | Performance | Total Power Output | Cost |
|---|---|---|---|
| Global dMPC | 88 | 85 | 91 |
| MOOP dMPC | 63 | 71 | 68 |
| Method | Performance | Total Power Output | Cost |
|---|---|---|---|
| Global dMPC | 90 | 95 | 91 |
| MOOP dMPC | 87 | 91 | 88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionescu, C.M.; Caruntu, C.F.; Cajo, R.; Ghita, M.; Crevecoeur, G.; Copot, C. Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study. Processes 2019, 7, 778. https://doi.org/10.3390/pr7110778
Ionescu CM, Caruntu CF, Cajo R, Ghita M, Crevecoeur G, Copot C. Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study. Processes. 2019; 7(11):778. https://doi.org/10.3390/pr7110778
Chicago/Turabian StyleIonescu, Clara M., Constantin F. Caruntu, Ricardo Cajo, Mihaela Ghita, Guillaume Crevecoeur, and Cosmin Copot. 2019. "Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study" Processes 7, no. 11: 778. https://doi.org/10.3390/pr7110778
APA StyleIonescu, C. M., Caruntu, C. F., Cajo, R., Ghita, M., Crevecoeur, G., & Copot, C. (2019). Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study. Processes, 7(11), 778. https://doi.org/10.3390/pr7110778









