Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System
Abstract
1. Introduction
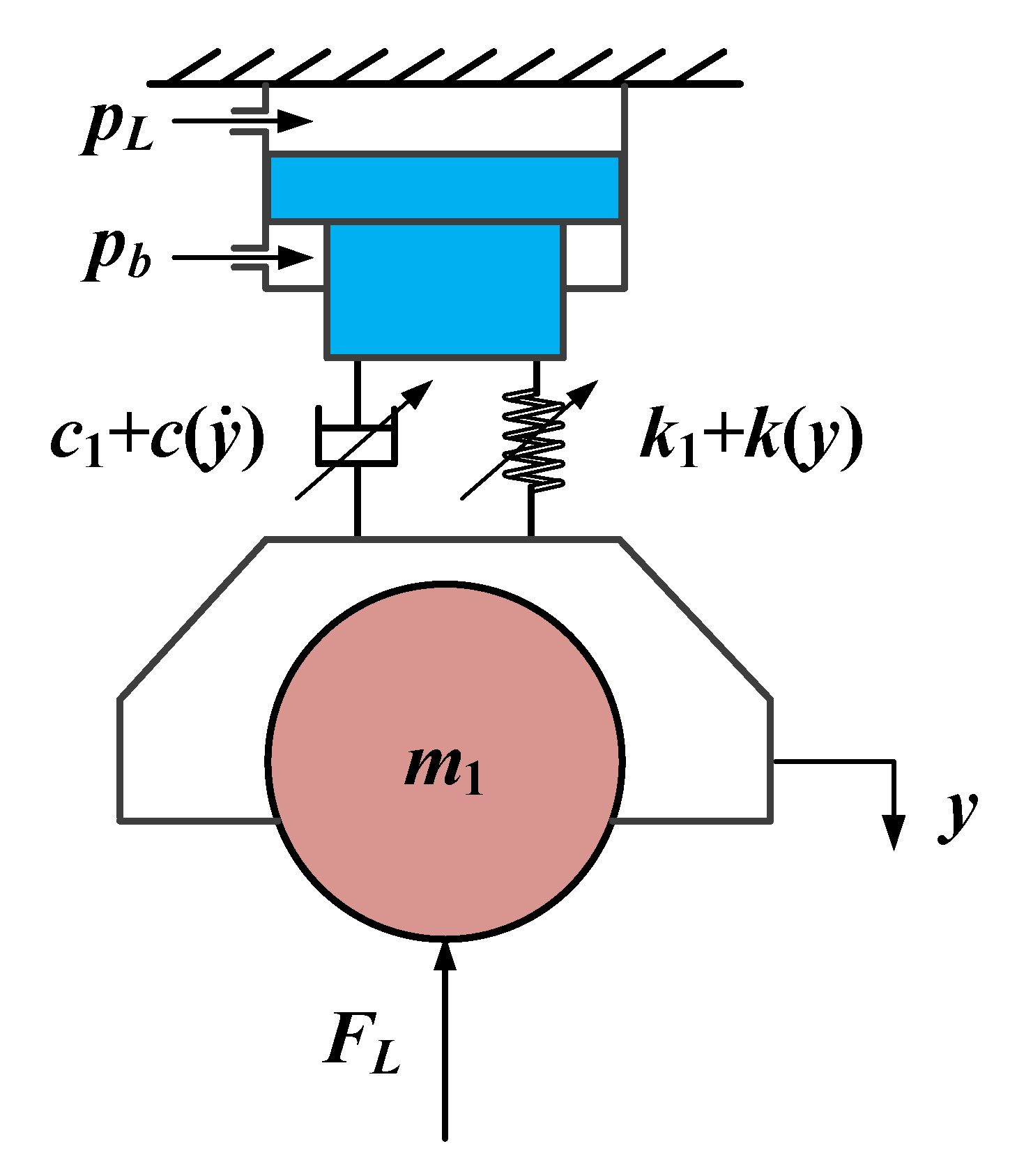
2. Vertical Vibration Model of Load
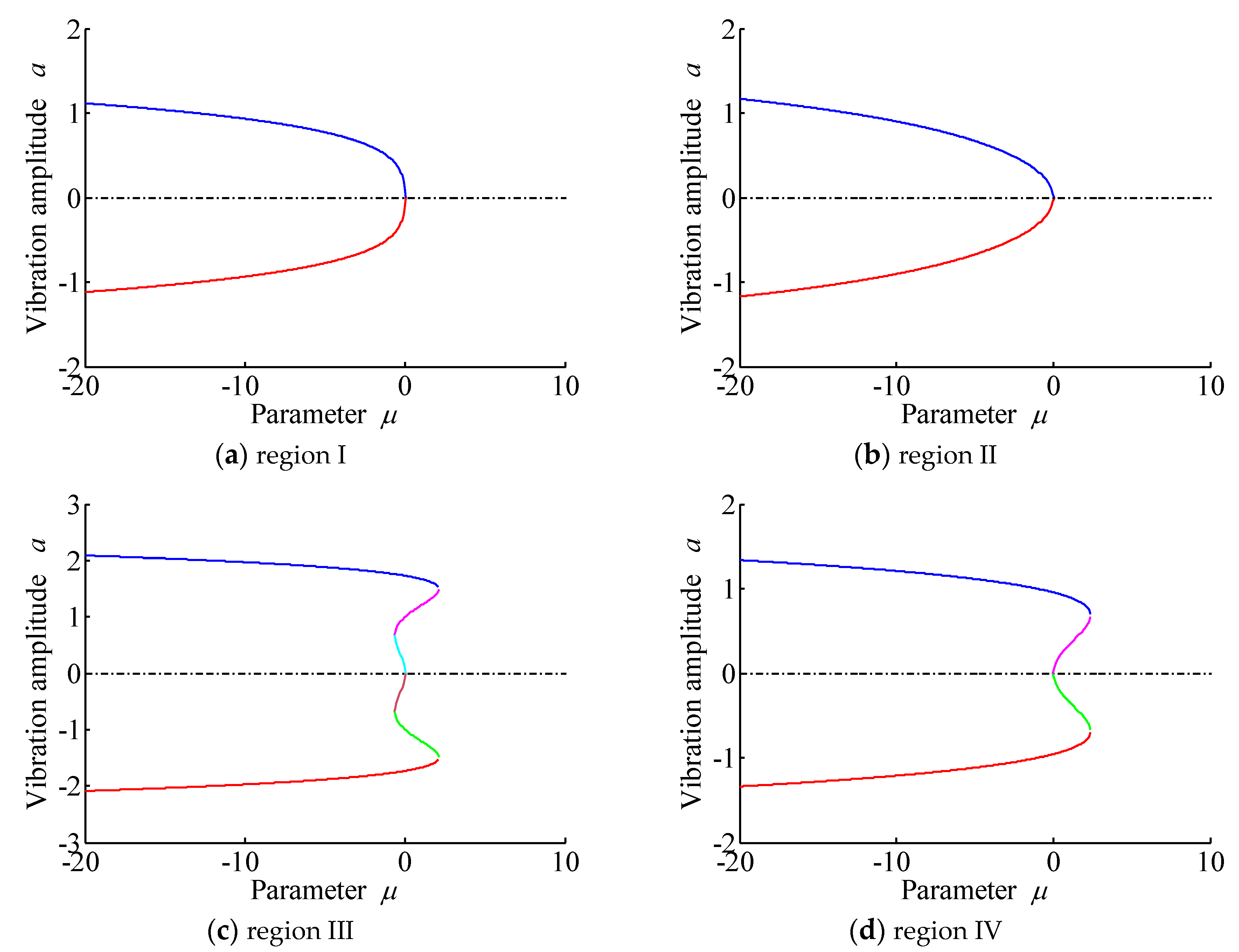
3. Analysis of Bifurcation Characteristic
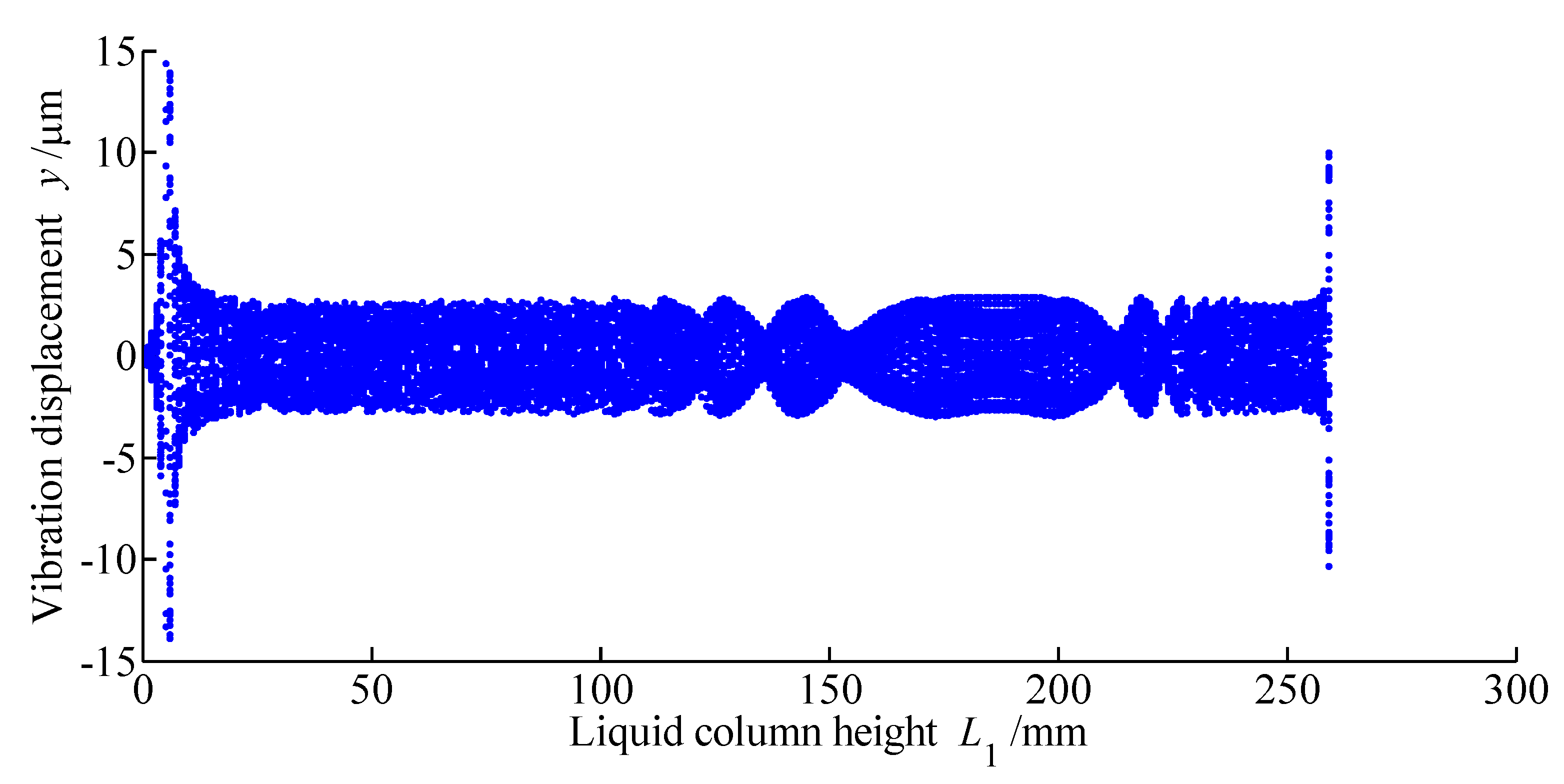
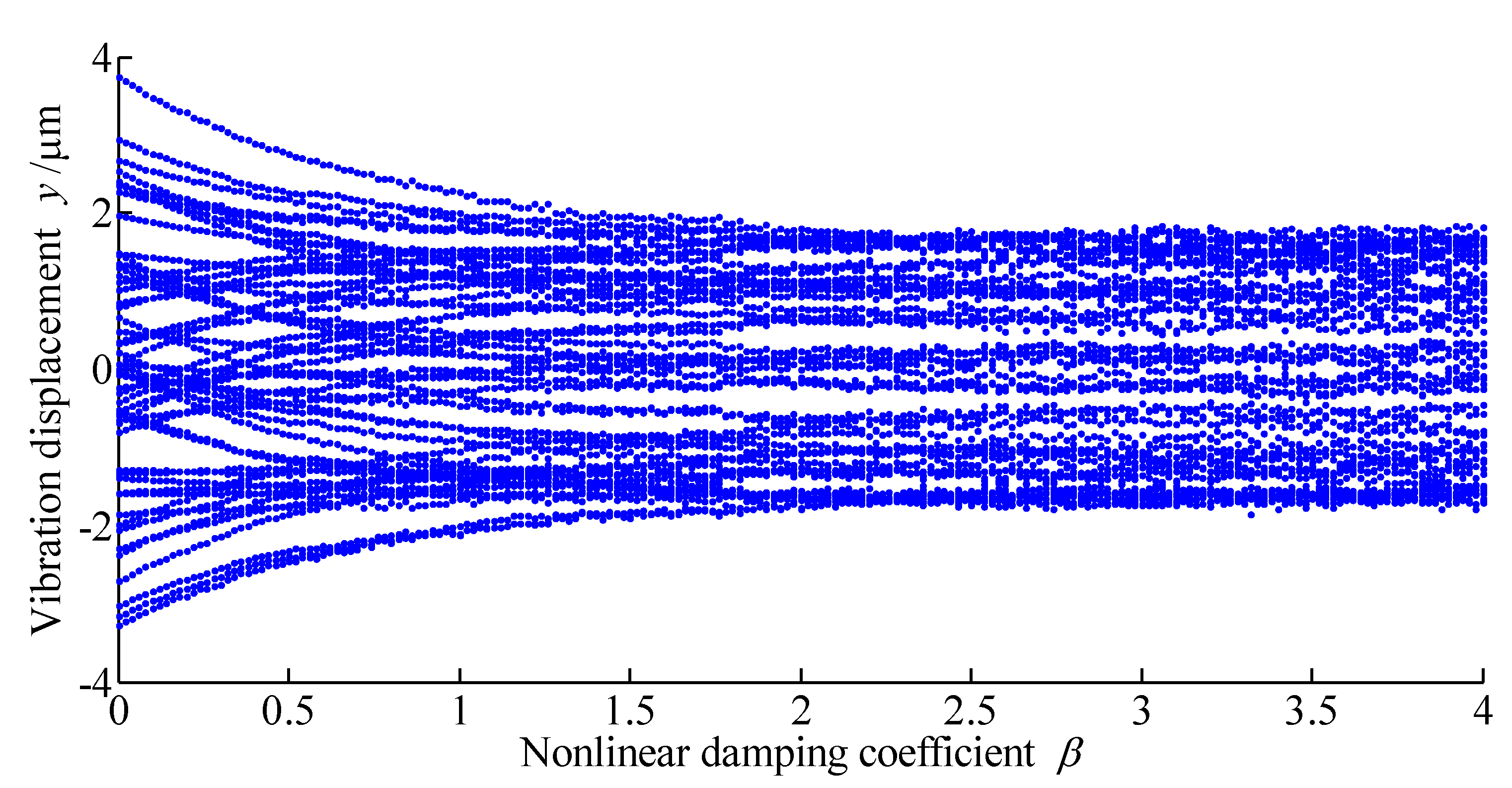
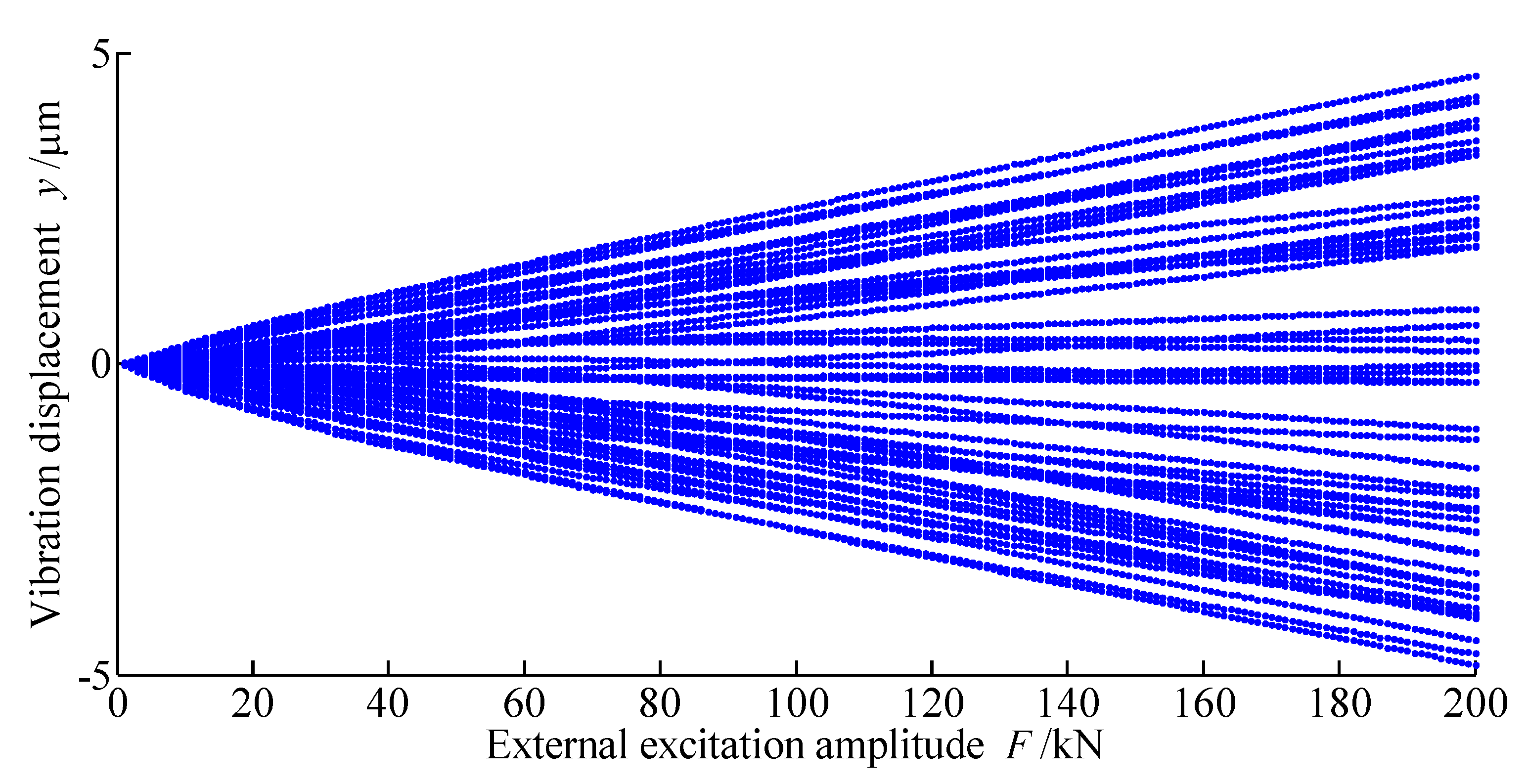
4. Research on Bifurcation Behavior
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, Y.J.; Li, Y.G.; Shen, G.X.; Xie, M.L. Spatial vibration characteristics of six-high cold strip rolling mills. Ironmak. Steelmak. 2017, 45, 1–6. [Google Scholar] [CrossRef]
- Shao, Y.; Deng, X.; Yuan, Y.; Mechefske, C.K.; Chen, Z. Characteristic recognition of chatter mark vibration in a rolling mill based on the non-dimensional parameters of the vibration signal. J. Mech. Sci. Technol. 2014, 28, 2075–2080. [Google Scholar] [CrossRef]
- Wu, S.; Shao, Y.; Wang, L.; Yuan, Y.; Mechefske, C.K. Relationship between chatter marks and rolling force fluctuation for twenty-high roll mill. Eng. Fail. Anal. 2015, 55, 87–99. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, W.L.; Kong, X.D.; Wang, H.N. Analytical solution for nonlinear vertical vibration model of mill roll system based on improved complexification averaging method. J. Vibroeng. 2016, 18, 5521–5536. [Google Scholar]
- Xue, Z.H.; Cao, X.; Wang, T.Z. Vibration test and analysis on the centrifugal pump. J. Drain. Irrig. Mach. Eng. 2018, 36, 472–477. [Google Scholar]
- Zhong, J.; Tang, H.P. Vibration problems of high speed rolling mill-study of dynamics of complex electromechanically coupled system. J. Vib. Meas. Diagn. 2002, 22, 1–8. [Google Scholar]
- Wang, Y.Q.; Sun, F.; Liu, J.; Sun, M.H.; Xie, Y.H. Application of smith predictor based on single neural network in cold rolling shape control. Chin. J. Mech. Eng. 2009, 22, 282–286. [Google Scholar] [CrossRef]
- Chen, Y.H.; Shi, T.L.; Yang, S.Z. Study on parametrically excited nonlinear vibrations on 4-H cold rolling mills. Chin. J. Mech. Eng. 2003, 39, 56–60. [Google Scholar] [CrossRef]
- Sun, J.L.; Peng, Y.; Liu, H.M. Vertical vibration of moving strip in rolling process based on beam theory. Chin. J. Mech. Eng. 2009, 22, 680–687. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, J.H.; Liu, F.; Northeastern University at Qinhuangdao; Institute of Information Technology and Engineering; Yanshan University. Nonlinear vibration characteristic of strip mill under the coupling effect of roll-rolled piece. J. Vibroengineering 2016, 18, 5492–5505. [Google Scholar] [CrossRef]
- Liu, H.R.; Shi, P.M.; Chen, H.; Hou, D.X. Study on nonlinear parametrically exited coupling vibrations of roller system on 4-H rolling mills. China Mech. Eng. 2011, 22, 1397–1401. [Google Scholar]
- Yan, X.Q. Machinery-electric-hydraulic coupong vibration control of hot continuous rolling mills. Chin. J. Mech. Eng. 2011, 47, 61–65. [Google Scholar] [CrossRef]
- Tang, S.N.; Zhu, Y.; Li, W.; Cai, J.X. Status and prospect of research in preprocessing methods for measured signals in mechanical systems. J. Drain. Irrig. Mach. Eng. 2019, 37, 822–828. [Google Scholar]
- Zhu, Y.; Tang, S.N.; Quan, L.X.; Jiang, W.L.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.Y.; Tong, C.N. Nonlinear vibration modeling and stability analysis of vertical roller system in cold rolling mill. J. Vib. Meas. Diagn. 2013, 33, 302–306. [Google Scholar]
- Bi, Q.S.; Ma, R.; Zhang, Z.D. Bifurcation mechanism of the bursting oscillations in periodically excited dynamical system with two time scales. Nonlinear Dyn. 2015, 79, 101–110. [Google Scholar] [CrossRef]
- Bi, Q.S.; Li, S.L.; Kurths, J.; Zhang, Z.D. The mechanism of bursting oscillations with different codimensional bifurcations and nonlinear structures. Nonlinear Dyn. 2016, 85, 993–1005. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Shi, W.; Wang, X.; Wang, X.; Qiu, N. Numerical study on pressure fluctuation of a multistage centrifugal pump based on whole flow field. AIP Adv. 2019, 9, 035118. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Zhang, D.; Hu, B.; Shi, W. Numerical and experimental study of the self-priming process of a multistage self-priming centrifugal pump. Int. J. Energy Res. 2019, 43, 4074–4092. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.; Wang, X.; Jiang, X.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- He, X.; Jiao, W.; Wang, C.; Cao, W. Influence of surface roughness on the pump performance based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W.D. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.Y.; Gao, Z.X.; Liu, B.Z.; Jin, Z.J. Parametric study on fluid dynamics of pilot-control angle globe valve. Asme J. Fluids Eng. 2018, 140, 111103. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.P.; Pang, Q.L.; Ye, D.X. Vibration in a multistage centrifugal pump under varied conditions. Shock Vib. 2019, 2019, 2057031. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W.D. Numerical study of pressure fluctuation and unsteady flow in a centrifugal pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.L.; Wang, K.; Zhou, L.; Jiang, X.P.; Li, Y. Numerical simulation of the sound field of a five-stage centrifugal pump with different turbulence models. Water 2019, 11, 1777. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B.; Zhu, S.Q. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Process. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Zhang, J.H.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018, 139, 1–7. [Google Scholar] [CrossRef]
- Pei, J.; Zhang, F.; Appiah, D.; Hu, B.; Asomani, S.N. Performance prediction based on effects of wrapping angle of a side channel pump. Energies 2019, 12, 139. [Google Scholar] [CrossRef]
- Niziol, J.; Światoniowski, A. Numerical analysis of the vertical vibrations of rolling mills and their negative effect on the sheet quality. J. Mater. Process. Technol. 2005, 162–163, 546–550. [Google Scholar] [CrossRef]
- Heidari, A.; Forouzan, M.R.; Akbarzadeh, S. Development of a rolling chatter model considering unsteady lubrication. ISIJ Int. 2014, 54, 165–170. [Google Scholar] [CrossRef]
- Heidari, A.; Forouzan, M.R.; Akbarzadeh, S. Effect of friction on tandem cold rolling mills chattering. ISIJ Int. 2014, 54, 2349–2356. [Google Scholar] [CrossRef]
- Drzymala, Z.; Świątoniowski, A.; Bar, A. Non-linear vibrations in cold rolling mills. Mécanique Ind. 2003, 4, 151–158. [Google Scholar] [CrossRef]
- Xu, H.; Cui, L.L.; Shang, D.G. A study of nonlinear coupling dynamic characteristics of the cold rolling mill system under different rolling parameters. Adv. Mech. Eng. 2017, 9, 1–15. [Google Scholar] [CrossRef]
- Wang, Q.L.; Li, X.; Hu, Y.J.; Sun, J.; Zhang, D.H. Numerical analysis of intermediate roll shifting-induced rigidity characteristics of UCM cold rolling mill. Steel Res. Int. 2018, 89, 1700454. [Google Scholar] [CrossRef]
- Chen, T.U.; Liu, X.; Gong, Y. Research on fatigue failure of agc servo hydraulic cylinder. Mach. Tool Hydraul. 2017, 45, 158–161. [Google Scholar]
- Mosayebi, M.; Zarrinkolah, F.; Farmanesh, K. Calculation of stiffness parameters and vibration analysis of a cold rolling mill stand. Int. J. Adv. Manuf. Technol. 2017, 91, 1–11. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, W.L.; Kong, X.D.; Zheng, Z. Study on nonlinear dynamics characteristics of electro-hydraulic servo system. Nonlinear Dyn. 2015, 80, 723–737. [Google Scholar] [CrossRef]
- Khalid, M.S.U.; Imran, A.; Dong, H.; Ahsan, N.; Wu, B. Bifurcations and route to chaos for flow over an oscillating airfoil. J. Fluids Struct. 2018, 80C, 262–274. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Han, X.J.; Bi, Q.S. Dynamical behavior analysis and bifurcation mechanism of a new 3-D nonlinear periodic switching system. Nonlinear Dyn. 2013, 73, 1873–1881. [Google Scholar] [CrossRef]
- Zhu, Y.; Qian, P.F.; Tang, S.N.; Jiang, W.L.; Li, W.; Zhao, J.H. Amplitude-frequency characteristics analysis for vertical vibration of hydraulic AGC system under nonlinear action. AIP Adv. 2019, 9, 035019. [Google Scholar] [CrossRef]
- Liu, F.; Liu, B.; Shi, P.M.; Hou, D.X. Vibration behavior of roll system under nonlinear constraints of the hydraulic cylinder. J. Mech. Eng. 2014, 50, 59–65. [Google Scholar] [CrossRef]
- Ling, Q.H.; Yan, X.Q.; Zhang, Q.D.; Zhang, Y.F. Research on vibration characteristics of the hot rolling mill by dual power source driven. J. Vib. Meas. Diagn. 2014, 34, 534–538. [Google Scholar]
- Liu, B.; Li, P.; Liu, F.; Liu, H.R.; Jiang, J.H. Vibration behavior and control of roll system under nonlinear stiffness of a hydraulic cylinder. China Mech. Eng. 2016, 27, 3190–3196. [Google Scholar]
- Xuan, B.T.; Hafizah, N.; Yanada, H. Modeling of dynamic friction behaviors of hydraulic cylinders. Mechatronics 2012, 22, 65–75. [Google Scholar]
- Pennestrì, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dyn. 2016, 83, 1785–1801. [Google Scholar]
- Salahshoor, E.; Ebrahimi, S.; Maasoomi, M. Nonlinear vibration analysis of mechanical systems with multiple joint clearances using the method of multiple scales. Mech. Mach. Theory 2016, 105, 495–509. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Liu, B.B.; Bi, Q.S. Non-smooth bifurcations on the bursting oscillations in a dynamic system with two timescales. Nonlinear Dyn. 2015, 79, 195–203. [Google Scholar] [CrossRef]
- Cirillo, G.I.; Habib, G.; Kerschen, G.; Sepulchre, R. Analysis and design of nonlinear resonances via singularity theory. J. Sound Vib. 2017, 392, 295–306. [Google Scholar] [CrossRef]
- Zhang, C.; Han, X.J.; Bi, Q.S. On symmetry-breaking bifurcation in the periodic parameter-switching Lorenz oscillator. Sci. China-Technol. Sci. 2013, 56, 2310–2316. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Zhang, Z.D.; Bi, Q.S. Nonlinear behaviors as well as the bifurcation mechanism in switched dynamical systems. Nonlinear Dyn. 2015, 79, 465–471. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Yu, P.; Wang, K.Q. Bifurcation analysis on a self-excited hysteretic system. Int. J. Bifurc. Chaos 2004, 14, 2825–2842. [Google Scholar] [CrossRef]




| Physical Quantity | Value | Unit | Physical Quantity | Value | Unit |
|---|---|---|---|---|---|
| equivalent mass m1 | 8656 | kg | bulk modulus βe | 780 × 106 | Pa |
| equivalent linear stiffness coefficient k1 | 1.6724 × 109 | N/m | dynamic friction factor μm | 0.01 | — |
| equivalent linear damping coefficient c1 | 1.2923 × 105 | N·s/m | static friction factor μs | 0.02 | — |
| total stroke L | 260 | mm | vibration velocity vm | 0.01 | m/s |
| effective working area Ap | 19.635 × 10−2 | m2 | positive pressure FN | 0.04 × 106 | N |
| effective working area Ab | 3.0159 × 10−2 | m2 | oil density ρ | 872 | kg/m3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System. Processes 2019, 7, 718. https://doi.org/10.3390/pr7100718
Zhu Y, Tang S, Wang C, Jiang W, Yuan X, Lei Y. Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System. Processes. 2019; 7(10):718. https://doi.org/10.3390/pr7100718
Chicago/Turabian StyleZhu, Yong, Shengnan Tang, Chuan Wang, Wanlu Jiang, Xiaoming Yuan, and Yafei Lei. 2019. "Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System" Processes 7, no. 10: 718. https://doi.org/10.3390/pr7100718
APA StyleZhu, Y., Tang, S., Wang, C., Jiang, W., Yuan, X., & Lei, Y. (2019). Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System. Processes, 7(10), 718. https://doi.org/10.3390/pr7100718








