Computational Molecular Modeling of Transport Processes in Nanoporous Membranes
Abstract
1. Introduction
- Transport of water and ions in reverse osmosis (RO) nanoporous membranes and the role played by ion-solvation in such membranes.
- Ion exchange in zeolite membranes and our finding that the separations were almost completely enthalpically driven rather than entropically.
- Separation of gases using zeolite membranes and the role of membrane loading and diffusion in the observed separation factors achieved in the membranes.
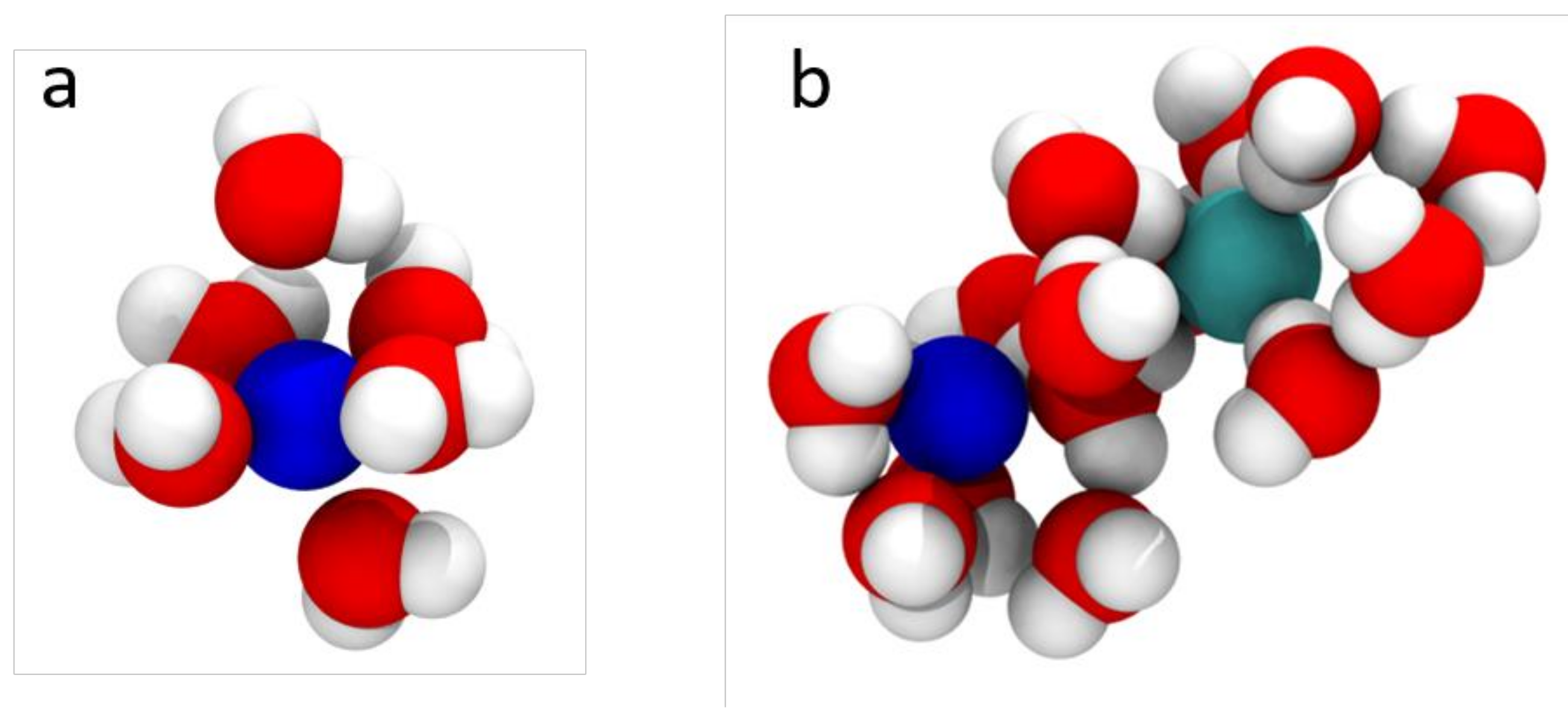
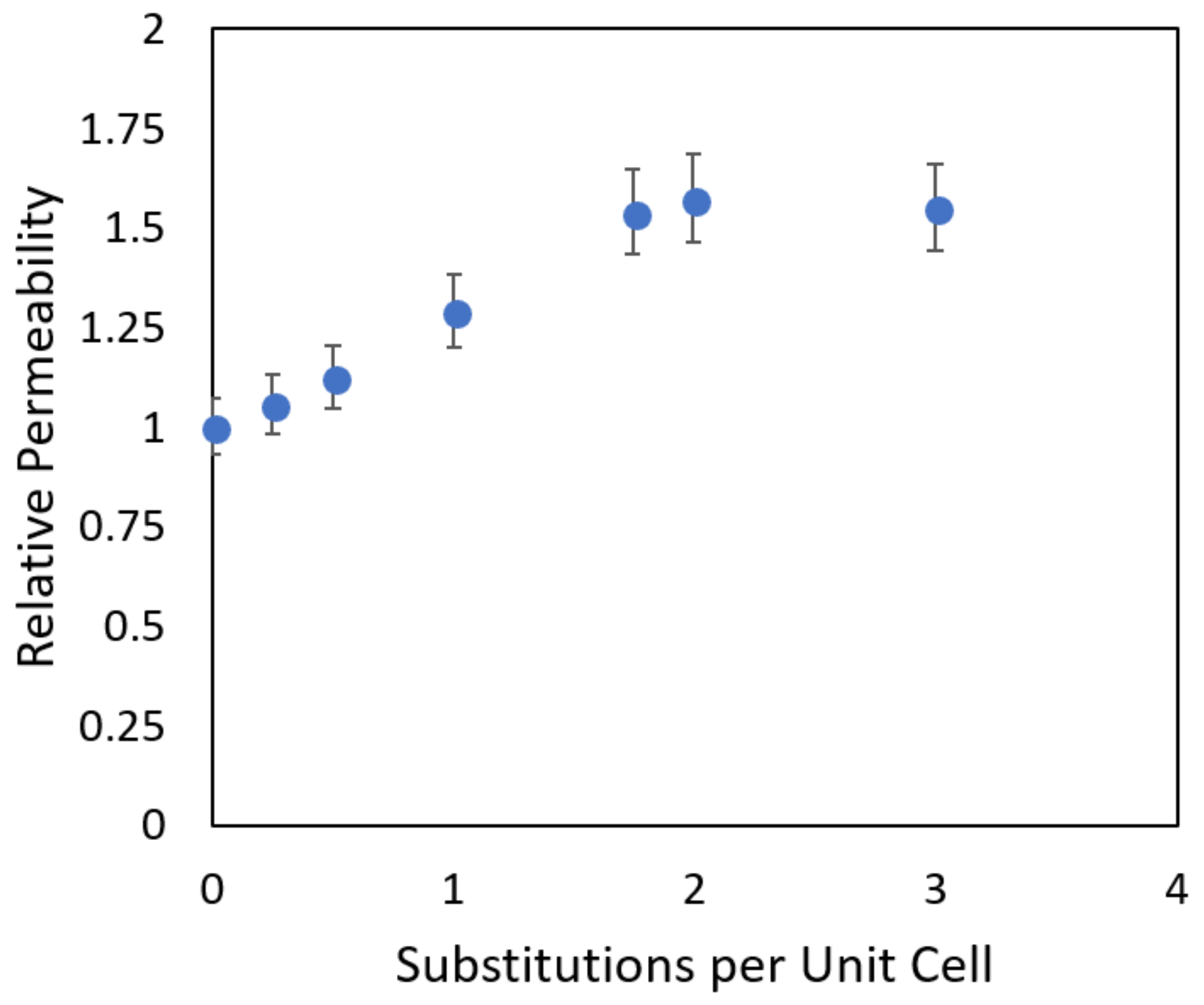
- We describe our investigations of multiple zeolite framework types to determine their transport behavior regarding water, protons, and vanadium ions, and investigate at the molecular level the requirements for their suitability in ion exchange membrane (IEM) applications. In addition to investigating different zeolite frameworks, the effect of composition is also examined by introducing different levels of aluminum substitution into the crystalline structure of a specific zeolite framework. By investigating two characteristics, membrane loading and intramembrane diffusion, it was possible for us to predict the overall ion permeability with the goal of optimizing the amount of aluminum substitution for high proton permeability while maintaining selectivity to undesirable ions. These and similar studies can be instrumental in designing more efficient membranes for important applications such as water purification/desalination and in many proposed applications in energy sustainability.
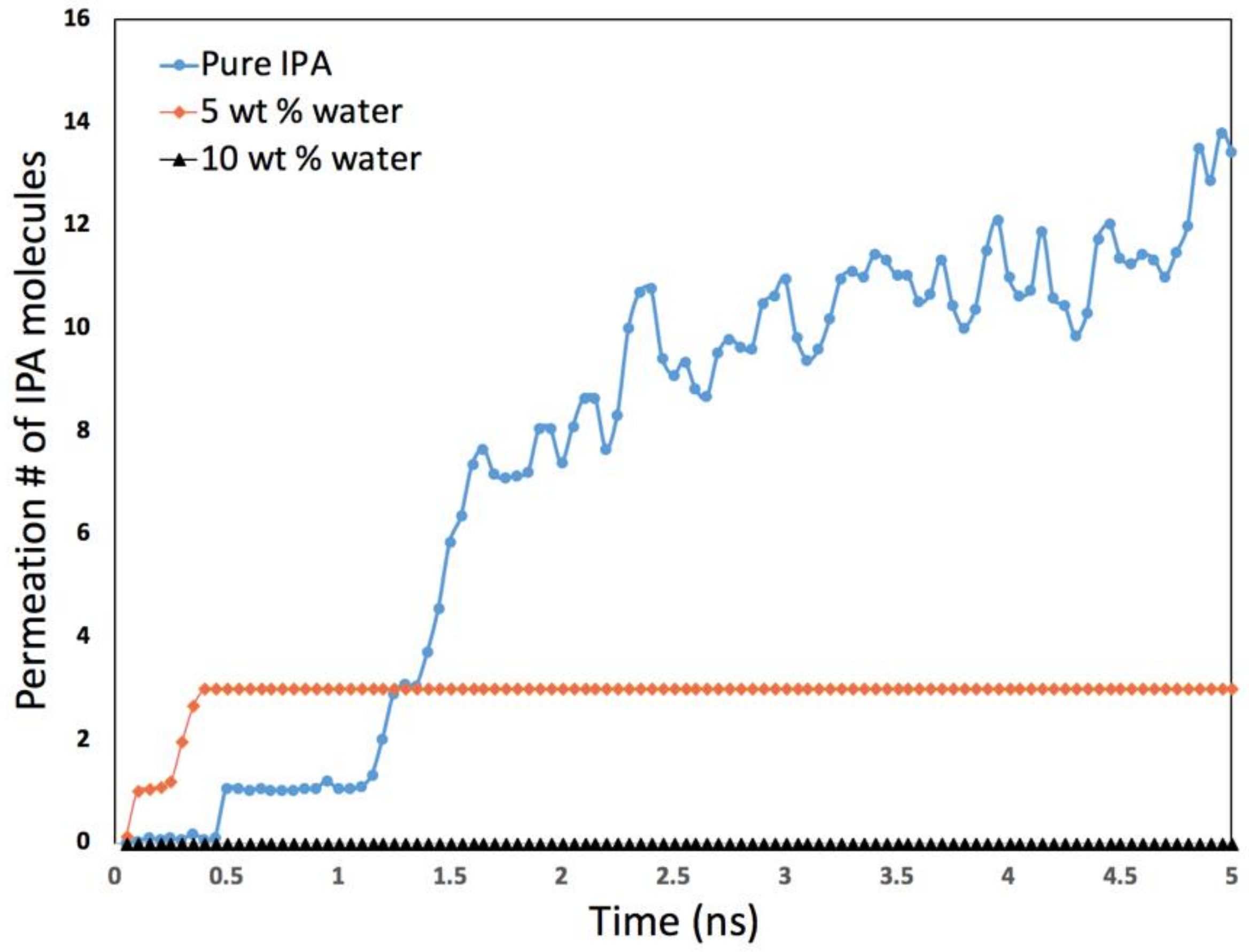
- The second application focuses on how molecular simulations can help to understand unexpected or non-intuitive results obtained during experiments. A recent experimental study on the dehydration of alcohols using zeolite membranes showed [7] that the membrane was effective in dehydrating alcohol when 5% water was present but became surprisingly ineffective when the water content was 1%. This was an intriguing observation that molecular simulation was able to explain because of the fine spatial and temporal resolution accessible in such investigations that may not be possible experimentally.
2. Molecular Simulations Applied to Various Membrane Applications
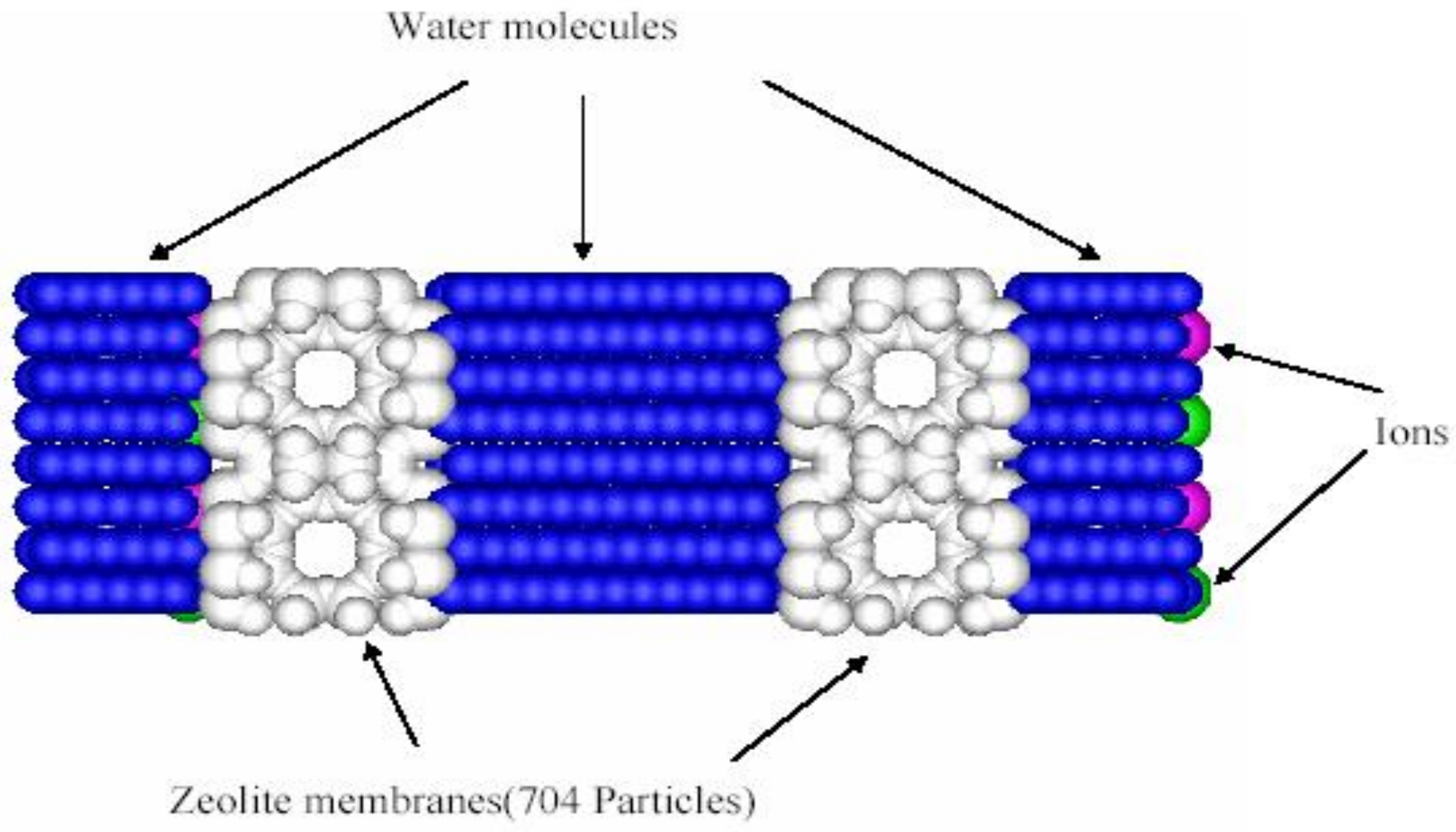
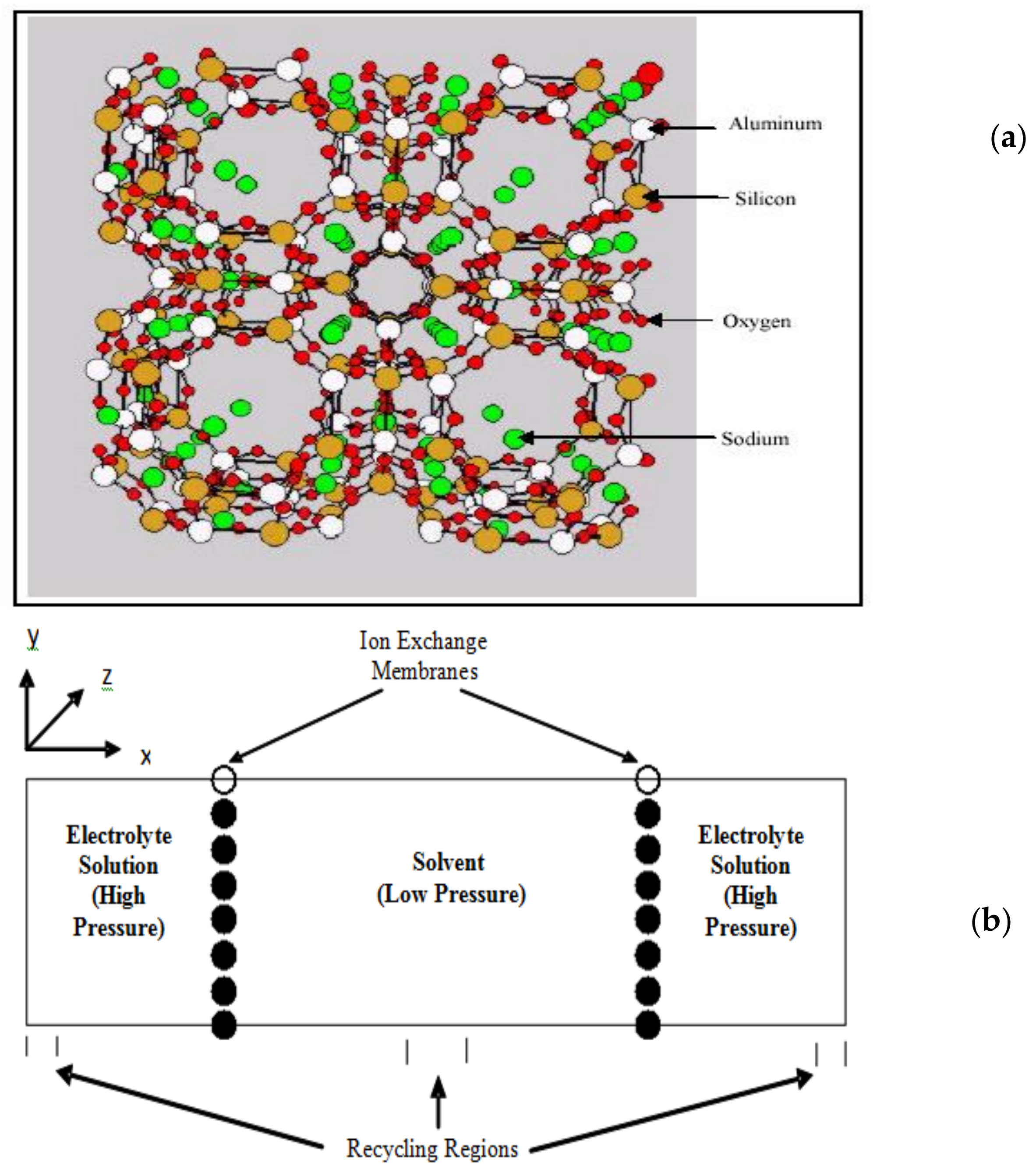
2.1. Transport in Reverse Osmosis Membranes
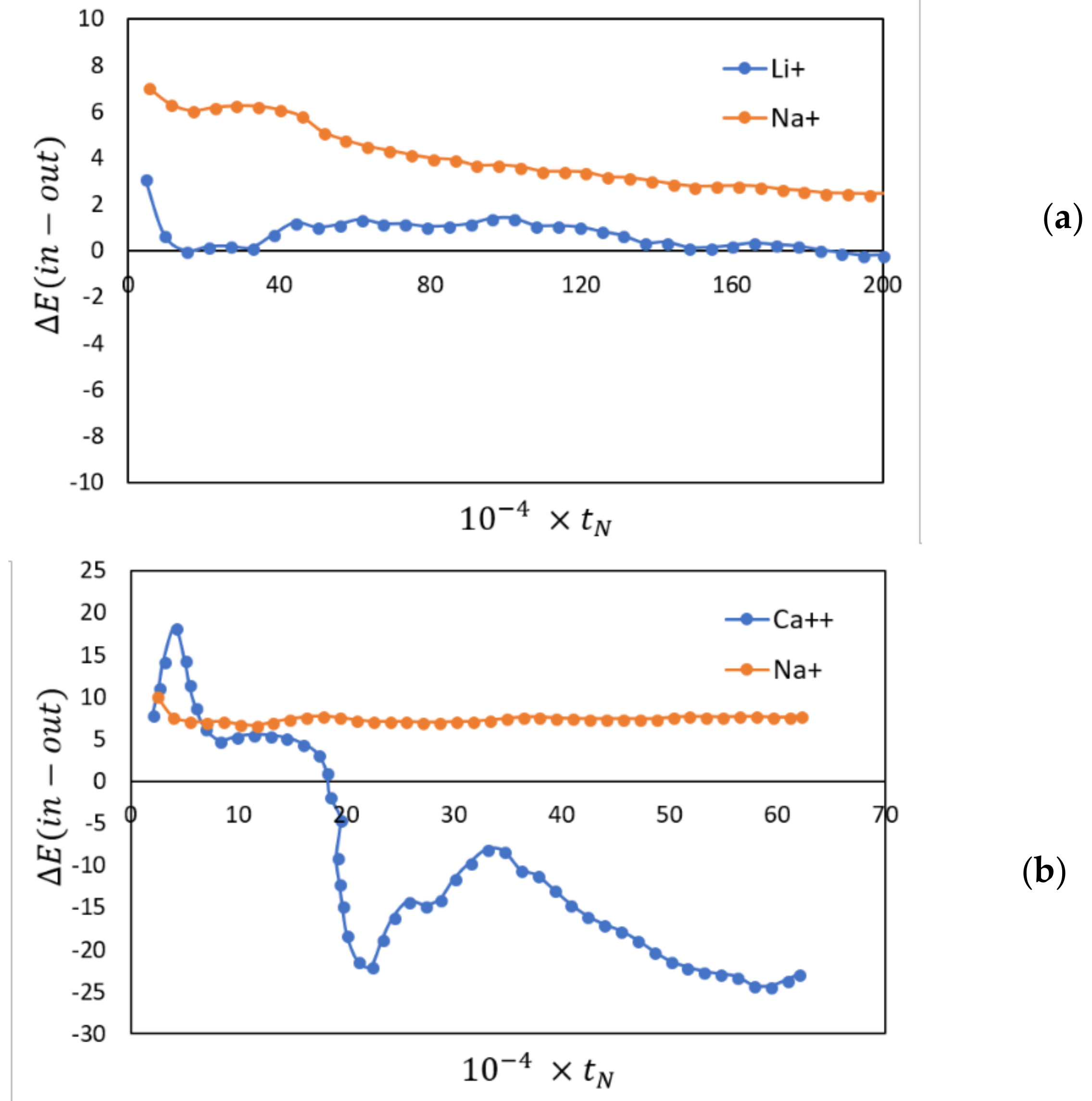
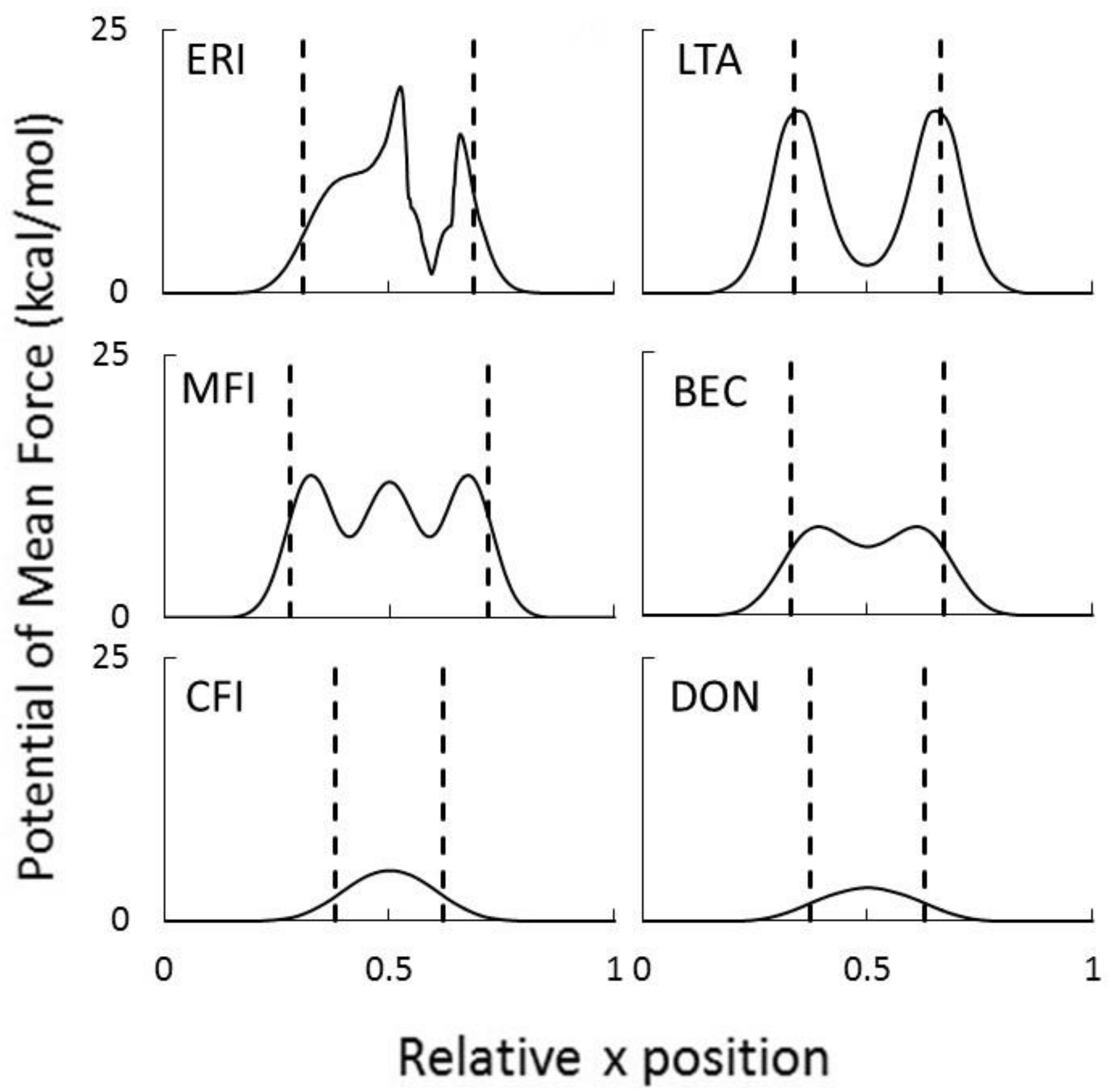
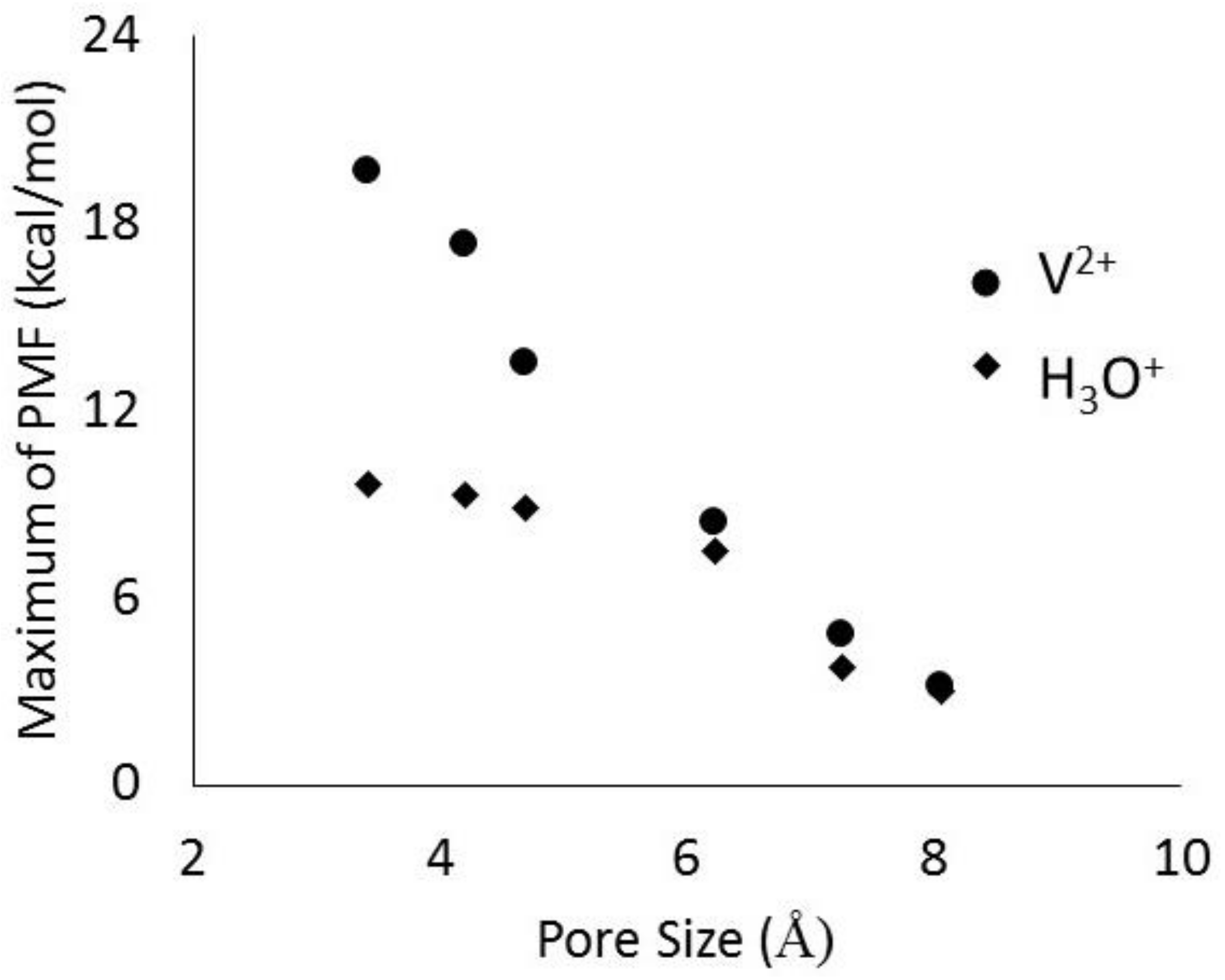
2.2. Transport in Ion-Exchange Membranes
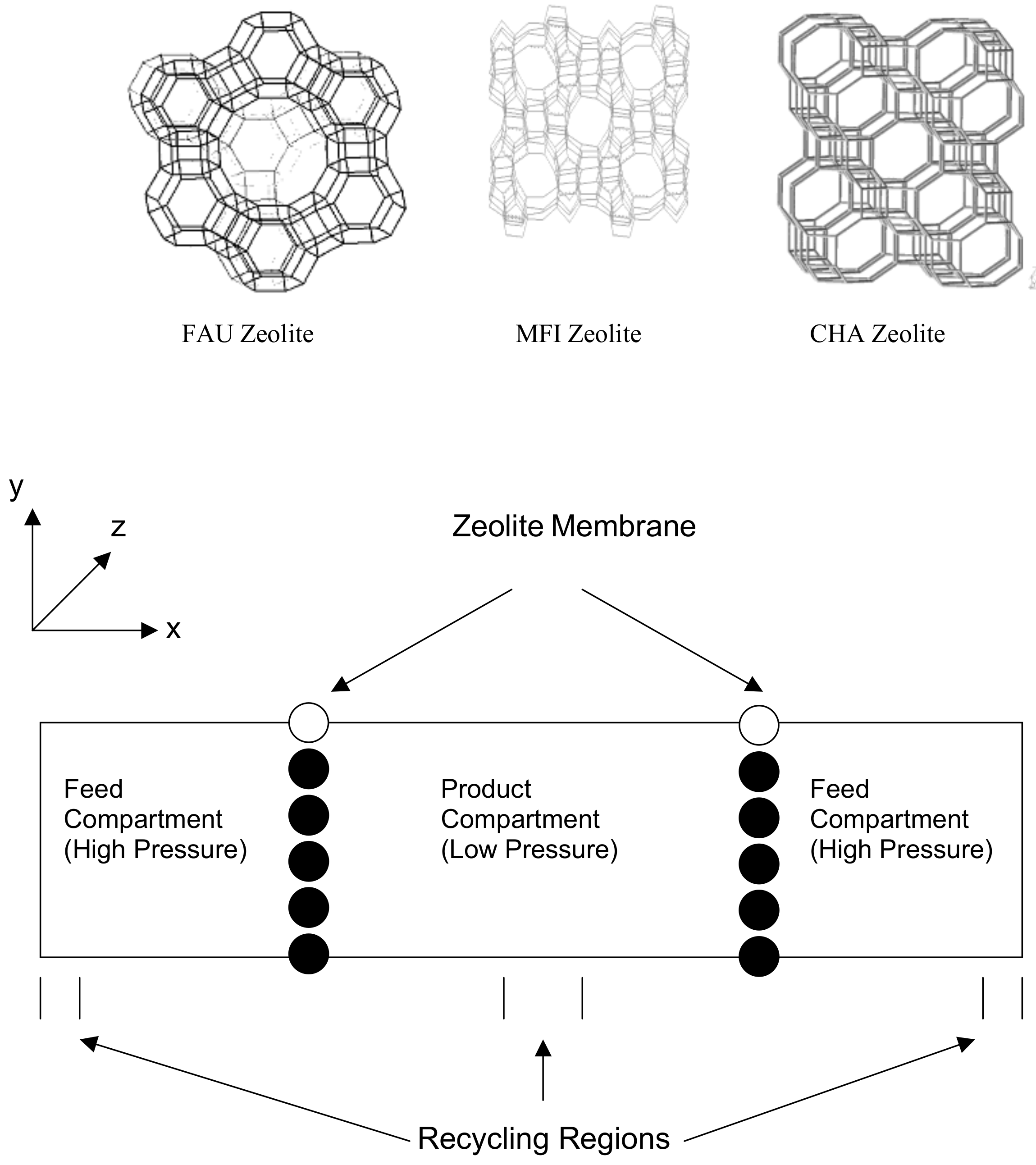
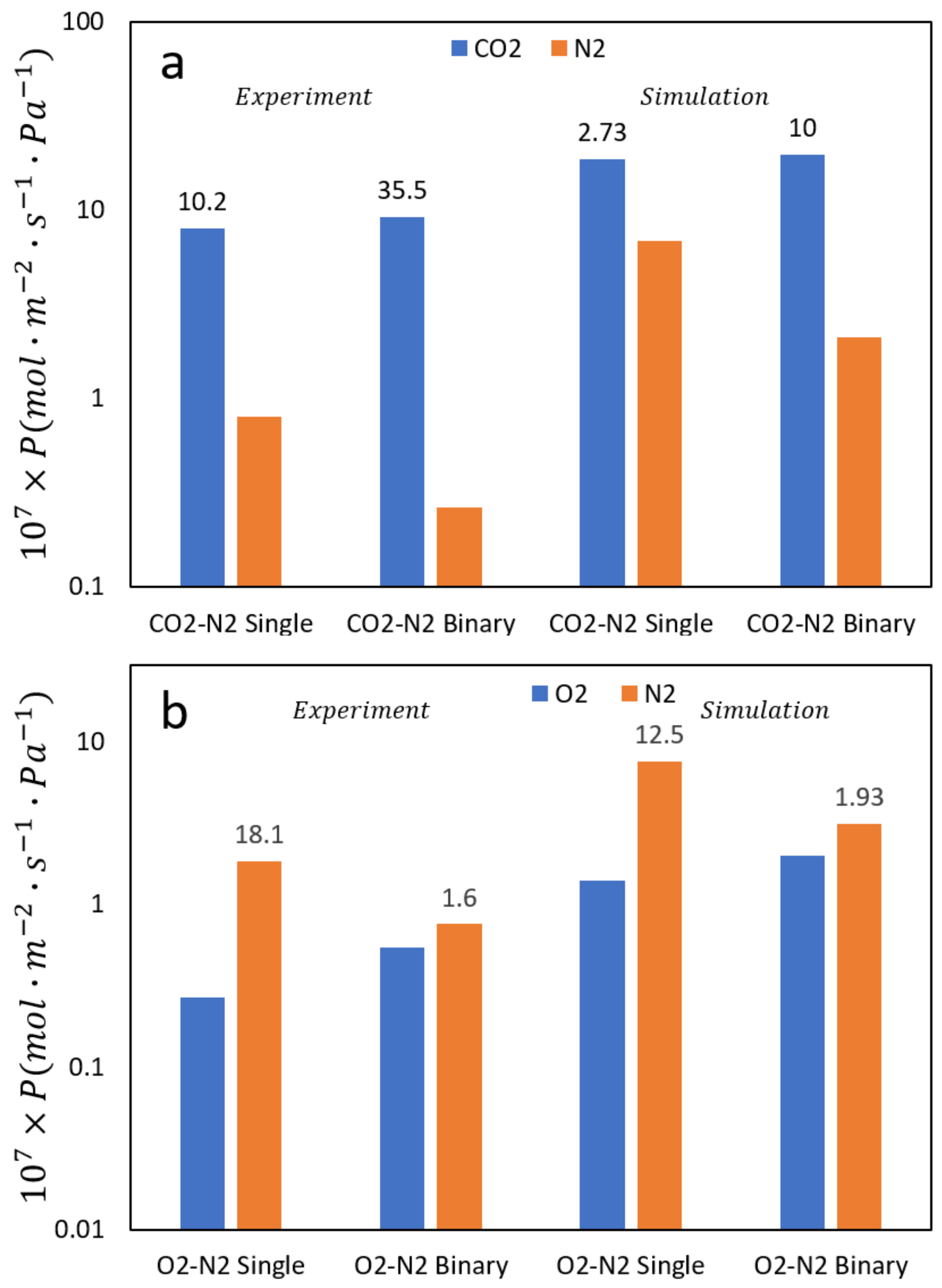
2.3. Transport in Gas Separations Membranes
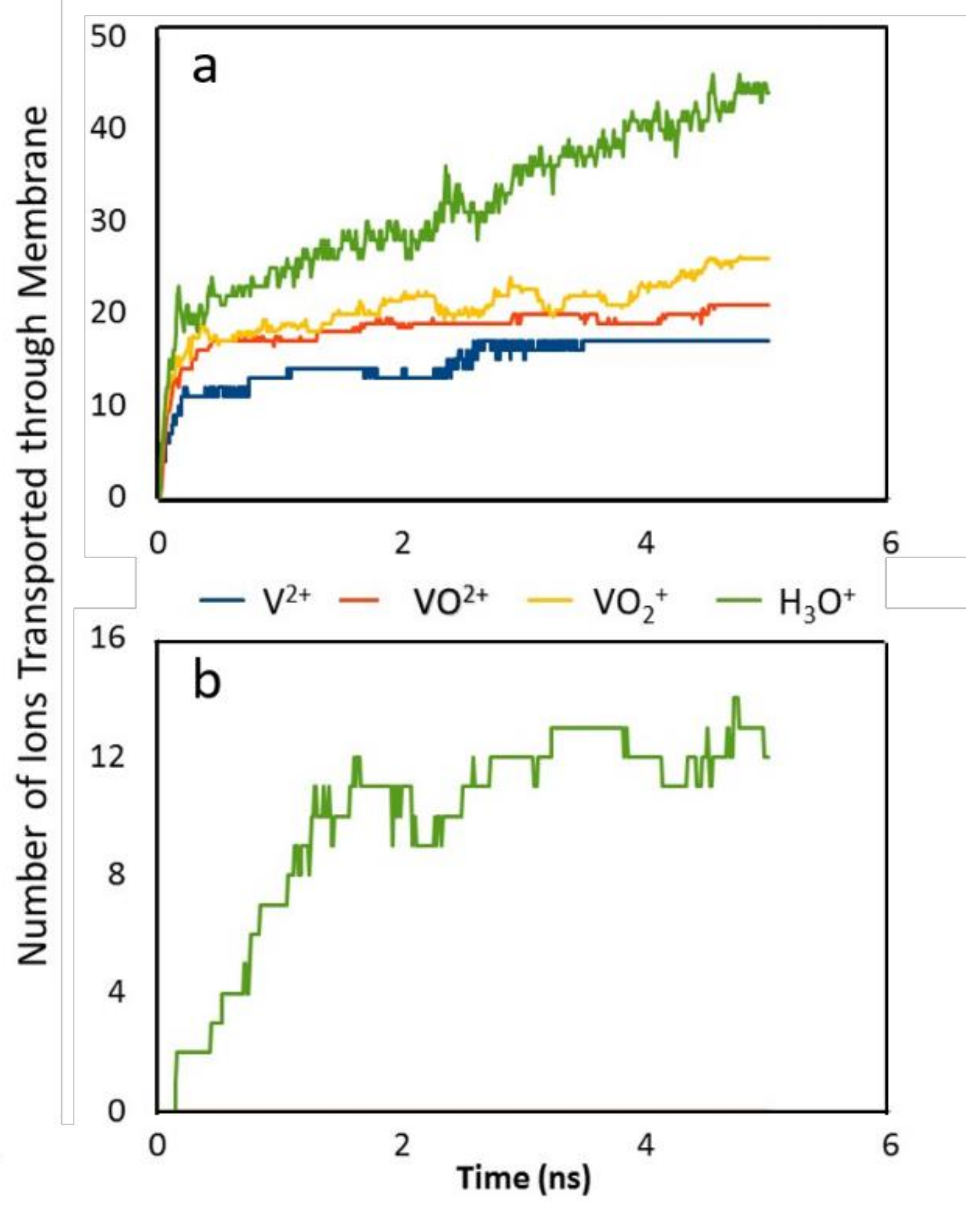
2.4. Membranes for Redox Flow Batteries
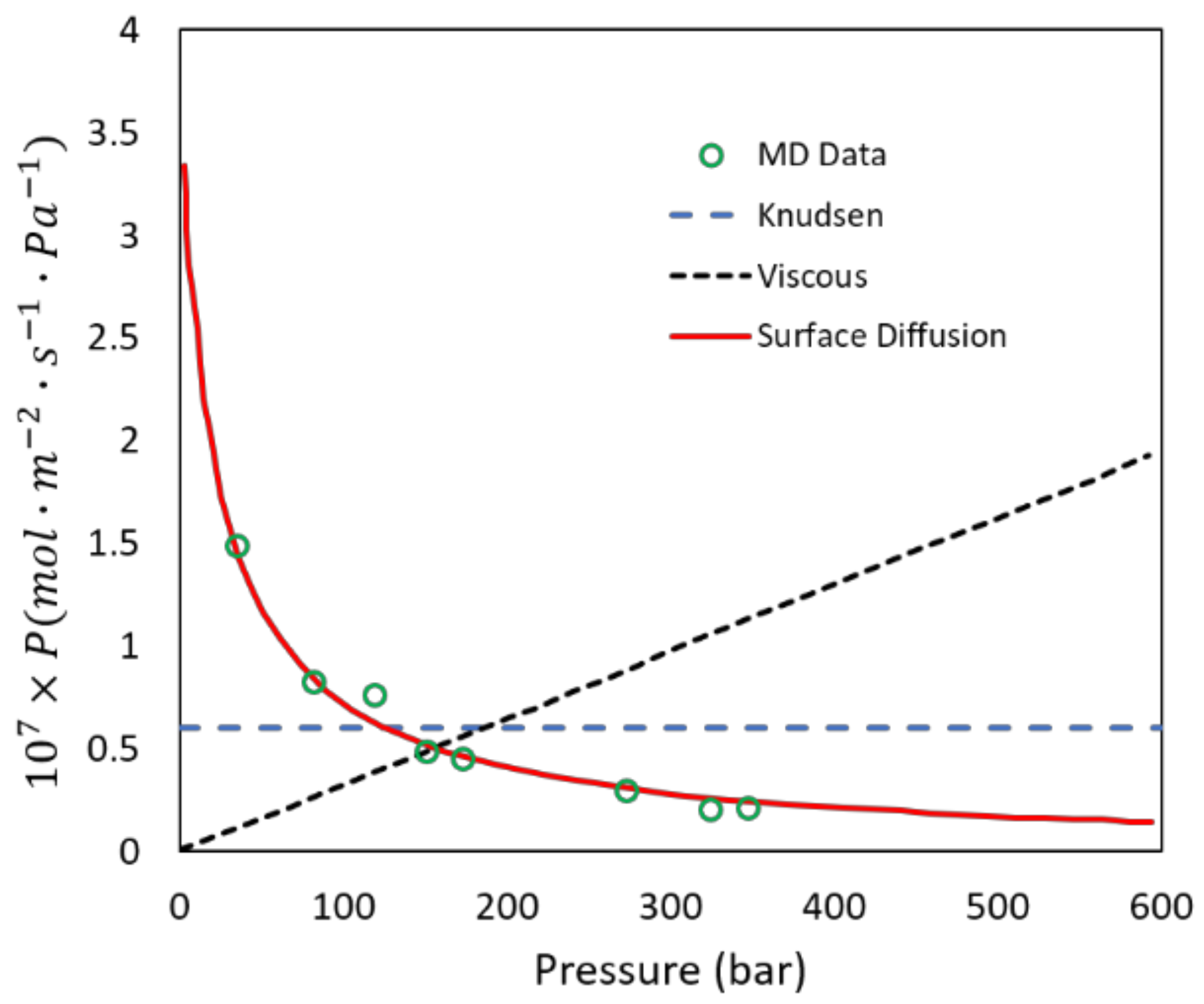
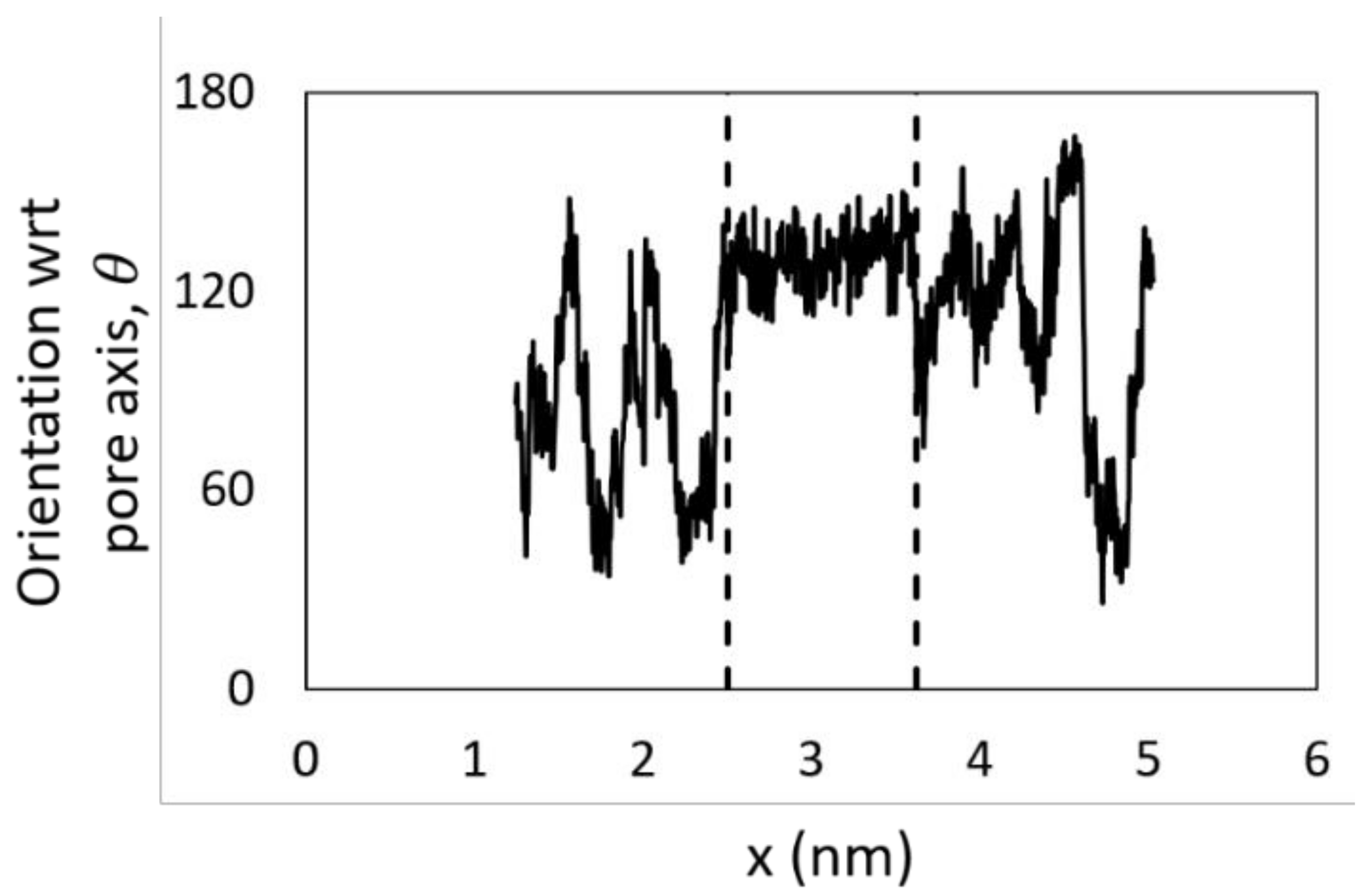
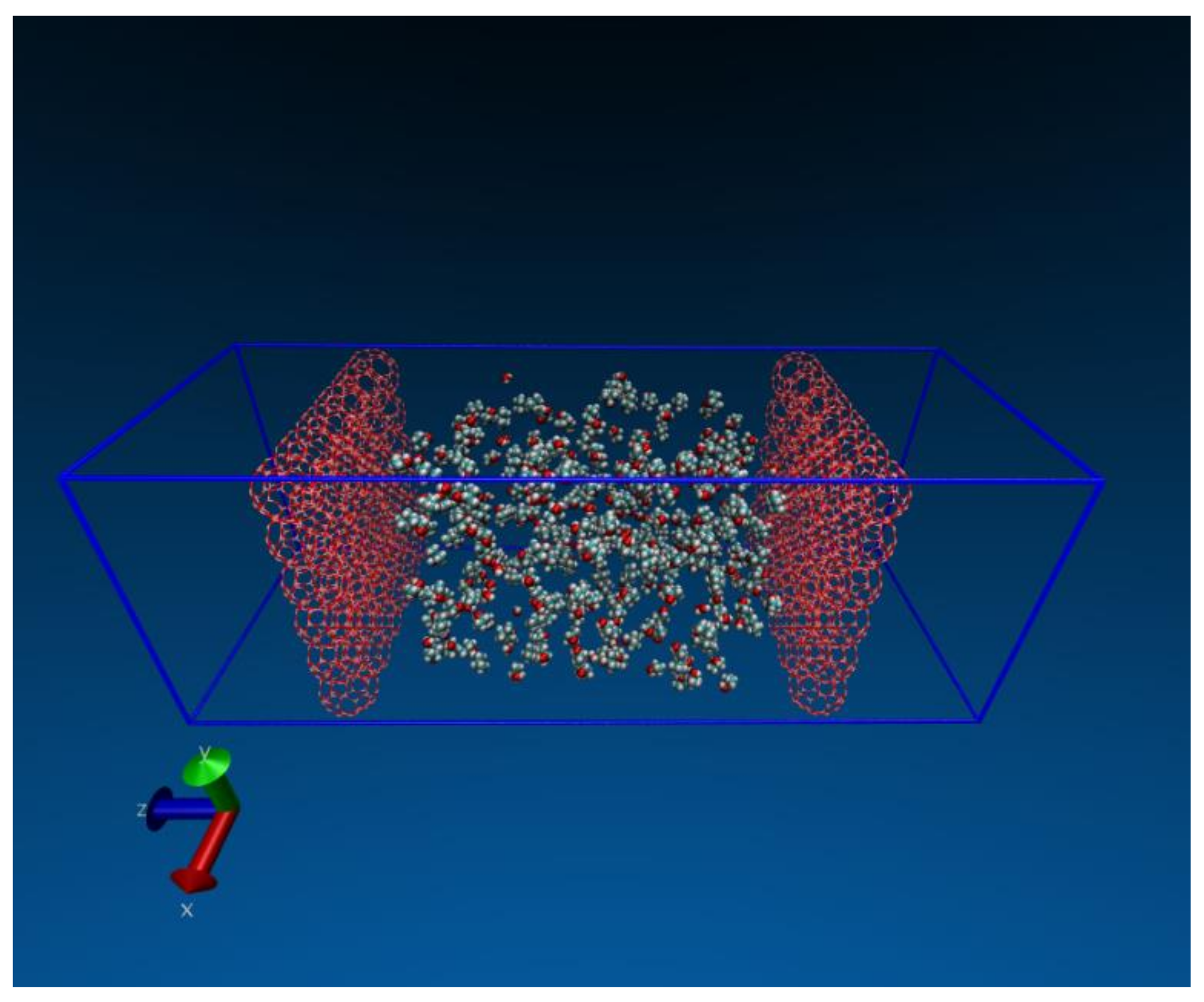
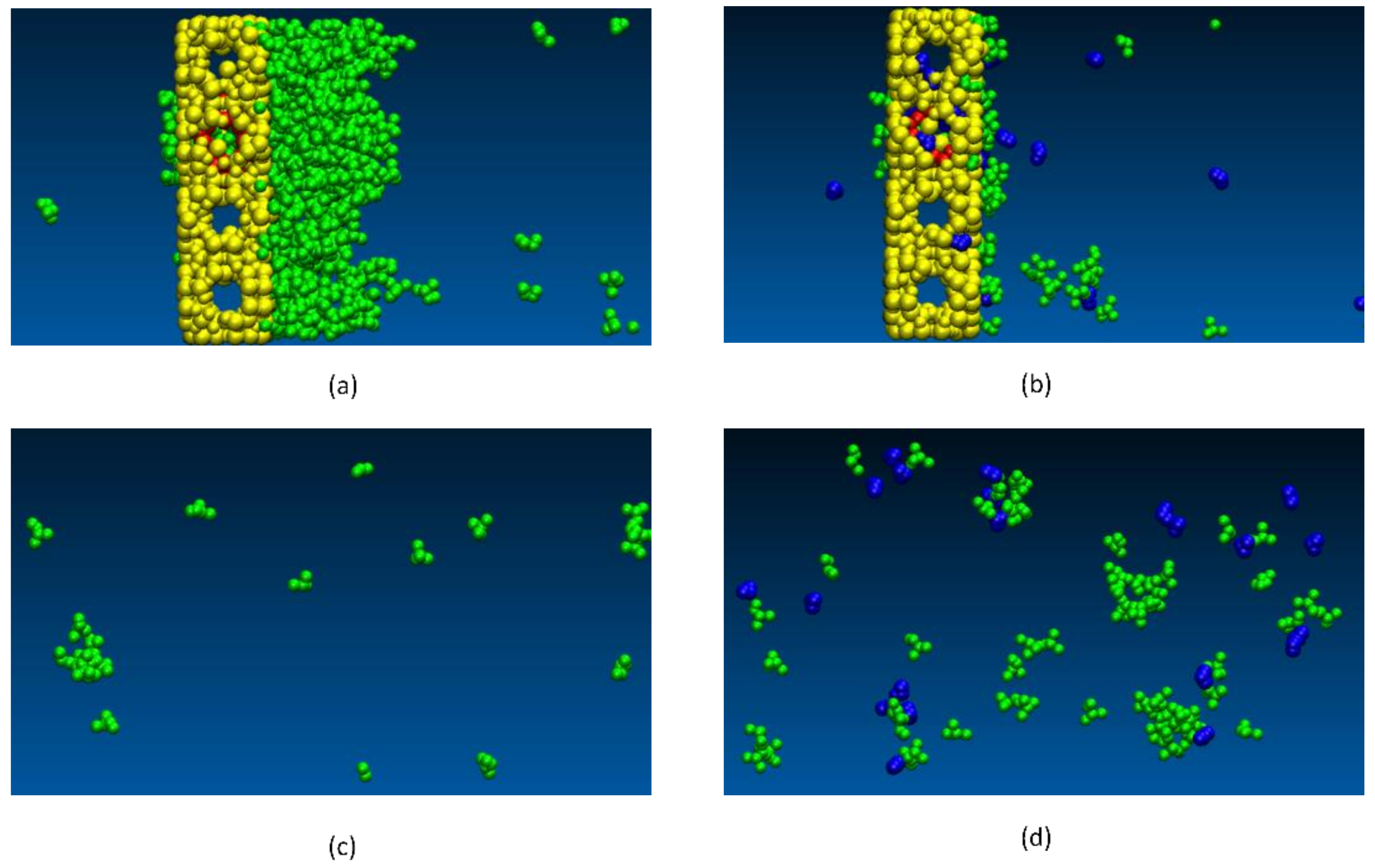
2.5. Dehydration of Alcohol
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef] [PubMed]
- Lively, R.P.; Sholl, D.S. From water to organics in membrane separations. Nat. Mater. 2017, 16, 276–279. [Google Scholar] [CrossRef] [PubMed]
- Widodo, S.; Khoiruddin; Ariono, D.; Subagjo; Wenten, I.G. Membrane separation for non-aqueous solution. IOP Conf. Ser. Mater. Sci. Eng. 2018, 285, 012008. [Google Scholar] [CrossRef]
- Yuan, H.; Yu, B.; Cong, H.; Peng, Q.; Yang, R.; Yang, S.; Yang, Z.; Luo, Y.; Xu, T.; Zhang, H.; et al. Modification Progress of Polymer Membranes for Gas Separation. Rev. Adv. Mater. Sci. 2016, 44, 207–220. [Google Scholar]
- Soleimany, A.; Hosseini, S.S.; Gallucci, F. Recent progress in developments of membrane materials and modification techniques for high performance helium separation and recovery: A review. Chem. Eng. Process. Process Intensif. 2017, 122, 296–318. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; ISBN 978-0-19-252470-6. [Google Scholar]
- Qu, F.; Shi, R.; Peng, L.; Zhang, Y.; Gu, X.; Wang, X.; Murad, S. Understanding the effect of zeolite crystal expansion/contraction on separation performance of NaA zeolite membrane: A combined experimental and molecular simulation study. J. Membr. Sci. 2017, 539, 14–23. [Google Scholar] [CrossRef]
- Lin, J.; Murad, S. A computer simulation study of the separation of aqueous solutions using thin zeolite membranes. Mol. Phys. 2001, 99, 1175–1181. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces; The Jerusalem Symposia on Quantum Chemistry and Biochemistry; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. ISBN 978-90-481-8368-5. [Google Scholar]
- Jorgensen, W.L.; Bigot, B.; Chandrasekhar, J. Quantum and statistical mechanical studies of liquids. 21. The nature of dilute solutions of sodium and methoxide ions in methanol. J. Am. Chem. Soc. 1982, 104, 4584–4591. [Google Scholar] [CrossRef]
- Tironi, I.G.; Sperb, R.; Smith, P.E.; van Gunsteren, W.F. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 1995, 102, 5451–5459. [Google Scholar] [CrossRef]
- Murad, S.; Oder, K.; Lin, J. Molecular simulation of osmosis, reverse osmosis, and electro-osmosis in aqueous and methanolic electrolyte solutions. Mol. Phys. 1998, 95, 401–408. [Google Scholar] [CrossRef]
- Kotelyanskii, M.J.; Wagner, N.J.; Paulaitis, M.E. Atomistic simulation of water and salt transport in the reverse osmosis membrane FT-30. J. Membr. Sci. 1998, 139, 1–16. [Google Scholar] [CrossRef]
- Murad, S.; Jia, W.; Krishnamurthy, M. Ion-exchange of monovalent and bivalent cations with NaA zeolite membranes: A molecular dynamics study. Mol. Phys. 2004, 102, 2103–2112. [Google Scholar] [CrossRef]
- Townsend, R.P.; Harjula, R. Ion Exchange in Molecular Sieves by Conventional Techniques. In Post-Synthesis Modification I; Molecular Sieves; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–42. ISBN 978-3-540-64334-0. [Google Scholar]
- Ponce de León, C.; Frías-Ferrer, A.; González-García, J.; Szánto, D.A.; Walsh, F.C. Redox flow cells for energy conversion. J. Power Sources 2006, 160, 716–732. [Google Scholar] [CrossRef]
- Cheng, F.; Liang, J.; Tao, Z.; Chen, J. Functional Materials for Rechargeable Batteries. Adv. Mater. 2011, 23, 1695–1715. [Google Scholar] [CrossRef] [PubMed]
- Codina, G.; Perez, J.R.; Lopez-Atalaya, M.; Vasquez, J.L.; Aldaz, A. Development of a 0.1 kW power accumulation pilot plant based on an Fe/Cr redox flow battery Part I. Considerations on flow-distribution design. J. Power Sources 1994, 48, 293–302. [Google Scholar] [CrossRef]
- Lim, H.S.; Lackner, A.M.; Knechtli, R.C. Zinc-Bromine Secondary Battery. J. Electrochem. Soc. 1977, 124, 1154–1157. [Google Scholar] [CrossRef]
- Clarke, R.L.; Dougherty, B.J.; Harrison, S.; Millington, J.P.; Mohanta, S. Battery with Bifunctional Electrolyte. U.S. Patent 6,986,966, 17 January 2006. [Google Scholar]
- Skyllas-Kazacos, M.; Rychcik, M.; Robins, R.G.; Fane, A.G.; Green, M.A. New All-Vanadium Redox Flow Cell. J. Electrochem. Soc. 1986, 133, 1057–1058. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Mai, Z.; Zhang, H.; Vankelecom, I. Ion exchange membranes for vanadium redox flow battery (VRB) applications. Energy Environ. Sci. 2011, 4, 1147–1160. [Google Scholar] [CrossRef]
- Li, X. Principles of Fuel Cells; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 978-1-59169-022-1. [Google Scholar]
- Vijayakumar, M.; Bhuvaneswari, M.S.; Nachimuthu, P.; Schwenzer, B.; Kim, S.; Yang, Z.; Liu, J.; Graff, G.L.; Thevuthasan, S.; Hu, J. Spectroscopic investigations of the fouling process on Nafion membranes in vanadium redox flow batteries. J. Membr. Sci. 2011, 366, 325–334. [Google Scholar] [CrossRef]
- Mohammadi, T.; Kazacos, M.S. Evaluation of the chemical stability of some membranes in vanadium solution. J. Appl. Electrochem. 1997, 27, 153–160. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Zhong, H.; Li, X.; Xiao, S.; Mai, Z. High performance composite membranes with enhanced dimensional stability for use in PEMFC. Int. J. Hydrog. Energy 2010, 35, 4209–4214. [Google Scholar] [CrossRef]
- Lew, C.M.; Cai, R.; Yan, Y. Zeolite Thin Films: From Computer Chips to Space Stations. Acc. Chem. Res. 2010, 43, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.G.; Lin, Y.S. Sulfur Dioxide Sorption Properties and Thermal Stability of Hydrophobic Zeolites. Ind. Eng. Chem. Res. 1995, 34, 4063–4070. [Google Scholar] [CrossRef]
- Auerbach, S.M.; Carrado, K.A.; Dutta, P.K. Handbook of Zeolite Science and Technology; CRC Press: Boca Raton, FL, USA, 2003; ISBN 978-0-203-91116-7. [Google Scholar]
- Li, L.; Dong, J.; Nenoff, T.M.; Lee, R. Desalination by reverse osmosis using MFI zeolite membranes. J. Membr. Sci. 2004, 243, 401–404. [Google Scholar] [CrossRef]
- Lia, L.; Dong, J.; Nenoff, T.M.; Lee, R. Reverse osmosis of ionic aqueous solutions on a MFI zeolite membrane. Desalination 2004, 170, 309–316. [Google Scholar] [CrossRef]
- Yang, R.; Xu, Z.; Yang, S.; Li, L.; Angelopoulos, A.; Dong, J. Nonionic Zeolite Membrane as Potential Ion Separator in Redox-Flow Battery. J. Membr. Sci. 2014, 450, 12–17. [Google Scholar] [CrossRef]
- Hinkle, K.R.; Jameson, C.J.; Murad, S. Transport of Vanadium and Oxovanadium Ions Across Zeolite Membranes: A Molecular Dynamics Study. J. Phys. Chem. C 2014, 118, 23803–23810. [Google Scholar] [CrossRef]
- Baerlocher, C.; McCusker, L.B.; Olson, D.H. Atlas of Zeolite Framework Types; Elsevier: New York, NY, USA, 2007; ISBN 978-0-08-055434-1. [Google Scholar]
- Xu, Z.; Michos, I.; Wang, X.; Yang, R.; Gu, X.; Dong, J. A zeolite ion exchange membrane for redox flow batteries. Chem. Commun. 2014, 50, 2416–2419. [Google Scholar] [CrossRef] [PubMed]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Song, B.; Yuan, H.; Jameson, C.J.; Murad, S. Role of surface ligands in nanoparticle permeation through a model membrane: A coarse-grained molecular dynamics simulations study. Mol. Phys. 2012, 110, 2181–2195. [Google Scholar] [CrossRef]
- Olson, D.H.; Khosrovani, N.; Peters, A.W.; Toby, B.H. Crystal Structure of Dehydrated CsZSM-5 (5.8Al): Evidence for Nonrandom Aluminum Distribution. J. Phys. Chem. B 2000, 104, 4844–4848. [Google Scholar] [CrossRef]
- Sethia, G.; Pillai, R.S.; Dangi, G.P.; Somani, R.S.; Bajaj, H.C.; Jasra, R.V. Sorption of Methane, Nitrogen, Oxygen, and Argon in ZSM-5 with different SiO2/Al2O3 Ratios: Grand Canonical Monte Carlo Simulation and Volumetric Measurements. Ind. Eng. Chem. Res. 2010, 49, 2353–2362. [Google Scholar] [CrossRef]
- Bell, R.G.; Jackson, R.A.; Catlow, C.R.A. Löwenstein’s rule in zeolite A: A computational study. Zeolites 1992, 12, 870–871. [Google Scholar] [CrossRef]
- Catlow, C.R.A.; George, A.R.; Freeman, C.M. Ab initio and molecular-mechanics studies of aluminosilicate fragments, and the origin of Lowenstein’s rule. Chem. Commun. 1996, 0, 1311–1312. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Xu, Z.; Michos, I.; Cao, Z.; Jing, W.; Gu, X.; Hinkle, K.; Murad, S.; Dong, J. Proton-Selective Ion Transport in ZSM-5 Zeolite Membrane. J. Phys. Chem. C 2016, 120, 26386–26392. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss mechanism. Chem. Phys. Lett. 1995, 244, 456–462. [Google Scholar] [CrossRef]
- Lobaugh, J.; Voth, G.A. The quantum dynamics of an excess proton in water. J. Chem. Phys. 1996, 104, 2056–2069. [Google Scholar] [CrossRef]
- Schmitt, U.W.; Voth, G.A. Multistate Empirical Valence Bond Model for Proton Transport in Water. J. Phys. Chem. B 1998, 102, 5547–5551. [Google Scholar] [CrossRef]
- Schmitt, U.W.; Voth, G.A. The computer simulation of proton transport in water. J. Chem. Phys. 1999, 111, 9361–9381. [Google Scholar] [CrossRef]
- Day, T.J.F.; Schmitt, U.W.; Voth, G.A. The Mechanism of Hydrated Proton Transport in Water. J. Am. Chem. Soc. 2000, 122, 12027–12028. [Google Scholar] [CrossRef]
- Kusaka, I.; Wang, Z.-G.; Seinfeld, J.H. Binary nucleation of sulfuric acid-water: Monte Carlo simulation. J. Chem. Phys. 1998, 108, 6829–6848. [Google Scholar] [CrossRef][Green Version]
| No. of Substitutions Per Unit Cell | Si/Al Ratio | Hydronium Ion Concentration, mol/L |
|---|---|---|
| 0.00 | ∞ | 1.86 ± 0.46 |
| 0.25 | 383 | 2.02 ± 0.50 |
| 0.50 | 191 | 2.22 ± 0.57 |
| 1.00 | 95 | 2.77 ± 0.54 |
| 1.75 | 54 | 4.36 ± 0.52 |
| 2.00 | 47 | 5.42 ± 0.63 |
| 3.00 | 31 | 6.37 ± 0.61 |
| No. of Substitutions Per Unit Cell | Si/Al Ratio | Hydronium Ion Diffusion, ×105 cm2/s |
|---|---|---|
| 0.00 | ∞ | 2.66 ± 0.11 |
| 0.25 | 383 | 2.56 ± 0.24 |
| 0.50 | 191 | 2.40 ± 0.11 |
| 1.00 | 95 | 2.35 ± 0.25 |
| 1.75 | 53.86 | 2.31 ± 0.23 |
| 2.00 | 47 | 2.09 ± 0.18 |
| 3.00 | 31 | 1.98 ± 0.31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinkle, K.R.; Wang, X.; Gu, X.; Jameson, C.J.; Murad, S. Computational Molecular Modeling of Transport Processes in Nanoporous Membranes. Processes 2018, 6, 124. https://doi.org/10.3390/pr6080124
Hinkle KR, Wang X, Gu X, Jameson CJ, Murad S. Computational Molecular Modeling of Transport Processes in Nanoporous Membranes. Processes. 2018; 6(8):124. https://doi.org/10.3390/pr6080124
Chicago/Turabian StyleHinkle, Kevin R., Xiaoyu Wang, Xuehong Gu, Cynthia J. Jameson, and Sohail Murad. 2018. "Computational Molecular Modeling of Transport Processes in Nanoporous Membranes" Processes 6, no. 8: 124. https://doi.org/10.3390/pr6080124
APA StyleHinkle, K. R., Wang, X., Gu, X., Jameson, C. J., & Murad, S. (2018). Computational Molecular Modeling of Transport Processes in Nanoporous Membranes. Processes, 6(8), 124. https://doi.org/10.3390/pr6080124





