Mathematical Modeling of Metastatic Cancer Migration through a Remodeling Extracellular Matrix
Abstract
1. Introduction
2. Methods
2.1. Cancer Cells
2.2. Extracellular Matrix Collagen Fibers
2.3. Enzyme MMP
2.4. Enzyme LOX
2.5. Nondimensionalization and Parameter Values
2.6. Initial and Boundary Conditions
2.7. Numerical Methods and Code Repository
3. Results and Discussion
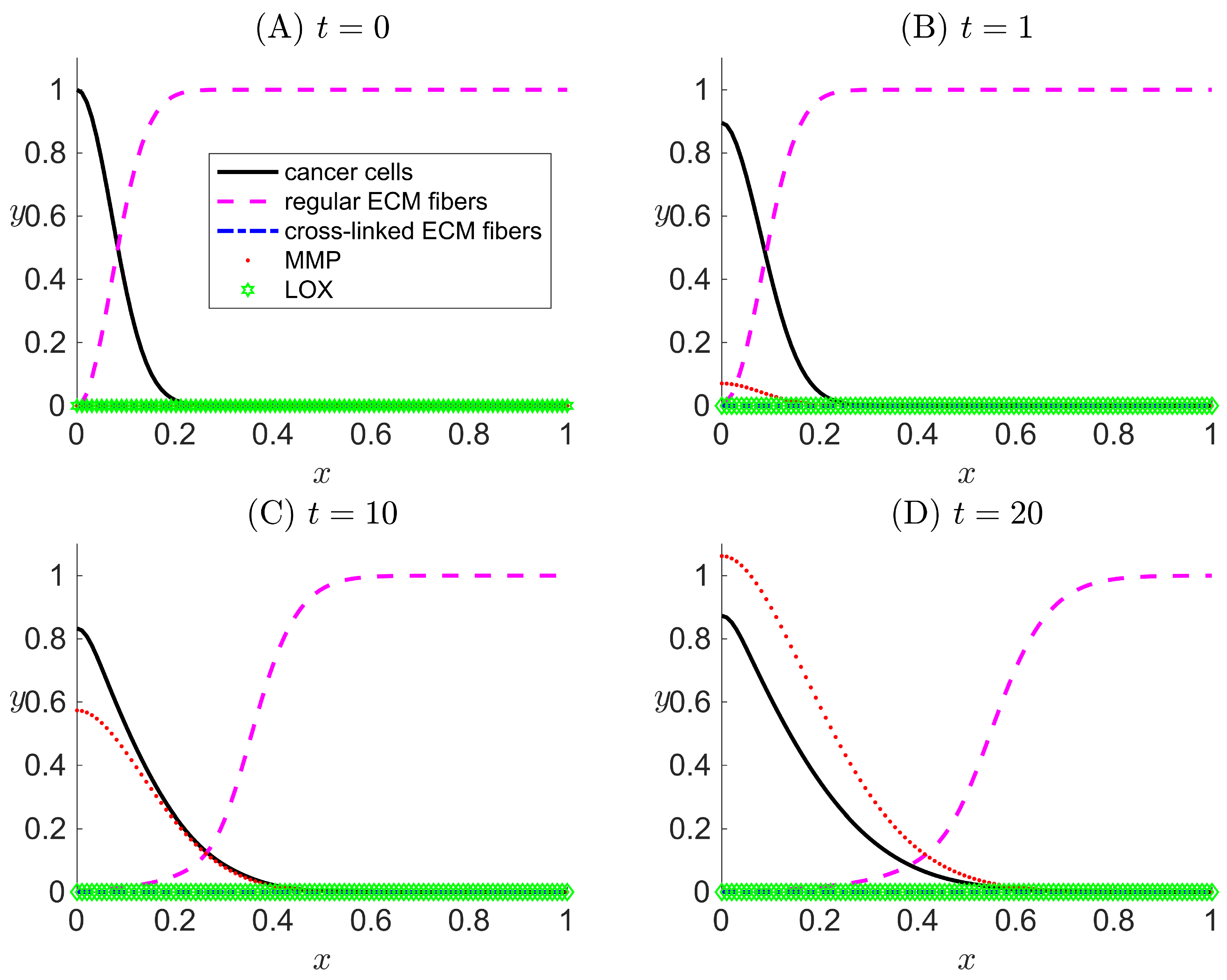
3.1. Case I: LOX Is Absent
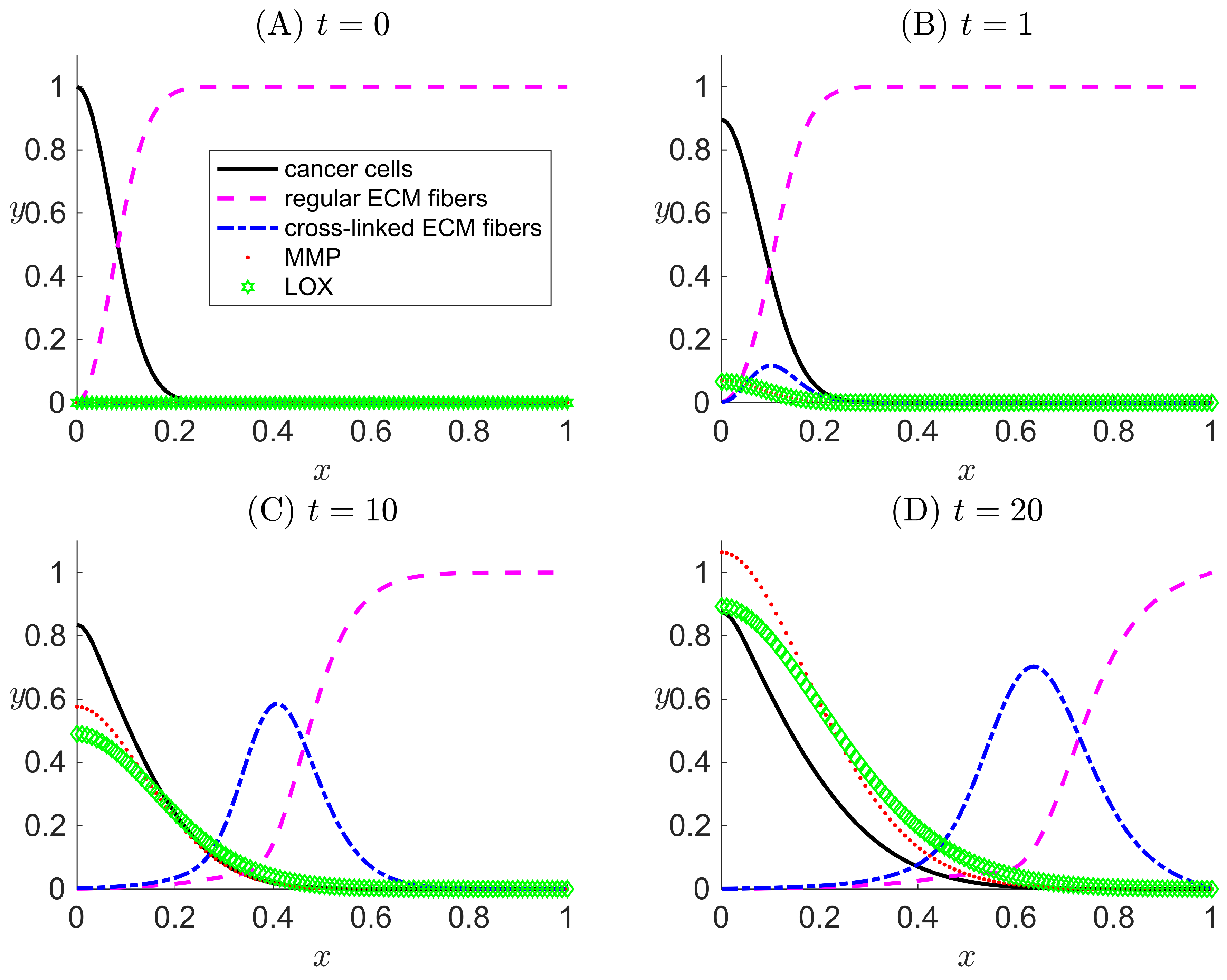
3.2. Case II: LOX Is Present But Not Coupled to the Haptotactic Migration of Cancer Cells
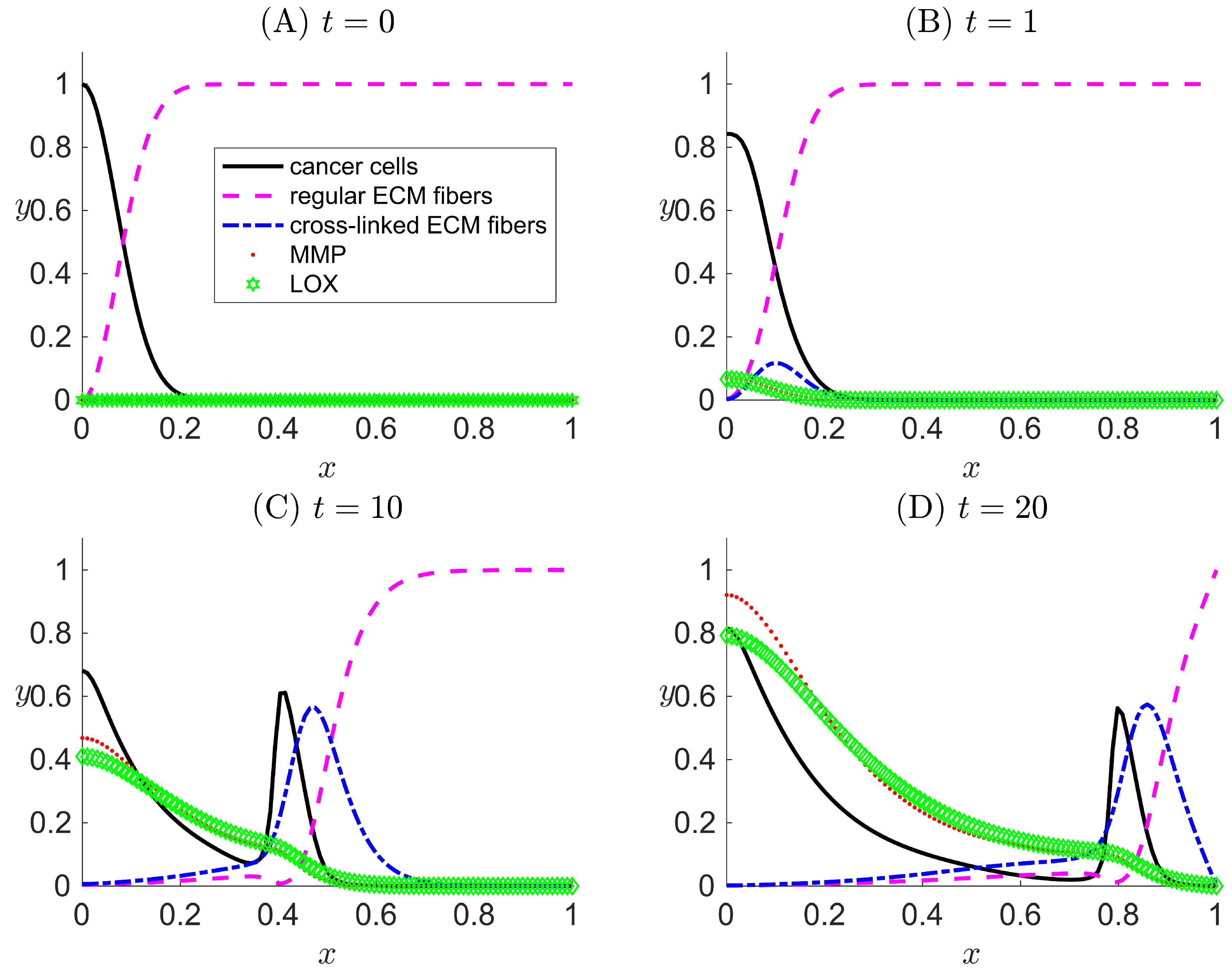
3.3. Case III: LOX Is Present and Is Coupled to the Haptotactic Migration of Cancer Cells
3.4. Sensitivity Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cox, T.R.; Gartland, A.; Erler, J.T. Lysyl oxidase, a targetable secreted molecule involved in cancer metastasis. Cancer Res. 2016, 76, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, M.; Khanna, C. Revisiting the seed and soil in cancer metastasis. Int. J. Biochem. Cell Biol. 2009, 41, 1452–1462. [Google Scholar] [CrossRef] [PubMed]
- Bagley, R. The Tumor Microenvironment; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kahlert, C.; Kalluri, R. Exosomes in tumor microenvironment influence cancer progression and metastasis. J. Mol. Med. 2013, 91, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhao, J.; Zhang, L.; Wei, F.; Lian, Y.; Wu, Y.; Gong, Z.; Zhang, S.; Zhou, J.; Cao, K.; et al. Role of tumor microenvironment in tumorigenesis. J. Cancer 2017, 8, 761–773. [Google Scholar] [CrossRef] [PubMed]
- Keeratichamroen, S.; Lirdprapamongkol, K.; Svasti, J. Mechanism of ECM-induced dormancy and chemoresistance in A549 human lung carcinoma cells. Oncol. Rep. 2018, 39, 1765–1774. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, K. Basement membrane (type IV) collagen. Matrix Biol. 1995, 14, 439–445. [Google Scholar] [CrossRef]
- Clark, A.G.; Vignjevic, D.M. Modes of cancer cell invasion and the role of the microenvironment. Curr. Opin. Cell Biol. 2015, 36, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Provenzano, P.P.; Eliceiri, K.W.; Campbell, J.M.; Inman, D.R.; White, J.G.; Keely, P.J. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 2006, 4, 38. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Takai, K.; Weaver, V.M.; Werb, Z. Extracellular matrix degradation and remodeling in development and disease. Cold Spring Harb. Perspect. Biol. 2011, 3, a005058. [Google Scholar] [CrossRef] [PubMed]
- Oudin, M.J.; Jonas, O.; Kosciuk, T.; Broye, L.C.; Guido, B.C.; Wyckoff, J.; Riquelme, D.; Lamar, J.M.; Asokan, S.B.; Whittaker, C.; et al. Tumor cell-driven extracellular matrix remodeling drives haptotaxis during metastatic progression. Cancer Discov. 2016, 6, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Bonnans, C.; Chou, J.; Werb, Z. Remodelling the extracellular matrix in development and disease. Nat. Rev. Mol. Cell Biol. 2014, 15, 786–801. [Google Scholar] [CrossRef] [PubMed]
- Frantz, C.; Stewart, K.M.; Weaver, V.M. The extracellular matrix at a glance. J. Cell Sci. 2010, 123, 4195–4200. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Mouw, J.K.; Weaver, V.M. Forcing form and function: Biomechanical regulation of tumor evolution. Trends Cell Biol. 2011, 21, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Quaranta, V. Cell migration through extracellular matrix: Membrane-type metalloproteinases make the way. J. Cell Biol. 2000, 149, 1167–1170. [Google Scholar] [CrossRef] [PubMed]
- Condeelis, J.; Segall, J.E. Intravital imaging of cell movement in tumours. Nat. Rev. Cancer 2003, 3, 921–930. [Google Scholar] [CrossRef] [PubMed]
- Wyckoff, J.B.; Wang, Y.; Lin, E.Y.; Li, J.F.; Goswami, S.; Stanley, E.R.; Segall, J.E.; Pollard, J.W.; Condeelis, J. Direct visualization of macrophage-assisted tumor cell intravasation in mammary tumors. Cancer Res. 2007, 67, 2649–2656. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Weaver, V.M.; Werb, Z. The extracellular matrix: A dynamic niche in cancer progression. J. Cell Biol. 2012, 196, 395–406. [Google Scholar] [CrossRef] [PubMed]
- Cawston, T.E.; Young, D.A. Proteinases involved in matrix turnover during cartilage and bone breakdown. Cell Tissue Res. 2010, 339, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Cathcart, J.; Pulkoski-Gross, A.; Cao, J. Targeting matrix metalloproteinases in cancer: Bringing new life to old ideas. Genes Dis. 2015, 2, 26–34. [Google Scholar] [CrossRef] [PubMed]
- Gialeli, C.; Theocharis, A.D.; Karamanos, N.K. Roles of matrix metalloproteinases in cancer progression and their pharmacological targeting. Cell Tissue Res. 2010, 339, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Coussens, L.M.; Fingleton, B.; Matrisian, L.M. Matrix metalloproteinase inhibitors and cancer: Trials and tribulations. Science 2002, 295, 2387–2392. [Google Scholar] [CrossRef] [PubMed]
- Fingleton, B. Chapter 36: MMP inhibitor clinical trials - the past, present, and future. In The Cancer Degradome: Proteases and Cancer Biology; Edwards, D., Hoyer-Hansen, G., Blasi, F., Sloane, B., Eds.; Springer: New York, NY, USA, 2008; pp. 759–785. [Google Scholar]
- Smith-Mungo, L.I.; Kagan, H.M. Lysyl oxidase: Properties, regulation and multiple functions in biology. Matrix Biol. 1998, 16, 387–398. [Google Scholar] [CrossRef]
- Egeblad, M.; Rasch, M.G.; Weaver, V.M. Dynamic interplay between the collagen scaffold and tumor evolution. Curr. Opin. Cell Biol. 2010, 22, 697–706. [Google Scholar] [CrossRef] [PubMed]
- Rasmuson, A.; Andersson, B.; Olsson, L.; Andersson, R. Mathematical Modeling in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Gatenby, R.A. Models of tumor-host interaction as competing populations: Implications for tumor biology and treatment. J. Theor. Biol. 1995, 176, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A.; Gawlinski, E.T. A reaction-diffusion model of cancer invasion. Cancer Res. 1996, 56, 5745–5753. [Google Scholar] [PubMed]
- Orme, M.E.; Chaplain, M.A. A mathematical model of the first steps of tumour-related angiogenesis: Capillary sprout formation and secondary branching. IMA J. Math. Appl. Med. Biol. 1996, 13, 73–98. [Google Scholar] [CrossRef] [PubMed]
- Perumapanani, A.J.; Sherratt, J.A.; Norbury, J.; Byrne, H.M. Biological inferences from a mathematical model for malignant invasion. Invasion Metastasis 1996, 16, 209–221. [Google Scholar]
- Perumapanani, A.J.; Simmons, D.L.; Gearing, A.J.H.; Miller, K.M.; Ward, G.; Norbury, J.; Schneemann, M.; Sherratt, J.A. Extracellular matrix-mediated chemotaxis can impede cell migration. Proc. Biol. Sci. 1998, 265, 2347. [Google Scholar] [CrossRef]
- Anderson, A.R.A.; Chaplain, M.A.J. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull. Math. Biol. 1998, 60, 857–899. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.A.; Chaplain, M.A.J.; Newman, E.L.; Steele, R.J.C.; Thompson, A.M. Mathematical modelling of tumour invasion and metastasis. J. Theor. Med. 2000, 2, 129–154. [Google Scholar] [CrossRef]
- Turner, S.; Sherratt, J.A. Intercellular adhesion and cancer invasion: A discrete simulation using the extended Potts model. J. Theor. Biol. 2002, 16, 85–100. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.A. A hybrid mathematical model of solid tumour invasion: The importance of cell adhesion. Math. Med. Biol. 2005, 22, 163–186. [Google Scholar] [CrossRef] [PubMed]
- Chaplain, M.A.J.; Lolas, G. Mathematical modeling of cancer cell invasion of tissue: The role of the urokinase plasminogen activation system. Math. Models Methods Appl. Sci. 2005, 15, 1685–1734. [Google Scholar] [CrossRef]
- Chaplain, M.A.J.; Lolas, G. Mathematical modeling of cancer invasion of tissue: Dynamic heterogeneity. Netw. Heterog. Media 2006, 1, 399–439. [Google Scholar]
- Frieboes, H.B.; Zheng, X.; Sun, C.; Tromberg, B.; Gatenby, R.; Cristini, V. An Integrated computational/experimental model of tumor invasion. Cancer Res. 2006, 66, 1597–1604. [Google Scholar] [CrossRef] [PubMed]
- Hillen, T. M5 mesoscopic and macroscopic models for mesenchymal motion. J. Math. Biol. 2006, 53, 585–616. [Google Scholar] [CrossRef] [PubMed]
- Gerisch, A.; Chaplain, M.A.J. Mathematical modelling of cancer cell invasion of tissue: Local and non-local models and the effect of adhesion. J. Theor. Biol. 2008, 250, 684–704. [Google Scholar] [CrossRef] [PubMed]
- Ramis-Conde, I.; Drasdo, D.; Anderson, A.R.A.; Chaplain, M.A.J. Modeling the influence of the E-cadherin-β-catenin pathway in cancer cell invasion: A multiscale approach. Biophys. J. 2008, 95, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.; Rejniak, K.; Gerlee, P.; Quaranta, V. Microenvironment driven invasion: A multiscale multimodel investigation. J. Math. Biol. 2009, 58, 579–624. [Google Scholar] [CrossRef] [PubMed]
- Poplawski, N.J.; Agero, U.; Gens, J.S.; Swat, M.; Glazier, J.A.; Anderson, A.R.A. Front instabilities and invasiveness of simulated avascular tumors. Bull. Math. Biol. 2009, 71, 1189–1227. [Google Scholar] [CrossRef] [PubMed]
- Szymanska, Z.; Rodrigo, C.M.; Lachowicz, M.; Chaplain, M.A.J. Mathematical modelling of cancer invasion of tissue: The role and effect of nonlocal interactions. Math. Models Methods Appl. Sci. 2009, 19, 257–281. [Google Scholar] [CrossRef]
- Painter, K.J. Modelling cell migration strategies in the extracellular matrix. J. Math. Biol. 2009, 58, 511–543. [Google Scholar] [CrossRef] [PubMed]
- Painter, K.J.; Armstrong, N.A.; Sherratt, J.A. The impact of adhesion on cellular invasion processes in cancer and development. J. Theor. Biol. 2010, 264, 1057–1067. [Google Scholar] [CrossRef] [PubMed]
- Andasari, V.; Gerisch, A.; Lolas, G.; South, A.P.; Chaplain, M.A.J. Mathematical modeling of cancer cell invasion of tissue: Biological insight from mathematical analysis and computational simulation. J. Math. Biol. 2011, 63, 141–171. [Google Scholar] [CrossRef] [PubMed]
- Kolev, M.; Zubik-Kowal, B. Numerical solutions for a model of tissue invasion and migration of tumour cells. Comput. Math. Methods Med. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Toma, A.; Mang, A.; Schuetz, T.A.; Becker, S.; Buzug, T.M. A novel method for simulating the extracellular matrix in models of tumour growth. Comput. Math. Methods Med. 2012, 2012. [Google Scholar] [CrossRef] [PubMed]
- Deakin, N.E.; Chaplain, M.A.J. Mathematical modeling of cancer invasion: The role of membrane-bound matrix metalloproteinases. Front. Oncol. 2013, 3, 70. [Google Scholar] [CrossRef] [PubMed]
- Evje, S. An integrative multiphase model for cancer cell migration under influence of physical cues from the microenvironment. Chem. Eng. Sci. 2017, 165, 240–259. [Google Scholar] [CrossRef]
- Rejniak, K.A. Systems Biology of Tumor Microenvironment: Quantitative Modeling and Simulations; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Kessenbrock, K.; Plaks, V.; Werb, Z. Matrix metalloproteinases: Regulators of the tumor microenvironment. Cell 2010, 141, 52–67. [Google Scholar] [CrossRef] [PubMed]
- Pittayapruek, P.; Meephansan, J.; Prapapan, O.; Komine, M.; Ohtsuki, M. Role of matrix metalloproteinases in photoaging and photocarcinogenesis. Int. J. Mol. Sci. 2016, 17, 868. [Google Scholar] [CrossRef] [PubMed]
- Brower, M.; Carney, D.N.; Oie, H.K.; Gazdar, A.F.; Minna, J.D. Growth of cell lines and clinical specimens of human non-small cell lung cancer in serum-free defined medium. Cancer Res. 1986, 46, 798–806. [Google Scholar] [PubMed]
- Kremmer, T.; Palyi, I.; Daubner, D.; Boldizsar, M.; Vincze, B.; Paulik, E.; Sugar, J.; Pokorny, E.; Tury, E. Comparative studies on the polyamine metabolism and DFMO treatment of MCF-7 and MDA-MB-231 breast cancer cell lines and xenografts. Anticancer Res. 1991, 11, 1807–1813. [Google Scholar] [PubMed]
- Limame, R.; Wouters, A.; Pauwels, B.; Fransen, E.; Peeters, M.; Lardon, F.; de Wever, O.; Pauwels, P. Comparative analysis of dynamic cell viability, migration and invasion assessments by novel real-time technology and classic endpoint assays. PLoS ONE 2012, 7, e46536. [Google Scholar] [CrossRef] [PubMed]
- Oraiopoulou, M.E.; Tzamali, E.; Tzedakis, G.; Vakis, A.; Papamatheakis, J.; Sakkalis, V. In vitro/in silico study on the role of doubling time heterogeneity among primary glioblastoma cell lines. BioMed Res. Int. 2017, 2017, 8569328. [Google Scholar] [CrossRef] [PubMed]
- Bray, D. Cell Movements: From Molecules to Motility; Garland Publishing: New York, NY, USA, 2001. [Google Scholar]
- Collier, I.E.; Legant, W.; Marmer, B.; Lubman, O.; Saffarian, S.; Wakatsuki, T.; Elson, E.; Goldberg, G.I. Diffusion of MMPs on the surface of collagen fibrils: The mobile cell surface—Collagen substratum interface. PLoS ONE 2011, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Terranova, V.P.; Diflorio, R.; Lyall, R.M.; Hic, S.; Friesel, R.; Maciag, T. Human endothelial cells are chemotactic to endothelial cell growth factor and heparin. J. Cell Biol. 1985, 101, 2330–2334. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Das, A.; Barai, A.; Sen, S. MMP secretion rate and inter-invadopodia spacing collectively govern cancer invasiveness. Biophys. J. 2018, 114, 650–662. [Google Scholar] [CrossRef] [PubMed]
- Higham, D.J. MATLAB Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Nguyen Edalgo, Y.T.; Ford Versypt, A.N. MetastaticCancerECMRemodeling. 2018. Available online: http://github.com/ashleefv/MetastaticCancerECMRemodeling (accessed on 22 April 2018). [CrossRef]
- Kim, M.J.; Gillies, R.J.; Rejniak, K.A. Current advances in mathematical modeling of anti-cancer drug penetration into tumor tissues. Front. Oncol. 2013, 3, 278. [Google Scholar] [CrossRef] [PubMed]

| Term | Description | Value | Unit | Sources |
|---|---|---|---|---|
| L | Reference length | 1 | cm | [33] |
| Reference time | 32 | hours | [55,56,57,58] | |
| Reference number of cancer cells per volume | cells/cm | [33] | ||
| Reference value for | M | [61] | ||
| , | Reference value for m, l | M | [47] | |
| Diffusion coefficient of cancer cells | cms | [59] | ||
| Diffusion coefficient of MMP | cms | [60] | ||
| D | Reference chemical diffusion coefficient | cms | [59] | |
| Haptotaxis coefficient toward f | cm M s | [32] |
| Term | Description | Value | Sources |
|---|---|---|---|
| Diffusion coefficient of cell | 0.001 | Calculated [59] | |
| Rate expression for tumor proliferation | Assumed | ||
| Haptotaxis toward f | Calculated [59,61] | ||
| Haptotaxis toward | Assumed | ||
| Space fraction per unit | 1 | By definition from [40] | |
| Space fraction per unit | 1 | By definition from [40] | |
| Space fraction per unit | 1 | By definition from [40] | |
| Rate constant for MMP cleavage of f | 10 | Estimated from [33] | |
| Rate constant for production of f | 0.15 | Estimated from [47] | |
| Rate constant for LOX remodeling of f | 18 | Assumed | |
| Diffusion of MMP | Calculated [33,59,60] | ||
| Rate constant for decay of MMP | Estimated from [33,62] | ||
| Rate constant for secretion of MMP by cells | Estimated from [33] | ||
| Diffusion coefficient of LOX | Assumed | ||
| Rate constant for decay of LOX | Assumed | ||
| Rate constant for secretion of LOX by cells | Assumed |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen Edalgo, Y.T.; Ford Versypt, A.N. Mathematical Modeling of Metastatic Cancer Migration through a Remodeling Extracellular Matrix. Processes 2018, 6, 58. https://doi.org/10.3390/pr6050058
Nguyen Edalgo YT, Ford Versypt AN. Mathematical Modeling of Metastatic Cancer Migration through a Remodeling Extracellular Matrix. Processes. 2018; 6(5):58. https://doi.org/10.3390/pr6050058
Chicago/Turabian StyleNguyen Edalgo, Yen T., and Ashlee N. Ford Versypt. 2018. "Mathematical Modeling of Metastatic Cancer Migration through a Remodeling Extracellular Matrix" Processes 6, no. 5: 58. https://doi.org/10.3390/pr6050058
APA StyleNguyen Edalgo, Y. T., & Ford Versypt, A. N. (2018). Mathematical Modeling of Metastatic Cancer Migration through a Remodeling Extracellular Matrix. Processes, 6(5), 58. https://doi.org/10.3390/pr6050058






