1. Introduction
Tuberculosis (TB) is the second leading cause of death in the world next to the Human Immunodeficiency Virus (HIV) [
1], which is mainly caused by the bacteria called
Mycobacterium tuberculosis and usually acquired via air born infection from someone who has active TB. It particularly affects the lungs (pulmonary TB) but can also affect other organs of the body such as kidney, brain, blood, bones, glands (extra-pulmonary TB) [
1,
2,
3,
4]. Not all individuals infected by TB develop active TB. Only around 10% of those infected with
Mycobacterium tuberculosis develop active TB disease and become infectious. Whereas, around 90% of the people infected with the bacteria remain latently infected and individuals in the latent stage do not transmit TB. However, there is a high risk of developing an active TB for individuals whose immune system is weakened due to the presence of HIV, malnutrition or diabetes. Infected individuals can be treated through anti-TB drugs such as Isoniazid, Rifampicin, Pyrazinamide, Ethambutol and Streptomycin [
1,
3].
The global report of TB by World Health Organization (WHO) indicated that in 2015, 10.4 million people were infected with TB and 1.8 million died due to the disease (including 0.4 million among people with HIV) [
5]. Over 95% of TB deaths occur in low and middle income countries. In the same year, an estimated 1 million children became infected with TB and 170,000 children died of TB (excluding children with HIV) and an estimated 49 million lives were saved through TB diagnosis and treatment between 2000 and 2015. More than 20% of TB cases worldwide are attributed to smoking and people who are infected with HIV are 26 to 31 times more likely to become infected with TB [
4].
The Human Immunodeficiency Virus (HIV) infects cells of immune system such as helper T cells (specifically CD4+ T cells), macrophages, and dendritic cells. HIV compromises the human immune system and reduces the ability of the body to fight back infections and diseases. The most advanced stages of HIV infection is usually called Acquired Immunodeficiency Syndrome (AIDS). AIDS is one of the leading causes of death worldwide that is affecting virtually every nation. Even if HIV/AIDS is not permanently curable, main methods used to fight against it are preventive mechanisms (which include: abstinence, faithfulness and protection) which mainly rely on the level of behavioral change of the population, and providing Antiretroviral Therapy (ART) for those infected.
In 2016, an estimated 36.7 million people were living with HIV (including 1.8 million newly infected people in the same year) and 1 million people died of AIDS related illness. Since the start of the epidemic, an estimated 76.1 million people have been infected with HIV and 35 million people died of AIDS related illness [
6]. Individuals infected with HIV are more likely to develop TB disease because of the deficiency in their immunity, and HIV infection is the most powerful risk factor for progression from TB infection directly to the infectious stage [
7]. In the WHO report of 2017, it is indicated that TB remains the leading cause of death among people living with HIV, accounting for around one in three AIDS related deaths [
8]. Collaborative TB/HIV activities (including HIV testing, ART and TB preventive measures) are crucial for the reduction of TB-HIV co-infection. Even though, those collaborative activities can save people from dying, significant challenges are there to fully implement them. As has been indicated in literature, ART is not being delivered to TB-HIV co-infected patients in the majority of the countries with the largest number of TB/HIV patients; the pace of treatment scale-up for TB/HIV patients has slowed, and only a small fraction of TB/HIV infected individuals received TB preventive therapy [
9]. As a result, the reduction of TB related deaths among people living with HIV has slowed in recent years.
Since epidemiological and mathematical models play fundamental role in the study of the dynamics of such diseases, various models have been used to investigate the transmission dynamics and treatment strategy of different infectious diseases such as TB and HIV/AIDS. One of the classical models to describe the transmission dynamics of TB was formulated in 1962 by Waaler et al. [
10]. They used a particular linear function to model infection rates. In this model, the equation for the latent and infectious classes were assumed to be uncoupled with the equation for the susceptible class. Following this and by modifying some part of the model structure, a lot of mathematical models have been developed and analyzed for TB (drug sensitive and drug resistant) disease transmission [
10,
11,
12,
13,
14,
15]. Multi-drug resistance (MDR) TB strain has also been developed in the course of time partly due to the mismanagement in the treatment of TB patients. This includes wrong diagnosis and delayed diagnosis, wrong or interrupted treatment, and the misuse of TB drugs [
4,
16]. Hence, mathematical models (such as [
11,
12,
15]) that include multiple strain of TB have been used to study the effect of these new strains. A two strain model is formulated and mathematically analyzed by Castillo- Chavez and Feng [
15]. In this model, the drug resistant strain is assumed to be not treatable; latently infected, infectious and treated individuals are assumed to be re-infected with the drug resistant strain. However, the model did not take into account long and variable periods of latency as well as the role of preventive education for the society. Another mathematical model to study a two strain TB infection that include diagnosis, treatment and health education as an intervention mechanism is proposed by Maliyani et al. [
17]. In the study of this model, it is indicated that diagnosis of the MDR-TB strain has a major impact in the eradication of drug sensitive TB and in the reduction of MDR-TB.
The role of vaccination at birth and behavior change through education in a two age group TB model in the presence of medical treatment was investigated by Awoke T.D. and Kassa S.M. [
3]. The authors used optimal control theory to propose a cost effective strategy for intervention in reducing the burden of the drug sensitive TB in the population. Moreover, it is shown that in addition to vaccination and medical treatment, behavior change through education about the preventive mechanisms of the disease have significant impact to reduce the burden of the disease.
Different researchers have also studied the dynamics of HIV/AIDS disease transmission (see for example, [
18,
19,
20,
21]). Since proper HIV/AIDS medical treatment could decrease not only HIV prevalence but also TB notification rate, different researchers have developed a two strain TB-HIV/AIDS co-infection model and studied the dynamics of such a model (see for instance, [
9,
22,
23,
24,
25,
26,
27,
28]). However, the mathematical analysis of these models remain challenging as the transmission modes are very different.
Due to the role of optimal control theory to determine the best intervention control strategy with minimum aggregate cost of intervention, Silva et al. [
9] and Agusto et al. [
27] studied TB-HIV/AIDS co-infection model. From their optimal control simulations they came up independently with a result that treating co-infected individuals at optimal level can decrease the prevalence of the disease in addition to case finding and case holding strategies. However, the model in [
9,
27] assume that human behaviour remains constant, and hence the contact rates of the population remain unchanged while the disease progressed even if the size of the epidemics grows. However, it is well known that human behaviour changes as the burden of the disease increases [
29]. Moreover, preventive education and the participation of the population in reducing their risky behaviour are well accepted public health strategy in combating communicable diseases. Therefore, it is necessary to include in the model both preventive mechanisms as well as treatment interventions and study the effect.
In this paper, we introduce the behaviour change function in to the TB-HIV/AIDS co-infection model and analyze the model. We will also study the mathematical control analysis of the model to propose an optimal control strategy for the public health planning in combating the two diseases. The current model aims to answer specific questions about the likely impact of change of behaviour by individuals on the burden of TB-HIV/AIDS co-infection in a hypothetical population.
The paper is organized as follows: in
Section 2 we give the description of the model and analyze the model mathematically. In
Section 3, we formulate the control problem for the model and apply the mathematical control analysis to find the necessary conditions for the optimal controls. Some numerical simulations are shown in
Section 4 to illustrate the trajectory of the subpopulation in the dynamics when various combination of controls are applied. The paper is then concluded with some conclusive remarks in
Section 5.
2. Mathematical Model with Behavior Change and Treatment
We modified the usual TB-HIV co-infection model (for example the one in [
9]) by introducing two additional cohorts,
which represents the section of the population that decided to use any of the available preventive mechanisms against TB infection, and
which represents the section of the population that uses any of the mechanisms that prevent or reduce the risk of infection by HIV. The population in each of these two cohorts are assumed to enjoy a reduced susceptibility against the infection of the corresponding disease. Therefore, the total population at time
t, is divided into the following epidemiological subgroups:
, Susceptible individuals;
, Educated individuals about TB;
, individuals infected with TB in latent stage;
, TB-infected individuals who have active TB disease and are infectious;
, Successfully treated with TB;
, Educated individuals about HIV/AIDS ;
, HIV-infected individuals with no clinical symptoms of AIDS;
, TB-latent individuals co-infected with HIV;
, HIV-infected individuals (pre-AIDS) co-infected with active TB disease;
, HIV-infected individuals under treatment for HIV infection;
, HIV-infected individuals with AIDS clinical symptoms;
, HIV-infected individuals with AIDS symptoms and co-infected with active TB;
, TB-recovered individuals with HIV-infection without AIDS symptoms.
The total population at time
t, denoted by
, is given by
. The Susceptible population is increased by the recruitment of individuals (assumed susceptible) into the population at a rate
. Susceptible individuals acquire TB infection from individuals with active TB at a variable rate
, which is given by,
where,
is the effective transmission rate for TB infection. Similarly, susceptible individuals acquire HIV infection at a variable rate
, given by
where
is the effective transmission rate for HIV. The modification parameter
accounts for the relative infectiousness of individuals with AIDS symptoms, in comparison to those infected with HIV with no AIDS symptoms. Individuals with AIDS symptoms are more infectious than HIV-infected individuals (pre-AIDS) because they have a higher viral load and there is a positive correlation between viral load and infectiousness [
30]. On the other hand,
accounts to the partial restoration of the immune function of individuals with HIV infection that use correctly ART [
31].
Only approximately
of infected people with
Mycobacterium tuberculosis are considered to develop active TB disease. While the rest (approximately
) of infected people will develop latent TB disease [
4]. Hence, if a fraction
g of infected people develop latent TB, then the remaining
proportion of infected population will develop or progress to the stage of active TB disease and suffer from the additional disease induced death at a rate of
. Latently infected individuals progress to the
class due to the presence of reactivation at a rate
b or due to reinfection at a rate of
k.
When the risk of the disease in the population increases, people may get more awareness about the disease and they may apply different self-protective measures. This will affect the contact rate per unit of time, by decreasing the incidence rate of the disease. Therefore, behavior change through awareness creation is important in fighting against the disease. If we add an ‘educated’ compartment (
or
) into the usual SIR model, it is possible to observe that individuals in educated class are exposed to the infection with a rate smaller than other susceptible individuals. However, the recruitment rate into educated classes vary through time corresponding to the total proportion of people affected by the disease. This recruitment function describes the learning effect of population which can be measured indirectly by observing behavior modification of individuals towards their exposedness to the disease [
29]. The behavior change function (
) is assumed to be described as a function of the prevalence
of the disease at any time
t. At the beginning of the outbreak, normally people understand very little about the disease and the reaction could be almost none whereas at high prevalence some susceptible individuals will change their behavior and start applying any of the possible self protective measures to reduce the risk of any possible infection. This implies that
and
. Here, self-protective measures for TB and HIV may be any of the following. Applying any of the existing protective measures against HIV infection (from abstinence to using self-protective devices, such as condoms) similarly for TB infection, one may apply any of the protective measures, like opening windows of public transport vehicles while in use, keeping the rooms used by infected individuals ventilated, advising and helping a friend or a family member who shows some symptoms of TB to be diagnosed at a health center, separating the nutritional equipments of infectious individuals and using gloves in the case of helping them in cleaning their sputum, and wearing appropriate masks while meeting people who are possibly infectious.
Therefore, we can describe the two behaviour change functions as
and
where
and
are the prevalence producing half of the maximum behavioral change value of TB and HIV respectively;
and
represent the force of infection for TB and HIV respectively with
and
;
n is a hill coefficient that portrays the rate of reaction by the population and
is the saturation level of
e (which we took it to be one in this context). If we denote by
the mean education rate at which susceptible individuals receive a convincing message about TB to move into the educated class per unit of time,
will give us the actual recruitment rate to the cohort of TB educated class from the susceptible class. Similarly if
is the counterpart of
for the HIV educated cohort,
will give us the actual recruitment rate to the cohort of HIV/AIDS educated class from the susceptible class.
However, every protective measure may not be absolutely effective due to the choice of different measures taken by the population with varying coefficients of effectiveness. If we denote the average effectiveness of all existing self protective measures for TB disease by , then will be the average failure of self-protective measures for TB. Hence, we assumed that individuals in the TB educated class may be infected with TB only due to the failure of existing self-protective measures. Similarly, if we denote the average effectiveness of all existing self protective measures about HIV/AIDS by , then will represent the average failure of self-protective measures for HIV, and we assumed that individuals in class get infected by HIV only due to the failure of the self-protective measures.
Educated individuals about HIV/AIDS in the class may be well informed about HIV/AIDS disease transmission, symptoms and their mode of transmission but they may not have the required information about preventive, control and treatment mechanisms of the TB disease in its full form. Then proportion () of individuals from class may contract TB infection and join the latent stage (). Therefore, it is assumed that individuals in the HIV/AIDS class may be infected with TB like any of the individuals in other epidemiological classes but with a reduced rate. Similarly, those in the class may also get infected with HIV, but with a reduced rate of (). For simplicity of the analysis, it is assumed that there is no intersection between the class of and the class of .
We assume that TB treated or recovered individuals
acquire partial immunity and hence their rate of infection is reduced by
with
. Individuals with active TB disease suffer from additional TB-induced death rate of
. On the other hand, since individuals who are infected by active TB,
, are more susceptible to HIV infection, it is assumed that they get infected at a rate of
, where the modification parameter
accounts for higher probability of individuals in class
to become HIV positive. HIV infected individuals with (no AIDS symptoms) progress to the AIDS class
at a rate of
. HIV infected individuals with AIDS symptoms are treated for HIV at a rate of
and suffer from additional AIDS-induced death rate of
. Individuals in the class
are also susceptible to TB infection at a rate
, where
is a modification parameter depicting the fact that HIV infection is a driver of TB epidemic [
32]. HIV infected individuals (pre-AIDS) could be co-infected by TB disease and are assumed to join the active stage
. A fraction
r of
individuals are assumed to receive simultaneously TB and HIV treatments at a rate of
p and hence they will get cured from TB but remain in
. Moreover, assume that there are a fraction
of
individuals who show symptoms of TB but are not diagnosed for HIV. These individuals will be recruited at a rate of
to receive only TB treatment. Individuals in the class
that do not take any of the TB or HIV treatments are assumed to progress to the class
at a rate of
, and suffer from the additional TB-HIV/AIDS induced death rate of
. Moreover, a fraction
from the class of
are also assumed to recover from TB. Individuals in the class
are assumed to be more likely to progress to active TB disease either due to reactivation at a rate of
or through reinfection at a rate of
. Similarly, HIV infection make individuals more susceptible to TB reinfection when compared to non HIV positive individuals. The modification parameter associated to the TB reinfection rate, for individuals in the class of
, is taken to be
with
. Individuals in this class are assumed to progress to class
at a constant rate of
. In addition, people in the classes of
and
are recruited to receive ART in the same rate as those in
. However, individuals in AIDS group (
) are assumed to receive ART at a rate of
and those who are co-infected with TB (
) are also recruited at a rate of
to receive treatments for both HIV/AIDS and TB and then progress to the
class. The description of the parameter used in the model is given in
Table 1.
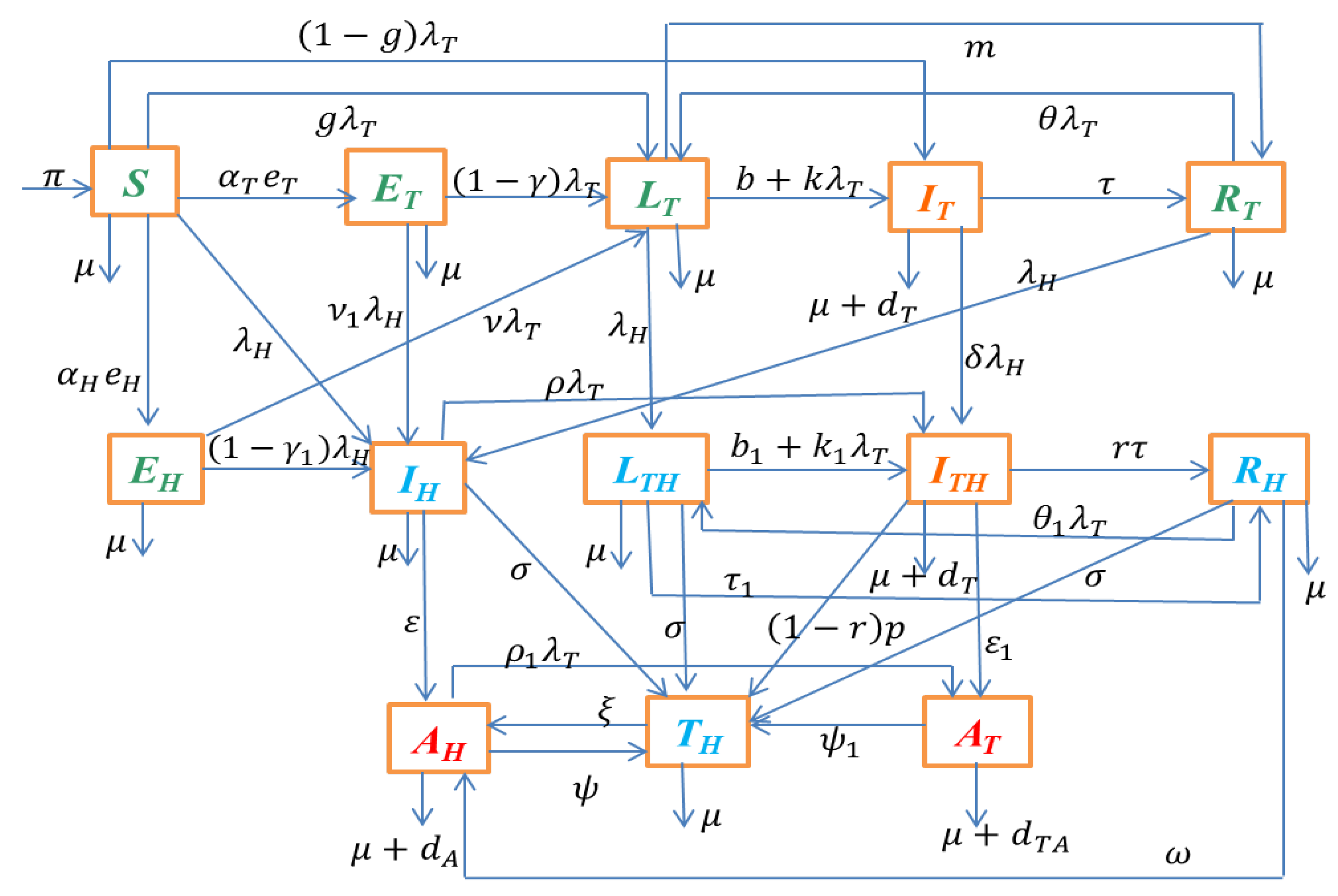
With the above assumptions and description of the model variables, the TB-HIV co-infection dynamics, whose schematic diagram is given in
Figure 1, can be described by the following deterministic system of non-linear ODE:
where,
| | |
| | |
| | |
2.1. Positivity and Boundedness of Solutions
For the TB-HIV/AIDS co-infection model system (
3) to be epidemiologically meaningful, it is important to analyze that all its state variables are non-negative at all times. In other words, solutions of the model system (
3) with non-negative initial data will remain non-negative for all time
.
Indeed, since the model (
3) considers human populations, all the variables and parameters of the model are non-negative. Then consider the following biological feasible region.
We establish in the following the positive invariance of
(i.e., all solutions in
remain in
at all times). The rate of change of total population, which is obtained by adding all the equations in the model system (
3), is given by
It is simple to observe that for
,
. Using the Standard Comparison Theorem [
33], it is possible to show the boundedness of
as follows.
Therefore, from this last inequality it follows that
Then, if
, we get
for all
. That means, the model system (
3) can be considered as bieng epidemiologically and mathematically well posed [
34]. Therefore, every solution of the model system (
3) with initial conditions in
remains there for
. This result can be summarized in the following Lemma.
Lemma 1. The region Ω
is positively invariant for the model system (3) with non-negative conditions in , where represents the non-negative orthant of the 13-dimensional real space . 2.2. Analysis of the Sub-Models
In this section, we analyze the models for HIV only (in the absence of TB) and for TB only (in the absence of HIV) separately to draw some conclusions.
2.2.1. TB-Only Model
The sub-model of system (
3) with no HIV/AIDS disease, that is when
, is analyzed as follows.
where,
and
.
Analogous to Lemma 1 we can prove that is positively invariant and attracting. Thus, the dynamics of TB only model will be considered in .
2.2.2. Local Stability of Disease Free Equilibrium
The model subsystem (
5) has a disease free equilibrium (DFE), obtained by setting the right hand side of the equations in the model to zero in the absence of TB infection, is given by
. The local stability of
can be established using the next-generation operator method on the system (
5).
Definition 1. The basic reproduction number, basic reproduction ratio or basic reproductive rate is defined as the average number of secondary infections that occur when one infective is introduced into a completely susceptible host populatio [35]. We can calculate the basic reproduction ratio(number),
, using the next generation approach proposed by van den Driesseche and Watmough [
36]. According to this approach, in order to compute the basic reproduction number, it is important to distinguish new infections from all other class transitions in the population. The infected classes are
and
. We can write system (
5) as:
,
, where
).
is the rate of appearance of new infection in each class,
is the rate of transfer into each class by all other means, and
is the rate of transfer of the infectious individuals out of each class.
Using system of differential equations below (where the underlined terms represent the new infections in each class),
the associated matrices,
for the new infection terms, and
for the remaining transition terms are respectively given by,
Evaluating the partial derivatives of (
6) at
and bearing in mind that system (
3) has two TB only infected classes, namely
and
, we obtain
Similarly, partial differentiation of (
7) with respect to
and
at
gives
The basic reproduction number of TB only sub-model is defined, following van den Driessche and Watmough [
36], as the spectral radius of the next generation matrix,
and it is given by:
Therefore, we have the following conclusion from [
36].
Lemma 2. The disease free equilibrium (DFE) of the TB-only model system (5) is locally asymptotically stable (LAS) if and unstable if . The threshold quantity is the reproduction number for TB and it measures the average number of new TB infections generated by a single TB-infected individual in a population where a certain fraction of infected individuals are treated.
2.2.3. HIV-Only Model
The sub-model of (
3) with no TB disease, that is when (
), is analyzed as follows.
where,
and
.
Analogous to Lemma 2, we can prove that is positively invariant and attracting. Thus, the dynamics of HIV only model will be considered in .
2.2.4. Local Stability of Disease Free Equilibrium
The model subsystem (
9) has a DFE, obtained by setting the right hand side of the equations in the model zero and in the absence of HIV infection is given by
. The local stability of
can be established using the next-generation operator method on the system (
9). Using a similar procedure as in the previous subsection on the subsystem:
the associated matrices,
for the new infection terms, and
for the remaining transition terms are respectively given by,
Evaluating the partial derivatives of (
11) at
and bearing in mind that system (
3) has three HIV/AIDS only infected classes, namely
,
and
, we obtain
Similarly, partial differentiation of (
12) with respect to
,
and
at
gives
The basic reproduction number of HIV/AIDS only sub-model is defined, following van den Driessche and Watmough [
36], as the spectral radius of the next generation matrix,
and it is given by:
where,
, and
The basic reproduction number represents the expected average number of new HIV infections produced by a single HIV-infected individual when in contact with a completely susceptible population.
2.3. Analysis of the Full Model
Consider now the full model (
3), with DFE given by
Using the same procedure like in
Section 2.2.1 to calculate basic reproduction number, the associated matrices
and
can be determined as below. Here the underlined terms are new infections in each class.
The associated matrices
for new infections terms, and
for the remaining transition terms are respectively given by
Evaluating the partial derivatives of (
15) at
and bearing in mind that system (
14) has nine infected classes, namely
and
, we obtain
Similarly, partial differentiation of (
16) with respect to
and
at
gives
Then, following van den Driessche and Watmough [
36], the basic reproduction number is given by the spectral radius of the next generation matrix. Then, the dominant eigenvalues of the matrix
are,
where,
,
, and
Thus, the basic reproduction number
of the model (
3) is given by
Lemma 3. Suppose the disease transmission of the full model is given by (3). If is a DFE of the model, then is locally asymptotically stable if and unstable otherwise, where is the reproduction number defined in (17). 3. Formulation of the Control
The possible interventions for TB and HIV/AIDS co-infection can be categorized as (1) applying preventive education and (2) treatment of infected individuals. In the following we will describe what specific control measures can be taken corresponding to each of the two intervention categories.
After applying all these four control functions described above in to the model system, the corresponding system of differential equation can be written as follows.
where,
For all , , , . The total size of population is bounded above by and bounded below by some . Since the state variables are partitions of the total population, the suprimum of the total population is also the suprimum of each of the state variables. This implies that each of the state variables are bounded below by 0 and bounded above by the same bound with the total population.
Thus, with controlled model system (
18) and given initial population size of each compartment to be
and
,
our main goal in this work is to find or propose the best strategy in terms of either in combination or independent efforts of preventive education and treatment that will minimize the total number of new infections and the total number of people that die due to the two infectious diseases (TB and HIV) in the planning period while at the same time also minimizing the total cost of interventions. We considered the optimal control problem with a fixed terminal time problem because most governments cannot continue the implementation of the interventions indefinitely; rather they may choose a program that the disease is eradicated or is driven below specified level within a set time frame.
If we are given the initial value for the populations size of each cohort to be
and the control trajectory, i.e., the values of
over the whole time interval
, then we can integrate (
18) to get the state trajectory, i.e., the values of
and
, over the same time interval. We want to choose the control trajectory so that the control and the corresponding state trajectories minimize the objective cost function, or simply the objective function which is given by.
where the constants
,
,
,
,
,
,
and
can be considered as values that will balance the units of measurement and also may indicate the importance of one type of intervention over the other.
,
,
,
and
represent the cost on the population of actively infected individuals with TB, that of HIV infected individuals with no clinical symptoms of AIDS, that of TB infected individuals who are also co-infected with HIV, and that of individuals who progressed to AIDS stage respectively. Moreover, the terms
and
represent the cost of individual treatment for TB and HIV respectively, where as
represent the cost of producing and administering educational materials about TB, about HIV, and the cost of production and administration of treatment for TB patients, and for HIV/AIDS patients respectively. The treatment cost may include the cost of the medical tests and diagnosis, drug cost, hospitalization cost and the like. However, the cost of initial investment for the educational materials and pharmaceutical drugs as well as their administrative costs are not linearly related with the number of individuals persuaded or treated. The variables in this part are squared to amplify the effects of large variations and to de-emphasize contributions of small variations. Since implementation of any public health intervention has increasing costs with reaching higher fraction of the population, we took a quadratic cost function to represent this situation. On the the other hand the unit cost of drugs used for treatment depends linearly with the number of units applied (or number of people treated), hence we used the linear cost to capture this fact.
So we seek to find optimal controls
such that
where
Existence and Characterization of Optimal Control Solution
Theorem 1 (Existence of optimal control solution).
There exists an optimal control and corresponding solutions and to the state initial value problem (18)–(20) that minimizes over . Proof. The non trivial requirements on the set of admissible controls and on the set of end conditions are verified by Fleming and Rishel’s theorem.
- A.
The set of all solutions to system (
18)–(
20) with corresponding control functions in
is non-empty.
- B.
The state system can be written as a linear function of the control variables with coefficients dependent on time and the state variables.
- C.
The integrand
L in (
19) from objective functional with
is convex on
, and additionally it satisfies
where
and
.
In order to establish condition A, we refer to Picard-Lindelöf’s theorem from [
38,
39]. If the solutions to the state equations are bounded and if the state equations are continuous and Lipschitz in the state variables, then there is a unique solution corresponding to every admissible control
.
It is indicated that the total population is bounded below by a positive nonzero number
and bounded above by
as well as each of the state variables are bounded. With the bounds established above, it follows that the state system is continuous and bounded. It is equally direct to show the boundedness of the partial derivatives with respect to the state variables in the state system, which establishes that the system is Lipschitz with respect to the state variables (see [
40]). This completes the proof that condition A holds.
Condition B is verified by observing the linear dependence of the state equations on controls
and
. Finally, to verify condition C by definition from [
41,
42] any constant, linear and quadratic functions are convex. Therefore,
is convex on
. To prove the bound on the
L we note that by the definition of
, we have
☐
The necessary conditions that an optimal solution must satisfy come from Pontryagin’s maximum principle (PMP). This principle converts (
18)–(
20) in to a problem of minimizing a Hamiltonian,
H, with respect to
together with the state equation and the adjoint condition. Here, the Hamiltonian is given by
where, the
’s represent the right hand side of the differential equation of the
ith state variable in system (
18),
,
and
.
If is an optimal control vector for the problem (which is yet to be determined), then from Pontryagin’s Maximum Principle we have the following conditions:
Optimality Conditions:
The first conditions that we will consider from the Pontryagin’s Maximum principle is the minimization of the Hamiltonian H with respect to the control variables, . Since the cost function is convex, if the optimal control occurs in the interior region we must have . Therefore,
- (i)
for the control
we must have,
- (ii)
for the control
we must have
- (iii)
for the control
we must have
- (iv)
Similarly, for the control
we must have
And therefore, the optimal controls on the given bounded intervals are given by
The adjoint (co-state) equations:
From the second condition of the Pontryagin’s Maximum Principle, we must have at the optimal controls for each .
Therefore, we need to calculate and solve the system,
together with the transversality conditions,
Solving the above two conditions together with the state equation (equation system (
18)) gives us the required optimal solution and the corresponding state variables.
4. Numerical Simulation and Results
In this section we shall carry out simulations to demonstrate the output of optimal control values and the corresponding impacts on the dynamics of the disease by varying some of the parameter values. In addition, we will also consider the what if analysis on the system when some of the controls are missing and when all of the controls are being used.
We estimate the results by using fourth order Runge-Kutta method in solving the state equation system (
18), and the adjoint (or co-state) equation system (
23), together with the optimality Equation (
22).
The process begins with an initial guess on the control variables. Then, the state equations are simultaneously solved forward in time starting from the initial conditions and the adjoint equations are solved backward in time starting from the transversality conditions (
24). The control is updated by inserting the new values of the state and adjoint vectors into its characterization (Equation (
22)), and the process is repeated until convergence occurs.
We used fixed final time
years and the initial conditions are estimated as follows. We assumed that more than half of the population (55%) belongs to the subgroup of susceptible class (
16,500) and that a big percentage about 31% is infected with TB in latent stage (i.e.,
. This is justified from the fact that “about one third of the world’s population has latent TB”, as it is indicated from the webpage of the World Health Organization (WHO [
5]). The value for the fraction of people infected with HIV is assumed to be about 4.17% (
based on HIV and AIDS information from AVERT.org [
8]. We also assumed that there is very little information about the disease in the population; and hence only 0.2% is educated about TB preventions (i.e.,
) and only about 0.27% is educated about HIV preventions (i.e.,
). Other initial values of the sub-populations are assumed for numerical purpose to be as below.
,
,
.
The constants in the cost functional are taken as follows: coefficients for cost of infection are , coefficients for cost of individual treatment are , and coefficients for cost of production and administering the control efforts are . These constants can also serve as values that balance the different measure of quantities in the sum and may also indicate the level of importance of one of the control type over the other.
Therefore, using the parameter values from
Table 2 and the above initial population data the state system evolves according to the trajectories indicated in
Figure 2.
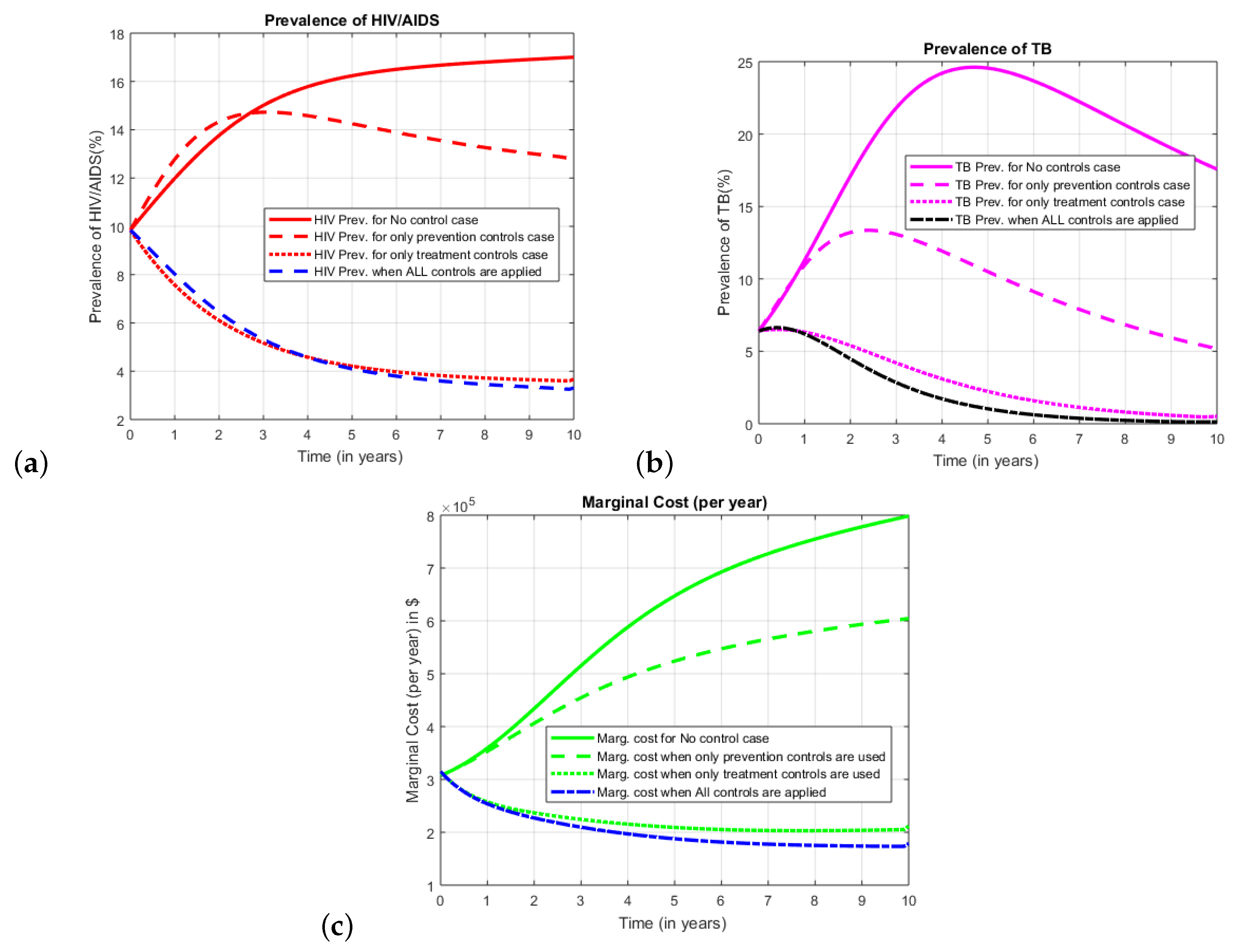
The result of using various control mechanisms can be summarized from the graph of prevalence (in
Figure 3a,b) and the graph of the corresponding marginal cost functions (in
Figure 3c). In the simulation, we first integrated the system without any control values. The second phase is to optimize the objective function
by using only the prevention controls (
and
) and then using only the treatment controls (
and
), finally using all the controls together. As can be seen from the graph, when all the interventions are applied simultaneously the gain in prevalence is significant in both diseases with very less total cost as compared to other combinations. Treatment is more effective as compared to the prevention controls. However, the combination of both preventive and treatment controls yields in less aggregate cost, with a slight gain also in the prevalence of both diseases.
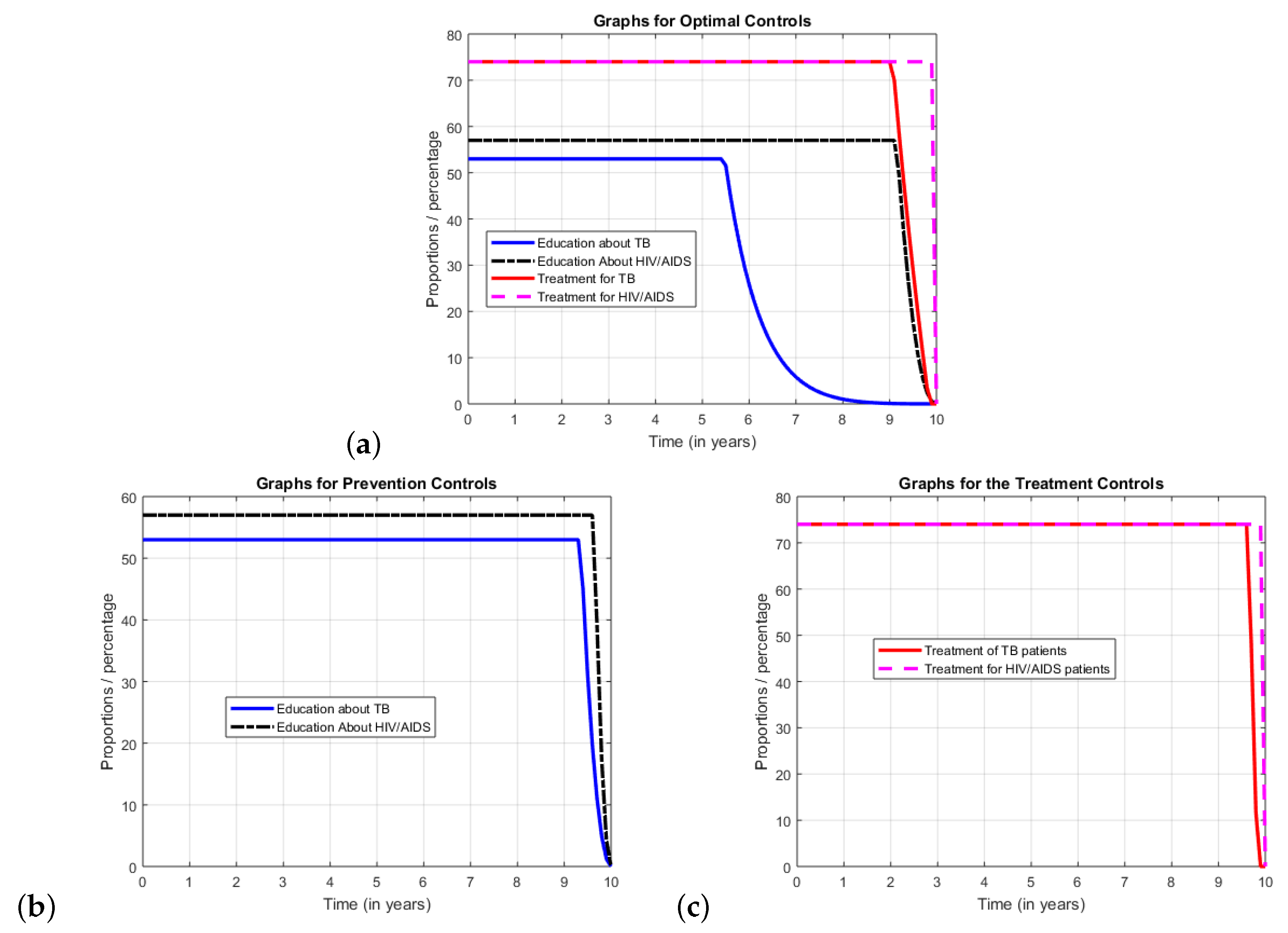
In the strategy where all the controls are being applied concurrently, it it is optimal to apply all available resources to each of the control measures at the initial stage of the planning period. However, since our objective is to minimize the total aggregate cost of the population, it is optimal to decrease the intensity of the effort for educating people to apply all possible prevention methods against TB after nearly 4 years. Then, after nearly 9 years the effort on HIV education and on recruiting additional people for TB treatment can be reduced. However, giving treatment for HIV positive individuals should continue in its full intensity until the end of the planning period (see
Figure 4a. On the other hand when either only prevention or only treatment controls are applied, one has to apply all the corresponding control measures at their full scale in the entire planning period (see graphs (b) and (c) in
Figure 4). We observe that the result obtained when only treatment controls are applied is similar to the result reported in [
9].
It can be seen from the results in the prevalence and marginal cost that it is optimal to include the preventive educational efforts in the control strategy. Otherwise, apply treatment control with all its full intensity could be costly for the authorities. In addition, applying the optimal control strategy reduces the burden of the two diseases to a level that they are unrecognizable in the society within 10 years. The trajectories for all the sub-populations in course of the optimal control strategy is shown in
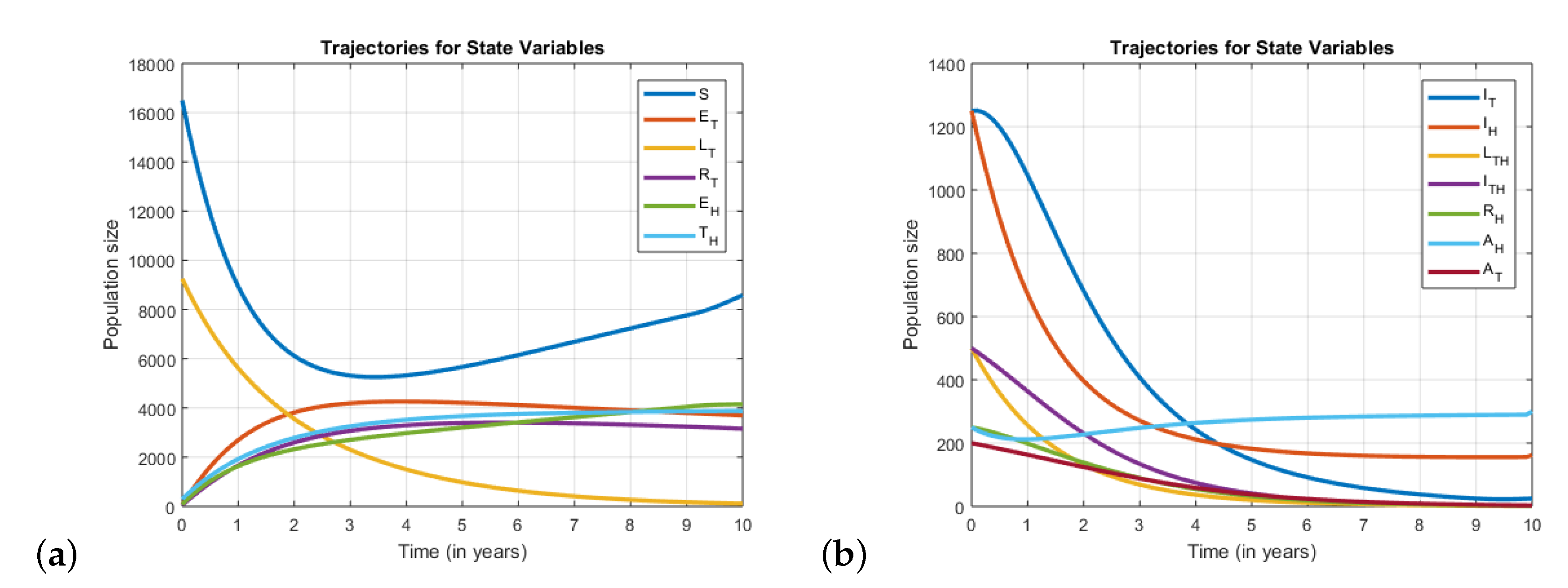
Figure 5.
When all controls are applied the size of the subpopulation under infection reduce significantly. Some of them, especially those related to TB decrease to values very close to zero. However, those values related to HIV/AIDS only cases may still remain high as compared to the TB case counterparts. This could be explained due to the fact that the treatment for TB makes the infected individuals recover from infection and their effect is seen within 6 months. However, the treatment for HIV does not make individuals fully non-infectious and the impact is seen in a longer time period. In addition, when only preventive controls are used the impact seems negligible or non at the beginning but one get a significant effect after a while. This could justified that preventive actions will make difference on the general population not immediately but at a latter stage. At the beginning even the prevalence increases slightly as there is no additional treatment regiment for those newly infected.