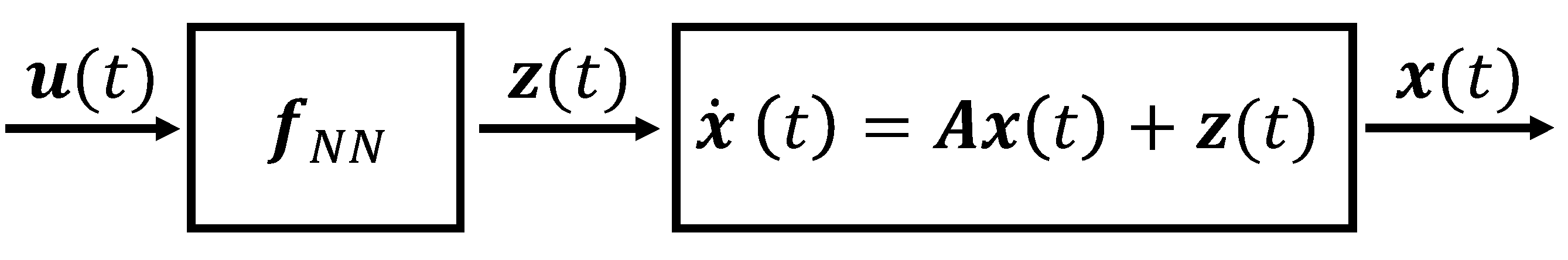1. Introduction
The industrial continuous production of complex fluids still encounters to date issues in terms of quality control of products. Parameters like shear rate dependent viscosity, which affects product quality, could easily go out of specifications if the ingredient characteristics or other variables of the process move away from the original formulation. The main issue is represented by the difficulty of controlling such processes because there aren’t commercial sensors capable of providing real-time information about the rheological properties of the fluid. Available in-line sensors can measure the viscosity only for a punctual shear rate value, therefore their use for controlling the production process of non-Newtonian fluid is not possible. Furthermore, very few in-line rheometers have been tested and few studies have been presented for non-Newtonian and opaque industrial fluids [
1].
Because of the importance of the continuous monitoring of rheological parameters of industrial fluids during production, in the last years many steps have been accomplished for designing and developing sensors capable of providing rheological proprieties of complex fluids in real-time. Many recent works focus their efforts on non-invasive techniques which seem the most promising for this type of problems. Kotzé et al. [
2] studied a technique based on ultrasonic velocity profiling (UVP) which measures an instantaneous one-dimensional velocity profile in a fluid containing particles across the ultrasonic beam axis or measurement line. The method combines the UVP technique with pressure difference (PD) measurements, it is non-invasive, it can be used to measure opaque and concentrated suspensions. Preliminary results obtained in concentrated cement pastes showed that UVP is a feasible and promising technique for flow characterisation in viscous fluids. Meacci et al. [
1] presented an efficient, fully programmable and integrated system for in-line fluids characterisation of a wide range of non-Newtonian and opaque fluids. This system, named Flow-Viz exploits ultrasounds to detect the velocity profile of the flow moving in the pipe, and it is designed for industrial use. Recently, Yoshida et al. [
3] proposed a sensor based on ultrasonic spinning rheometry (USR), which is expected to provide details of various rheological properties. The proposed USR capabilities were assessed for three test fluids chosen as examples of thixotropic fluids, shear-thinning fluids, and multiphase fluids.
The recent results on innovative sensors encourage the efforts for developing control strategies which provide the target rheological characteristics in the production of non-Newtonian fluids. The present study is aimed to design a controller for the production of a detergent obtained by mixing different ingredients, which should lead to specific rheological and physical properties. The product is characterised by a complex rheological behavior and, in a previous work [
4] the authors developed a one-point control of viscosity curve for the continuous production process, showing how the choice of the point on the viscosity-vs-shear rate curve was crucial for the quality of the product. Results also evidenced that it is possible to partly reject disturbances using only one point as controlled variable, but this configuration was not adequate for the severe specifics required in the plant under investigation. In this situation, a model predictive control (MPC) can improve the performance of the system. MPC can handle non-square system, therefore the two available manipulated inputs can be used to control more than two points on the viscosity-vs-shear rate curve in an efficient way. It is worth noting that the plant under consideration is characterised by high time delay, if compared to the characteristic time of the mixing process, and again the MPC algorithm is effective in this case [
5]. The multivariable control performances have been assessed by simulating the process at different operating conditions, including time delay and measurement noise.
2. Process Description
The production of a detergent on pilot plant scale (facilities made available by the Brussels Innovation Centre in Belgium, BIC) is considered in this work. The product is a compound which contains several ingredients with different rheological properties, obtaining a final mixture with a highly complex rheological behavior. It is important to underline that blends rheology is affected by factors such rheology of single components but also temperature and polydispersity [
6,
7]. Details on the ingredients cannot be reported for confidentiality reasons.
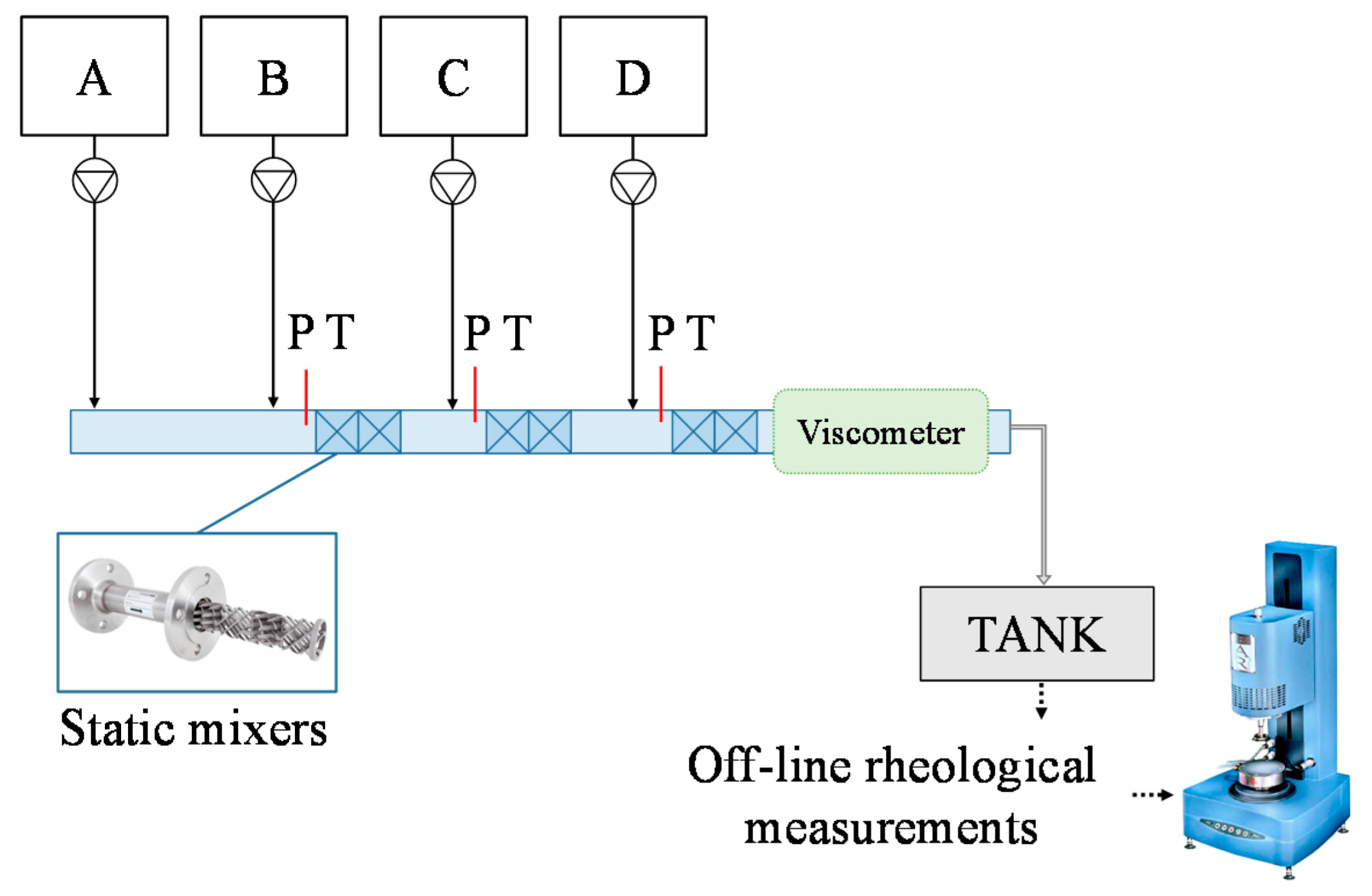
The pilot plant (
Figure 1) is designed as a main pipe connected to a series of tanks, each of them containing one ingredient, through secondary pipes. Ingredients are pumped in the main line and a series of static mixer between inputs ensure a good blending of the mixture. At the end of the line the product is collected in a tank for off-line rheological measurements (for further details see [
8]).
An in-line Endress-Hauser Proline Promass 83I Coriolis flowmeter, located in the main pipe after the 4 inputs of the ingredients, is used to gain information about system dynamics, along with pressure and temperature sensors. Such a flowmeter can provide only a point measurement of viscosity. Such measure is not exhaustive when dealing with non-Newtonian fluids but can provide a rough estimation about dynamics.
Off-line rheological measurements were carried out on the samples collected in the final tank with a rheometer AR-2000 TA stress controlled equipped with a 40 mm cone and plate fixture, used to obtain the viscosity dependence on shear rate.
3. Problem Statement
The quality of the product under study is determined through its rheological properties, which can be summarised by the viscosity-vs-shear rate curve. The rheological properties may deviate from the nominal ones, because of process disturbances, and they can be adjusted by varying the ingredients flow rates which have a major impact without affecting too much detergent characteristics.
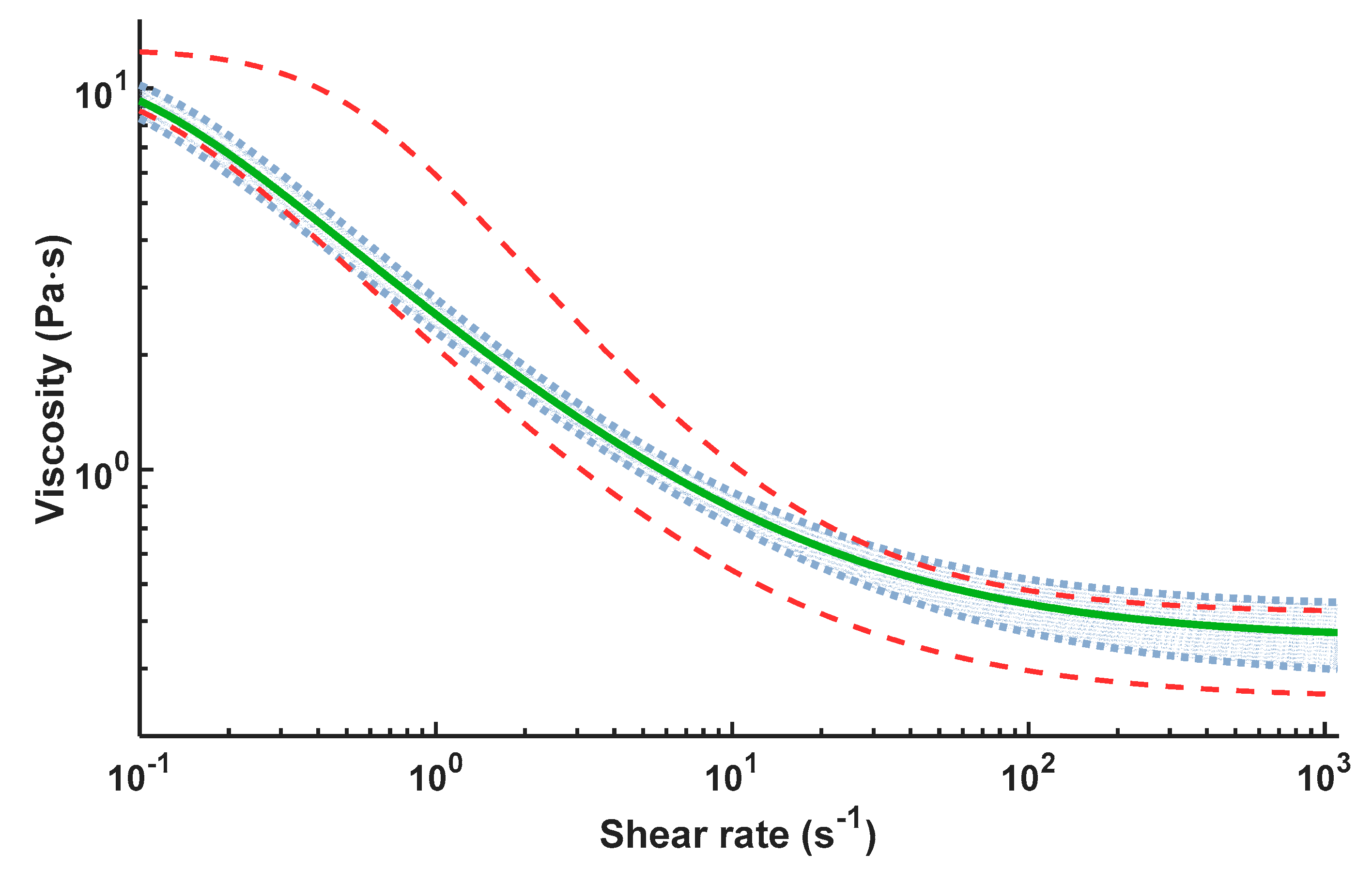
As representative example,
Figure 2 reports a typical viscosity curve for the detergent produced in the plant (schematised in
Figure 1), with a target reported with the green continuous line and the region (grey shaded area) of accepted viscosity values limited by the upper and lower curves. Such region was obtained by considering a maximum error of 10% at low shear rate (lower than 10 s
−1), while 20% has been set at high shear rate. The red dashed lines are two examples of undesired output values, when the process is out-of-control. It is worth noting that the target of the control problem is not a point value but infinite points lying on a one-dimensional manifold (the viscosity curve) and the entire curve should stay within the grey region of allowable viscosity. The main issue is to individuate the points on the curve that guarantee the respect of the limits at every condition in the plant. Based on the previous investigation of the authors [
4], the viscosities (
) of the studied compound at shear-rate (
) values equal to 0.1, 1, 10 and 1100 s
−1 have been selected. Such points are the most representative for the rheological behavior of the considered system.
4. Process Simulator
A process simulator has been developed for designing and evaluating a rheological controller for the continuous production of a detergent. The role of this simulator is to give time responses for the viscosities of the produced compound taking as inputs the ingredient amounts. Because the rheological behavior of the system is very complex, a first principle description of the process is not possible, and a data-driven model has been preferred. The experimental apparatus used in this work cannot give on-line information about the quality of the ingredients which are fed in the plant, meaning that it is only possible to describe the input-output relationship between ingredient flow rates and product’s rheological properties. For model development, several step tests were carried out at different inlet flow rates and plant setup (distance between the last mixer and the sample collection), and the products were analysed analyzed off-line with the rheometer described in the previous section. The rheological information obtained with such tests can be related to steady state conditions. The transient response was on the other hand observed using the data collected with the in-line viscometer (Promass).
A simple description of the data collected in the pilot plant can be attained by means of a continuous-time Hammerstein model [
9], where the nonlinear no-memory gain is calculated with a Neural Network (NN) model [
10,
11]. The time invariant state space representation of a nonlinear continuous-time Hammerstein system (
Figure 3) that cascades a static nonlinearity followed by a linear dynamic system may be described by Equation (1)
where
x is the
n-dimensional state vector,
u is the
m-dimensional input vector,
A is a constant matrix and
fNN indicates the memoryless NN model.
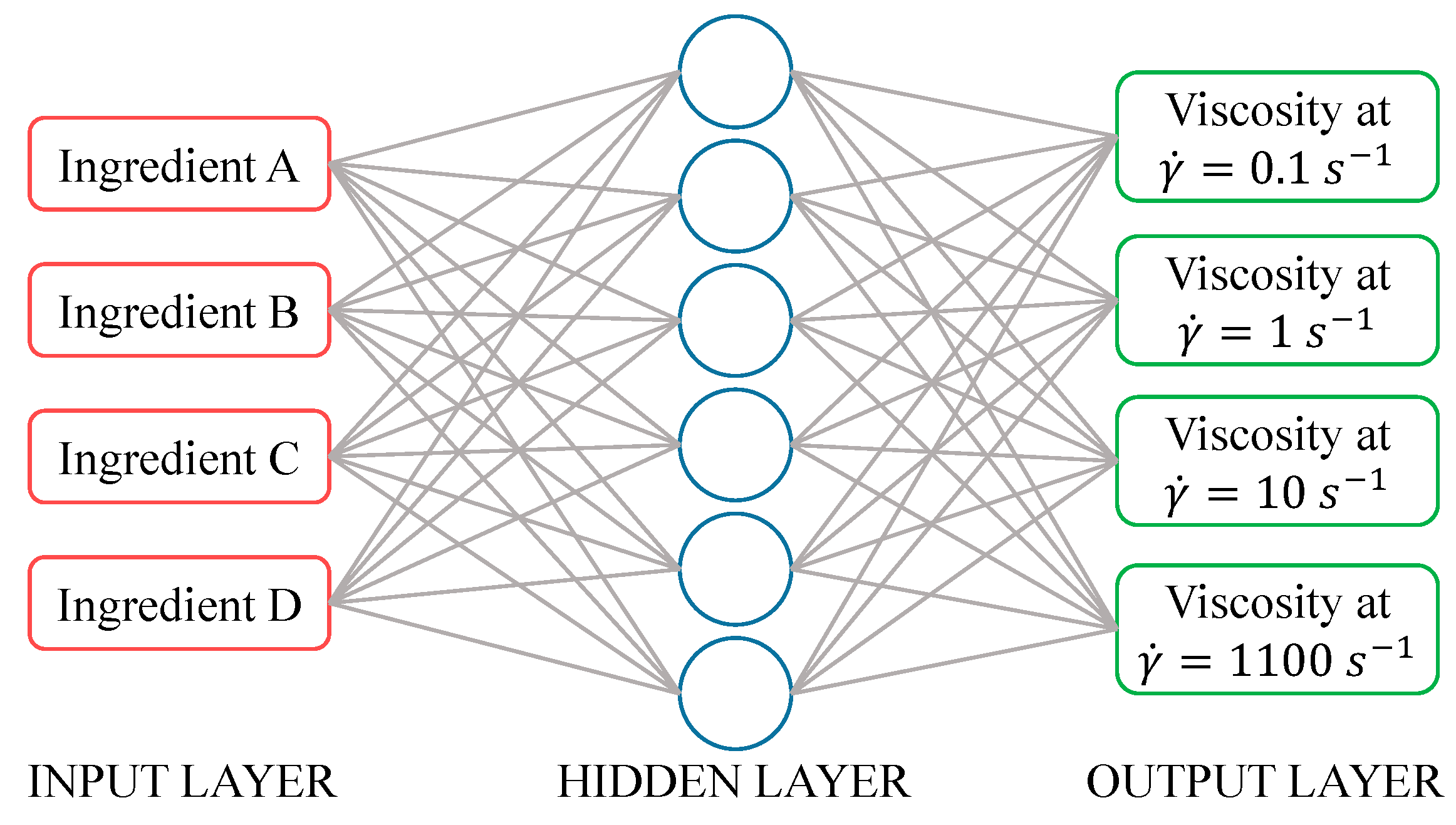
The neural network between the inputs
u and the variable
z on
Figure 3 has been designed and tested to relate viscosities measured off-line at different shear rate values with the inputs of the pilot plant, in terms of ingredient mass fraction in the feed. Mass fractions were chosen instead of mass flows to avoid problems concerning the use of different order of mass flows magnitude. The outputs (
z) are the off-line viscosities (η) of the studied compound at shear-rate (
) values equal to 0.1, 1, 10 and 1100 s
−1, as reported in the previous section. The NN structure is represented in
Figure 4, where it is shown that the input vector consists of four units, the output layer has four neurons and the hidden layer has six neurons. For both the hidden and output layers a sigmoidal activation function is used. The experimental data used for model calibration were obtained varying the percentage of the ingredient flow rates within the interval reported in
Table 1. In more details, 27 different operating conditions were used in the pilot plant and with the repeated experiments allowed the collection of 171 viscosity curves. The model parameter estimation was carried out using 70% of points for the training step, 15% for the validation and 15% for the test.
Model’s performance is evaluated by considering the coefficient
R2 and the mean absolute deviation (MAD) defined in Equation (2), where
yi is the measured viscosity,
fi is the calculated viscosity, is the mean viscosity value and
N is the number of experimental points.
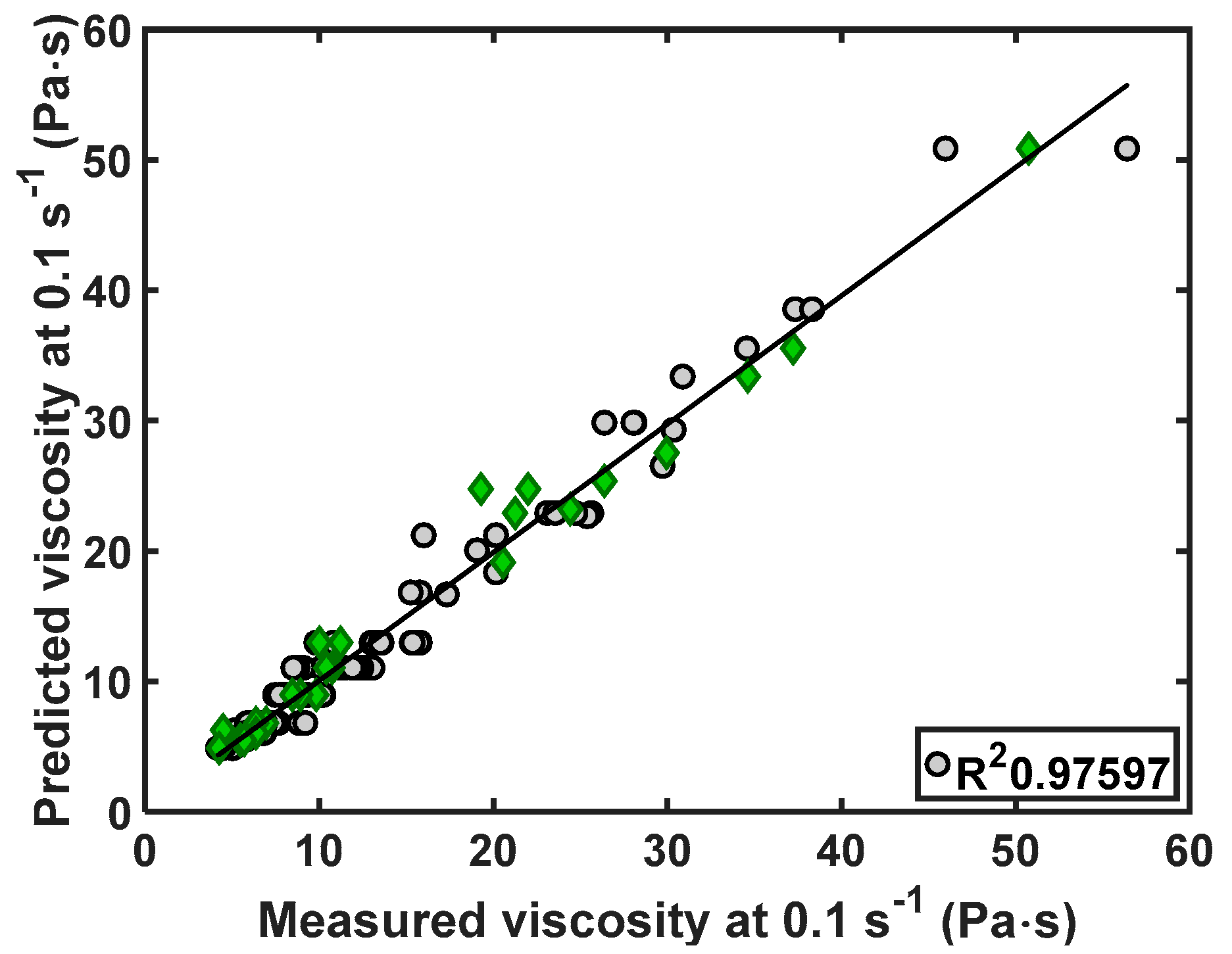
The developed NN is capable to predict viscosities of the compound with good results, as reported in
Table 2, where the performance indexes are shown for the four output variables. Measured viscosities against predicted NN viscosities are reported, by way of example, in
Figure 5 for shear-rate equal to 0.1 s
−1. The test dataset is evidenced in the figure to better evaluate the performance of the model, because in this case the neural model uses data which have not been used during the training/validation step. The obtained results are in the main quite good, but at = 1100 s
−1,
R2 is relatively low (about 0.93) showing some predictability limits of the model. It should be considered that the viscosity variations at high shear-rate value are however rather small (from 0.1 to 0.5 Pa·s). Standard residuals (
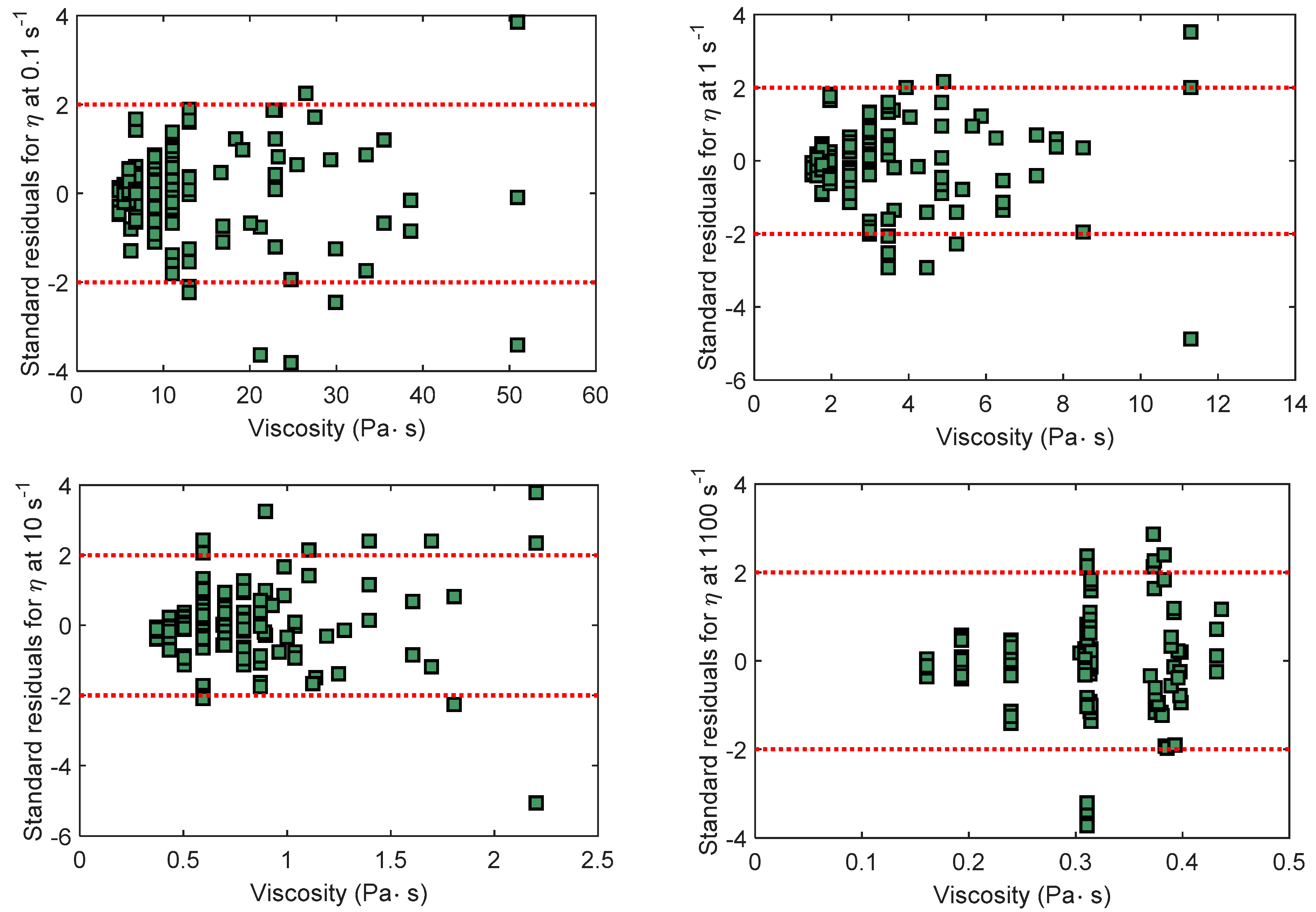
Figure 6) appear without a deterministic structure, indicating that the model captures the essential features of the data and they validate the reliability of the NN to predict the steady state values of off-line viscosities for different amounts of ingredients, at least for the investigated conditions.
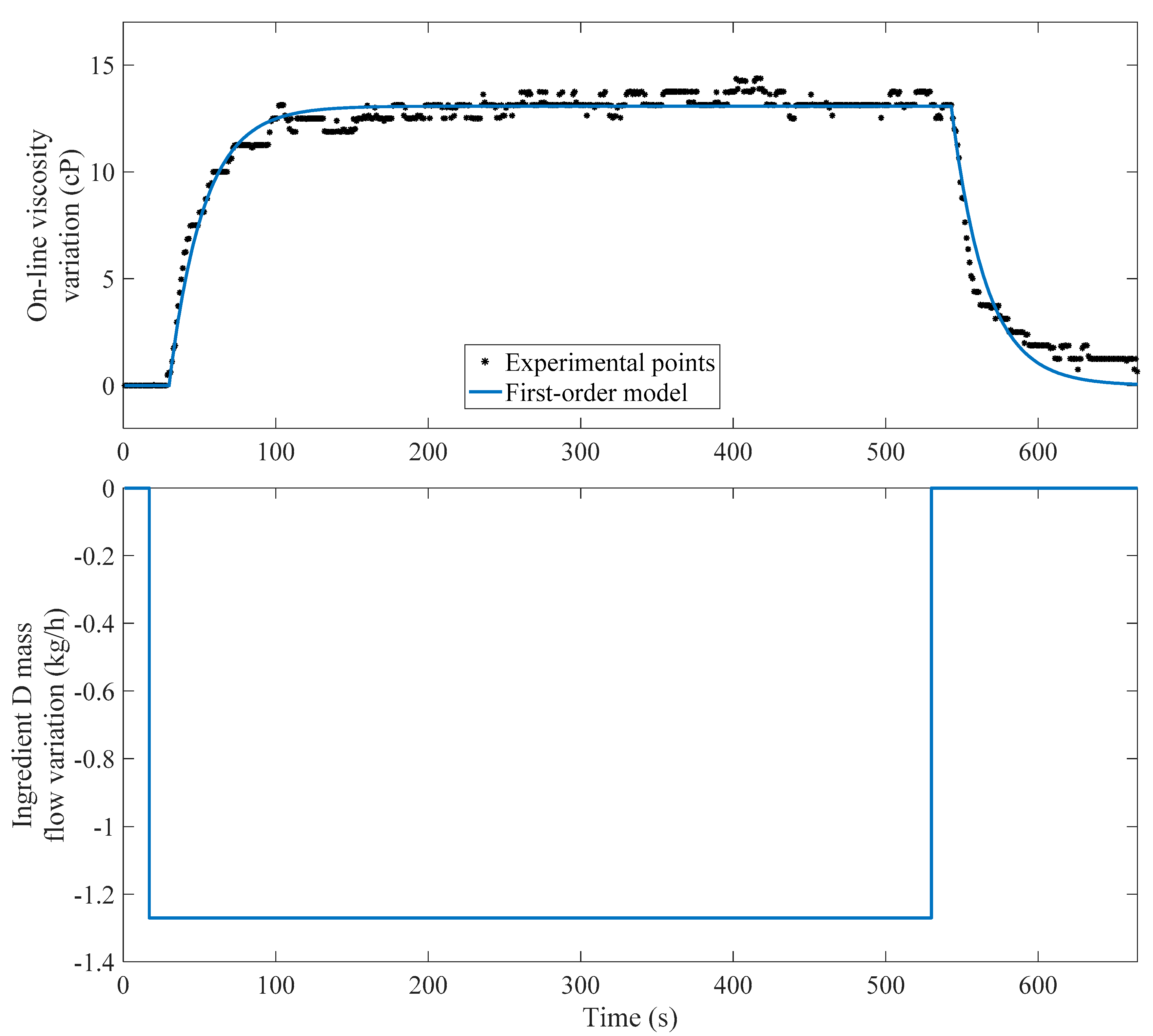
The second block in the Hammerstein model (
Figure 3) describes the dynamic behaviour and it has been obtained using the in-line measurements. Because only a point viscosity is available with Promass, a unique characteristic time is adopted for the four output variables, in the understanding that the rheological changes in the mixture happens at the same moment for each shear rate. By the same token, the time delay is assumed equal for each calculated output. A comparison between the measured viscosity and the one obtained using a first-order plus time delay system is reported in
Figure 7, with the purpose of showing the dynamics assessment. It is worth noticing that it is not possible to compare the viscosity predicted by the NN, calculated offline, and the one of the flowing detergents in the plant, because it is not possible to relate the in-line viscosity given by Promass with the off-line values. This means that a comparison between the model and plant behaviour is possible only when the in-line sensor is available. In this work, the impact of process conditions on the characteristic time is neglected and it is set equal to 20 s. Time delay has been calculated considering one configuration of the plant and it is set equal to 8 s.
5. Control Algorithm
The control problem is addressed using a model predictive control (MPC) in its basic formulation of dynamic matrix control (DMC), where the controlled outputs are selected among the ones given by the simulator. In more details, because the small variations at
= 1100 s
−1 can be challenging for the robustness of the controller [
12] only the viscosities at
= 0.1, 1 and 10 s
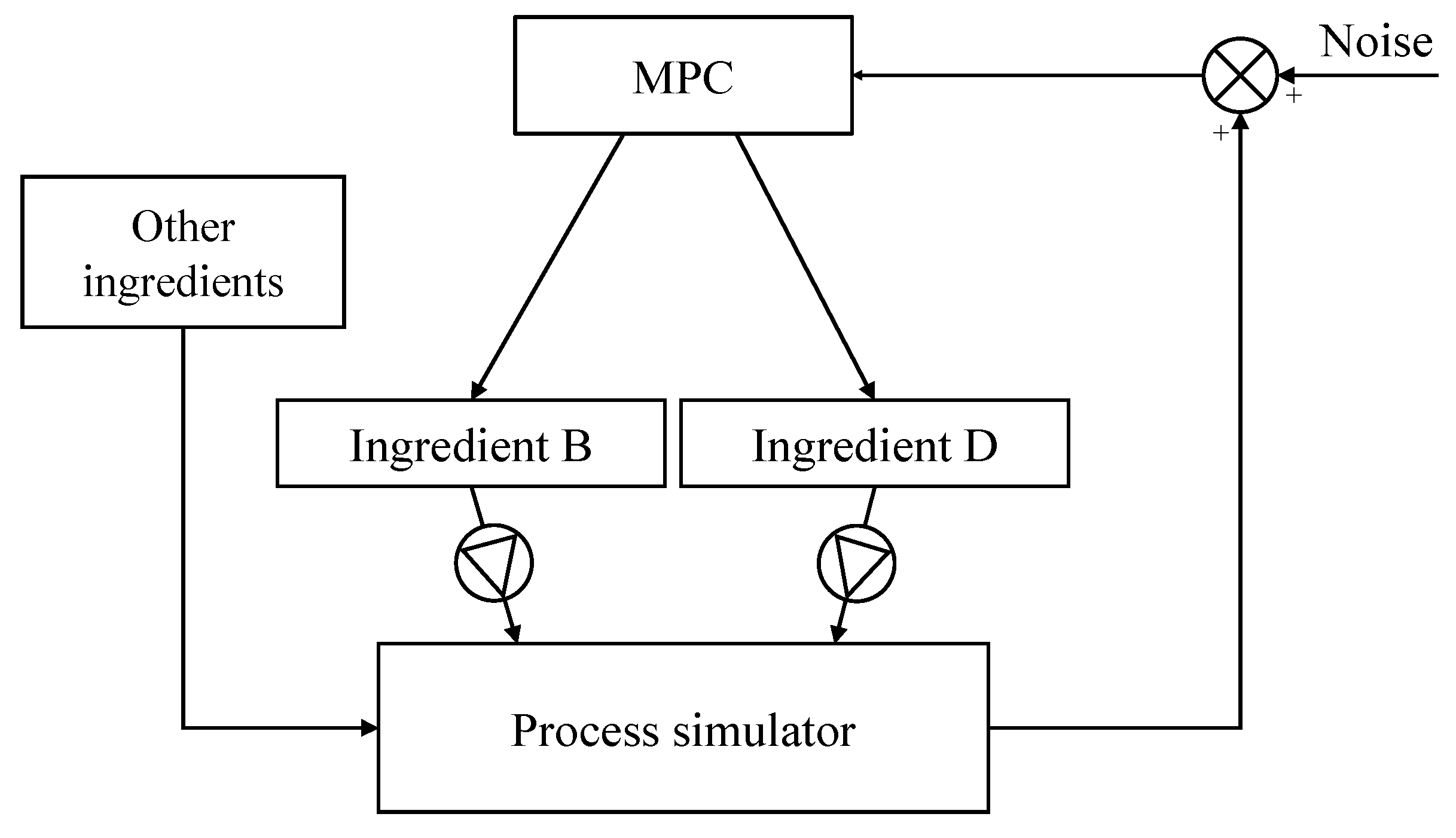
−1 have been considered as controlled variable, while the ingredient B and D flow rates are the manipulated inputs. The evaluation of the control configuration has been carried out using the simulator reported in
Section 4 to act as a virtual plant and a schematic representation of the control loop is reported in
Figure 8.
The objective function
J used to calculate the manipulated action in the DMC is reported in Equation (3)
where
k denotes the time index,
e(
k + 1) is the 3xH
p dimensional vector representing the difference between the desired outputs and the current output prediction without further control action,
F is the dynamic matrix [
5], H
p is the prediction horizon,
u is 2xH
u dimensional vector of the future control moves, H
u is the control horizon,
K is a block diagonal matrix used to penalise changes of manipulated inputs,
W is a weighting matrix used as a tuning parameter. The prediction error is corrected by the measured outputs available at the sampling instant. More in details,
W is a positive (3xH
p)x(3xH
p) block diagonal matrix which in turn is composed of three diagonal matrixes, one for each output (Equation (4)).
The matrices diag(wi), with i = 1, 2, 3, have dimensions HpxHp and the element on the diagonal is the positive weight for a specific output. The matrix K is a positive (2xHu)x(2xHu) block diagonal matrix which in turn is composed of two diagonal matrixes, one for each input.
The matrices diag(ki), with i = 1, 2, have dimensions HuxHu and the element on the diagonal is positive and it penalises a specific input. The process simulator (Equation (1)) provides the four points of the rheological curve corresponding to the actual situation of the process. Random noise is then added to the outputs in order to simulate measurement noise.
A linear predictive model is required to implement the DMC in its traditional form. This task is addressed using the simulator to carry on step response tests from which the dynamic matrix
F is obtained [
5]. The simulator model is excited by varying the input corresponding to the manipulated variables, starting from the reference condition and considering step changes of different sizes [
13,
14]. It is worth noting that the simulator does not model the variations of ingredients quality (composition and rheological behavior). The coefficients of the dynamic matrix
F are obtained by averaging the responses of the different step changes.
6. Results
Various tests have been carried out with the intention of assessing the performance of the control strategy. The main purpose of the simulations is to understand how the quality of the on-line measurements (delay and noise) can affect the rheological control behavior, in view of a future implementation of continuous monitoring of rheological parameters in industrial plants. Ultrasound sensors are indeed candidate to monitor and control the production of materials with complex characteristic behavior (e.g., [
1]), but information on their in-line response such as time required for calculation of the viscosity curve, measurement noise, reliability, repeatability is not available yet for the fluid under investigation. In particular, it could be useful to understand what happens if the time interval for the ultrasound sensor to collect measurements and calculate the velocity profile is much greater than the characteristic time of the process.
6.1. MPC for Set-Point Tracking
The parameters related to the MPC development, such as prediction and control horizon, sampling time and weights, are found by analysing the dynamic response of the process and by tuning. Considering a measurement delay equal to 30 s, the following parameters have been selected in order to achieve an acceptable dynamic matrix conditioning while maintaining good controller performances: (i) the control action is applied every 10 s, and (ii) the dimension of the prediction horizon H
p is set equal to 16. The control horizon H
u is set equal to 4 for the entire control configuration, as suggested by [
5], and only the first control move is applied at each sampling time.
Table 3 summarises the process conditions and MPC parameters for a reference case.
Figure 9 shows the system responses to step variation of the set points. The controller works well and it is capable to bring the three controlled viscosities (viscosity at shear-rates equal to 0.1, 1 and 10 s
−1) to the desired values in a relatively low time. Actions on the two manipulated variables have been penalised to avoid excessive overshoots.
The effects of a greater measurement delay on the controlled process is represented in
Figure 10. In this case measurements are available every 60 s, and H
p was set equal to 19. The controller is capable to bring the viscosities to the desired values but the response is slower than the reference case.
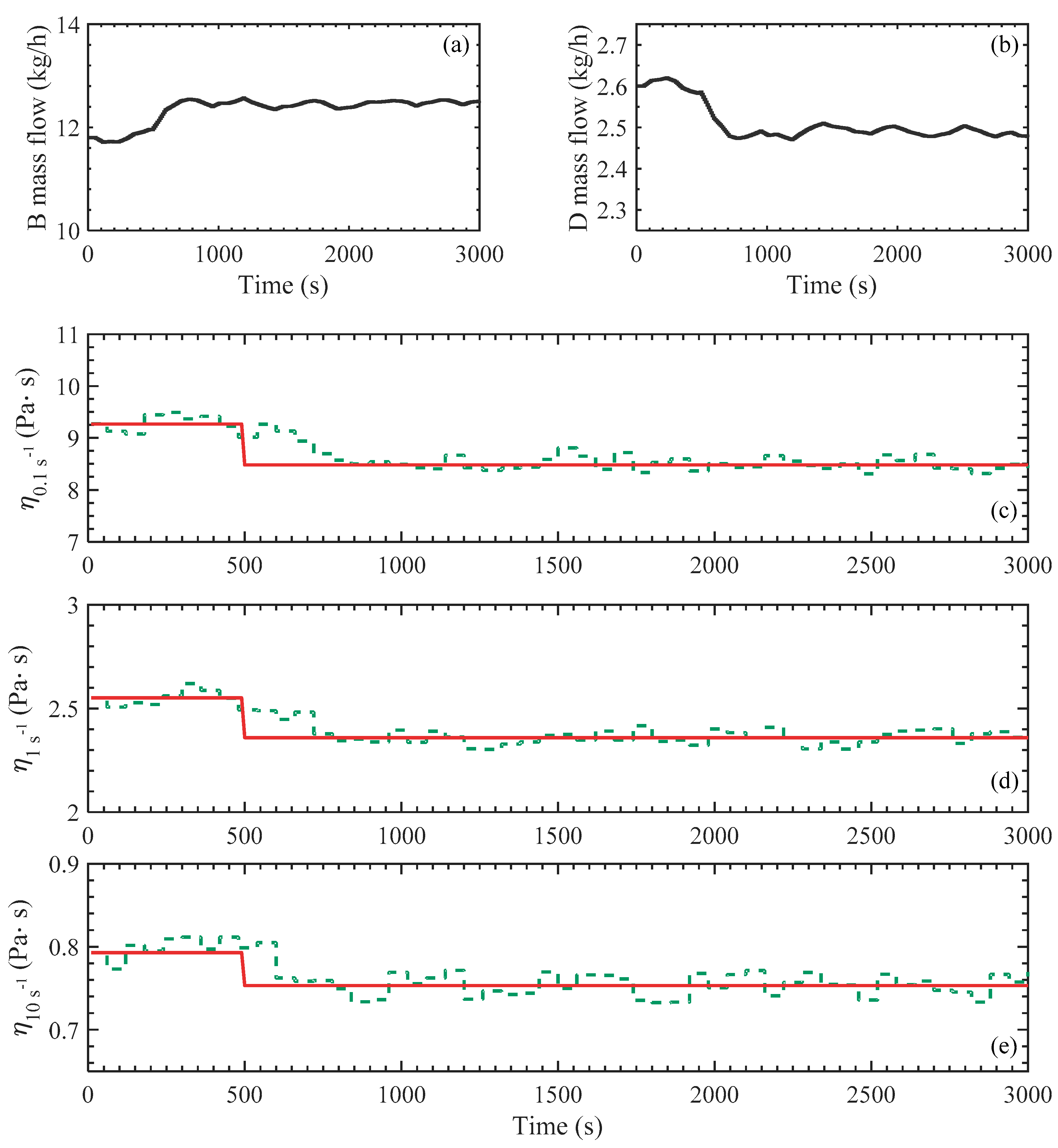
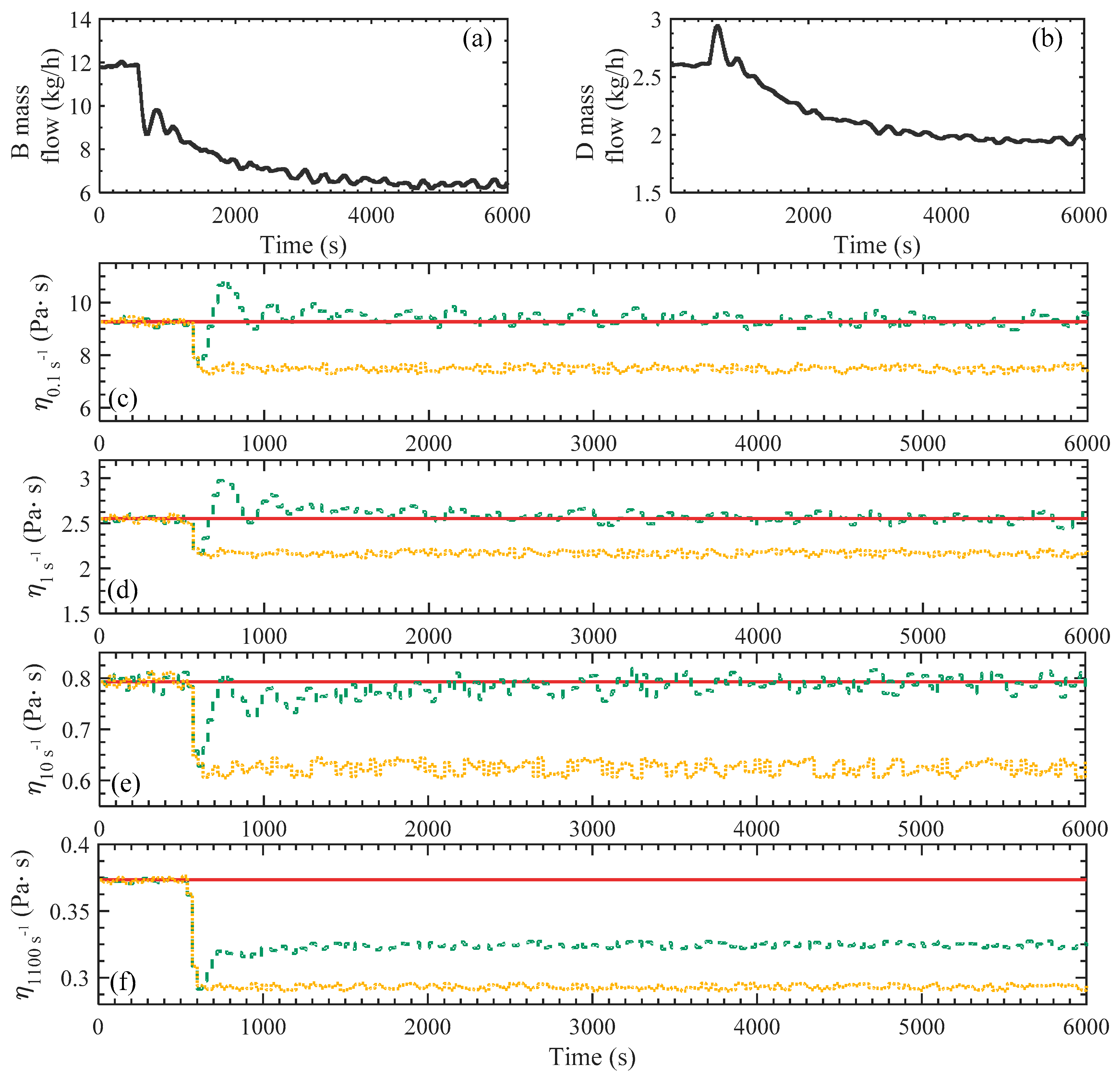
6.2. MPC for Disturbance Rejection
To study the performance of the MPC controller when different batches of ingredients are used, another test has been designed and developed. More in details, a different type of ingredient B has been used in the process.
Another neural network (hereafter indicated as NN_d) with the same structure shown in
Figure 3 has been trained using data coming from tests where another type of ingredient B (type 2) has been used. The second linear block of the Hammerstein model, which is only related to the dynamic behavior, is the same of the previous case. The new model NN_d has been used to simulate a disturbance entering the process, as explained in the following. Time intervals for process simulation, control action and sampling are the same reported in
Table 2. The magnitude of noise in the measurements is respectively ±0.2 Pa·s for
, ±0.05 Pa·s for
and ±0.02 Pa·s for
.
To simulate the disturbance, at a certain point in the timeline of the simulation (when relative time is equal to 500 s), the neural network used for the process simulator (NN) has been replaced with the other one (NN_d). It’s important to highlight that only the simulator is affected by this change, while the dynamic matrix F is the same. This action has the goal to simulate what happens to the real process when a different batch of ingredient B, which has a different rheological behavior with respect to the previous one, is suddenly used (maybe to replace a finished batch).
The response of the system to this change of ingredient is reported in
Figure 11. As shown in the figure, the controller is capable to maintain the controlled viscosities to target. The dotted orange line represents the response of the process to the change of ingredient B in an open loop configuration, while the green dotted line represents the controlled process. In this case, also the behavior of the viscosity at high shear rate is reported in the figure, in order to evaluate if controllability for the four states is satisfied. Indeed, the viscosity at 1100 s
−1 is not controlled, nonetheless the difference between target and actual value is reduced indicating a correct behavior of the proposed controller.