Computational Package for Copolymerization Reactivity Ratio Estimation: Improved Access to the Error-in-Variables-Model
Abstract
:1. Introduction
2. A Brief Overview of EVM for Reactivity Ratio Estimation
2.1. Copolymerization Models
2.2. Error-in-Variables-Model (EVM)
3. Program Description
3.1. Overview
3.2. Program Requirements
3.2.1. Instantaneous Model
3.2.2. Cumulative Model
3.2.3. Default Settings
3.3. Results & Diagnostics
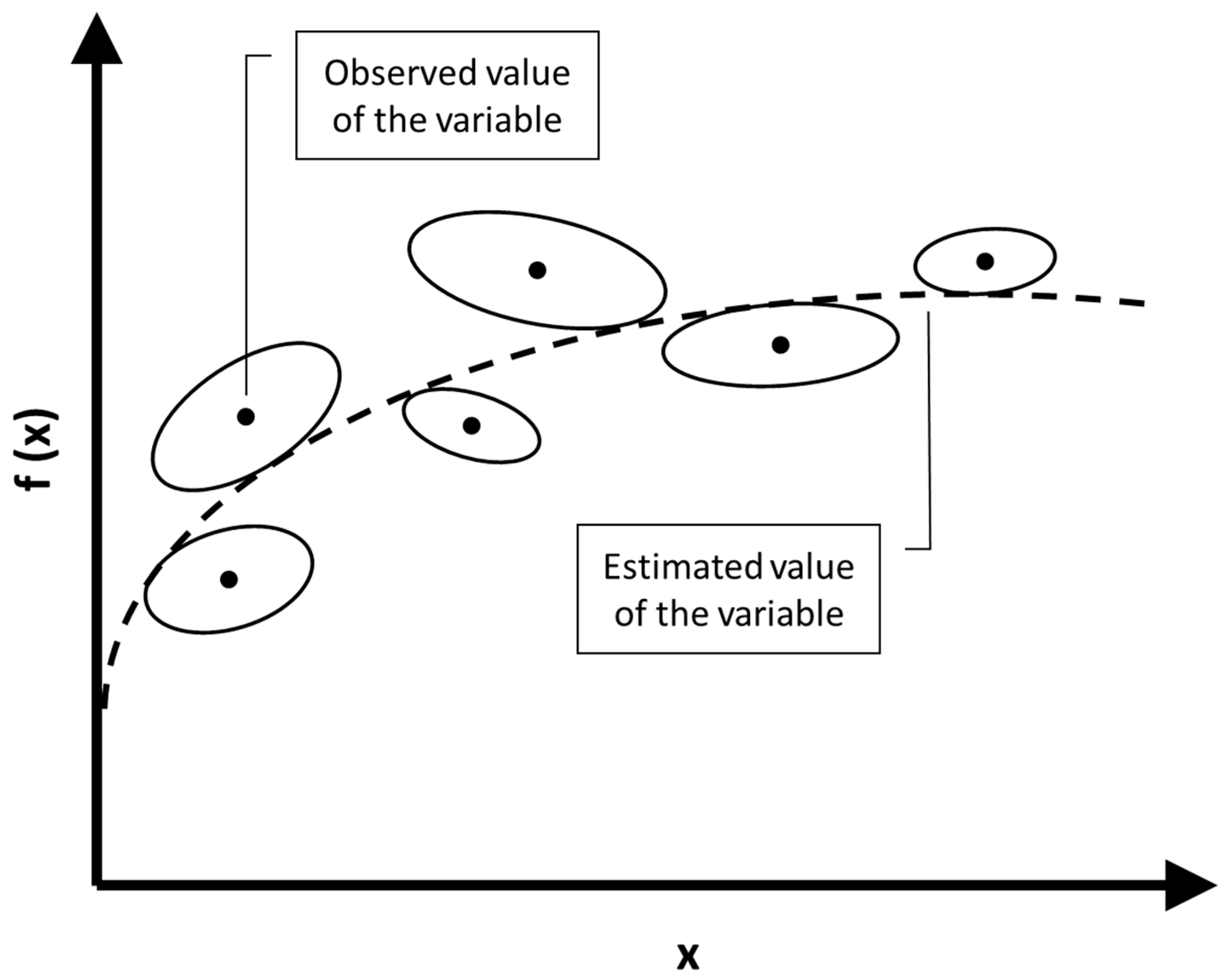
Joint Confidence Regions
4. Case Studies
4.1. Current “Best Practices” and Their Shortcomings
4.1.1. Exhibit A: Why Do Researchers Continue to Use Linear Parameter Estimation Techniques?
Evaluation of MDO/VAc Copolymerization Data: Fineman-Ross vs. EVM
4.1.2. Exhibit B: Are Researchers Addressing the Limitations of Low Conversion Data Analysis?
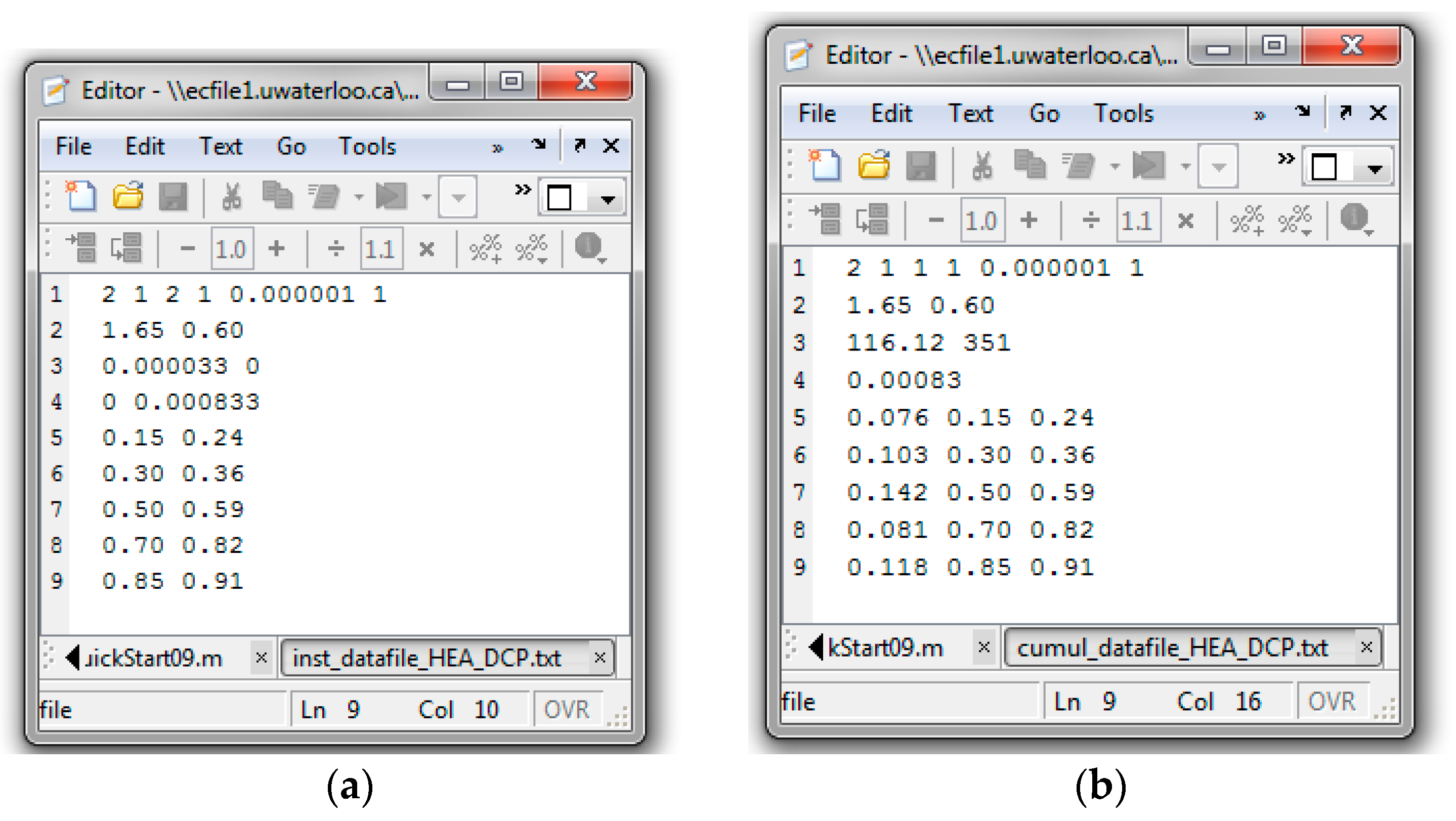
Evaluation of HEA/DCP Copolymerization Data
4.2. Maximizing and Exploiting Information Content
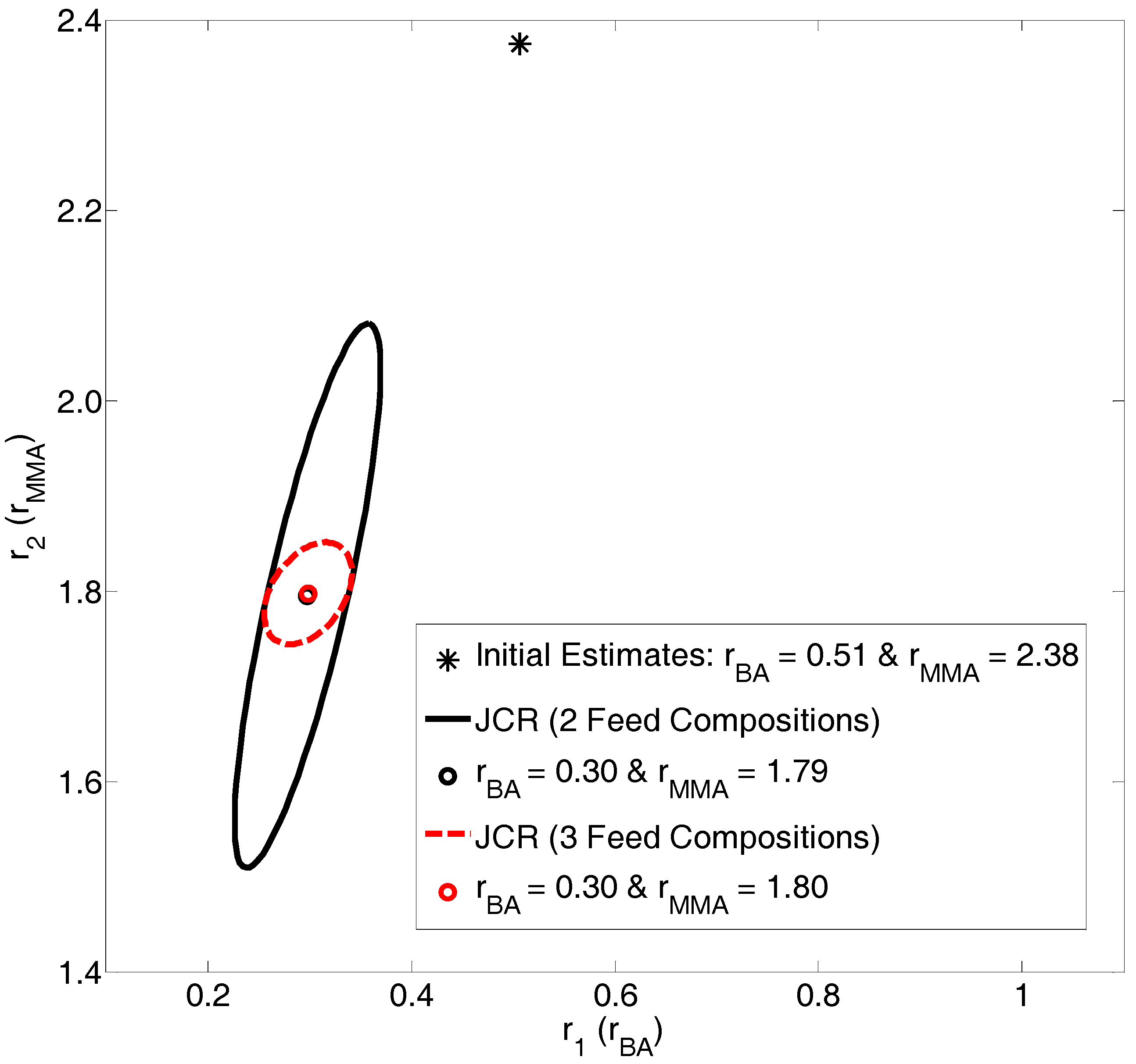
4.2.1. Exhibit C: What Happens when We Take Advantage of ALL Copolymerization Data?
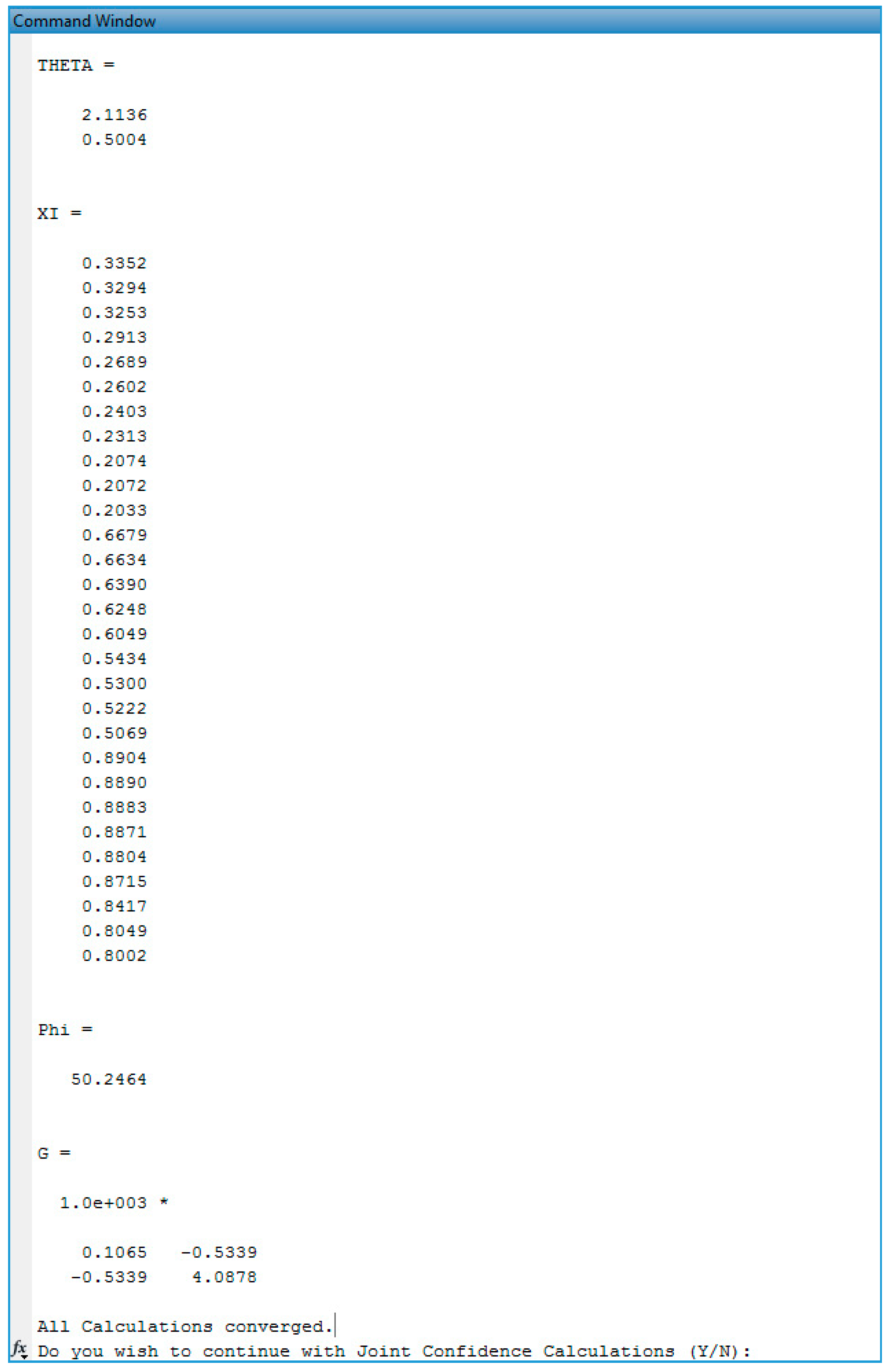
Evaluation of BMA/BA Copolymerization Data: Low Conversion Analysis
Evaluation of BMA/BA Copolymerization Data: Medium-High Conversion Analysis
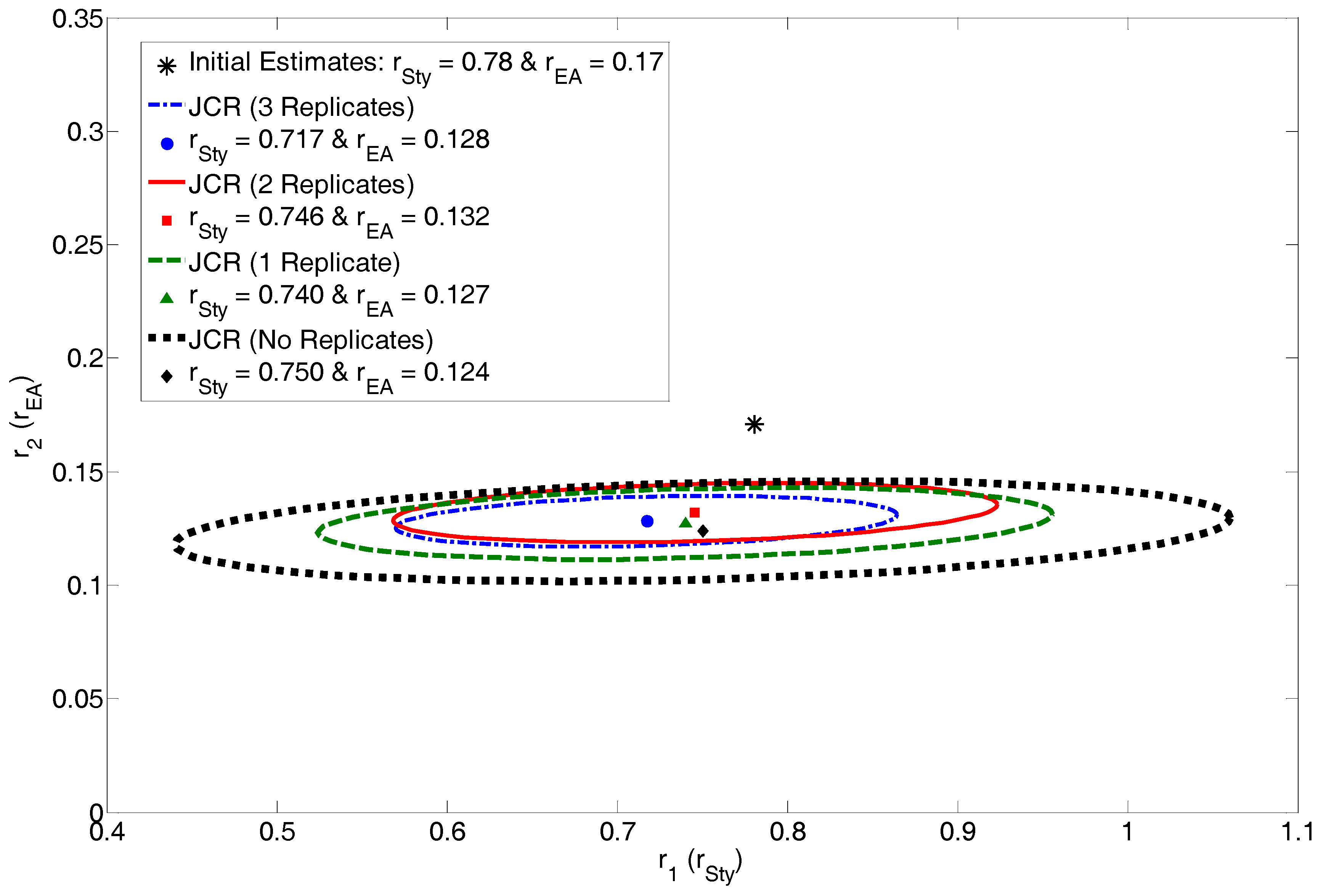
4.2.2. Exhibit D: How Many Replicates Do We Really Need?
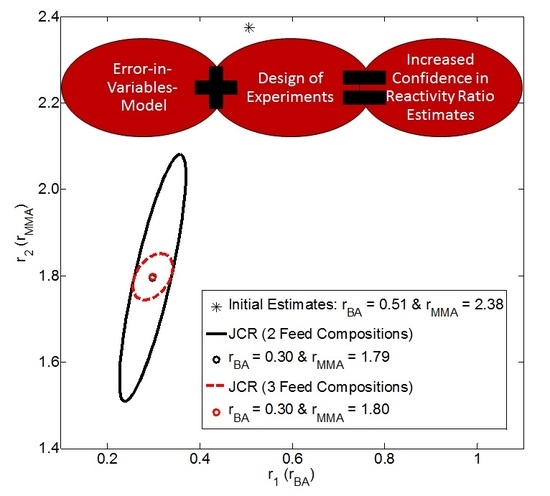
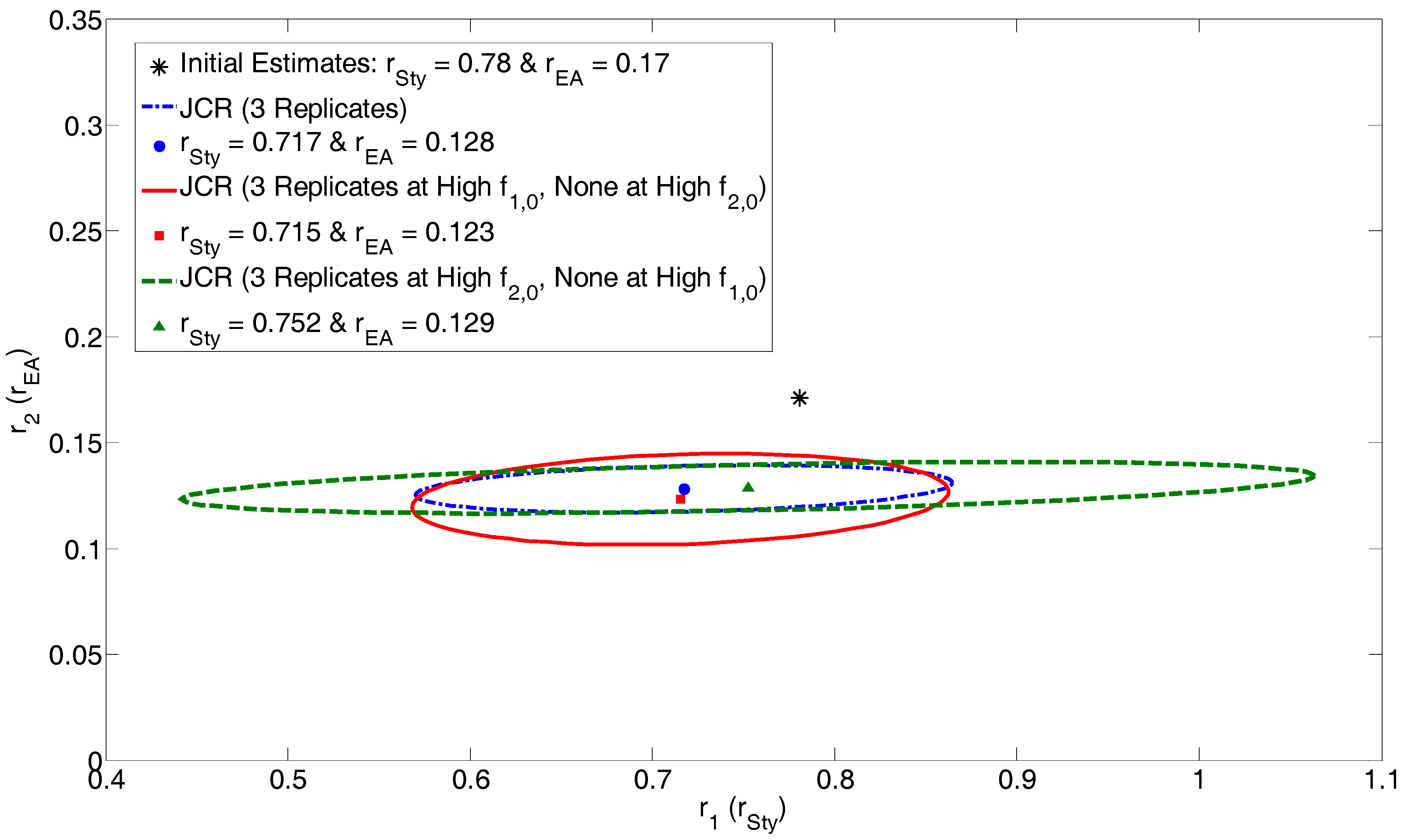
4.2.3. Exhibit E: Can We Use Design of Experiments to Increase Confidence in Our Results?
- (1)
- EVM is applied to instantaneous (low conversion) data (from [22]) to estimate reactivity ratios. Feed compositions are selected according to Tidwell-Mortimer design and four runs are done at each level: f1,0 = 0.543 and f1,0 = 0.798.
- (2)
- Parameter estimation results from EVM are recorded (see Appendix C, Section C.5). Specifically, reactivity ratio estimates (r1 and r2) and the G matrix (Appendix A) are required for sequential design of experiments.
- (3)
- The EVM-based sequential design of experiments program (using data from step (2), as well as the preliminary feed compositions from step (1)) is employed. Details on the design have been reported by Kazemi et al. [8].
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
An Overview of the Appendices
Appendix A. Relevant Statistical Principles
Appendix A.1. Additive and Multiplicative Error
Appendix A.2. Calculation of G as an EVM Program Output
Appendix B. General Program Description

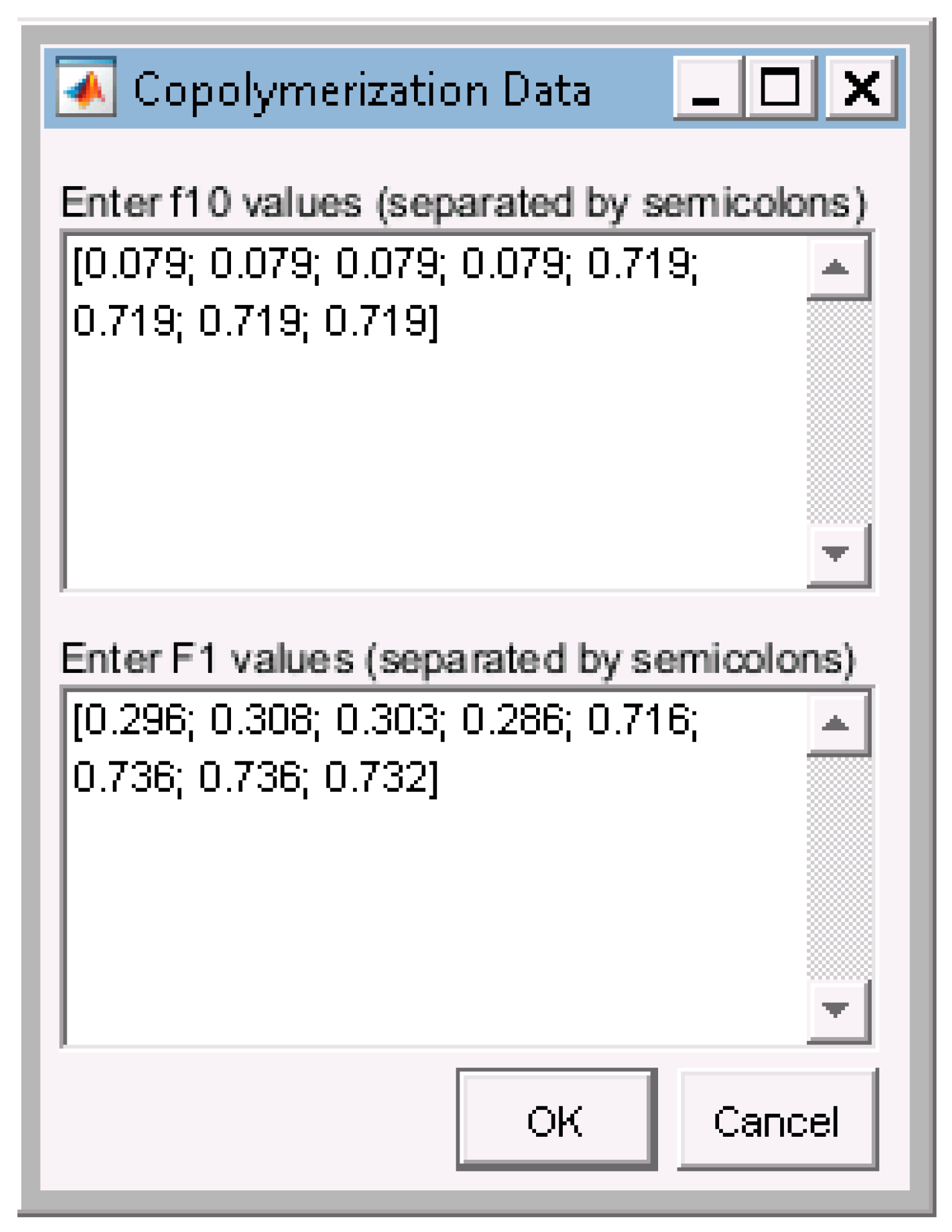
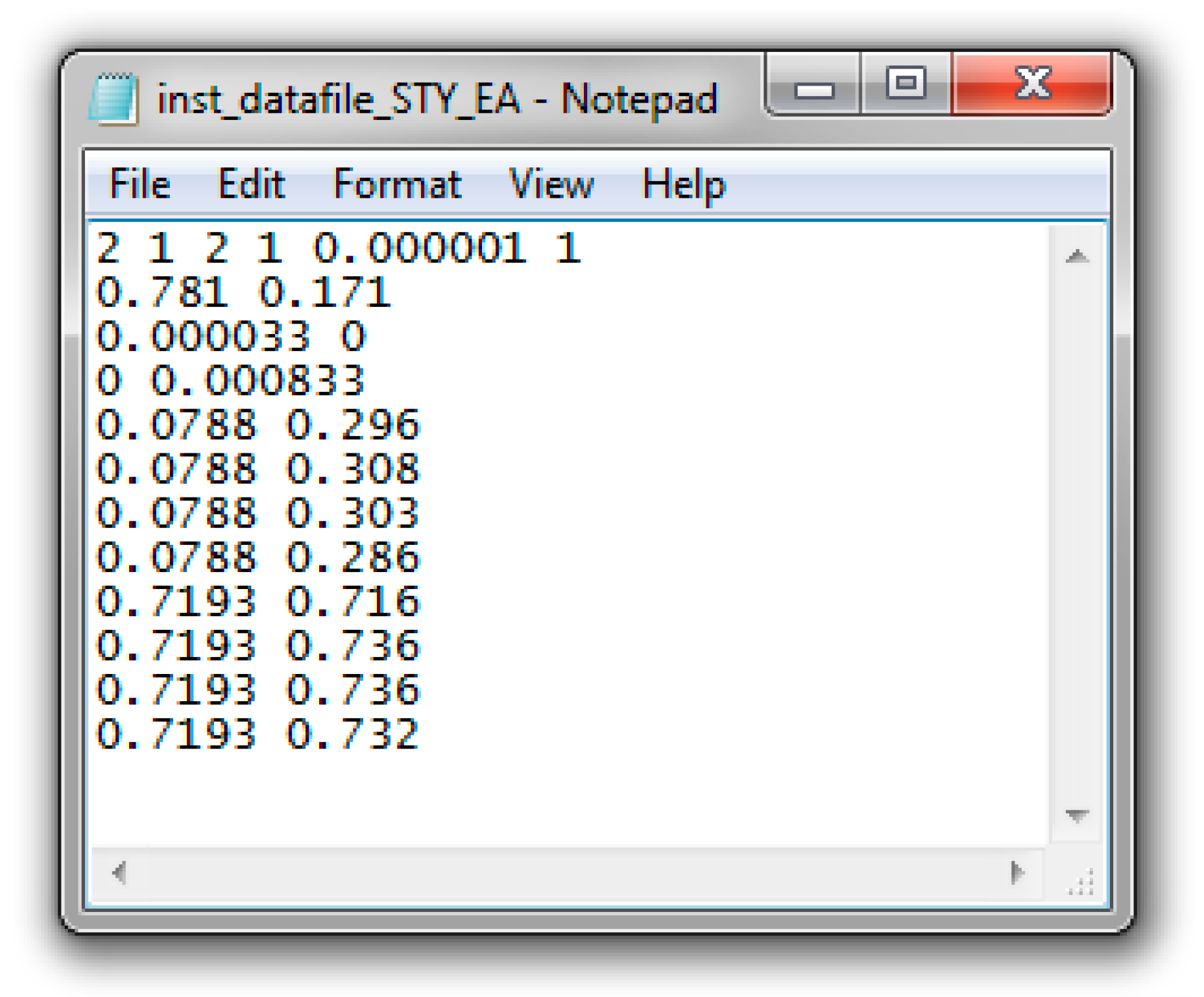
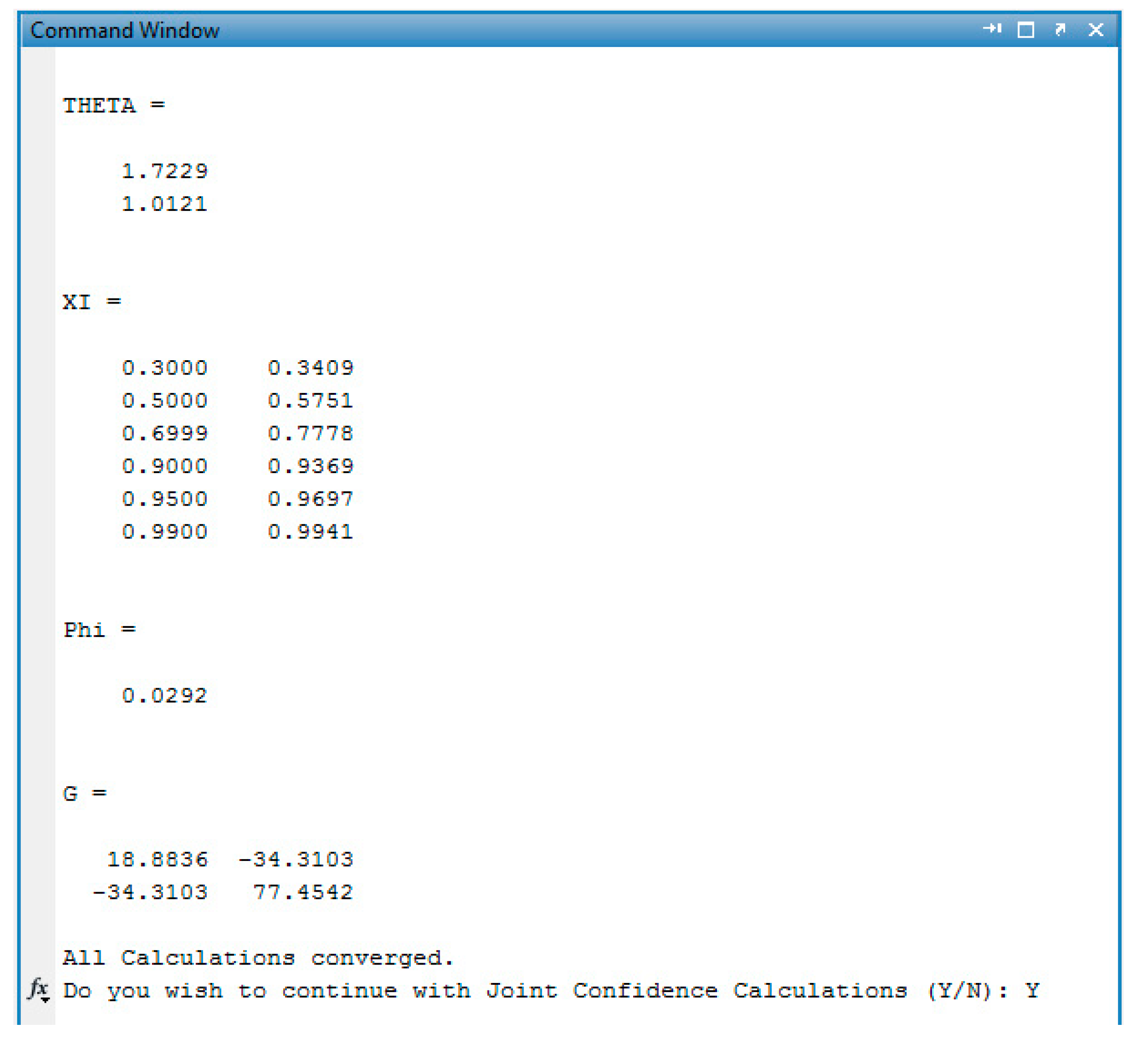
Appendix C. Data & Screenshots from Case Studies
Appendix C.1. Screenshots from MDO/VAc Copolymerization Analysis

Appendix C.2. Screenshots from HEA/DCP Copolymerization Analysis

Appendix C.3. Screenshots from BMA/BA Copolymerization Analysis


Appendix C.4. Screenshots from Sty/EA Copolymerization Analysis
| 3 Replicates | 2 Replicates | 1 Replicate | No Replicates | ||||
|---|---|---|---|---|---|---|---|
| f1,0 | F1 | f1,0 | F1 | f1,0 | F1 | f1,0 | F1 |
| 0.079 | 0.296 | 0.079 | 0.296 | 0.079 | 0.296 | ||
| 0.079 | 0.308 | ||||||
| 0.079 | 0.303 | 0.079 | 0.303 | 0.079 | 0.303 | 0.079 | 0.303 |
| 0.079 | 0.286 | 0.079 | 0.286 | ||||
| 0.719 | 0.716 | ||||||
| 0.719 | 0.736 | 0.719 | 0.736 | 0.719 | 0.736 | 0.719 | 0.736 |
| 0.719 | 0.736 | 0.719 | 0.736 | ||||
| 0.719 | 0.732 | 0.719 | 0.732 | 0.719 | 0.732 | ||
| r1 = 0.717 | r1 = 0.746 | r1 = 0.740 | r1 = 0.750 | ||||
| r2 = 0.128 | r2 = 0.132 | r2 = 0.127 | r2 = 0.124 | ||||
| 3 Replicates | High f1,0 Replicates | High f2,0 Replicates | |||
|---|---|---|---|---|---|
| f1,0 | F1 | f1,0 | F1 | f1,0 | F1 |
| 0.079 | 0.296 | 0.079 | 0.296 | ||
| 0.079 | 0.308 | 0.079 | 0.308 | ||
| 0.079 | 0.303 | 0.079 | 0.303 | 0.079 | 0.303 |
| 0.079 | 0.286 | 0.079 | 0.286 | ||
| 0.719 | 0.716 | 0.719 | 0.716 | ||
| 0.719 | 0.736 | 0.719 | 0.736 | 0.719 | 0.736 |
| 0.719 | 0.736 | 0.719 | 0.736 | ||
| 0.719 | 0.732 | 0.719 | 0.732 | ||
| r1 = 0.717 | r1 = 0.715 | r1 = 0.752 | |||
| r2 = 0.128 | r2 = 0.123 | r2 = 0.129 | |||
Appendix C.5. Screenshots from BA/MMA Copolymerization Analysis
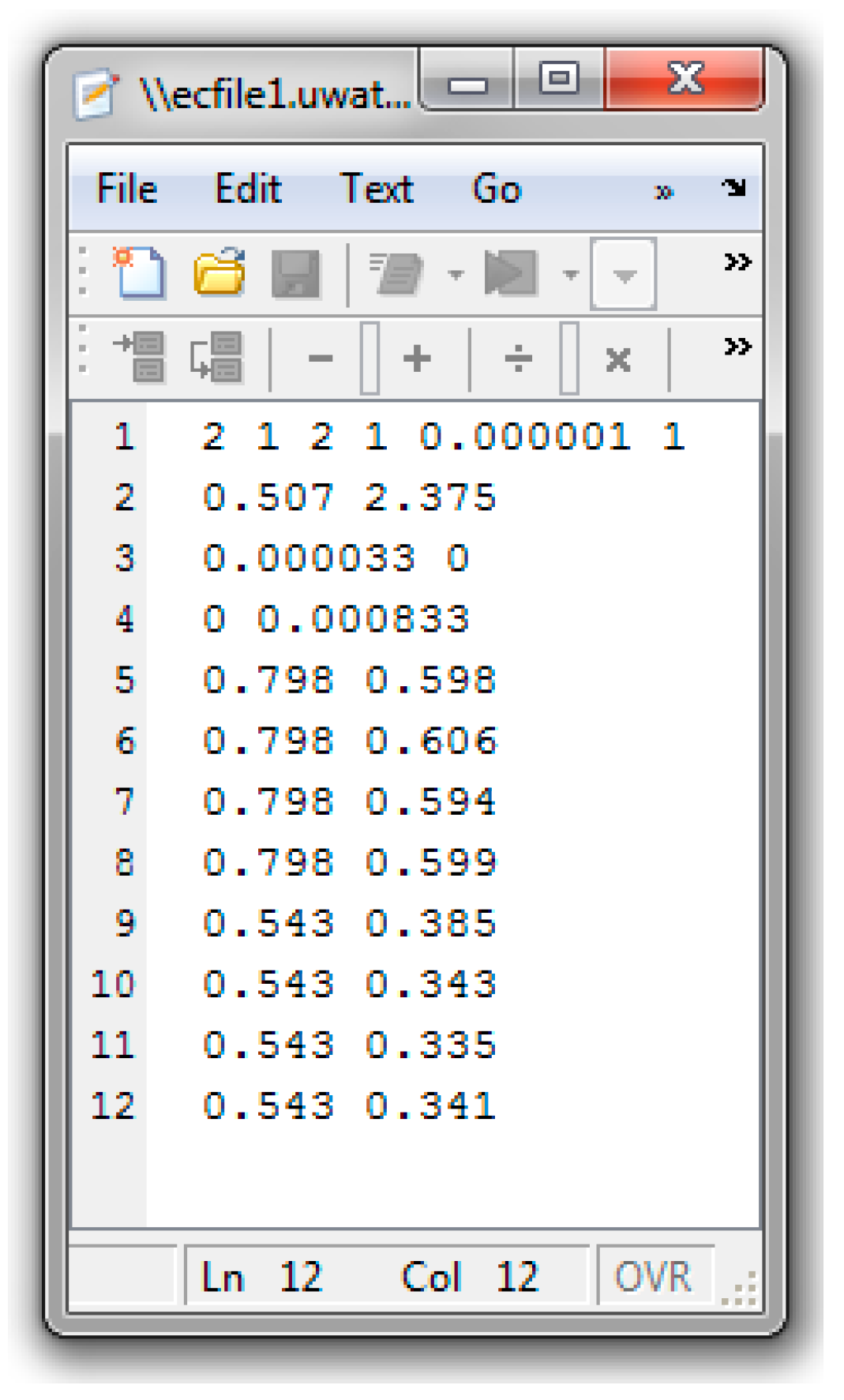
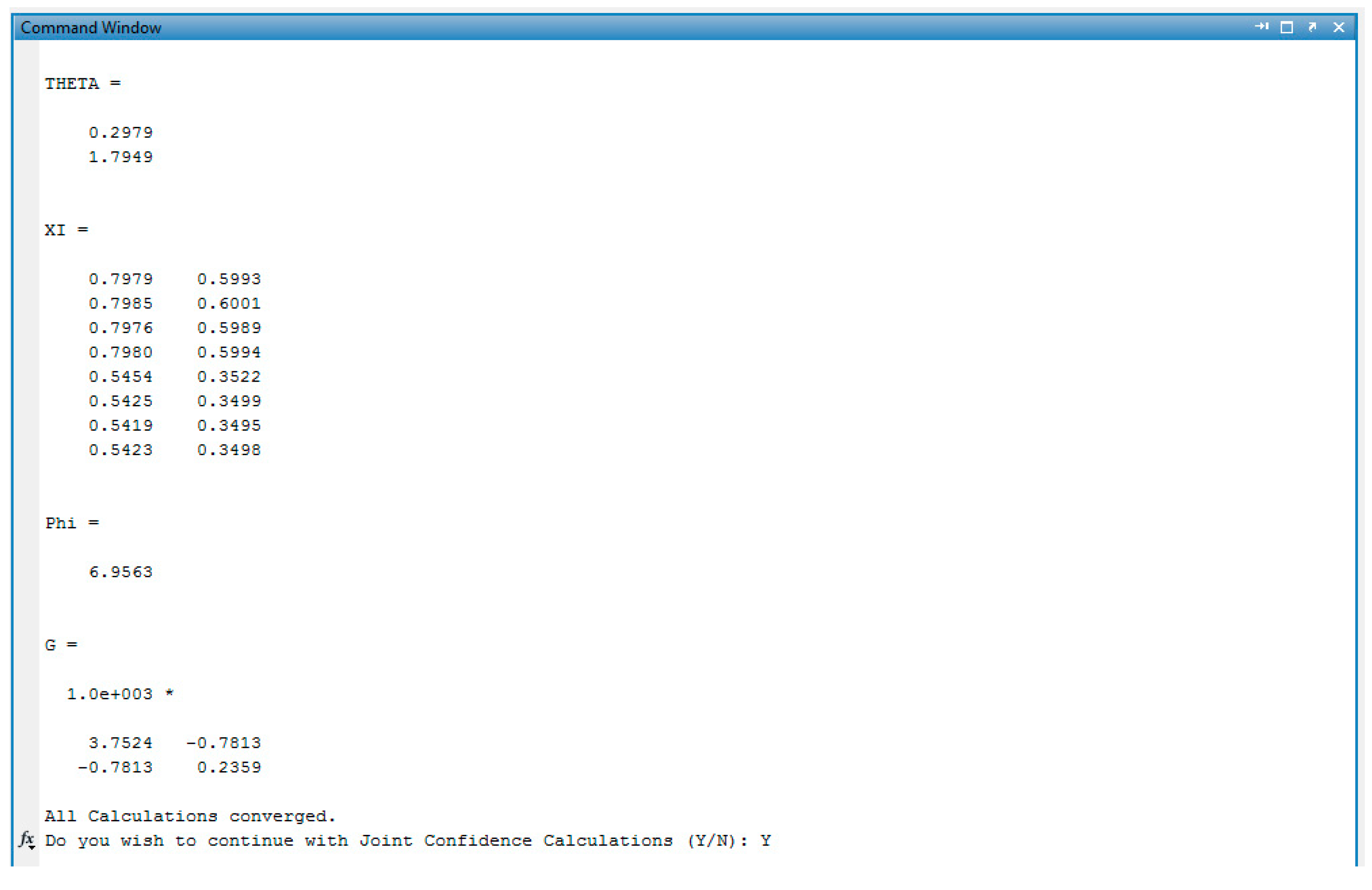
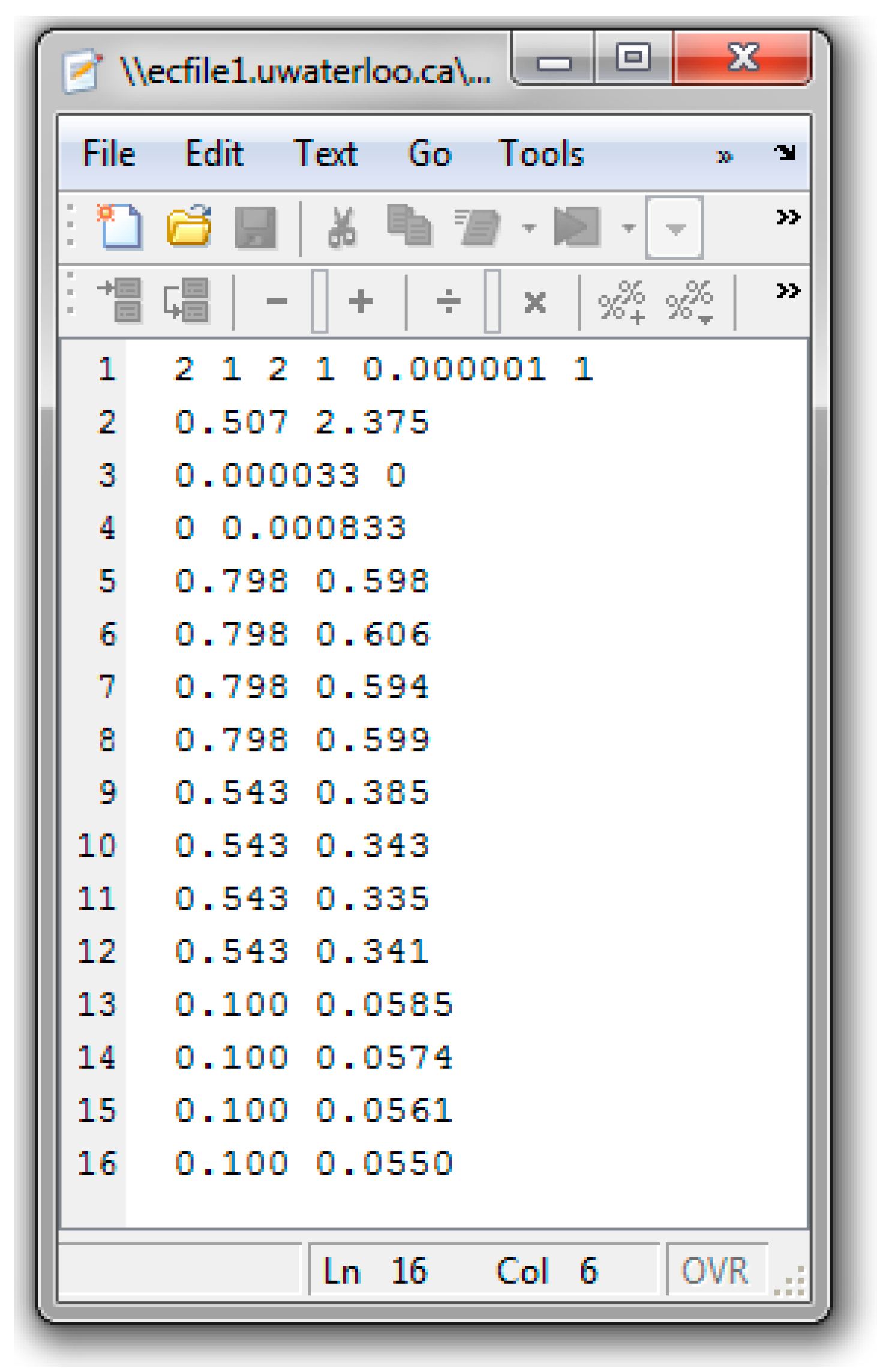

References
- Dubé, M.A.; Amin Sanayei, R.; Penlidis, A.; O’Driscoll, K.F.; Reilly, P.M. A microcomputer program for estimation of copolymerization reactivity ratios. J. Polym. Sci. Part A Polym. Chem. 1991, 29, 703–708. [Google Scholar] [CrossRef]
- Polic, A.L.; Duever, T.A.; Penlidis, A. Case studies and literature review on the estimation of copolymerization reactivity ratios. J. Polym. Sci. Part A Polym. Chem. 1998, 36, 813–822. [Google Scholar] [CrossRef]
- Kazemi, N.; Duever, T.A.; Penlidis, A. A powerful estimation scheme with the error-in-variables-model for nonlinear cases: Reactivity ratio estimation examples. Comput. Chem. Eng. 2013, 48, 200–208. [Google Scholar] [CrossRef]
- Scott, A.J.; Riahinezhad, M.; Penlidis, A. Optimal design for reactivity ratio estimation: A comparison of techniques for AMPS/acrylamide and AMPS/acrylic acid copolymerizations. Processes 2015, 3, 749–768. [Google Scholar] [CrossRef]
- Scott, A.J.; Penlidis, A. Copolymerization. In Elsevier Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Reedijk, J., Ed.; Elsevier: Waltham, MA, USA, 2017. [Google Scholar]
- Kazemi, N.; Duever, T.A.; Penlidis, A. Reactivity ratio estimation from cumulative copolymer composition data. Macromol. React. Eng. 2012, 5, 385–403. [Google Scholar] [CrossRef]
- Reilly, P.M.; Patino-Leal, H. A Bayesian study of the error-in-variables model. Technometrics 1981, 23, 221–231. [Google Scholar] [CrossRef]
- Kazemi, N.; Duever, T.A.; Penlidis, A. Design of experiments for reactivity ratio estimation in multicomponent polymerizations using the error-in-variables approach. Macromol. Theory Simul. 2013, 22, 261–272. [Google Scholar] [CrossRef]
- Scott, A.J.; Kazemi, N.; Penlidis, A. AMPS/AAm/AAc terpolymerization: Experimental verification of the EVM framework for ternary reactivity ratio estimation. Processes 2017, 5, 9. [Google Scholar] [CrossRef]
- Agarwal, S.; Kumar, R.; Kissel, T.; Reul, R. Synthesis of degradable materials based on caprolactone and vinyl acetate units using radical chemistry. Polym. J. 2009, 42, 650–660. [Google Scholar] [CrossRef]
- Undin, J.; Illanes, T.; Finne-Wistrand, A.; Albertsson, A. Random introduction of degradable linkages into functional vinyl polymers by radical ring-opening polymerization, tailored for soft tissue engineering. Polym. Chem. 2012, 3, 1260–1266. [Google Scholar] [CrossRef]
- Hedir, G.; Bell, C.; Ieong, N.; Chapman, E.; Collins, I.; O’Reilly, R.; Dove, A. Functional degradable polymers by xanthate-mediated polymerization. Macromolecules 2014, 47, 2847–2852. [Google Scholar] [CrossRef]
- Ding, D.; Pan, X.; Zhang, Z.; Li, N.; Zhu, J.; Zhu, X. A degradable copolymer of 2-methylene-1,3-dioxepane and vinyl acetate by photo-induced cobalt-mediated radical polymerization. Polym. Chem. 2016, 7, 5258–5264. [Google Scholar] [CrossRef]
- Feldermann, A.; Toy, A.; Phan, H.; Stenzel, M.; Davis, T.; Barner-Kowollik, C. Reversible addition fragmentation chain transfer copolymerization: Influence of the RAFT process on the copolymer composition. Polymer 2004, 45, 3997–4007. [Google Scholar] [CrossRef]
- Hagiopol, C. Copolymerization: Toward a Systematic Approach; Plenum Publishers: New York, NY, USA, 1999. [Google Scholar]
- Suresh, J.; Karthik, S.; Arun, A. Photocrosslinkable polymer based on 4-3-(2,4-dichlorophenyl)-3-oxoprop-1-enyl) phenylacrylate: Synthesis, reactivity ratio, and crosslinking studies. Mater. Sci. Pol. 2016, 34, 834–844. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, L.; Gao, H.; Konstantinov, I.; Arturo, S.; Yu, D.; Torkelson, J.; Broadbelt, L. A combined computational and experimental study of copolymerization propagation kinetics for 1-ethylcyclopentyl methacrylate and methyl methacrylate. Macromol. Theory Simul. 2016, 25, 263–273. [Google Scholar] [CrossRef]
- Ren, S.; Hinojosa-Castellanos, L.; Zhang, L.; Dubé, M.A. Bulk free-radical copolymerization of n-butyl acrylate and n-butyl methacrylate: Reactivity ratio estimation. Macromol. React. Eng. 2017, 11, 1600050. [Google Scholar] [CrossRef]
- Tidwell, P.W.; Mortimer, G.A. An improved method of calculating copolymerization reactivity ratios. J. Polym. Sci. Part A Polym. Chem. 1965, 3, 369–387. [Google Scholar] [CrossRef]
- Cochran, W.G.; Cox, G.M. Experimental Designs; John Wiley & Sons, Inc.: New York, NY, USA, 1957. [Google Scholar]
- McManus, N.; Penlidis, A. A kinetic investigation of styrene/ethyl acrylate copolymerization. J. Polym. Sci. Part A Polym. Chem. 1996, 34, 237–248. [Google Scholar] [CrossRef]
- Dubé, M.A.; Penlidis, A. A systematic approach to the study of multicomponent polymerization kinetics—The butyl acrylate/methyl methacrylate/vinyl acetate example: 1. Bulk copolymerization. Polymer 1995, 36, 587–598. [Google Scholar] [CrossRef]
- Zhang, Y.; Dubé, M.A. Copolymerization of n-butyl methacrylate and d-limonene. Macromol. React. Eng. 2014, 8, 805–812. [Google Scholar] [CrossRef]
- Grassie, N.; Torrance, B.; Fortune, J.; Gemell, J. Reactivity ratios for the copolymerization of acrylates and methacrylates by nuclear magnetic resonance spectroscopy. Polymer 1965, 6, 653–658. [Google Scholar] [CrossRef]
- Rossignoli, P.J.; Duever, T.A. The estimation of copolymer reactivity ratios: A review and case studies using the error-in-variables model and nonlinear least squares. Polym. React. Eng. 1995, 3, 361–395. [Google Scholar]

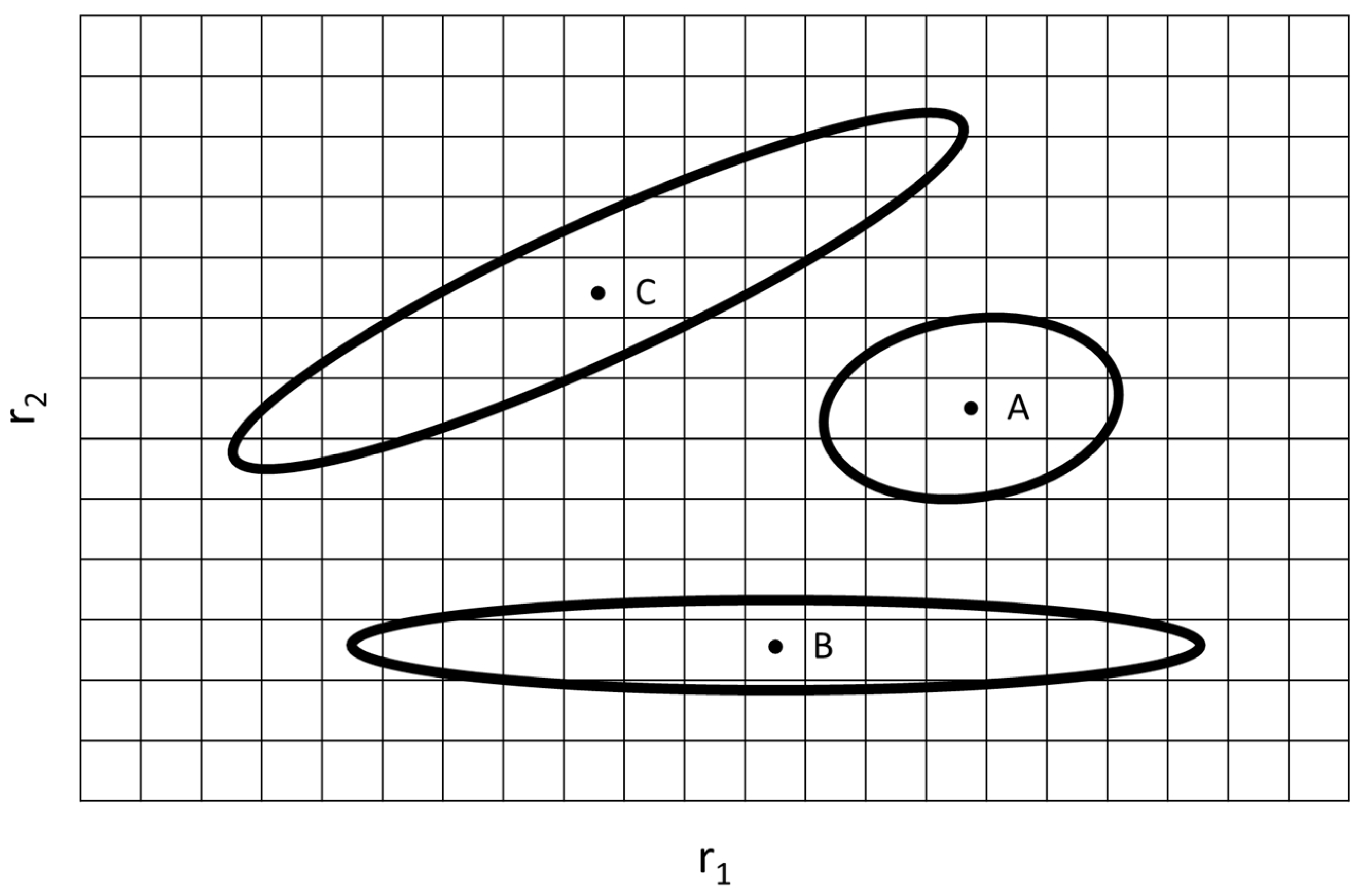
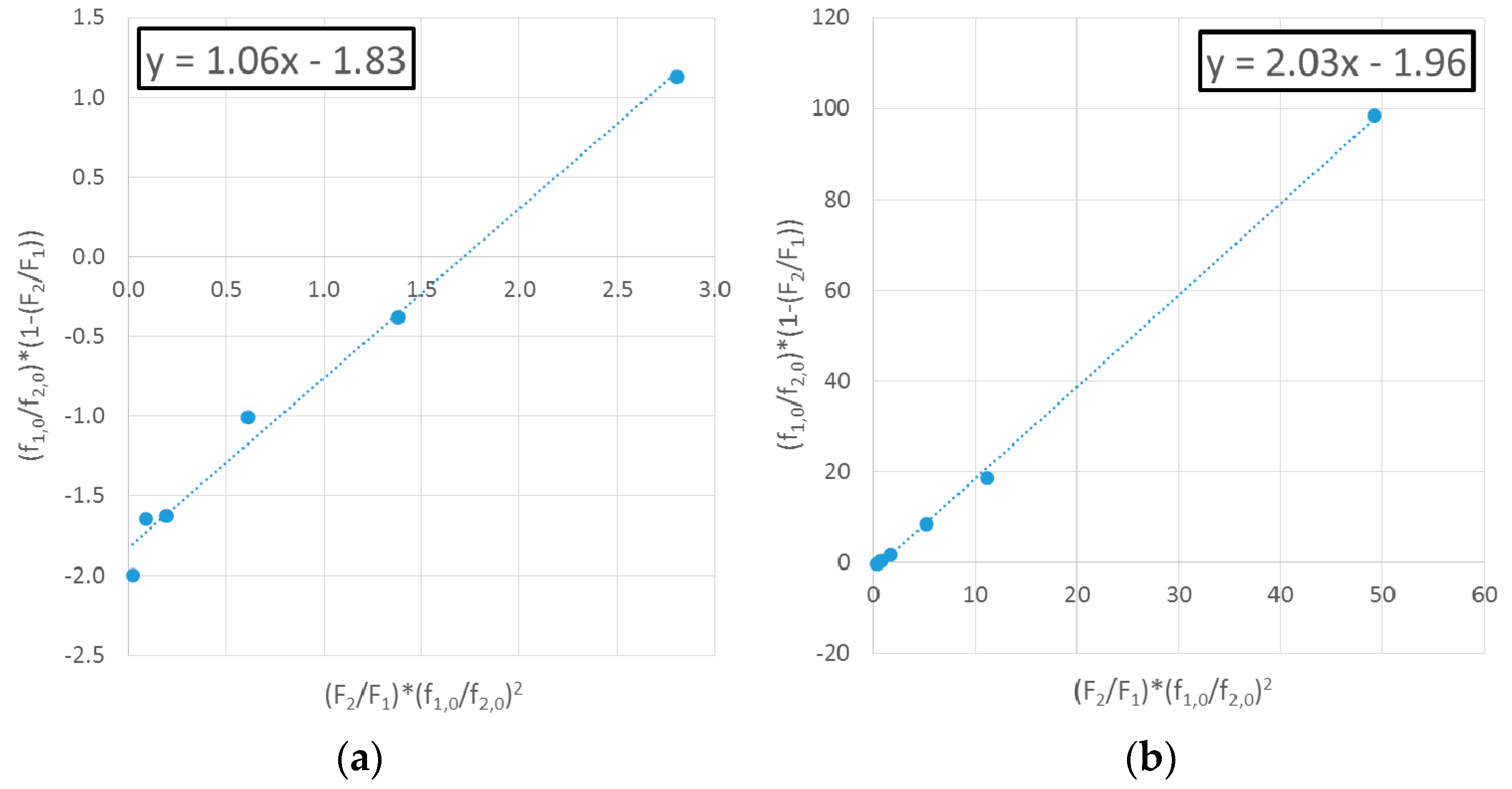
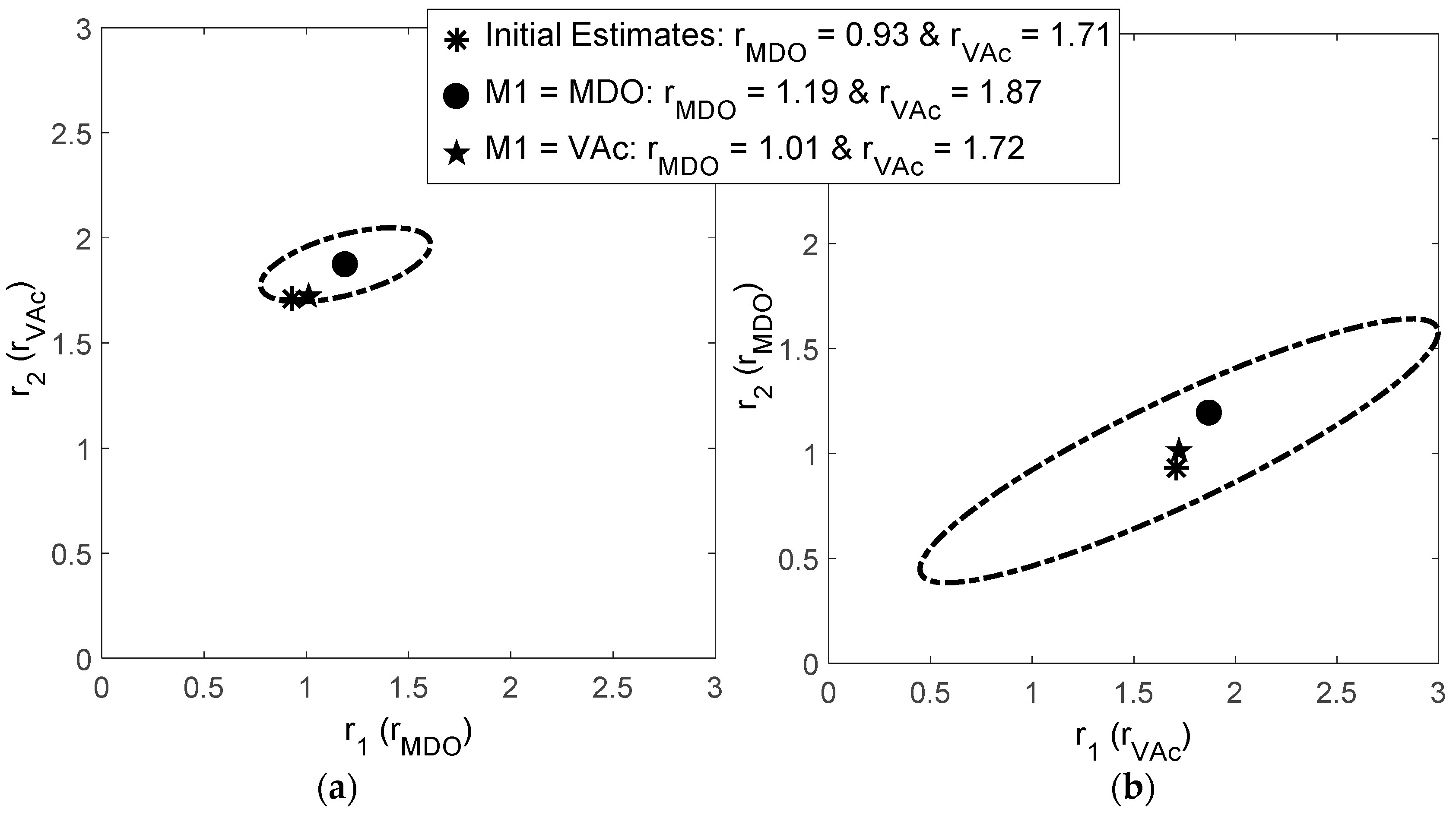
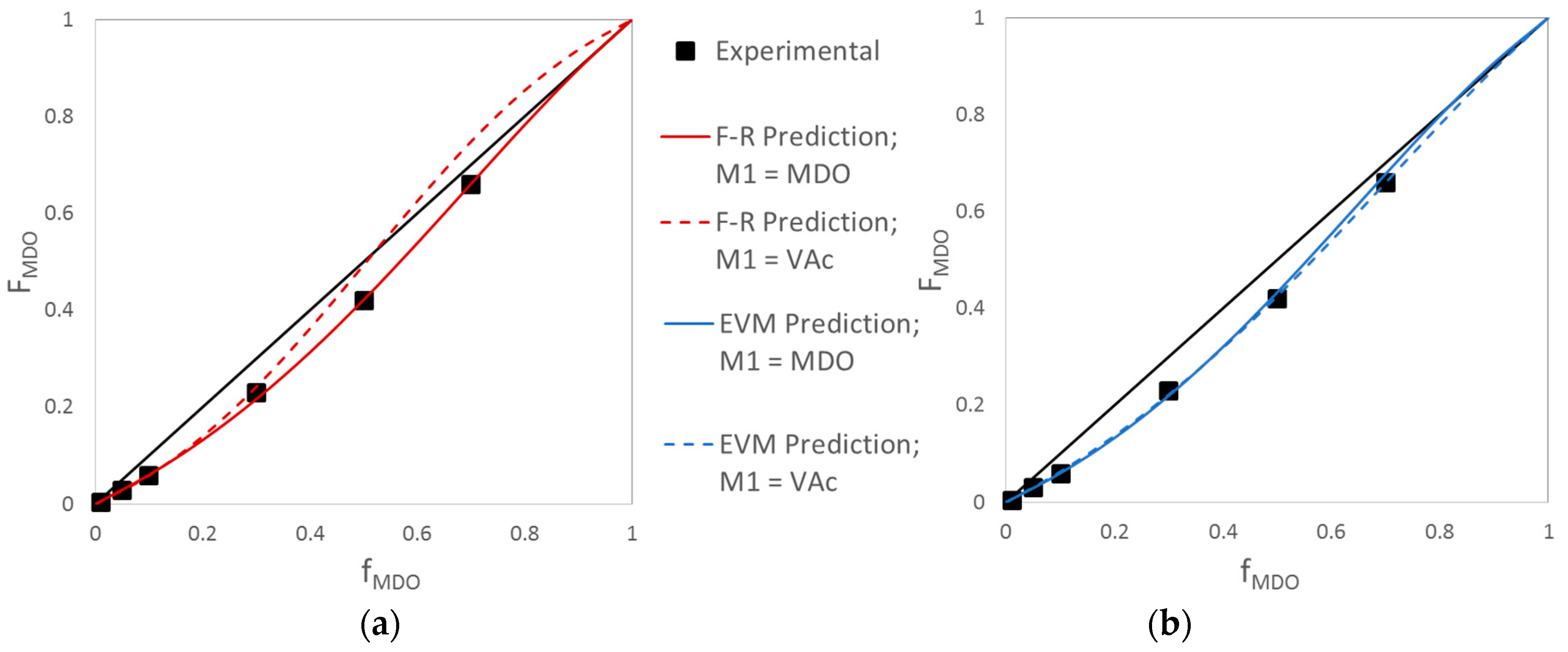
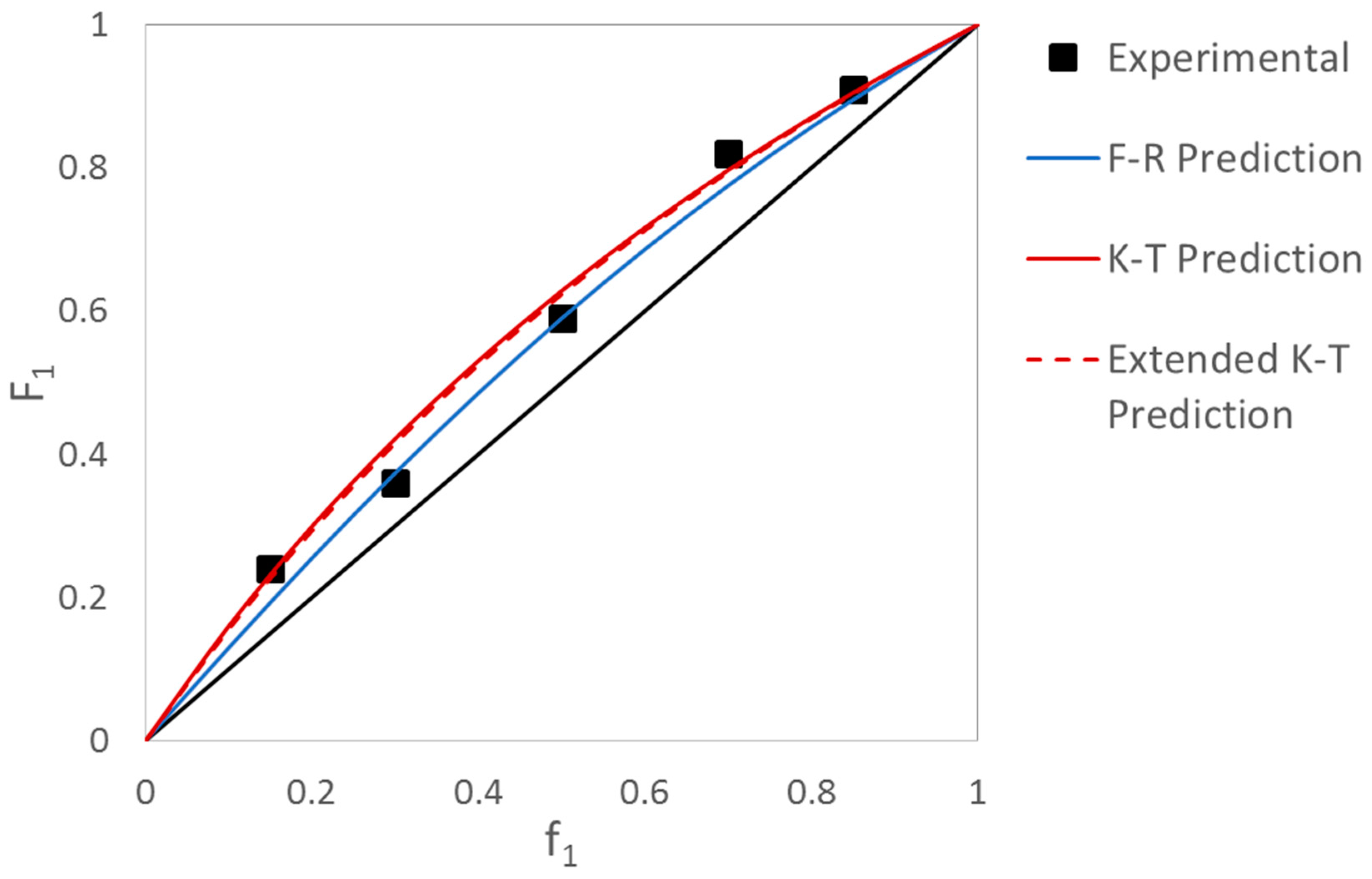
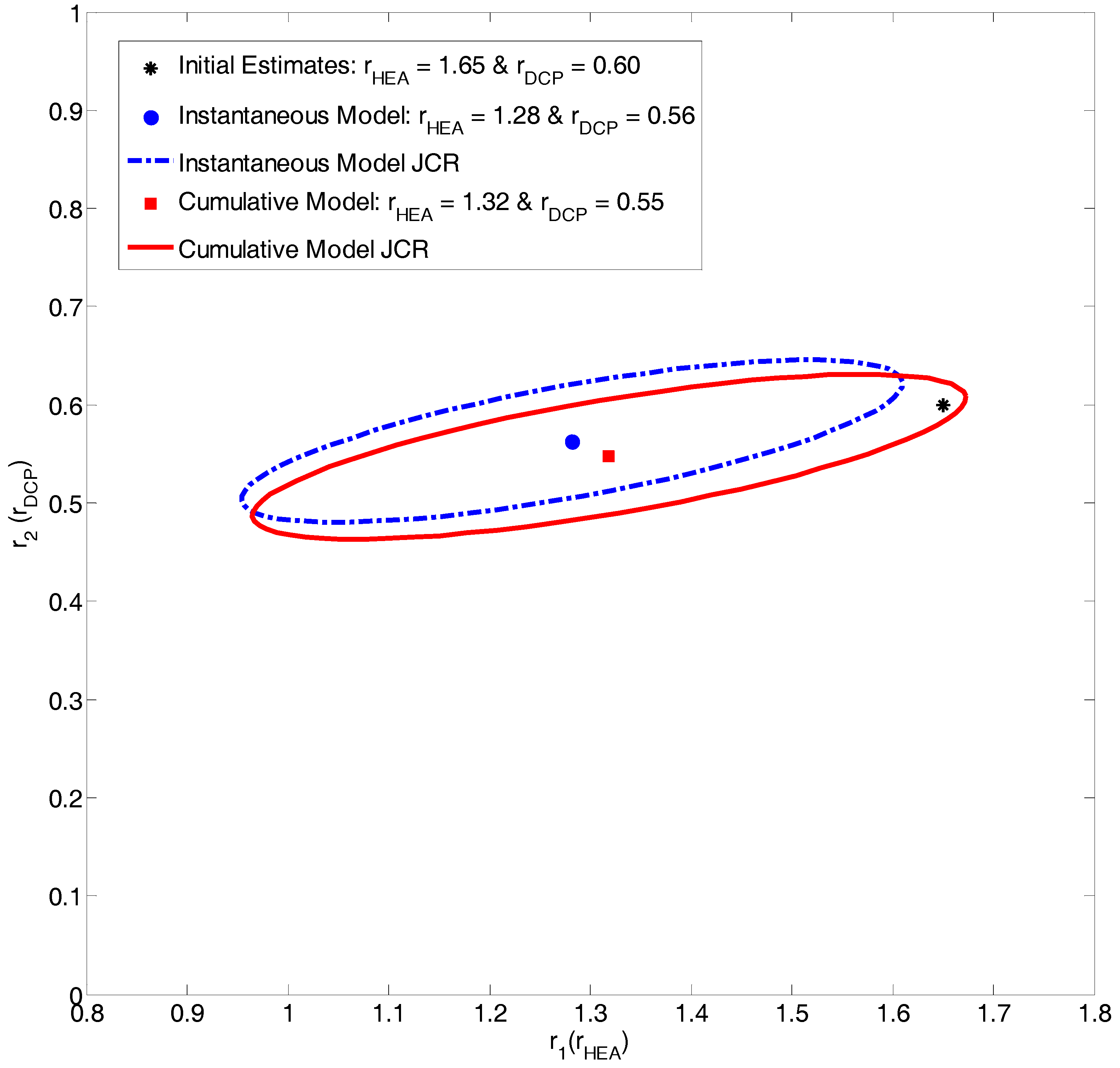
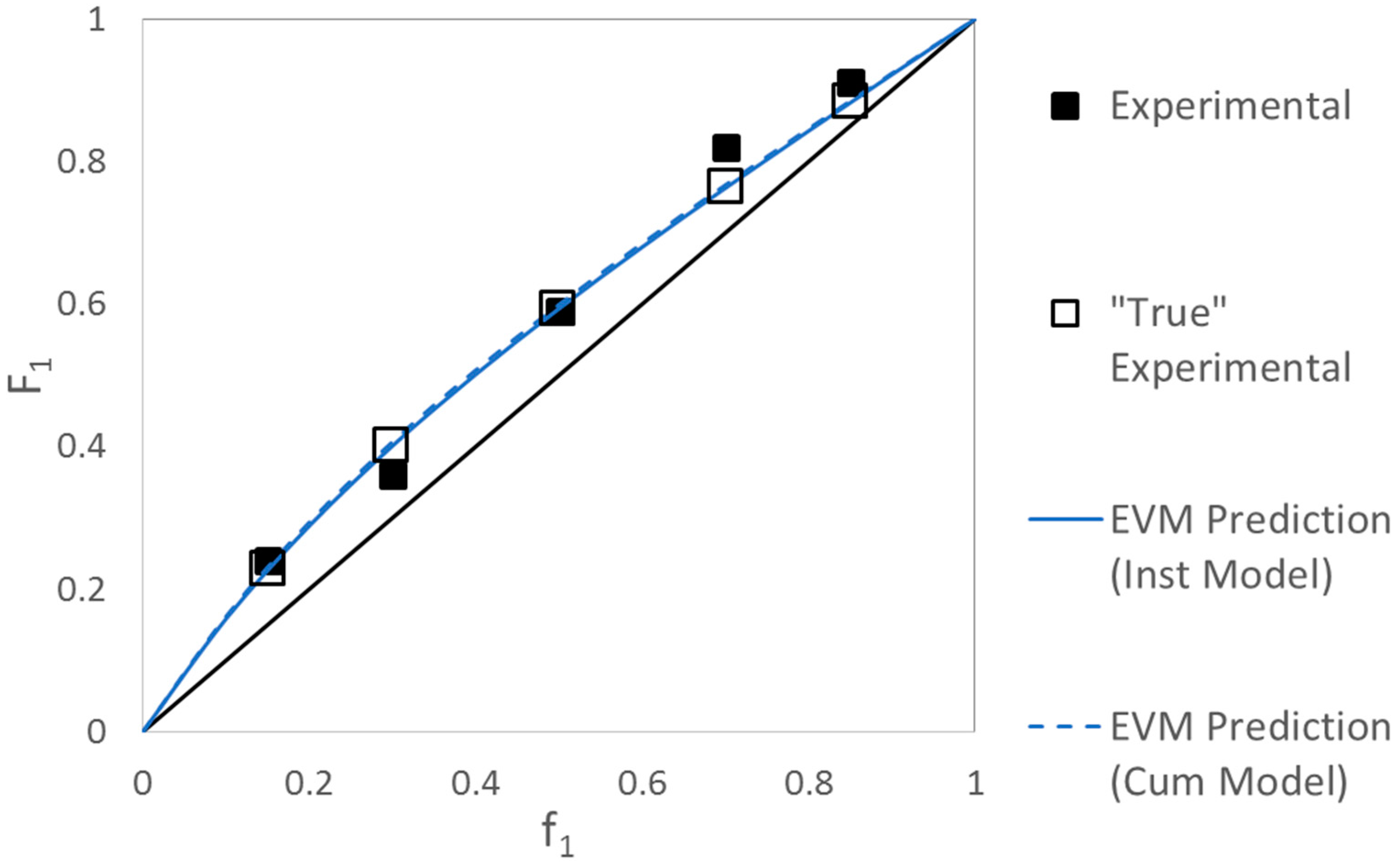
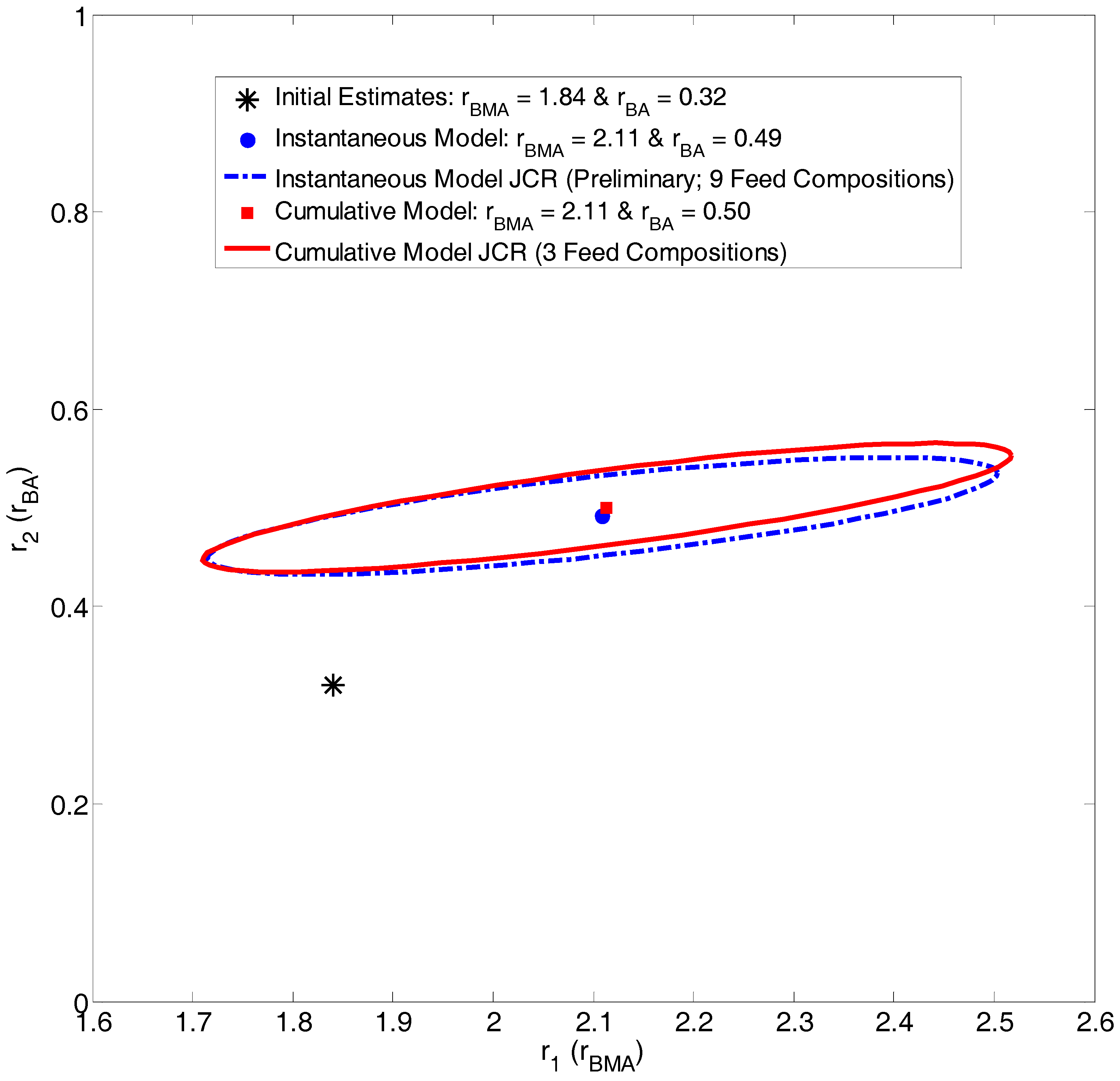
| Ref. | RRE Technique | RRE Results | Comments | |
|---|---|---|---|---|
| r1 | r2 | |||
| [10] | Kelen-Tüdös (K-T) | 0.47 | 1.56 |
|
| [11] | Fineman-Ross (F-R) | 0.93 | 1.71 |
|
| [12] | Non-Linear Least Squares (NLLS) | 1.03 | 1.22 |
|
| [13] | Fineman-Ross (F-R) | 0.14 | 1.89 |
|
| Sample | Monomer Feed | Copolymer Composition | ||
|---|---|---|---|---|
| f1,0 | f2,0 | |||
| MDO70 | 0.70 | 0.30 | 0.66 | 0.34 |
| MDO50 | 0.50 | 0.50 | 0.42 | 0.58 |
| MDO30 | 0.30 | 0.70 | 0.23 | 0.77 |
| MDO10 | 0.10 | 0.90 | 0.06 | 0.94 |
| MDO5 | 0.05 | 0.95 | 0.03 | 0.97 |
| MDO1 | 0.01 | 0.99 | 0.005 | 0.995 |
| Ref. | RRE Technique | RRE Results | |
|---|---|---|---|
| r1 | r2 | ||
| [16] | Fineman-Ross (F-R) | 1.53 ± 0.10 | 0.76 ± 0.16 |
| [16] | Kelen-Tüdös (K-T) | 1.67 ± 0.13 | 0.58 ± 0.05 |
| [16] | Extended K-T | 1.65 ± 0.13 | 0.60 ± 0.08 |
| Current Work | Instantaneous EVM | 1.28 * | 0.56 * |
| Current Work | Cumulative EVM | 1.32 * | 0.55 * |
| Ref. | RRE Technique | RRE Results | |
|---|---|---|---|
| r1 | r2 | ||
| [18] | Preliminary Estimates (RREVM) [1] | 2.100 | 0.489 |
| [18] | Estimates from Tidwell-Mortimer Designed Experiments (RREVM) [1,2] | 2.008 | 0.460 |
| Current Work | Instantaneous EVM (preliminary data) | 2.109 | 0.492 |
| Current Work | Instantaneous EVM (preliminary data & designed replicates) | 2.012 | 0.462 |
| Current Work | Cumulative EVM | 2.114 | 0.500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scott, A.J.; Penlidis, A. Computational Package for Copolymerization Reactivity Ratio Estimation: Improved Access to the Error-in-Variables-Model. Processes 2018, 6, 8. https://doi.org/10.3390/pr6010008
Scott AJ, Penlidis A. Computational Package for Copolymerization Reactivity Ratio Estimation: Improved Access to the Error-in-Variables-Model. Processes. 2018; 6(1):8. https://doi.org/10.3390/pr6010008
Chicago/Turabian StyleScott, Alison J., and Alexander Penlidis. 2018. "Computational Package for Copolymerization Reactivity Ratio Estimation: Improved Access to the Error-in-Variables-Model" Processes 6, no. 1: 8. https://doi.org/10.3390/pr6010008
APA StyleScott, A. J., & Penlidis, A. (2018). Computational Package for Copolymerization Reactivity Ratio Estimation: Improved Access to the Error-in-Variables-Model. Processes, 6(1), 8. https://doi.org/10.3390/pr6010008