Effect of Tariff Policy and Battery Degradation on Optimal Energy Storage
Abstract
1. Introduction
2. Problem Statement and Model Formulation
2.1. Objective Function
2.2. Constraints
- The battery cannot charge and discharge at the same timeThis restriction can be mathematically posted as
- For safety reasons, there is a maximum power that should not be exceeded neither during charge () nor during discharge (). Additionally, and will always be assumed as positive variables. Then:
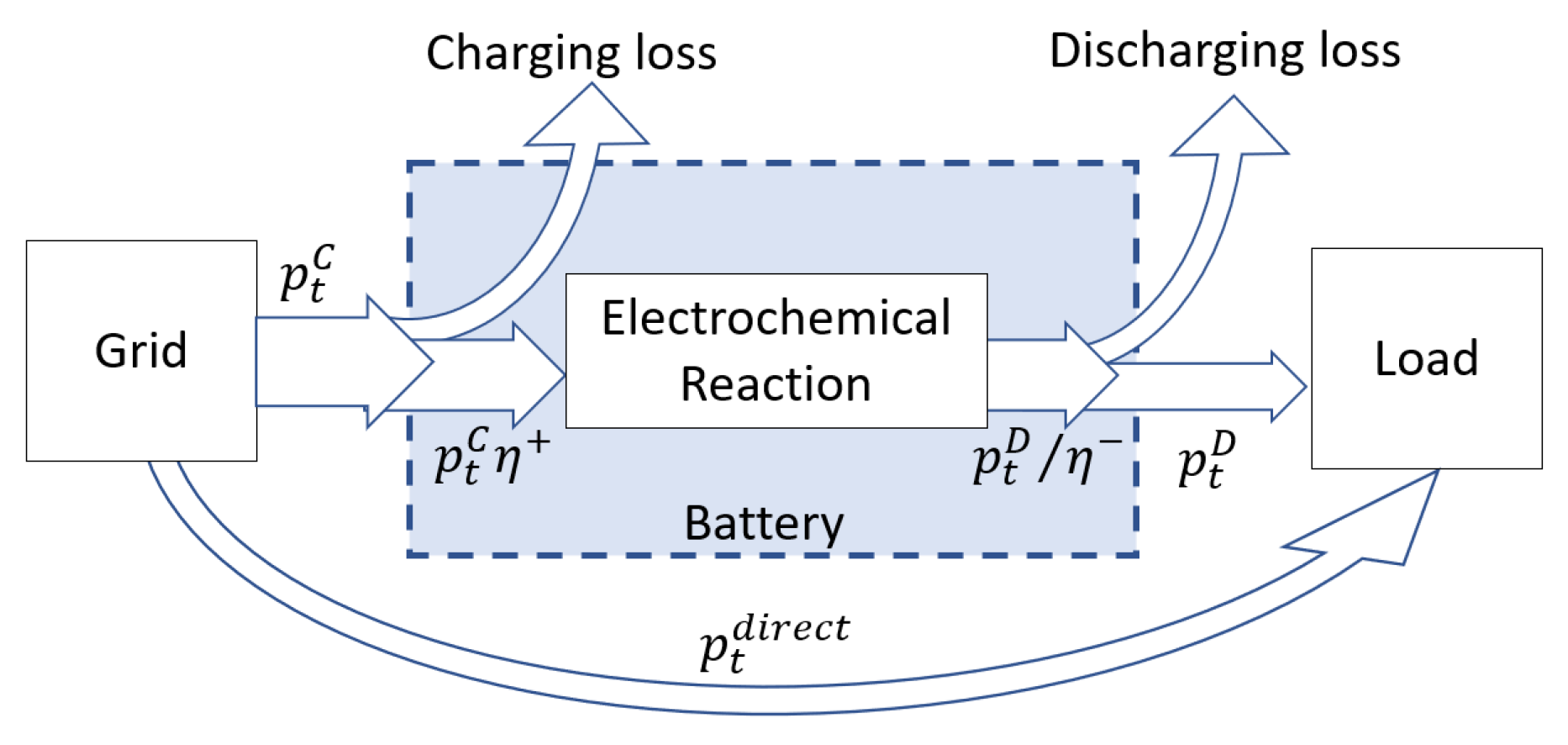
- Energy balance: the state of charge at a certain time, , depends on the state of charge at the immediately previous period of time and the amount of energy that is effectively used in electrochemical reactions during charge or discharge processes:where the efficiencies are as defined previously (see Figure 1).
- In order to preserve the battery life, the state of charge should neither be lower than a minimum fixed value () nor larger than a maximum (). Both these parameters correspond to different fractions of the total available capacity.
- Equations for battery degradation:Battery degradation kinetics are studied in the electrochemistry field by using a parameter known as the [16,17]. The is the inverse of the characteristic time that relates electric current during a time step, in units of A or mA, and the electrical charge capacity of the battery, in units of Ah or mAh.This coefficient allows a size-independent study of the kinetics of any reaction happening in batteries. The fraction of capacity lost by the battery can then be expressed as a function of the .where the functionality f is obtained experimentally by running charge/discharge cycles at different currents, and is usually a non-linear expression. Taking as a basis the experimental data reproduced in Figure S1, it can be seen that can be modeled as a convex second order polynomial.with and parameters that are adjusted to the experimental data.To relate the from its definition (Equation (12)) with the variables used in this problem, a nearly constant working potential of the cell needs to be assumed. In practice, this assumption implies disregarding the effects of the overpotentials in the potential vs. current (E-I) curve. Then, and:Notice that as charge and discharge do not happen simultaneously (see Equations (7) and (15)) can be rewritten to combine both processes in a single equation:At this point, it is worth commenting that natural aging phenomena (just a function of time) has not been considered here as calendar aging is not dependent on the rate of battery use.
2.3. Derivation of an Equivalent Convex Problem
2.3.1. Non-Simultaneous Charge and Discharge
“For energy storage capacity at bus where (the energy storage capacity) , if (the locational marginal price) is strictly positive then (...) simultaneous charging and discharging will not occur”.
2.3.2. Battery Degradation
2.3.3. Problem Statement in Convex Form
3. Optimal Scheduling for a 24 h Period
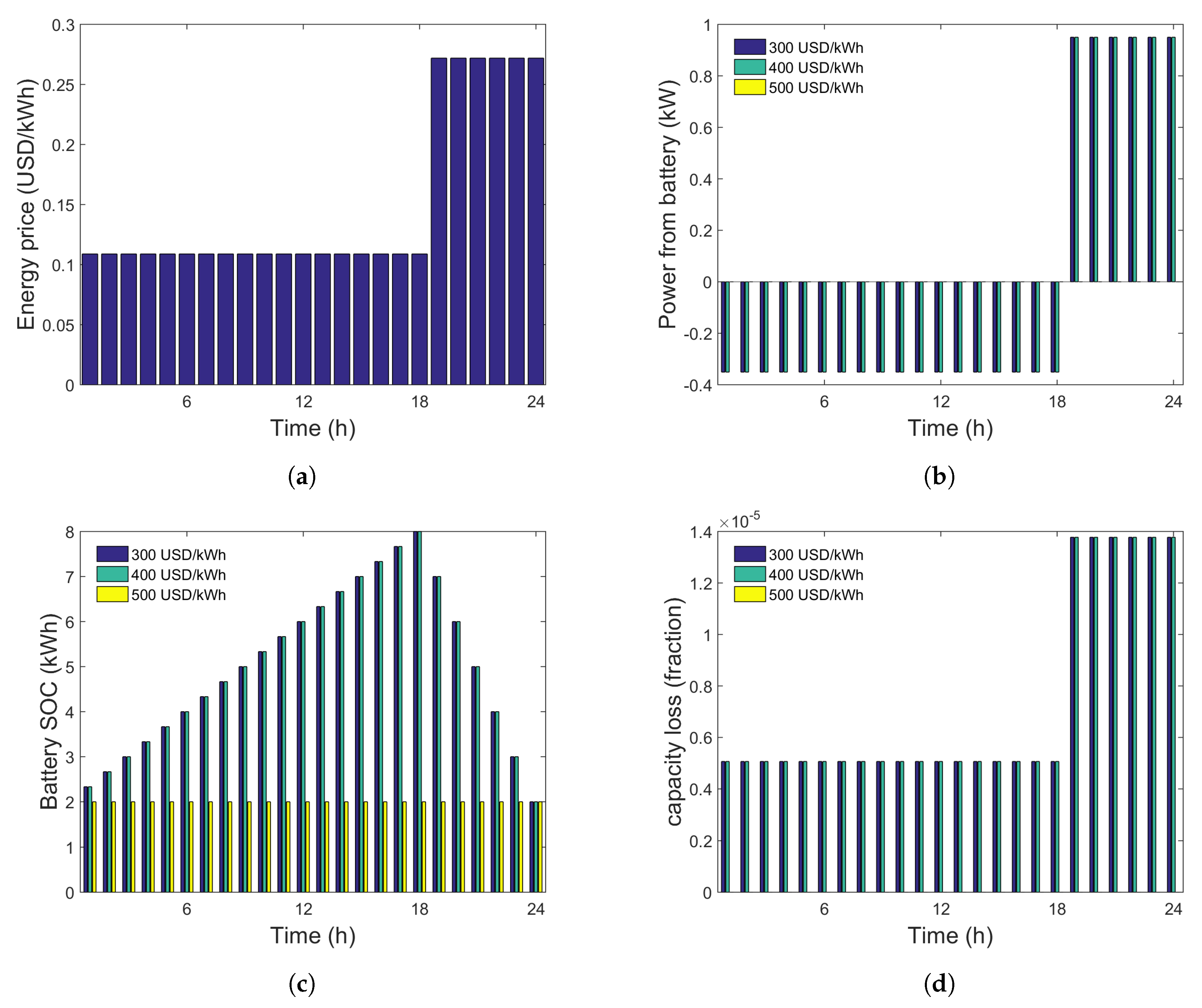
- The “simple tariff” refers to a pricing policy that only has two price steps: cheap (off-peak) and expensive (on-peak), and the daily price pattern is repeated throughout the year. Therefore, there are always some consecutive hours with exactly the same price.
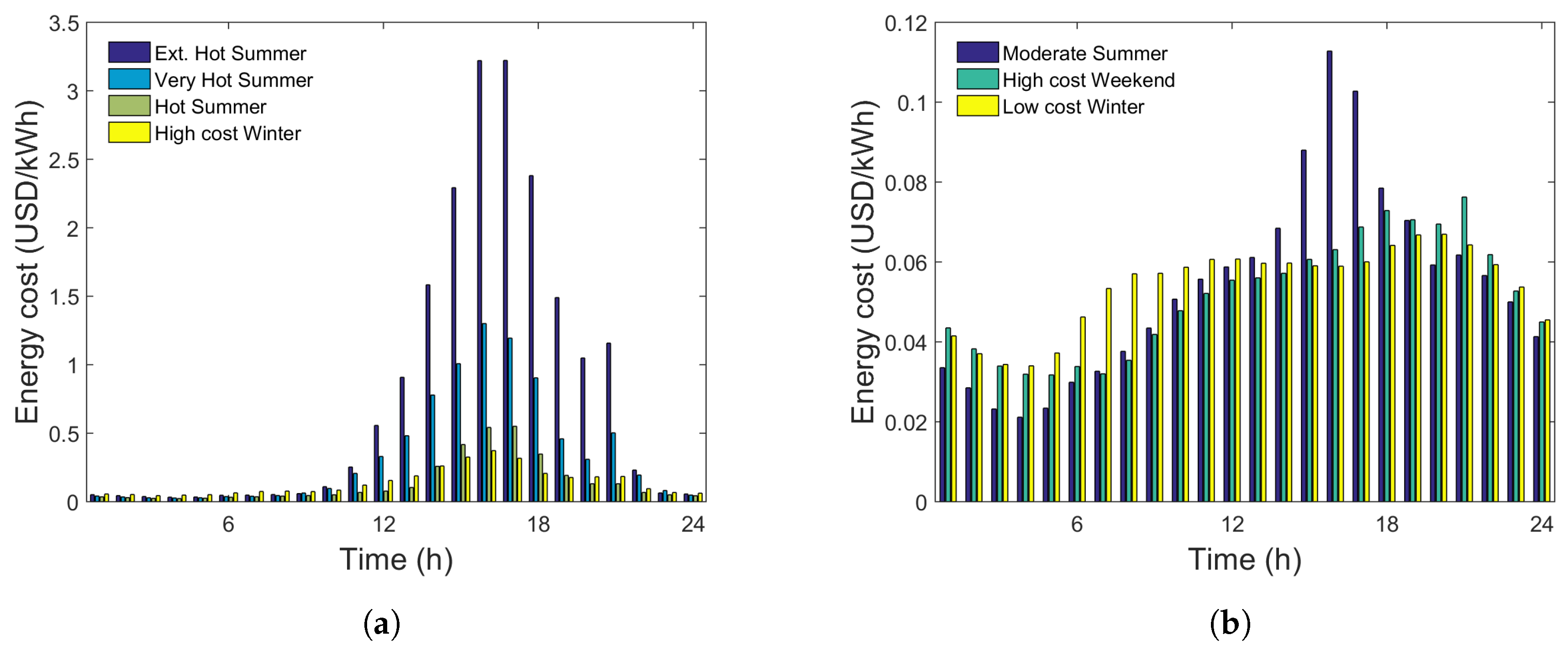
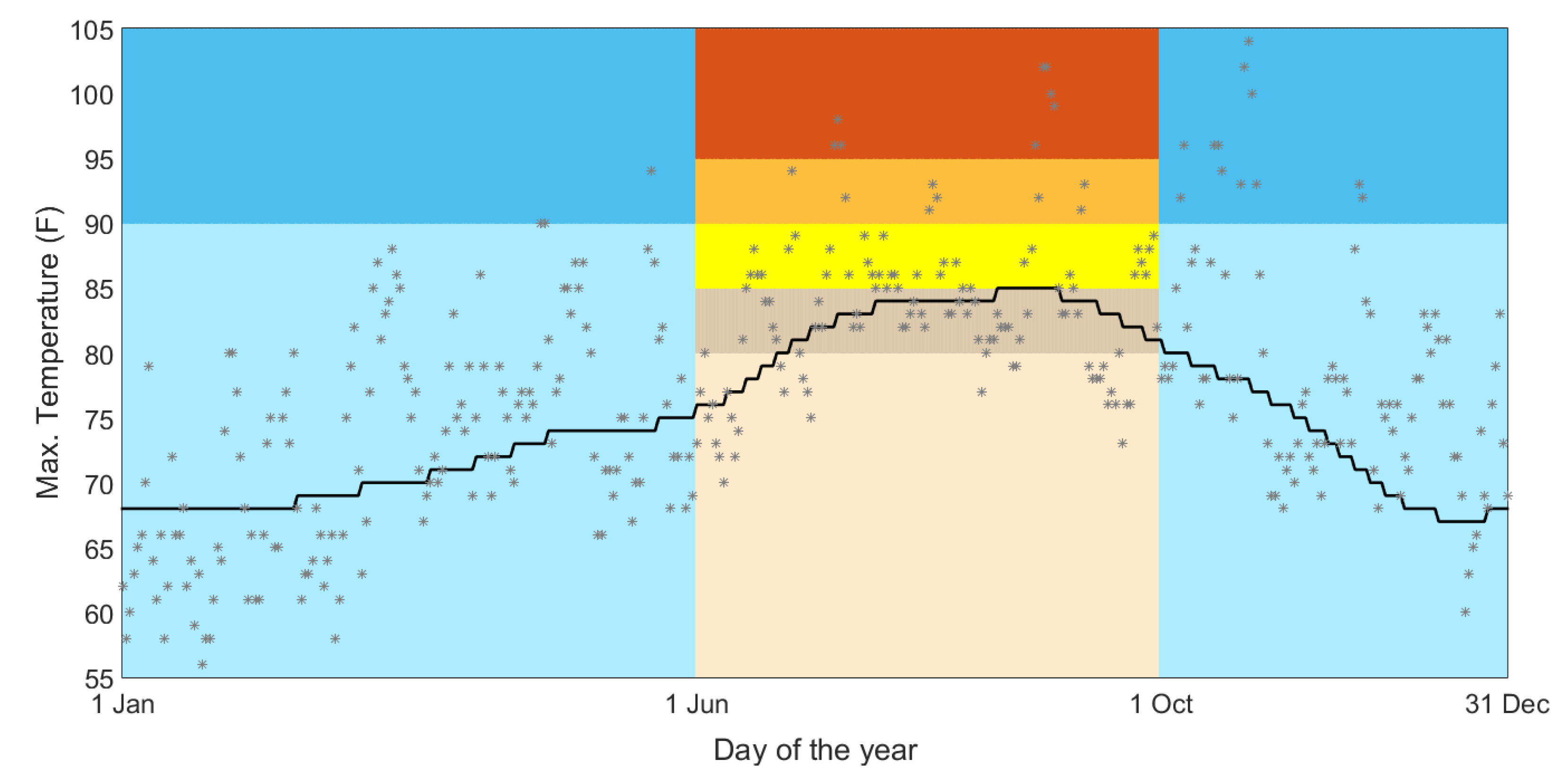
- The “complex tariff” refers to a pricing policy where there are several price steps during a single day (the price is still constant for each hour of the day), different days present different prices (weekdays are priced differently than weekends and holidays and there is also seasonal variation), and prices are dependent on the expected weather.
3.1. Results and Discussion: Simple tariff
3.2. Results and Discussion: Complex Tariff
4. Optimal Scheduling for Long-Term Periods
4.1. Modifications to the Original Problem
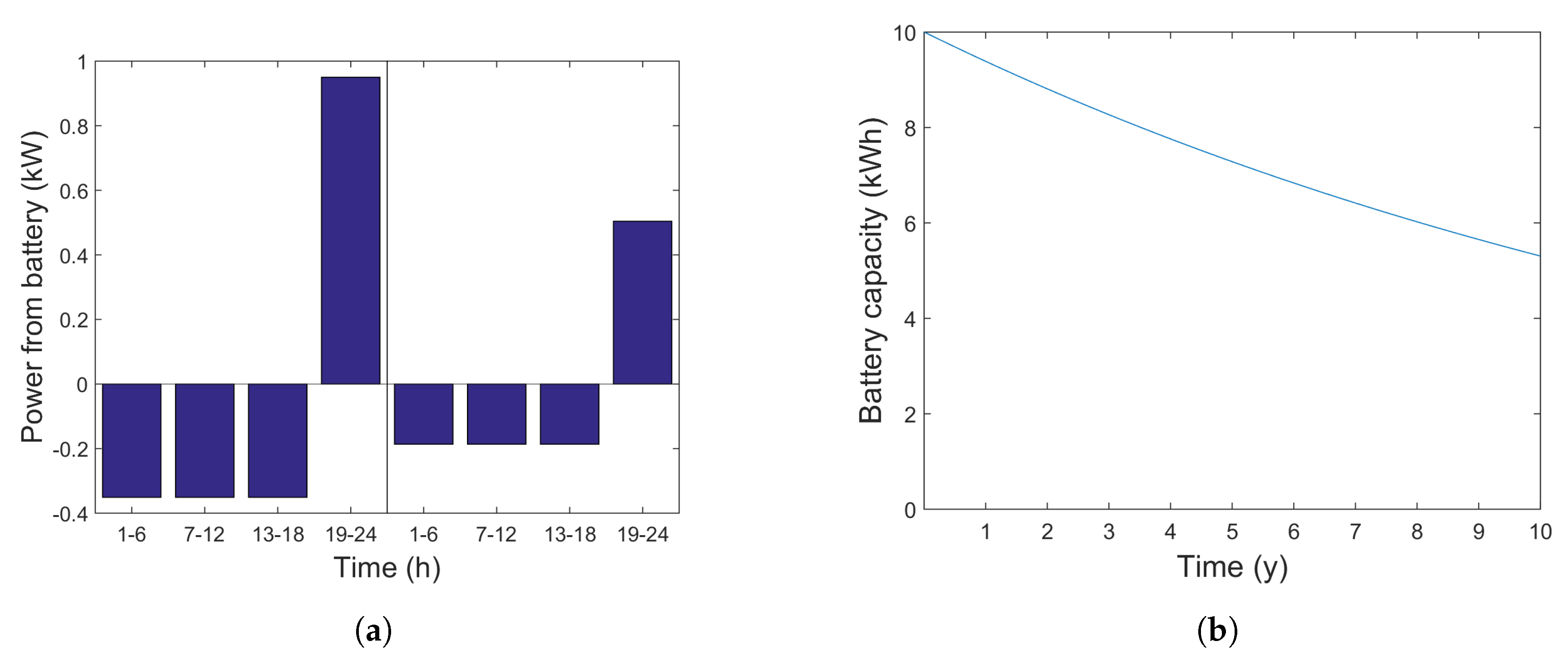
4.1.1. Variable Capacity
4.1.2. Restricted Time Span between Charge and Discharge Periods
- If energy is stored in batteries for a long period of time, self-discharge processes occur. For the sake of simplicity our model has not included these types of processes under the assumption that the charge and discharge cycle of the battery happens in a reasonably short period, most probably during the same day.
- Complex tariffs depend on weather conditions and thus a reliable forecast. In this work we have assumed that reasonable forecasts are given for periods no longer than a week.
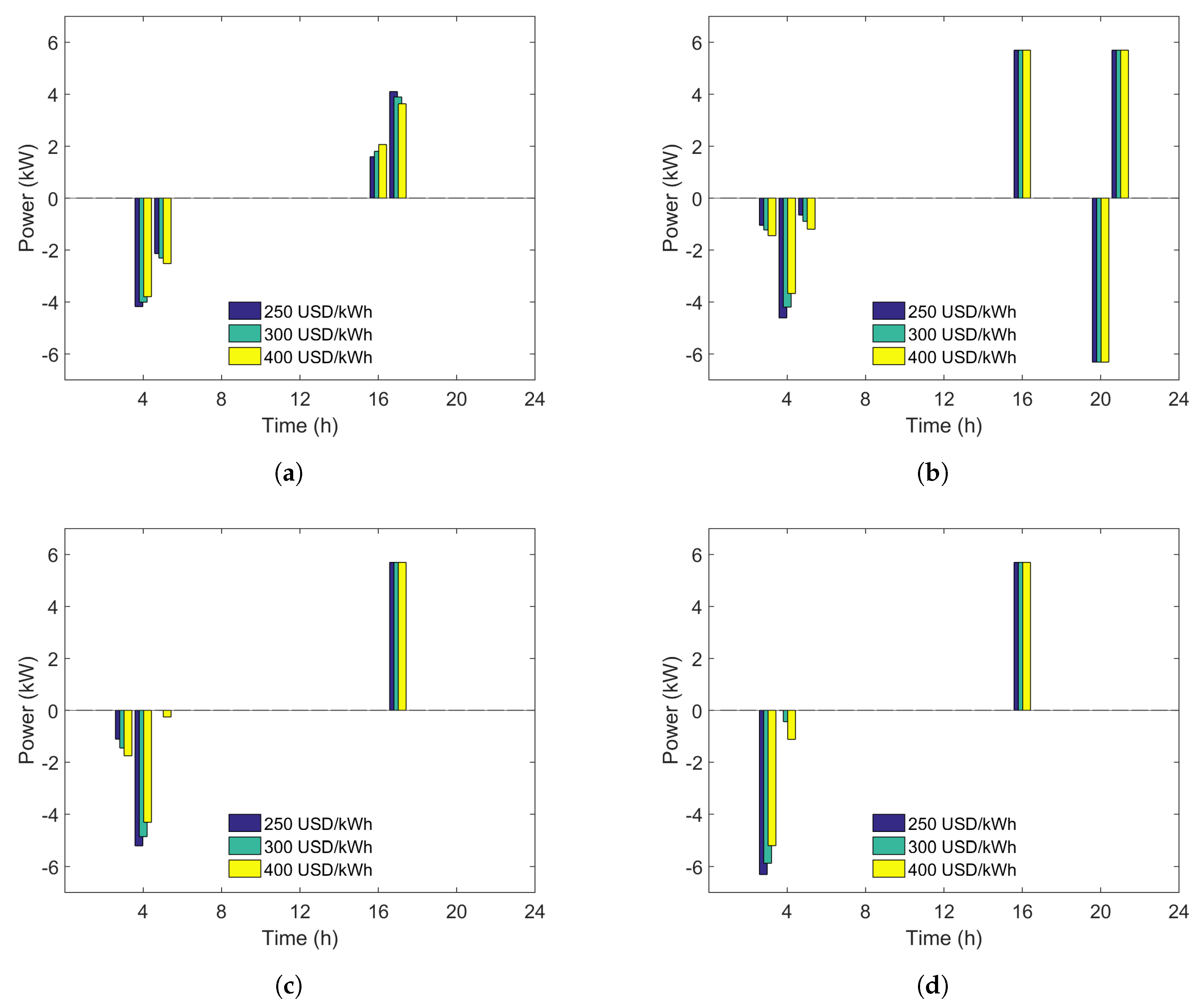
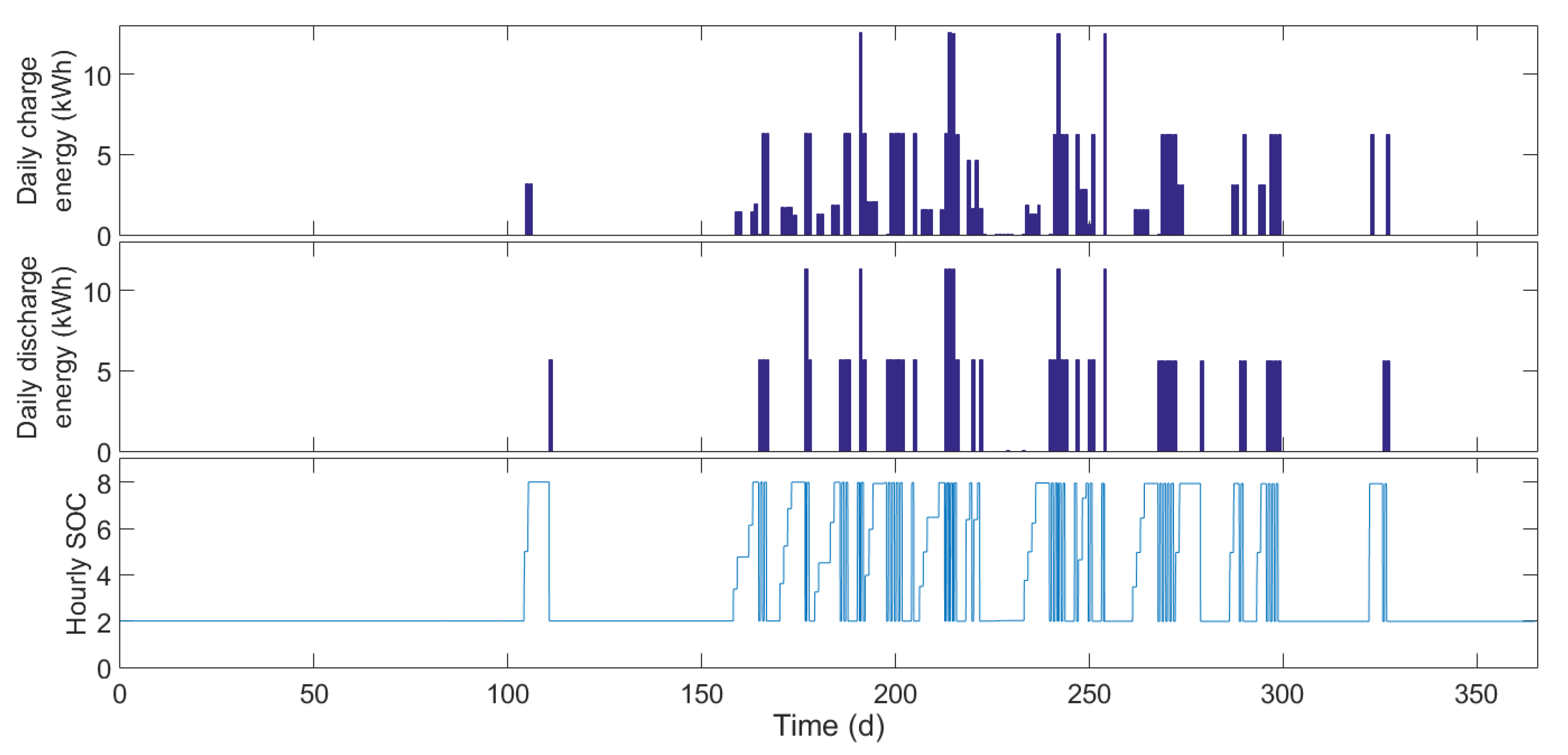
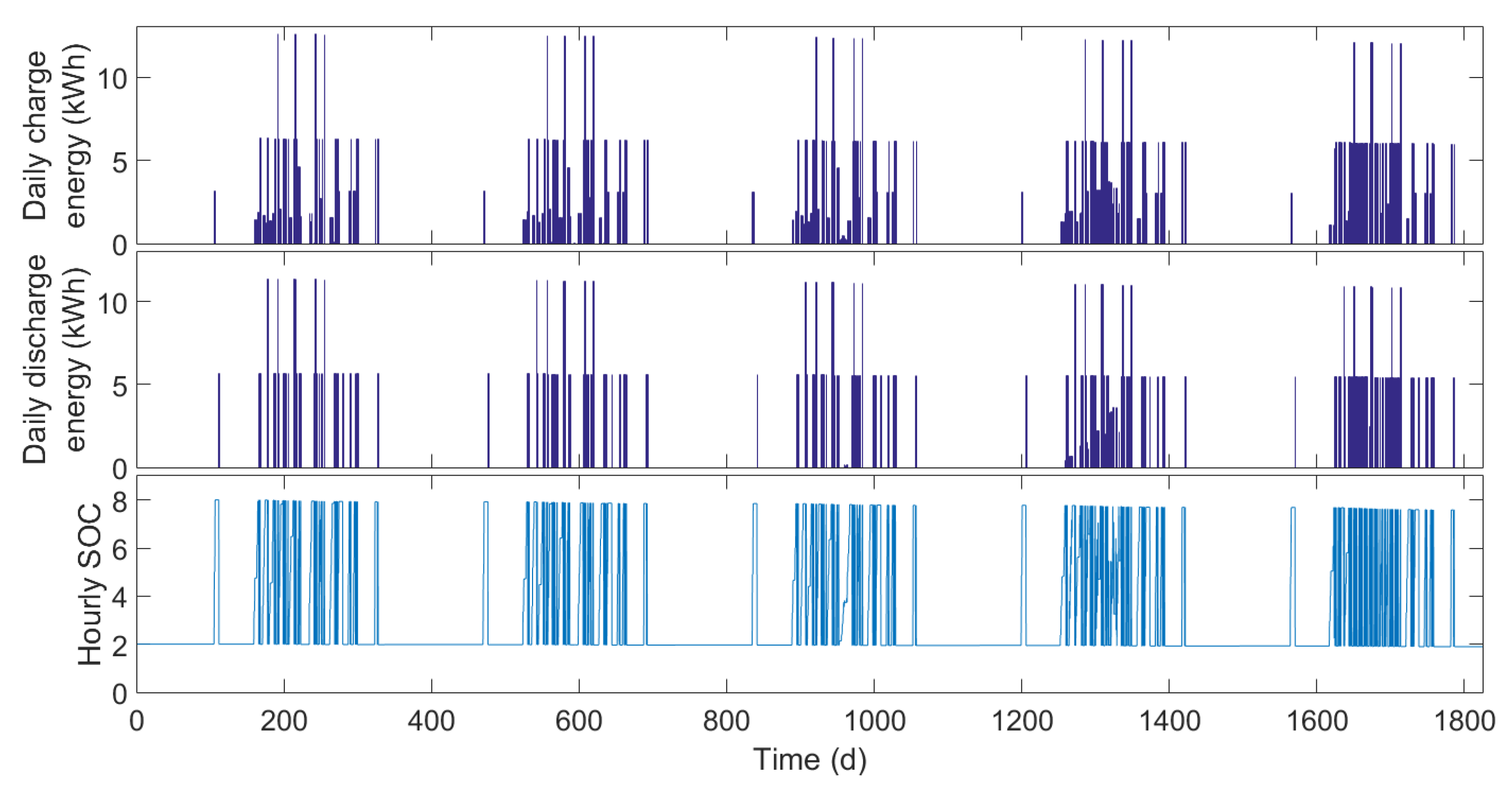
4.2. Results and Discussion: Simple Tariff
4.3. Results and Discussion: Complex Tariff
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| optimization total period of time | |
| battery charging efficiency | |
| battery discharging efficiency | |
| time step | |
| energy storage installed capacity (energy units) | |
| initial energy storage installed capacity (electrical charge units) | |
| energy storage capacity at t (energy units) | |
| dimensionless charge/discharge rate | |
| market cost of battery capacity | |
| terminal potential difference at time t | |
| open circuit potential difference at time t | |
| net current at time t | |
| maximum safe charging power | |
| charge power at time t | |
| maximum safe discharging power | |
| discharge power at time t | |
| r | discount rate |
| state of charge at time t | |
| Minimum required state of charge | |
| Maximum allowed state of charge | |
| fraction of capacity loss during the time step at t | |
| Energy grid price at time t |
References
- Castillo, A.; Gayme, D.F. Grid-scale energy storage applications in renewable energy integration: A survey. Energy Convers. Manag. 2014, 87, 885–894. [Google Scholar] [CrossRef]
- Morales, J.M.; Conejo, A.J.; Madsen, H.; Pinson, P.; Zugno, M. Facilitating Renewable Integration by Demand Response. In Integrating Renewables in Electricity Markets: Operational Problems; Morales, J.M., Conejo, A.J., Madsen, H., Pinson, P., Zugno, M., Eds.; Springer: Boston, MA, USA, 2014; pp. 289–329. [Google Scholar]
- Conejo, A.J.; Sioshansi, R. Rethinking restructured electricity market design: Lessons learned and future needs. Int. J. Electr. Power Energy Syst. 2018, 98, 520–530. [Google Scholar] [CrossRef]
- Mayer, K.; Trück, S. Electricity markets around the world. J. Commod. Mark. 2018, 9, 77–100. [Google Scholar] [CrossRef]
- Samad, T.; Kiliccote, S. Smart grid technologies and applications for the industrial sector. Comput. Chem. Eng. 2012, 47, 76–84. [Google Scholar] [CrossRef]
- Weitzel, T.; Glock, C.H. Energy management for stationary electric energy storage systems: A systematic literature review. Eur. J. Oper. Res. 2018, 264, 582–606. [Google Scholar] [CrossRef]
- United States Department of Energy–Office of Energy Efficiency and Renewable Energy. 2016–2020 Strategic Plan and Implementation Framework. Available online: https://www.energy.gov/ (accessed on 15 August 2018).
- International Energy Agency. Global EV Outlook 2017. Available online: https://www.iea.org/ (accessed on 10 August 2018).
- Reniers, J.M.; Mulder, G.; Ober-Blöbaum, S.; Howey, D.A. Improving optimal control of grid-connected lithium-ion batteries through more accurate battery and degradation modelling. J. Power Sources 2018, 379, 91–102. [Google Scholar] [CrossRef]
- Zhao, Y.; Choe, S.Y.; Kee, J. Modeling of degradation effects and its integration into electrochemical reduced order model for Li(MnNiCo)O2/Graphite polymer battery for real time applications. Electrochim. Acta 2018, 270, 440–452. [Google Scholar] [CrossRef]
- Zhao, X.; Bi, Y.; Choe, S.Y.; Kim, S.Y. An integrated reduced order model considering degradation effects for LiFePO4/graphite cells. Electrochim. Acta 2018, 280, 41–54. [Google Scholar] [CrossRef]
- Sarker, M.R.; Murbach, M.D.; Schwartz, D.T.; Ortega-Vazquez, M.A. Optimal operation of a battery energy storage system: Trade-off between grid economics and storage health. Electr. Power Syst. Res. 2017, 152, 342–349. [Google Scholar] [CrossRef]
- Yan, G.; Liu, D.; Li, J.; Mu, G. A cost accounting method of the Li-ion battery energy storage system for frequency regulation considering the effect of life degradation. Prot. Control Mod. Power Syst. 2018, 3, 4. [Google Scholar] [CrossRef]
- Hu, X.; Martinez, C.M.; Yang, Y. Charging, power management, and battery degradation mitigation in plug-in hybrid electric vehicles: A unified cost-optimal approach. Mech. Syst. Signal Process. 2017, 87, 4–16. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Crompton, T.R. 1–Introduction to battery technology. In Battery Reference Book, 3rd ed.; Crompton, T., Ed.; Newnes: Oxford, UK, 2000; pp. 1–64. [Google Scholar]
- Delacourt, C.; Safari, M. Mathematical Modeling of Aging of Li-Ion Batteries. In Physical Multiscale Modeling and Numerical Simulation of Electrochemical Devices for Energy Conversion and Storage: From Theory to Engineering to Practice; Franco, A.A., Doublet, M.L., Bessler, W.G., Eds.; Springer: London, UK, 2016; pp. 151–190. [Google Scholar]
- Jabr, R.A.; Karaki, S.; Korbane, J.A. Robust Multi-Period OPF With Storage and Renewables. IEEE Trans. Power Syst. 2015, 30, 2790–2799. [Google Scholar] [CrossRef]
- Castillo, A.; Gayme, D.F. Profit maximizing storage allocation in power grids. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 429–435. [Google Scholar] [CrossRef]
- Fortenbacher, P.; Andersson, G. Battery degradation maps for power system optimization and as a benchmark reference. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ruan, Y.; Song, X.; Fu, Y.; Song, C.; Battaglia, V. Structural evolution and capacity degradation mechanism of LiNi0.6Mn0.2Co0.2O2 cathode materials. J. Power Sources 2018, 400, 539–548. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- GAMS Documentation of IPOPT. Available online: https://www.gams.com/ (accessed on 26 September 2018).
- UTE. Pliego Tarifario 2018. Available online: https://portal.ute.com.uy (accessed on 7 May 2018).
- Southern California Edison. TOU-GS-2-RTP. Available online: https://www.sce.com/ (accessed on 20 February 2018).
- ANEEL. Tarifa Branca. Available online: http://www.aneel.gov.br/tarifa-branca (accessed on 20 August 2018).
- MidAmerican Energy. Electric Tariffs Iowa. Available online: https://www.midamericanenergy.com (accessed on 20 August 2018).
- LAZARD. LAZARD’s Levelized Cost of Storage Analysis—Version 3.0. Technical Report. 2017. Available online: https://www.lazard.com/perspective/levelized-cost-of-storage-2017/ (accessed on 9 July 2018).
- Asif, A.; Singh, R. Further Cost Reduction of Battery Manufacturing. Batteries 2017, 3, 17. [Google Scholar] [CrossRef]
- AccuWeather. Available online: https://www.accuweather.com (accessed on 15 August 2018).
| Operation Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Annual savings (USD) | 305 | 286 | 269 | 252 | 237 | 222 | 208 | 196 | 184 | 172 |
| (USD/kWh) | (USD) | (USD) | (USD) |
|---|---|---|---|
| 400 | −2374 | −2497 | −2606 |
| 300 | −1374 | −1497 | −1606 |
| 200 | −374 | −497 | −606 |
| 150 | 126 | 3 | −106 |
| 100 | 626 | 503 | 394 |
| (USD/kWh) | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 |
|---|---|---|---|---|---|
| Electricity annual savings (USD/year) | |||||
| 200 | 223 | 230 | 230 | 226 | 223 |
| 250 | 223 | 220 | 218 | 221 | 226 |
| 300 | 223 | 220 | 218 | 216 | 214 |
| Annual capacity loss (%) | |||||
| 200 | 0.96 | 1.29 | 1.37 | 1.35 | 1.34 |
| 250 | 0.94 | 0.93 | 0.93 | 1.09 | 1.34 |
| 300 | 0.94 | 0.93 | 0.92 | 0.92 | 0.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corengia, M.; Torres, A.I. Effect of Tariff Policy and Battery Degradation on Optimal Energy Storage. Processes 2018, 6, 204. https://doi.org/10.3390/pr6100204
Corengia M, Torres AI. Effect of Tariff Policy and Battery Degradation on Optimal Energy Storage. Processes. 2018; 6(10):204. https://doi.org/10.3390/pr6100204
Chicago/Turabian StyleCorengia, Mariana, and Ana I. Torres. 2018. "Effect of Tariff Policy and Battery Degradation on Optimal Energy Storage" Processes 6, no. 10: 204. https://doi.org/10.3390/pr6100204
APA StyleCorengia, M., & Torres, A. I. (2018). Effect of Tariff Policy and Battery Degradation on Optimal Energy Storage. Processes, 6(10), 204. https://doi.org/10.3390/pr6100204





