1. Introduction
Agglomeration and fragmentation (or breakage) processes are used to accommodate a change in the particle properties of the granules in the pharmaceutical and food industries. Other applications that involve these processes are crystallization, flocculation, the formation of water droplets, sprayed fluidized bed granulation (SFBG) and twin screw granulation (TSG) [
1,
2,
3]. Among sprayed fluidized bed granulation and twin screw granulation, SFBG is adopted for the production of granular materials due to its potential to conduct granulation or agglomeration at low costs [
4]. SFBG has applications in the food industry, as it is used for size enlargement of food ingredients. Moreover, it has major applications in the pharmaceutical industry because of its ability to produce identical granules, less dust content, superior wetting, etc. [
5]. In the literature, many authors have attempted to model SFBG by considering the system to be well mixed [
6], but in reality, it is a non-homogeneous system. The issue of inhomogeneity may be handled partially by introducing the compartmental modelling [
7,
8].
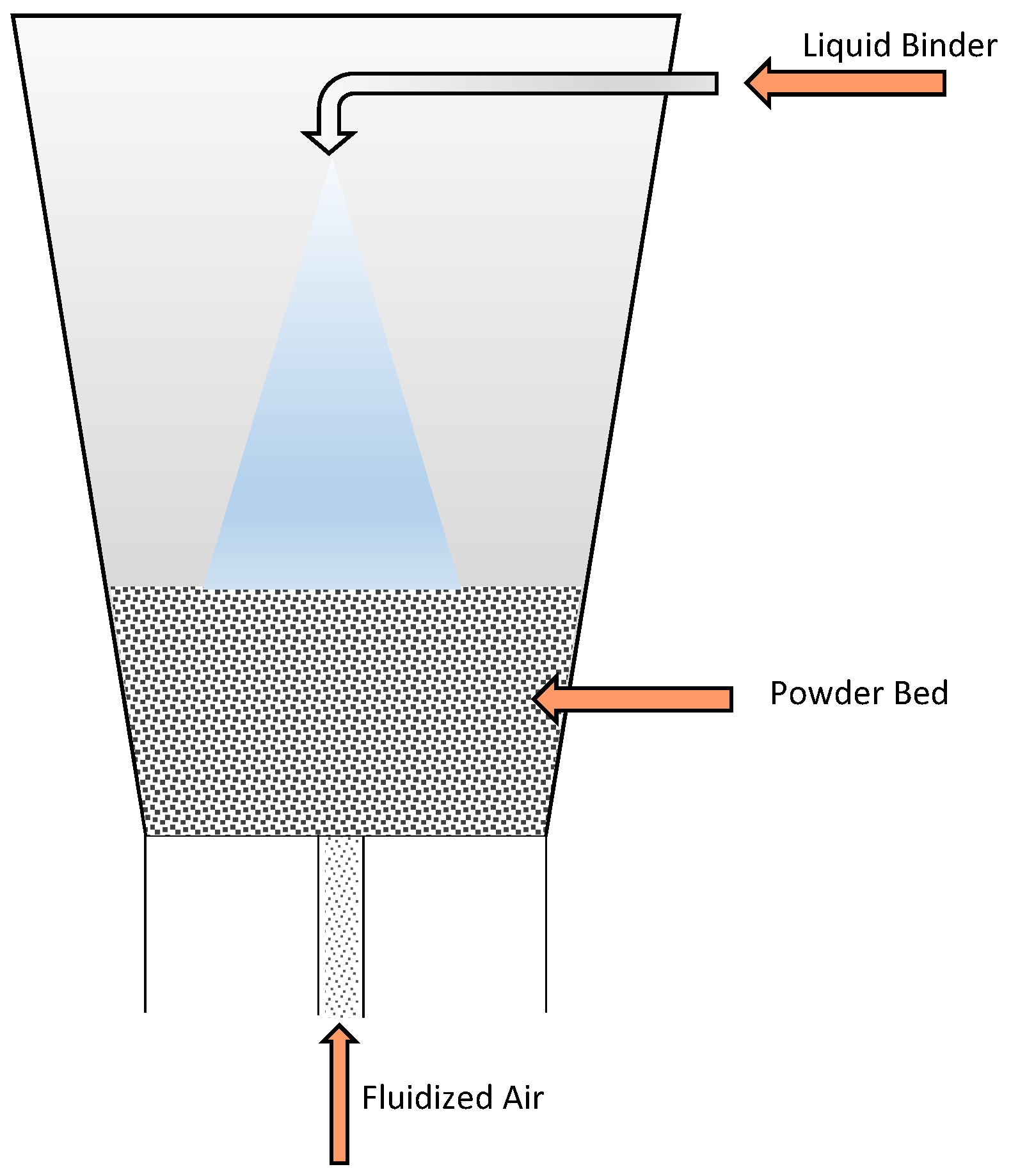
For our study, a top SFBG is divided into two compartments, as shown in
Figure 1.
In the wet zone, the particles are sprayed in and wetted with the binder, which leads to the formation of bridges between the particles or layering on the surface of the particles. In contrast, in the dry zone, breakage leads to the formation of the new particles due to the breaking of drying bridges, which were already formed due to solidification of the particles. During the compartmentalization of SFBG, the particle residence time in both zones plays a very important role. The residence time of particles in the wet zone and dry zone are of equal importance because the particle sizes are actually growing in the spray zone due to the aggregation process, whereas in the other zone, the particles will have a greater chance to be in contact with the hot air, which leads to the fragmentation of the particles into smaller classes. In this work, various sizes of wet zones are considered, ranging from 14% to 30%, and in the dry zone from 70–86% of the total size [
9]. In addition to this, the mass flow rate at which particles are exchanged between the two zones is also a major issue.
The dynamics of the particle size distribution inside the compartments of the compartmental model evolves due to the aggregation and breakage mechanisms and can be tracked by a population balance model. The aggregation and breakage population balance equations (PBEs) corresponding to wet and dry zones can be written as follows:
and:
with respect to the initial condition
The integrals present on the right-hand side of Equation (
1) represent the birth and death of particles in the system. Moreover, the aggregation kernel
denotes the rate at which the large-sized particles are formed from the smaller-sized particles due to aggregation. Additionally, the aggregation kernel is a non-negative function (
) and symmetric with respect to the internal coordinates, that is
. For the breakage Equation (
2),
is the selection function, and it expresses the rate at which particles of size
r are selected to break into smaller fragments. The fragmentation function
is the probability density function denoting the formation of daughter particles of size
r due to the breakage of the parent particles of size
s. The fragmentation function must satisfy the following conditions:
and:
Equation (
4) represents the mass conservation between the parent particle and the smaller-sized fragments. For a practical scenario,
must be greater than or equal to two. The integral properties such as the moments of the distribution corresponding to Equations (
1) and (
2) are also important to calculate. Moreover, the
i-th moment can be defined as:
Here, represents the total number of particles, whereas signifies the total mass of particles in the system.
In this study, our main objective is to propose a mathematical model and develop a new numerical approximation for solving the proposed compartmental model. Various earlier numerical methods were developed to solve these kinds of complex models. Among them, the cell average technique [
7,
10] and Hounslow’s discretization [
8,
11] are well-established methods known for their accuracy. However, the major disadvantage of these methods is that they have a very complex mathematical formulation and, hence, are computationally very expensive. This leads to the choice of finite volume schemes [
12,
13,
14]. In order to verify the accuracy of the mathematical model, the numerical results are validated by deriving the new analytical solutions by choosing various combinations of aggregation kernels and the binary fragmentation function with the linear selection function.
The rest of paper is structured as follows: In
Section 2, we briefly describe the two-compartment model and the assumptions considered for simulating a top SFBG. The next section is devoted to providing the formulation of the proposed numerical scheme for solving the set of equations. In
Section 4, the accuracy and efficiency of the proposed method are tested by comparing the results with the newly-developed analytical results for moments. Finally,
Section 5 summarizes the conclusions of this study.
2. Two-Compartment Model for Sprayed Fluidized Bed Granulation
In this section, a top-sprayed fluidized bed granulator and its compartmentalization are discussed in detail. At the top of the granulator, a nozzle is fixed by which the liquid binder is sprayed over the particles in the granulator. The particles are considered to be spherical, placed at the bottom of the granulator as shown in
Figure 1. When the hot air enters into the granulator from the bottom, the particles placed at the bottom put into a random motion, and collisions take place between the particles. At the same time, the particles become wet because of the liquid binder, which leads to the aggregation and breakage processes inside the SFBG.
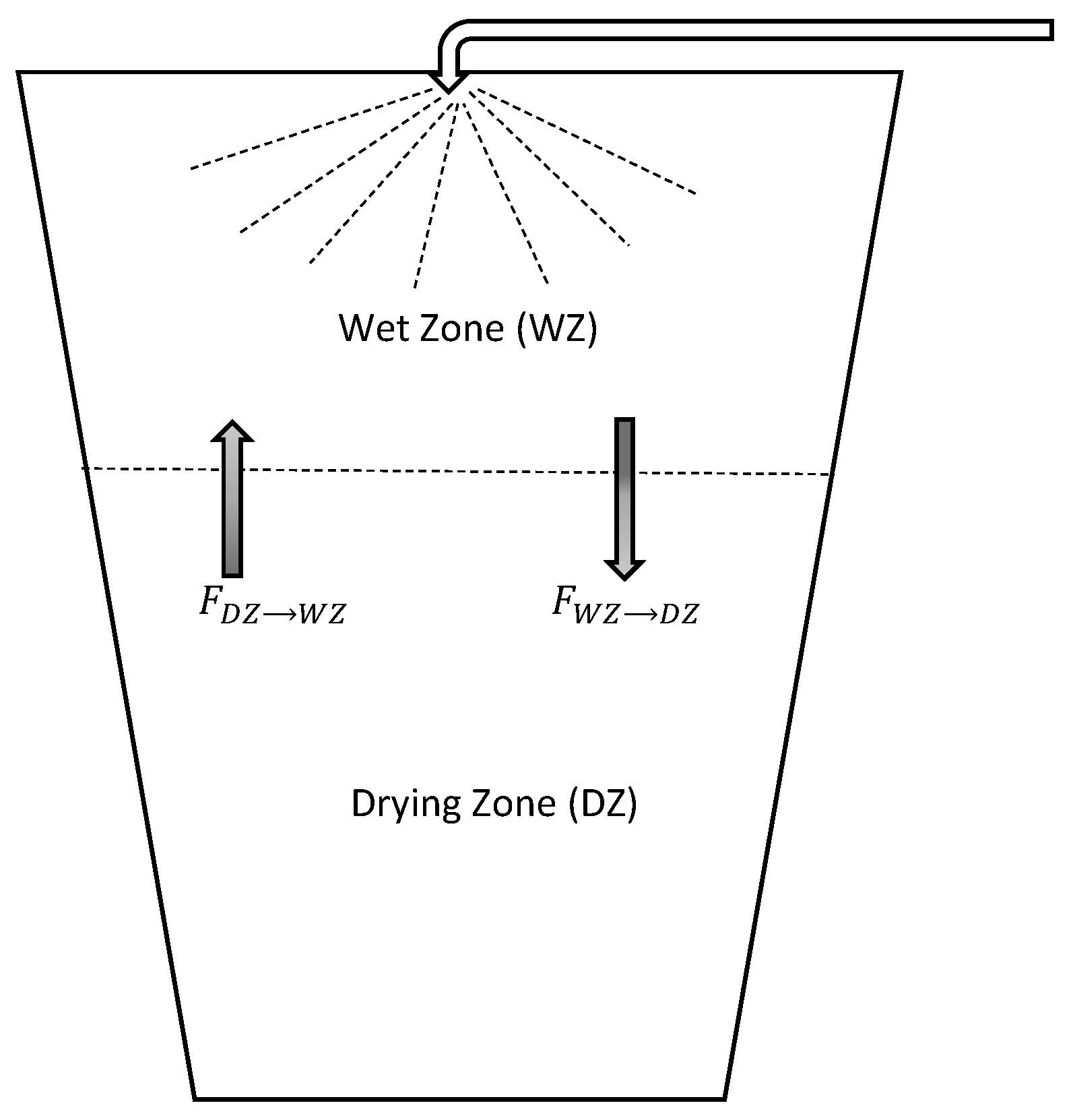
For the compartmental modelling, the granulator is divided into zones based on the dominating mechanism occurring in a particular part of the granulator. The top of the granulator is the first compartment, named the Wet Zone (
), as in this area, the particles are becoming wet; whereas, the bottom of the granulator is called the Drying Zone (
), as the liquid binder on the particles is becoming dry because of the hot air. The schematic diagram of the compartment modelling of the system is shown in
Figure 2. The assumptions that were made for the development of the model are given below:
The system is divided into two compartments:
- (a)
the first compartment, that is the wet zone, is represented by fraction , and the volume is ,
- (b)
the second compartment, that is the dry zone, is represented by the fraction , and the volume is , where V is the total volume of the reactor.
Each compartment (, as well as ) is considered to be a well-mixed system.
The size of both compartments remains constant during the process.
The mass in each compartment should be constant at each time step.
The rate of exchange of volume flux between the compartments is constant during the process.
The residence time in the wet zone and in the dry zone is taken to be
and
, respectively. Moreover, the total time taken by the particle to complete one cycle of the system is
. Assume
and
are the number density functions in
and
respectively. The volume flux from
to
is:
and volume flux from
to
is
Based on aforementioned notations and formulating population balances for both compartments, the mathematical model for the wet zone can be written as:
and for the dry zone, the mathematical model is given by:
corresponding to initial conditions
.
In Equation (
6),
is the aggregation kernel, which defines the rate at which the particles having properties
r and
s aggregate. In Equation (
7),
exhibits the selection function, which defines the selection of a particle property
s to break into smaller particles. Moreover,
is the probability density function, which defines the formation of particle size
r due to the breakage of particle property
s.
Finite Volume Scheme
In this section, the modification of the Finite Volume Schemes (FVS) developed by [
15,
16] is done to approximate the coupled system of Equations (
6) and (
7). The basic notion of the scheme is to convert the integro-partial differential equation into the system of ordinary differential equations. To solve the given system of equations using FVS, firstly, the particle size domain should be discretized into small bins. The lower and upper boundaries of the
i-th bin are
for
with
. Assume that the representative of the
i-th bin is denoted by
, which defines the average of the lower and upper boundaries of the
i-th bin, that is,
Let us define the set
as:
which consists of all those pairs of the indices of the bins
j and
k such that the aggregate of particle properties of bins
j and
k, that is
, will fall in the bin having indices
i. Moreover, the average value of
and
in the
i-th bin, which are approximations of the number density function
and
corresponding to wet and dry zones, respectively, are given by:
Here, denotes the step size of the domain.
Now, on integrating Equations (
6) and (
7) from
to
and implementing the idea of FVS on the aggregation and breakage birth and death terms, we get:
and:
with
. These factors
are defined as:
and
where
The detailed explanation of the formulations of both numerical schemes corresponding to aggregation and breakage processes can be found in [
15,
16], respectively. Moreover, it can be noticed from Equations (
10) and (
11) that the correction factors added to both equations are only responsible for conserving the total mass of the system (first order moment) in each zone. However, it does not give any account of the preservation of the total number of particles (zeroth order moment) in each zone. Therefore, it will be interesting to see how accurately the zeroth order moment of both zones is calculated by the modified finite volume schemes. Further, for the verification of the proposed methods, the analytical (or exact) solutions of the different order moments are found for different combinations of aggregation kernel
and breakage function
. In particular, simple structured aggregation kernels, that is sum and product kernels for the wet zone and binary breakage function with the linear selection function for the dry zone, are considered. In the next section, the detailed derivation of the analytical results to verify the numerical approximations is provided.
3. Derivation of the Analytical Solutions for Moments
To verify the discretization of the system of ordinary differential Equations (
10) and (
11), we validate it against the analytical results that will be derived in this section. Due to the pairing and complex nature of the system of Equations (
6) and (
7), the number density function cannot be easily obtained. Therefore, the exact solutions of the zeroth order moment and first order moment for specific combinations of kernels are derived. Let us define the zeroth moment in each compartment as:
and the first moment in each compartment as:
Now, the expressions for the zeroth moment of the number density model given in Equations (
6) and (
7) will be derived. Integrating both sides of Equations (
6) and (
7) with respect to
r from zero to ∞, applying the change of order of integration to (
6) and using Equations (
13) and (
14), the following equations are obtained:
and:
The analytical solutions of (
15) and (
16) are derived for the following combinations of kernels:
Case 1: additive aggregation kernel, linear selection function with binary breakage kernel, that is .
Case 2: product aggregation kernel, linear selection function with binary breakage kernel, that is .
3.1. Case 1
Firstly, we choose additive aggregation kernel () corresponding to the wet zone and binary breakage function () with linear selection function () for the dry zone. For the binary breakage function, only two objects are produced per fragmentation event.
On substituting the aggregation kernel
in Equation (
15), the following is obtained:
Similarly for the
, on putting the values of
and
in Equation (
16), this gives:
as
is the average number of fragments in which a particle of size
s has broken, and for the case of binary breakage, the value of
k is two.
Finally, the following set of equations is formed:
As we know,
, where
V is the total volume of the system, and for the simplicity, let us consider
. Let
,
,
,
and
. The expression for the zeroth moment, i.e., total number of particles in the wet zone and dry zone for this particular case, is:
where:
3.2. Case 2
Analogous to the previous case, analytical moments of the wet and dry zones are also derived for the combination of product kernel () corresponding to the wet zone and binary breakage function () with linear selection function ().
On putting the aggregation kernel
in Equation (
15), it gives:
For
, the simplified equation is the same as derived in the previous case,
Therefore, for this case, the system of equations comes out as:
The analytical solution for the above-defined system of equations is:
where:
However, the analytical solution of the total mass in each compartment for both combinations of kernels is:
as the total mass of particles in each zone remains constant. Here,
is the initial total mass of the particles in the system.
4. Results and Discussion
In this section, the compartmental model of the sprayed fluidised bed granulator solved numerically is tested with various combinations of aggregation and breakage kernels. To check the accuracy of the numerical methodologies, the numerical results are compared with analytical solutions derived for combinations of additive and product aggregations kernels and the binary breakage kernel with the linear selection function in
Section 4. In addition, the quantitative relative errors in the zeroth and first order moments obtained for sum and product kernels are also computed using the following expression:
where
and
denote the analytical and numerical number of particles predicted in the
j-th cell, respectively. Moreover, the values
and
denote the relative errors in the zeroth and first order moments, respectively. All the numerical simulations were carried out using MATLAB 2015a on a i5 CPU with 2.67 GHz and 8 GB RAM. The system of ODEs derived in Equations (
10) and (
11) were solved using ode15 s solver in MATLAB.
To compute the numerical results using finite volume schemes, the size domain range from to was divided into 151 cells. Moreover, the comparison is presented by varying the size of the wet zone, in particular the value of was taken to be and .
4.1. Additive Aggregation Kernel and Binary Breakage with the Linear Selection Function
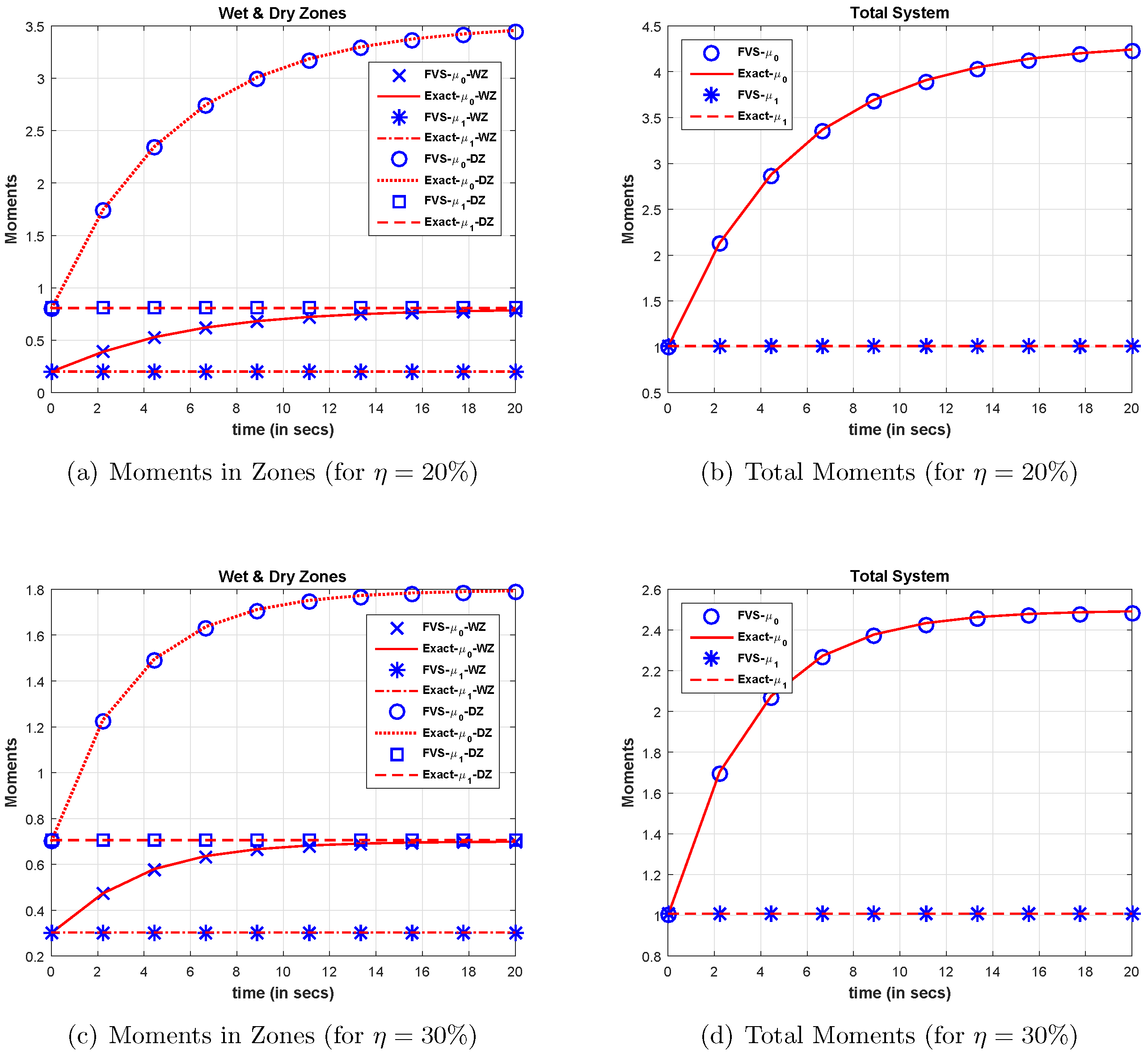
In this section, the comparison in terms of various moments obtained using is conducted with analytical moments for the additive kernel (). For the analytical solutions corresponding to the additive kernel, the value of was considered to be one. For calculating the numerical results, the simulations were run till time s.
Figure 3a,c reveals that the zeroth moments approximated numerically for wet and dry zones, respectively, matched well with the analytical moments. Moreover,
Figure 3b shows the comparison of the total number of particles in the system (combining wet and dry zones), which reveals that the modified FVS agreed well with the analytical total moment. It is important to note that no account for the preservation of the total number of particles in the system has been taken, but still, the modified finite volume scheme was highly accurate in computing the zeroth order moment. Moreover, it can also be observed that as the size of the wet zone increased from
to
, the total system acquired the steady state at time
s (for
wet zone), whereas for
wet zone, the system acquired the steady state at time
s. This is due to the fact that less particles were present in the wet zone for aggregation, whereas more particles in the dry zone were available that underwent the formation of smaller sized particles due to fragmentation process, which delayed the steady state. Additionally, when the size of the wet zone was increased, more particles were contributing towards the aggregation mechanism, and the number of particles in the dry zone decreased. Consequently, this further helped the system to achieve the steady state earlier.
In addition, the first order moments computed corresponding to both zones (wet and dry) showed consistent numerical results, that is they agreed well with the analytical first moments. This affirms that the total mass in both zones remained conserved. Moreover,
Figure 3d exhibits the comparison of the total mass in the system (combining wet and dry zones), which coincides well with the analytical total first moment. Furthermore, the quantitative relative errors of the zeroth and first order moments calculated using (
19) are listed in
Table 1. One can observe that the relative errors in the moments of both zones, as well as in the total system increased as the size of the wet zone was incremented from
to
.
4.2. Product Kernel and Binary Breakage with Linear Selection Function
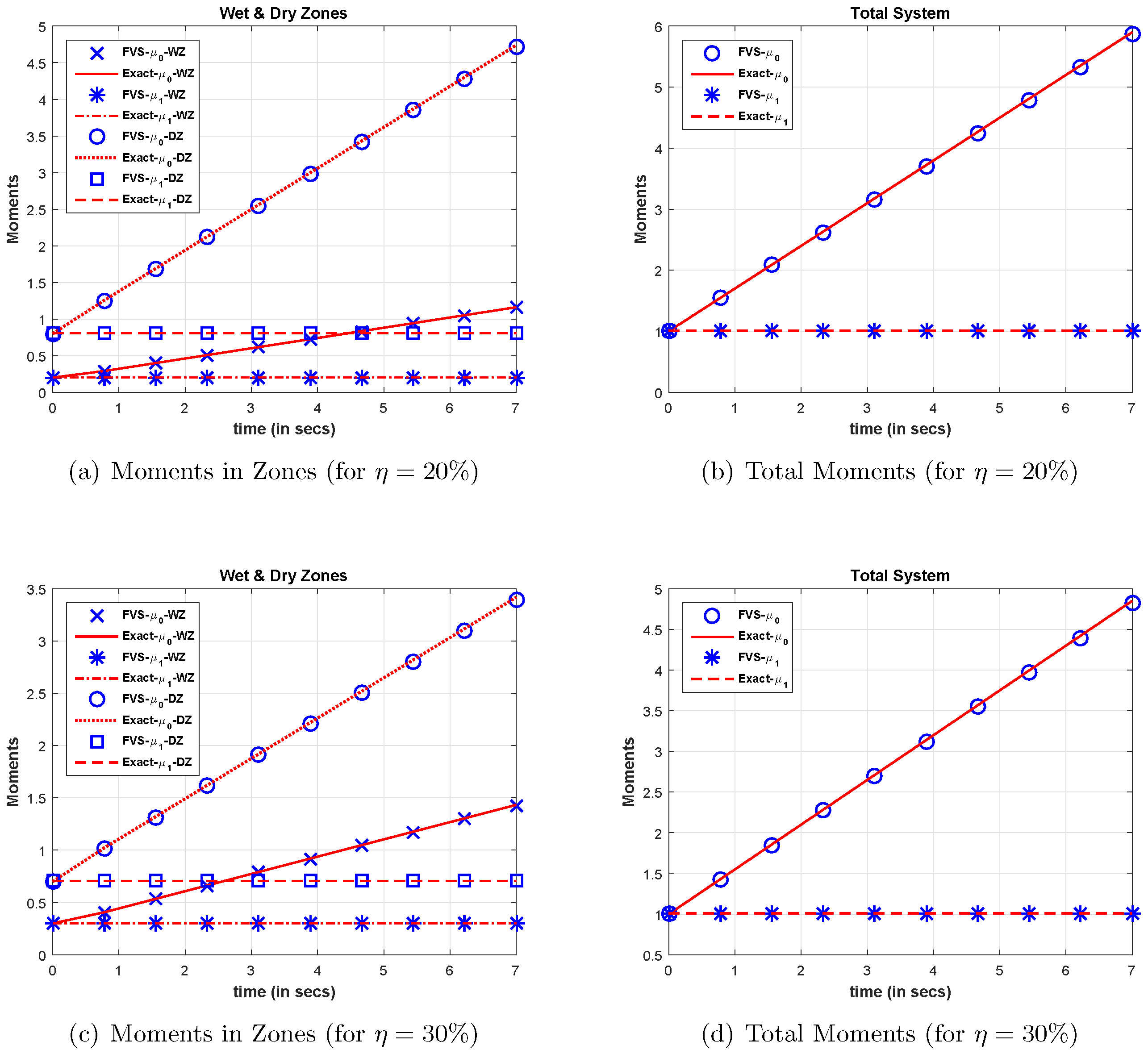
Similar to the sum kernel, for and , the numerical moments computed using finite volume scheme are compared with the newly-derived analytical results for a product kernel, that is . For the comparison, the value of was considered similar to the previous case. The simulations were run till time s for calculating the numerical results.
The product kernel was a gelling kernel for any arbitrary particle size distribution [
17]. Therefore, the simulation in this case was performed until the product kernel showed the gelling behaviour. The kernel exhibited gelling behaviour when the newly-forming particles aggregated at a greater frequency than their parents. The various order moments computed numerically were compared with the analytical moments, as shown in
Figure 4. The numerical results reveal that the zeroth and first order moments corresponding to wet and dry zones showed very consistent approximations and coincided well with the analytical moments (see
Figure 4a,c). Moreover, the numerical total zeroth and first order moments shown in
Figure 4b,d corresponding to the whole system matched well with the analytical results.
In contrast to the additive kernel, for the product kernel, no steady state was achieved by the system corresponding to
and
wet zones (see
Figure 4). This was due to the fact that a greater number of particles was available in the dry zone and hence produced a greater number of smaller particles. In contrast to the dry zone, a lesser number of particles was available for the formation (or aggregation) process, hence producing much smaller particles. Analogous to the additive kernel, the quantitative relative errors existing in zeroth and first order moments were also calculated for a product kernel using Expression (
19) (see
Table 2). The trend of the relative errors in both order moments was similar to the additive kernel, that is the relative errors in both order moments increased as the value of
varied from 20% to 30%.