A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations
Abstract
1. Introduction
2. Materials and Methods
2.1. Modeling of the Multicellular Dynamics
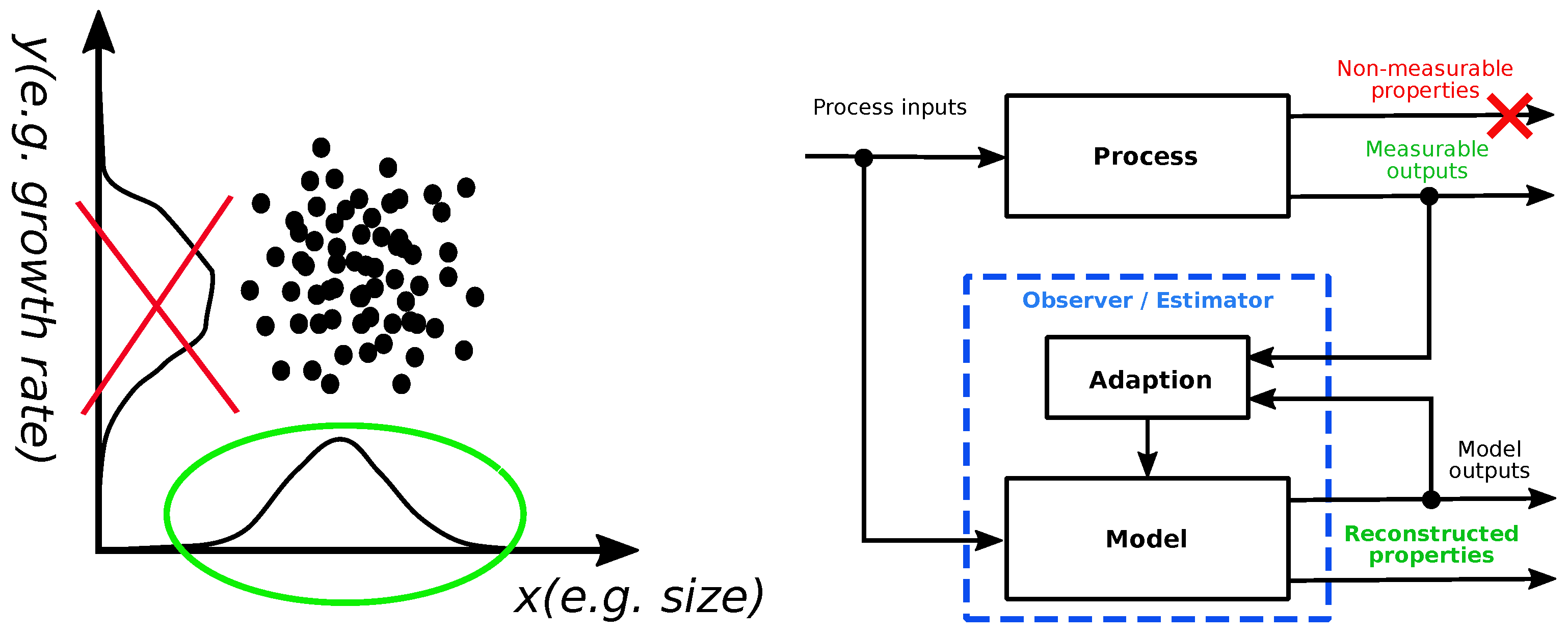
2.2. Observability of Multicellular Systems Dynamics
2.3. Estimator Design
- (I)
- Prediction step, a priori state and error covariance estimates:
- (II)
- Computation of the estimator gain:
- (III)
- Correction using current measurement , posterior estimates:
- (I)
- Initialization: A set of initial estimates (particles) is drawn from the initial state PDF:Subsequently, the following steps are executed recursively for :
- (II)
- Propagation: Each particle is propagated from to with Equation (12):
- (III)
- Weighting: The relative likelihood of each particle conditioned on the current measurement is computed by evaluating using Equation (13). Furthermore, all weights are normalized.
- (IV)
- Regularization and resampling: The posterior state PDF is approximated by a sum of weighted kernel functions, and a posteriori particles are generated from this PDF.From the posterior PDF, any desired statistical measures, e.g., mean and covariance, can be determined.
3. Results and Discussion
3.1. Comments on the Computational Implementation
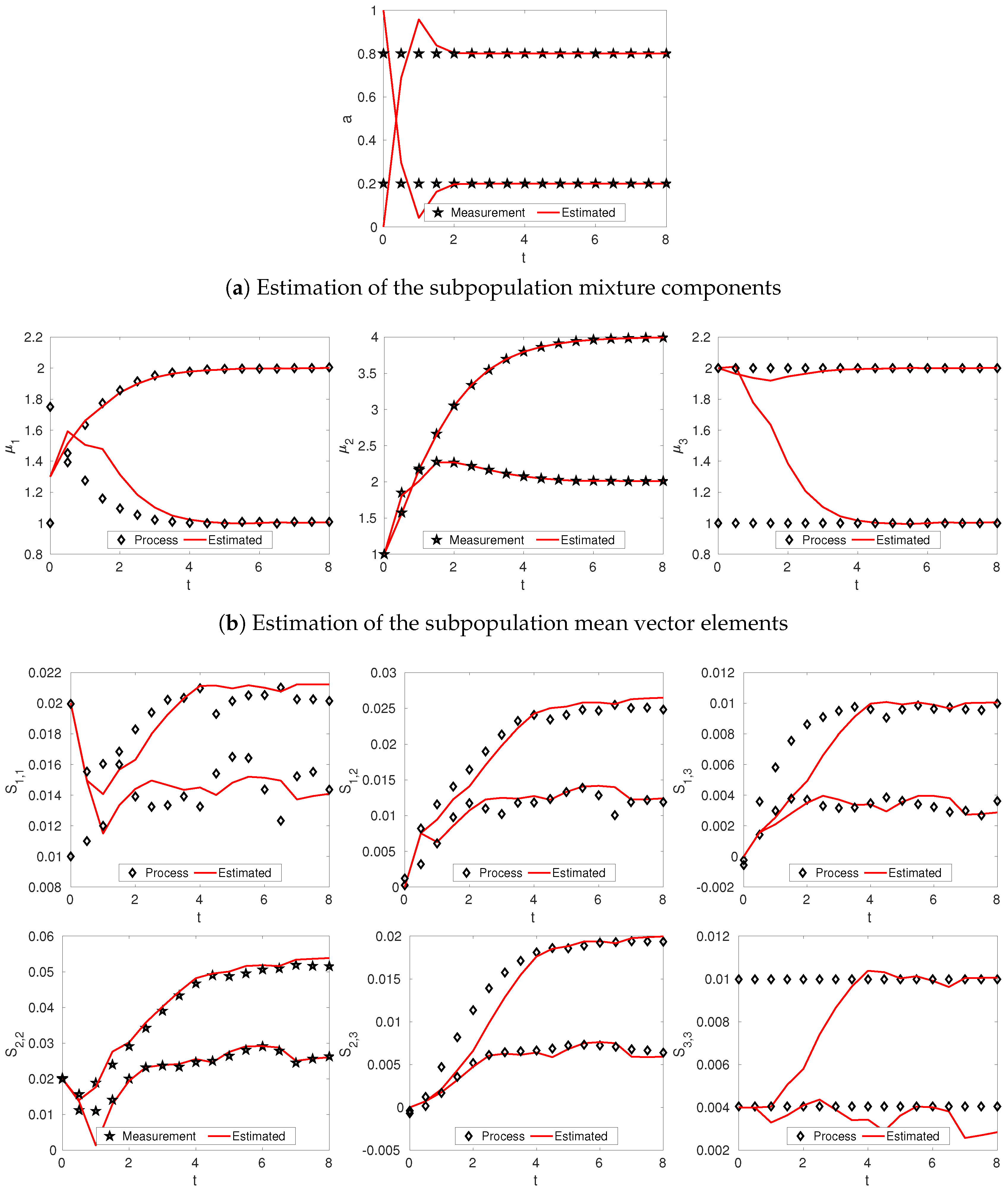
3.2. Linear Dynamics: Protein Expression
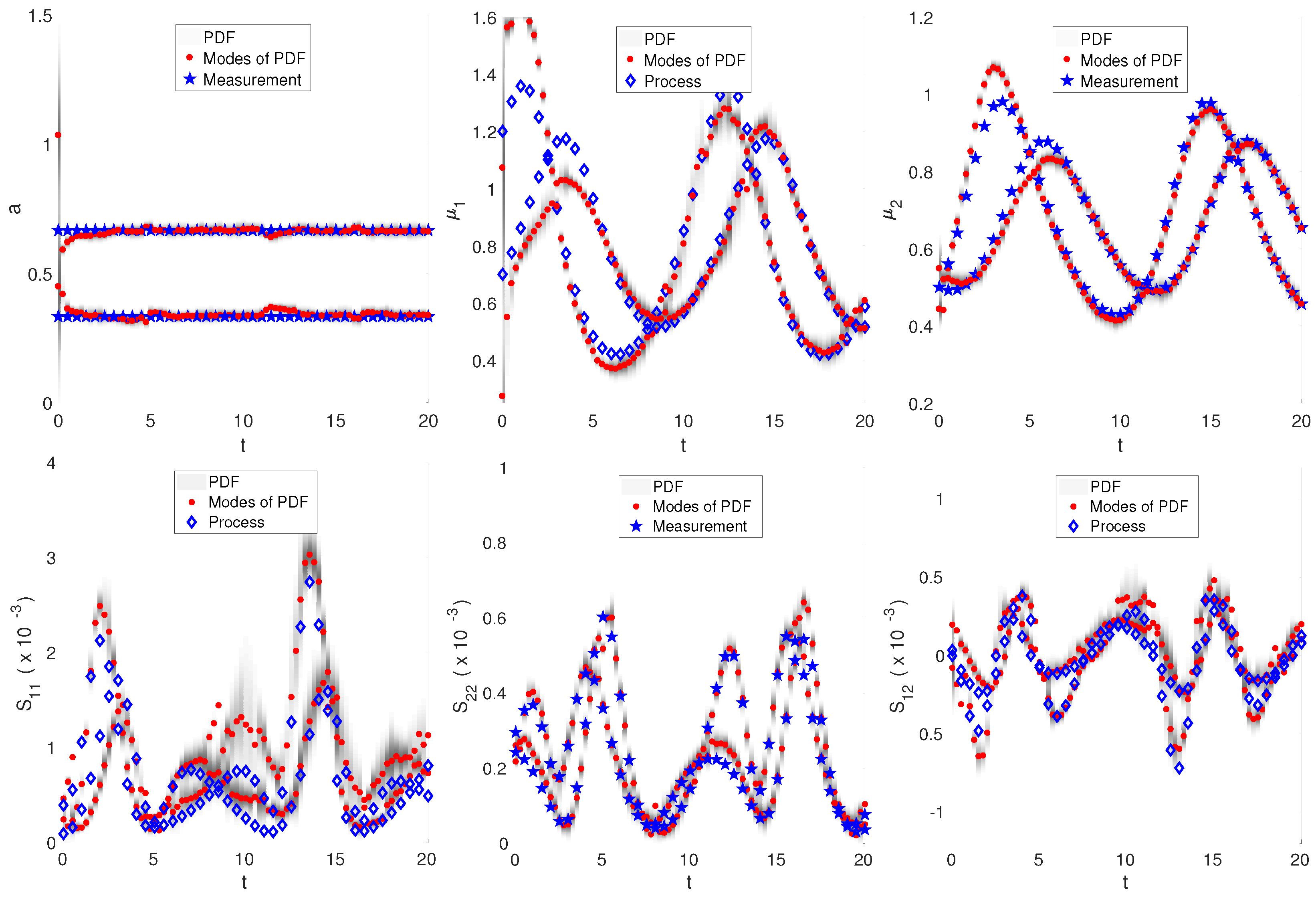
3.3. Nonlinear Dynamics: Intracellular Oscillator Modeled by Lotka–Volterra Dynamics
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NDF | Number density distribution function |
| ODE | Ordinary differential equation |
| PBE | Population balance equation |
| PBM | Population balance model |
| PDE | Partial differential equation |
| Probability density function | |
| SDE | Stochastic differential equation |
References
- Herberg, M.; Glauche, I.; Zerjatke, T.; Winzi, M.; Buchholz, F.; Roeder, I. Dissecting mechanisms of mouse embryonic stem cells heterogeneity through a model-based analysis of transcription factor dynamics. J. R. Soc. Interface 2016, 13, 201160167. [Google Scholar] [CrossRef] [PubMed]
- Müller, T.; Dürr, R.; Isken, B.; Schulze-Horsel, J.; Reichl, U.; Kienle, A. Distributed modeling of human influenza a virus-host cell interactions during vaccine production. Biotechnol. Bioeng. 2013, 110, 2252–2266. [Google Scholar] [CrossRef] [PubMed]
- Tapia, F.; Vázquez-Ramírez, D.; Genzel, Y.; Reichl, U. Bioreactors for high cell density and continuous multi-stage cultivations: Options for process intensification in cell culture-based viral vaccine production. Appl. Microbiol. Biotechnol. 2016, 100, 2121–2132. [Google Scholar] [CrossRef] [PubMed]
- Franz, A.; Dürr, R.; Kienle, A. Population Balance Modeling of Biopolymer Production in Cellular Systems. IFAC Proc. Vol. 2014, 47, 1705–1710. [Google Scholar] [CrossRef]
- Nopens, I.; Torfs, E.; Ducoste, J.; Vanrolleghem, P.; Gernaey, K. Population balance models: A useful complementary modelling framework for future WWTP modelling. Water Sci. Technol. 2015, 71, 159–167. [Google Scholar] [CrossRef]
- Pigou, M.; Morchain, J. Investigating the interactions between physical and biological heterogeneities in bioreactors using compartment, population balance and metabolic models. Chem. Eng. Sci. 2015, 126, 267–282. [Google Scholar] [CrossRef]
- Liou, J.; Fredrickson, A.G.; Srienc, F. Selective synchronization of Tetrahymena pyriformis cell populations and cell growth kinetics during the cell cycle. Biotechnol. Prog. 1998, 14, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Harms, H.; Bley, T. Origin and analysis of microbial population heterogeneity in bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Binder, D.; Drepper, T.; Jaeger, K.E.; Delvigne, F.; Wiechert, W.; Kohlheyer, D.; Grünberger, A. Homogenizing bacterial cell factories: Analysis and engineering of phenotypic heterogeneity. Metab. Eng. 2017, 42, 145–156. [Google Scholar] [CrossRef] [PubMed]
- de Vargas Roditi, L.; Claassen, M. Computational and experimental single cell biology techniques for the definition of cell type heterogeneity, interplay and intracellular dynamics. Curr. Opin. Biotechnol. 2015, 34, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Waldherr, S.; Doszczak, M.; Radde, N.; Scheurich, P.; Allgöwer, F. Identification of models of heterogeneous cell populations from population snapshot data. BMC Bioinform. 2011, 12, 125. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, A.; Srienc, F. Glucose uptake rates of single E. coli cells grown in glucose-limited chemostat cultures. J. Microbiol. Methods 2000, 42, 87–96. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fredrickson, A.G.; Ramkrishna, D.; Tsuchiya, H.M. Statistics and dynamics of procaryotic cell populations. Math. Biosci. 1967, 1, 327–374. [Google Scholar] [CrossRef]
- Mangold, M. Use of a Kalman filter to reconstruct particle size distributions from FBRM measurements. Chem. Eng. Sci. 2012, 70, 99–108. [Google Scholar] [CrossRef]
- McLachlan, G.; Peel, D. Finite Mixture Models; Wiley Series in Probability And Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Slack, M.D.; Martinez, E.D.; Wu, L.F.; Altschuler, S.J. Characterizing heterogeneous cellular responses to perturbations. Proc. Natl. Acad. Sci. USA 2008, 105, 19306–19311. [Google Scholar] [CrossRef] [PubMed]
- Altschuler, S.J.; Wu, L.F. Cellular Heterogeneity: Do Differences Make a Difference? Cell 2010, 141, 559–563. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Hasenauer, C.; Hucho, T.; Theis, F.J. ODE Constrained Mixture Modelling: A Method for Unraveling Subpopulation Structures and Dynamics. PLoS Comput. Biol. 2014, 10, e1003686. [Google Scholar] [CrossRef] [PubMed]
- Dürr, R.; Müller, T.; Duvigneau, S.; Kienle, A. An efficient approximate moment method for multi-dimensional population balance models—Application to virus replication in multi-cellular systems. Chem. Eng. Sci. 2017, 160, 321–334. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Luenberger, D. An introduction to observers. IEEE Trans. Autom. Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Zeitz, M. Observability canonical (phase-variable) form for non-linear time-variable systems. Int. J. Syst. Sci. 1984, 15, 949–958. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control, 3rd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Observability of complex systems. Proc. Natl. Acad. Sci. USA 2013, 110, 2460–2465. [Google Scholar] [CrossRef] [PubMed]
- Mangold, M.; Bück, A.; Schenkendorf, R.; Steyer, C.; Voigt, A.; Sundmacher, K. Two state estimators for the barium sulfate precipitation in a semi-batch reactor. Chem. Eng. Sci. 2009, 64, 646–660. [Google Scholar] [CrossRef]
- Zeng, S.; Waldherr, S.; Ebenbauer, C.; Allgöwer, F. Ensemble Observability of Linear Systems. IEEE Trans. Autom. Control 2016, 61, 1452–1465. [Google Scholar] [CrossRef]
- Wang, X.; Li, T.; Sun, S.; Corchado, J.M. A Survey of Recent Advances in Particle Filters and Remaining Challenges for Multitarget Tracking. Sensors 2017, 17, 2707. [Google Scholar] [CrossRef] [PubMed]
- Gerards, A. Chapter 3: Matching. In Network Models; Elsevier: Amsterdam, The Netherlands, 1995; Volume 7, pp. 135–224. [Google Scholar]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Drengstig, T.; Ni, X.Y.; Thorsen, K.; Jolma, I.W.; Ruoff, P. Robust Adaptation and Homeostasis by Autocatalysis. J. Phys. Chem. B 2012, 116, 5355–5363. [Google Scholar] [CrossRef] [PubMed]
- Isensee, J.; Diskar, M.; Waldherr, S.; Buschow, R.; Hasenauer, J.; Prinz, A.; Allgöwer, F.; Herberg, F.W.; Hucho, T. Pain modulators regulate the dynamics of PKA-RII phosphorylation in subgroups of sensory neurons. J. Cell Sci. 2014, 127, 216–229. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value |
|---|---|
| k | 2 |
| d | |
| V | |
| W |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.8 | V | ||
| 1.2 | W | ||
| 0.4 | 200 | ||
| 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dürr, R.; Waldherr, S. A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations. Processes 2018, 6, 187. https://doi.org/10.3390/pr6100187
Dürr R, Waldherr S. A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations. Processes. 2018; 6(10):187. https://doi.org/10.3390/pr6100187
Chicago/Turabian StyleDürr, Robert, and Steffen Waldherr. 2018. "A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations" Processes 6, no. 10: 187. https://doi.org/10.3390/pr6100187
APA StyleDürr, R., & Waldherr, S. (2018). A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations. Processes, 6(10), 187. https://doi.org/10.3390/pr6100187






