Abstract
In this present work, a study of the modelling and simulation for a top-sprayed fluidized bed granulator (SFBG) is presented, which is substantially used by the pharmaceutical industry to prepare granules. The idea is to build a number-based mathematical model using the notion of population balances by dividing a top SFBG into two different zones, namely the wet zone and dry zone. To solve a two-compartment model, an existing accurate and efficient finite volume scheme is implemented. In order to validate the compartmental model, a new class of analytical moments is derived corresponding to various combinations of aggregation and breakage kernels. To verify the accuracy of a modified finite volume scheme, the zeroth and first order moments computed using the finite volume scheme are compared with the newly-derived analytical results. Moreover, the stability of the compartmental model and the numerical scheme is tested by varying the size of the wet zone. It is also shown that the relative errors in both order moments increase with the increase in the size of the wet zone.
1. Introduction
Agglomeration and fragmentation (or breakage) processes are used to accommodate a change in the particle properties of the granules in the pharmaceutical and food industries. Other applications that involve these processes are crystallization, flocculation, the formation of water droplets, sprayed fluidized bed granulation (SFBG) and twin screw granulation (TSG) [1,2,3]. Among sprayed fluidized bed granulation and twin screw granulation, SFBG is adopted for the production of granular materials due to its potential to conduct granulation or agglomeration at low costs [4]. SFBG has applications in the food industry, as it is used for size enlargement of food ingredients. Moreover, it has major applications in the pharmaceutical industry because of its ability to produce identical granules, less dust content, superior wetting, etc. [5]. In the literature, many authors have attempted to model SFBG by considering the system to be well mixed [6], but in reality, it is a non-homogeneous system. The issue of inhomogeneity may be handled partially by introducing the compartmental modelling [7,8].
For our study, a top SFBG is divided into two compartments, as shown in Figure 1.
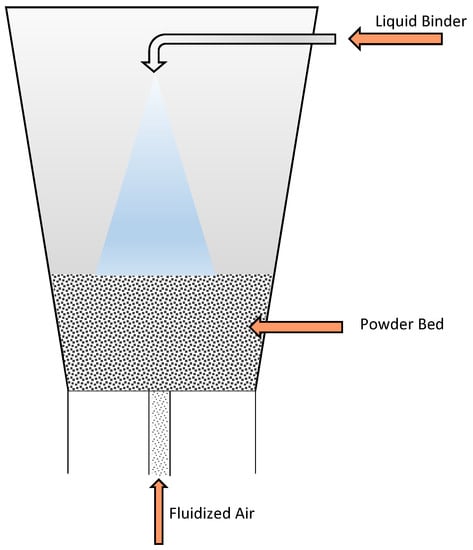
Figure 1.
Top-sprayed fluidized bed granulator.
In the wet zone, the particles are sprayed in and wetted with the binder, which leads to the formation of bridges between the particles or layering on the surface of the particles. In contrast, in the dry zone, breakage leads to the formation of the new particles due to the breaking of drying bridges, which were already formed due to solidification of the particles. During the compartmentalization of SFBG, the particle residence time in both zones plays a very important role. The residence time of particles in the wet zone and dry zone are of equal importance because the particle sizes are actually growing in the spray zone due to the aggregation process, whereas in the other zone, the particles will have a greater chance to be in contact with the hot air, which leads to the fragmentation of the particles into smaller classes. In this work, various sizes of wet zones are considered, ranging from 14% to 30%, and in the dry zone from 70–86% of the total size [9]. In addition to this, the mass flow rate at which particles are exchanged between the two zones is also a major issue.
The dynamics of the particle size distribution inside the compartments of the compartmental model evolves due to the aggregation and breakage mechanisms and can be tracked by a population balance model. The aggregation and breakage population balance equations (PBEs) corresponding to wet and dry zones can be written as follows:
and:
with respect to the initial condition
The integrals present on the right-hand side of Equation (1) represent the birth and death of particles in the system. Moreover, the aggregation kernel denotes the rate at which the large-sized particles are formed from the smaller-sized particles due to aggregation. Additionally, the aggregation kernel is a non-negative function () and symmetric with respect to the internal coordinates, that is . For the breakage Equation (2), is the selection function, and it expresses the rate at which particles of size r are selected to break into smaller fragments. The fragmentation function is the probability density function denoting the formation of daughter particles of size r due to the breakage of the parent particles of size s. The fragmentation function must satisfy the following conditions:
and:
Equation (4) represents the mass conservation between the parent particle and the smaller-sized fragments. For a practical scenario, must be greater than or equal to two. The integral properties such as the moments of the distribution corresponding to Equations (1) and (2) are also important to calculate. Moreover, the i-th moment can be defined as:
Here, represents the total number of particles, whereas signifies the total mass of particles in the system.
In this study, our main objective is to propose a mathematical model and develop a new numerical approximation for solving the proposed compartmental model. Various earlier numerical methods were developed to solve these kinds of complex models. Among them, the cell average technique [7,10] and Hounslow’s discretization [8,11] are well-established methods known for their accuracy. However, the major disadvantage of these methods is that they have a very complex mathematical formulation and, hence, are computationally very expensive. This leads to the choice of finite volume schemes [12,13,14]. In order to verify the accuracy of the mathematical model, the numerical results are validated by deriving the new analytical solutions by choosing various combinations of aggregation kernels and the binary fragmentation function with the linear selection function.
The rest of paper is structured as follows: In Section 2, we briefly describe the two-compartment model and the assumptions considered for simulating a top SFBG. The next section is devoted to providing the formulation of the proposed numerical scheme for solving the set of equations. In Section 4, the accuracy and efficiency of the proposed method are tested by comparing the results with the newly-developed analytical results for moments. Finally, Section 5 summarizes the conclusions of this study.
2. Two-Compartment Model for Sprayed Fluidized Bed Granulation
In this section, a top-sprayed fluidized bed granulator and its compartmentalization are discussed in detail. At the top of the granulator, a nozzle is fixed by which the liquid binder is sprayed over the particles in the granulator. The particles are considered to be spherical, placed at the bottom of the granulator as shown in Figure 1. When the hot air enters into the granulator from the bottom, the particles placed at the bottom put into a random motion, and collisions take place between the particles. At the same time, the particles become wet because of the liquid binder, which leads to the aggregation and breakage processes inside the SFBG.
For the compartmental modelling, the granulator is divided into zones based on the dominating mechanism occurring in a particular part of the granulator. The top of the granulator is the first compartment, named the Wet Zone (), as in this area, the particles are becoming wet; whereas, the bottom of the granulator is called the Drying Zone (), as the liquid binder on the particles is becoming dry because of the hot air. The schematic diagram of the compartment modelling of the system is shown in Figure 2. The assumptions that were made for the development of the model are given below:
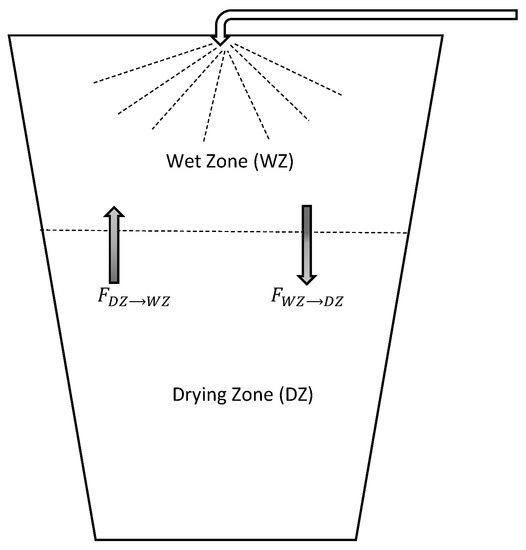
Figure 2.
Schematic representation of the two-compartment model.
- The system is divided into two compartments:
- (a)
- the first compartment, that is the wet zone, is represented by fraction , and the volume is ,
- (b)
- the second compartment, that is the dry zone, is represented by the fraction , and the volume is , where V is the total volume of the reactor.
- Each compartment (, as well as ) is considered to be a well-mixed system.
- The size of both compartments remains constant during the process.
- The mass in each compartment should be constant at each time step.
- The rate of exchange of volume flux between the compartments is constant during the process.
The residence time in the wet zone and in the dry zone is taken to be and , respectively. Moreover, the total time taken by the particle to complete one cycle of the system is . Assume and are the number density functions in and respectively. The volume flux from to is:
and volume flux from to is
Based on aforementioned notations and formulating population balances for both compartments, the mathematical model for the wet zone can be written as:
and for the dry zone, the mathematical model is given by:
corresponding to initial conditions .
In Equation (6), is the aggregation kernel, which defines the rate at which the particles having properties r and s aggregate. In Equation (7), exhibits the selection function, which defines the selection of a particle property s to break into smaller particles. Moreover, is the probability density function, which defines the formation of particle size r due to the breakage of particle property s.
Finite Volume Scheme
In this section, the modification of the Finite Volume Schemes (FVS) developed by [15,16] is done to approximate the coupled system of Equations (6) and (7). The basic notion of the scheme is to convert the integro-partial differential equation into the system of ordinary differential equations. To solve the given system of equations using FVS, firstly, the particle size domain should be discretized into small bins. The lower and upper boundaries of the i-th bin are for with . Assume that the representative of the i-th bin is denoted by , which defines the average of the lower and upper boundaries of the i-th bin, that is,
Let us define the set as:
which consists of all those pairs of the indices of the bins j and k such that the aggregate of particle properties of bins j and k, that is , will fall in the bin having indices i. Moreover, the average value of and in the i-th bin, which are approximations of the number density function and corresponding to wet and dry zones, respectively, are given by:
Here, denotes the step size of the domain.
Now, on integrating Equations (6) and (7) from to and implementing the idea of FVS on the aggregation and breakage birth and death terms, we get:
and:
with . These factors are defined as:
and where
The detailed explanation of the formulations of both numerical schemes corresponding to aggregation and breakage processes can be found in [15,16], respectively. Moreover, it can be noticed from Equations (10) and (11) that the correction factors added to both equations are only responsible for conserving the total mass of the system (first order moment) in each zone. However, it does not give any account of the preservation of the total number of particles (zeroth order moment) in each zone. Therefore, it will be interesting to see how accurately the zeroth order moment of both zones is calculated by the modified finite volume schemes. Further, for the verification of the proposed methods, the analytical (or exact) solutions of the different order moments are found for different combinations of aggregation kernel and breakage function . In particular, simple structured aggregation kernels, that is sum and product kernels for the wet zone and binary breakage function with the linear selection function for the dry zone, are considered. In the next section, the detailed derivation of the analytical results to verify the numerical approximations is provided.
3. Derivation of the Analytical Solutions for Moments
To verify the discretization of the system of ordinary differential Equations (10) and (11), we validate it against the analytical results that will be derived in this section. Due to the pairing and complex nature of the system of Equations (6) and (7), the number density function cannot be easily obtained. Therefore, the exact solutions of the zeroth order moment and first order moment for specific combinations of kernels are derived. Let us define the zeroth moment in each compartment as:
and the first moment in each compartment as:
Now, the expressions for the zeroth moment of the number density model given in Equations (6) and (7) will be derived. Integrating both sides of Equations (6) and (7) with respect to r from zero to ∞, applying the change of order of integration to (6) and using Equations (13) and (14), the following equations are obtained:
and:
- Case 1: additive aggregation kernel, linear selection function with binary breakage kernel, that is .
- Case 2: product aggregation kernel, linear selection function with binary breakage kernel, that is .
3.1. Case 1
Firstly, we choose additive aggregation kernel () corresponding to the wet zone and binary breakage function () with linear selection function () for the dry zone. For the binary breakage function, only two objects are produced per fragmentation event.
Similarly for the , on putting the values of and in Equation (16), this gives:
as is the average number of fragments in which a particle of size s has broken, and for the case of binary breakage, the value of k is two.
Finally, the following set of equations is formed:
As we know, , where V is the total volume of the system, and for the simplicity, let us consider . Let , , , and . The expression for the zeroth moment, i.e., total number of particles in the wet zone and dry zone for this particular case, is:
where:
3.2. Case 2
Analogous to the previous case, analytical moments of the wet and dry zones are also derived for the combination of product kernel () corresponding to the wet zone and binary breakage function () with linear selection function ().
For , the simplified equation is the same as derived in the previous case,
Therefore, for this case, the system of equations comes out as:
The analytical solution for the above-defined system of equations is:
where:
However, the analytical solution of the total mass in each compartment for both combinations of kernels is:
as the total mass of particles in each zone remains constant. Here, is the initial total mass of the particles in the system.
4. Results and Discussion
In this section, the compartmental model of the sprayed fluidised bed granulator solved numerically is tested with various combinations of aggregation and breakage kernels. To check the accuracy of the numerical methodologies, the numerical results are compared with analytical solutions derived for combinations of additive and product aggregations kernels and the binary breakage kernel with the linear selection function in Section 4. In addition, the quantitative relative errors in the zeroth and first order moments obtained for sum and product kernels are also computed using the following expression:
where and denote the analytical and numerical number of particles predicted in the j-th cell, respectively. Moreover, the values and denote the relative errors in the zeroth and first order moments, respectively. All the numerical simulations were carried out using MATLAB 2015a on a i5 CPU with 2.67 GHz and 8 GB RAM. The system of ODEs derived in Equations (10) and (11) were solved using ode15 s solver in MATLAB.
To compute the numerical results using finite volume schemes, the size domain range from to was divided into 151 cells. Moreover, the comparison is presented by varying the size of the wet zone, in particular the value of was taken to be and .
4.1. Additive Aggregation Kernel and Binary Breakage with the Linear Selection Function
In this section, the comparison in terms of various moments obtained using is conducted with analytical moments for the additive kernel (). For the analytical solutions corresponding to the additive kernel, the value of was considered to be one. For calculating the numerical results, the simulations were run till time s.
Figure 3a,c reveals that the zeroth moments approximated numerically for wet and dry zones, respectively, matched well with the analytical moments. Moreover, Figure 3b shows the comparison of the total number of particles in the system (combining wet and dry zones), which reveals that the modified FVS agreed well with the analytical total moment. It is important to note that no account for the preservation of the total number of particles in the system has been taken, but still, the modified finite volume scheme was highly accurate in computing the zeroth order moment. Moreover, it can also be observed that as the size of the wet zone increased from to , the total system acquired the steady state at time s (for wet zone), whereas for wet zone, the system acquired the steady state at time s. This is due to the fact that less particles were present in the wet zone for aggregation, whereas more particles in the dry zone were available that underwent the formation of smaller sized particles due to fragmentation process, which delayed the steady state. Additionally, when the size of the wet zone was increased, more particles were contributing towards the aggregation mechanism, and the number of particles in the dry zone decreased. Consequently, this further helped the system to achieve the steady state earlier.
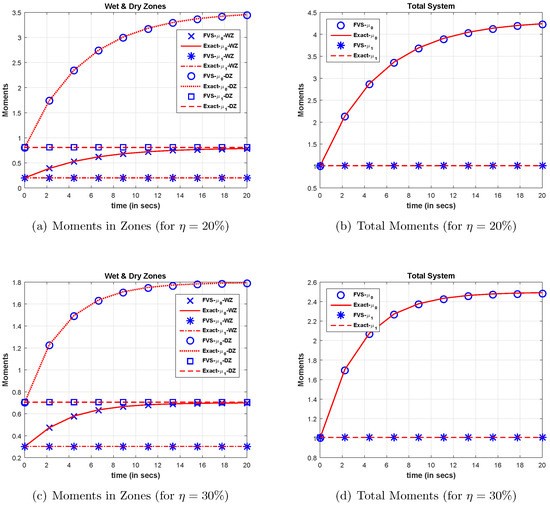
Figure 3.
Different order moments and number density for the additive kernel. FVS, Finite Volume Scheme.
In addition, the first order moments computed corresponding to both zones (wet and dry) showed consistent numerical results, that is they agreed well with the analytical first moments. This affirms that the total mass in both zones remained conserved. Moreover, Figure 3d exhibits the comparison of the total mass in the system (combining wet and dry zones), which coincides well with the analytical total first moment. Furthermore, the quantitative relative errors of the zeroth and first order moments calculated using (19) are listed in Table 1. One can observe that the relative errors in the moments of both zones, as well as in the total system increased as the size of the wet zone was incremented from to .

Table 1.
Quantitative relative errors in the zeroth and first order moments for the additive kernel.
4.2. Product Kernel and Binary Breakage with Linear Selection Function
Similar to the sum kernel, for and , the numerical moments computed using finite volume scheme are compared with the newly-derived analytical results for a product kernel, that is . For the comparison, the value of was considered similar to the previous case. The simulations were run till time s for calculating the numerical results.
The product kernel was a gelling kernel for any arbitrary particle size distribution [17]. Therefore, the simulation in this case was performed until the product kernel showed the gelling behaviour. The kernel exhibited gelling behaviour when the newly-forming particles aggregated at a greater frequency than their parents. The various order moments computed numerically were compared with the analytical moments, as shown in Figure 4. The numerical results reveal that the zeroth and first order moments corresponding to wet and dry zones showed very consistent approximations and coincided well with the analytical moments (see Figure 4a,c). Moreover, the numerical total zeroth and first order moments shown in Figure 4b,d corresponding to the whole system matched well with the analytical results.
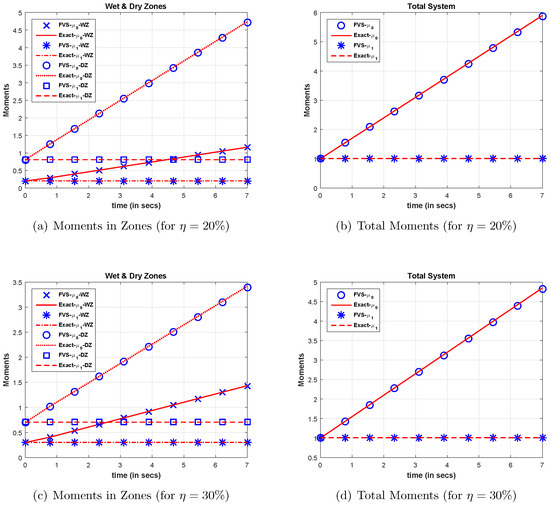
Figure 4.
Different order moments and number density for the product kernel.
In contrast to the additive kernel, for the product kernel, no steady state was achieved by the system corresponding to and wet zones (see Figure 4). This was due to the fact that a greater number of particles was available in the dry zone and hence produced a greater number of smaller particles. In contrast to the dry zone, a lesser number of particles was available for the formation (or aggregation) process, hence producing much smaller particles. Analogous to the additive kernel, the quantitative relative errors existing in zeroth and first order moments were also calculated for a product kernel using Expression (19) (see Table 2). The trend of the relative errors in both order moments was similar to the additive kernel, that is the relative errors in both order moments increased as the value of varied from 20% to 30%.

Table 2.
Quantitative relative errors in the zeroth and first order moments for the product kernel.
5. Conclusions
In this study, a two-compartment model for a top-sprayed fluidized bed granulator is proposed using population balances. The model has been analysed by varying the size of the compartments. Moreover, a modification of the existing finite volume scheme has been done to solve the proposed compartmental model. For the verification of the modified finite volume scheme, new analytical solutions for zeroth and first order moments are derived for various combinations of aggregation and breakage kernels. It has been demonstrated that the modified finite volume scheme has the stability to track the zeroth and first order moments accurately, even if different sizes of wet zone are chosen. Moreover, the relative errors existing in both order moments increased as the size of the wet zone was varied from 20% to 30%. Finally, we concluded that the proposed model, as well as the numerical discretization behaved well for various kernels and sizes of compartments.
Author Contributions
G.K. conceived of the presented idea, developed the theory and performed analytical calculations. G.K. and M.S. performed the numerical simulations. I.N. encouraged G.K. and M.S. to investigate and supervised the findings of this work. Supervisors J.K., T.D.B. and I.N. contributed to the final version of the manuscript. I.N. supervised the project.
Funding
This research was funded by International Mobility Programme for Academic and Knowledge Transfer (IMPAKT Project), Erasmus Mundus Programme to Gurmeet Kaur and grant number is IT16DM0434.
Acknowledgments
The authors gratefully acknowledge financial support provided by the International Mobility Programme for Academic and Knowledge Transfer (IMPAKT Project), Erasmus Mundus Programme, to Gurmeet Kaur.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marchal, P.; David, R.; Klein, J.; Villermaux, J. Crystallization and precipitation engineering-I. an efficient method for solving population balance in crystallization with agglomeration. Chem. Eng. Sci. 1988, 43, 59–67. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Wang, T.; Wang, J.; Jin, Y. Population balance model for gas-liquid flows: Influence of bubble coalescence and breakup models. Ind. Eng. Chem. Res. 2005, 44, 7540–7549. [Google Scholar] [CrossRef]
- Börner, M.; Peglow, M.; Tsotsas, E. Particle residence times in fluidized bed granulation equipments. Chem. Eng. Technol. 2011, 34, 1116–1122. [Google Scholar] [CrossRef]
- Teunou, E.; Poncelet, D. Batch and continuous fluid bed coating–review and state of the art. J. Food Eng. 2002, 53, 325–340. [Google Scholar] [CrossRef]
- Vreman, A.; Van Lare, C.; Hounslow, M. A basic population balance model for fluid bed spray granulation. Chem. Eng. Sci. 2011, 64, 4389–4398. [Google Scholar] [CrossRef]
- Hussain, M.; Kumar, J.; Peglow, M.; Tsotsas, E. On two-compartment population balance modelling of spray fluidized bed agglomeration. Comput. Chem. Eng. 2014, 61, 185–202. [Google Scholar] [CrossRef]
- Liu, H.; Li, M. Two-compartmental population balance modelling of a pulsed spray fluidized bed granulation based on computational fluid dynamics (cfd) analysis. Int. J. Pharm. 2014, 475, 256–269. [Google Scholar] [CrossRef] [PubMed]
- Turchiuli, C.; Jimenèz, T.; Dumoulin, E. Identification of thermal zones and population balance modelling of fluidized bed spray granulation. Powder Technol. 2011, 208, 542–552. [Google Scholar] [CrossRef]
- Kumar, J.; Peglow, M.; Warnecke, G.; Heinrich, S.; Mörl, L. Improved accuracy and convergence of discretized population balance for aggregation: The Cell Average Technique. Chem. Eng. Sci. 2006, 61, 3327–3342. [Google Scholar] [CrossRef]
- Hounslow, M.; Ryall, R.; Marshall, V. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Kumar, J.; Kaur, G.; Tsotsas, E. An accurate and efficient discrete formulation of aggregation population balance equation. Kinet. Relat. Model. 2016, 9, 373–391. [Google Scholar]
- Singh, M.; Kaur, G.; Kumar, J.; De Beer, T.; Nopens, I. A comparative study of numerical approximations for solving smoluchowski coagulation equation. Braz. J. Chem. Eng. 2017, 35. Available online: https://www.researchgate.net/profile/Mehakpreet_Singh/publication/318129362_A_Comparative_Study_of_Numerical_Approximations_for_Solving_Smoluchowski_Coagulation_Equation/links/5a3bb40fa6fdccb29dca325f/A-Comparative-Study-of-Numerical-Approximations-for-Solving-Smoluchowski-Coagulation-Equation.pdf (accessed on 1 September 2018).
- Singh, M.; Kumar, J.; Bück, A. A volume conserving discrete formulation of aggregation population balance equations on non-uniform meshes. IFAC-PapersOnLine 2015, 48, 192–197. [Google Scholar] [CrossRef]
- Saha, J.; Kumar, J.; Bück, A.; Tsotsas, E. Finite volume approximations of breakage population balance equation. Chem. Eng. Res. Des. 2016, 110, 114–122. [Google Scholar] [CrossRef]
- Singh, M.; Kumar, J.; Bück, A.; Tsotsas, E. A volume-consistent discrete formulation of aggregation population balance equations. Math. Methods Appl. Sci. 2015, 39, 2275–2286. [Google Scholar] [CrossRef]
- Smit, D.; Hounslow, M.; Paterson, W. Aggregation and gelation-I. analytical solutions for cst and batch operation. Chem. Eng. Sci. 1994, 49, 1025–1035. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).