Automated Detection of Shading Faults in Photovoltaic Modules Using Convolutional Neural Networks and I–V Curves
Abstract
1. Introduction
2. Theoretical Background
2.1. Photovoltaic Panels
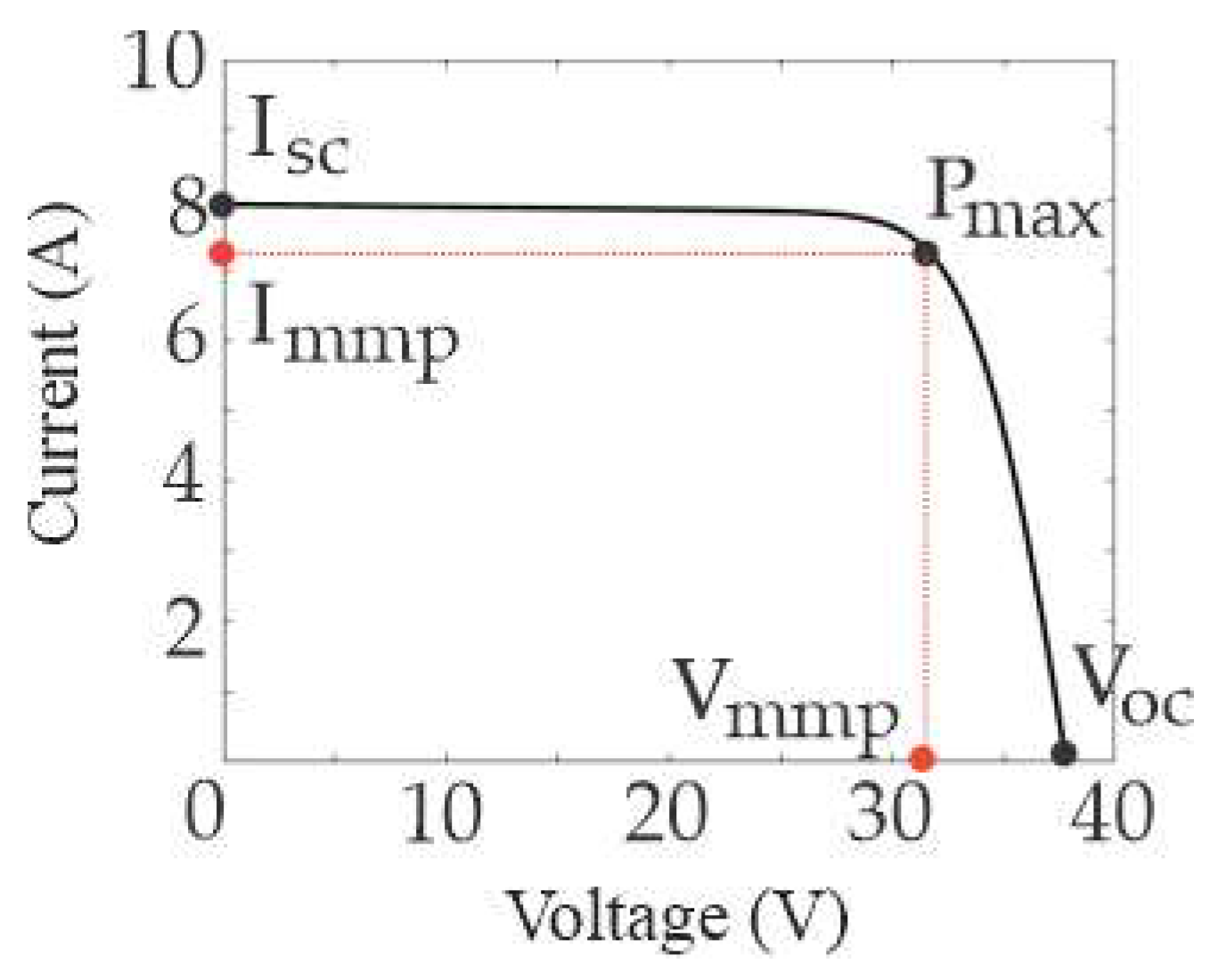
2.2. Current–Voltage (I–V) Curves
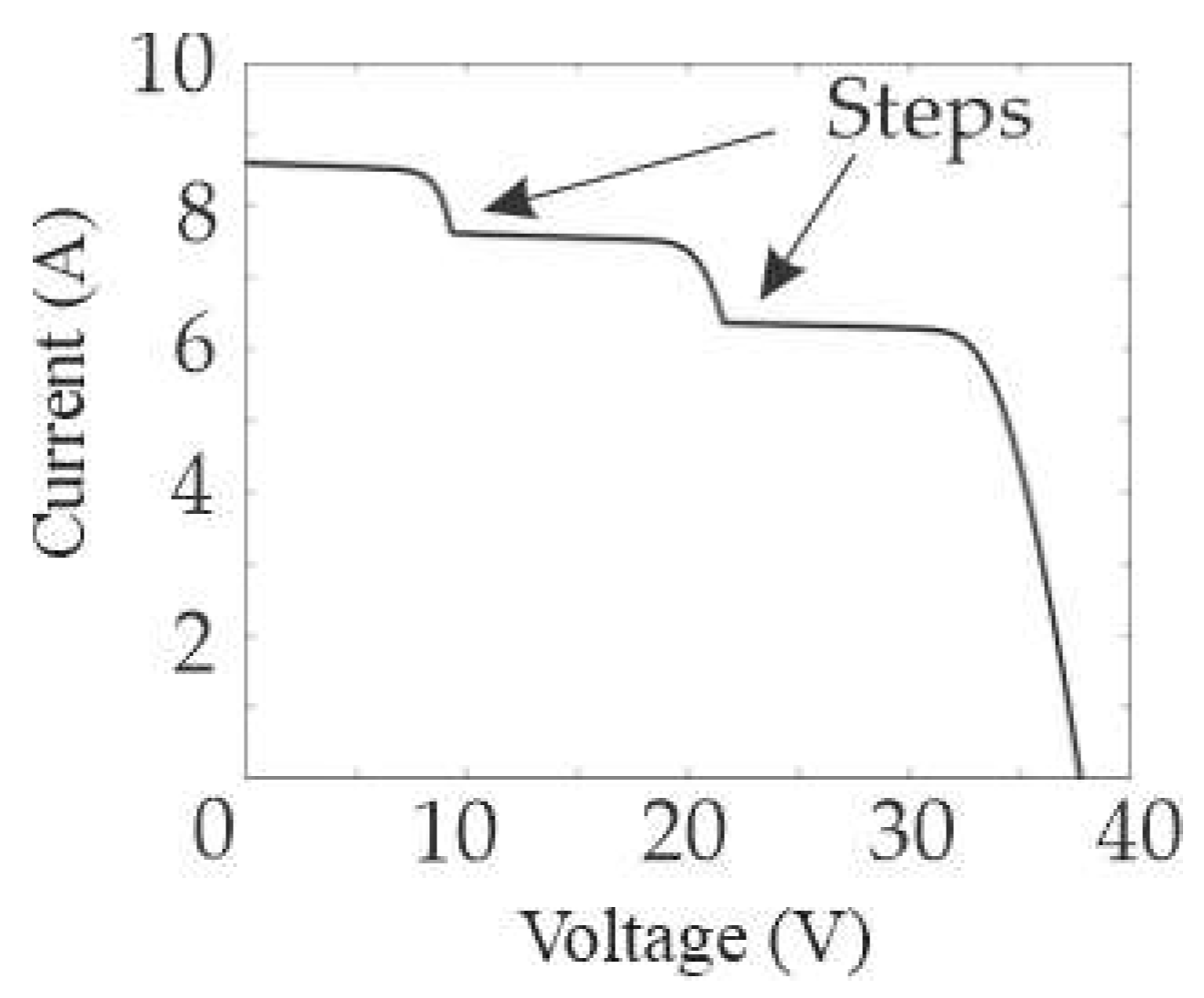
2.3. Shading Faults
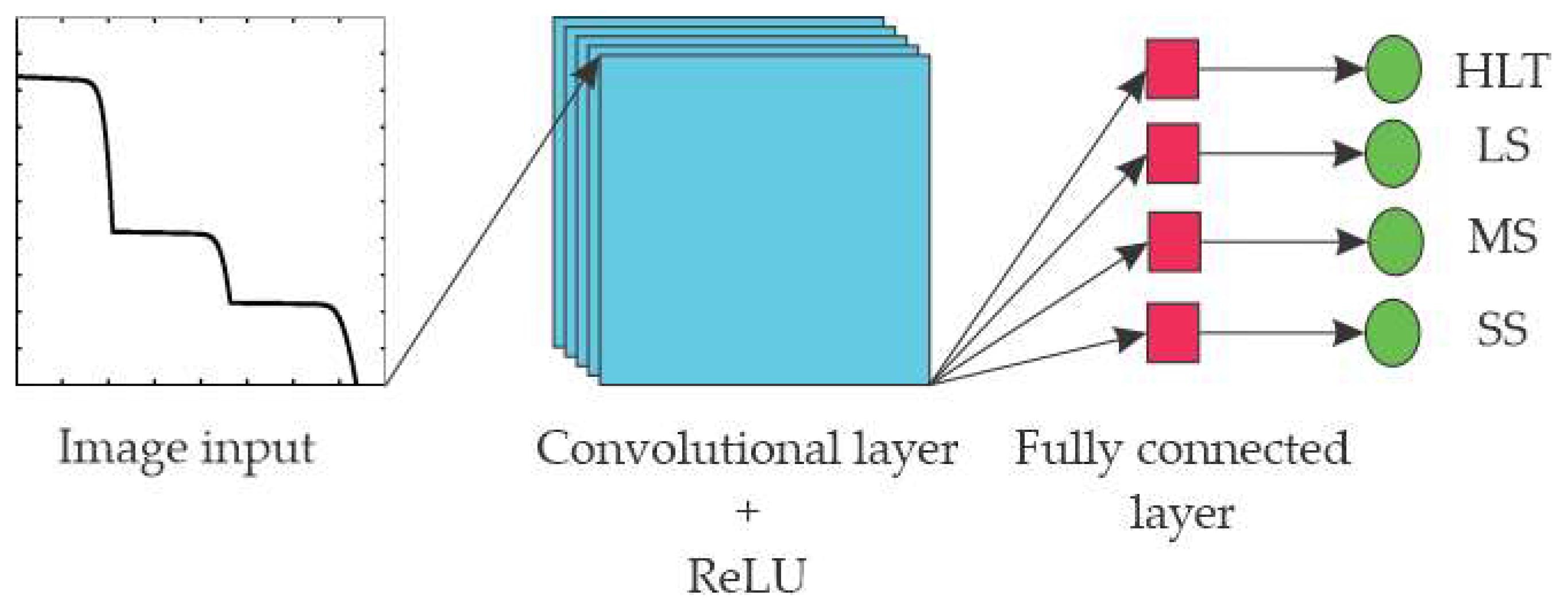
2.4. Convolutinal Neural Networks
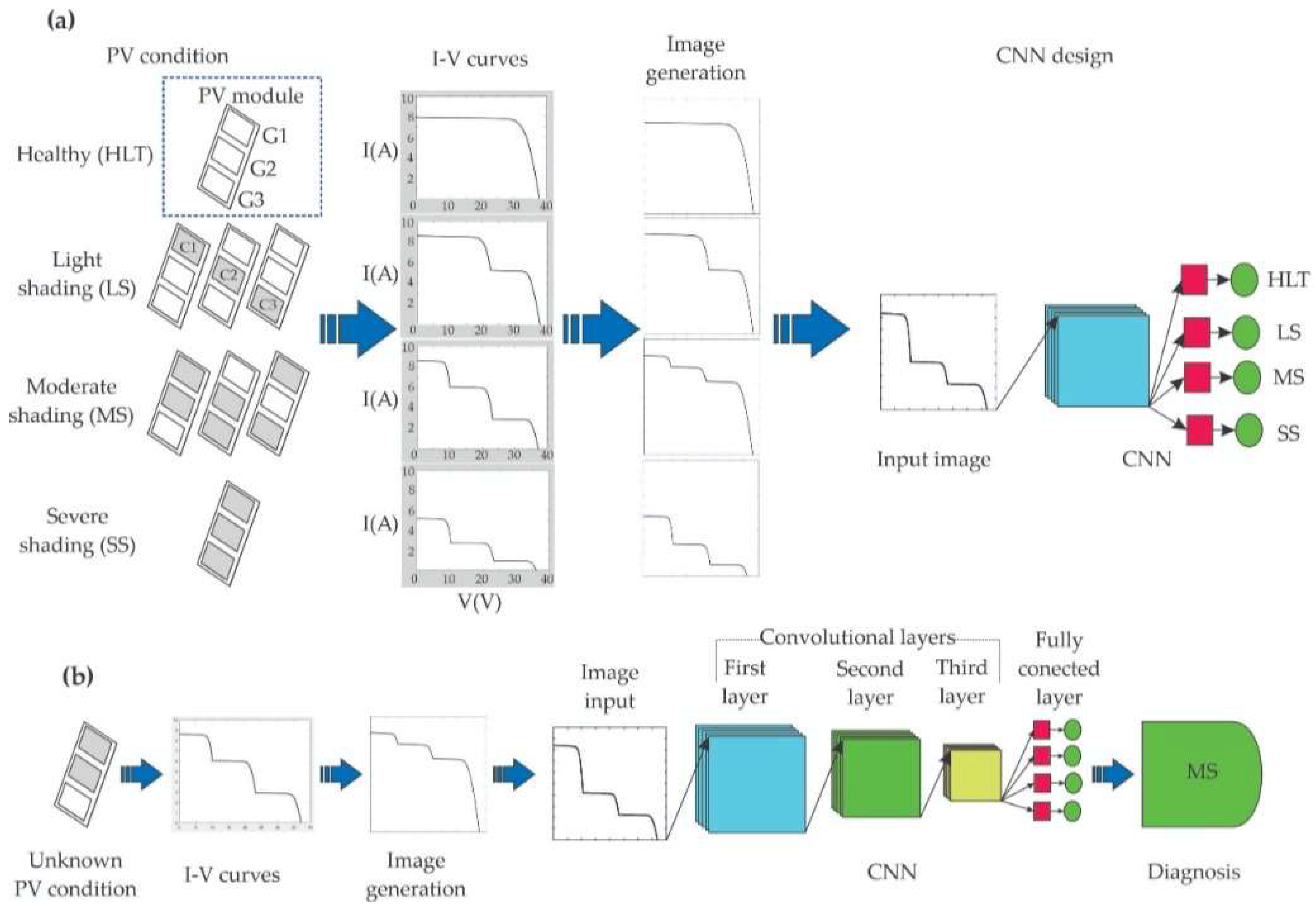
3. Methodology
4. Experimentation and Results
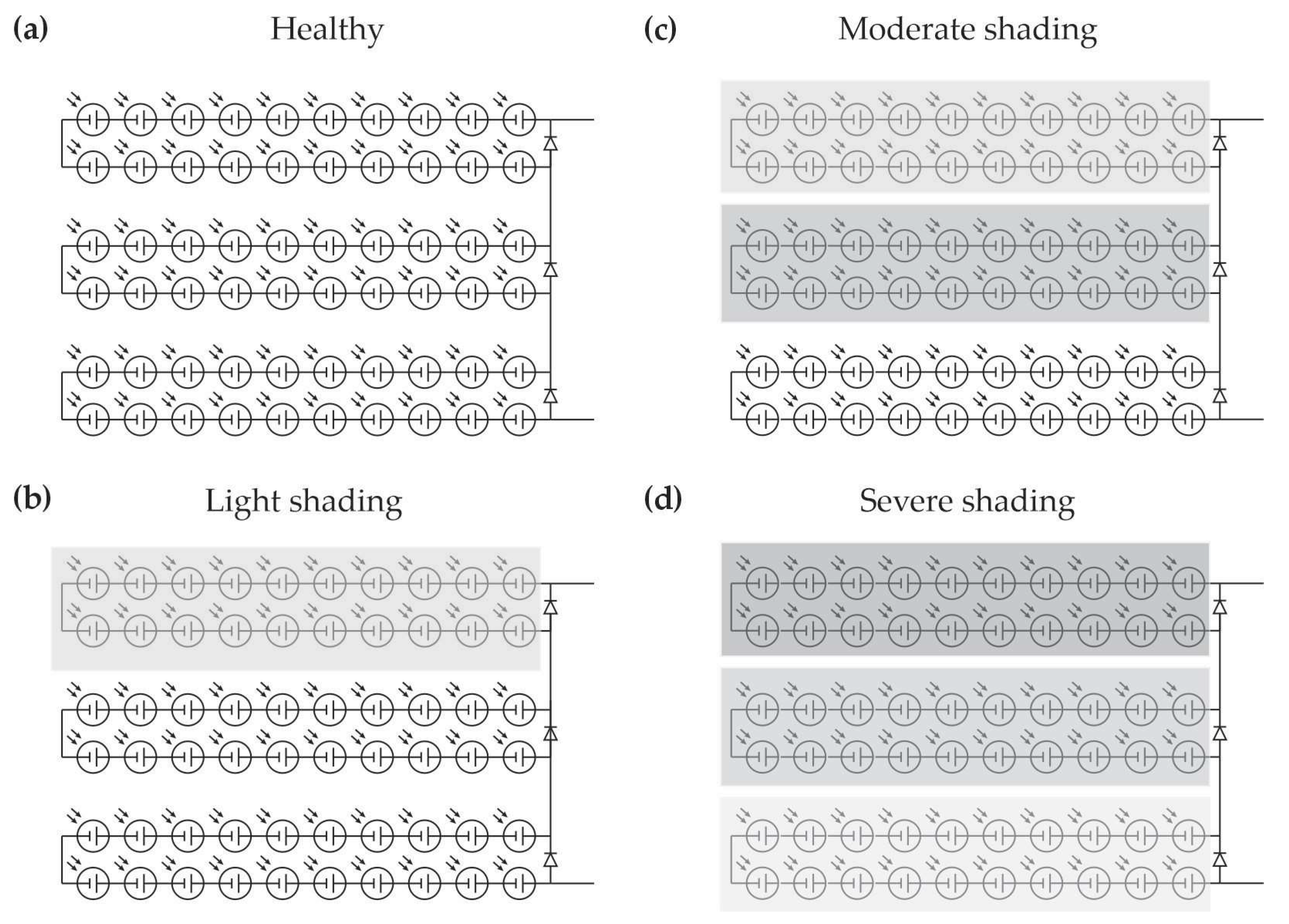
4.1. Experiment Setup
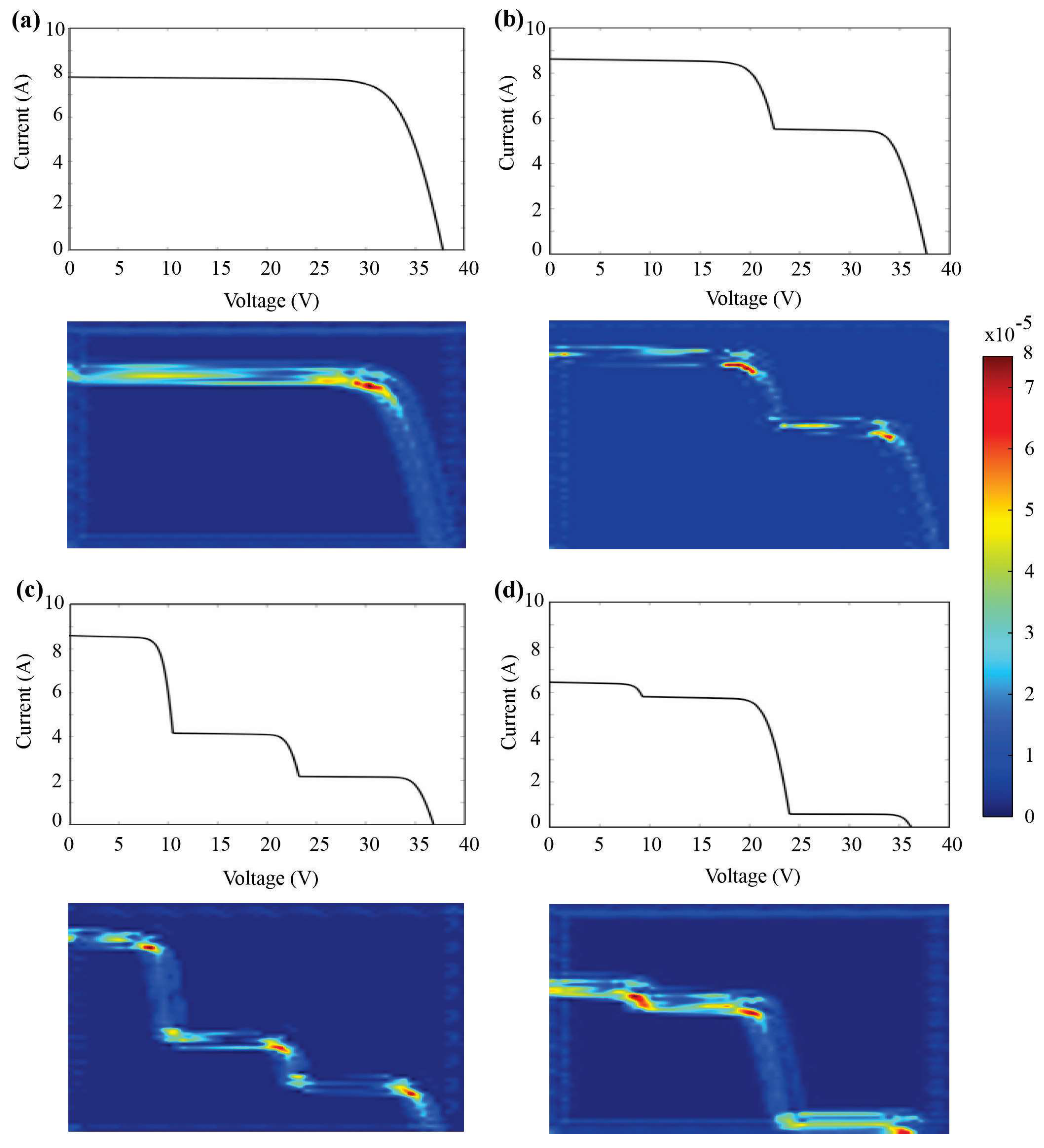
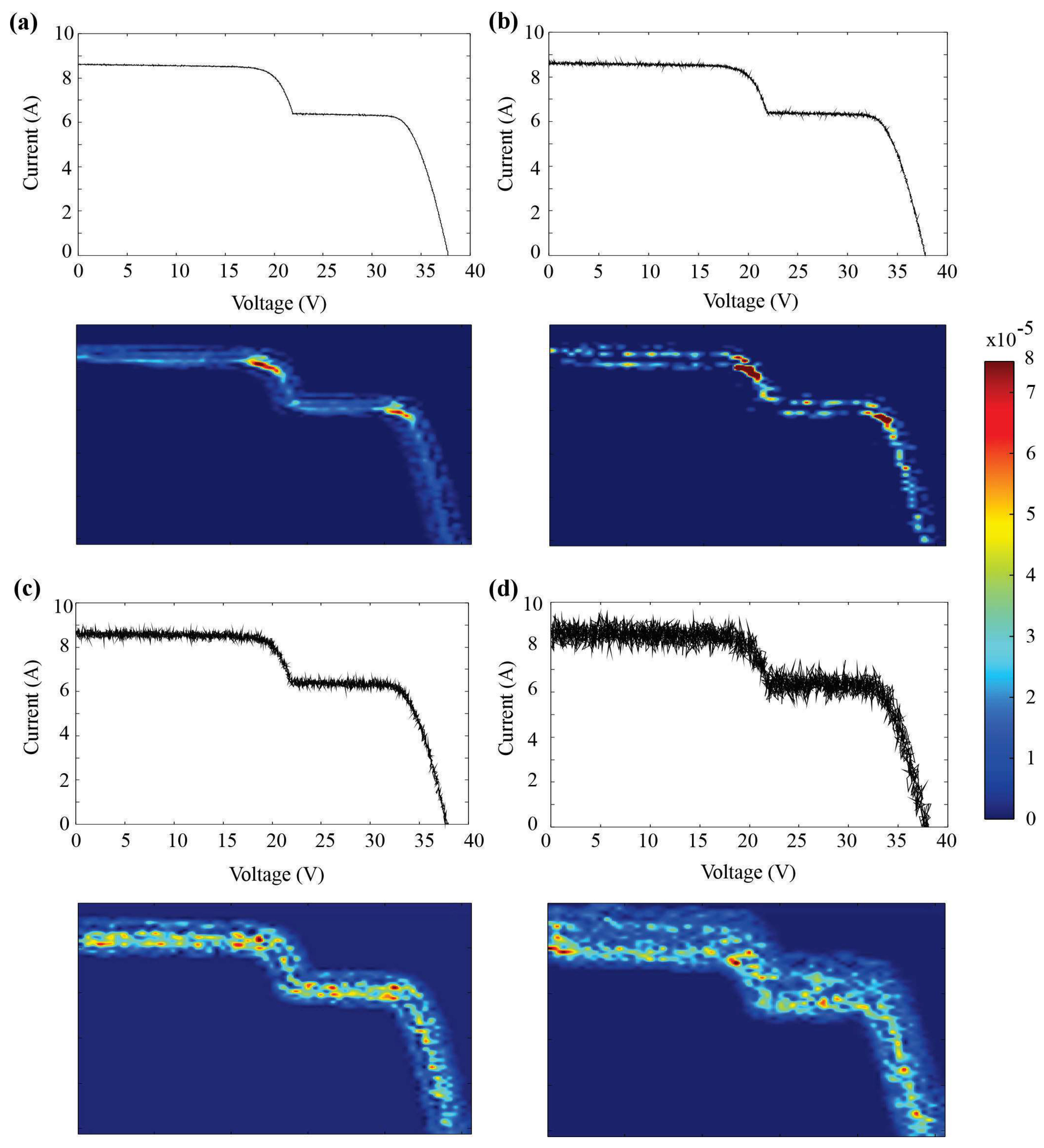
- HLT: All three sections of 20 cells each receive uniform irradiance values (1000 W/m2 in Figure 4), representing the baseline performance of the module. Under uniform high irradiance, no bypass diode conducts. Consequently, the I–V curve exhibits a single knee with nominal Isc and Voc, and a high fill factor. The HLT label is assigned when all substrings remain forward-biased and no step features appear in the curve [11,40].
- LS: A reduction in irradiance is applied to one section (either cells 1–20, 21–40, or 41–60), simulating partial obstruction such as mild dirt accumulation or small object shadows. Due to the non-uniform irradiance, the current produced by the shaded section cannot reach the total module current, causing its bypass diode to conduct. Therefore, the I–V curve exhibits a single shallow step corresponding to this partial bypass [10,11].
- MS: Two of the three sections are subjected to reduced irradiance. For example, string 2 (cells 21–40) receives 300 W/m2, while string 3 (cells 41–60) receives 600 W/m2. This configuration simulates more significant power loss and uneven shadowing. In this case, the shaded substrings are reverse-biased when the total current exceeds their maximum output, activating their bypass diodes and producing two steps in the I–V curve [11,40].
- SS: All three sections are shaded, each with different irradiance levels to reflect highly variable conditions. This setup represents the most critical degradation scenario for power output and voltage stability. Substrings are bypassed as their diodes conduct when their current limits are exceeded, and the I–V curve shows two steps along with a substantial reduction in voltage and power [40,41].
4.2. CNN Results
4.2.1. Evaluation of the Convolutional Layers
- Number of filters: 4, 8, 16, and 32
- Filter sizes: 3 × 3, 5 × 5, and 8 × 8
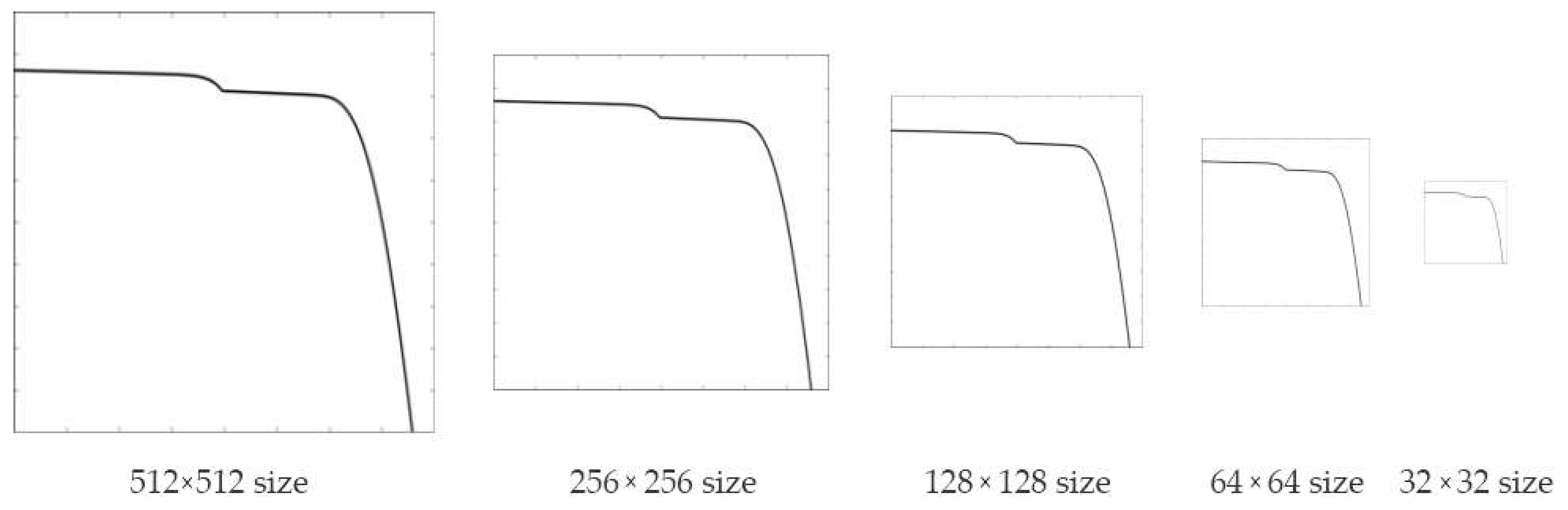
4.2.2. Evaluation of Image Resolution
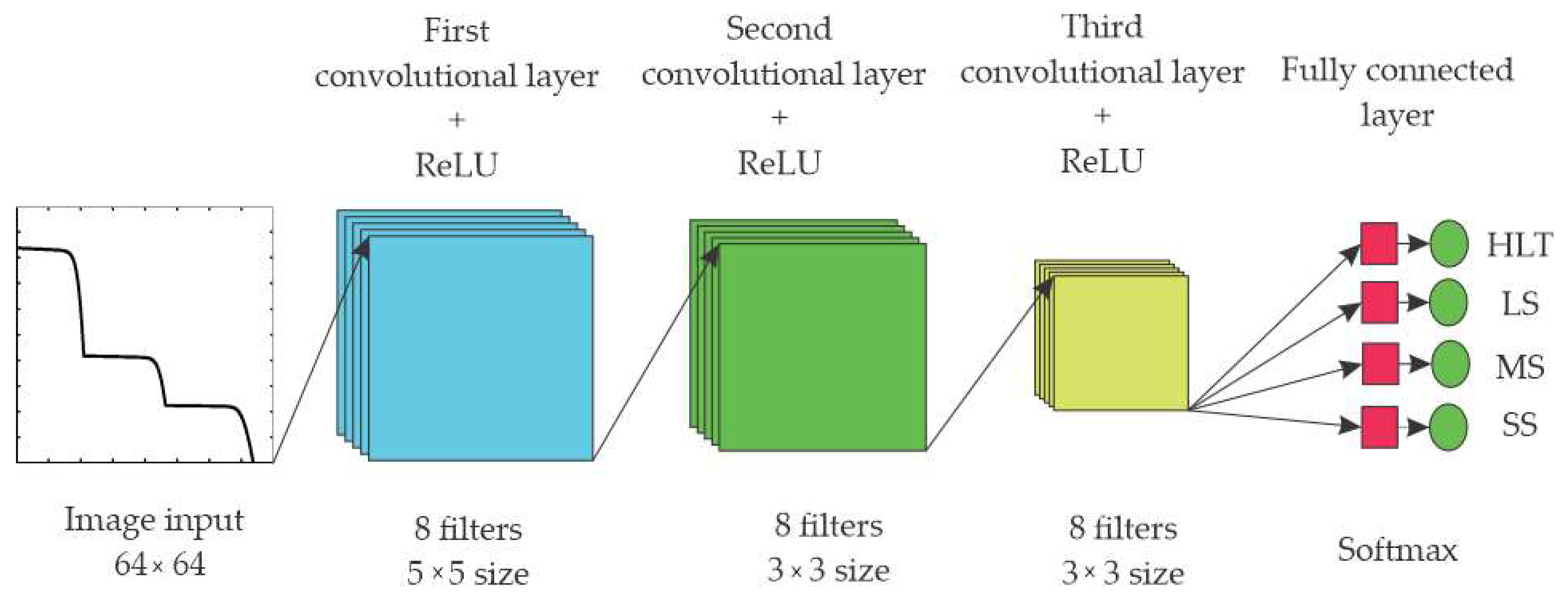
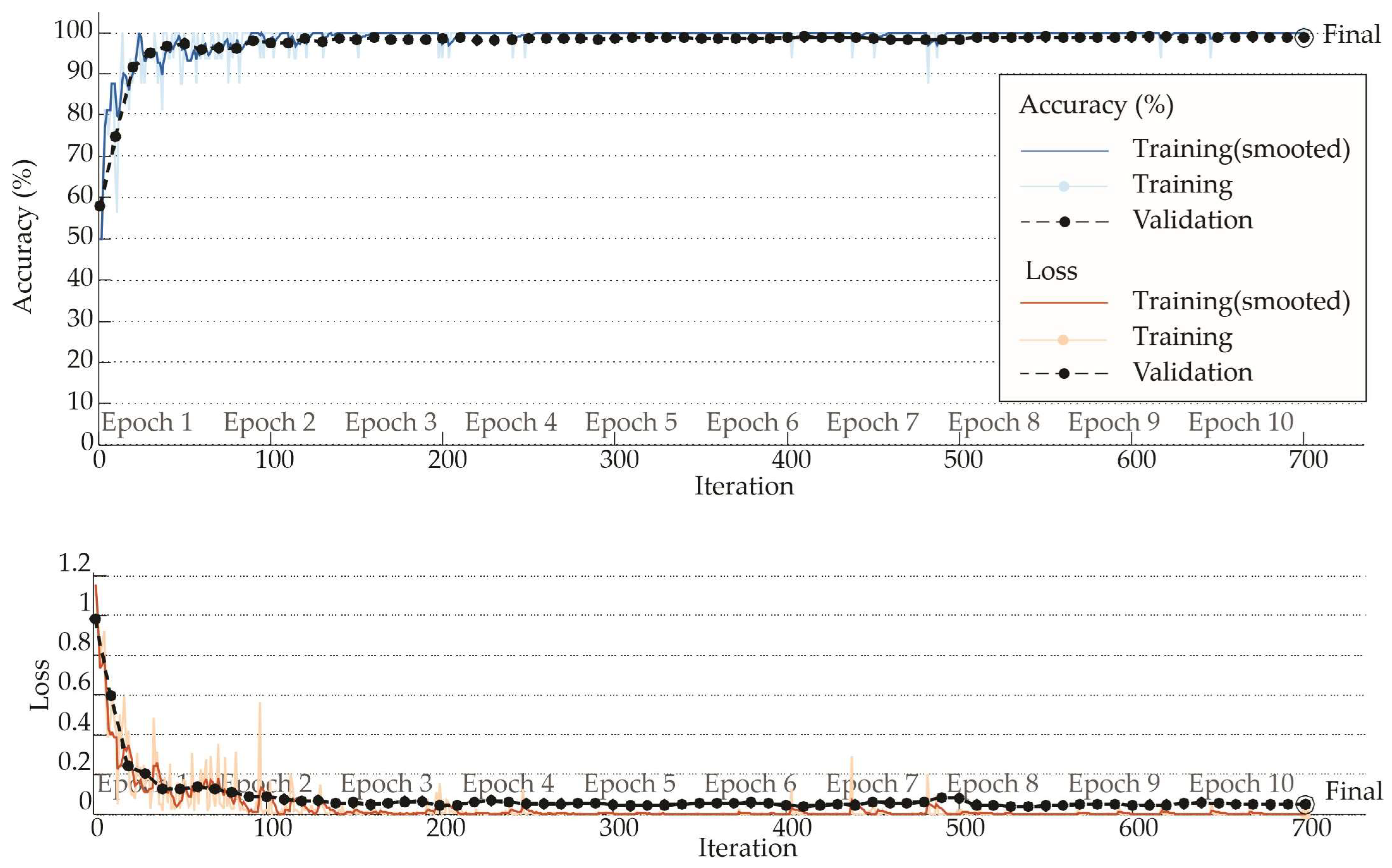
4.2.3. Final Configuration and Training Performance
- Input resolution: 64 × 64 pixels.
- CNN structure: three convolutional layers with eight filters (first layer: 5 × 5, second: 3 × 3, third: 5 × 5).
- Stride and padding: stride = 1, same padding for all layers.
- Pooling: two max-pooling layers with pool size 2 × 2.
- Activation functions: ReLU for convolutional layers and softmax for classification.
- Cross-validation: k-fold used, with k = 5, to ensure robustness of results.
- Training parameters: batch size = 32, epochs = 10, optimizer = Adam, learning rate = 0.001, early stopping not applied due to convergence in under 10 epochs.
- Conventional dataset split: 70% training, 15% validation, 15% testing.
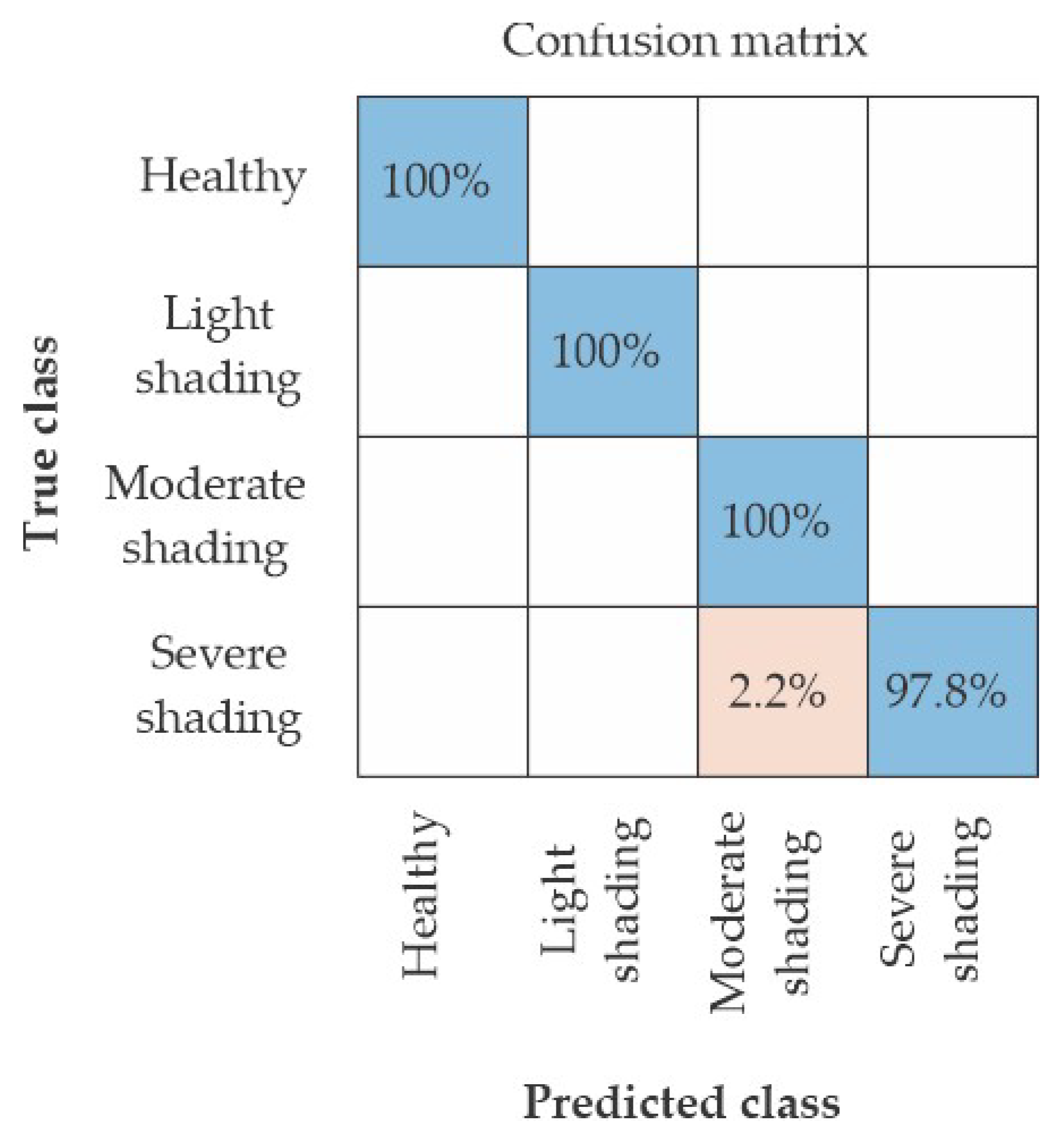
4.3. Gradient-Weighted Class Activation Mapping (Grad-CAM) Results
4.4. Robustness Evaluation Under Noisy Conditions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV | Photovoltaic |
| CNN | Convolutional neural network |
| ANN | Artificial neural network |
| DC | Direct current |
| HLT | Healthy |
| LS | Light shading |
| MS | Moderate shading |
| ReLU | Severe shading |
| Grad-CAM | Gradient-weighted class activation mapping |
| SNR | Signal-to-noise ratio |
References
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable energy and energy storage systems. Energies 2023, 16, 1415. [Google Scholar] [CrossRef]
- Obeidat, F. A comprehensive review of future photovoltaic systems. Sol. Energy 2018, 163, 545–551. [Google Scholar] [CrossRef]
- Uddin, M.; Kazemi, A. A Fault Detection Scheme Utilizing Convolutional Neural Network for PV Solar Panels with High Accuracy. In Proceedings of the 2022 IEEE 1st Industrial Electronics Society Annual On-Line Conference (ONCON), Indian Institute of Technology Kharagpur, Virtual Conference, Kharagpur, India, 9–11 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Khan, M.; Khan, A.; Ahmad, Z.; Khan, S.; Mohammed, A. A Model-Based Approach for Detecting and Identifying Faults on the D.C. Side of a P.V. System Using Electrical Signatures from I-V Characteristics. PLoS ONE 2022, 17, e0260771. [Google Scholar] [CrossRef]
- Lin, W.-T.; Chang, C.-M.; Huang, Y.-C.; Wu, C.-C.; Kuo, C.-C. Fault Diagnosis in Solar Array I-V Curves Using Characteristic Simulation and Multi-Input Models. Appl. Sci. 2024, 14, 5417. [Google Scholar] [CrossRef]
- Khan, Z.U.; Khan, A.D.; Khan, K.; Al Khatib, S.A.K.; Khan, S.; Khan, M.Q.; Ullah, A. A Review of Degradation and Reliability Analysis of a Solar PV Module. IEEE Access 2024, 12, 185036–185054. [Google Scholar] [CrossRef]
- Mustafa, R.J.; Gomaa, M.R.; Al-Dhaifallah, M.; Rezk, H. Environmental Impacts on the Performance of Solar Photovoltaic Systems. Sustainability 2020, 12, 608. [Google Scholar] [CrossRef]
- Köntges, M.; Kurtz, S.; Packard, C.; Jahn, U.; Berger, K.A.; Kato, K.; Friesen, T.; Liu, H.; Van Iseghem, M. Review of Failures of Photovoltaic Modules; Report IEA-PVPS T13-01:2014; International Energy Agency Photovoltaic Power Systems Programme: Paris, France, 2014. [Google Scholar]
- Virtuani, A.; Pavanello, D.; Friesen, T.; Caccivio, M.; Leanza, G.; Ballif, C. The Ageing of Crystalline Silicon Photovoltaic Modules: Materials and Performance. Renew. Energy 2021, 163, 1891–1907. [Google Scholar]
- Meyer, E.L.; van Dyk, E.E. Assessing the Reliability and Degradation of Photovoltaic Module Performance Parameters. IEEE Trans. Reliab. 2004, 53, 83–92. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. (Eds.) Handbook of Photovoltaic Science and Engineering; Wiley: Chichester, UK, 2003. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Vieira, R.G.; de Araújo, F.M.U.; Dhimish, M.; Guerra, M.I.S. A Comprehensive Review on Bypass Diode Application on Photovoltaic Modules. Energies 2020, 13, 2472. [Google Scholar] [CrossRef]
- Özkalay, E.; Valoti, F.; Caccivio, M.; Virtuani, A.; Friesen, G.; Ballif, C. The Effect of Partial Shading on the Reliability of Photovoltaic Modules in the Built-Environment. EPJ Photovolt. 2024, 15, 7. [Google Scholar] [CrossRef]
- Zbib, B.; Al-Sheikh, H. Fault Detection and Diagnosis of Photovoltaic Systems through I-V Curve Analysis. In Proceedings of the 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Istanbul, Turkey, 12–13 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Fadhel, S.; Migan, A.; Delpha, C.; Diallo, D.; Bahri, I.; Trabelsi, M.; Mimouni, M. Data-Driven Approach for Isolated PV Shading Fault Diagnosis Based on Experimental I-V Curves Analysis. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 927–932. [Google Scholar] [CrossRef]
- Hopwood, M.; Stein, J.; Braid, J.; Seigneur, H. Physics-Based Method for Generating Fully Synthetic IV Curve Training Datasets for Machine Learning Classification of PV Failures. Energies 2022, 15, 5085. [Google Scholar] [CrossRef]
- Lu, S.; Wang, M.-H.; Wei, S.-E.; Liu, H.D.; Wu, C.-C. Photovoltaic Module Fault Detection Based on a Convolutional Neural Network. Processes 2021, 9, 1635. [Google Scholar] [CrossRef]
- Fadhel, S.; Delpha, C.; Diallo, D.; Bahri, I.; Migan, A.; Trabelsi, M.; Mimouni, M. PV Shading Fault Detection and Classification Based on I-V Curve Using Principal Component Analysis: Application to Isolated PV System. Sol. Energy 2018, 179, 1–10. [Google Scholar] [CrossRef]
- Pierdicca, R.; Malinverni, E.; Piccinini, F.; Paolanti, M.; Felicetti, A. Deep Convolutional Neural Network for Automatic Detection of Damaged Photovoltaic Cells. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Göttingen, Germany, 10–12 May 2018; Volume XLII-2, pp. 893–900. [Google Scholar] [CrossRef]
- Spataru, S.; Sera, D.; Kerekes, T.; Teodorescu, R. Diagnostic method for photovoltaic systems based on light I–V measurements. Sol. Energy 2015, 119, 29–44. [Google Scholar] [CrossRef]
- Bressan, M.; El Basri, Y.; Gutierrez, A.; Alonso, C. A Shadow Fault Detection Method Based on the Standard Error Analysis of I-V Curves. Renew. Energy 2016, 99, 1181–1190. [Google Scholar] [CrossRef]
- Zabihi, A.; Sadeghkhani, I.; Fani, B. A partial shading detection algorithm for photovoltaic generation systems. J. Sol. Energy Res. 2021, 6, 678–687. [Google Scholar]
- Yuan, Z.; Xiong, G.; Fu, X. Artificial Neural Network for Fault Diagnosis of Solar Photovoltaic Systems: A Survey. Energies 2022, 15, 8693. [Google Scholar] [CrossRef]
- Hopwood, M.; Gunda, T.; Seigneur, H.; Walters, J. Neural Network-Based Classification of String-Level IV Curves from Physically-Induced Failures of Photovoltaic Modules. IEEE Access 2020, 8, 161480–161487. [Google Scholar] [CrossRef]
- Nehme, B.; M’Sirdi, N.; Namaane, A.; Akiki, T. Analysis and Characterization of Faults in PV Panels. Energy Procedia 2017, 111, 1020–1029. [Google Scholar] [CrossRef]
- Haque, A.; Kurukuru, V.S.B.; Khan, M.; Khan, I.; Jaffery, Z. Fault Diagnosis of Photovoltaic Modules. Energy Sci. Eng. 2019, 7, 622–644. [Google Scholar] [CrossRef]
- Mehta, S.; Azad, A.P.; Chemmengath, S.A.; Raykar, V.; Kalyanaraman, S. DeepSolarEye: Power Loss Prediction and Weakly Supervised Soiling Localization via Fully Convolutional Networks for Solar Panels. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 333–342. [Google Scholar]
- Salem, F.; Awadallah, M.A. Detection and assessment of partial shading in photovoltaic arrays. J. Electr. Syst. Inf. Technol. 2016, 3, 23–32. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Cheng, S.; Lin, P.; Wu, Y.; Lin, W. Intelligent fault diagnosis of photovoltaic arrays based on optimized kernel extreme learning machine and IV characteristics. Appl. Energy 2017, 204, 912–931. [Google Scholar] [CrossRef]
- Deitsch, S.; Christlein, V.; Berger, S.; Buerhop-Lutz, C.; Maier, A.; Gallwitz, F.; Riess, C. Automatic Classification of Defective Photovoltaic Module Cells in Electroluminescence Images Using Convolutional Neural Networks. Sol. Energy 2019, 185, 455–468. [Google Scholar] [CrossRef]
- Latoui, A.; Daachi, M.E.H. Real-time monitoring of partial shading in large PV plants using Convolutional Neural Network. Sol. Energy 2023, 253, 428–438. [Google Scholar] [CrossRef]
- Wang, M.-H.; Lin, Z.-H.; Lu, S.-D. A Fault Detection Method Based on CNN and Symmetrized Dot Pattern for PV Modules. Energies 2022, 15, 6449. [Google Scholar] [CrossRef]
- Cipriani, G.; D’Amico, A.; Guarino, S.; Manno, D.; Traverso, M.; Di Dio, V. Convolutional Neural Network for Dust and Hotspot Classification in PV Modules. Energies 2020, 13, 6357. [Google Scholar] [CrossRef]
- Teta, A.; Korich, B.; Bakria, D.; Hadroug, N.; Rabehi, A.; Alsharef, M.; Bajaj, M.; Zaitsev, I.; Ghoneim, S.S.M. Fault detection and diagnosis of grid-connected photovoltaic systems using energy valley optimizer based lightweight CNN and wavelet transform. Sci. Rep. 2024, 14, 18907. [Google Scholar] [CrossRef]
- Nelson, J. The Physics of Solar Cells; Imperial College Press: London, UK, 2003. [Google Scholar]
- Green, M.A. Solar Cells: Operating Principles, Technology, and System Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Würfel, P.; Würfel, U. Physics of Solar Cells: From Basics to Advanced Concepts, 3rd ed.; Wiley-VCH: Weinheim, Germany, 2016. [Google Scholar]
- Markvart, T.; Castañer, L. (Eds.) Practical Handbook of Photovoltaics, 2nd ed.; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Sera, D.; Teodorescu, R.; Rodriguez, P. Photovoltaic Module Diagnostics by Series Resistance Monitoring and Temperature and Rated Power Estimation. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics (IECON), Orlando, FL, USA, 10–13 November 2008; pp. 2195–2199. [Google Scholar] [CrossRef]
- Maghami, M.R.; Mutambara, A.G.O. Challenges associated with hybrid energy systems: An artificial intelligence solution. Energy Rep. 2023, 9, 924–940. [Google Scholar] [CrossRef]
- Khalil, I.U.; Ul-Haq, A.; Mahmoud, Y.; Jalal, M.; Aamir, M.; Ahsan, M.U.; Mehmood, K. Comparative analysis of photovoltaic faults and performance evaluation of its detection techniques. IEEE Access 2020, 8, 26676–26700. [Google Scholar] [CrossRef]
- Bhimrao, B.; Vishwakarma, S. Study of partial shading effect on solar module using MATLAB. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2017, 6, 5303–5308. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. Eur. Conf. Comput. Vis. 2014, 8689, 818–833. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Lujan-Olalde, A.G.; Rangel-Rodriguez, A.H.; Perez-Sanchez, A.V.; Valtierra-Rodriguez, M.; Machorro-Lopez, J.M.; Amezquita-Sanchez, J.P. Graphical Empirical Mode Decomposition–Convolutional Neural Network-Based Expert System for Early Corrosion Detection in Truss-Type Bridges. Infrastructures 2025, 10, 177. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE international conference on computer vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Brockmann, S.; Schlippe, T. Optimizing convolutional neural networks for image classification on resource-constrained microcontroller units. Computers 2024, 13, 173. [Google Scholar] [CrossRef]




| Single Layer | Filter Size | |||
|---|---|---|---|---|
| 3 × 3 | 5 × 5 | 8 × 8 | ||
| Number of filters | 4 | 92.1% | 92.9% | 93.1% |
| 8 | 94.6% | 95.8% | 95.6% | |
| 16 | 91.5% | 93.3% | 95.2% | |
| 32 | 92.1% | 93.7% | 95.4% | |
| Two Layers | Filter Size | |||
|---|---|---|---|---|
| 3 × 3 | 5 × 5 | 8 × 8 | ||
| Number of filters | 4 | 96.2% | 95.8% | 96.1% |
| 8 | 96.9% | 96.0% | 96.2% | |
| 16 | 95.6% | 96.0% | 95.9% | |
| 32 | 96.2% | 94.7% | 96.1% | |
| Three Layers | Filter Size | |||
|---|---|---|---|---|
| 3 × 3 | 5 × 5 | 8 × 8 | ||
| Number of filters | 4 | 96.4% | 97.1% | 97.1% |
| 8 | 99.5% | 99.1% | 99.2% | |
| 16 | 98.7% | 99.3% | 98.9 | |
| 32 | 96.0% | 97.5% | 98.1 | |
| Image Size | Accuracy |
|---|---|
| 512 | 99.54% |
| 256 | 99.46% |
| 128 | 99.51% |
| 64 | 99.58% |
| 32 | 94.54% |
| Results | |
|---|---|
| Validation accuracy | 99.5% |
| Training finishing | Max epoch completed |
| Training cycle | |
| Epoch | 10 of 10 |
| Iteration | 700 of 700 |
| Iteration per epoch | 70 |
| Maximum iteration | 700 |
| Validation | |
| Frequency | 10 iterations |
| Other information | |
| Hardware resource | Single GPU |
| Learning rate schedule | Constant |
| Learning rate | 0.001 |
| Activation functions | ReLU and softmax |
| Optimizer | Adam |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arenas-Prado, J.A.; Rangel-Rodriguez, A.H.; Amezquita-Sanchez, J.P.; Granados-Lieberman, D.; Tapia-Tinoco, G.; Valtierra-Rodriguez, M. Automated Detection of Shading Faults in Photovoltaic Modules Using Convolutional Neural Networks and I–V Curves. Processes 2025, 13, 2999. https://doi.org/10.3390/pr13092999
Arenas-Prado JA, Rangel-Rodriguez AH, Amezquita-Sanchez JP, Granados-Lieberman D, Tapia-Tinoco G, Valtierra-Rodriguez M. Automated Detection of Shading Faults in Photovoltaic Modules Using Convolutional Neural Networks and I–V Curves. Processes. 2025; 13(9):2999. https://doi.org/10.3390/pr13092999
Chicago/Turabian StyleArenas-Prado, Jesus A., Angel H. Rangel-Rodriguez, Juan P. Amezquita-Sanchez, David Granados-Lieberman, Guillermo Tapia-Tinoco, and Martin Valtierra-Rodriguez. 2025. "Automated Detection of Shading Faults in Photovoltaic Modules Using Convolutional Neural Networks and I–V Curves" Processes 13, no. 9: 2999. https://doi.org/10.3390/pr13092999
APA StyleArenas-Prado, J. A., Rangel-Rodriguez, A. H., Amezquita-Sanchez, J. P., Granados-Lieberman, D., Tapia-Tinoco, G., & Valtierra-Rodriguez, M. (2025). Automated Detection of Shading Faults in Photovoltaic Modules Using Convolutional Neural Networks and I–V Curves. Processes, 13(9), 2999. https://doi.org/10.3390/pr13092999








