Failure Analysis and Safety De-Icing Strategy of Local Transmission Tower-Line Structure System Based on Orthogonal Method in Power System
Abstract
1. Introduction
2. Transmission Tower-Line System Model
3. Orthogonal Test Design of De-Icing for Each Wire
3.1. Design of the Orthogonal Array
3.2. Apply Loads and Calculations According to the Orthogonal Table
3.2.1. Calculation of Load
3.2.2. Load Application and Calculation
4. Analysis of Orthogonal Test Results
5. Tower Failure Analysis Under the Most Dangerous Ice Melting Condition
- (1)
- The structure of the tower becomes a single mechanism. The criterion is that after the failure of some components, the total stiffness matrix of the residual components is singular.
- (2)
- The structural deformation is greater than the allowable value. If the top displacement of the tower exceeds a certain value, the transmission tower will be considered a failure.
- (3)
- The structure cannot bear the extra load or a lower structural bearing capacity occurs for the first time. Generally speaking, the transmission tower will be considered a failure when the stress ratio of the main components of the tower is too large.
6. Conclusions
- (1)
- Orthogonal test results show that conductors 1, 5, and 6 and ground lines 11 and 12 icing or not has a great impact on the mechanical failure situation of the whole tower-line system, and conductors and ground lines with large span lengths and large altitude differences in icing have a greater impact. Meanwhile, from the results of optimal combination, no icing at the windward side and icing at the leeward side can cause larger unbalanced tension on the tower, wherein the risk of tower collapse is significantly elevated. Therefore, the ice on these lines should be preferentially removed when melting ice.
- (2)
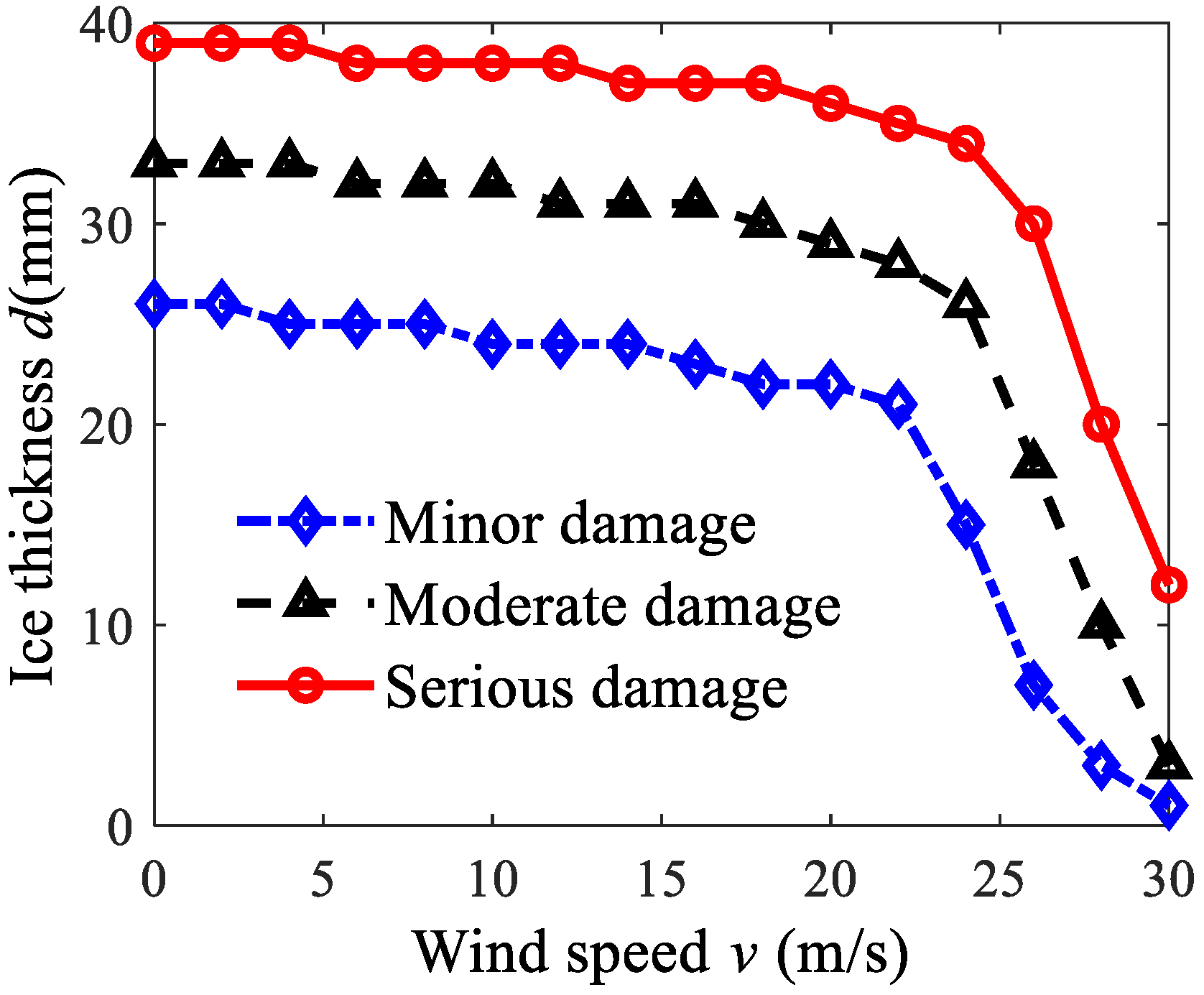
- The ice thickness–wind speed critical failure curves of the tower-line system have been proposed. When the ice thickness of the transmission lines is above 25 mm, some ice melting measures should be taken in a timely manner. When the wind speed exceeds 20 m/s, the ice thickness of the tower failure reduces evidently. When the wind speed exceeds 26 m/s, even if the ice thickness is smaller than about 10 mm, the tower still has a risk of mechanical failure.
- (3)
- Next, research on the real-time de-icing system can be carried out based on the work of this paper. The ice–wind critical failure curve is pre-input into the system, thereby enabling the prediction of ice disaster on transmission lines and the determination of the conditions for ice-melting initiation. Subsequently, based on the current situation of the ice-melting equipment, differentiated efforts will be made to conduct ice melting on specific sections of the conductors and ground wires. The application of the system will help reduce the hazards and losses caused by ice formation on transmission lines.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, B.; Jiang, X.; Yin, F. Development and prospect of monitoring and prevention methods of icing disaster in China power grid. IET Gener. Transm. Distrib. 2022, 16, 4480–4493. [Google Scholar] [CrossRef]
- Farzaneh, M.; Chisholm, W.A. Insulators for Icing and Polluted Environments; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Huang, J.; Zhou, X. Study on transmission line icing prediction based on micro-topographic correction. AIP Adv. 2022, 12, 085103. [Google Scholar] [CrossRef]
- Couture, P. Smart Power Line and photonic de-icer concepts for transmission-line capacity and reliability improvement. Cold Reg. Sci. Technol. 2011, 65, 13–22. [Google Scholar] [CrossRef]
- Lu, J.; Wu, C.; Li, B.; Zhang, H.-X. Comparative research on topology of DC de-icing equipment. Power Syst. Prot. Control 2014, 42, 83–88. (In Chinese) [Google Scholar]
- Mao, X.; Tan, Y.; Zhu, Y.; Huang, Q.; Liu, H.; Xu, B. The Portable DC De-icer with Emergency Power Supply Function. In Proceedings of the 2019 3rd IEEE Conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019; pp. 2364–2369. [Google Scholar]
- Fan, R.; Sun, M.; He, Z.; Yan, S. Design and system test of movable DC de-icer for Jiangxi power grid. Autom. Elect. Power Syst. 2009, 33, 67–71. (In Chinese) [Google Scholar]
- Yan, M.; Ai, X.; Shahidehpour, M.; Li, Z.; Wen, J.; Bahramira, S.; Paaso, A. Enhancing the Transmission Grid Resilience in Ice Storms by Optimal Coordination of Power System Schedule with Pre-Positioning and Routing of Mobile DC De-Icing Devices. IEEE Trans. Power Syst. 2019, 34, 2663–2674. [Google Scholar] [CrossRef]
- Zhou, X.; Yao, Y.; Li, Z.; Chen, L.; Chen, J. Multi-Physics Optimization Study of Permanent Magnet Synchronous Generator for Direct Current De-icing Based on Surrogate Model. In Proceedings of the 2023 10th International Forum on Electrical Engineering and Automation (IFEEA), Nanjing, China, 3–5 November 2023; pp. 783–787. [Google Scholar]
- Zhou, X.; Yao, Y.; Ma, X.; Feng, Z.; Yu, X. The Scheme of Movable DC Ice Melting Device Based on the Engine-Generator Topology. In Proceedings of the 2023 4th International Conference on Electrical, Electronic Information and Communication Engineering, EEICE, Dalian, China, 21–23 April 2023; Volume 2023, pp. 1–8. [Google Scholar]
- Xie, D.; Song, W.; Wang, W.; Sun, T.; Huang, T.; Cai, X. Research on ice removal blasting parameters of HV Transmission Lines. J. North Univ. China 2018, 39, 746–751. (In Chinese) [Google Scholar]
- Cao, Y.; Xue, K.; Miao, L.; Li, H.; Guan, X.; Zhang, J.; Li, G. Dynamic response analysis of ice tower line system after blasting deicing. J. North Univ. China Nat. Sci. Ed. 2019, 40, 198–205. (In Chinese) [Google Scholar]
- Zhao, J.; Guo, R.; Cao, L.; Zhang, F. Improvement of LineROVer: A mobile robot for de-icing of transmission lines. In Proceedings of the 2010 1st International Conference on Applied Robotics for the Power Industry, Montreal, QC, Canada, 5–7 October 2010; pp. 1–4. [Google Scholar]
- Zhang, Z.; Zhang, H.; Yue, S.; Zeng, W. A Review of Icing and Anti-Icing Technology for Transmission Lines. Energies 2023, 16, 601. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, J.; Deng, Y.; Hu, J.; Ren, X. Research on Uneven Icing of Lines in Adjacent Towers Under Pass Micro-topography. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2023, 44, 2462–2474. (In Chinese) [Google Scholar]
- Lu, J.; Liu, C.; Chen, H.; Hu, B. Finite element calculation of 500 kV iced power transmission system. High Volt. Eng. 2007, 33, 167–169. (In Chinese) [Google Scholar]
- Zhang, Z.; Liu, J.; Shao, K.; Zhang, P. Analysis of wind-sand-load-induced dynamic response of transmission tower-line systems. Shock Vib. 2022, 2022, 4924091. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, X.; Song, X.; Deng, H.; Ma, X. Investigation on aerodynamic characteristics for steel tubular cross-arms of transmission tower under skew wind. J. Wind Eng. Ind. Aerodyn. 2022, 222, 1–13. [Google Scholar] [CrossRef]
- Rao, N.P.; Kalyanaraman, V. Nonlinear behaviour of lattice panel of angle towers. J. Constr. Steel Res. 2001, 57, 1337–1357. [Google Scholar]
- Yao, C.; Mao, F.; Xu, D.; Liu, X.; Zhou, Z.; Cui, Y. Mechanical properties of transmission tower-line system in non-uniformly iced condition. High Volt. Eng. 2011, 37, 3084–3092. (In Chinese) [Google Scholar]
- Dong, B.; Jiang, X.; Xiang, Z. Calculation model and experimental verification of equivalent ice thickness on overhead lines with tangent tower considering ice and wind loads. Cold Reg. Sci. Technol. 2022, 200, 103588. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, J.; Du, Z.; Zhou, W.; Li, G.; Gan, Y. Short-term failure warning for transmission tower under land subsidence condition. IEEE Access 2020, 8, 10455–10465. [Google Scholar] [CrossRef]
- Ghaderpour, E. Constructions for orthogonal designs using signed group orthogonal designs. Discret. Math. 2018, 341, 277–285. [Google Scholar] [CrossRef]
- GB 50545-2010; Code for Design of 110 kV~750 kV Overhead Transmission Line. PRC National Standard: Beijing, China, 2010.
- Han, F. Study on Reliability Analysis of UHV Transmission Tower-Line System with Wind Action. Ph.D. Thesis, Chongqing University, Chongqing, China, 2012. (In Chinese). [Google Scholar]
- Zhang, L.; Ruan, J.; Du, Z.; Huang, D.; Deng, Y. Transmission line tower failure warning based on FBG strain monitoring and prediction model. Electr. Power Syst. Res. 2023, 214, 108827. [Google Scholar] [CrossRef]



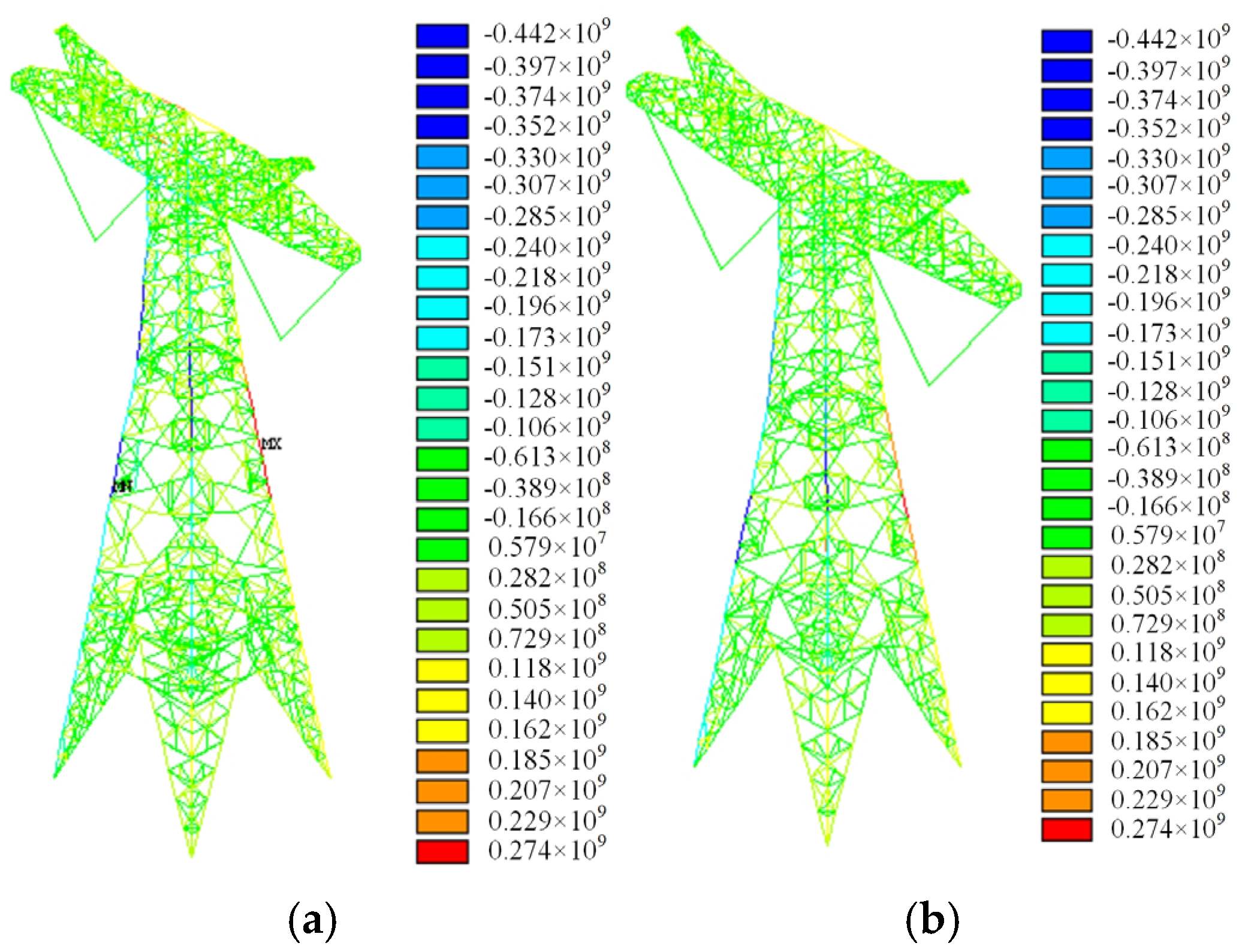
| Aspect | Existing Work | Inadequacy | References | Proposed Work |
|---|---|---|---|---|
| Local Line De-icing Technologies | Effectively removes the ice, overcomes the problems of inconvenient transportation in mountainous areas and difficulty in obtain-ing power supply. | Lack of ice-melting strategy. | [4,5,6,7,8,9,10,11,12,13,14] | Research on the de-icing strategy for local line de-icing. |
| Mechanical Analysis | The mechanical characteristics of the tower under various loads based on beam element finite element models have been studied. | Lack of research on the impact of local ice melting on the unbalanced tension of the tower. | [15,16,17,18,19,20,21,22] | Analyzed based on FEM and orthogonal design. |
| Optimization Strategy | Heuristic or single-factor approaches. | Lack of criteria for transmission tower failure, and the considerations are also very limited. | [17,18,19,22] | Considers both the tower displacement and the element stress. |
| Computational Efficiency | Finite element calculations can analyze the impact of ice melting on the mechanical properties of the tower. | The number of ice-melting combinations for the wires is large, resulting in low cal-culation efficiency. | [20,21] | Orthogonal tests to re-duce the calculation time. |
| No. | Type | Nominal Height/m | Total Height/m | Altitude/m | Span/m |
|---|---|---|---|---|---|
| 397 | Tension tower | JT61 | 46.5 | 64.5 | 249 |
| 398 | Tangent tower | Z30601 | 60 | 69.8 | 89 |
| 399 | Tangent tower | Z30601 | 72 | 81.8 | 320 |
| 400 | Tension tower | JT61 | 48 | 66 | / |
| Test No. | Ice Combination | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | G1 | G2 | G3 | G4 | G5 | G6 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 7 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 9 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 10 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 11 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 12 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 13 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 14 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 15 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 16 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| Wind Speed | Ice Thickness | Most Severe Combination | Wind Speed | Ice Thickness | Most Severe Combination | ||
|---|---|---|---|---|---|---|---|
| Index 1 | Index 2 | Index 1 | Index 2 | ||||
| 22 m/s | 20 mm | 110111010011 | 101010101010 | 26 m/s | 40 mm | 101011001011 | 101010101010 |
| 22 m/s | 30 mm | 110111000111 | 101010111010 | 26 m/s | 50 mm | 100011011011 | 101010101010 |
| 22 m/s | 40 mm | 110011000111 | 101010111010 | 30 m/s | 20 mm | 100011011011 | 101010111010 |
| 26 m/s | 20 mm | 110011000111 | 100010111010 | 30 m/s | 30 mm | 100011010011 | 101010111010 |
| 26 m/s | 30 mm | 101011001011 | 101010101110 | 30 m/s | 40 mm | 101011001011 | 101010101110 |
| Factor | Frequency of Occurrence | Factor | Most Severe Combination | ||
|---|---|---|---|---|---|
| Index 1 | Index 2 | Index 1 | Index 2 | ||
| 1 | 6 | 10 | 7 | 0 | 0 |
| 2 | 4 | 10 | 8 | 0 | 0 |
| 3 | 0 | 5 | 9 | 0 | 5 |
| 4 | 3 | 10 | 10 | 0 | 0 |
| 5 | 10 | 10 | 11 | 9 | 10 |
| 6 | 7 | 10 | 12 | 8 | 9 |
| Category | Minor Damage | Moderate Damage | Serious Damage |
|---|---|---|---|
| Stress ratio of main beam | ξ > 1.0 | ξ > 1.15 | —— |
| Stress ratio of diagonal beam | 0.8 < ξ < 1.0 | 1.0 < ξ < 1.15 | ξ > 1.15 |
| Horizontal displacement of the tower top | —— | 3h/1000 < l < h/100 | l > h/100 |
| Convergence of program | —— | —— | Program cannot converge |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhou, X.; Ruan, J.; Feng, Z.; Shen, Y.; Yao, Y. Failure Analysis and Safety De-Icing Strategy of Local Transmission Tower-Line Structure System Based on Orthogonal Method in Power System. Processes 2025, 13, 1782. https://doi.org/10.3390/pr13061782
Zhang L, Zhou X, Ruan J, Feng Z, Shen Y, Yao Y. Failure Analysis and Safety De-Icing Strategy of Local Transmission Tower-Line Structure System Based on Orthogonal Method in Power System. Processes. 2025; 13(6):1782. https://doi.org/10.3390/pr13061782
Chicago/Turabian StyleZhang, Li, Xueming Zhou, Jiangjun Ruan, Zhiqiang Feng, Yu Shen, and Yao Yao. 2025. "Failure Analysis and Safety De-Icing Strategy of Local Transmission Tower-Line Structure System Based on Orthogonal Method in Power System" Processes 13, no. 6: 1782. https://doi.org/10.3390/pr13061782
APA StyleZhang, L., Zhou, X., Ruan, J., Feng, Z., Shen, Y., & Yao, Y. (2025). Failure Analysis and Safety De-Icing Strategy of Local Transmission Tower-Line Structure System Based on Orthogonal Method in Power System. Processes, 13(6), 1782. https://doi.org/10.3390/pr13061782







