Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation
Abstract
1. Introduction
2. Dynamic Model of Mobile Robots
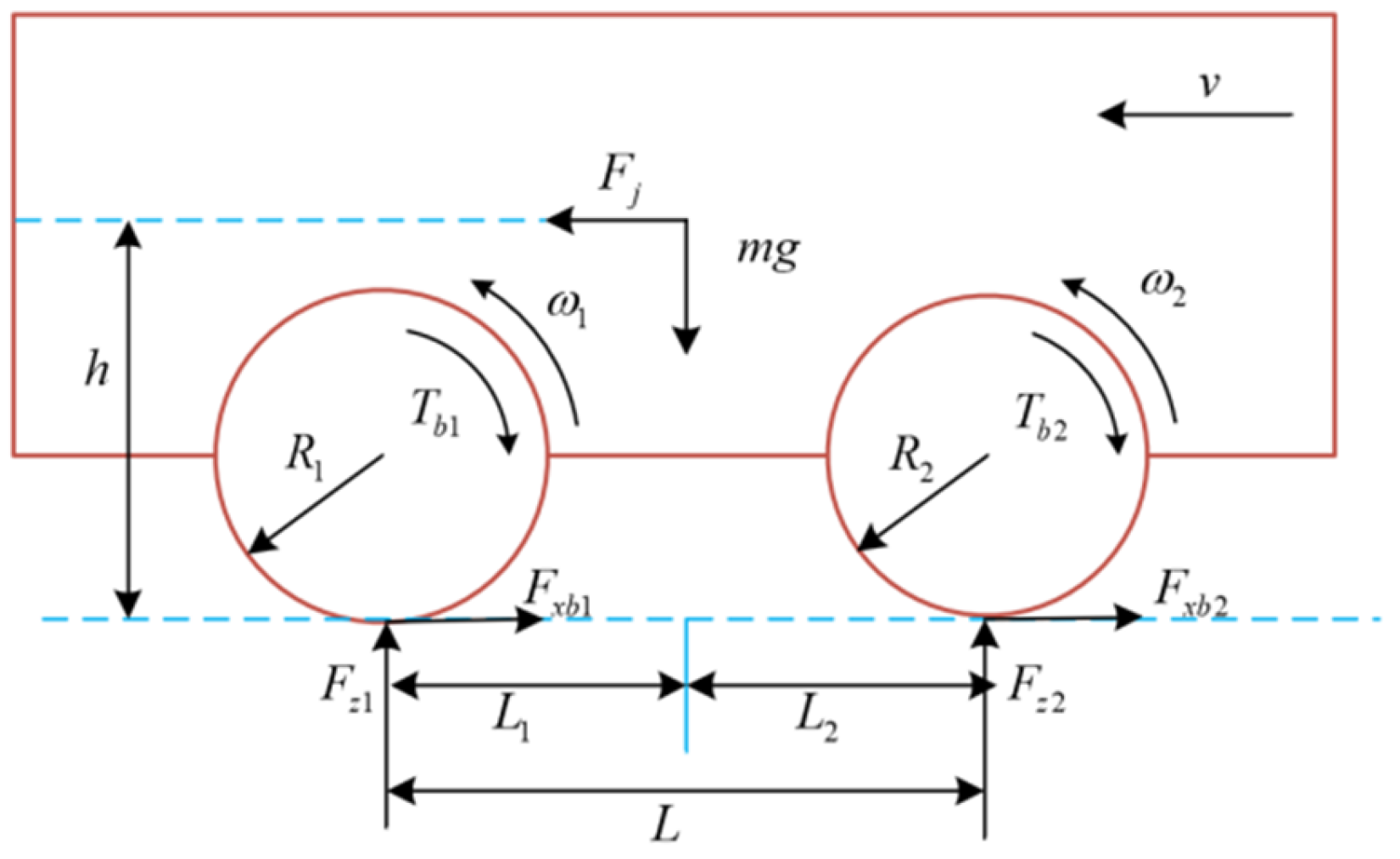
2.1. Wheel Model
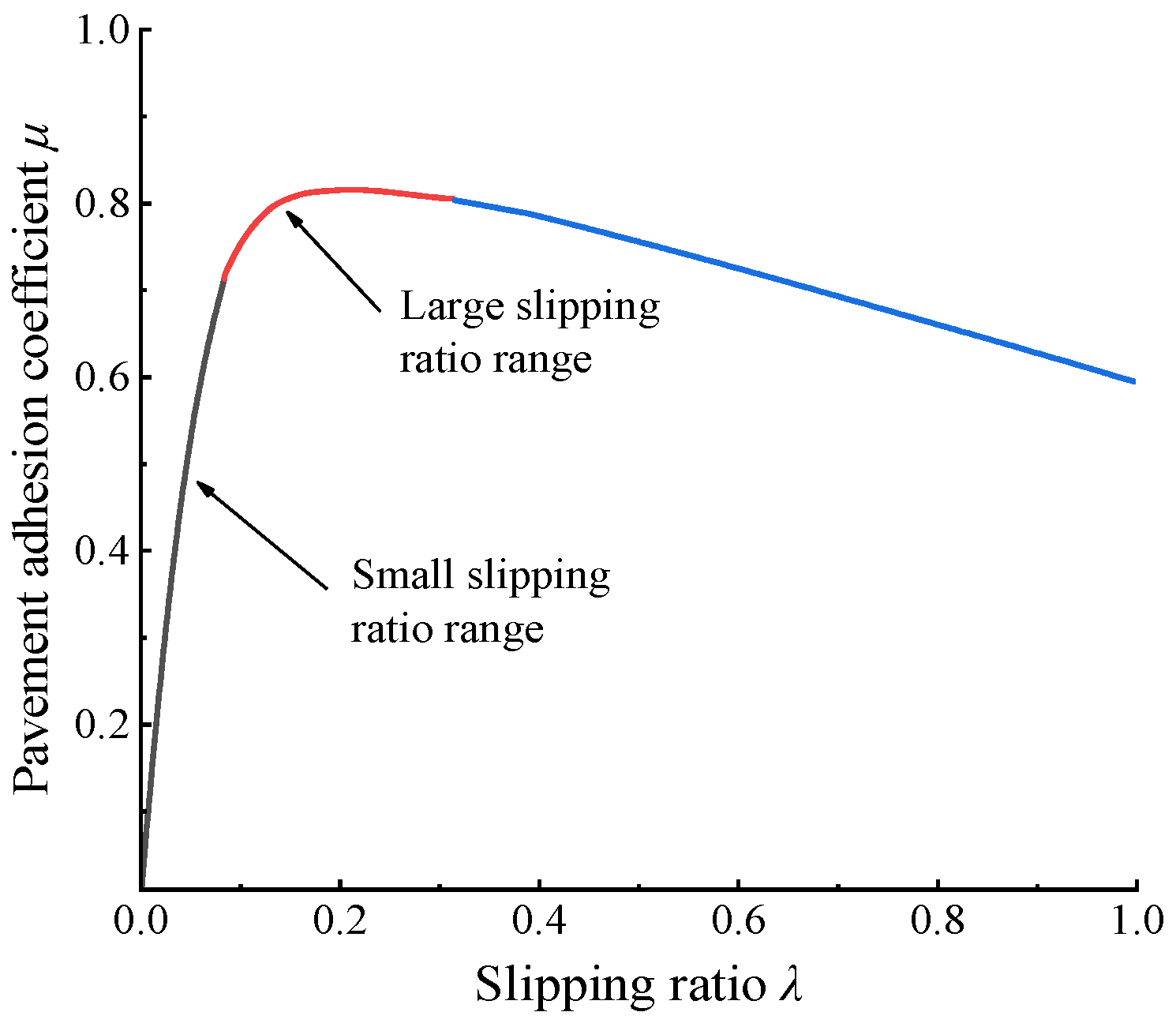
2.2. Tire Model
3. Design of Integral Sliding-Mode Controller
3.1. Estimation of Pavement Adhesion Coefficient
3.2. Design of Integral Sliding-Mode Surface
3.3. Design of the Composite Convergence Law
3.4. Design of Integral Sliding-Mode Algorithm Regulated by a Composite Convergence Law
4. Simulation Verification
4.1. Simulation Model
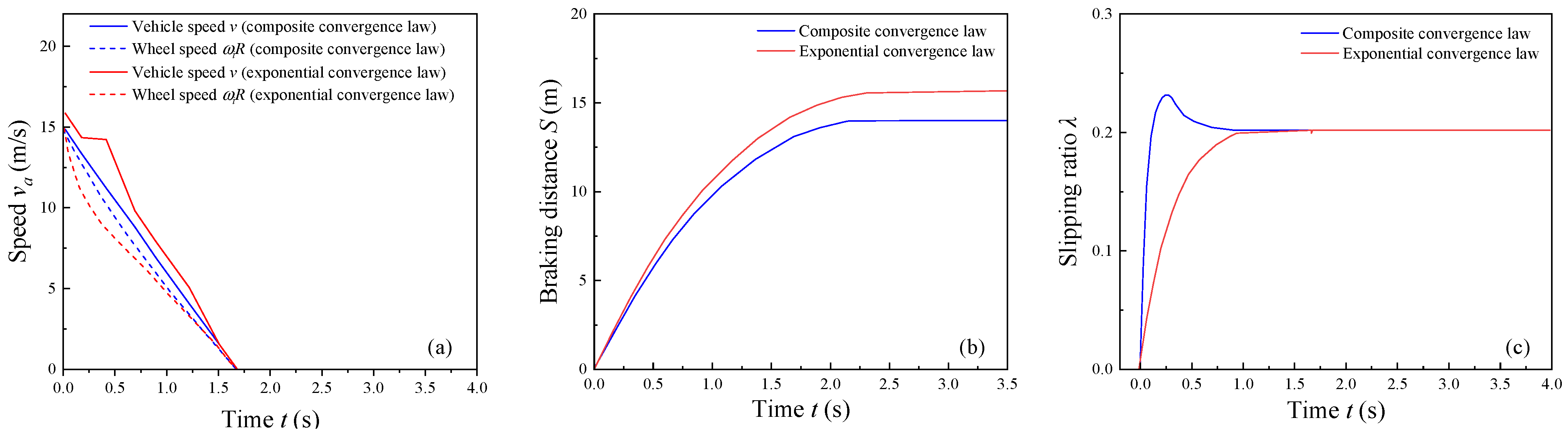
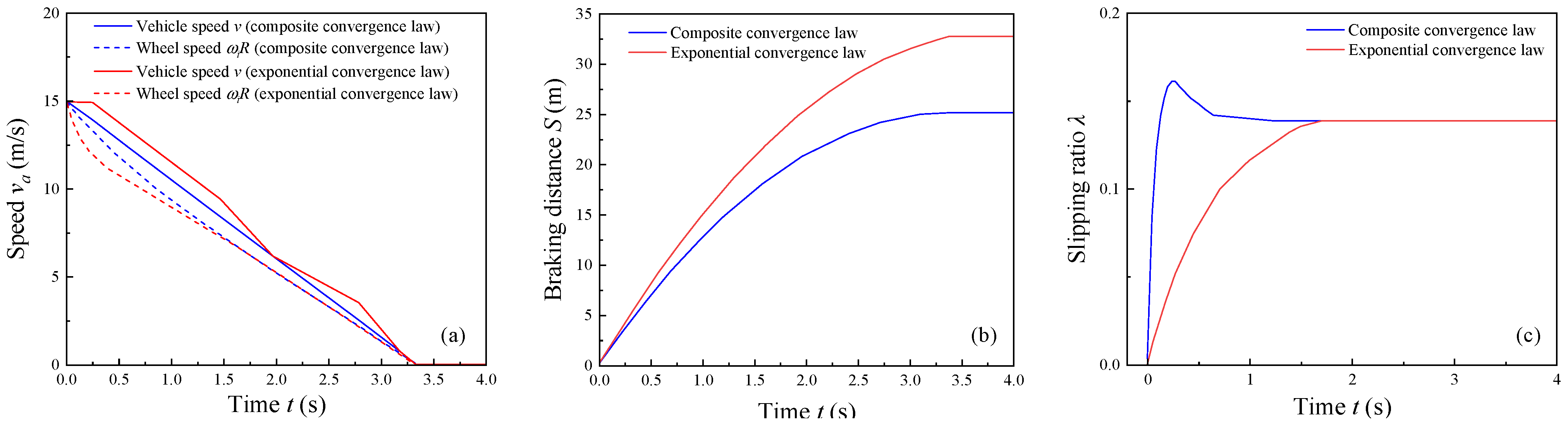
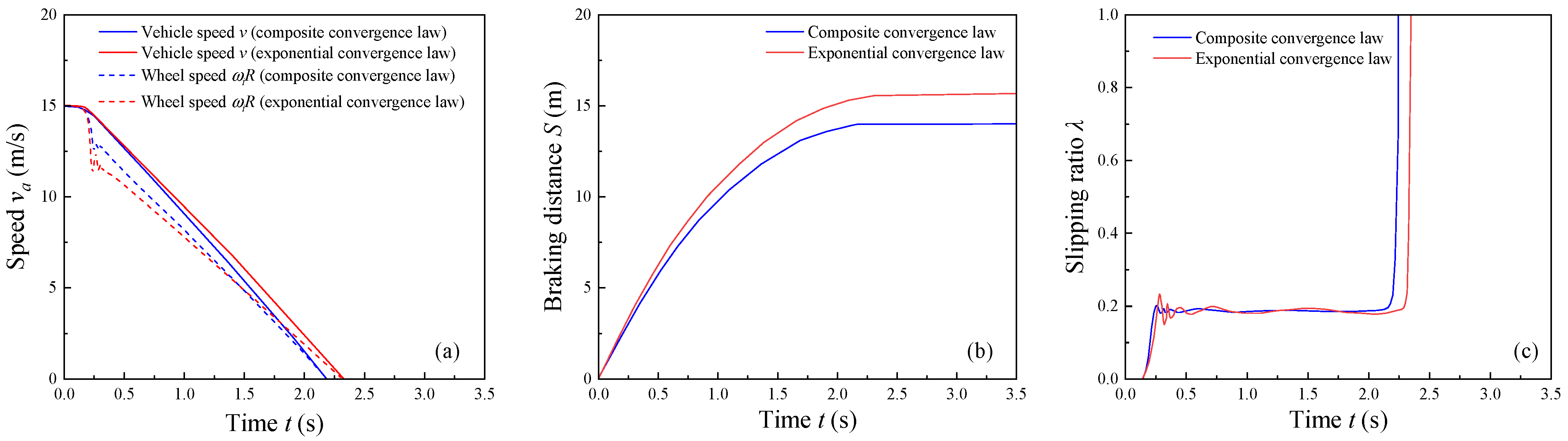
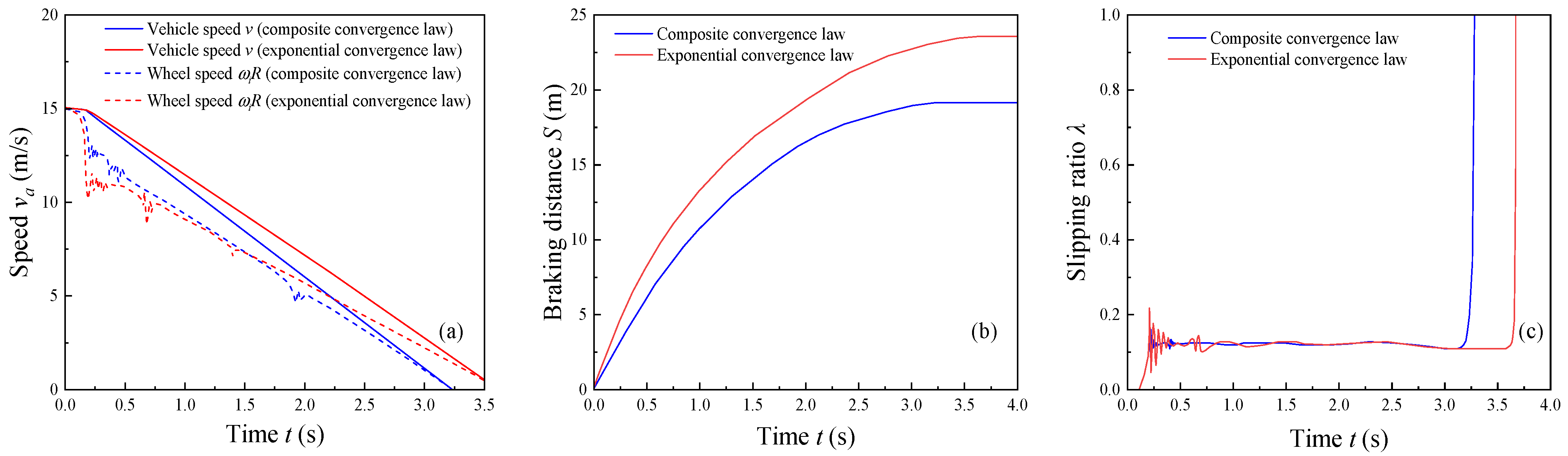
4.2. Simulation Results
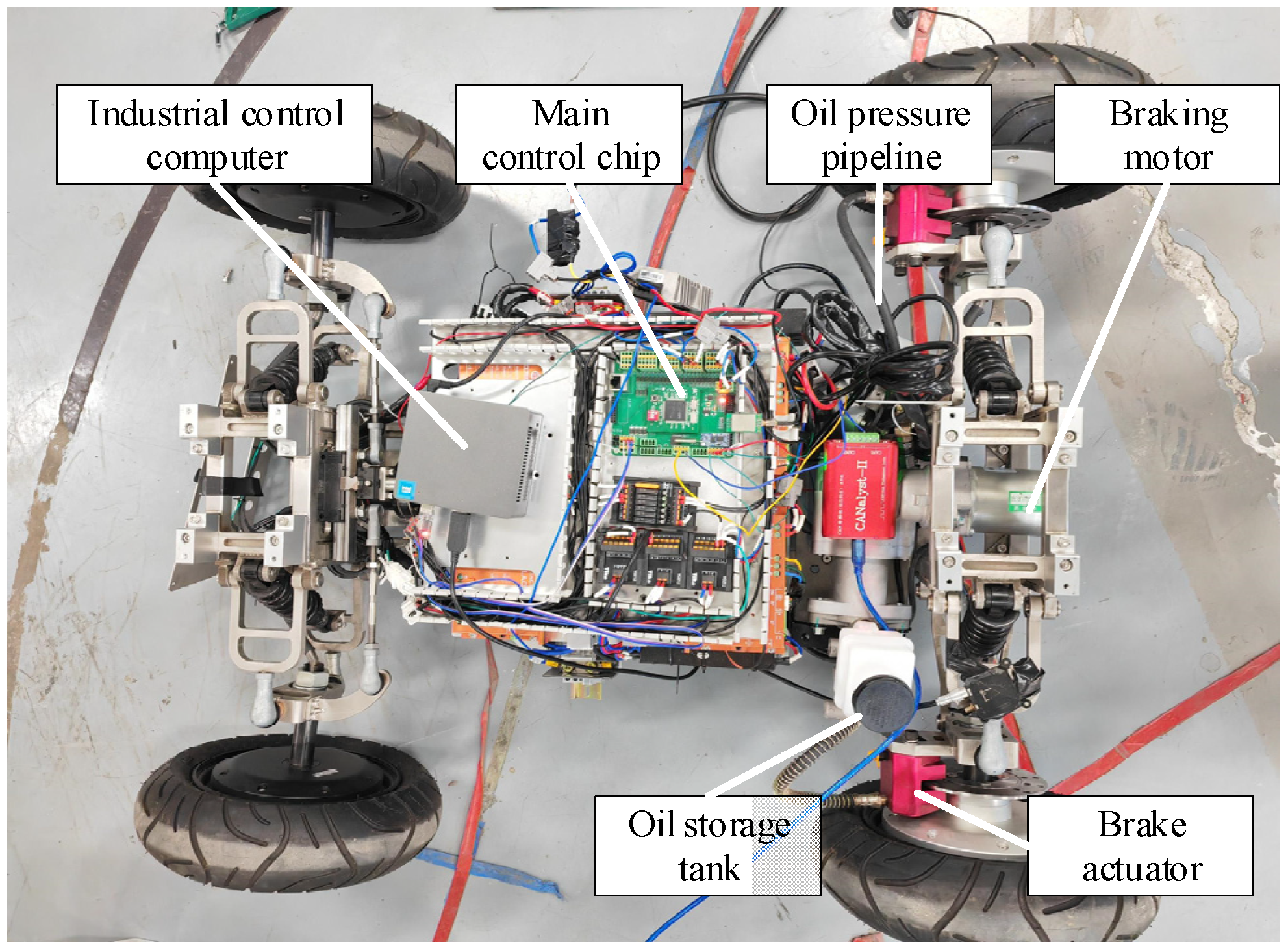
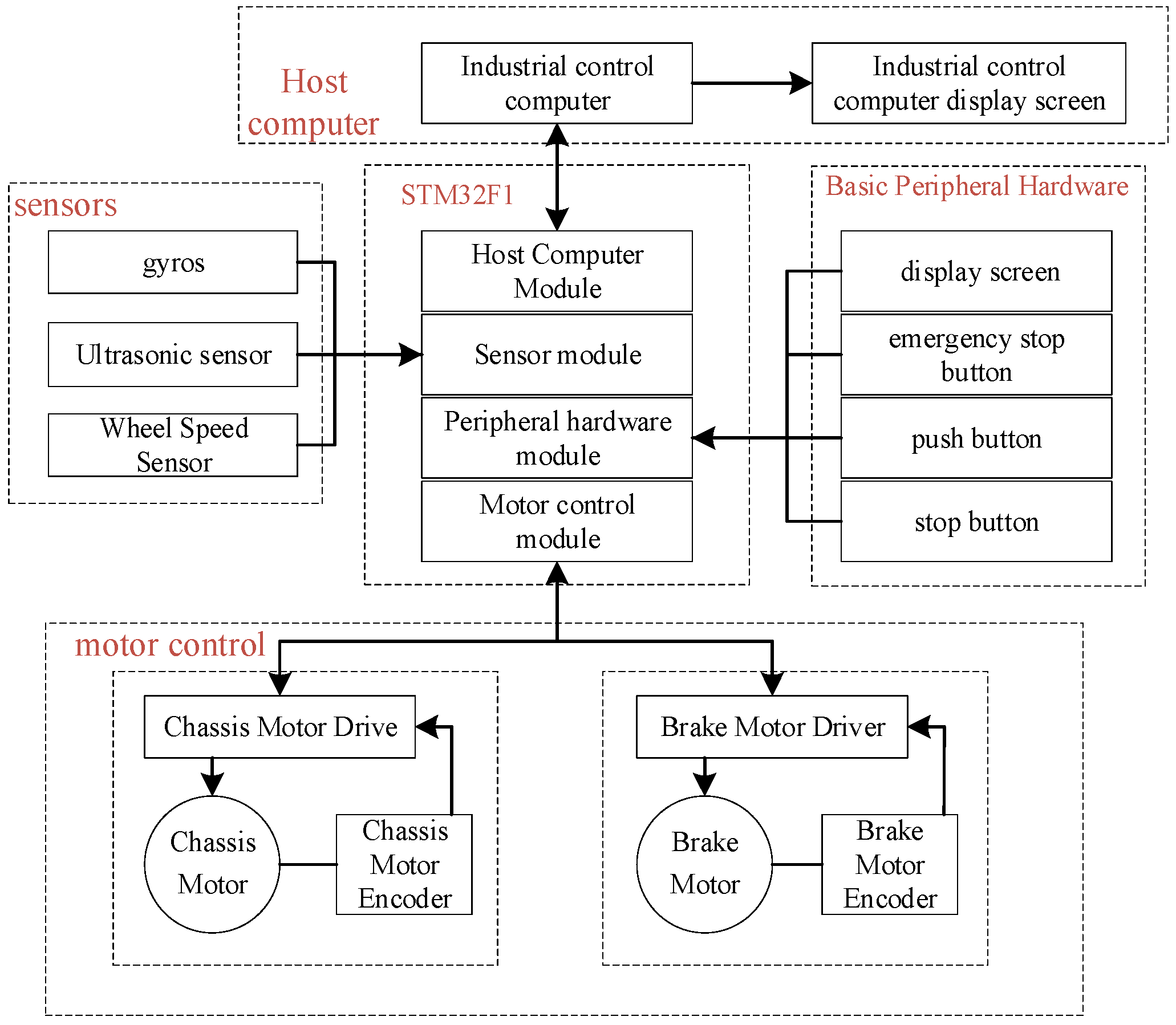
4.3. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henry, A.I.; Hesham, E.S.; Manzoor, K. An overview of sensors in Autonomous Vehicles. Proc. Comp. Sci. 2022, 198, 736–741. [Google Scholar]
- Zhu, S.; Fan, X.; Qi, G.; Wang, P. Review of Control Algorithms of Vehicle Anti-lock Braking System. Recent Pat. Eng. 2023, 17, 30–45. [Google Scholar] [CrossRef]
- Unsal, C.; Kachroo, P. Sliding mode measurement feedback control for anti-lock braking systems. IEEE Trans. Control Syst. Technol. 1999, 7, 271–281. [Google Scholar] [CrossRef]
- Yin, Z.; Cui, C.; Wang, R.; Su, R.; Ma, X. Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems. Machines 2025, 13, 271. [Google Scholar] [CrossRef]
- Yao, S.; Xue, L.; Huang, J.; Zou, Y.; Zhang, R. Research on the Configuration of Wheeled Mobile Welding Robots Under Multiple Working Conditions. Machines 2025, 13, 315. [Google Scholar] [CrossRef]
- Mi, J.; Liu, J.; Xu, Y.; Long, Z.; Wang, J.; Xu, W.; Ji, T. A Reinforcement Learning-Based Double Layer Controller for Mobile Robot in Human-Shared Environments. Appl. Sci. 2025, 15, 7812. [Google Scholar] [CrossRef]
- Chiu, C.S.; Yao, S.Y.; Santiago, C. Type-2 Fuzzy-Controlled Air-Cleaning Mobile Robot. Symmetry 2025, 17, 1088. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Z.; Hu, J.; Zeng, S.; Liu, X.; Zhang, T. Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments. Appl. Sci. 2025, 15, 7551. [Google Scholar] [CrossRef]
- Yin, Z.; Ma, X.; Su, R.; Huang, Z.; Zhang, C. Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy. Processes 2023, 11, 2985. [Google Scholar] [CrossRef]
- Ait Dahmad, H.; Ayad, H.; García Cerezo, A.; Mousannif, H. Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance. Sensors 2025, 25, 3805. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zhang, L.; Wang, Y. Automotive ABS/DYC coordinated control under complex driving conditions. IEEE Access 2018, 6, 32769–32779. [Google Scholar] [CrossRef]
- Chereji, E.; Radac, M.B.; Szedlak-Stinean, A.I. Sliding Mode Control Algorithms for Anti-Lock Braking Systems with Performance Comparisons. Algorithms 2021, 14, 2. [Google Scholar] [CrossRef]
- Rishabh, B.; Sangram, P.; Ramesh, K.S. Surface prediction and control algorithms for anti-lock brake system. Transp. Res. Part C Emerg. Technol. 2012, 21, 181–195. [Google Scholar]
- Feng, X.; Hu, J. Discrete fuzzy adaptive PID control algorithm for automotive anti-lock braking system. J. Ambient Intell. Humaniz. Comput. 2021, 3, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Wu, S.; Wang, Q. Global Sliding Mode Control for Nonlinear Vehicle Antilock Braking System. IEEE Access 2021, 9, 40349–40359. [Google Scholar] [CrossRef]
- Emir, K.; Hermann, W. Validation of vehicle dynamics simulation models—A review. Veh. Syst. Dynam. 2014, 52, 186–200. [Google Scholar]
- Stawczyk, P. Costless Improvement of Converter Efficiency in a Regenerative Braking System with a Brushless DC Machine. Electronics 2025, 14, 2390. [Google Scholar] [CrossRef]
- Gerdes, J.C.; Hedrick, J.K. Brake System Modeling for Simulation and Control. J. Dyn. Syst. Meas. Control 1999, 121, 496–503. [Google Scholar] [CrossRef]
- Kaspar, S.; Stroph, D.R.; Pruckner, D.A.; Hohmann, P.-D.S. Single wheel drives for wheel slip control. World Electr. Veh. J. 2013, 6, 223–229. [Google Scholar] [CrossRef]
- Shi, P.; Min, Y.; Wang, H.; Lv, L. Dynamic Simulation of Ground Braking Force Control Based on Fuzzy Adaptive PID for Integrated ABS-RBS System with slipping ratio Consideration. World Electr. Veh. J. 2025, 16, 372. [Google Scholar] [CrossRef]
- Bi, J.; Han, Y.; Hou, M.; Wang, C. Adaptive Second-Order Sliding Mode Wheel Slip Control for Electric Vehicles with In-Wheel Motors. World Electr. Veh. J. 2024, 15, 538. [Google Scholar] [CrossRef]
- Jeon, W.; Chakrabarty, A.; Zemouche, A.; Rajamani, R. Simultaneous State Estimation and Tire Model Learning for Autonomous Vehicle Applications. IEEE ASME Trans. Mechatron. 2021, 26, 1941–1950. [Google Scholar] [CrossRef]
- De Castro, R.; Araújo, R.E.; Freitas, D. Real-time estimation of tyre–road friction peak with optimal linear parameterization. IET Control Theory Appl. 2012, 6, 2257–2268. [Google Scholar] [CrossRef]
- David, V.; Rodolfo, O.; Matthias, S.; Michel, B. An adapted Burckhardt tire model for off-road vehicle applications. J. Terramech. 2022, 104, 15–24. [Google Scholar]
- Xiao, F.; Hu, J.; Jia, M.; Zhu, P.; Deng, C. A novel estimation scheme of tyre–road friction characteristics based on parameter constraints on varied-µ roads. Measurement 2022, 194, 111077. [Google Scholar] [CrossRef]
- Kang, S.; Chen, J.; Qiu, G.; Tong, H. Slipping ratio Adaptive Control Based on Wheel Angular Velocity for Distributed Drive Electric Vehicles. World Electr. Veh. J. 2023, 14, 119. [Google Scholar] [CrossRef]
- Leng, B.; Jin, D.; Xiong, L.; Yang, X.; Yu, Z. Estimation of tire-road peak adhesion coefficient for intelligent electric vehicles based on camera and tire dynamics information fusion. Mech. Syst. Signal. Process. 2021, 150, 107275. [Google Scholar] [CrossRef]
- Guan, H.; Wang, B.; Lu, P.; Xu, L. Identification of maximum road friction coefficient and optimal slip ratio based on road type recognition. Chin. J. Mech. Eng. 2014, 27, 1018–1026. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, J.; Huang, D.; Xu, M.; Zhai, S.; Zhang, W.; Jiang, P. Prediction and Experimental Study of Tire Slip Rate Based on Chassis Sinkage Amount. Agriculture 2023, 13, 665. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lu, Y.; Li, H. Estimation Strategy for the Adhesion Coefficient of Arbitrary Pavements Based on an Optimal Adaptive Fusion Algorithm. Machines 2025, 13, 17. [Google Scholar] [CrossRef]
- Quan, L.; Chang, R.; Guo, C. Vehicle state and road adhesion coefficient joint estimation based on high-order cubature Kalman algorithm. Appl. Sci. 2023, 13, 10734. [Google Scholar] [CrossRef]
- Chen, X.; Li, S.; Li, L.; Zhao, W.; Cheng, S. Longitudinal-lateral-cooperative estimation algorithm for vehicle dynamics states based on adaptive-square-root-cubature-Kalman-filter and similarity-principle. Mech. Syst. Signal Process. 2022, 176, 109162. [Google Scholar] [CrossRef]
- Dong, P.; Li, J.; Guo, W.; Zhang, H.; Zhao, P.; Xu, X.; Wang, S. Robust Optimal Path Tracking Control for Intelligent Vehicles Equipped with Wheel Modules Based on Continuous Integral Sliding Mode Control. Autom. Innov. 2025, 8, 385–404. [Google Scholar] [CrossRef]
- Alika, R.; Mellouli, E.M.; Tissir, E.H. A modified sliding mode controller based on fuzzy logic to control the longitudinal dynamics of the autonomous vehicle. Results Eng. 2024, 22, 102120. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, Y.; Liu, H.; He, S.; Khan, Z. A composite sliding mode controller with extended disturbance observer for 4WSS agricultural robots in unstructured farmlands. Comput. Electron. Agric. 2025, 232, 110069. [Google Scholar] [CrossRef]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2021, 9, 363–378. [Google Scholar] [CrossRef]
- Zhou, P.; Hu, X.; Zhu, Z.; Ma, J. What is the most suitable Lyapunov function? Chaos Solitons Fractals 2021, 150, 111154. [Google Scholar] [CrossRef]
- Chu, Y.; Fu, S.; Hou, S.; Fei, J. Intelligent terminal sliding mode control of active power filters by self-evolving emotional neural network. IEEE Trans. Industr. Inform. 2022, 19, 6138–6149. [Google Scholar] [CrossRef]
- Hou, S.; Chu, Y.; Fei, J. Intelligent global sliding mode control using recurrent feature selection neural network for active power filter. IEEE Trans. Ind. Electron. 2020, 68, 7320–7329. [Google Scholar] [CrossRef]
- Mosayebi, M.; Sadeghzadeh, S.M.; Gheisarnejad, M.; Khooban, M.H. Intelligent and fast model-free sliding mode control for shipboard DC microgrids. IEEE Trans. Transport. Elect. 2020, 7, 1662–1671. [Google Scholar] [CrossRef]
- Zheng, K.; Hu, Y.; Wu, B. Intelligent fuzzy sliding mode control for complex robot system with disturbances. Eur. J. Control. 2020, 51, 95–109. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, S.G.; Sun, I.F. Intelligent sliding-mode position control using recurrent wavelet fuzzy neural network for electrical power steering system. Int. J. Fuzzy Syst. 2017, 19, 1344–1361. [Google Scholar] [CrossRef]
- Wang, S.; Hui, Y.; Sun, X.; Shi, D. Neural network sliding mode control of intelligent vehicle longitudinal dynamics. IEEE Access 2019, 7, 162333–162342. [Google Scholar] [CrossRef]
- Rizki, H.; Lamzouri, F.E.Z.; Boufounas, E.M.; El Amrani, A.; Bejjit, L. Advanced global MPPT strategy for PV systems using high-order sliding mode control, ABC optimization, and neural network prediction under partial shading conditions. Comput. Electr. Eng. 2025, 127, 110562. [Google Scholar] [CrossRef]



| Pavement Type | ||
|---|---|---|
| Dry asphalt | 0.193 | 1.170 |
| Dry cement | 0.1599 | 1.089 |
| Wet asphalt | 0.1308 | 0.801 |
| Pebble | 0.4004 | 1.002 |
| Snow | 0.0779 | 0.210 |
| Ice | 0.0314 | 0.023 |
| Parameter Name | Value |
|---|---|
| One quarter of the mass of the mobile robot m (kg) | 150 |
| Tire moment of inertia Ji (kg⋅m2) | 1.8 |
| Tire radius Ri (m) | 0.3 |
| Adhesion coefficient μ1 (wet asphalt) | 0.45 |
| Adhesion coefficient μ2 (dry asphalt) | 0.91 |
| Convergence coefficient α | 0.05 |
| Integral coefficient c | 6 |
| Switching gain ε | 0.15 |
| Gain coefficient k | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Long, D.; Liang, Y.; Wang, B.; Wang, X.; Su, R. Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation. Processes 2025, 13, 2887. https://doi.org/10.3390/pr13092887
Hu H, Long D, Liang Y, Wang B, Wang X, Su R. Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation. Processes. 2025; 13(9):2887. https://doi.org/10.3390/pr13092887
Chicago/Turabian StyleHu, Hanchun, Dengyan Long, Yi Liang, Buyun Wang, Xubo Wang, and Rong Su. 2025. "Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation" Processes 13, no. 9: 2887. https://doi.org/10.3390/pr13092887
APA StyleHu, H., Long, D., Liang, Y., Wang, B., Wang, X., & Su, R. (2025). Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation. Processes, 13(9), 2887. https://doi.org/10.3390/pr13092887







