Evaluation Method of Key Controlling Factors for Productivity in Deep Coalbed Methane Reservoirs—A Case Study of the 8+9^# Coal Seam in the Eastern Margin of the Ordos Basin

Abstract

Coalbed methane (CBM) resources hold broad development prospects in China, with deep CBM reservoirs increasingly becoming a focal point for exploration. However, compared to shallow CBM, the factors influencing the productivity of deep CBM are more complex and less studied. This study integrates statistical methods—grey correlation analysis and principal component analysis—with the machine learning approach of random forests, and further employs a fuzzy mathematics-based comprehensive evaluation method to propose a systematic evaluation framework for identifying key controlling factors of productivity. Using field data from the No. 8+9 coal seam in the eastern margin of the Ordos Basin, the results indicate that the primary geological factors affecting cumulative gas production are gas content and coal seam thickness, while the key engineering factors are proppant intensity and proppant volume. These findings align with practical field experience and provide a rational basis for the design of fracturing strategies in deep CBM reservoirs.

1. Evaluation Methodology for Key Controlling Factors

China possesses abundant coalbed methane (CBM) resources, with estimated geological reserves of approximately 30.05 × 10¹² m³ and recoverable reserves of 12.50 × 10¹² m³ at depths shallower than 2000 m. For reservoirs exceeding 2000 m in depth, the geological and recoverable reserves are approximately 40.71 × 10¹² m³ and 10.01 × 10¹² m³ respectively, demonstrating significant development potential. In 2023, China’s CBM production reached 11.77 billion m³, accounting for 5% of the nation’s natural gas supply, with an incremental contribution of 18%, thereby serving as a crucial supplement to domestic natural gas resources [1]. However, deep CBM reservoirs exhibit complex occurrence conditions characterized by “great depth, ultra-low porosity and permeability, strong heterogeneity, and high in situ stress” [2], presenting substantially greater exploration and development challenges compared to shallow CBM. Furthermore, the lack of universal development techniques adaptable to varying geological conditions has resulted in generally low productivity. Consequently, in-depth research into the key controlling factors of deep CBM well productivity is of paramount importance for enhancing resource utilization efficiency and achieving economically viable development [3,4,5].

The factors influencing deep coalbed methane (CBM) productivity are highly complex, with production performance being jointly determined by both geological and engineering parameters. Current research on these influencing factors remains limited, with most studies employing conventional statistical methods such as grey correlation analysis and principal component analysis (PCA) to evaluate either geological or engineering parameters’ individual impacts on productivity. Alternatively, some studies have conducted simplified evaluations of key controlling factors primarily to facilitate subsequent productivity prediction modelling or parameter optimization. However, given the multitude of factors affecting deep CBM productivity and the inherent correlations among certain parameters, a comprehensive methodology for evaluating these key controlling factors has yet to be established [6,7,8,9,10,11].

With the increasing adoption and application of artificial intelligence technologies, intelligent and digital solutions have emerged as pivotal drivers in advancing reservoir fracturing techniques. Extensive literature review reveals that researchers have successfully employed machine learning algorithms, including random forest and gradient boosting, to determine feature importance among various productivity-influencing factors. These data-driven approaches have enabled the establishment of robust productivity evaluation models [12,13,14].

This study integrates statistical approaches with machine learning methodologies, combining grey correlation analysis, principal component analysis (PCA), entropy weight method, and random forest algorithms to develop a comprehensive evaluation framework for identifying key productivity-controlling factors in deep coalbed methane (CBM) reservoirs. The proposed methodology was applied to historical production data from the 8+9^# coal seam in the eastern margin of Ordos Basin, establishing a solid foundation for subsequent productivity prediction and parameter optimization in this reservoir.

1.1. Grey Relational Analysis

Grey relational analysis is a methodology for assessing the degree of association between factors based on sample data, which quantitatively characterizes the strength, magnitude, and sequence of inter-element relationships. When the variation trends of two factors in the sample data demonstrate substantial consistency, their mutual correlation is stronger, and conversely weaker [15,16]. The analytical procedure initiates with data standardization using Equation (1), where each element is normalized by the mean value of its corresponding indicator:

$$x_{ij}^{\prime }={\displaystyle \frac{x_{ij}}{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{x}_{ij}}}}$$

(1)

where x_ij represents the matrix element corresponding to each parameter, n denotes the number of elements per parameter, $x_{ij}^{\prime }$ indicates the standardized result of each parameter element.

Subsequently, the correlation degree between each element in the standardized independent variable sequence and its corresponding element in the dependent variable sequence is computed. Let the dependent variable sequence be denoted as $x_0=\left\{x_0\right(1),x_0(2),\dots ,x_0(n\left)\right\}$, and the independent variable sequences as $x_1=\left\{x_1\right(1),x_1(2),\dots ,x_1(n\left)\right\}$, $x_2=\left\{x_2\right(1),x_2(2),\dots ,x_2(n\left)\right\},\dots ,$$x_k=\left\{x_k\right(1),x_k(2),\dots ,x_k(n\left)\right\}$. The calculation procedure initiates with determining the minimum and maximum differences between the independent and dependent variable sequences:

$$a=\min \left|x_0\left(j\right)-x_k\left(j\right)\right|,\forall k,j$$

(2)

$$b=\max \left|x_0\left(j\right)-x_k\left(j\right)\right|,\forall k,j$$

(3)

where a and b represent the minimum and maximum differences between the independent and dependent variable sequences, respectively, k = 1, 2,…, denoting the index of distinct independent variable sequences.

Whereupon, we define the following mathematical expression:

$$\gamma \left(x_0\left(j\right),x_k\left(j\right)\right)={\displaystyle \frac{a+\rho b}{\left|x_0\left(j\right)-x_k\left(j\right)\right|+\rho b}},\forall k,j$$

(4)

where ρ denotes the distinguishing coefficient, conventionally assigned a value of 0.5.

Finally, the relational degree between each sequence (i.e., the association measure between independent and dependent variables) is computed as follows:

$$\gamma \left(x_0,x_k\right)={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n}\gamma \left(x_0\left(j\right),x_k\left(j\right)\right)}{n}}$$

(5)

The relational degree [0, 1] is bounded within the unit interval, where a higher value indicates stronger influence of the independent variable on the dependent variable.

1.2. Random Forest Methodology

The Random Forest algorithm is an ensemble learning method that fundamentally employs bagging (bootstrap aggregating) with multiple decision trees through iterative combination. Utilizing decision trees as base learners, this technique incorporates both random feature selection and bootstrap sampling during training, thereby maintaining the low-bias characteristics of individual decision trees while effectively mitigating overfitting. In the context of correlation analysis, Random Forest primarily performs feature importance evaluation, which quantitatively assesses the contribution of each feature to model predictions [17].

Within the Random Forest algorithm, decision trees are constructed by recursively selecting optimal feature splits to minimize node impurity measures—specifically, variance reduction for regression tasks and Gini impurity or entropy for classification tasks [18]. The assessment of feature importance is principally achieved through computation of the aggregate impurity reduction attributable to each feature across all decision nodes. As this investigation constitutes a regression analysis, node impurity is quantified using the Mean Squared Error (MSE) metric, expressed as

$$MSE\left(t\right)={\displaystyle \frac{1}{N_t}}{{\displaystyle \sum _{i\in t}\left(y_i{\overline{y}}_t\right)}}^2$$

(6)

where $t$ denotes an arbitrary node during feature splitting, $N_t$ represents the number of samples contained in node $t$, $y_i$ indicates the $i$-th sample value, $\overline{y_t}$ signifies the mean value of all samples in node $t$.

The impurity reduction metric for regression tasks is computed as follows:

$$△MSE\left(j\right)=MSE\left(t\right)-\left({\displaystyle \frac{N_L}{N_t}}MSE\left(t_L\right)+{\displaystyle \frac{N_R}{N_t}}MSE\left(t_R\right)\right)$$

(7)

when a node $t$ undergoes splitting via a given feature, this partition generates two child nodes $t_L$ and $t_R$; $N_L$ and $N_R$ denote the sample sizes in nodes $t_L$ and $t_R$.

Within a given decision tree T, the importance measure $I_j\left(T\right)$ of feature $j$ is computed as the summation of impurity reduction gains across all nodes where $j$ serves as the splitting feature:

$$I_j\left(T\right)={\displaystyle \sum _{t\in T}△MSE\left(j,t\right)}$$

(8)

In Random Forest algorithms, the importance of feature $j$ is computed as the mean value across all individual trees in the ensemble:

$$I_j={\displaystyle \frac{1}{N_{trees}}}{\displaystyle \sum _{k=1}^{N_{trees}}{I}_j\left(T_k\right)}$$

(9)

where $N_{trees}$ denotes the total number of trees in the Random Forest ensemble, and $T_k$ represents the $k$-th decision tree.

1.3. Principal Component Analysis–Entropy Weight Method

1.3.1. Principal Component Analysis

Principal Component Analysis (PCA) is a statistical methodology employed for dimensionality reduction and data analysis. The primary objective of PCA is to project high-dimensional data onto a lower-dimensional subspace while preserving maximal information from the original dataset. The fundamental principle of PCA involves an orthogonal transformation that reorients the original data into a new coordinate system, where the derived axes—termed principal components—are mutually orthogonal and ordered by their explained variance [19]. The first principal component captures the maximum variance in the data, followed by the second principal component, which accounts for the next highest variance under the constraint of orthogonality to the first, and so forth.

Since features may exhibit heterogeneous measurement scales that could bias analytical results, data standardization must precede Principal Component Analysis. The standardization equation is given by

$$x_{ij}^{*}={\displaystyle \frac{x_{ij}-{\mu }_j}{{\sigma }_j}}$$

(10)

where $i$ denotes the number of samples in the dataset, $j$ represents the index of the feature column, $x_{ij}$ is the original observed value, ${\mu }_j$ stands for the mean of the $j$-th feature, ${\sigma }_j$ indicates its standard deviation, and $x_{ij}^{*}$ refers to the standardized value after normalization.

Then, the covariance matrix of the standardized data is computed and undergoes eigenvalue decomposition to obtain the eigenvalues ${\lambda }_j$ and corresponding eigenvectors ${\nu }_j$ of the covariance matrix. Finally, the linear combination relationship between each principal component and the original features is derived [20]:

$$z_n={\nu }_{1n}{X}_1+{\nu }_{2n}{X}_2+\cdots +{\nu }_{jn}{X}_n$$

(11)

where $n$ denotes the number of principal components, ${\nu }_{jn}$ represents the $n$-th component of the $j$-th feature, $X_n$ indicates the $n$-th feature

The cumulative variance contribution rate of the principal components is given by:

$${\alpha }_k={\displaystyle \frac{{\displaystyle \sum _{j=1}^k{\lambda }_j}}{{\displaystyle \sum _{i=1}^n{\lambda }_i}}}\left(k\le n\right)$$

(12)

where ${\alpha }_k$ represents the cumulative variance contribution rate of the first $k$ principal components.

Generally, when the cumulative variance contribution rate of principal components reaches 85%, it can capture the primary information of the original dataset, and the number of principal components selected typically satisfies this condition. However, for the analysis of key productivity-controlling factors, it is necessary to consider incorporating as much of the complete data characteristics as possible. Therefore, the number of principal components obtained corresponds to the number of features involved in the selection.

1.3.2. Entropy Weight Method

The Entropy Weight Method (EWM) is a multi-criteria comprehensive evaluation approach based on information entropy that objectively assigns weights according to the relative variation degree of indicators and their systemic impacts, thereby accurately reflecting intrinsic information relationships while eliminating subjectivity from empirical judgments [21]. This method determines each indicator’s weight in comprehensive evaluations by calculating its information entropy—a quantitative measure of information uncertainty—which EWM employs to assess indicators’ information content for weight allocation. The core principle of EWM lies in determining weights based on indicators’ value distributions: indicators exhibiting greater inter-sample variability possess higher information content and consequently receive larger weights, whereas those with minimal variability contain less information and are assigned proportionally smaller weights [22].

Similarly, to eliminate the influence of different measurement units across indicators, data standardization must be performed prior to calculation using the following normalization equation:

$$\overline{x_{ij}}={\displaystyle \frac{x_{ij}-x_{\min ,j}}{x_{\max ,j}-x_{\min ,j}}}$$

(13)

where $x_{ij}$ represents the original data, $x_{\min ,j}$ denotes the minimum value of the $j$-th column in the original data, $x_{\max ,j}$ indicates the maximum value of the $j$-th column in the original data, and $\overline{x_{ij}}$ signifies the standardized data.

Following standardization, the entropy values of each indicator in the normalized dataset must be calculated. First, compute the proportion of the j-th indicator in the i-th sample as:

$$p_{ij}={\displaystyle \frac{\overline{x_{ij}}}{{\displaystyle {\sum }_{i=1}^n\overline{x_{ij}}}}}$$

(14)

where $p_{ij}$ represents the sample proportion.

Subsequently, the information entropy for each feature indicator is calculated [23]:

$$e_j=-k{\displaystyle \sum _{i=1}^n{p}_{ij}}\ln \left(p_{ij}\right)$$

(15)

where $k$ is a constant (typically set to $k={\displaystyle \frac{1}{\ln \left(n\right)}}$), $n$ represents the total number of samples, and $e_j$ denotes the information entropy.

The weight $w_j$ for each feature indicator is calculated based on its entropy value. First, compute the information utility value $d_j$ for each feature indicator:

$$d_j=1-e_j$$

(16)

Then, the weight of each feature indicator is calculated as:

$$w_j={\displaystyle \frac{d_j}{{\displaystyle {\sum }_{j=1}^m{d}_j}}}$$

(17)

where $m$ represents the total number of feature indicators.

Finally, a comprehensive evaluation score $S_i$ can be obtained by applying the calculated weights to the sample data:

$$S_i={\displaystyle \sum _{j=1}^m{w}_j\overline{x_{ij}}}$$

(18)

where $S_i$ represents the comprehensive score of the $i$-th sample.

The entropy weight method is employed to calculate the weight coefficients of each principal component. The principal component with the largest weight is selected, and the absolute values of its corresponding feature coefficients are ranked. This yields the contribution degree of each feature to that principal component, where a higher contribution degree indicates greater influence.

The three aforementioned methods each possess distinct characteristics, but also exhibit certain limitations. The grey correlation analysis is adept at quantifying linear relationships but fails to capture nonlinear interactions and is more suitable for small-sample data analysis. The random forest method can capture nonlinear relationships but is susceptible to interference from feature correlations. The principal component analysis-entropy weight method can extract information-intensive principal components; however, it tends to obscure the actual physical meaning of the original parameters and may dilute their individual contributions. Consequently, integrating them into a comprehensive evaluation methodology allows them to mutually compensate for their respective weaknesses. Specifically, the capability of random forests to capture nonlinearity compensates for the neglect of feature interaction effects in grey correlation analysis. The dimensionality reduction and redundancy removal offered by principal component analysis-entropy weight method counteracts the bias from correlated features in random forests. The strength of grey correlation analysis in preserving parameter relationships compensates for the weakening of original parameter significance in the principal component analysis-entropy weight method, leading to more precise analytical results. Therefore, the following fuzzy mathematics-based comprehensive evaluation method is proposed.

1.4. Fuzzy Mathematics Comprehensive Evaluation

Fuzzy Mathematics is a mathematical tool for addressing uncertainty and ambiguity. Unlike conventional precise mathematics, it permits partial membership and uncertainty. The fuzzy comprehensive evaluation method can systematically assess complex problems influenced by multiple factors, including those difficult to quantify, to produce accurate evaluation results [24], it is mostly used to solve evaluation problems involving multi-level and multi-index systems [25]. In this study, the three aforementioned evaluation methods yield three sets of assessment results. These results are combined into an evaluation index matrix. Using the entropy weight method, the respective weights of each set of indicators are calculated. By integrating these weights with the evaluation index matrix, the comprehensive evaluation score for each feature parameter is obtained according to Equation (18), leading to the identification of key controlling factors.

2. Case Study: 8+9^# Coal Seam in the Eastern Margin of the Ordos Basin

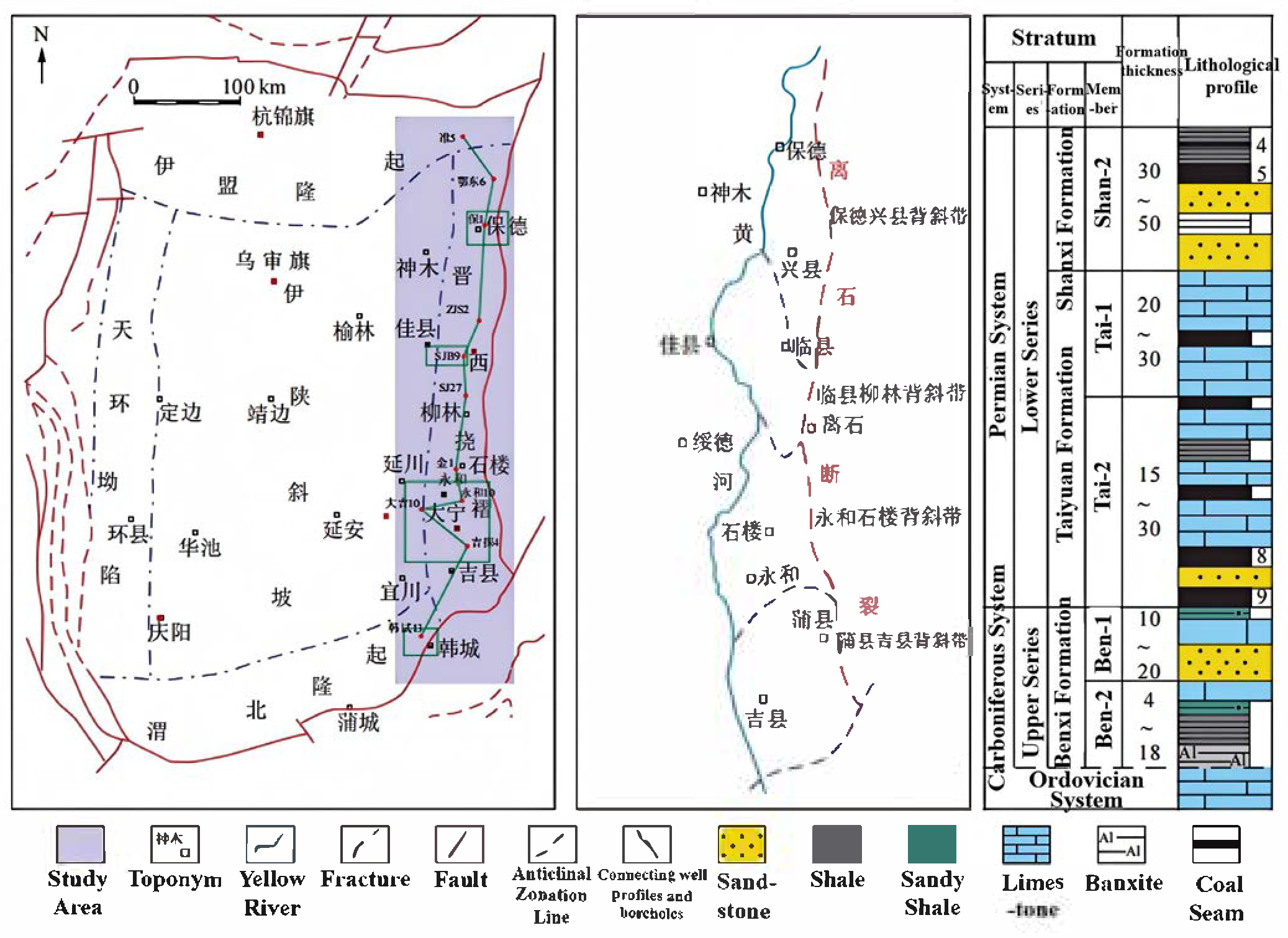
2.1. Regional Geological Setting

The Ordos Basin, as one of the most stable cratonic basins in China, is characterized by a large west-dipping monocline structure and relatively weak internal tectonic activities [26]. The eastern margin of the Ordos Basin formed during the Carboniferous to Permian periods, with depositional environments transitioning progressively from paralic to continental facies. This evolution facilitated the development of diverse peat-forming environments, resulting in the formation of stable and continuous thick coal seams. Structurally, the eastern Ordos margin is situated at the junction of the western Shanxi Flexural Fold Belt, the eastern Weibei Uplift, and the eastern Yimeng Uplift, exhibiting an overall west-dipping monoclinal structure (Figure 1) [27,28]. Compared with interior basin gas fields such as Daniudi and Sulige, this area demonstrates greater structural complexity with more developed fault systems [29,30].

The study area is divided into two blocks—Block A and Block B, with coal-bearing strata primarily consisting of the Benxi, Taiyuan, and Shanxi Formations. The target 8+9^# coal seam is distributed within the Benxi Formation, characterized by considerable thickness and excellent lateral continuity. The vertically stacked, thick coal seams provide favourable material conditions for hydrocarbon generation [32]. The coal-bearing strata exhibit a parallel unconformity contact with the weathering surface of the Lower Paleozoic Majiagou Formation, with a total thickness ranging from 51 to 70 m and containing 1 to 4 coal seams. Based on sedimentary sequences and lithological assemblages, the Benxi Formation can be subdivided into two members. The Benxi-2 Member (22–49 m thick) consists of grey to off-white bauxitic mudstone in the lower section, often intercalated with lenticular limonite and hematite deposits at the base, while the upper section comprises dark grey sandy mudstone with interbeds of bauxitic mudstone and thin fine sandstone layers, containing 1–2 uneconomic coal seams. The Benxi-1 Member (20–56 m thick) is dominated by fine- to coarse-grained quartz sandstone in the lower section, transitioning to greyish-black mudstone and siltstone in the middle-upper sections, with the 8+9^# coal seam occurring at the top [33].

2.2. Analysis of Key Productivity Controls

Based on field data from stimulated wells in the target 8+9^# coal seam, the aforementioned evaluation methods were applied to analyze factors influencing average cumulative gas production and peak gas production rates, encompassing both geological and engineering parameters. Preliminary screening of available data identified key geological characteristics (

Table 1. Screening Results of Geological–Engineering Characteristics.

Sample	Perforation Thickness	Effective Perforation Count	Proppant Volume	Clean Fluid Volume	Pumping Rate	Vertical Thickness	Proppant Intensity	Fluid Intensity	Pad Fluid Ratio	Slurry Volume	Displacement Volume	Average Sand Ratio	Flowback Ratio	Density	GSI	Gas Content
Unit	m	piece	m3	m3	m3/min	m	m2	m2	%	m3	m3	%	%	g/cm3	-	m3/t
1	5	80	314	2881.6	17	17.4	18.04	165.6	28.8%	2053.8	27.0	14.8%	13.2%	1.27	64.5	5.9
2	3	48	211.5	1981.4	18	10.6	19.95	186.9	23.7%	1536.9	28.3	14.7%	4.6%	1.27	44.9	11.1
3	3.5	56	301.9	2754.8	18	13.6	22.19	202.5	22.7%	2028.3	31.1	14.6%	10.7%	1.47	61.2	17.04

), including gas content, Geological Strength Index (GSI), vertical thickness, and density, along with engineering parameters such as perforation thickness, effective perforation count, average sand ratio, flowback ratio, proppant intensity, pad fluid ratio, proppant volume, clean fluid volume, fluid intensity, pumping rate, slurry volume, and displacement volume.

2.2.1. Data Preprocessing

Prior to the key controlling factor analysis, data preprocessing was conducted to ensure analytical accuracy. The boxplot method was employed to eliminate outliers, followed by Pearson correlation analysis to calculate inter-parameter correlation coefficients. For highly correlated parameter pairs, one parameter from each pair was removed to reduce feature dimensionality.

The boxplot is a statistical chart used to display data distribution and identify outliers within a dataset. The principle of handling outliers using the boxplot method is based on quartiles and the interquartile range (IQR) to define the range of normal values. Data points outside this range are considered outliers and are removed.

Due to the characteristics of deep coalbed methane productivity influencing factors—such as numerous parameters, complex interactions, and intricate relationships—this chapter employs the Pearson correlation coefficient method to investigate the correlations between geological/engineering parameters and productivity indicators. This approach helps uncover potential influencing patterns on productivity. The Pearson correlation coefficient is a statistical measure used to quantify the strength and direction of the linear relationship between two variables, with values ranging from −1 to 1. Specifically:

①

When the coefficient is 1, it indicates a perfect positive linear relationship between the two variables, meaning that as one variable increases, the other increases in a fixed proportion.

②

When the coefficient is −1, it indicates a perfect negative linear relationship, meaning that as one variable increases, the other decreases in a fixed proportion.

③

When the coefficient is close to 0, it suggests little to no linear relationship between the two variables.

The formula for calculating the Pearson correlation coefficient is as follows [34]:

$$r={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}\sqrt{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}}$$

(19)

where x_i and y_i represent the i-th observations of variables X and Y, respectively, while $\overline{x}$ and $\overline{ y}$ denote the mean values of these two variables.

The preprocessed geological and engineering data from Blocks A and B for deep coalbed methane were combined with the average cumulative gas production and peak gas production for Pearson correlation coefficient calculations. Figure 2 and Figure 3 illustrate the correlations between various geological and engineering parameters and productivity in Blocks A and B. To reduce data complexity and enhance the interpretability of subsequent key controlling factor analysis models, one of the two strongly correlated parameters was filtered out, thereby decreasing the number of feature parameters.

2.2.2. Comprehensive Geological–Engineering Factor Analysis

The preprocessed datasets from Blocks A and B were analyzed using the aforementioned evaluation methods. The results, including grey correlation degrees, feature importance, and principal component coefficients for each parameter relative to average cumulative gas production and peak gas production, are shown in Figure 4 (Block A) and Figure 5 (Block B).

An evaluation index matrix was established based on results from the grey correlation analysis, random forest method, and principal component analysis-entropy weight method. The weight coefficients of these three evaluation methods for Blocks A and B were calculated as shown in

Table 2. Weighting coefficients of evaluation methods for Block A.

Method	Weight (Average Cumulative Production)	Weight (Peak Production)
Grey Correlation Analysis	0.416	0.447
Random Forest Method	0.343	0.295
PCA–Entropy Weight Method	0.241	0.258

and

Table 3. Weighting coefficients of evaluation methods for Block B.

Method	Weight (Average Cumulative Production)	Weight (Peak Production)
Grey Correlation Analysis	0.408	0.415
Random Forest Method	0.368	0.357
PCA–Entropy Weight Method	0.224	0.228

. Using these weights, comprehensive evaluation scores for different geological-engineering parameters were computed through fuzzy mathematics comprehensive evaluation and ranked in descending order (Figure 6 and Figure 7). The analysis reveals that the primary productivity-controlling factors in Block A are gas content, GSI value, proppant volume, and proppant intensity, while the top factors in Block B are proppant volume, vertical thickness, proppant intensity, and pad fluid ratio.

The differences in the analysis results between Blocks A and B also indicate that Block A may be characterized by “geology-driven reservoir conditions with precision engineering adjustments.” In contrast, the geological reservoir conditions of the coal seam in Block B are likely inferior to those in Block A. Therefore, subsequent completion designs for Block B should adhere to a development strategy of “compensating for geological limitations through engineering solutions.”

Given the inherent differences in geological conditions and operational parameters between the two blocks, the analytical results exhibit distinct variations. To validate the comprehensive findings, separate analyses were conducted for geological factors and engineering factors within each block.

2.2.3. Univariate Factor Analysis Validation

The compiled dataset was segregated into geological parameter and engineering parameter datasets, which were then analyzed using the proposed key controlling factor evaluation methodology. The comprehensive evaluation scores of each parameter were ranked in descending order, as shown in Figure 8 and Figure 9.

The univariate analysis of geological and engineering factors in Blocks A and B demonstrates consistent results: for both average cumulative gas production and peak gas production, Block A’s top three influential geological factors were gas content, GSI value, and vertical thickness, while the leading engineering factors were average sand ratio, proppant volume, and proppant intensity—findings that align closely with the fuzzy comprehensive evaluation results. Similarly, Block B’s primary engineering controls were proppant volume, pad fluid ratio, and proppant intensity, showing agreement with its comprehensive evaluation outcomes.

3. Highlights

In this paper, we propose a comprehensive analysis method for main controlling factors of productivity, which integrates grey correlation analysis, random forest, and principal component analysis-entropy weight method. This method is applied to the field wells of the 8+9^# deep coalbed methane (CBM) in the eastern margin of the Ordos Basin. Through discussion, the key highlights are summarized as follows:

• A comprehensive analysis method for main controlling factors of production capacity is proposed, which integrates grey relational analysis, random forest, and principal component analysis-entropy weight method.
• The key geological and engineering controlling factors for the productivity of deep coalbed methane in the 8+9^# coal seams on the eastern margin of the Ordos Basin have been clarified.
• Formulate a differentiated development strategy: for Block A, form a “geology-led, engineering-regulated” plan; for Block B, propose a “engineering supplementation for geological deficiencies” strategy.
• This analysis method still has certain limitations. The accuracy of its analysis results can be further improved by integrating more advanced feature evaluation methods.

4. Conclusions and Findings

• This study analyzed Pearson correlations and comprehensive influence degrees between average cumulative gas production, peak gas production, and multiple geological/engineering parameters using data from 38 directional wells in the 8+9^# deep coalbed methane reservoir of the Ordos Basin’s eastern margin. The key controlling factors for average cumulative production were identified as gas content, vertical thickness, and GSI value among geological parameters, and proppant intensity, pad fluid ratio, and proppant volume among engineering parameters.
• By integrating grey correlation analysis, principal component analysis-entropy weight method, and random forest algorithm through fuzzy mathematics, we developed a comprehensive evaluation methodology for identifying key productivity controls in deep CBM reservoirs, which provides a scientific basis for future fracturing design optimization.
• Although the comprehensive evaluation method proposed in this study integrates three single methods, it still has certain limitations. Specifically, this method is more suitable for analyzing continuous data. When dealing with discrete data, preprocessing such as recoding may be required to convert it into a continuous form; however, this process might overlook the actual meaning of discrete values and potentially reduce the accuracy of the analysis. In addition, since this method combines three independent technologies for analyzing controlling factors, it can also be integrated with newer and more advanced analytical methods. Nevertheless, before conducting such integration, the advantages and disadvantages of the newly added method must be carefully evaluated to determine whether it can complement those of the current framework; otherwise, the accuracy of the final results may be compromised.