Computational Analysis of Two Micro-Vortex Generator Configurations for Supersonic Boundary Layer Flow Control
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Methods
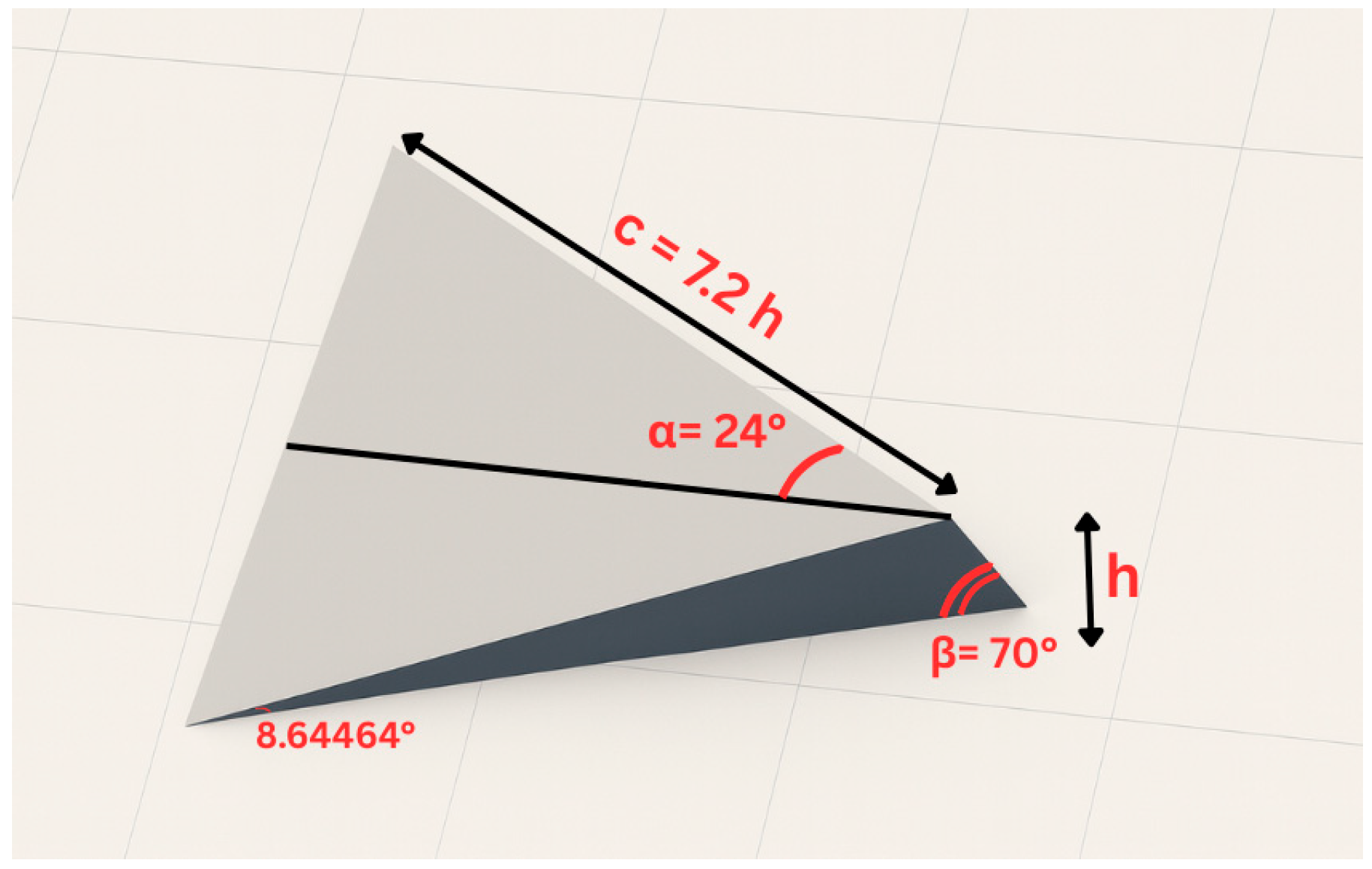
2.2. Case Setup
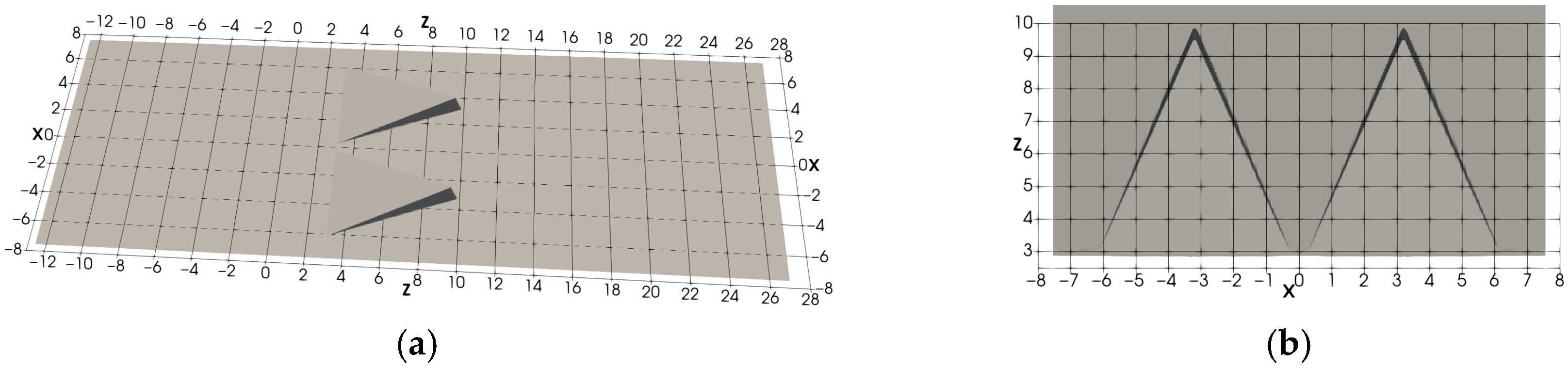
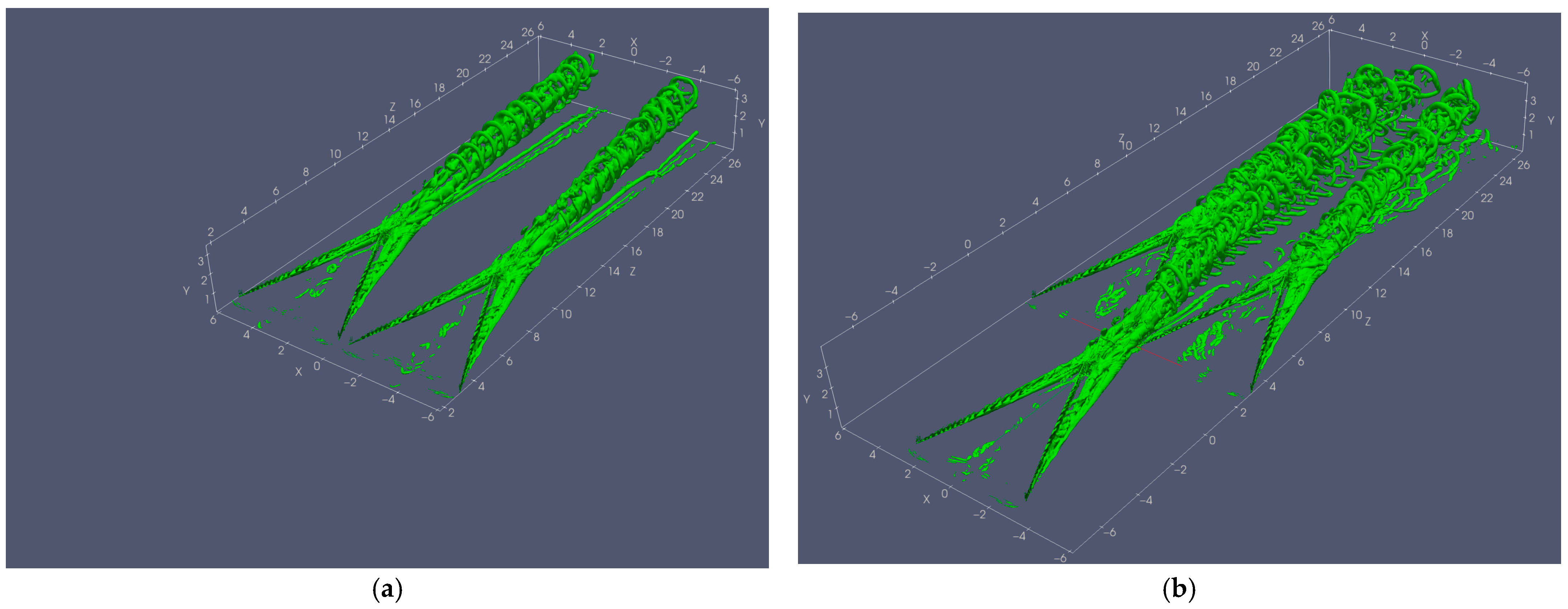
- The two-MVG case: Two MVGs are placed next to each other in the spanwise direction (X), see Figure 1. The computational domain spans (where h is the MVG height) in the spanwise (X), wall-normal (Y), and streamwise (Z) directions, respectively, with a grid resolution of 269 × 200 × 846.
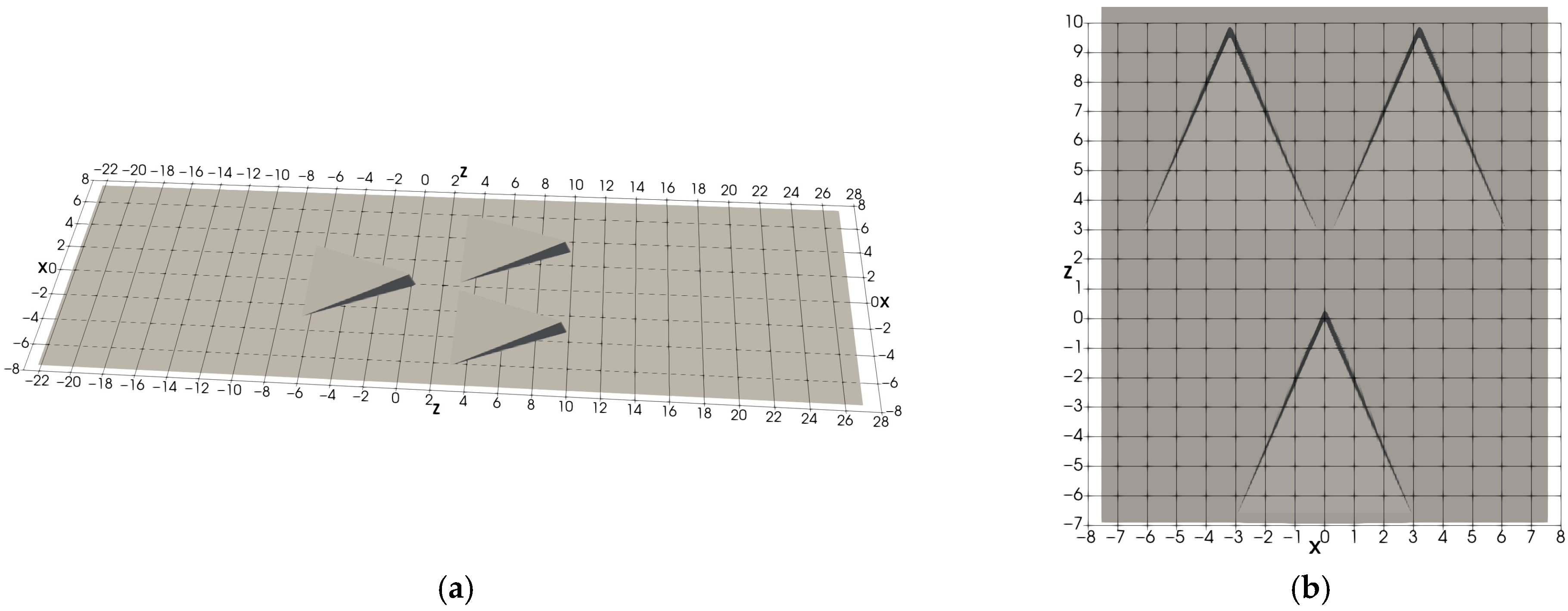
- The three-MVG case: Three MVGs are arranged with two MVGs positioned identically to the Two-MVG case and a third MVG placed upstream at the midpoint between them, with a streamwise offset of 3h, see Figure 2. The computational domain spans in the spanwise (X), wall-normal (Y), and streamwise (Z) directions, respectively, with a grid resolution of 269 × 200 × 1091.
3. Results
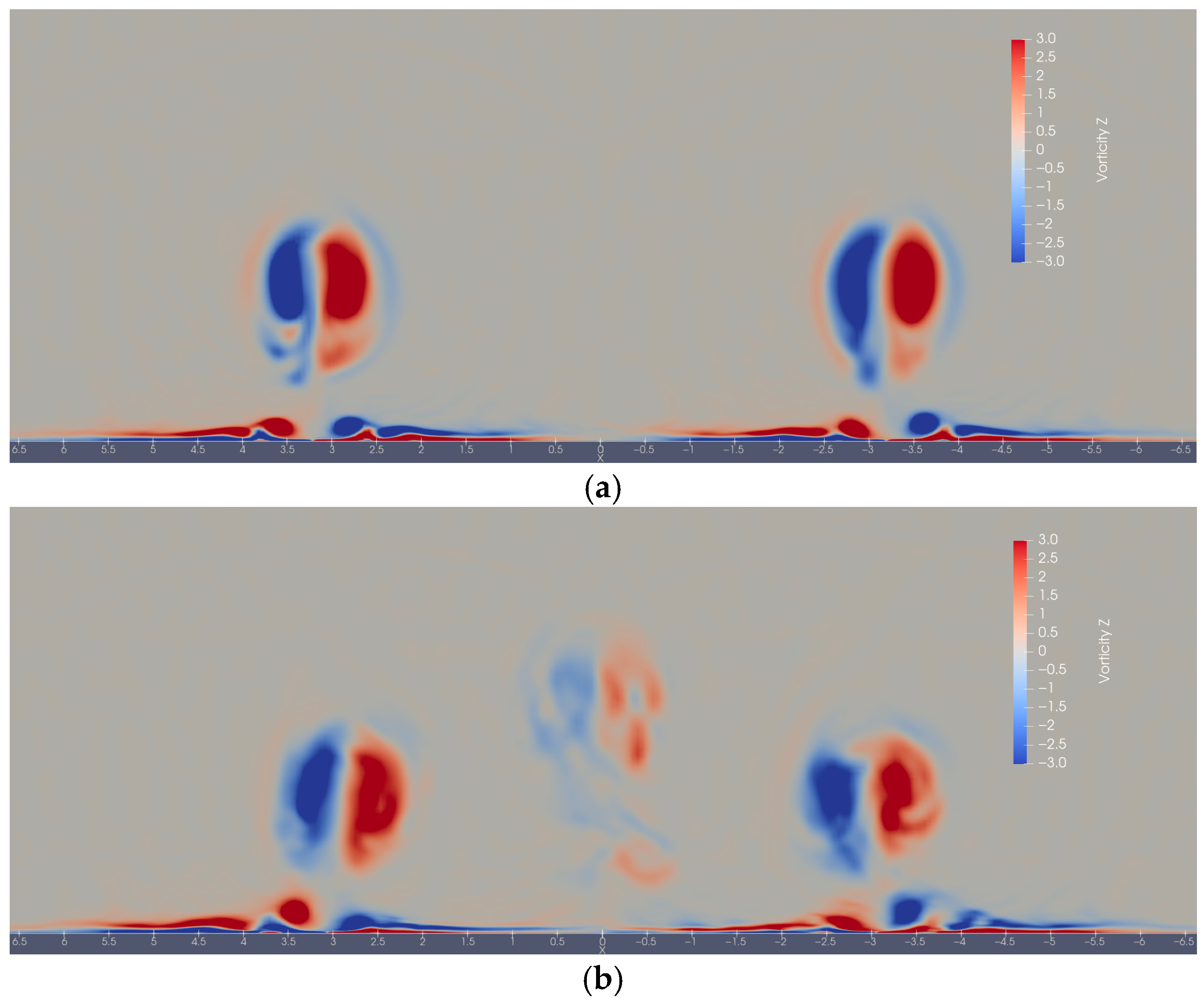
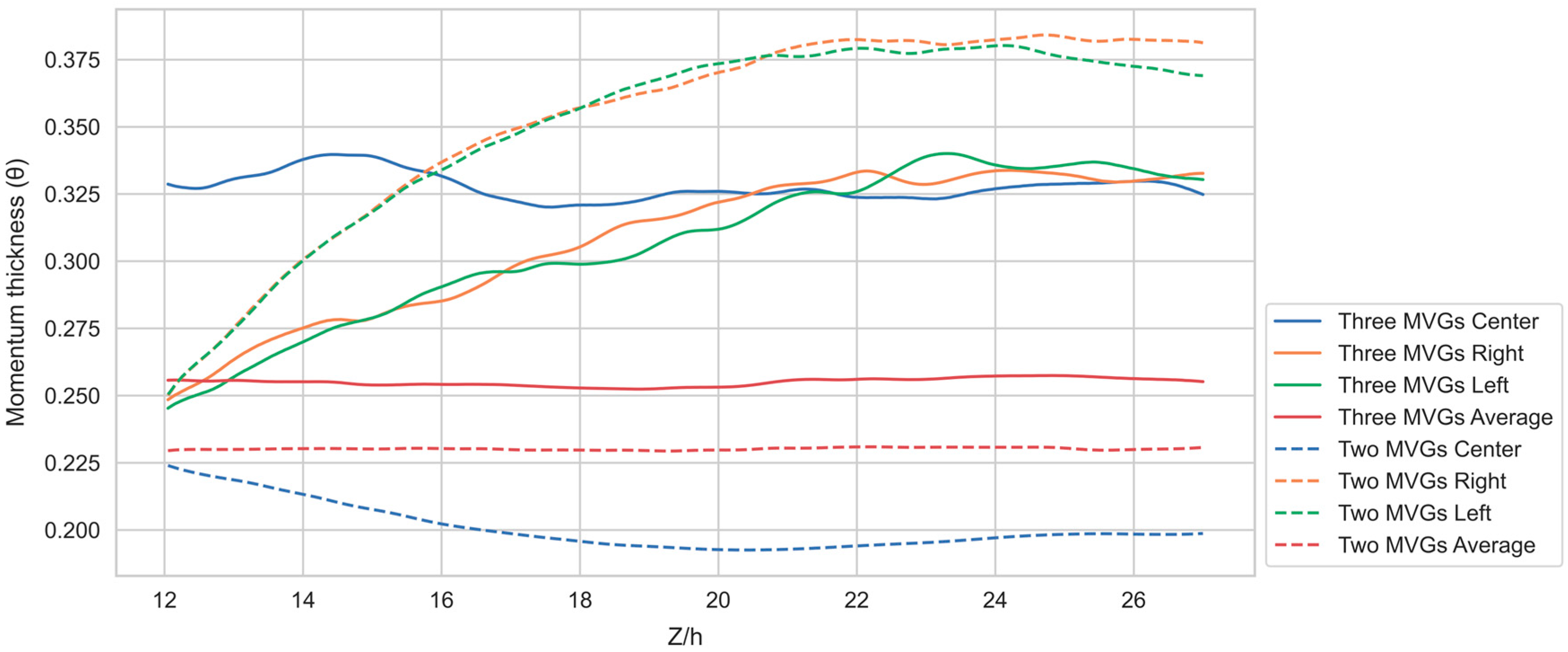
3.1. Mean Flow Structures
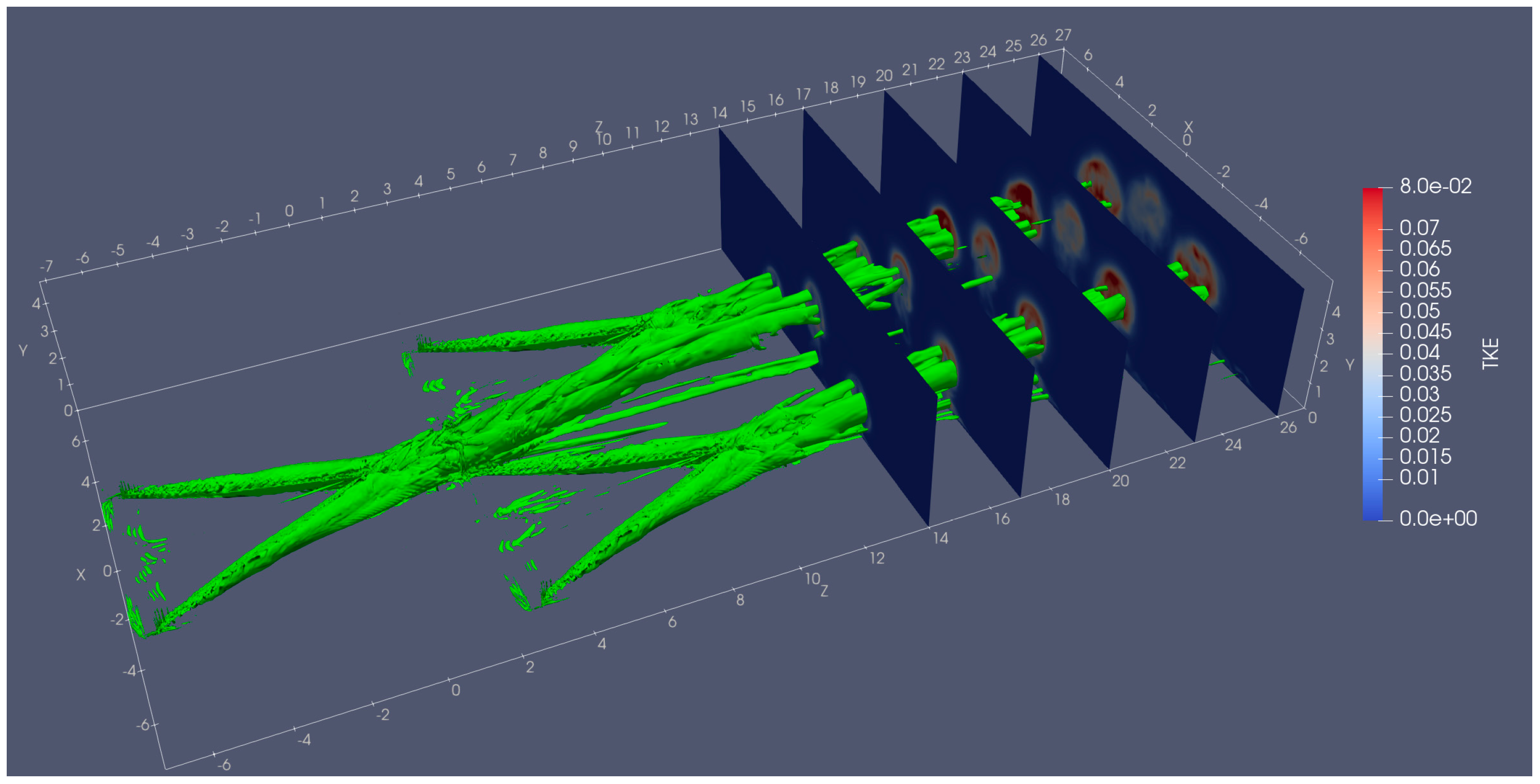
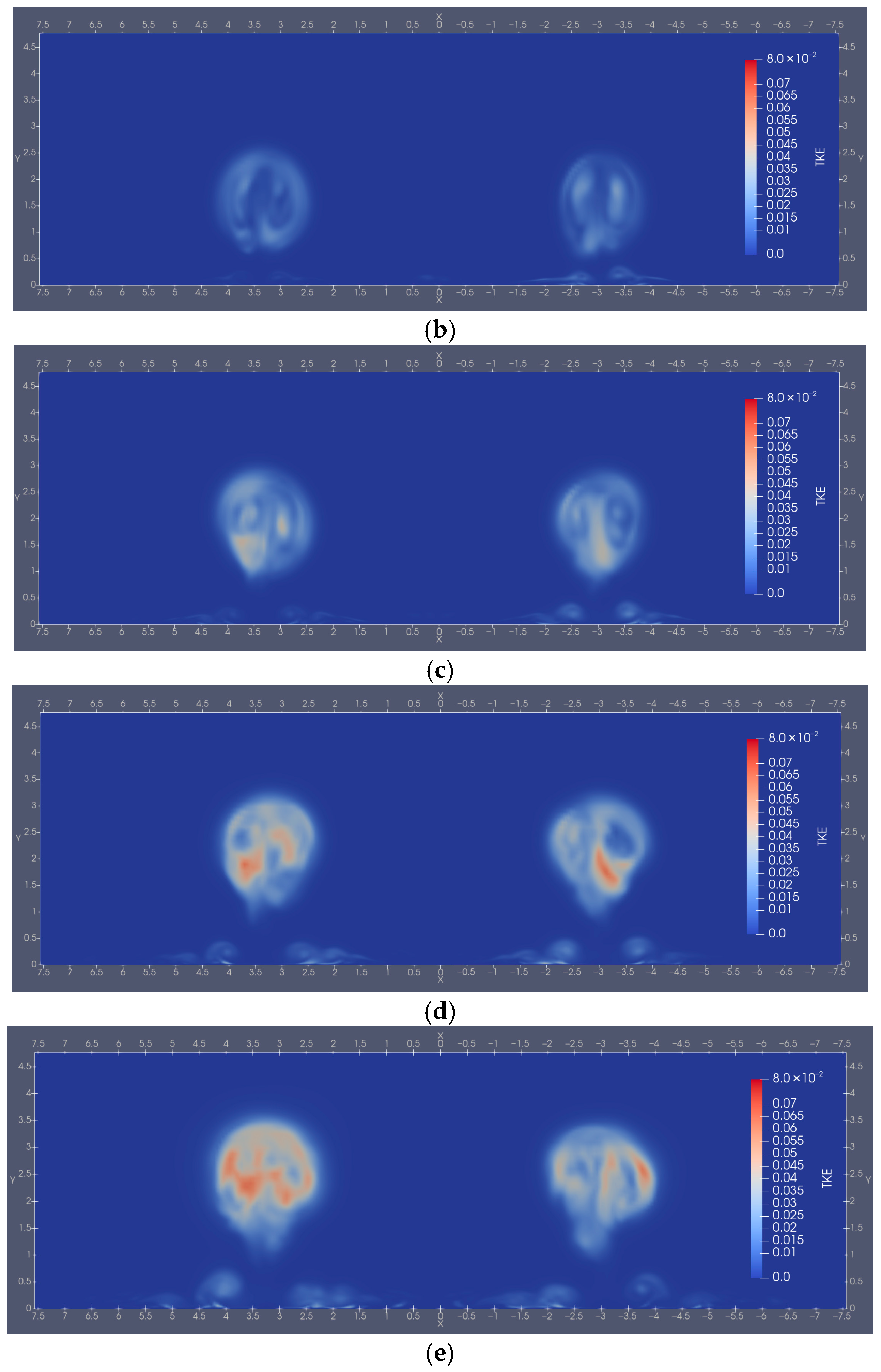
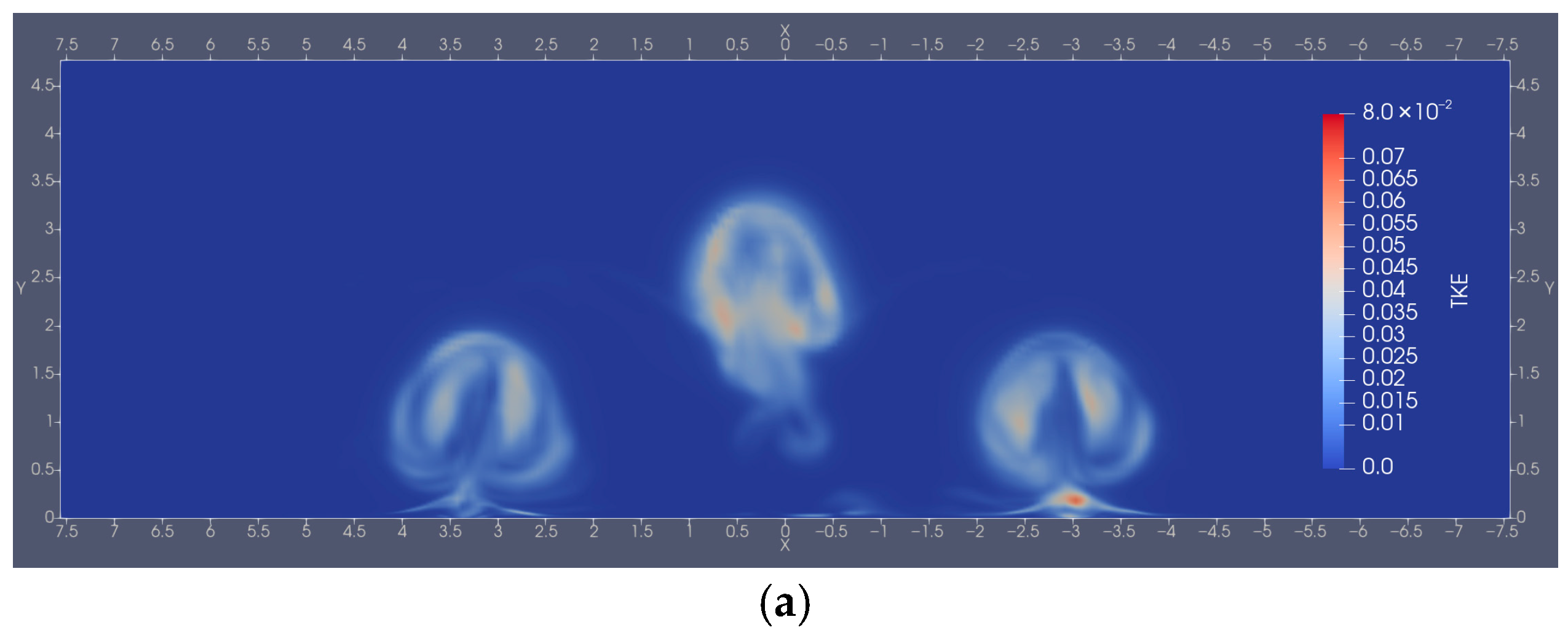
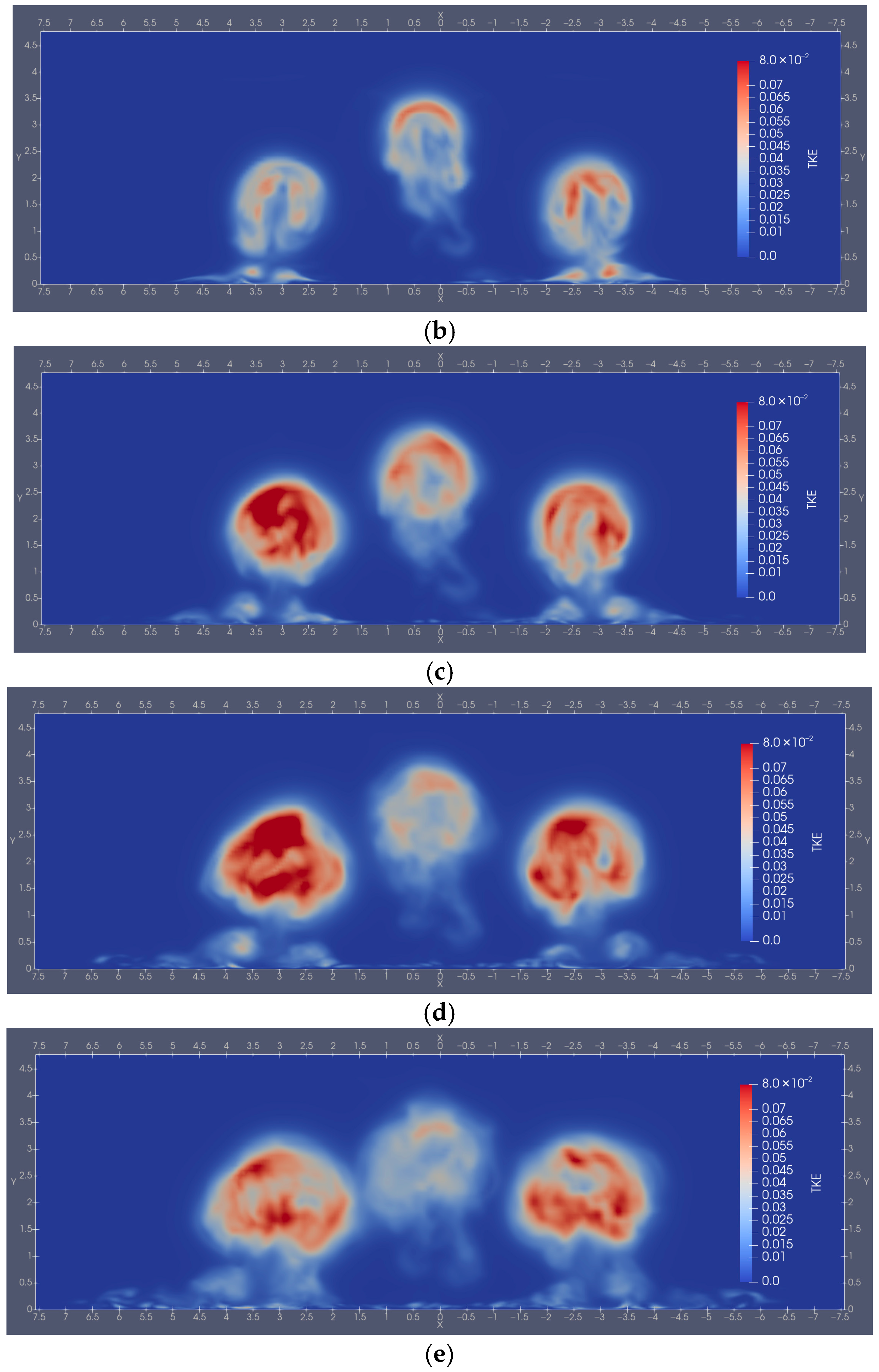
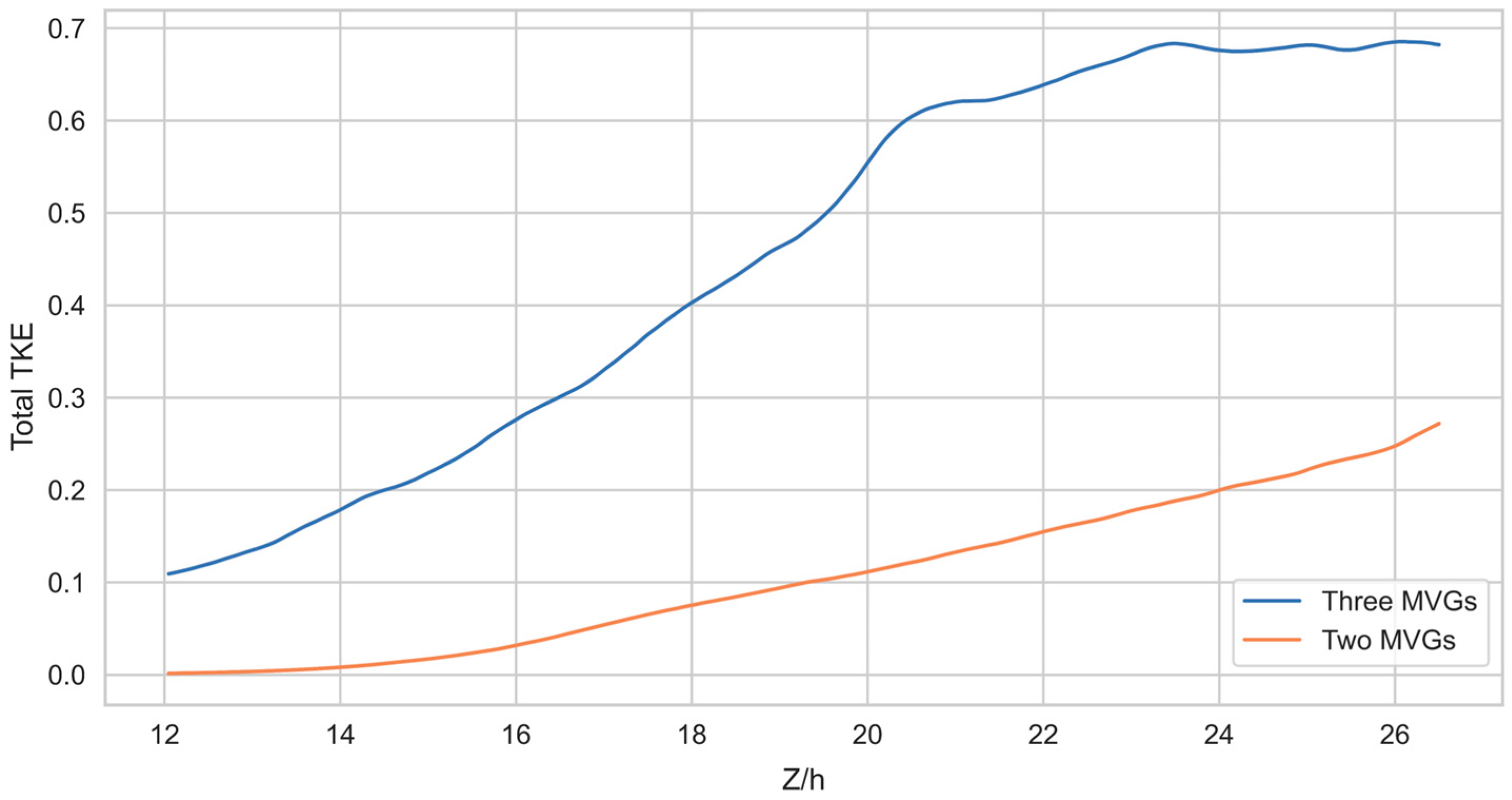
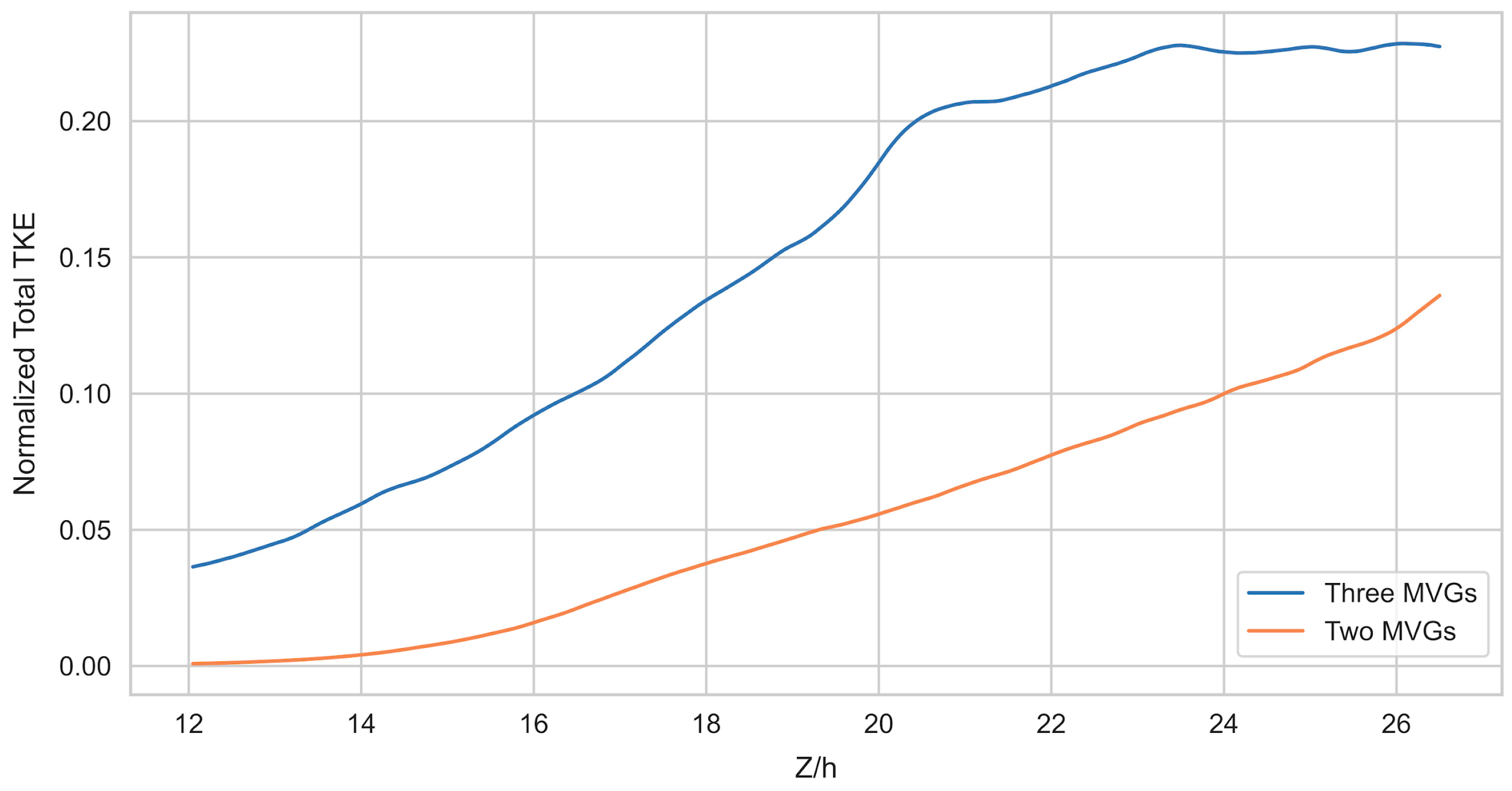
3.2. Turbulence Analysis
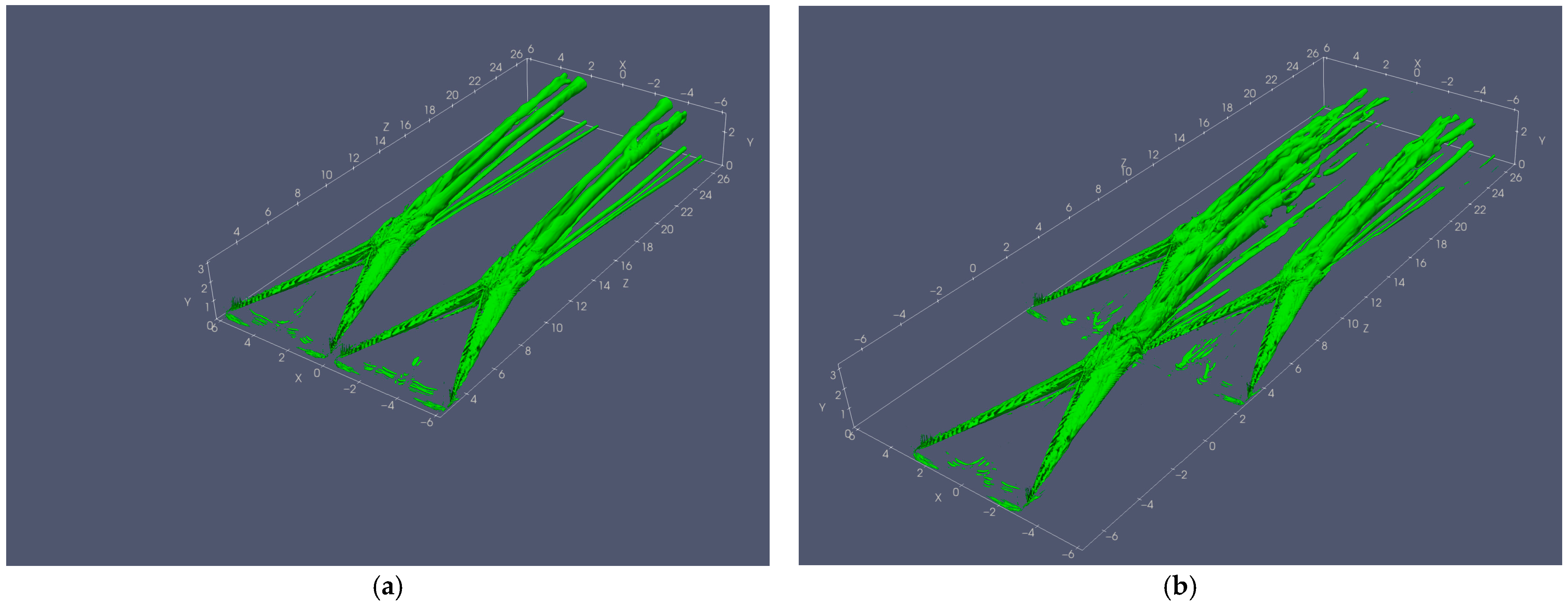
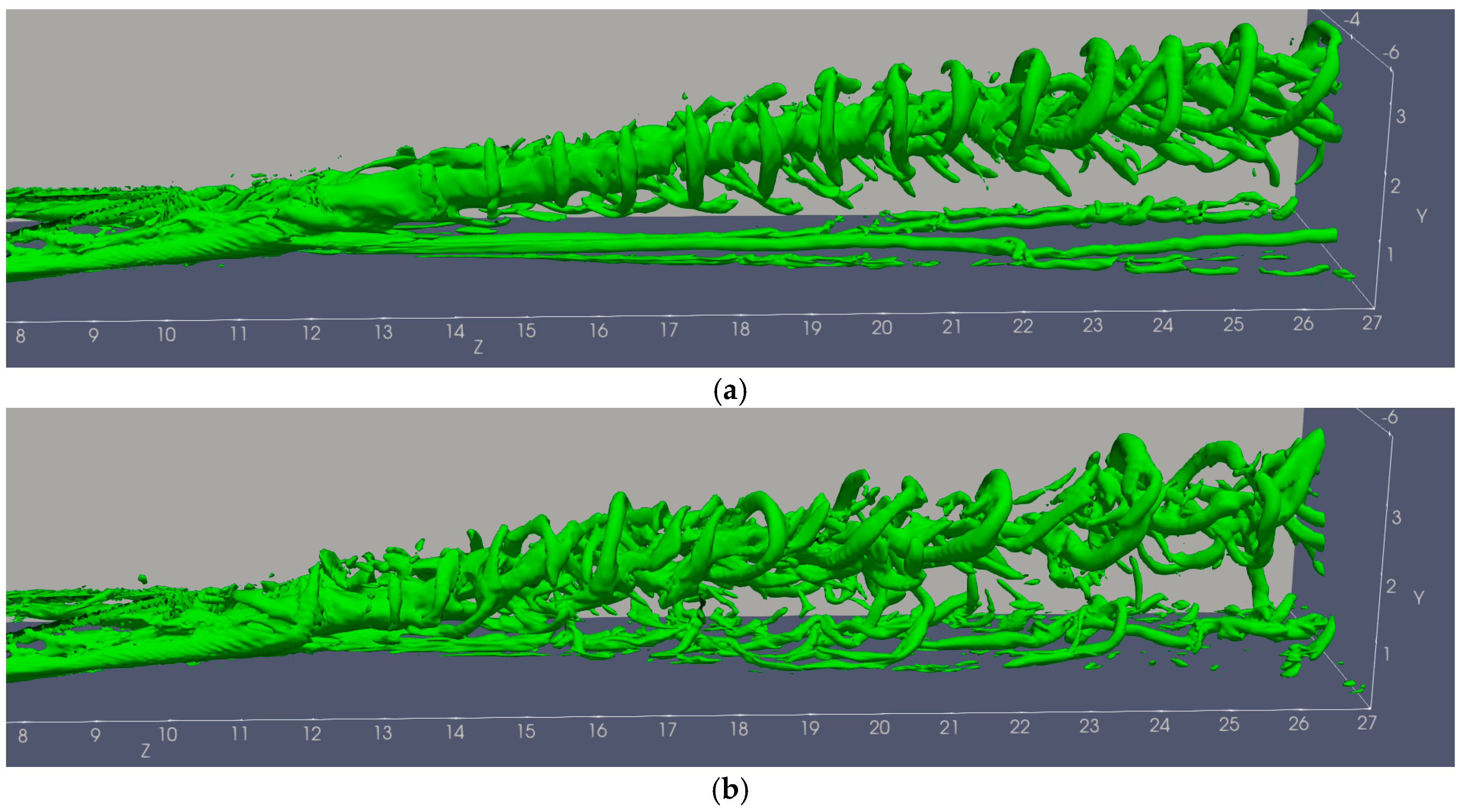
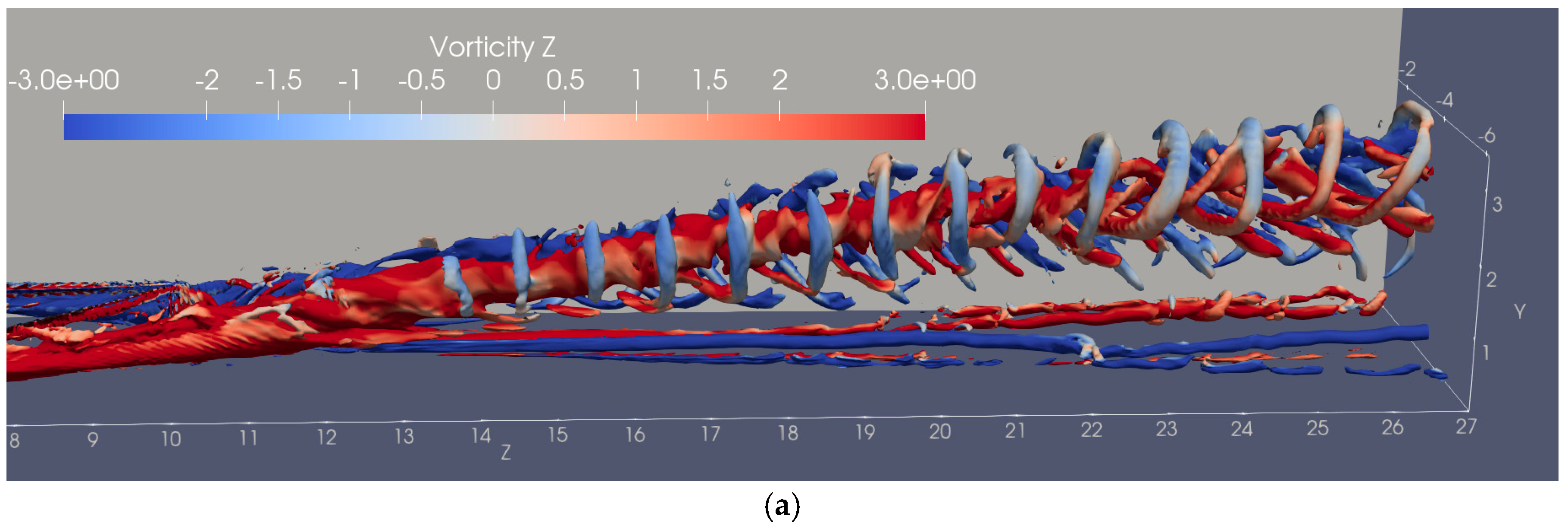
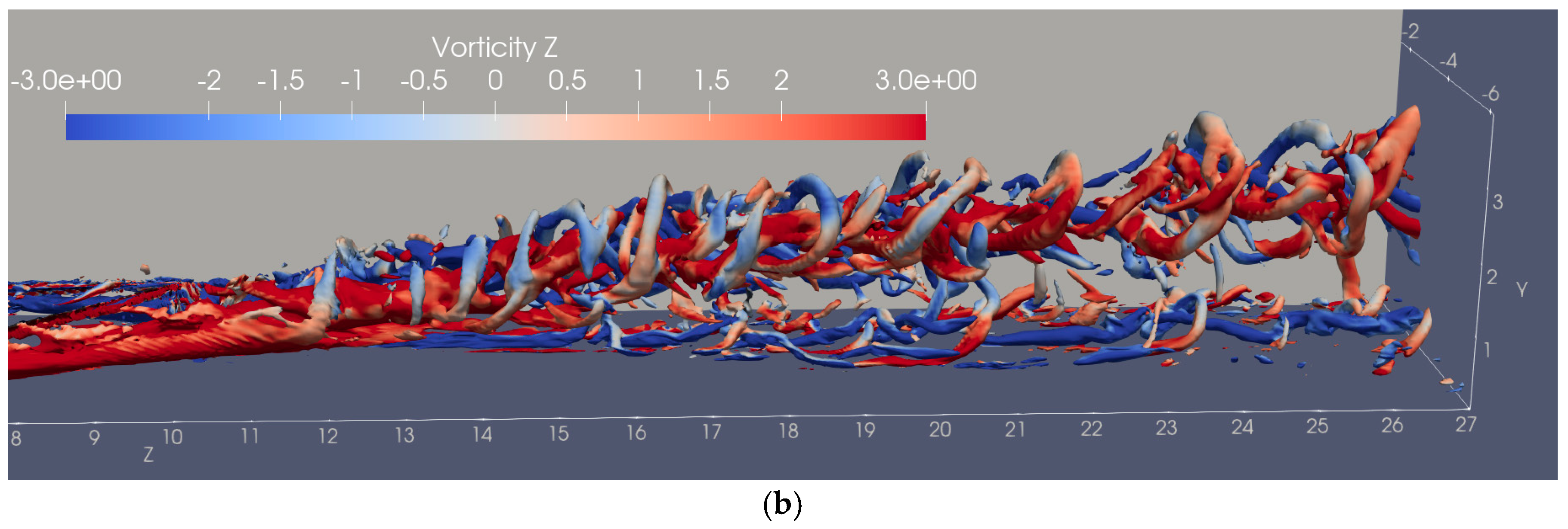
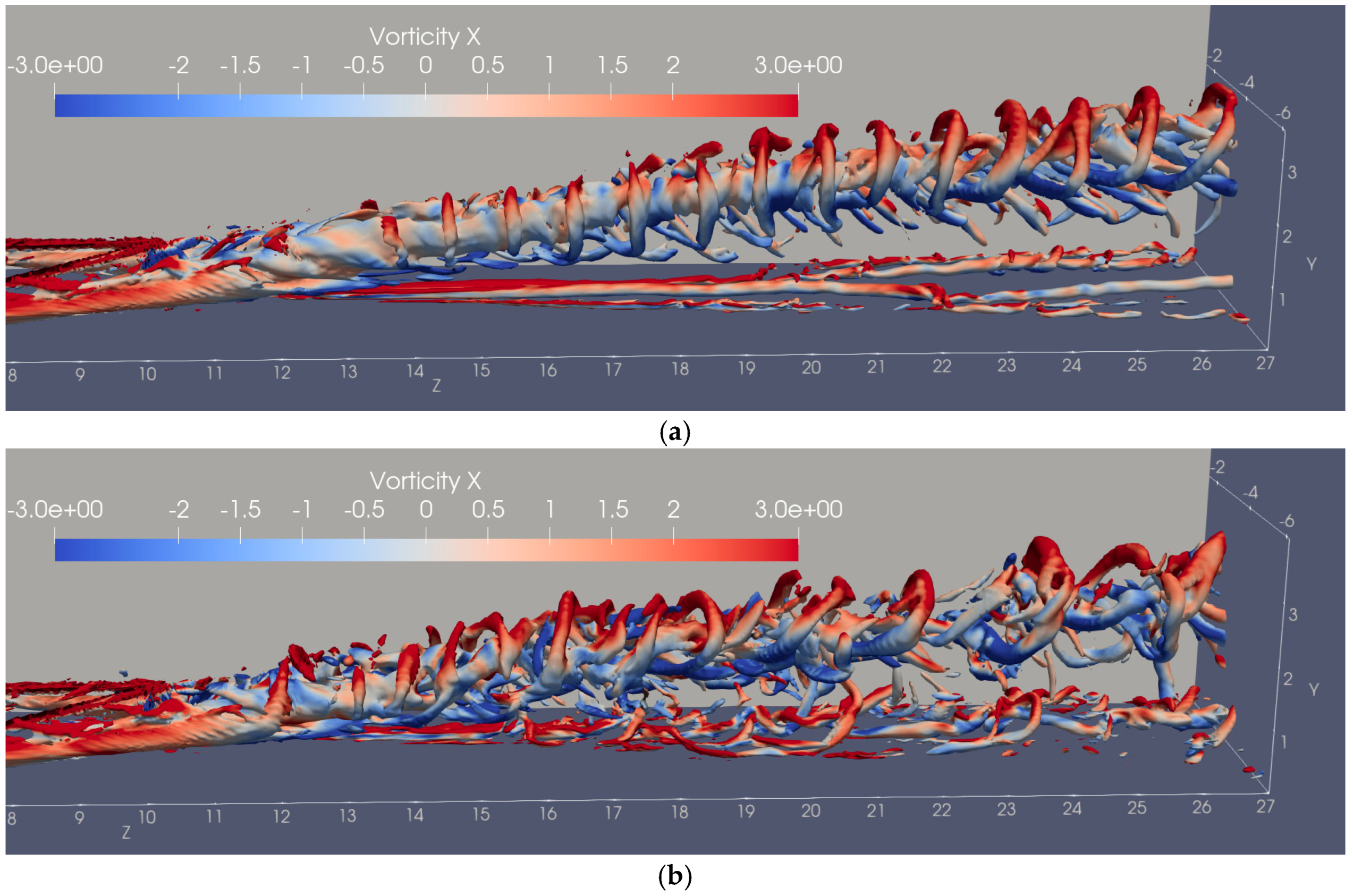
3.3. Vortex Structures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNS | Direct Numerical Simulation |
| LES | Large Eddy Simulation |
| MVG | Micro-Vortex Generator |
| SBLI | Shock-Wave Boundary Layer Interaction |
| TVD | Total Variation Diminishing |
| WENO | Weighted Essentially Non-Oscillatory |
| TKE | Turbulent Kinetic Energy |
References
- Délery, J.; Dussauge, J.P. Some physical aspects of shock wave/boundary layer interactions. Shock Waves 2009, 19, 453–468. [Google Scholar] [CrossRef]
- Babinsky, H.; Li, Y.; Pitt Ford, C.W. Microramp Control of Supersonic Oblique Shock-Wave/Boundary-Layer Interactions. AIAA J. 2009, 47, 668–675. [Google Scholar] [CrossRef]
- Sun, Z.; Scarano, F.; van Oudheusden, B.W.; Schrijer, F.F.J.; Yan, Y.; Liu, C. Numerical and Experimental Investigations of the Supersonic Microramp Wake. AIAA J. 2014, 52, 1518–1527. [Google Scholar] [CrossRef][Green Version]
- Wang, B.; Liu, W.; Zhao, Y.; Fan, X.; Wang, C. Experimental Investigation of the Micro-Ramp Based Shock Wave and Turbulent Boundary Layer Interaction Control. Phys. Fluids 2012, 24, 055110. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, Q.; Xiang, X.; Xu, J. An Improved Micro-Vortex Generator in Supersonic Flows. Aerosp. Sci. Technol. 2015, 47, 210–215. [Google Scholar] [CrossRef]
- Liu, J.; Khine, Y.Y.; Saleem, M.; Lopez Rodriguez, O.; Gutmark, E. Supersonic Jet Noise Reduction Using Micro Vortex Generators. In Proceedings of the AIAA AVIATION 2021 FORUM, Virtual Event, 2–6 August 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar]
- Xue, D.; Chen, Z.; Jiang, X.; Fan, B. Numerical Investigations on the Wake Structures of Micro-Ramp and Micro-Vanes. Fluid Dyn. Res. 2014, 46, 015505. [Google Scholar] [CrossRef]
- Wang, B.; Liu, W.D.; Sun, M.B.; Zhao, Y.X. Fluid Redistribution in the Turbulent Boundary Layer Under the Microramp Control. AIAA J. 2015, 53, 3777–3787. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, L.; Li, Q.; Liu, C. Numerical Study of Micro-Ramp Vortex Generator for Supersonic Ramp Flow Control at Mach 2.5. Shock Waves 2017, 27, 79–96. [Google Scholar] [CrossRef]
- Nishantt, N.; Baraiya, N.A. Flow Control Using MVG in Shock Wave/Boundary Layer Interaction. In Recent Advances in Fluid Dynamics; Banerjee, J., Shah, R.D., Agarwal, R.K., Mitra, S., Eds.; Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2023; pp. 175–190. ISBN 978-981-19-3378-3. [Google Scholar]
- Saleem, M.; Karnam, A.; Rodriguez, O.; Liu, J.; Gutmark, E. Flow and Acoustic Fields Investigation of Noise Reduction by Micro Vortex Generators in Supersonic Nozzles. Phys. Fluids 2023, 35, 106111. [Google Scholar] [CrossRef]
- Lu, F.; Pierce, A.; Shih, Y. Experimental Study of near Wake of Micro Vortex Generators in Supersonic Flow. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Reddy, H.S.B. Optimum micro-vortex generator design for planar symmetric diffuser under fully developed turbulent flow. Phys. Fluids 2024, 36, 125160. [Google Scholar] [CrossRef]
- Chen, C.; Yang, Y.; Yan, Y. Computational Analysis of Tandem Micro-Vortex Generators for Supersonic Boundary Layer Flow Control. Computation 2025, 13, 101. [Google Scholar] [CrossRef]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex—A New Vortex Vector Definition and Vorticity Tensor and Vector Decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef]
- LarKermani, E.; Roohi, E.; Porté-Agel, F. Evaluating the Modulated Gradient Model in Large Eddy Simulation of Channel Flow with OpenFOAM. J. Turbul. 2018, 19, 600–620. [Google Scholar] [CrossRef]
- Zahiri, A.-P.; Roohi, E. Anisotropic Minimum-Dissipation (AMD) Subgrid-Scale Model Implemented in OpenFOAM: Verification and Assessment in Single-Phase and Multi-Phase Flows. Comput. Fluids 2019, 180, 190–205. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Chen, C.; Yan, Y.; Al Shaaban, M. Computational Analysis of Two Micro-Vortex Generator Configurations for Supersonic Boundary Layer Flow Control. Processes 2025, 13, 2818. https://doi.org/10.3390/pr13092818
Yang Y, Chen C, Yan Y, Al Shaaban M. Computational Analysis of Two Micro-Vortex Generator Configurations for Supersonic Boundary Layer Flow Control. Processes. 2025; 13(9):2818. https://doi.org/10.3390/pr13092818
Chicago/Turabian StyleYang, Yong, Caixia Chen, Yonghua Yan, and Mai Al Shaaban. 2025. "Computational Analysis of Two Micro-Vortex Generator Configurations for Supersonic Boundary Layer Flow Control" Processes 13, no. 9: 2818. https://doi.org/10.3390/pr13092818
APA StyleYang, Y., Chen, C., Yan, Y., & Al Shaaban, M. (2025). Computational Analysis of Two Micro-Vortex Generator Configurations for Supersonic Boundary Layer Flow Control. Processes, 13(9), 2818. https://doi.org/10.3390/pr13092818







