Data-Driven Prediction of Li-Ion Battery Thermal Behavior: Advances and Applications in Thermal Management
Abstract
1. Introduction
2. Overview of Data-Driven Modeling Methods
2.1. Statistical Modeling Methods
2.1.1. Linear Regression
2.1.2. Grey Relational Analysis
2.2. Traditional Machine Learning Methods
2.2.1. Support Vector Machine
2.2.2. Gaussian Process Regression
2.2.3. Decision Tree and Random Forest
2.3. Deep Learning Methods
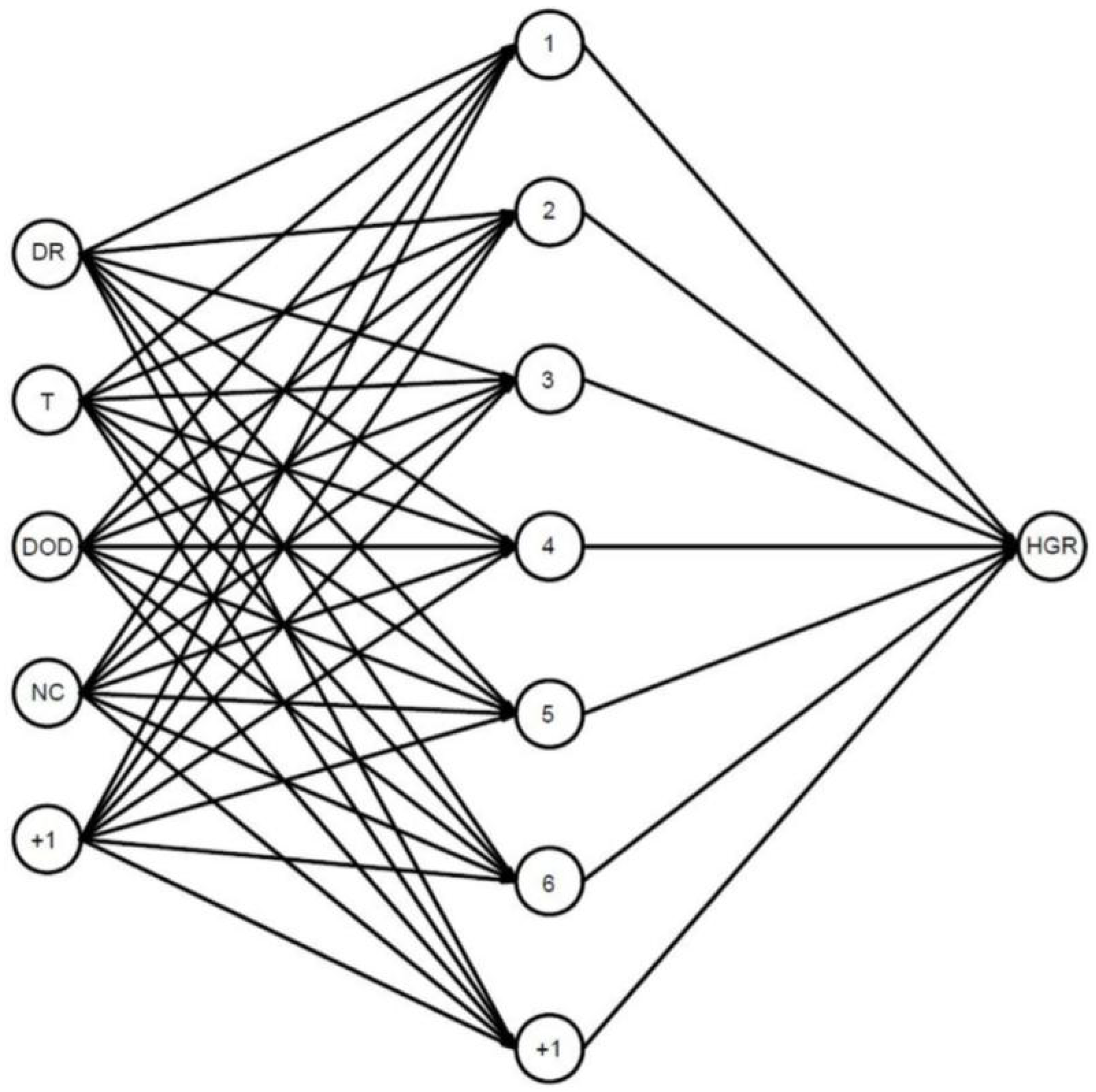
2.3.1. Multi-Layer Perceptron
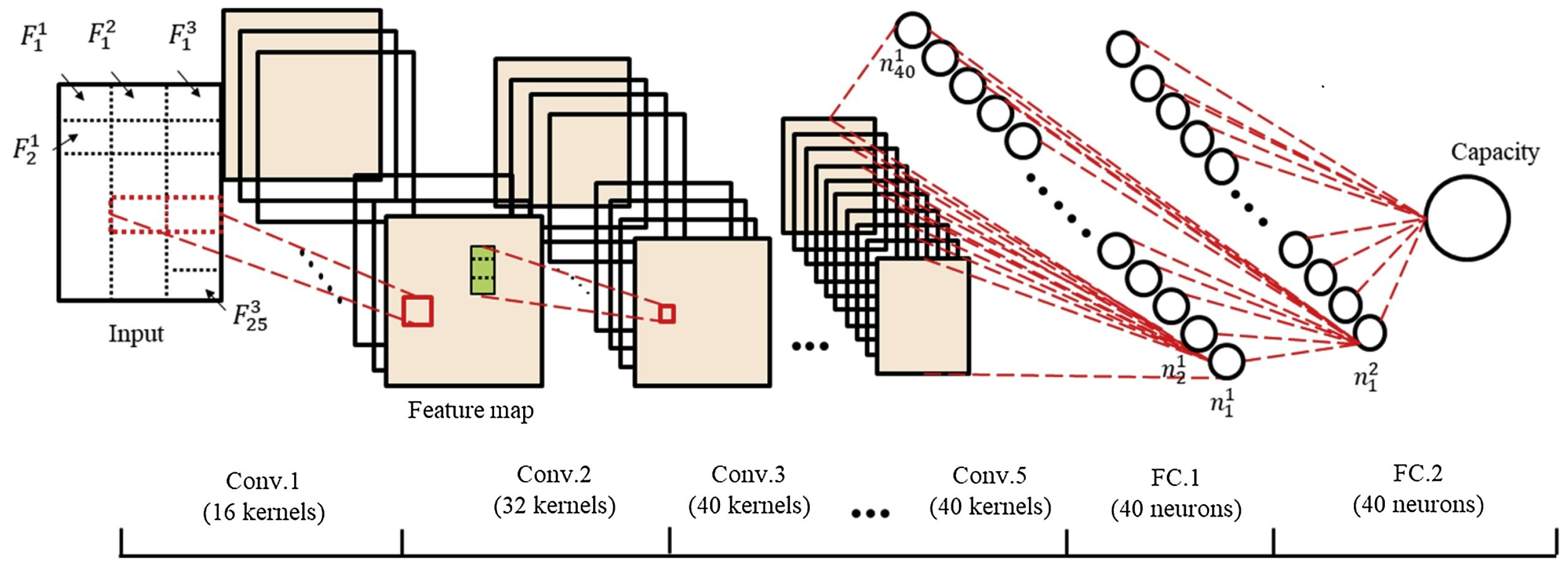
2.3.2. Convolutional Neural Network
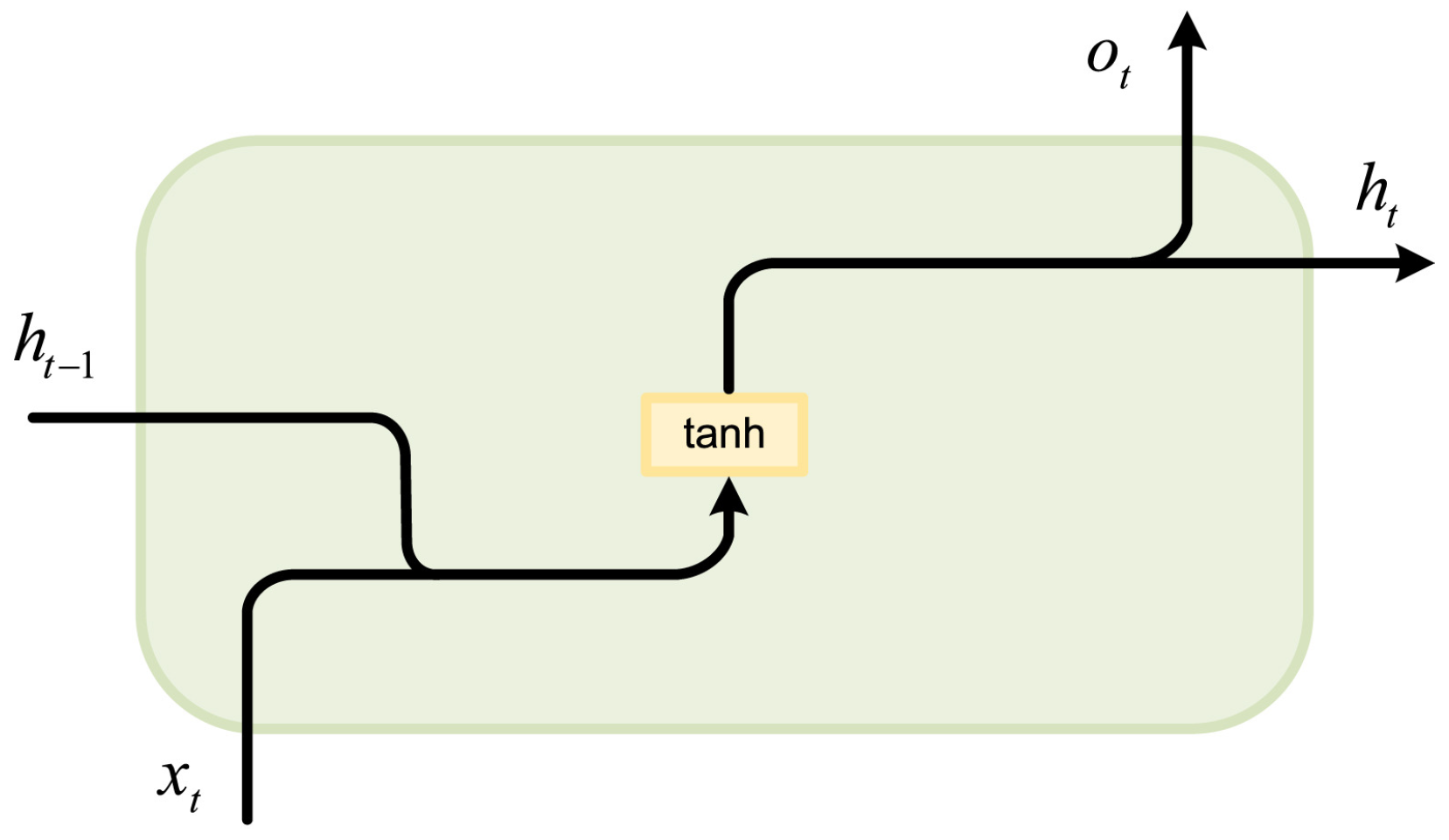
2.3.3. Recurrent Neural Network and Long Short-Term Memory Networks
2.4. Hybrid Methods
2.5. Reinforcement Learning
3. Prediction and Modeling of Thermal Properties
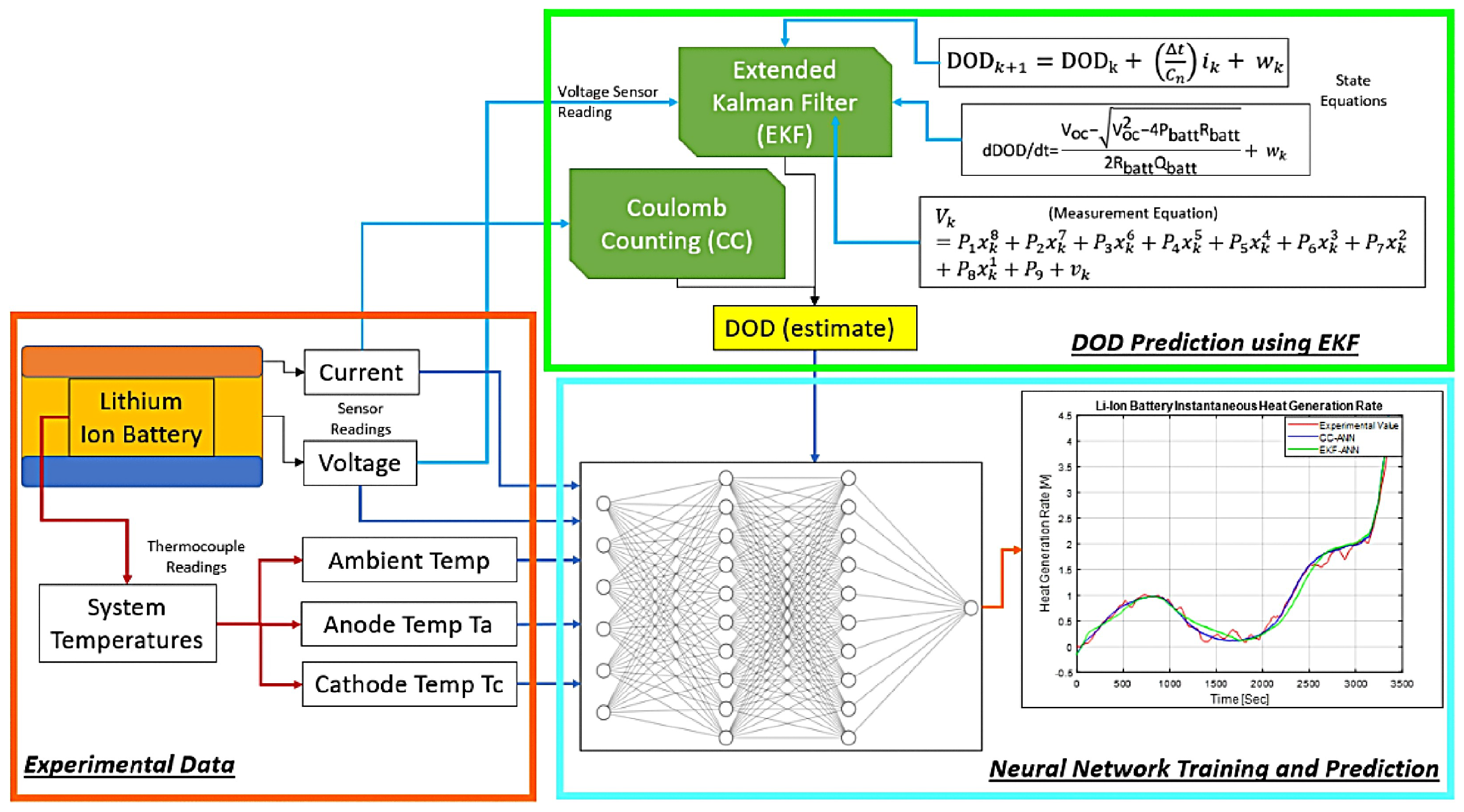
3.1. Heat-Generation Rate
3.2. Heat Conductivity
4. Prediction of Battery Temperature
5. Design of Thermal Management System
6. Discussion and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ANN | artificial neural network |
| BTMS | battery thermal management system |
| CFD | computational fluid dynamics |
| CNN | convolutional neural network |
| DNN | deep neural network |
| DOD | depth of discharge |
| DRL | deep reinforcement learning |
| DT | decision tree |
| EIS | electrochemical impedance spectroscopy |
| FNN | feedforward neural network |
| GPR | Gaussian process regression |
| GRA | grey relational analysis |
| GRG | grey relational grade |
| HGR | heat-generation rate |
| LIB | Lithium-ion battery |
| LR | linear regression |
| LSTM | long short-term memory |
| MLP | multi-layer perceptron |
| PINN | physical-informed neural network |
| PDE | partial differential equation |
| PSO | particle swarm optimization |
| PCA | principal component analysis |
| RF | random forest |
| RUL | remaining useful life |
| RMSE | root mean square error |
| RL | reinforcement learning |
| RNN | recurrent neural network |
| SVM | support vector machine |
| SVR | support vector regression |
| SOC | state of charge |
| SOH | state of health |
| TR | thermal runaway |
References
- Han, J.; Wang, F. Design and testing of a small orchard tractor driven by a power battery. Eng. Agric. 2023, 2, e20220195. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J. Key Challenges for Grid-Scale Lithium-Ion Battery Energy Storage. Adv. Energy Mater. 2022, 12, 2202197. [Google Scholar] [CrossRef]
- Yang, S.; Ling, C.; Fan, Y.; Yang, Y.; Tan, X.; Dong, H. A Review of Lithium-Ion Battery Thermal Management System Strategies and the Evaluate Criteria. Int. J. Electrochem. Sci. 2019, 14, 6077–6107. [Google Scholar] [CrossRef]
- Feng, X.; Zheng, S.; Ren, D.; He, X.; Wang, L.; Cui, H.; Liu, X.; Jin, C.; Zhang, F.; Xu, C.; et al. Investigating the thermal runaway mechanisms of lithium-ion batteries based on thermal analysis database. Appl. Energy 2019, 246, 53–64. [Google Scholar] [CrossRef]
- Gharebaghi, M.; Rezaei, O.; Li, C.; Wang, Z.; Tang, Y. A Survey on Using Second-Life Batteries in Stationary Energy Storage Applications. Energies 2025, 18, 42. [Google Scholar] [CrossRef]
- Zeng, Y.; Chalise, D.; Lubner, S.D.; Kaur, S.; Prasher, R.S. A review of thermal physics and management inside lithium-ion batteries for high energy density and fast charging. Energy Storage Mater. 2021, 41, 264–288. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes 2022, 10, 1192. [Google Scholar] [CrossRef]
- Pal, S.; Kashyap, P.; Panda, B.; Gao, L.; Garg, A. A comprehensive review of thermal runaway for batteries: Experimental; modelling, challenges and proposed framework. Int. J. Green Energy 2025, 22, 2399–2422. [Google Scholar] [CrossRef]
- Chalise, D.; Lu, W.; Srinivasan, V.; Prasher, R. Heat of Mixing During Fast Charge/Discharge of a Li-Ion Cell: A Study on NMC523 Cathode. J. Electrochem. Soc. 2020, 167, 090560. [Google Scholar] [CrossRef]
- An, K.; Barai, P.; Smith, K.; Mukherjee, P.P. Probing the Thermal Implications in Mechanical Degradation of Lithium-Ion Battery Electrodes. J. Electrochem. Soc. 2014, 161, A1058. [Google Scholar] [CrossRef]
- Li, X.; Chang, X.; Feng, Y.; Dai, Z.; Zheng, L. Investigation on the heat generation and heat sources of cylindrical NCM811 lithium-ion batteries. Appl. Therm. Eng. 2024, 241, 122403. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Marinescu, M.; Offer, G.J.; Martinez-Botas, R.F.; Brandon, N.P. Coupled thermal–electrochemical modelling of uneven heat generation in lithium-ion battery packs. J. Power Sources 2013, 243, 544–554. [Google Scholar] [CrossRef]
- Wang, H.; Li, P.; Wang, K.; Zhang, H. Coupled Electrochemical-Thermal-Mechanical Modeling and Simulation of Multi-Scale Heterogeneous Lithium-Ion Batteries. Adv. Theory Simul. 2025, e00250. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A review of air-cooling battery thermal management systems for electric and hybrid electric vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Northrop, P.W.C.; Suthar, B.; Ramadesigan, V.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Efficient Simulation and Reformulation of Lithium-Ion Battery Models for Enabling Electric Transportation. J. Electrochem. Soc. 2014, 161, E3149. [Google Scholar] [CrossRef]
- Le Houx, J.; Kramer, D. Physics based modelling of porous lithium ion battery electrodes—A review. Energy Rep. 2020, 6, 1–9. [Google Scholar] [CrossRef]
- Habib, M.K.; Ayankoso, S.A.; Nagata, F. Data-Driven Modeling: Concept, Techniques, Challenges and a Case Study. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 1000–1007. [Google Scholar] [CrossRef]
- Li, M.; Dong, C.; Xiong, B.; Mu, Y.; Yu, X.; Xiao, Q.; Jia, H. STTEWS: A sequential-transformer thermal early warning system for lithium-ion battery safety. Appl. Energy 2022, 328, 119965. [Google Scholar] [CrossRef]
- Shahrabi, A.; Nikpanjeh, F.; Hamounian, A.; Mohebbi, H.; Shekari, M.; Parvandi, Z.; Asoudeh, M.; Tabar, M.R.R. Data-driven stability analysis of complex systems with higher-order interactions. Commun. Phys. 2025, 8, 239. [Google Scholar] [CrossRef]
- Al Miaari, A.; Ali, H.M. Batteries temperature prediction and thermal management using machine learning: An overview. Energy Rep. 2023, 10, 2277–2305. [Google Scholar] [CrossRef]
- Haghi, S.; Hidalgo, M.F.V.; Niri, M.F.; Daub, R.; Marco, J. Machine Learning in Lithium-Ion Battery Cell Production: A Comprehensive Mapping Study. Batter. Supercaps 2023, 6, e202300046. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, R.; Ren, Y.; Jiao, M.; Liu, H.; Lian, C. Advanced data-driven techniques in AI for predicting lithium-ion battery remaining useful life: A comprehensive review. Green Chem. Eng. 2025, 6, 139–153. [Google Scholar] [CrossRef]
- Jaime-Barquero, E.; Bekaert, E.; Olarte, J.; Zulueta, E.; Lopez-Guede, J.M. Artificial Intelligence Opportunities to Diagnose Degradation Modes for Safety Operation in Lithium Batteries. Batteries 2023, 9, 388. [Google Scholar] [CrossRef]
- Duquesnoy, M.; Liu, C.; Dominguez, D.Z.; Kumar, V.; Ayerbe, E.; Franco, A.A. Machine learning-assisted multi-objective optimization of battery manufacturing from synthetic data generated by physics-based simulations. Energy Storage Mater. 2023, 56, 50–61. [Google Scholar] [CrossRef]
- Tagade, P.; Hariharan, K.S.; Ramachandran, S.; Khandelwal, A.; Naha, A.; Kolake, S.M.; Han, S.H. Deep Gaussian process regression for lithium-ion battery health prognosis and degradation mode diagnosis. J. Power Sources 2020, 445, 227281. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, J.; Wu, B.; Zhao, C.; Sun, J.; Dai, C. Discrimination of Chinese Liquors Based on Electronic Nose and Fuzzy Discriminant Principal Component Analysis. Foods 2019, 8, 38. [Google Scholar] [CrossRef] [PubMed]
- Geng, W.; Haruna, S.A.; Li, H.; Kademi, H.I.; Chen, Q. A Novel Colorimetric Sensor Array Coupled Multivariate Calibration Analysis for Predicting Freshness in Chicken Meat: A Comparison of Linear and Nonlinear Regression Algorithms. Foods 2023, 12, 720. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, H.; Wang, B.; Qu, W.; Wali, A.; Zhou, C. Relationships between the structure of wheat gluten and ACE inhibitory activity of hydrolysate: Stepwise multiple linear regression analysis. J. Sci. Food Agric. 2016, 96, 3313–3320. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, L.; Liu, H. Grey relational analysis, principal component analysis and forecasting of carbon emissions based on long short-term memory in China. J. Clean. Prod. 2019, 209, 415–423. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.; Buttar, N.A. Analysis of mechanical properties for tea stem using grey relational analysis coupled with multiple linear regression. Sci. Hortic. 2020, 260, 108886. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Zhang, C.; Li, N. Machine Learning Methods for Weather Forecasting: A Survey. Atmosphere 2025, 16, 82. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Wong, K.K.L. Support Vector Machine. In Cybernetical Intelligence; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2023; Chapter 8; pp. 149–176. [Google Scholar] [CrossRef]
- Huang, W.; Zhu, W.; Ma, C.; Guo, Y.; Chen, C. Identification of group-housed pigs based on Gabor and Local Binary Pattern features. Biosyst. Eng. 2018, 166, 90–100. [Google Scholar] [CrossRef]
- Fan, C.; Liu, Y.; Cui, T.; Qiao, M.; Yu, Y.; Xie, W.; Huang, Y. Quantitative Prediction of Protein Content in Corn Kernel Based on Near-Infrared Spectroscopy. Foods 2024, 13, 4173. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Lian, Y.; Chen, J.; Guan, Z.; Song, J. Development of a monitoring system for grain loss of paddy rice based on a decision tree algorithm. Int. J. Agric. Biol. Eng. 2021, 14, 224–229. [Google Scholar] [CrossRef]
- Louppe, G. Understanding Random Forests: From Theory to Practice. Ph.D. Thesis, University of Liege, Liege, Belgium, 2014. [Google Scholar] [CrossRef]
- Yu, J.; Zhangzhong, L.; Lan, R.; Zhang, X.; Xu, L.; Li, J. Ensemble Learning Simulation Method for Hydraulic Characteristic Parameters of Emitters Driven by Limited Data. Agronomy 2023, 13, 986. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Srivastava, A.; Deng, J.; Li, Z.; Raza, A.; Khadke, L.; Yu, Z.; El-Rawy, M. Forecasting vapor pressure deficit for agricultural water management using machine learning in semi-arid environments. Agric. Water Manag. 2023, 283, 108302. [Google Scholar] [CrossRef]
- Qian, W.; Hui, X.; Wang, B.; Kronenburg, A.; Sung, C.J.; Lin, Y. An investigation into oxidation-induced fragmentation of soot aggregates by Langevin dynamics simulations. Fuel 2023, 334, 126547. [Google Scholar] [CrossRef]
- Qian, W.; Yang, S.; Liu, W.; Xu, Q.; Zhu, W. Research on Flow Field Prediction in a Multi-Swirl Combustor Using Artificial Neural Network. Processes 2024, 12, 2435. [Google Scholar] [CrossRef]
- Suk, H.I. An Introduction to Neural Networks and Deep Learning. In Deep Learning for Medical Image Analysis; Zhou, S.K., Greenspan, H., Shen, D., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 3–24. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Hyperspectral technique combined with deep learning algorithm for detection of compound heavy metals in lettuce. Food Chem. 2020, 321, 126503. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Han, J.; Norton, T. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1–14. [Google Scholar] [CrossRef]
- Maffezzoni, D.; Barbierato, E.; Gatti, A. Data-Driven Diagnostics for Pediatric Appendicitis: Machine Learning to Minimize Misdiagnoses and Unnecessary Surgeries. Future Internet 2025, 17, 147. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, K.; Fan, W.; Li, C.; Qian, W. Prediction of swirling flow field in combustor based on deep learning. Acta Astronaut. 2022, 201, 302–316. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, J.; Liu, W.; Yue, R.; Shi, J.; Zhou, C.; Hu, J. SN-CNN: A Lightweight and Accurate Line Extraction Algorithm for Seedling Navigation in Ridge-Planted Vegetables. Agriculture 2024, 14, 1446. [Google Scholar] [CrossRef]
- Qiu, D.; Guo, T.; Yu, S.; Liu, W.; Li, L.; Sun, Z.; Peng, H.; Hu, D. Classification of Apple Color and Deformity Using Machine Vision Combined with CNN. Agriculture 2024, 14, 978. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xiang, H.; Xiong, X.; Wang, Y.; Chen, Z. Benchmarking core temperature forecasting for lithium-ion battery using typical recurrent neural networks. Appl. Therm. Eng. 2024, 248, 123257. [Google Scholar] [CrossRef]
- Taha, M.F.; Mao, H.; Mousa, S.; Zhou, L.; Wang, Y.; Elmasry, G.; Al-Rejaie, S.; Elwakeel, A.E.; Wei, Y.; Qiu, Z. Deep Learning-Enabled Dynamic Model for Nutrient Status Detection of Aquaponically Grown Plants. Agronomy 2024, 14, 2290. [Google Scholar] [CrossRef]
- Yuan, A.; Cai, T.; Luo, H.; Song, Z.; Wei, B. Core temperature estimation of lithium-ion battery based on numerical model fusion deep learning. J. Energy Storage 2024, 102, 114148. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Qian, W.; Hui, X.; Wang, B.; Zhang, Z.; Lin, Y.; Yang, S. Physics-Informed neural network for inverse heat conduction problem. Heat Transf. Res. 2023, 54, 65–76. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, Z.; Yang, L. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction. J. Power Sources 2019, 412, 442–450. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, Z.; Sun, W.; He, L. A Decision-Making System for Cotton Irrigation Based on Reinforcement Learning Strategy. Agronomy 2024, 14, 11. [Google Scholar] [CrossRef]
- Feng, X.; Ren, D.; He, X.; Ouyang, M. Mitigating Thermal Runaway of Lithium-Ion Batteries. Joule 2020, 4, 743–770. [Google Scholar] [CrossRef]
- Feng, X.; Fang, M.; He, X.; Ouyang, M.; Lu, L.; Wang, H.; Zhang, M. Thermal runaway features of large format prismatic lithium ion battery using extended volume accelerating rate calorimetry. J. Power Sources 2014, 255, 294–301. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Neural network based computational model for estimation of heat generation in LiFePO4 pouch cells of different nominal capacities. Comput. Chem. Eng. 2017, 101, 81–94. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, X.; Yang, H. Prediction of the heat-generation rate of lithium-ion batteries based on three machine learning algorithms. Batteries 2023, 9, 165. [Google Scholar] [CrossRef]
- Yalçın, S.; Panchal, S.; Herdem, M.S. A CNN-ABC model for estimation and optimization of heat generation rate and voltage distributions of lithium-ion batteries for electric vehicles. Int. J. Heat Mass Transf. 2022, 199, 123486. [Google Scholar] [CrossRef]
- Legala, A.; Li, X. Hybrid data-based modeling for the prediction and diagnostics of Li-ion battery thermal behaviors. Energy AI 2022, 10, 100194. [Google Scholar] [CrossRef]
- Cho, G.; Kim, Y.; Kwon, J.; Su, W.; Wang, M. Impact of Data Sampling Methods on the Performance of Data-driven Parameter Identification for Lithium ion Batteries. IFAC-PapersOnLine 2021, 54, 534–539. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J.; Ringbeck, F.; Jöst, D.; Zhang, L.; Wei, Z.; Sauer, D.U. Physics-informed neural networks for electrode-level state estimation in lithium-ion batteries. J. Power Sources 2021, 506, 230034. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, T.; Zhang, C.; Yuan, L.; Xu, Z.; Jin, L. Non-uniform heat generation model of pouch lithium-ion battery based on regional heat-generation rate. J. Energy Storage 2023, 63, 107074. [Google Scholar] [CrossRef]
- Koo, B.; Goli, P.; Sumant, A.V.; dos Santos Claro, P.C.; Rajh, T.; Johnson, C.S.; Balandin, A.A.; Shevchenko, E.V. Toward Lithium Ion Batteries with Enhanced Thermal Conductivity. ACS Nano 2014, 8, 7202–7207. [Google Scholar] [CrossRef] [PubMed]
- Werner, D.; Loges, A.; Becker, D.J.; Wetzel, T. Thermal conductivity of Li-ion batteries and their electrode configurations—A novel combination of modelling and experimental approach. J. Power Sources 2017, 364, 72–83. [Google Scholar] [CrossRef]
- Bazinski, S.J.; Wang, X. Experimental study on the influence of temperature and state-of-charge on the thermophysical properties of an LFP pouch cell. J. Power Sources 2015, 293, 283–291. [Google Scholar] [CrossRef]
- Wei, L.; Lu, Z.; Cao, F.; Zhang, L.; Yang, X.; Yu, X.; Jin, L. A comprehensive study on thermal conductivity of the lithium-ion battery. Int. J. Energy Res. 2020, 44, 9466–9478. [Google Scholar] [CrossRef]
- Leng, X.; Li, Y.; Xu, G.; Xiong, W.; Xiao, S.; Li, C.; Chen, J.; Yang, M.; Li, S.; Chen, Y.; et al. Prediction of lithium-ion battery internal temperature using the imaginary part of electrochemical impedance spectroscopy. Int. J. Heat Mass Transf. 2025, 240, 126664. [Google Scholar] [CrossRef]
- Choi, C.; Park, S.; Kim, J. Uniqueness of multilayer perceptron-based capacity prediction for contributing state-of-charge estimation in a lithium primary battery. Ain Shams Eng. J. 2023, 14, 101936. [Google Scholar] [CrossRef]
- Zheng, Y.; Cui, Y.; Han, X.; Ouyang, M. A capacity prediction framework for lithium-ion batteries using fusion prediction of empirical model and data-driven method. Energy 2021, 237, 121556. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Lin, M.; Zeng, X.; Wu, J. State of health estimation of lithium-ion battery based on an adaptive tunable hybrid radial basis function network. J. Power Sources 2021, 504, 230063. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, H.; Feng, F.; Liu, B. An enhanced multi-state estimation hierarchy for advanced lithium-ion battery management. Appl. Energy 2020, 257, 114019. [Google Scholar] [CrossRef]
- Hasib, S.A.; Islam, S.; Ali, M.F.; Sarker, S.K.; Li, L.; Hasan, M.M.; Saha, D.K. Enhancing prediction accuracy of Remaining Useful Life in lithium-ion batteries: A deep learning approach with Bat optimizer. Future Batter. 2024, 2, 100003. [Google Scholar] [CrossRef]
- Qian, C.; Guan, H.; Xu, B.; Xia, Q.; Sun, B.; Ren, Y.; Wang, Z. A CNN-SAM-LSTM hybrid neural network for multi-state estimation of lithium-ion batteries under dynamical operating conditions. Energy 2024, 294, 130764. [Google Scholar] [CrossRef]
- Jaliliantabar, F.; Mamat, R.; Kumarasamy, S. Prediction of lithium-ion battery temperature in different operating conditions equipped with passive battery thermal management system by artificial neural networks. Mater. Today Proc. 2022, 48, 1796–1804. [Google Scholar] [CrossRef]
- Hussein, A.A.; Chehade, A.A. Robust Artificial Neural Network-Based Models for Accurate Surface Temperature Estimation of Batteries. IEEE Trans. Ind. Appl. 2020, 56, 5269–5278. [Google Scholar] [CrossRef]
- Xiong, R.; Li, X.; Li, H.; Zhu, B.; Avelin, A. Neural network and physical enable one sensor to estimate the temperature for all cells in the battery pack. J. Energy Storage 2024, 80, 110387. [Google Scholar] [CrossRef]
- Yravedra, F.A.; Li, Z. A complete machine learning approach for predicting lithium-ion cell combustion. Electr. J. 2021, 34, 106887. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Vidal, C.; Emadi, A. Accurate Surface Temperature Estimation of Lithium-Ion Batteries Using Feedforward and Recurrent Artificial Neural Networks. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 52–57. [Google Scholar] [CrossRef]
- Han, J.; Seo, J.; Kim, J.; Koo, Y.; Ryu, M.; Lee, B.J. Predicting temperature of a Li-ion battery under dynamic current using long short-term memory. Case Stud. Therm. Eng. 2024, 63, 105246. [Google Scholar] [CrossRef]
- Zhu, S.; He, C.; Zhao, N.; Sha, J. Data-driven analysis on thermal effects and temperature changes of lithium-ion battery. J. Power Sources 2021, 482, 228983. [Google Scholar] [CrossRef]
- Yi, Y.; Xia, C.; Feng, C.; Zhang, W.; Fu, C.; Qian, L.; Chen, S. Digital twin-long short-term memory (LSTM) neural network based real-time temperature prediction and degradation model analysis for lithium-ion battery. J. Energy Storage 2023, 64, 107203. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Z.; Shu, X.; Xiao, R.; Shen, J.; Liu, Y.; Liu, Y. Online surface temperature prediction and abnormal diagnosis of lithium-ion batteries based on hybrid neural network and fault threshold optimization. Reliab. Eng. Syst. Saf. 2024, 243, 109798. [Google Scholar] [CrossRef]
- Zafar, M.H.; Bukhari, S.M.S.; Houran, M.A.; Mansoor, M.; Khan, N.M.; Sanfilippo, F. DeepTimeNet: A novel architecture for precise surface temperature estimation of lithium-ion batteries across diverse ambient conditions. Case Stud. Therm. Eng. 2024, 61, 105002. [Google Scholar] [CrossRef]
- Kleiner, J.; Stuckenberger, M.; Komsiyska, L.; Endisch, C. Advanced Monitoring and Prediction of the Thermal State of Intelligent Battery Cells in Electric Vehicles by Physics-Based and Data-Driven Modeling. Batteries 2021, 7, 31. [Google Scholar] [CrossRef]
- Hasan, M.M.; Ali Pourmousavi, S.; Jahanbani Ardakani, A.; Saha, T.K. A data-driven approach to estimate battery cell temperature using a nonlinear autoregressive exogenous neural network model. J. Energy Storage 2020, 32, 101879. [Google Scholar] [CrossRef]
- Kleiner, J.; Stuckenberger, M.; Komsiyska, L.; Endisch, C. Real-time core temperature prediction of prismatic automotive lithium-ion battery cells based on artificial neural networks. J. Energy Storage 2021, 39, 102588. [Google Scholar] [CrossRef]
- Tran, M.K.; Panchal, S.; Chauhan, V.; Brahmbhatt, N.; Mevawalla, A.; Fraser, R.; Fowler, M. Python-based scikit-learn machine learning models for thermal and electrical performance prediction of high-capacity lithium-ion battery. Int. J. Energy Res. 2022, 46, 786–794. [Google Scholar] [CrossRef]
- Pathmanaban, P.; Arulraj, P.; Raju, M.; Hariharan, C. Optimizing electric bike battery management: Machine learning predictions of LiFePO4 temperature under varied conditions. J. Energy Storage 2024, 99, 113217. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Emadi, A. Application of Deep Neural Networks for Lithium-Ion Battery Surface Temperature Estimation Under Driving and Fast Charge Conditions. IEEE Trans. Transp. Electrif. 2023, 9, 1153–1165. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Song, M.; Zhao, X.; Li, G. Instantaneous estimation of internal temperature in lithium-ion battery by impedance measurement. Int. J. Energy Res. 2020, 44, 3082–3097. [Google Scholar] [CrossRef]
- Ströbel, M.; Pross-Brakhage, J.; Kopp, M.; Birke, K.P. Impedance Based Temperature Estimation of Lithium Ion Cells Using Artificial Neural Networks. Batteries 2021, 7, 85. [Google Scholar] [CrossRef]
- Amiri, M.N.; Håkansson, A.; Burheim, O.S.; Lamb, J.J. Lithium-ion battery digitalization: Combining physics-based models and machine learning. Renew. Sustain. Energy Rev. 2024, 200, 114577. [Google Scholar] [CrossRef]
- Cho, G.; Zhu, D.; Campbell, J.J.; Wang, M. An LSTM-PINN Hybrid Method to Estimate Lithium-Ion Battery Pack Temperature. IEEE Access 2022, 10, 100594–100604. [Google Scholar] [CrossRef]
- Kuzhiyil, J.A.; Damoulas, T.; Widanage, W.D. Neural equivalent circuit models: Universal differential equations for battery modelling. Appl. Energy 2024, 371, 123692. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical–thermal–neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; Shen, W.; Lin, X. Extreme Learning Machine-Based Thermal Model for Lithium-Ion Batteries of Electric Vehicles under External Short Circuit. Engineering 2021, 7, 395–405. [Google Scholar] [CrossRef]
- He, Y.B.; Wang, B.C.; Deng, H.P.; Li, H.X. Physics-reserved spatiotemporal modeling of battery thermal process: Temperature prediction, parameter identification, and heat-generation rate estimation. J. Energy Storage 2024, 75, 109604. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; Ma, S.; Lin, X. Characterization of external short circuit faults in electric vehicle Li-ion battery packs and prediction using artificial neural networks. Appl. Energy 2020, 260, 114253. [Google Scholar] [CrossRef]
- Li, M.; Dong, C.; Yu, X.; Xiao, Q.; Jia, H. Multi-step ahead thermal warning network for energy storage system based on the core temperature detection. Sci. Rep. 2021, 11, 15332. [Google Scholar] [CrossRef]
- Sarchami, A.; Tousi, M.; Darab, M.; Kiani, M.; Najafi, M.; Houshfar, E. Novel AgO-based nanofluid for efficient thermal management of 21700-type lithium-ion battery. Sustain. Energy Technol. Assess. 2024, 70, 103934. [Google Scholar] [CrossRef]
- Lin, J.; Liu, X.; Li, S.; Zhang, C.; Yang, S. A review on recent progress, challenges and perspective of battery thermal management system. Int. J. Heat Mass Transf. 2021, 167, 120834. [Google Scholar] [CrossRef]
- Jindal, P.; Kumar, B.S.; Bhattacharya, J. Coupled electrochemical-abuse-heat-transfer model to predict thermal runaway propagation and mitigation strategy for an EV battery module. J. Energy Storage 2021, 39, 102619. [Google Scholar] [CrossRef]
- Sadeh, M.; Tousi, M.; Sarchami, A.; Sanaie, R.; Kiani, M.; Ashjaee, M.; Houshfar, E. A novel hybrid liquid-cooled battery thermal management system for electric vehicles in highway fuel-economy condition. J. Energy Storage 2024, 86, 111195. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, W.; Chen, Q. Evaluating aroma quality of black tea by an olfactory visualization system: Selection of feature sensor using particle swarm optimization. Food Res. Int. 2019, 126, 108605. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Li, H.; Tang, P.; Chen, C. Synchronization Optimization of Pipe Diameter and Operation Frequency in a Pressurized Irrigation Network Based on the Genetic Algorithm. Agriculture 2022, 12, 673. [Google Scholar] [CrossRef]
- Pang, Y.; Tang, P.; Li, H.; Marinello, F.; Chen, C. Optimization of sprinkler irrigation scheduling scenarios for reducing irrigation energy consumption. Irrig. Drain. 2024, 73, 1329–1343. [Google Scholar] [CrossRef]
- Li, H.; Pan, X.; Jiang, Y.; Zhou, X. Optimising and analysis of the hydraulic performance of a water dispersion needle sprinkler using RF-NSGA II and CFD. Biosyst. Eng. 2025, 254, 104113. [Google Scholar] [CrossRef]
- Fayaz, H.; Afzal, A.; Samee, A.M.; Soudagar, M.E.M.; Akram, N.; Mujtaba, M.; Jilte, R.; Islam, M.T.; Ağbulut, Ü.; Saleel, C.A. Optimization of thermal and structural design in lithium-ion batteries to obtain energy efficient battery thermal management system (BTMS): A critical review. Arch. Comput. Methods Eng. 2022, 29, 129–194. [Google Scholar] [CrossRef]
- Shrinet, E.S.; Akula, R.; Kumar, L. Improvement in serpentine channel based battery thermal management system geometry using variable contact area and its multi-objective design optimization. J. Energy Storage 2024, 96, 112726. [Google Scholar] [CrossRef]
- Monika, K.; Punnoose, E.M.; Datta, S.P. Multi-objective optimization of cooling plate with hexagonal channel design for thermal management of Li-ion battery module. Appl. Energy 2024, 368, 123423. [Google Scholar] [CrossRef]
- Tang, X.; Guo, Q.; Li, M.; Wei, C.; Pan, Z.; Wang, Y. Performance analysis on liquid-cooled battery thermal management for electric vehicles based on machine learning. J. Power Sources 2021, 494, 229727. [Google Scholar] [CrossRef]
- Feng, X.H.; Li, Z.Z.; Gu, F.S.; Zhang, M.L. Structural design and optimization of air-cooled thermal management system for lithium-ion batteries based on discrete and continuous variables. J. Energy Storage 2024, 86, 111202. [Google Scholar] [CrossRef]
- Yuan, L.; Li, W.; Deng, W.; Sun, W.; Huang, M.; Liu, Z. Cell temperature prediction in the refrigerant direct cooling thermal management system using artificial neural network. Appl. Therm. Eng. 2024, 254, 123852. [Google Scholar] [CrossRef]
- Billert, A.M.; Erschen, S.; Frey, M.; Gauterin, F. Predictive battery thermal management using quantile convolutional neural networks. Transp. Eng. 2022, 10, 100150. [Google Scholar] [CrossRef]
- Mokhtari Mehmandoosti, M.; Kowsary, F. Artificial neural network-based multi-objective optimization of cooling of lithium-ion batteries used in electric vehicles utilizing pulsating coolant flow. Appl. Therm. Eng. 2023, 219, 119385. [Google Scholar] [CrossRef]
- Yetik, O.; Karakoc, T.H. Estimation of thermal effect of different busbars materials on prismatic Li-ion batteries based on artificial neural networks. J. Energy Storage 2021, 38, 102543. [Google Scholar] [CrossRef]
- Oyewola, O.M.; Idowu, E.T. Numerical and artificial neural network inspired study on step-like-plenum battery thermal management system. Int. J. Thermofluids 2024, 24, 100897. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.C.Y.; Wang, W.; Chen, T.B.Y.; Lai, C.S.; Yang, W.; Wu, W.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Integration of Computational Fluid Dynamics and Artificial Neural Network for Optimization Design of Battery Thermal Management System. Batteries 2022, 8, 69. [Google Scholar] [CrossRef]
- Najafi Khaboshan, H.; Jaliliantabar, F.; Abdullah, A.A.; Panchal, S.; Azarinia, A. Parametric investigation of battery thermal management system with phase change material, metal foam, and fins; utilizing CFD and ANN models. Appl. Therm. Eng. 2024, 247, 123080. [Google Scholar] [CrossRef]
- Jin, L.; Xi, H. Multi-objective parameter optimization of the Z-type air-cooling system based on artificial neural network. J. Energy Storage 2024, 86, 111284. [Google Scholar] [CrossRef]
- Zheng, A.; Gao, H.; Jia, X.; Cai, Y.; Yang, X.; Zhu, Q.; Jiang, H. Deep learning-assisted design for battery liquid cooling plate with bionic leaf structure considering non-uniform heat generation. Appl. Energy 2024, 373, 123898. [Google Scholar] [CrossRef]
- Fini, A.T.; Fattahi, A.; Musavi, S. Machine learning prediction and multiobjective optimization for cooling enhancement of a plate battery using the chaotic water-microencapsulated PCM fluid flows. J. Taiwan Inst. Chem. Eng. 2023, 148, 104680. [Google Scholar] [CrossRef]
- Ye, L.; Li, C.; Wang, C.; Zheng, J.; Zhong, K.; Wu, T. A multi-objective optimization approach for battery thermal management system based on the combination of BP neural network prediction and NSGA-II algorithm. J. Energy Storage 2024, 99, 113212. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Z.; Li, J.; Cao, X. Performance analysis and prediction of hybrid battery thermal management system integrating PCM with air cooling based on machine learning algorithm. Appl. Therm. Eng. 2024, 257, 124474. [Google Scholar] [CrossRef]
- Li, W.; Li, A.; Yin Yuen, A.C.; Chen, Q.; Yuan Chen, T.B.; De Cachinho Cordeiro, I.M.; Lin, P. Optimisation of PCM passive cooling efficiency on lithium-ion batteries based on coupled CFD and ANN techniques. Appl. Therm. Eng. 2025, 259, 124874. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, Y.; Zhao, S.; Zhao, T.; Ni, M. Modeling and optimization of micro heat pipe cooling battery thermal management system via deep learning and multi-objective genetic algorithms. Int. J. Heat Mass Transf. 2023, 207, 124024. [Google Scholar] [CrossRef]
- Qian, X.; Xuan, D.; Zhao, X.; Shi, Z. Heat dissipation optimization of lithium-ion battery pack based on neural networks. Appl. Therm. Eng. 2019, 162, 114289. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, W.; Shi, X.; She, C.; Zheng, Z.; Zhou, J.; Zhu, Y. Machine learning assisted multi-objective design optimization for battery thermal management system. Appl. Therm. Eng. 2024, 253, 123826. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, S.; Zhang, B.; Wang, A.; Zhang, L.; Zhu, Q. Research Status and Development Trends of Deep Reinforcement Learning in the Intelligent Transformation of Agricultural Machinery. Agriculture 2025, 15, 1223. [Google Scholar] [CrossRef]
- He, L.; Tan, L.; Liu, Z.; Zhang, Y.; Wu, L.; Feng, Y.; Tong, B. Optimization of thermal management performance of direct-cooled power battery based on backpropagation neural network and deep reinforcement learning. Appl. Therm. Eng. 2025, 258, 124661. [Google Scholar] [CrossRef]
- Xie, F.; Guo, Z.; Li, T.; Feng, Q.; Zhao, C. Dynamic Task Planning for Multi-Arm Harvesting Robots Under Multiple Constraints Using Deep Reinforcement Learning. Horticulturae 2025, 11, 88. [Google Scholar] [CrossRef]
- Cheng, H.; Jung, S.; Kim, Y.B. Battery thermal management system optimization using Deep reinforced learning algorithm. Appl. Therm. Eng. 2024, 236, 121759. [Google Scholar] [CrossRef]
- Ebbs-Picken, T.; Da Silva, C.M.; Amon, C.H. Hierarchical thermal modeling and surrogate-model-based design optimization framework for cold plates used in battery thermal management systems. Appl. Therm. Eng. 2024, 253, 123599. [Google Scholar] [CrossRef]


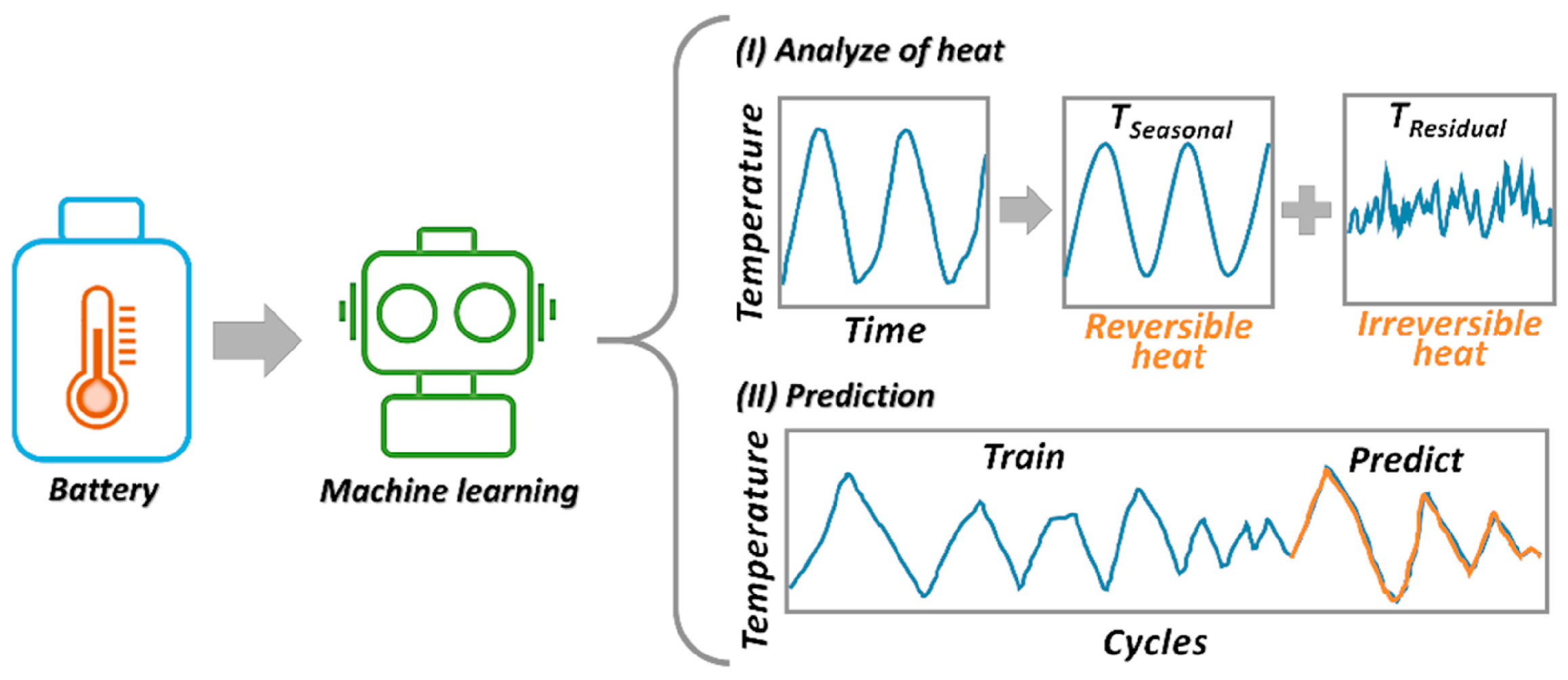


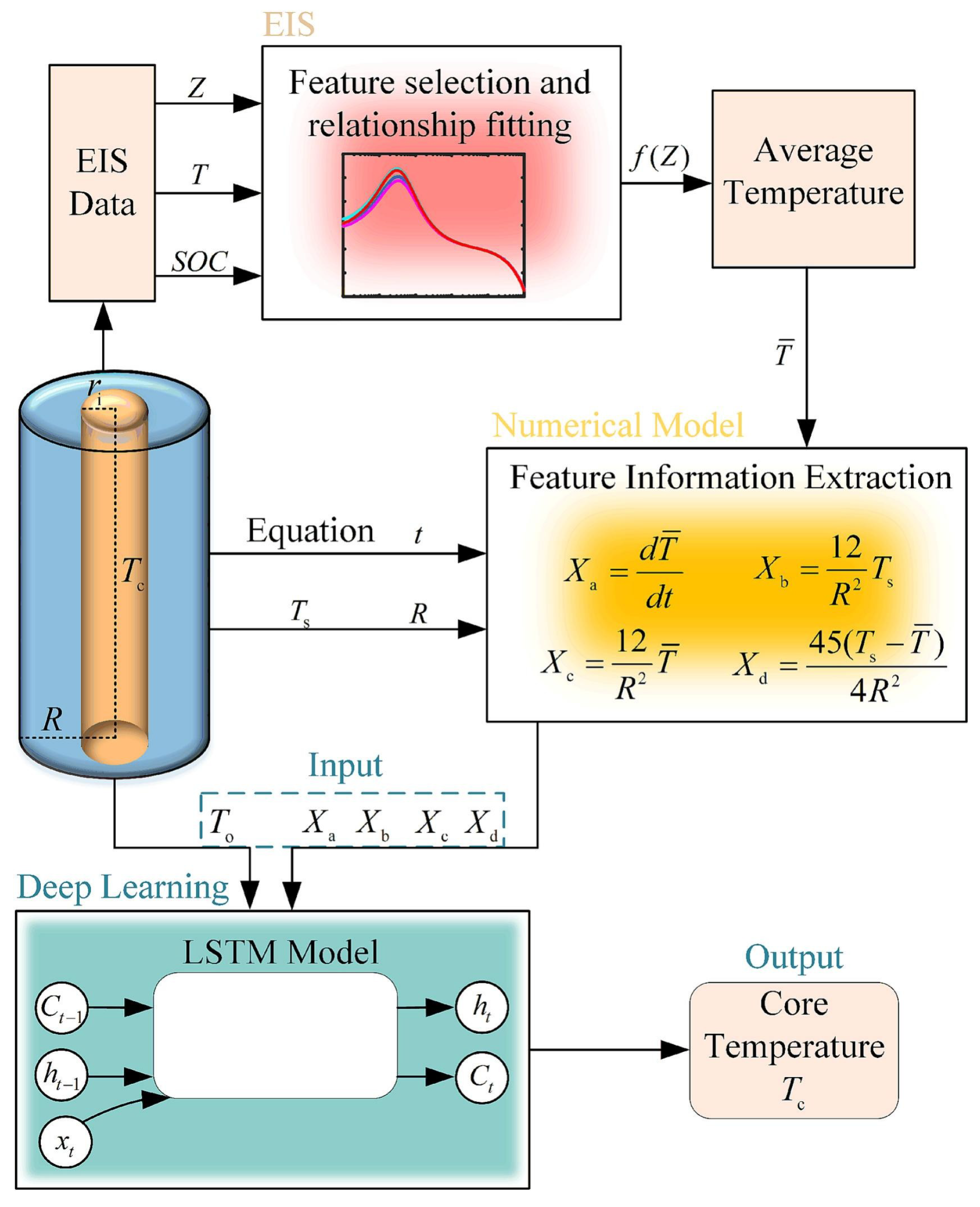
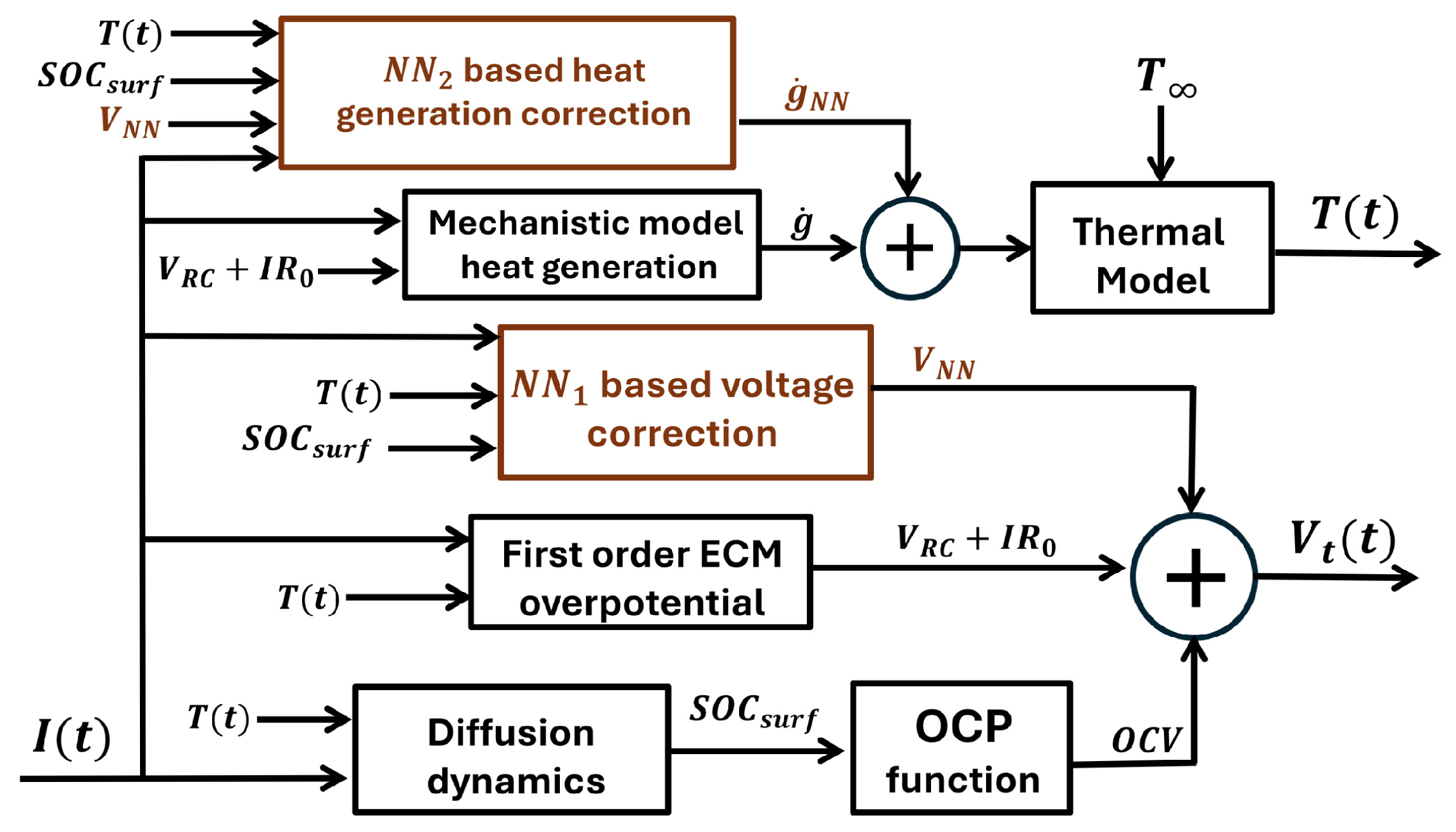
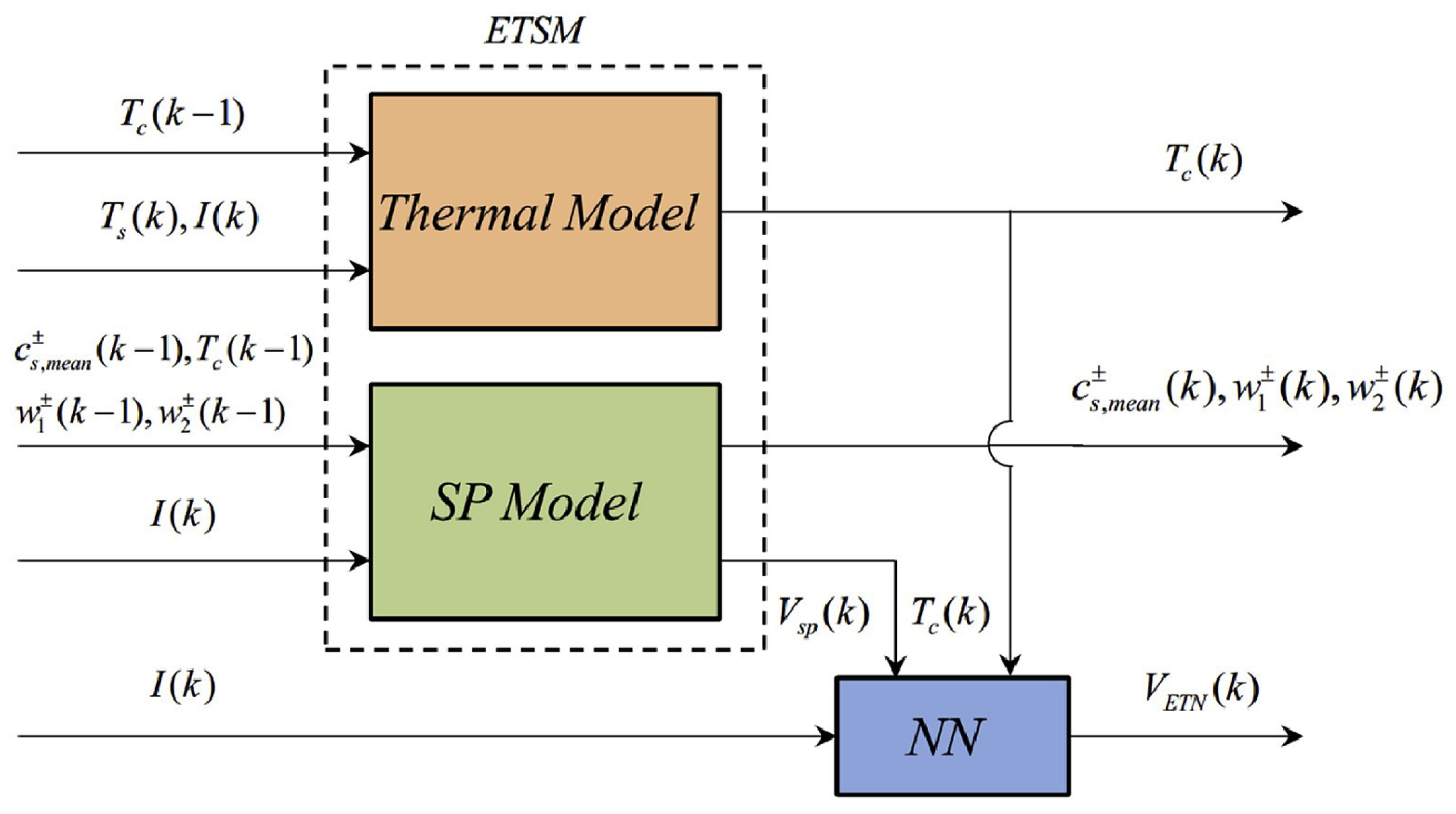

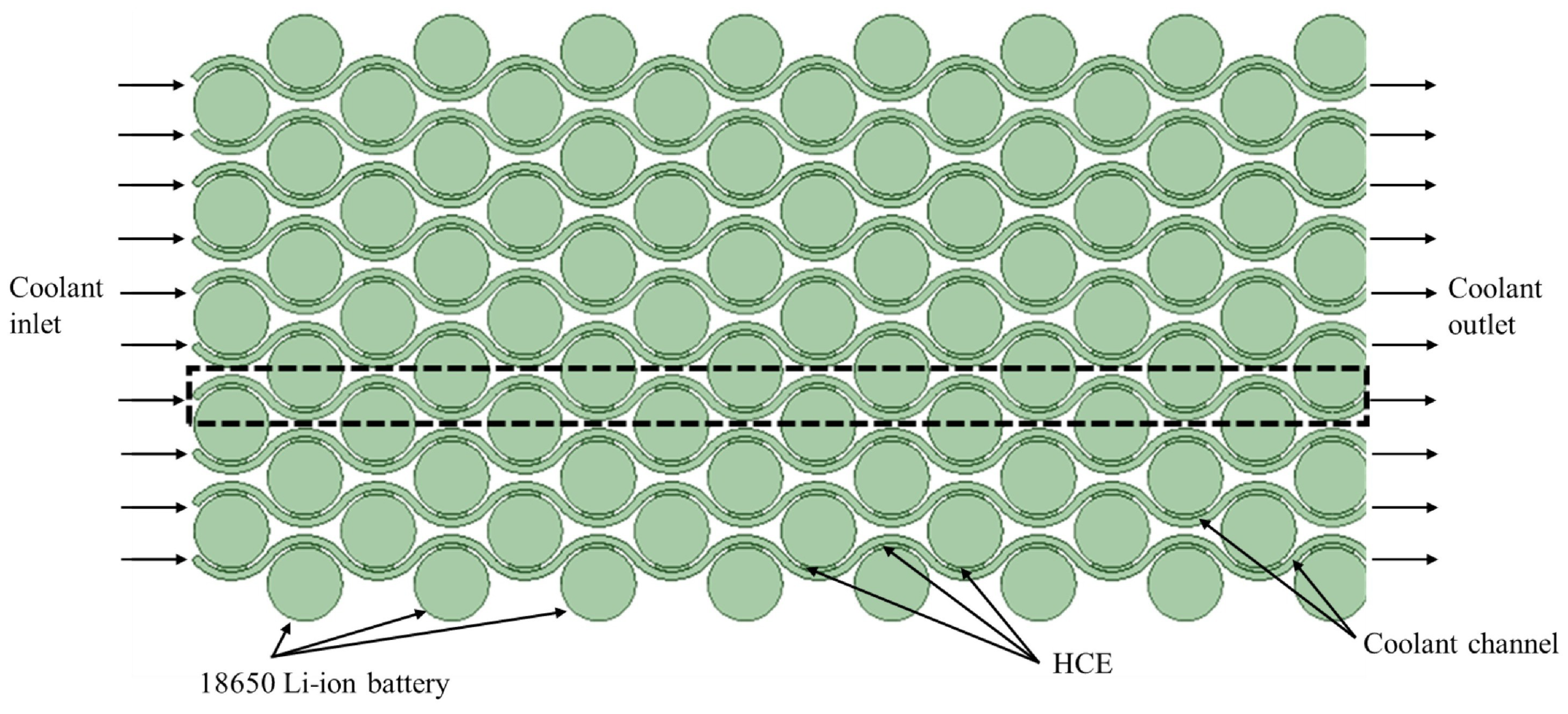

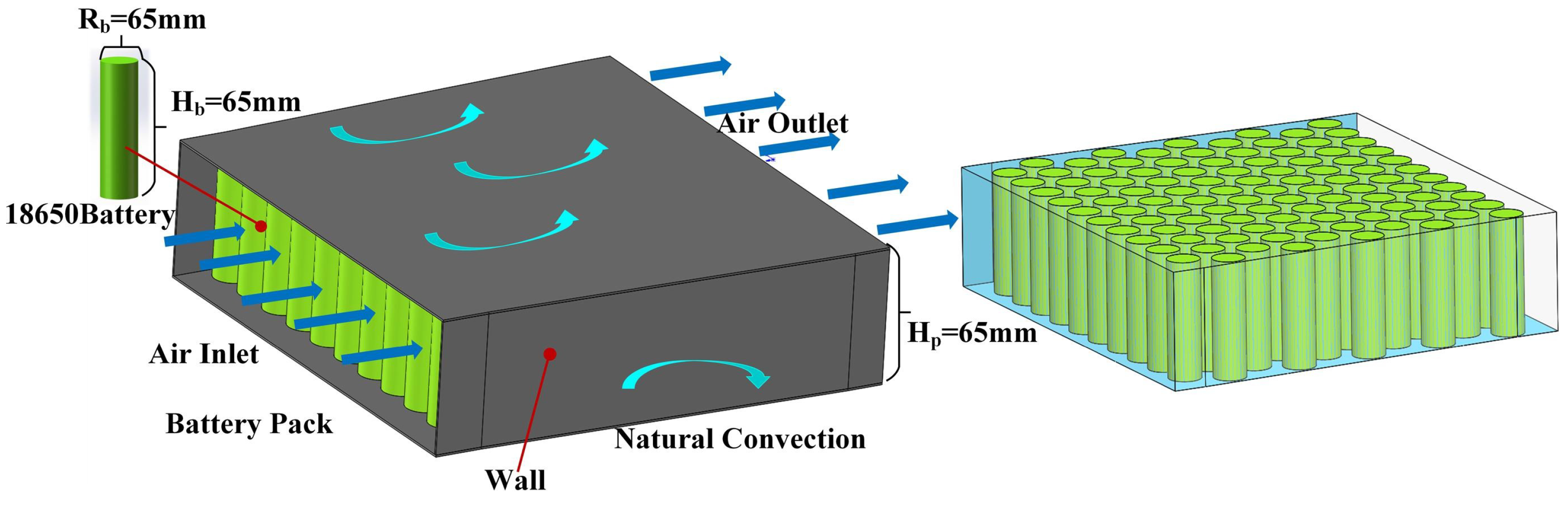
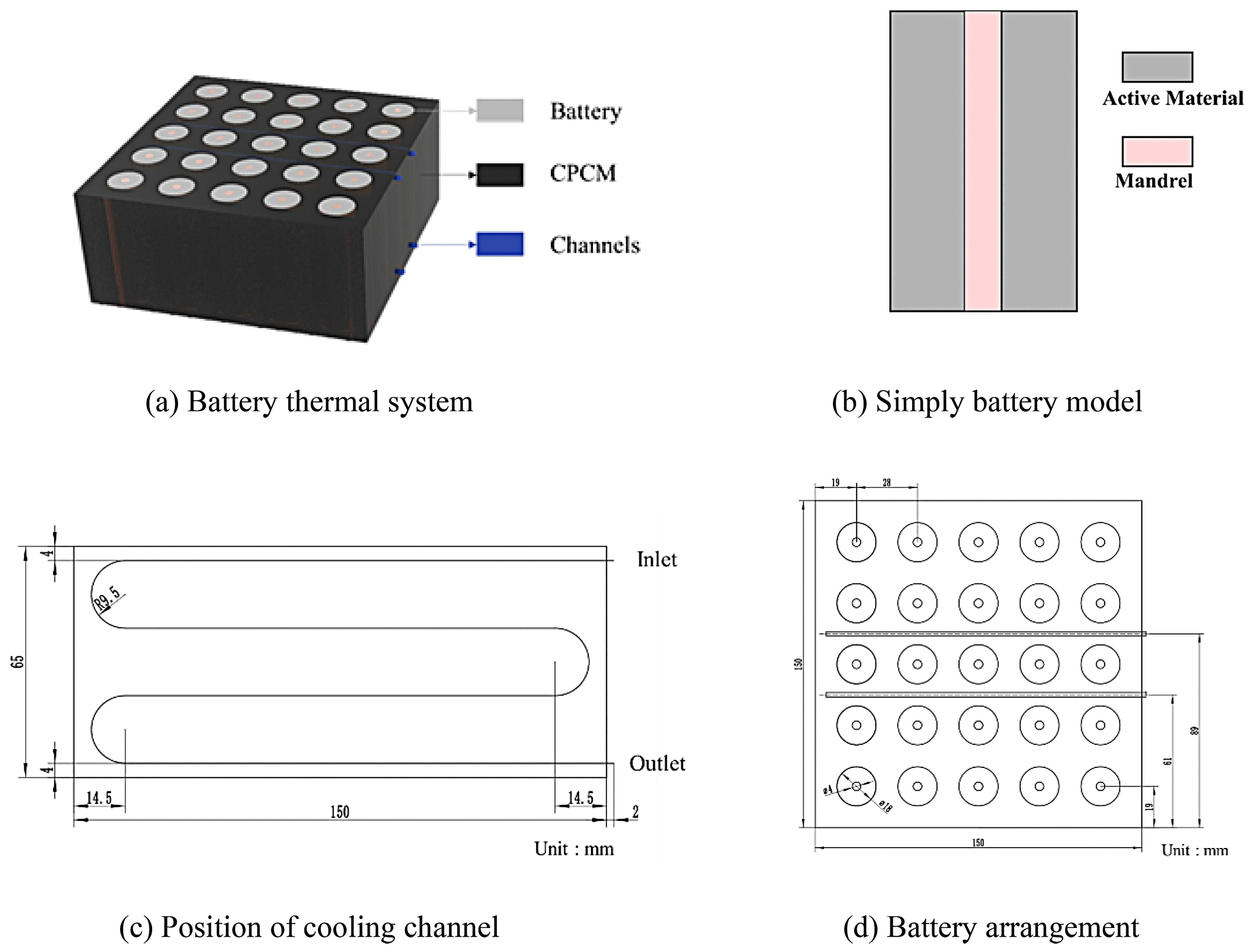

| Work | Input Parameters | Model |
|---|---|---|
| Arora et al. [65] | DOD, T, capacity, discharge rate | FNN |
| Cao et al. [66] | DOD, I, | FNN |
| Yalçın et al. [67] | I, V, T | CNN |
| Legala and Li [68] | I, V, Surface T, , DOD | FNN |
| Work | Cooling System Type | Input | Output |
|---|---|---|---|
| Mehmandoosti and Kowsary [125] | Pulsating liquid cooling | frequency and amplitude of pulsating flow | , |
| Yetik and Karakoc [126] | Air cooling | busbar material, C-rate, , , t | |
| Oyewola and Idowu [127] | Air cooling | Structural parameters, , | , , , |
| Li et al. [128] | Air cooling | Structural parameters, , | , |
| Khaboshan et al. [129] | PCM | Structural parameters | T |
| Jin and Xi [130] | Air cooling | Structural parameters, | , , |
| Zheng et al. [131] | Liquid cooling | Structural parameters | , , |
| Fini et al. [132] | PCM liquid flow | Re, volume fraction | Nu, |
| Ye et al. [133] | PCM and Liuqid Cooling | Structural parameters, | , , |
| Zhang et al. [134] | PCM and air cooling | Structural parameters, , C rate, | , |
| Li et al. [135] | PCM and immersion cooling | Property and configuration parameters | , |
| Guo et al. [136] | Micro heat pipe | Structural parameters | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, W.; Fang, W.; Tian, Y.; Dai, G.; Yan, T.; Yang, S.; Wang, P. Data-Driven Prediction of Li-Ion Battery Thermal Behavior: Advances and Applications in Thermal Management. Processes 2025, 13, 2769. https://doi.org/10.3390/pr13092769
Qian W, Fang W, Tian Y, Dai G, Yan T, Yang S, Wang P. Data-Driven Prediction of Li-Ion Battery Thermal Behavior: Advances and Applications in Thermal Management. Processes. 2025; 13(9):2769. https://doi.org/10.3390/pr13092769
Chicago/Turabian StyleQian, Weijia, Wenda Fang, Yongjun Tian, Guangwu Dai, Tao Yan, Siheng Yang, and Ping Wang. 2025. "Data-Driven Prediction of Li-Ion Battery Thermal Behavior: Advances and Applications in Thermal Management" Processes 13, no. 9: 2769. https://doi.org/10.3390/pr13092769
APA StyleQian, W., Fang, W., Tian, Y., Dai, G., Yan, T., Yang, S., & Wang, P. (2025). Data-Driven Prediction of Li-Ion Battery Thermal Behavior: Advances and Applications in Thermal Management. Processes, 13(9), 2769. https://doi.org/10.3390/pr13092769








