Fourier Transform-Based Inversion of Surface Deformation for Risk Assessment of Casing Damage: A Case Study of the Daqing Oilfield

Abstract

The intrinsic mechanism linking surface deformation to casing damage due to layer slippage remains unclear. Moreover, no method currently exists for calculating the slip deformation field of horizontal structural weakness planes from surface deformation. Therefore, we present a novel approach to infer formation pore pressure using surface deformation data based on Fourier transform and Wiener filtering. A forward modeling method is used to determine slippage along horizontal structural weakness planes, and a theoretical method is developed to derive slippage from observed surface deformation. We also apply a critical slippage threshold for casing damage to delineate risk zones via a maximum slip calculation model using data from the Daqing Oilfield in China. Our results reveal a strong correlation between casing damage occurrence and identified risk areas; within 6 months, 12 new casing damage wells appeared in high-risk areas, compared with 5 in low-risk zones. This method provides a scientific basis for the formulation of prevention schemes against shear casing damage in oilfields with weak horizontal structures.

1. Introduction

Shear-type casing damage has been a technical challenge in oilfield development and is particularly prominent in the Daqing Oilfield of China, accounting for approximately two-thirds of the total casing damage [1,2]. This type of damage is primarily concentrated in the bottom layer of the Nen-2 section, which is only 10 m thick and contains fossilized oil shale. Owing to its unique well-logging characteristics, this layer is referred to as the “standard layer”. The 2.5 m apparent resistivity logging curve exhibits six distinct peak values. The oil-bearing degree of the standard layer does not meet the development abundance criteria and is not exploited as an oil reservoir during the extraction process in the Daqing Oilfield. Located approximately 70 m above the oil reservoir, the standard layer exhibits stable planar distribution characteristics and a broad distribution range [3]. The standard layer is rich in fossil materials and displays low horizontal compressive strength characteristics [4]. During continuous extraction, the production layers, ranging from 100 to 300 m in thickness, experience uneven deformation owing to changes in pore pressure. This uneven deformation in the strata has a substantial impact on the standard layer; it induces fractures in the horizontal structural weakness planes of the standard layer and leads to the development of large-scale horizontal fracture surfaces and corresponding relative slippage, ultimately evolving into a characteristic form of shear-type casing damage. This type of casing damage exhibits a clear regional concentration at a planar scale and has resulted in the formation of over 30 large-scale high-incidence casing damage areas in the Daqing Oilfield. In some concentrated areas, the rate of casing damage can reach 70% [5]. Shear casing damage, caused by changes in the reservoir pressure, pose a serious threat to the safe and efficient development of the oilfield and have become a major obstacle to the full utilization of production capacity in the region [6].

Shear-type casing damage influenced by formation pore pressure has been reported in numerous oilfields; however, progress in understanding its underlying mechanisms remains limited. Dusseault et al. [7] considered the crack conditions of the structural weakness plane and proposed that overpressure injection could cause the upper part of the reservoir to form an upthrust deformation, could generate high pressure, and form a high-shear zone. They quantitatively analyzed the slip degree of the crack plane in the high-shear zone and proposed a mechanism of the shear casing damage of the structural weakness plane due to overall slip under the action of injection and production pressure. Liu et al. [8] conducted an 11-year survey on 3D geodetic deformation in the Naner Oilfield in Daqing, revealing correlations between subsurface pressure changes and surface elevation shifts during high-pressure production/injection. The researchers proposed a poroelastic-based mathematical model to quantify deformation patterns, providing theoretical guidance for casing preservation and waterflooding optimization in stressed reservoirs. They established a stress-prediction model validated using field data, to guide multilayer fracturing optimization. Liu et al. [9] established a semi-analytical model for calculating induced stress and slip along the fault caused by hydraulic fracture; the proposed method for calculating fault slippage was effective in field applications. Wang et al. [10] developed a fluid–solid coupling model for shear-induced casing damage in water-soaked standard layer shale, integrating rock mechanics theory and numerical experiments. Three-level orthogonal simulations for five influencing factors revealed critical strain thresholds via multiple regression analysis, enabling the prediction of casing strain and early warning systems for damage. Although a relatively stable theoretical framework for casing damage issues in the Daqing Oilfield has been established in recent years with fewer innovative breakthroughs, it is still not possible to control the forms of casing damage effectively, and effective means of monitoring and prevention are still lacking.

We have dedicated our research efforts toward understanding the mechanism of casing damage caused by shear forces in the Daqing Oilfield. Accordingly, in recent years, we have conducted theoretical and experimental research on the mechanism of casing damage in the standard layers of the Daqing Oilfield. A theoretical calculation model for the amount of formation slip was established by performing finite-element simulations of the correlation between the slip amount and casing damage [11]. Moreover, we developed an experimental method based on abnormal similarity theory to simulate formation slipping triggered by interregional pore-pressure differences. Our apparatus quantified slip conditions at varying pressure gradients and structural depths, revealing that slippage intensity correlates with oil layer burial depth and weak layers [12].

In the study of inferring subsurface parameters through surface state inversion, Brown et al. [13] introduced a one-dimensional compaction relation connecting pore pressure changes to surface deformation in confined aquifers, offering a computationally efficient method for groundwater models. By comparing modeled deformation with geodetic observations via InSAR, parameters are constrained, demonstrated through wastewater injection-induced uplift scenarios. Li et al. [14] analyzed the impact of factors influencing reservoir stability and sediment subsidence during long-term offshore gas hydrate gas production, with a thorough examination of the underlying mechanisms driving reservoir deformation and sediment subsidence. Li et al. [15] employed attenuated total reflectance Fourier-transform infrared spectroscopy to quantitatively assess the adsorption behavior of CO₂ thickeners onto kaolinite surfaces and complemented this with scanning electron microscopy for a comprehensive understanding of surface adsorption mechanisms.

The slippage of the structural weakness plane is the most critical parameter for determining whether the casing is damaged. However, current technological processes cannot directly acquire the slip conditions of the structural weakness plane [16,17]. The slippage of the structural weakness plane is fundamentally caused by the uneven deformation of the production layers induced by changes in the pore pressure within the layers. In addition to causing slippage of the upper horizontal structural weakness plane, production layer deformation results in surface deformation; both deformations share a homologous relationship.

Surface deformation can serve as the most direct parameter for predicting the deformation of standard layers in the Daqing Oilfield. Currently, surface deformation is measured using preset surface markers; however, the relationship between surface deformation and underground deformation is not one-to-one. To calculate the slippage of easily damaged layers (standard layers) using surface deformation, this study bridges the critical knowledge gap between surface deformation and casing damage mechanisms by establishing a quantitative link between surface monitoring data and subsurface structural responses. This study presents a method of obtaining formation pore pressure from surface deformation; the method is based on Fourier transform and Wiener filtering of deformation data. A forward modeling method is used to obtain the slippage of horizontal structural weakness plane in the formation. The accuracy of the inversion results under different grid sizes and measurement precision conditions is analyzed. A method for dividing the casing damage risk area is proposed according to the slip degree of the structural weakness plane, and the risk grades of high and low casing shear failure are determined. Both virtual test data and field data from the Daqing Oilfield are used as examples; the variation and distribution of formation pore pressure is calculated depending on the surface deformation measured by the surface stake in the target block, and the casing damage risk grade area is divided. The method described in this study can provide guidance on the steps needed to be taken to prevent and control shear casing damage due to formation slip.

2. Inversion Method of Average Reservoir Pore Pressure

The main factor influencing both standard layer slippage and surface deformation is the pore pressure within the oil-bearing formation. If the pore pressure can be accurately determined, the calculation of standard layer slippage and surface deformation becomes more straightforward. Stratum deformation can be modeled using a fluid–structure coupling finite-element method based on the interaction model between rock deformation and pore pressure proposed by Biot [18]. However, in practice, only surface deformation can be currently measured directly, whereas the distribution of pore pressure within the oil formation must be inferred using inversion. The fluid–structure coupling finite-element method can be used to calculate the stratum deformation field from a unit pressure change in each grid element. Considering that the deformation of stratum rocks during standard layer slippage remains within the linear elastic range [19], surface deformation can be estimated through convolution, as expressed in Equation (1).

w (x, y) = k_w (x, y) * p (x, y),

(1)

where the symbol “*” represents the convolution operation.

In Equation (1), k_w(x, y) denotes the distribution field of the surface vertical deformation caused by a grid change a unit pressure. The parameter field, as actually measured or computed, constitutes a plane composed of a finite data grid. When the number of grids is within a certain computational range, the two-dimensional discrete convolution equation can be represented as in Equation (2):

$$w(x,y)=k_{\mathrm{w}}(x,y)*p(x,y)={\displaystyle \sum _{i=0}^M{\displaystyle \sum _{j=0}^{N}k(i,j)p(x+i,y+j)}}$$

(2)

where the convolution kernel k_w(x, y) can be obtained from numerical simulations. Therefore, the surface’s vertical displacement induced by formation pore pressure can be calculated through forward modeling using an explicit formulation. Specifically, for any surface location, the vertical displacement w(x, y) can be determined directly without involving any unknowns during the solution process.

However, inverting the formation pore pressure p(x, y) from the surface vertical displacement w(x, y) is not straightforward. The vertical displacement at any given surface point results from the superposition of pore pressure contributions from multiple subsurface locations. The extent of this superposition is determined by the number of grid cells discretized by the convolution kernel. In the resulting linear system, the number of equations equals the total number of grids in the computational domain, and the coefficients of the unknowns are determined by the convolution kernel values. Given that the coefficients near the edges of the convolution kernel are close to zero, many coefficients in the linear system are also close to zero, which considerably affects the accuracy of the solution. Consequently, directly solving the linear system does not yield usable inversion results.

The Fourier convolution theorem can be used to resolve the problem of convolution. The expression of the Fourier convolution theorem is:

F[k_w (x, y) * p (x, y)] = K_w (u, v) ⋯ P(u, v),

(3)

where F is the Fourier operator. The Fourier transform of Equation (3) is [20]:

$$\mathrm{F}[a(x,y)]={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }a(x,y)e^{-i(ux-vy)}\mathrm{d}u\mathrm{d}v}}=A(u,v)$$

(4)

where a(x, y) denotes any function, A(u, v) is the Fourier transform of a(x, y), and i is the imaginary unit of the complex number. The function obtained via Fourier transform is a complex number. For two-dimensional discrete Fourier transform, the function may be described as follows:

$$\mathrm{F}[a(x,y)]={\displaystyle \sum _{x=0}^{N-1}{\displaystyle \sum _{y=0}^{M-1}a(x,y)e^{-i2\pi (\frac{ux}{N}-\frac{vy}{M})}}}=A(u,v)$$

(5)

Some errors were observed between the measured vertical deformation of the stratum at the marker-stake position and the actual value owing to the limited precision of the observation instrument; the actual value is given by Equation (6):

w′ (x, y) = k_w (x, y) * p (x, y) + n (x, y)

(6)

Fourier transform was applied on both sides simultaneously, as presented in Equation (7):

W′(u, v) = K_w (u, v) ⋯ P(u, v) + N (u, v),

(7)

where W′(u, v), K_w (u, v), and P(u, v) are the Fourier transforms of w′(x, y), k(x, y), and p(x, y), respectively; and N(u, v) is the measurement error in the Fourier function (m).

To prevent the division of the partial position by zero, the Wiener filtering method [21] (expressed by Equation (8)) was used to avoid a small divisor.

$$P(u,v)=W^{\prime }(u,v)\left({\displaystyle \frac{1}{K_{\mathrm{w}}(u,v)}}{\displaystyle \frac{|K_{\mathrm{w}}(u,v){|}^2}{|K_{\mathrm{w}}(u,v){|}^2+\mathrm{NSR}}}\right)$$

(8)

The pore-pressure distribution was obtained via inverse Fourier transform:

p (x, y) = F⁻¹[P (u, v)],

(9)

where F⁻¹ is the Fourier inverse function, and two-dimensional discrete grids are described by Equation (10) [22]:

$${\mathrm{F}}^{-1}[A(u,v)]={\displaystyle \frac{1}{NM}}{\displaystyle \sum }_{u=0}^{N-1}\sum _{v=0}^{M-1}A(u,v)e^{i2\pi ({\displaystyle \frac{ux}{N}}+{\displaystyle \frac{vy}{M}})}$$

(10)

Thus, we can obtain the inverted pore-pressure function (see Equation (11)):

$$p_{\mathrm{w}}(x,y)={\displaystyle \frac{1}{NM}}{\displaystyle \sum _{u=0}^{N-1}{\displaystyle \sum _{v=0}^{M-1}\left[W^{\prime }(u,v)\left(\frac{1}{K_{\mathrm{w}}(u,v)}\frac{|K_{\mathrm{w}}(u,v){|}^2}{|K_{\mathrm{w}}(u,v){|}^2+\mathrm{NSR}}\right)e^{i2\pi (\frac{ux}{N}+\frac{vy}{M})}\right]}}$$

(11)

In addition to vertical deformation, the oil-formation pore-pressure also causes horizontal deformation, observable at the surface. Using the same method, the oil formation pore pressure can be inverted by the surface displacement u in the x direction and v in the y direction. The calculation equations are:

$$\begin{array}{l}{p}_u(x,y)={\displaystyle \frac{1}{NM}}{\displaystyle \sum _{u=0}^{N-1}{\displaystyle \sum _{v=0}^{M-1}\left[U^{\prime }(u,v)\left(\frac{1}{K_u(u,v)}\frac{|K_u(u,v){|}^2}{|K_u(u,v){|}^2+\mathrm{NSR}}\right)e^{i2\pi (\frac{ux}{N}+\frac{vy}{M})}\right]}}\\ p_v(x,y)={\displaystyle \frac{1}{NM}}{\displaystyle \sum _{u=0}^{N-1}{\displaystyle \sum _{v=0}^{M-1}\left[V^{\prime }(u,v)\left(\frac{1}{K_v(u,v)}\frac{|K_v(u,v){|}^2}{|K_v(u,v){|}^2+\mathrm{NSR}}\right)e^{i2\pi (\frac{ux}{N}+\frac{vy}{M})}\right]}}\end{array}$$

(12)

Three reservoir pore-pressure fields were obtained using the surface vertical and horizontal displacements, where the two horizontal directions had equal weights. The reservoir pore pressure (inverted from surface horizontal displacement) was averaged with the inverted pressure from the surface vertical displacement, resulting in the final inversion result of reservoir pore pressure, as indicated by Equation (13):

$$p(x,y)={\displaystyle \frac{1}{2}}{p}_{\mathrm{w}}(x,y)+{\displaystyle \frac{1}{4}}{p}_{\mathrm{u}}(x,y)+{\displaystyle \frac{1}{4}}{p}_{\mathrm{v}}(x,y)$$

(13)

3. Calculation Model of Structural Weakness Plane Slippage

After the change of formation pore pressure, surface deformation was generated, and a slip was formed at the position of the horizontal structural weakness plane. However, the slip was a relative displacement with directivity and cannot be calculated directly by stacking. The slip amount has direction, and slip amounts in the same direction can be superimposed. Therefore, the slip amount on the structural weakness plane can be divided into components in two mutually perpendicular directions. After superimposing the slip quantity in the same direction at each point, the final slip amount can be obtained by adding vectors, as expressed by Equations (14)–(16):

s_x(x, y) = k_sx(x, y) * p (x, y),

(14)

s_y(x, y) = k_sy(x, y) * p (x, y),

(15)

$$s(x,y)=\sqrt{s_x(x,y)+s_y(x,y)}$$

(16)

where k_sx(x, y) and k_sy(x, y) respectively denote grid changes the distribution of X- and Y-direction slippages on the crack surface caused by unit pressure; k_sx(x, y) and k_sy(x, y) can be calculated as:

s_x(x, y) = cos[arg(x + iy)] k_s (x, y),

(17)

s_y(x, y) = sin[arg(x + iy)] k_s (x, y),

(18)

where arg(z) denotes the argument of the complex number z = x + iy at the point (x, y).

A geological model can be established for the calculation of k_s(x, y) in the corresponding relationship between formation pressure and crack surface slip. First, the finite-element method was used to calculate the formation slip after the change in formation pressure difference among inter-regions. The classification standard of casing damage risk area is determined by calculating the maximum slip amount and the limit of shear casing damage.

The COMSOL Multiphysics 6.1 finite-element software was used to establish a geomechanical model of a rectangular prism with dimensions of 10,000 (length) × 10,000 (width) × 3000 m (height) to calculate the surface-deformation caused by unit grid pressure difference and slip of cracked surface. The reservoir thickness was calculated as the total thickness of the vertical sandstone of the reservoir, which was 300 m. To analyze the interplay between fluid flow and rock mechanics, the Porous Media (Poro Model in COMSOL) module was employed. This module allows for the coupling of Darcy dynamics with elastic deformation under reservoir conditions. As the calculation involves the deformation of the strata caused by changes in pore pressure, and the deformation and stress levels are within the scope of elastic mechanics [23], a linear elastic model was adopted. Except for the surface, which was treated with a normal displacement of zero, the boundary effect was minimal owing to the sufficiently large lateral length. The standard layer positions were set with conditions of continuous vertical displacement and discontinuous lateral displacement. For the layers of the reservoir, standard layer, and surface, square grid planes of 12.5 m, 50 m, 150 m, 300 m, or 900 m were used for the output of results. Other parameters are listed in

Table 1. Conditions and mechanical parameters of formation used in mechanical models.

Parameters		Value	Unit
Model	Thickness	3000	m
	Length	6000	m
	Unit pressure difference	1.0	MPa
	Side length of per unit grid	150	m
Reservoir	Top depth	800	m
	Thickness	300	m
	Biot coefficient	0.95	1
	Elastic modulus	15	GPa
	Poisson’s ratio	0.2	1
Rock at reservoir’s top part	Elastic modulus	8	GPa
	Poisson’s ratio	0.2	1
Rock at reservoir’s bottom part	Elastic modulus	25	GPa
	Poisson’s ratio	0.2	1

.

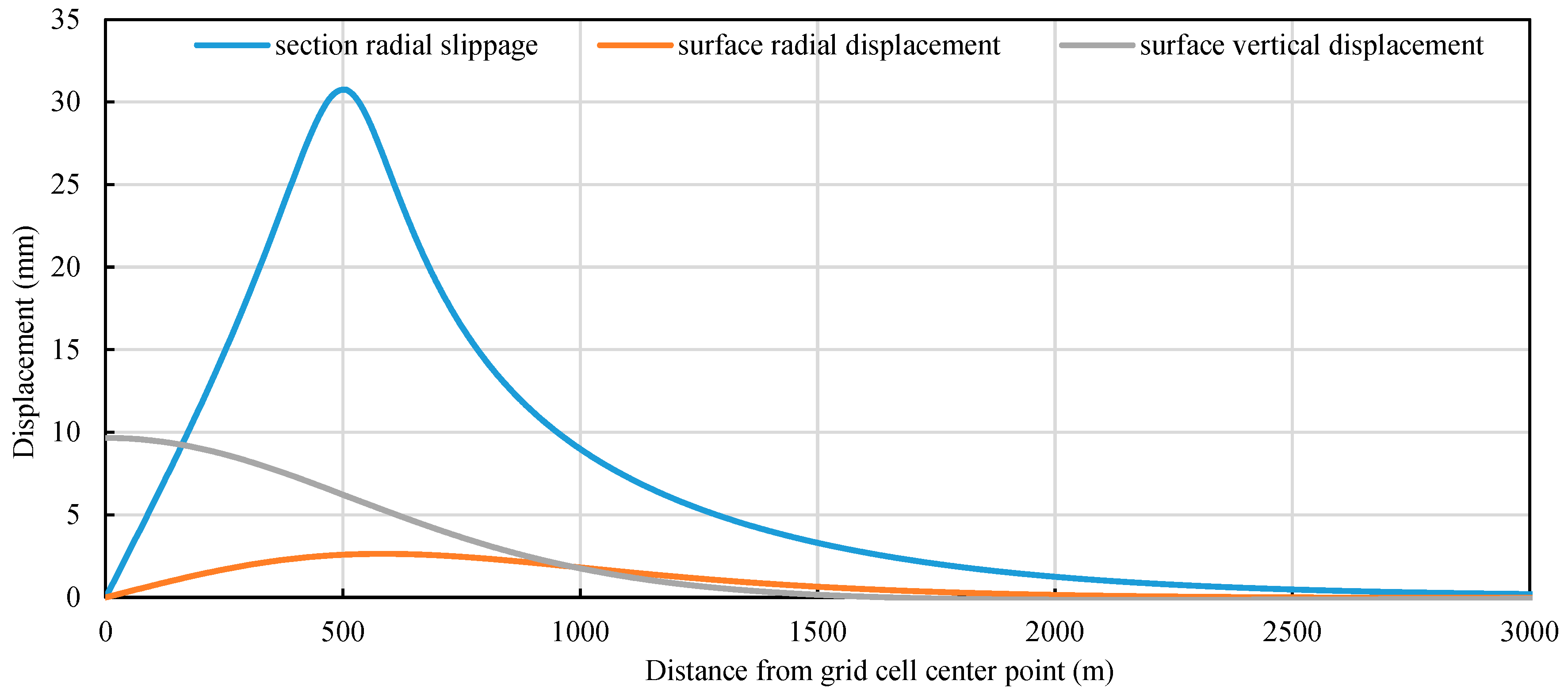
Using a 900 × 900 m grid as an example, the finite-element method was employed to calculate the surface displacement distribution and sectional slip caused by the pressure difference within the unit grid, which is used to get the convolutional kernels in Equations (11), (12), (14) and (15), as illustrated in Figure 1.

The surface deformation per unit pressure can be used as the convolution kernel for the inversion calculation of formation pore pressure. The convolution kernels after dispersion can be obtained from the two-dimensional discrete results of the radial slippage and surface radial displacement curves in Figure 1. The crack surface slippage curve can be used to delineate the risk level. When the pore pressure of the 900 × 900 m² grid is 1 MPa, a maximum crack slippage of 30.75 mm is generated in this target block. From the finite-element results, we can obtain k_w(x, y), k_u(x, y), k_v(x, y), k_sx(x, y), and k_sy(x, y).

To verify the theoretical effectiveness of this method, a simulation was conducted based on the assumption of unstable seepage of weakly compressible fluids, and the two-dimensional Laplace equation was used to simulate the average formation pressure based on the explicit difference method. The average formation pressure of 450 injection–production wells in a 4500 × 4500 m² area was simulated under random pressure conditions (to avoid the influence of boundary effects, the actual range involved in subsequent calculations was expanded to 6300 × 6300 m²). 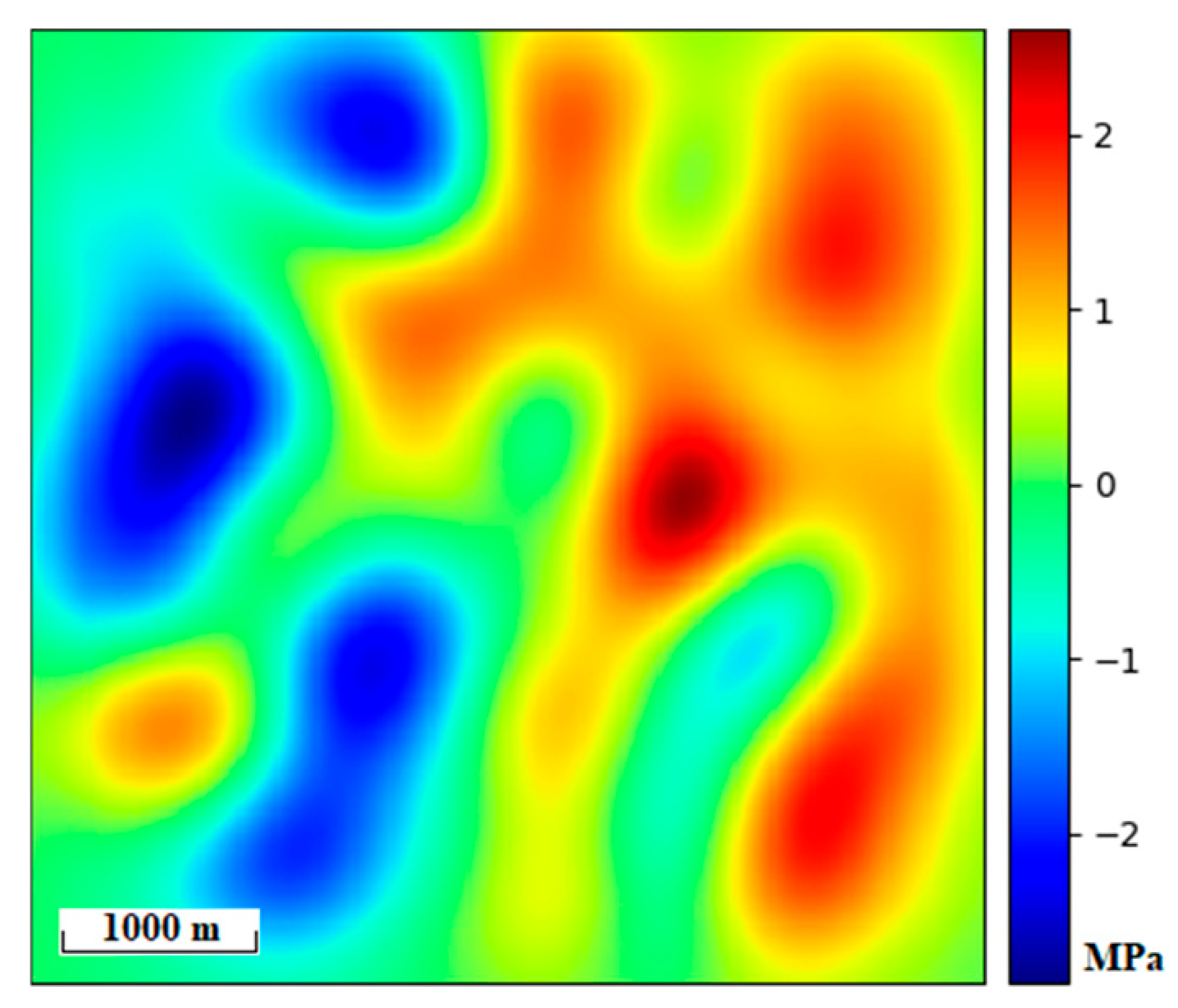To highlight the actual average formation pressure difference characteristics in the casing damage area, the average injection–production pressure in the western half was set at 1 MPa lower than that in the eastern half (the average formation pressure difference value between areas (>1 MPa) is the external cause of standard layer casing damage [5]). The grid size used in the simulation was a square unit with a side length of 12.5 m. The formation pressure distribution is shown in Figure 2.

Figure 2 illustrates the pore pressure of the oil reservoir represented as a difference value to the original formation pressure. The vertical surface deformation under the formation pressure state was calculated based on Equation (2), and a similar approach was employed to compute the horizontal surface deformation. The results are presented in Figure 3.

In practical applications, calculations are performed using different grid sizes, such as 50 m, 150 m, 300 m, and 900 m, considering the level of density and precision constraints in surface deformation measurements. The maximum grid sizes selected for this calculation is 900 m. Since the pressure field, displacement field, and convolution kernel all require an equal grid size during the calculation process, an excessively large grid size can lead to excessive deviation in the position of the maximum value on the convolution kernel, causing significant errors. To address measurement precision issues, the calculated surface deformation parameters were truncated and coarsened according to a gradient settings of ±0.1 mm, ±1 mm, ±2 mm, ±4 mm, ±6 mm, and ±10 mm. Utilizing the processed surface deformation field, the pore pressure of the underground oil reservoir was inverted using Equations (6) and (7), and the inversion accuracy was evaluated by comparing the results with the simulated formation pressure results. Based on the numerical characteristics of formation pressure, the difference between the maximum and minimum values within the block was adopted as the basis for measuring calculation accuracy, as expressed by Equation (19).

$$A=100\%-{\displaystyle \frac{1}{M_{\mathrm{p}}{N}_{\mathrm{p}}}}{\displaystyle \sum \frac{|p(i,j)-p^{\prime }(i,j)|}{p_{\max }-p_{\min }}},$$

(19)

where A(x, y) is calculation accuracy, M_p and N_p are the number of horizontal and vertical grids of pressure field, respectively, p(i, j) and p′(i, j) are calculation pressure and true pressure of oil formation, respectively, and p_max and p_min are the maximum and minimum pressure, respectively.

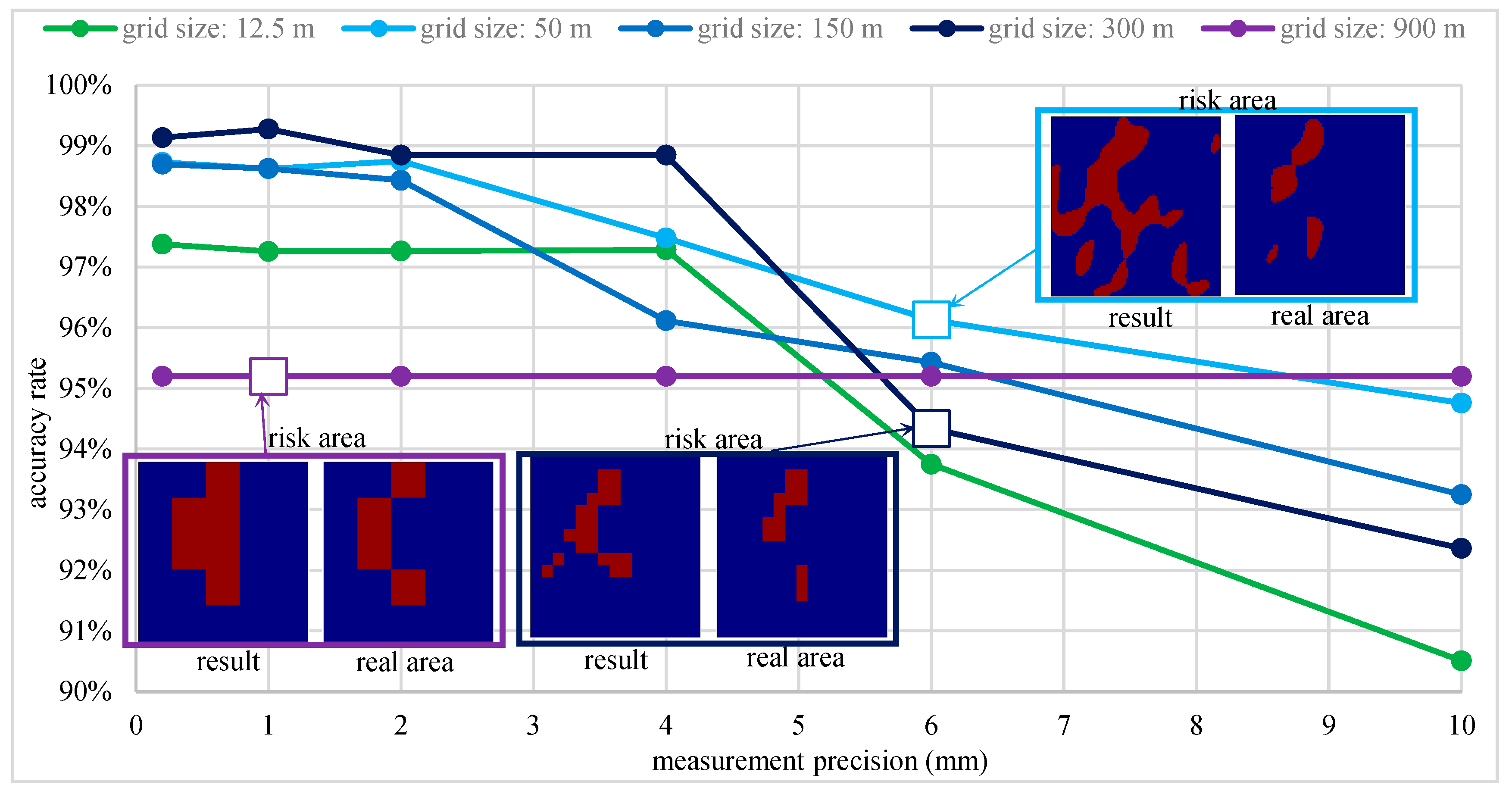
Different measurement precisions can lead to varying errors in the measurement results of surface deformation, which can be regarded as noise in the calculations of Equation (12). The value of NSR in the calculation process can be determined by the ratio of measurement precision to the range of measured values. Since the inversion process needs to overcome the situation where many regions of the convolution kernel are close to 0, the NSR value is generally set to 0.1 when using micro-nano filtering. In this study, when the ratio of measurement precision to the range of measured values is less than 0.1, the NSR value is set to 0.1. Under the combined conditions of grid sizes ranging from 12.5 m to 900 m and measurement precisions from ±0.1 mm to ±10 mm, the average accuracy of the inversion for formation pore pressure is illustrated in Figure 4.

The abscissa in Figure 4 illustrates the impact of different ground surface measurement precision on the displacement identification effect. When the measurement precision gradually increased from 0.1 mm to 10 mm, the identification precision of ground surface displacement tended to decrease. The image at the bottom of the x-axis in Figure 4 visually presents the evolution characteristics of measurement results during this accuracy variation process: when the measurement precision reached 10 mm, the identification results of all the grid measurement points could only distinguish among six measurement outcomes. Each curve in Figure 4 corresponds to the inversion accuracy under different grid sizes (requiring a certain number of surface marker stakes). When the grid size was 12.5 m, at least 129,600 stakes were required to cover an area of 4500 × 4500 m; whereas, when the grid was expanded to 900 m, only 25 marker stakes were needed, but this resulted in a considerable decrease in the clarity of the deformation field measurement. Each point on the curve represents the accuracy of the inverted formation pore pressure based on the surface deformation measured under different grid sizes and measurement precisions.

The computational results indicate that measurement precision has the greatest impact on inversion accuracy. When precision decreased from ±6 mm to ±10 mm, the calculation error increased by 66.65%. Notably, the inversion performance of the 12.5 m fine grid was inferior to that of the 50–300 m large grid, which is attributed to Wiener filtering errors caused by the excessively large size of the inversion convolution kernel. However, even with a 900 m large grid and a measurement precision of ±10 mm, the inversion accuracy still reached 92.04%, thereby confirming the robustness and effectiveness of the proposed method.

Wiener filtering is not the sole approach for inversion, with common foundational inversion methods including solving linear equations and applying the least squares method to overdetermined equations. However, these methods are not applicable in inversion calculations involving convolution kernels with a significant number of grid points approaching zero, resulting in poor inversion results with low robustness and values exceeding physical plausibility under error influences. This study involves a high noise-to-signal ratio, rendering conventional linear equation methods impractical.

Regarding the prediction of the standard layer slip, the accuracy of slip under different grid sizes and measurement precisions was ascertained based on the inversion results of stratum pressure and in conjunction with Equations (14)–(16). The results are presented in Figure 5.

Similar to the results of stratigraphic pressure inversion, the measurement precision has a major impact on the accuracy of predictions. Notably, even with a large grid size of 900 m and a precision of ±10 mm for surface deformation inversion, the prediction accuracy for standard layer slip can still reach 89.03%.

The core objective of this study was to predict the risk areas of casing damage in standard layers. In the standard layers of the Daqing Oilfield, voids are typically reserved without cementing, with a void length of approximately 20 mm. After shear deformation, the formation undergoes compression deformation but does not immediately fail. When the slip exceeds 20 mm, the casing will be affected by the shear deformation of the formation; when the slip exceeds 30 mm, it is typically considered the threshold value affecting production operations [24,25]. Therefore, in high-risk areas of casing damage in the Daqing Oilfield, the slip should be greater than 30 mm, while in low-risk areas, it should be less than 30 mm. The accuracy rates under various conditions, based on the criteria for casing damage risk assessment, are shown in Figure 6.

To reflect the engineering application value of the casing damage risk zone identification results, this study adopted the average of the identification accuracy rates for high- and low-risk zones as the overall identification accuracy indicator. Otherwise, if a model classifies all areas as low-risk casing damage zones, it may achieve a high level of computational accuracy; however, this model lacks practical application value. The calculation results indicate that both grid size and measurement precision have an impact on the delineation of casing damage risk areas. The grid size depends on the number of ground measurement marker stakes. A larger grid size provides fewer data points during the inversion process, which affects the accuracy of the model inversion. Similarly, the measurement precision of surface deformation also increases the noise-to-signal ratio of the measurement results, thereby affecting the inversion effect. When the measurement precision is controlled to values within ±4 mm, the accuracy of the prediction results fluctuates minimally. When the measurement precision is improved to ±4 mm, the identification accuracy rate for casing damage zones can exceed 95%, validating the engineering effectiveness of this method. The prediction results for a large grid size of 900 m do not fluctuate with changes in measurement accuracy. The fundamental reason for this is that the identification results for casing damage zones in all 25 grid units are identical for data with different accuracies.

The aforementioned research conclusions are based on numerical simulation data. Given the consistency between the actual formation pressure field and the simulated data in terms of pressure distribution characteristics and gradient variations, the results are derived from the simulated data. The characteristics of the actual formation pressure data align with those of the simulated data, and the indicators from the simulated data are more comprehensive, enabling a deeper understanding of the theoretical feasibility of this method.

4. Oilfield Test

The X block in the Sazhong Development Area of the Daqing Oilfield exhibits extensive casing damage in the standard layer, remaining in an unstable state for a long time. In this block, 2523 oil and water wells covered three series of development well groups. The block area was 19.28 km². The top depth of the oil layer was approximately 800 m, and the bottom depth was approximately 1250 m. The total effective thickness of the oil layer was approximately 300 m.

Currently, the X block uses ground survey piles to monitor surface deformation and guide the prevention and control of casing damage in the standard layer. The displacement measurement marker piles were constructed from composite steel plates, embedded 4 m into the ground, and exposed above the ground by 1.5 m, effectively shielding deformation of the shallow soil layer. During measurements, precise leveling instruments were used to measure the height difference and angular changes between adjacent marker piles, thereby determining the ground deformation over a specific period.

For the precision construction monitoring of the B-class network, four plane reference points were selected around the X block. Among them, two were installed on the roof of the stable area, which was marked as the monitoring pier inlaid with a forced alignment device. The other two were installed on the concrete-cast underground valve maintenance roof, marked by a direct inlaid forced aligning device. A Dini03 precision electronic level (Trimble company, Westminster, CO, USA) was used for leveling, with a round-trip measurement standard deviation of ±0.3 mm/km. The average side length of the benchmark frame network was 11.2 km. The monitoring network was measured according to the precision of a C-class network. The monitoring points were the monitoring piles constructed in the Daqing Oilfield in March 2017. Twenty-seven monitoring piles were used, and the spacing of the posts ranged between 700 m and 1000 m; the posts were evenly distributed in the monitoring area, and the area covered by the ground marker stakes was 16.2 km².

Between June and November 2023, the displacement of the marker stakes was measured. Surface displacement, measured twice, was the surface deformation at the marker-stake locations. The starting points of the elevation survey were first-class leveling points “H149-1” and “H153”, which were 1.5 km and 2.6 km away from the target area, respectively. The two tests in June and November 2023 were performed by leveling first, and the total length of the route was 5.25 km. The height difference between the two points was 1.42 mm, and the difference between the two points was 0.27 mm/km. Using H149-1 as the starting point, the leveling route was observed in a round trip according to the network that comprised three base points. Finally, the 27 monitoring points comprised 9 closed loops, and the leveling routes were observed repeatedly to obtain the location difference of each route; 2 leveling surveys were completed. The location and monitoring results of 27 monitoring points are shown in Figure 7.

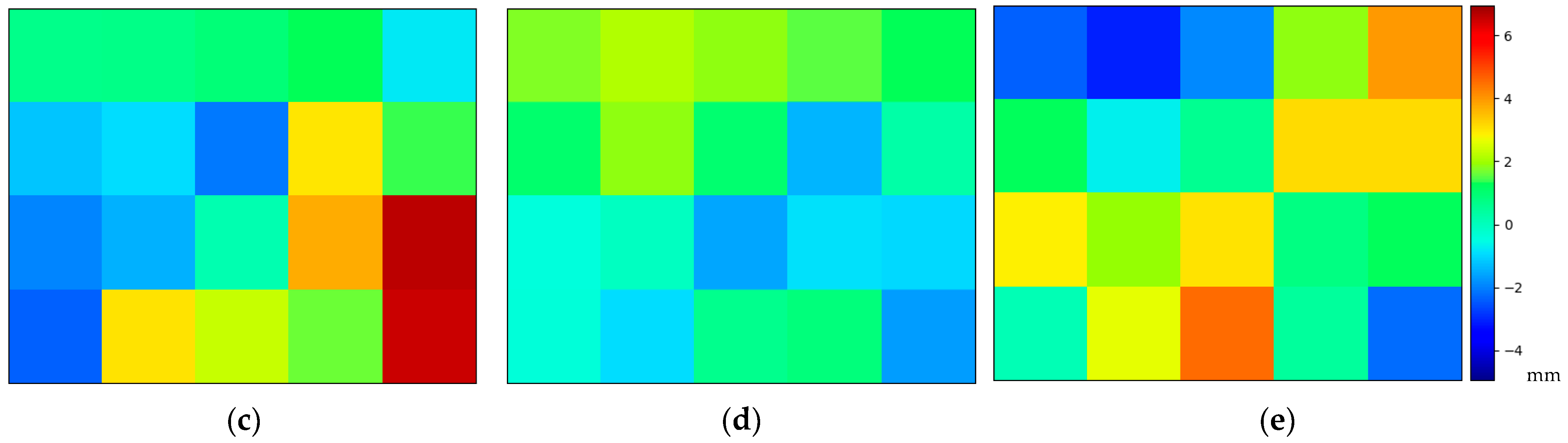
We established 27 marker-stake position points in the central and eastern regions of the X block and generated a surface displacement field distribution map based on the cubic spline interpolation method for ease of presentation (The calculation area is marked in red frames shown in Figure 7a,b). All interpolation results were not involved in the calculation. The reliability of the interpolation results for small-scale grids is relatively low owing to the insufficient density of the measured points. Therefore, the surface deformation field obtained from the 27 marker-stake points underwent a spatial scale coarsening process, utilizing a grid division of 900 × 900 m, resulting in 4 × 5 grid cells, as shown in Figure 7c–e.

Using the vertical displacement as an example in the inversion process, W(u, v) was obtained through Fourier transform, as expressed by Equation (5). Given that W(u, v) is a complex number, displaying only the real part or the virtual component results in disordered patterns without clear physical meaning. Therefore, analyzing the spectrum figure |G(u, v)| and phase figure ϕ(u, v) was necessary, as expressed by Equations (20) and (21):

$$\left|G(u,v)\right|=\sqrt{R^2(u,v)+I^2(u,v)},$$

(20)

$$\varphi (u,v)=\arctan {\displaystyle \frac{I(u,v)}{R(u,v)}}$$

(21)

where R(u, v) and I(u, v) are the real and imaginary parts of the surface’s vertical displacement after inversion, respectively, and W′(u, v) = R(u, v) + i I(u, v).

Owing to the large dynamic range of spectral values, the spectrum is typically displayed by adding one to each value to facilitate visualization. The resulting image is commonly referred to as a spectral diagram (Equation (22)):

Y(u, v) = ln[|G(u, v)| + 1]

(22)

The frequency spectrum and phase diagrams of the vertical deformation of the Earth’s surface are shown in Figure 8.

The energy spectrum and phase diagrams of the formation pore pressure distribution were obtained (as shown in Figure 9) by applying the Wiener filter in Equation (8) to divide the vertical displacement W′(u, v) by the convolution kernel K_w(u, v).

In the same way, the formation pore pressure inversed by surface horizontal displacement was calculated. The slippage of the structural weakness plane in the X- and Y-directions was calculated using Equations (14) and (15), respectively, and the maximum slippage of the target block was calculated using Equation (16) to obtain the maximum slippage of each grid, as shown in Figure 10.

The risk classification of the sliding displacement in the oil and water wells of the Daqing Oilfield revealed that within the measurement interval, the maximum sliding displacement in three grid blocks exceeded the safety threshold of 30 mm stander layer slippage for casing damage, reaching a high-risk level. When validating this casing-damage risk-classification method, the 6-month interval between the occurrence and detection of casing damage in the oilfield was considered. The standard layer casing damage conditions discovered within the measurement interval and within 6 months after the second surface deformation measurement were statistically analyzed, as shown in Figure 11.

During the observation period, 1446 non-casing damage wells were continuously active and showed no abnormalities, and 17 wells exhibited standard layer shear casing damage. Twelve new standard casing damage wells were identified in three high-risk areas (with 192 non-casing damage wells), and five new casing damage wells were discovered in 17 low-risk areas (with 1254 non-casing damage wells). This study effectively identified the spatiotemporal distribution characteristics of standard casing damage by establishing a risk classification system, providing technical support for subsequent investigation and prevention strategies for casing damage hazards.

This study has some limitations. Owing to the limited number of surface measurement points and the fact that experiments were only conducted in a small number of blocks, verifying the accuracy of standard layer slip inversion using measured data requires long-term and multiblock measurement support. In the future, remote sensing technologies (such as InSAR) can be employed to enhance the measurement of surface deformation; combined with the collection of more data from surface marker stakes, a more reliable method can be formed. In addition, the convolution kernels involved in this model were derived from the stratigraphic conditions of the measured area. For different areas of the Daqing Oilfield or other oilfields, the convolution kernels need to be calculated based on the actual situation.

5. Conclusions

In this study, we devised a new inversion method to determine changes in formation pore pressure. Based on the vertical deformation monitoring data of the surface, the Wiener filter method was used for deconvolution calculations in the frequency domain after Fourier transformation to obtain the change in the formation pore pressure.

Surface deformation measurements can effectively reflect the slippage of the standard layer in the Daqing Oilfield. When the measurement density of surface deformation was 900 m × 900 m per measurement point, and the measurement precision was within ±10 mm, the accuracy rate of the inverted slippage of the standard layer in the Daqing Oilfield exceeded 89.03%.

The Daqing Oilfield in China was used as a case study to demonstrate that applying Fourier transform in frequency-domain deconvolution provides strong performance in identifying areas of standard layer slip risk. The adopted risk-level classification method was effective in identifying high-incidence areas of casing damage.

The method employed in this study exhibits certain limitations, as it relies on the support of the number of marker stakes and measurement precision. Furthermore, for different oil fields, or even different blocks, it is necessary to recalculate several convolutional kernels in the model based on actual conditions, and also to revise them in conjunction with actual data.