Energy Management for Integrated Energy System Based on Coordinated Optimization of Electric–Thermal Multi-Energy Retention and Reinforcement Learning
Abstract
1. Introduction
2. Energy Management Framework and User Preference Model
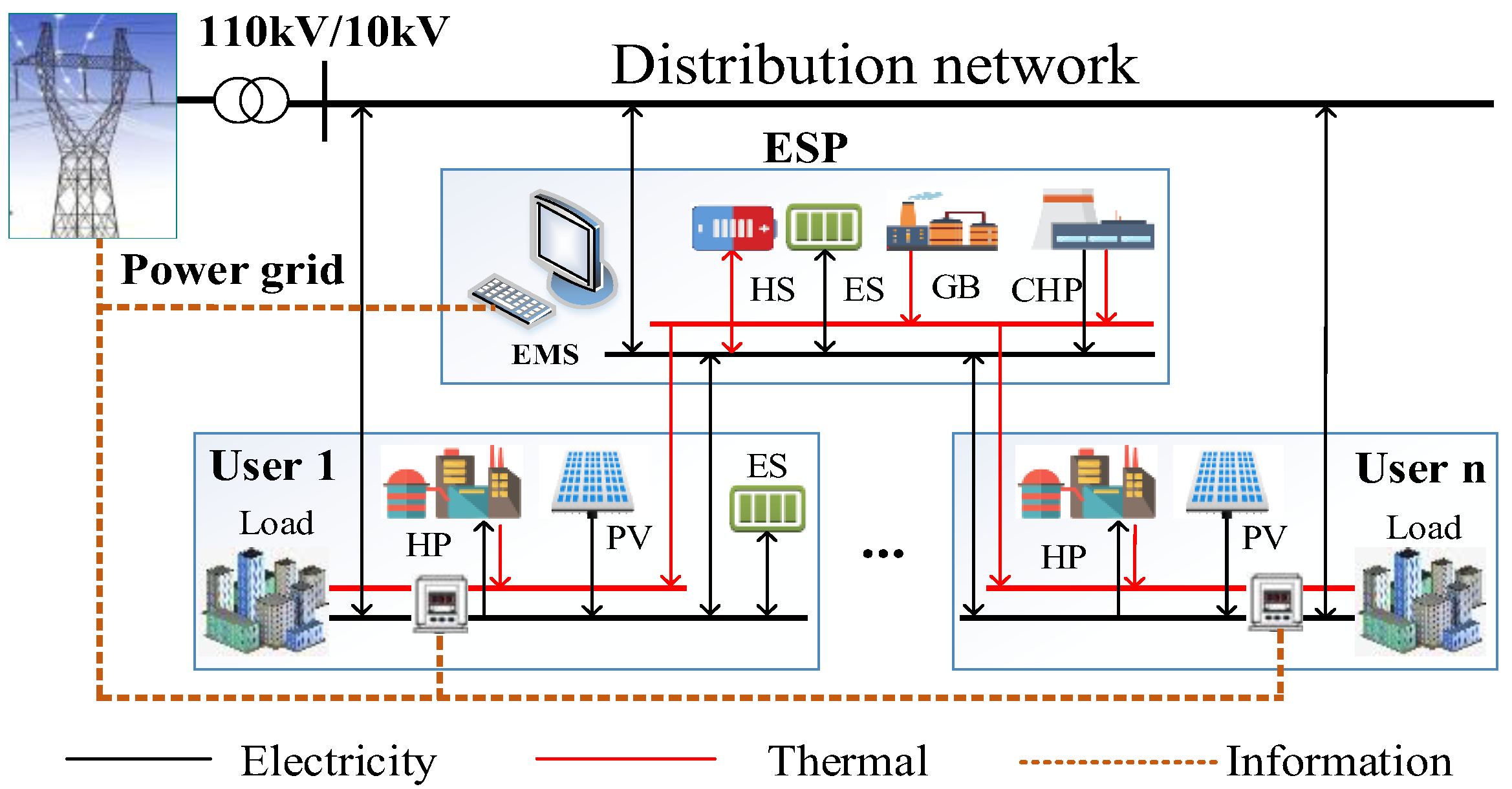
2.1. Energy Management Framework
2.2. User Energy Preference Model
2.2.1. Electricity Energy Preference Model
2.2.2. Thermal Energy Preference Model
3. ESP and User Benefit Model
3.1. ESP Benefit Model
3.2. User Benefit Model
4. Energy Management Model Based on Reinforcement Learning
4.1. Energy Management Model
4.1.1. Action Space Model
4.1.2. State Space Model
4.1.3. Reward Function Model
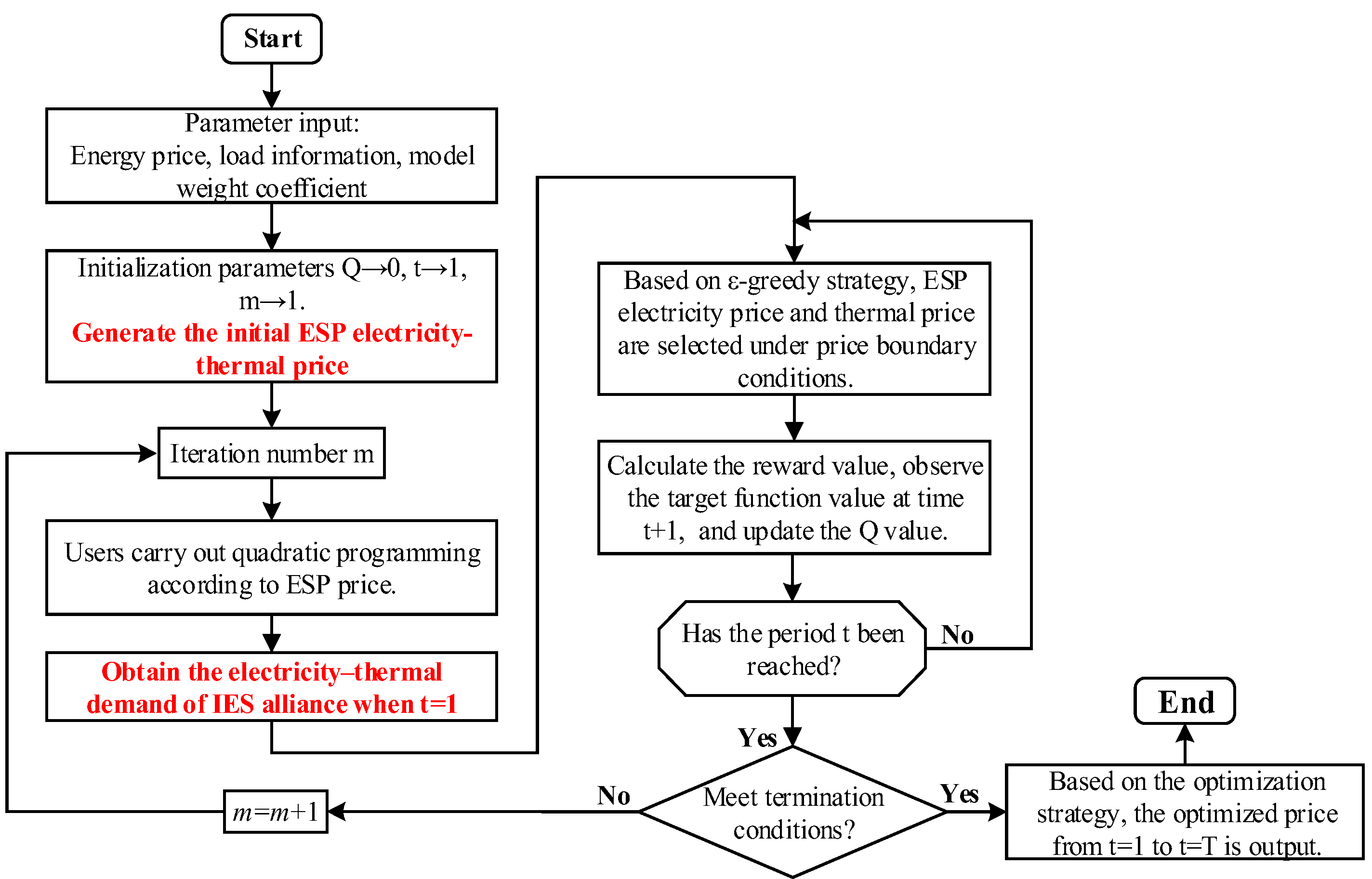
4.2. Model Solving Method Based on Q-Learning–QP
5. Case Study
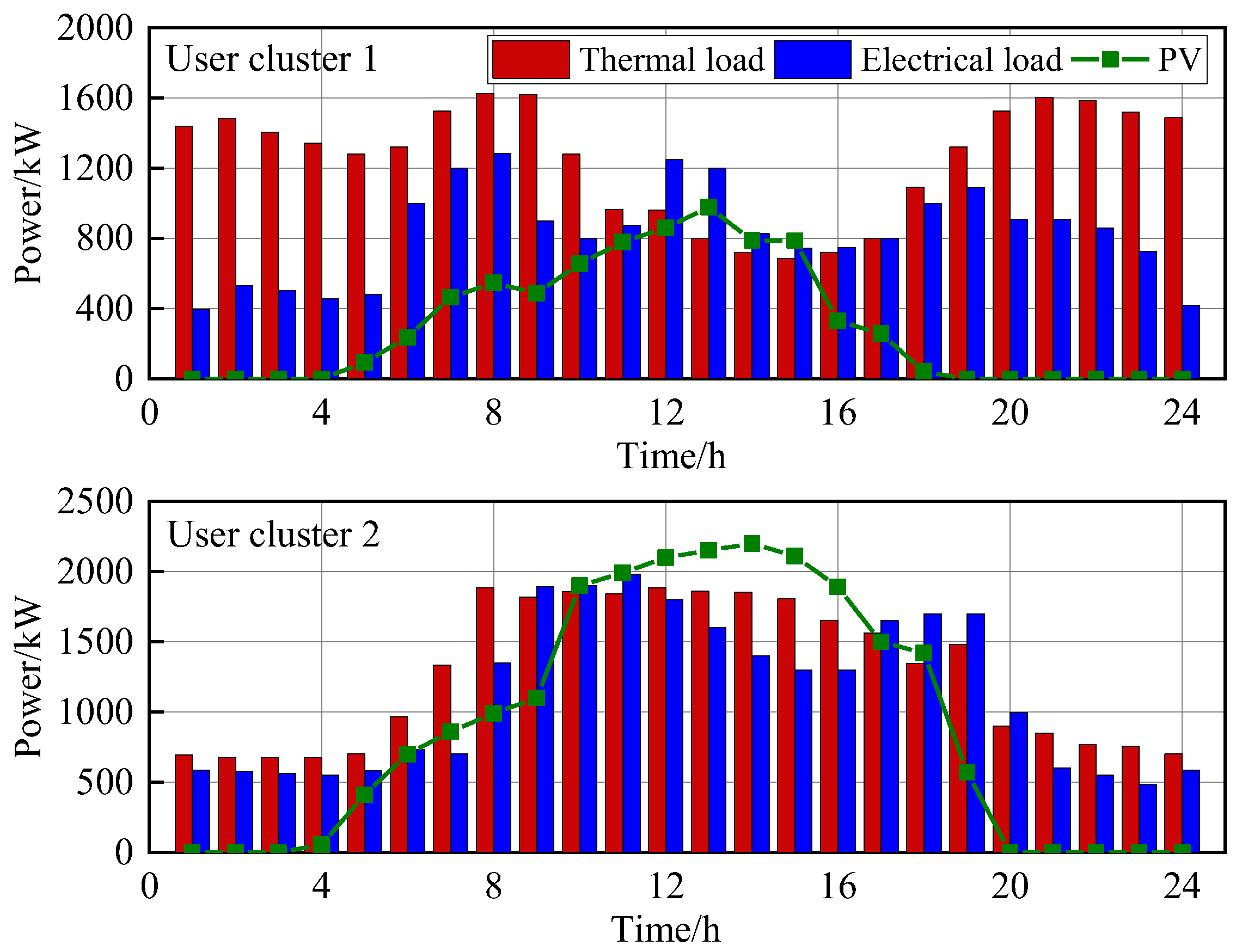
5.1. Basic Data
5.2. Simulation Results
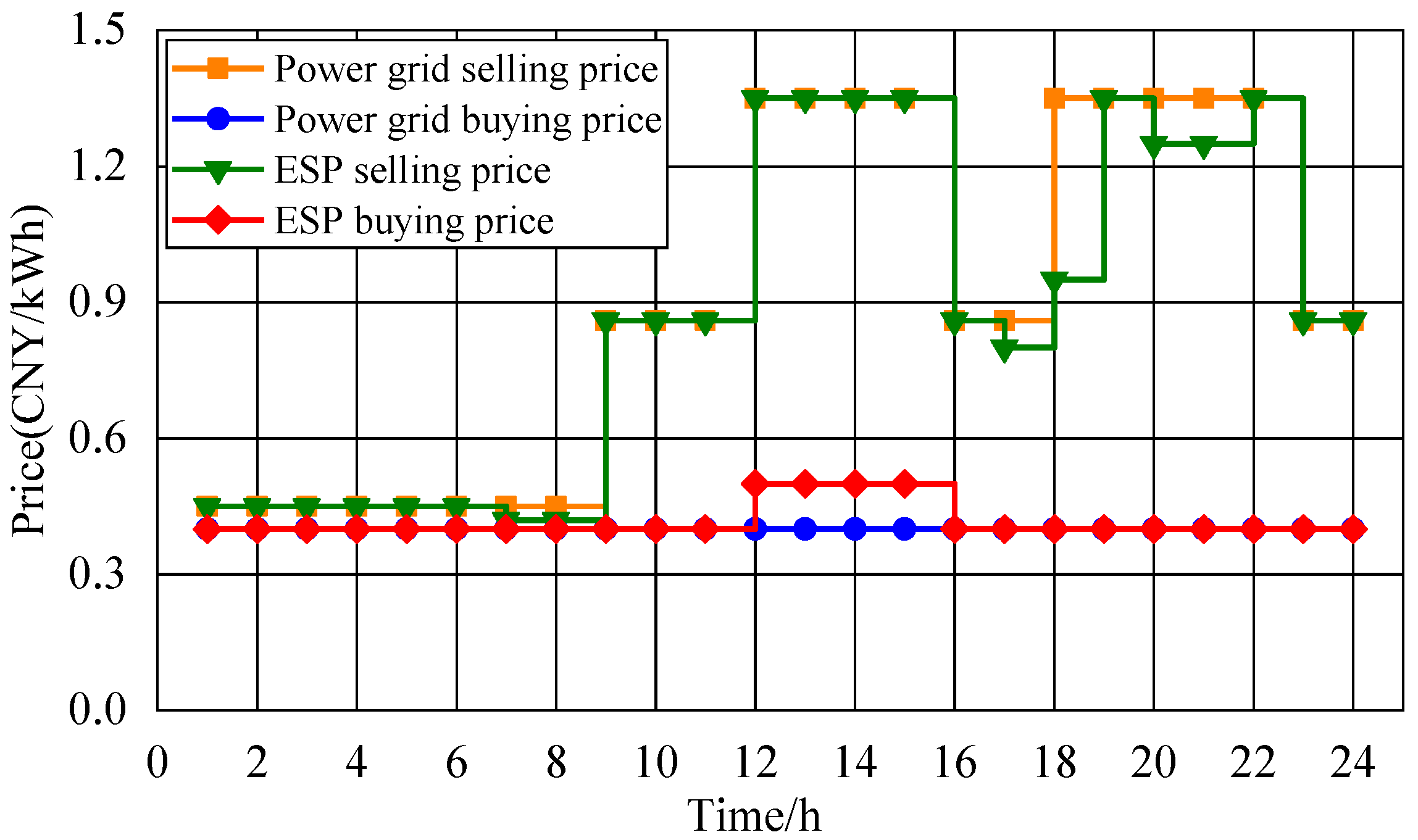
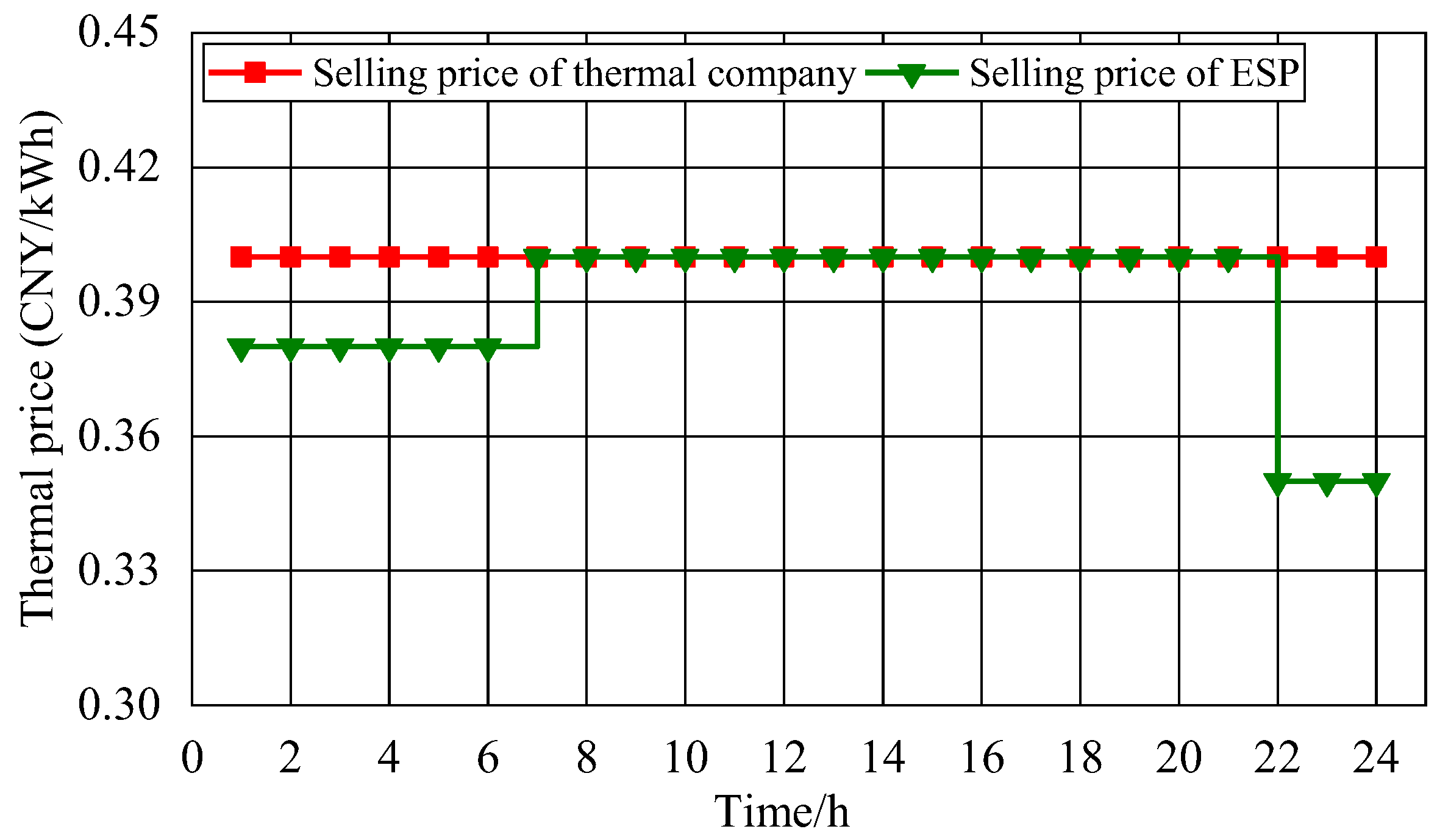
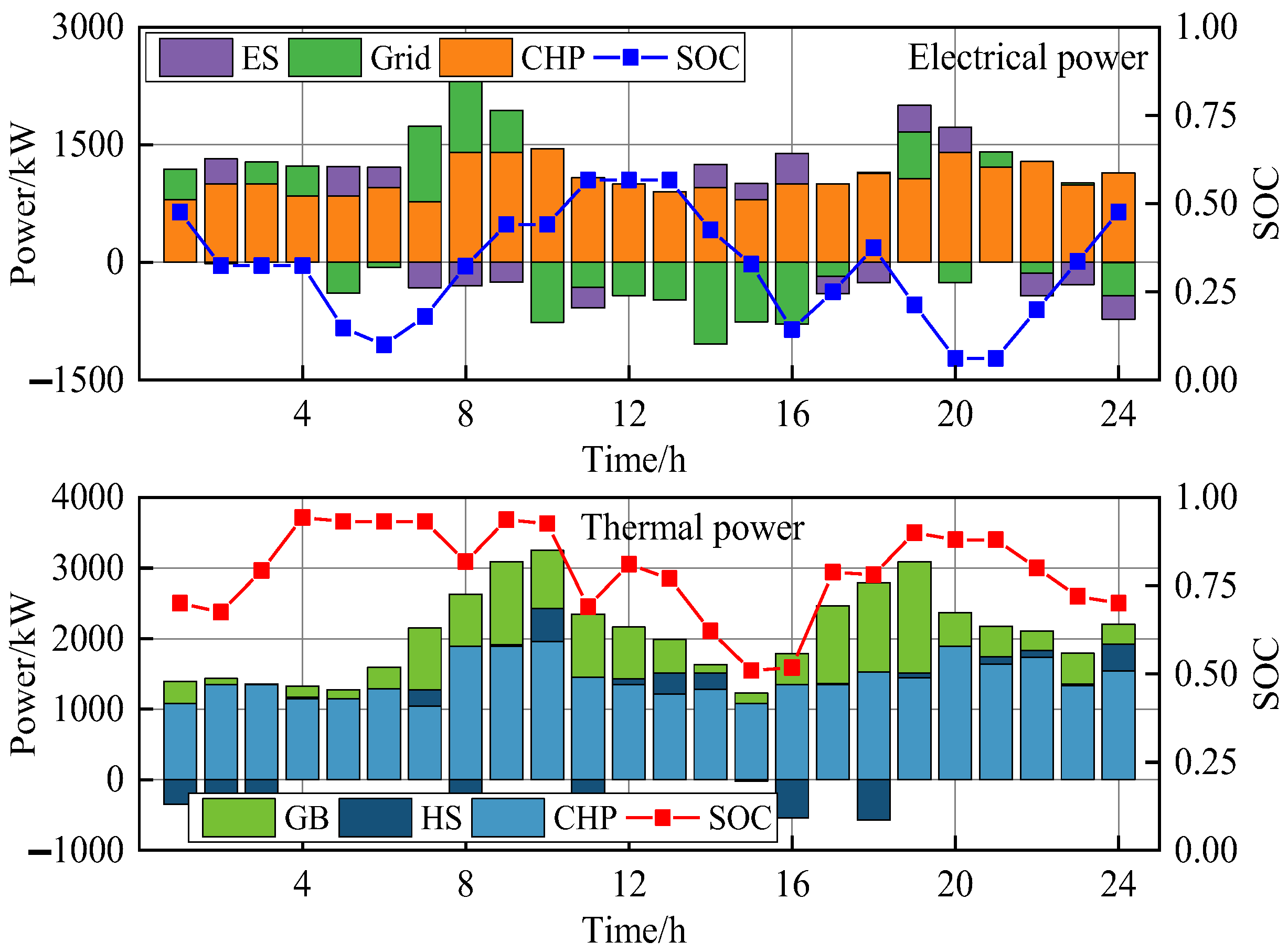
5.2.1. Optimization Result of ESP Pricing and Operation Strategy
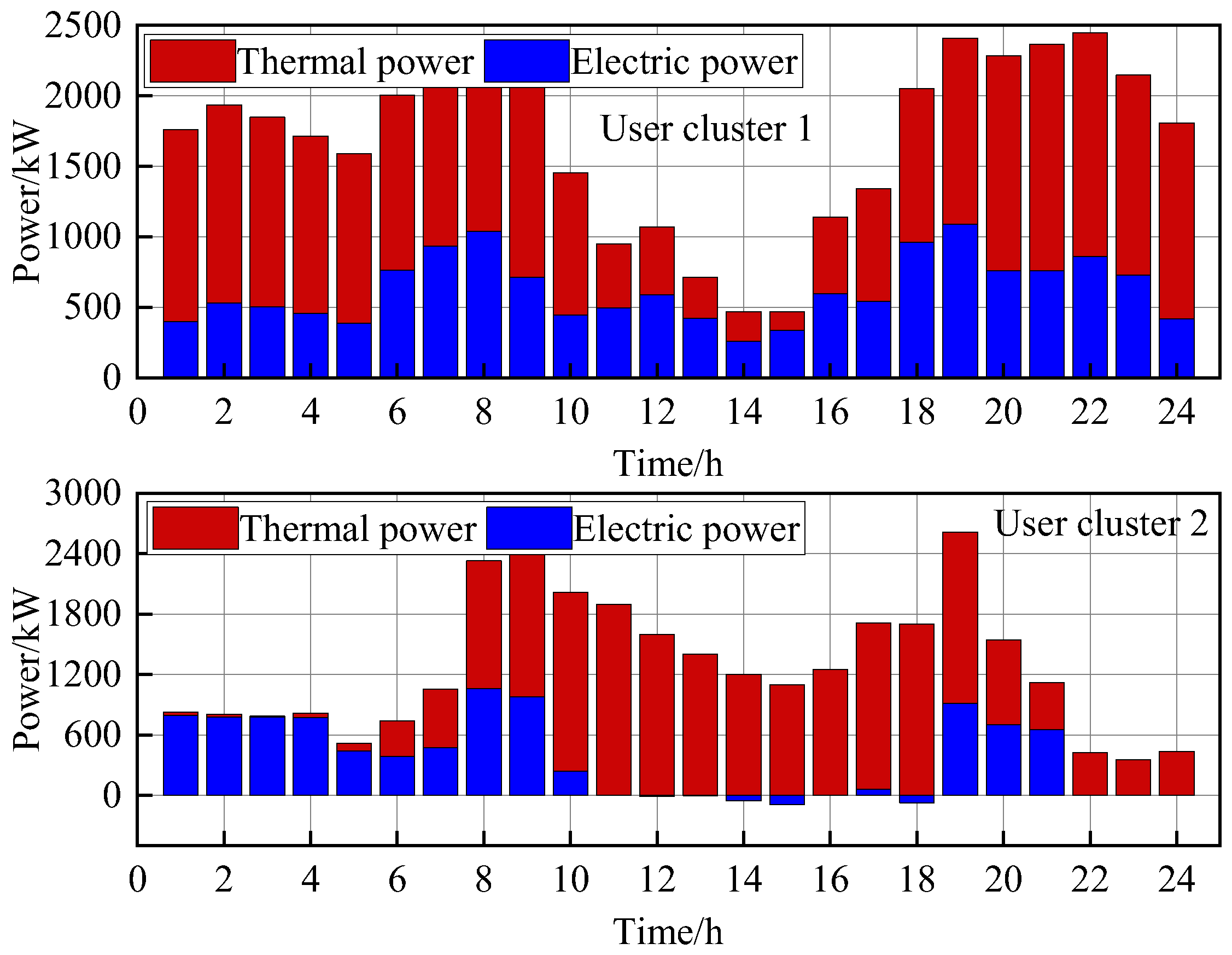
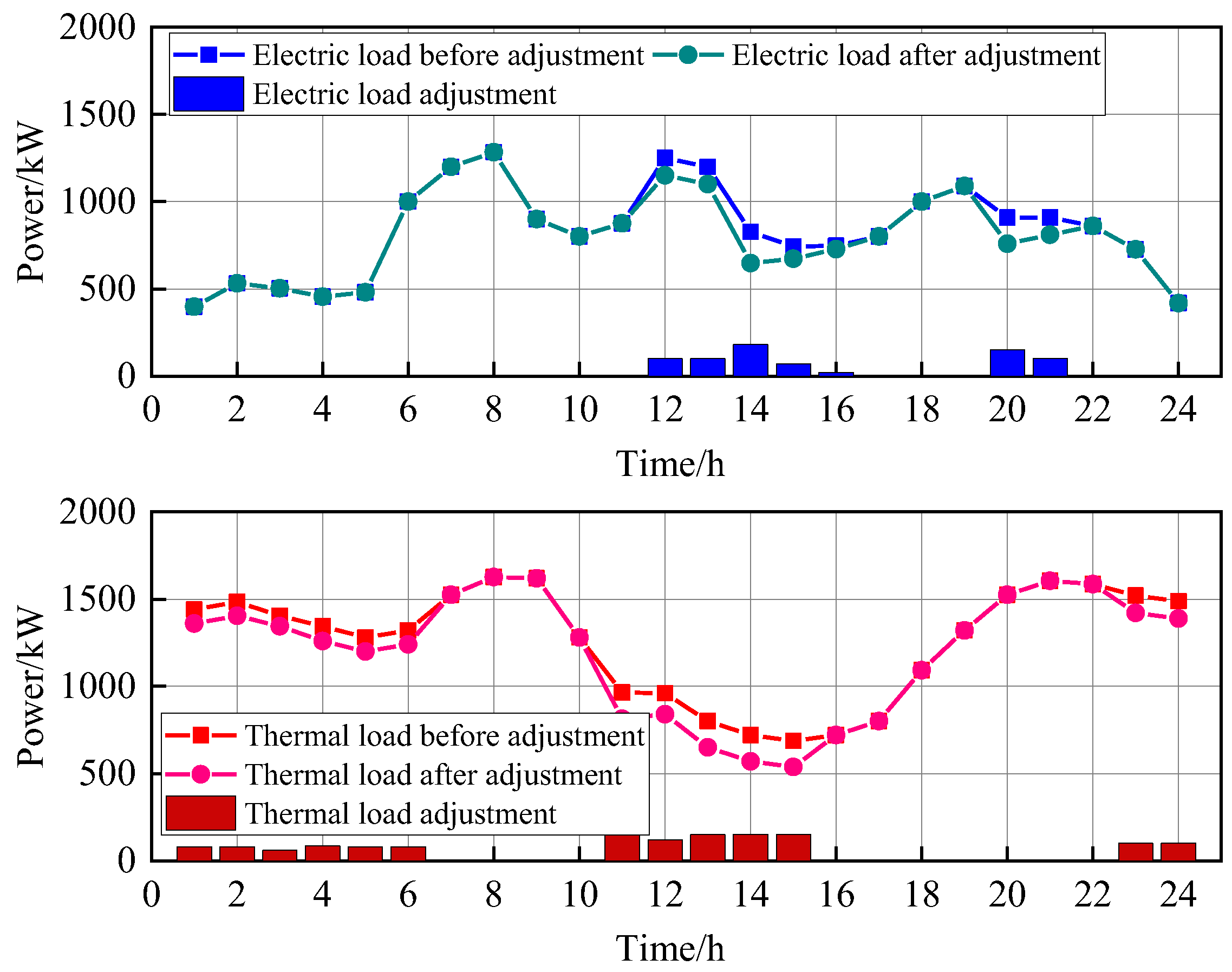
5.2.2. Optimization Result of User Energy Management
5.3. Discussion and Analysis
5.3.1. Analysis of Operation Economy and Carbon Emission
5.3.2. Scalability Verification of the Proposed Method
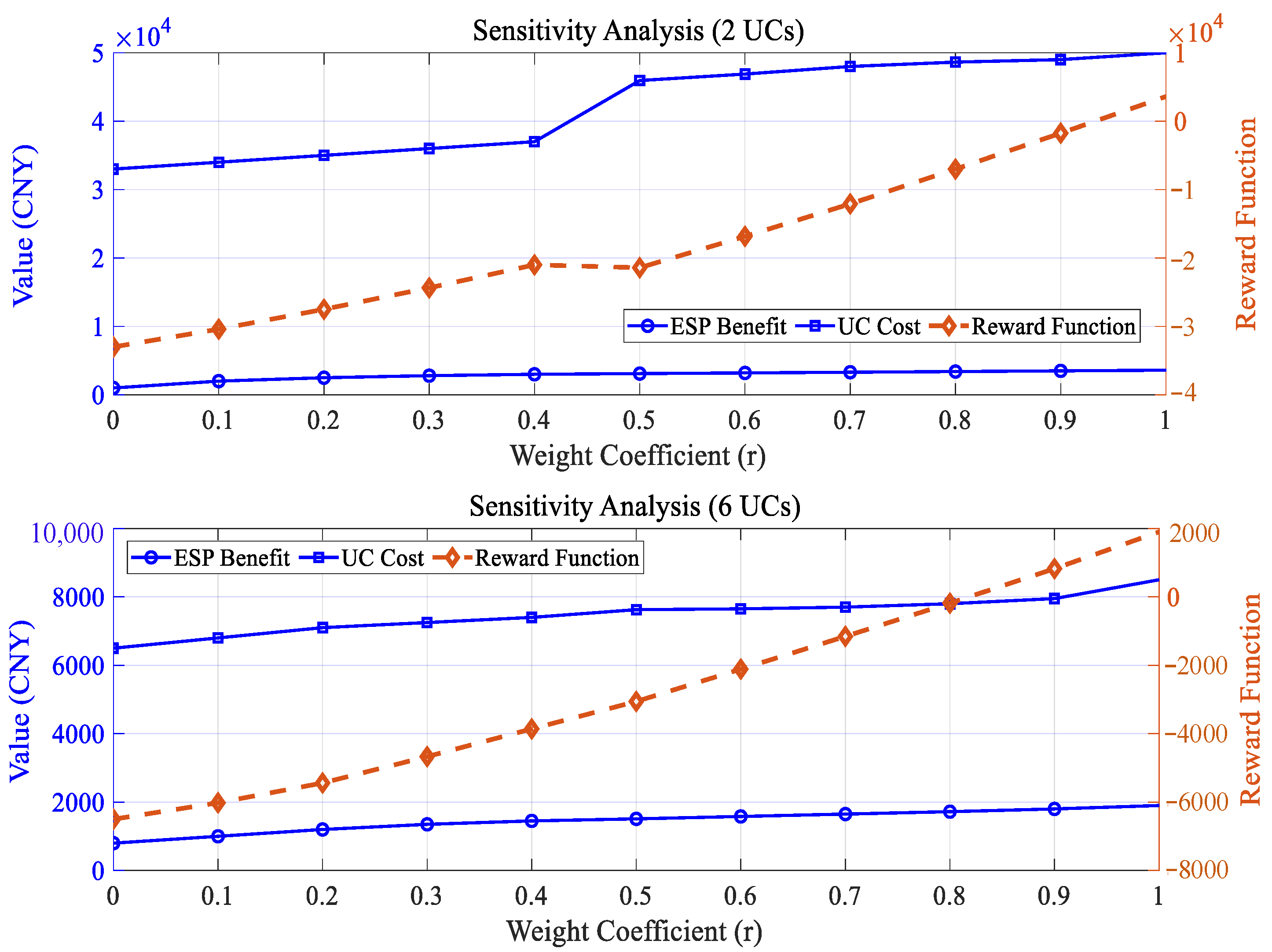
5.3.3. Sensitivity Analysis of Key Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Viewpoints | Participating Subject | Energy Form | DR Price | Pricing Decision | Optimization Method | |
| Demand response | Ref. [5] | User cluster | Electricity; thermal; hydrogen | Electricity price | No | Distributionally robust optimization model |
| Ref. [6] | User cluster | Electricity | Electricity price | No | Multi-objective optimization; horse herd optimization algorithm | |
| Ref. [7] | User cluster | Electricity; thermal | Electricity price; thermal price | No | Two-stage optimal operation; nondominated sorting genetic algorithm (NSGA-II) | |
| Ref. [8] | User cluster | Electricity | Electricity price | No | Segmented linearization approach | |
| Ref. [9] | User cluster | Electricity; thermal | Electricity price | No | Robust optimization technique | |
| Ref. [10] | User cluster | Electricity; thermal | Electricity price | No | Mixed-integer linear programming approach | |
| Ref. [11] | ESP; user cluster | Electricity | Electricity price | Electricity pricing | Stackelberg game approach; distributed algorithm | |
| Ref. [12] | ESP; user cluster | Electricity | Electricity price | Electricity pricing | Two-stage energy sharing; Stackelberg game approach | |
| This paper | ESP; user cluster | Electricity; thermal | Electricity price; thermal price | Electricity and thermal pricing | Reinforcement learning | |
| Energy management and operation optimization | Ref. [13] | User cluster | Electricity | Electricity price | No | Hybrid deep learning |
| Ref. [15] | User cluster | Electricity | Electricity price | Electricity pricing | DR optimization of electric load; mathematical programming | |
| Ref. [16] | User cluster | Electricity | Electricity price | No | Blockchain-based solution | |
| Ref. [17] | User cluster | Electricity | Electricity price | No | Bi-level mixed integer nonlinear programming | |
| Ref. [18] | User cluster | Electricity | Electricity price | No | PSO algorithm | |
| Ref. [19] | User cluster | Electricity | Electricity price | No | Mathematical programming | |
| Ref. [20] | ESP; user cluster | Electricity | Electricity price | Electricity pricing | DR optimization of electric load; Stackelberg game approach | |
| Ref. [21] | User cluster | Electricity | Electricity price | No | Multi-stage RL algorithm | |
| Ref. [22] | User cluster | Electricity | Electricity price | No | Deep reinforcement learning | |
| Ref. [23] | User cluster | Electricity | Electricity price | No | Deep–fuzzy logic control | |
| Ref. [24] | User cluster | Electricity; thermal | Electricity price | No | Electric-thermal collaborative optimization; multiscale multiphysics model | |
| This paper | ESP; user cluster | Electricity; thermal | Electricity price; thermal price | Electricity and thermal pricing | Electric–thermal collaborative optimization; DR optimization of electric–thermal load; reinforcement learning | |
| Solution method | Ref. [31] Ref. [32] | User cluster | Electricity | Electricity price | No | Markov decision making; deep reinforcement learning |
| Ref. [33] | User cluster | Electricity | Electricity price | No | Markov decision making; multi-Agent reinforcement learning | |
| Ref. [34] | User cluster | Electricity | Electricity price | No | Markov decision making; adaptive personalized federated reinforcement learning | |
| This paper | ESP; user cluster | Electricity; thermal | Electricity price; thermal price | Electricity and thermal pricing | Markov decision making; reinforcement learning | |
References
- Hung, Y.; Liu, N.; Chen, Z.; Xu, J. Collaborative optimization for interconnected energy hubs based on cluster partition of electric-thermal energy network. Energy 2025, 321, 135403. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, X.; Huang, Y. Low-Carbon-Oriented Capacity Optimization Method for Electric–Thermal Integrated Energy System Considering Construction Time Sequence and Uncertainty. Processes 2024, 12, 648. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Dong, L. Low carbon-oriented planning of shared energy storage station for multiple integrated energy systems considering energy-carbon flow and carbon emission reduction. Energy 2024, 290, 130139. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J. Two-stage energy management method of integrated energy system considering pre-transaction behavior of energy service provider and users. Energy 2023, 271, 127065. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, D.; Yun, J.; Siqin, Z. Distributionally Robust Optimization Model of the Integrated Energy System with Integrated Demand Response. J. Energy Eng. 2025, 151, 04025022. [Google Scholar] [CrossRef]
- Du, X.; Yang, Y.; Guo, H. Optimizing integrated hydrogen technologies and demand response for sustainable multi-energy microgrids. Electr. Eng. 2025, 107, 2621–2643. [Google Scholar] [CrossRef]
- Wang, X.; Jiao, Y.; Cui, B.; Zhu, H.; Wang, R. Two-Stage Optimal Operation of Integrated Energy System Considering Electricity–Heat Demand Response and Time-of-Use Energy Price. Int. J. Energy Res. 2025, 2025, 6106019. [Google Scholar] [CrossRef]
- Ma, C.; Hu, Z. Low-Carbon Economic Scheduling of Integrated Energy System Considering Flexible Supply–Demand Response and Diversified Utilization of Hydrogen. Sustainability 2025, 17, 1749. [Google Scholar] [CrossRef]
- Mobarakeh, S.I.; Sadeghi, R.; Saghafi, H.; Delshad, M. Hierarchical integrated energy system management considering energy market, demand response and uncertainties: A robust optimization approach. Comput. Electr. Eng. 2025, 123, 110138. [Google Scholar] [CrossRef]
- Moosavi, M.; Olamaei, J.; Shourkaei, H.M. Optimizing microgrid performance a multi-objective strategy for integrated energy management with hybrid sources and demand response. Sci. Rep. 2025, 15, 17827. [Google Scholar] [CrossRef]
- Lin, W.-T.; Chen, G.; Li, J.; Lei, Y.; Zhang, W.; Yang, D.; Ming, T. Privacy-preserving incentive mechanism for integrated demand response: A homomorphic encryption-based approach. Int. J. Electr. Power Energy Syst. 2025, 164, 110407. [Google Scholar] [CrossRef]
- Bian, Y.; Xie, L.; Ma, L.; Cui, C. A novel two-stage energy sharing model for data center cluster considering integrated demand response of multiple loads. Appl. Energy 2025, 384, 125454. [Google Scholar] [CrossRef]
- Ibude, F.; Otebolaku, A.; Ameh, J.E.; Ikpehai, A. Multi-Timescale Energy Consumption Management in Smart Buildings Using Hybrid Deep Artificial Neural Networks. J. Low Power Electron. Appl. 2024, 14, 54. [Google Scholar] [CrossRef]
- Ahmad, W.; Lucas, A.; Carvalhosa, S.M.P. Battery Control for Node Capacity Increase for Electric Vehicle Charging Support. Energies 2024, 17, 5554. [Google Scholar] [CrossRef]
- Asaleye, D.A.; Murphy, D.J.; Shine, P.; Murphy, M.D. The Practical Impact of Price-Based Demand-Side Management for Occupants of an Office Building Connected to a Renewable Energy Microgrid. Sustainability 2024, 16, 8120. [Google Scholar] [CrossRef]
- Kolahan, A.; Maadi, S.R.; Teymouri, Z.; Schenone, C. Blockchain-based solution for energy demand-side management of residential buildings. Sustain. Cities Soc. 2021, 75, 103316. [Google Scholar] [CrossRef]
- Al-Quraan, A.; Al-Mhairat, B. Sizing and energy management of standalone hybrid renewable energy systems based on economic predictive control. Energy Convers. Manag. 2024, 300, 117948. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, Z.; Li, Y.; Zhao, T. Grey-box model-based demand side management for rooftop PV and air conditioning systems in public buildings using PSO algorithm. Energy 2024, 296, 131052. [Google Scholar] [CrossRef]
- Zhang, K.; Saloux, E.; Candanedo, J.A. Enhancing energy flexibility of building clusters via supervisory room temperature control: Quantification and evaluation of benefits. Energy Build. 2024, 302, 113750. [Google Scholar] [CrossRef]
- Ying, C.; Zou, Y.; Xu, Y. Decentralized energy management of a hybrid building cluster via peer-to-peer transactive energy trading. Appl. Energy 2024, 372, 123803. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, F.; Ran, Y.; Li, Y.; Xu, Y. Scalable energy management approach of residential hybrid energy system using multi-agent deep reinforcement learning. Appl. Energy 2024, 367, 123414. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-Line Building Energy Optimization Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 3698–3708. [Google Scholar] [CrossRef]
- Cavus, M.; Dissanayake, D.; Bell, M. Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies 2025, 18, 995. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Wang, L.X.; Wang, B.Y.; Chen, Y.; Ran, C.X.; Wu, Z.B. Polarization management of photonic crystals to achieve synergistic optimization of optical, thermal, and electrical performance of building-integrated photovoltaic glazing. Appl. Energy 2024, 372, 123827. [Google Scholar] [CrossRef]
- Liang, H.; Lin, C.; Pang, A. Expert knowledge data-driven based actor–critic reinforcement learning framework to solve computationally expensive unit commitment problems with uncertain wind energy. Int. J. Electr. Power Energy Syst. 2024, 159, 110033. [Google Scholar] [CrossRef]
- Alharbi, M.; Alghamdi, A.S. Hybrid CNN-GRU Forecasting and Improved Teaching–Learning-Based Optimization for Cost-Efficient Microgrid Energy Management. Processes 2025, 13, 1452. [Google Scholar] [CrossRef]
- Ding, L.; Cui, Y.; Yan, G.; Huang, Y.; Fan, Z. Distributed energy management of multi-area integrated energy system based on multi-agent deep reinforcement learning. Int. J. Electr. Power Energy Syst. 2024, 157, 109867. [Google Scholar] [CrossRef]
- Shuai, Q.; Yin, Y.; Huang, S.; Chen, C. Deep Reinforcement Learning-Based Real-Time Energy Management for an Integrated Electric–Thermal Energy System. Sustainability 2025, 17, 407. [Google Scholar] [CrossRef]
- Li, Y.; Ma, W.; Li, Y.; Li, S.; Chen, Z.; Shahidehpour, M. Enhancing cyber-resilience in integrated energy system scheduling with demand response using deep reinforcement learning. Appl. Energy 2025, 379, 124831. [Google Scholar] [CrossRef]
- Gong, J.; Yu, N.; Han, F.; Tang, B.; Wu, H.; Ge, Y. Bias Correction of Data-Driven Deep Reinforcement Learning in Economic Scheduling of Integrated Energy Systems. In Proceedings of the International Conference on Life System Modeling and Simulation, International Conference on Intelligent Computing for Sustainable Energy and Environment, Suzhou, China, 13–15 September 2024; Springer: Singapore, 2025. [Google Scholar] [CrossRef]
- Lian, J.; Li, D.; Li, L. Real-Time Energy Management Strategy for Fuel Cell/Battery Plug-In Hybrid Electric Buses Based on Deep Reinforcement Learning and State of Charge Descent Curve Trajectory Control. Energy Technol. 2025, 13, 2401696. [Google Scholar] [CrossRef]
- Li, Y.; Chang, W.; Yang, Q. Deep reinforcement learning based hierarchical energy management for virtual power plant with aggregated multiple heterogeneous microgrids. Appl. Energy 2025, 382, 125333. [Google Scholar] [CrossRef]
- Liao, Z.; Li, C.; Zhang, X.; Hu, Q.; Wang, B. A Bidding Strategy for Power Suppliers Based on Multi-Agent Reinforcement Learning in Carbon–Electricity–Coal Coupling Market. Energies 2025, 18, 2388. [Google Scholar] [CrossRef]
- Wang, T.; Dong, Z.Y. Adaptive personalized federated reinforcement learning for multiple-ESS optimal market dispatch strategy with electric vehicles and photovoltaic power generations. Appl. Energy 2024, 365, 123107. [Google Scholar] [CrossRef]
- Wang, L.; Tao, Z.; Zhu, L.; Wang, X.; Yin, C.; Cong, H.; Bi, R.; Qi, X. Optimal dispatch of integrated energy system considering integrated demand response resource trading. IET Gener. Transm. Distrib. 2022, 16, 1727–1742. [Google Scholar] [CrossRef]
- Lu, J.; Liu, T.; He, C.; Nan, L.; Hu, X. Robust day-ahead coordinated scheduling of multi-energy systems with integrated heat-electricity demand response and high penetration of renewable energy. Renew. Energy 2021, 178, 466–482. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Zhang, X. A Dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Ma, L.; Liu, J.; Wang, Q. Energy Management and Pricing Strategy of Building Cluster Energy System Based on Two-Stage Optimization. Front. Energy Res. 2022, 10, 865190. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. Low-carbon economic dispatch and energy sharing method of multiple Integrated Energy Systems from the perspective of System of Systems. Energy 2022, 244, 122717. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, S.; Wang, S.; Zhao, Q. Distributed coordinated dispatching of district electric-thermal integrated energy system considering ladder-type carbon trading mechanism. Power Syst. Syst. Syst. Technol. 2023, 47, 217–229. [Google Scholar] [CrossRef]
- Gao, X.; Tao, H.; Miao, G.; Ping, Z. Joint optimization control of energy storage system management and demand response. J. Syst. Simul. 2016, 28, 1165–1172. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, Y. Optimal operation for park integrated energy system considering interruptible loads. J. Syst. Simul. 2022, 34, 817–825. [Google Scholar] [CrossRef]
- Huang, H.; Chen, X.; Cha, J. Partition autonomous energy cooperation community and its joint optimal scheduling for multi-park integrated energy system. Power Syst. Technol. 2022, 46, 2955–2965. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, T.; Li, Q.; He, C.; Xiao, H.; Qin, H. An Mixed Integer Quadratic Programming Model and Algorithm Study for Power Balance Problem of High Hydropower Proportion’s System. Proc. CSEE 2017, 37, 1114–1125. [Google Scholar] [CrossRef]
- Luo, J.; Li, Y.; Wang, H.; Li, G.; Song, Y.; Long, W. Optimal Scheduling of Integrated Energy System Considering Integrated Demand Response. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; Conference Series 2022. pp. 110–116. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. A two-stage energy management for heat-electricity integrated energy system considering dynamic pricing of Stackelberg game and operation strategy optimization. Energy 2022, 244, 122576. [Google Scholar] [CrossRef]


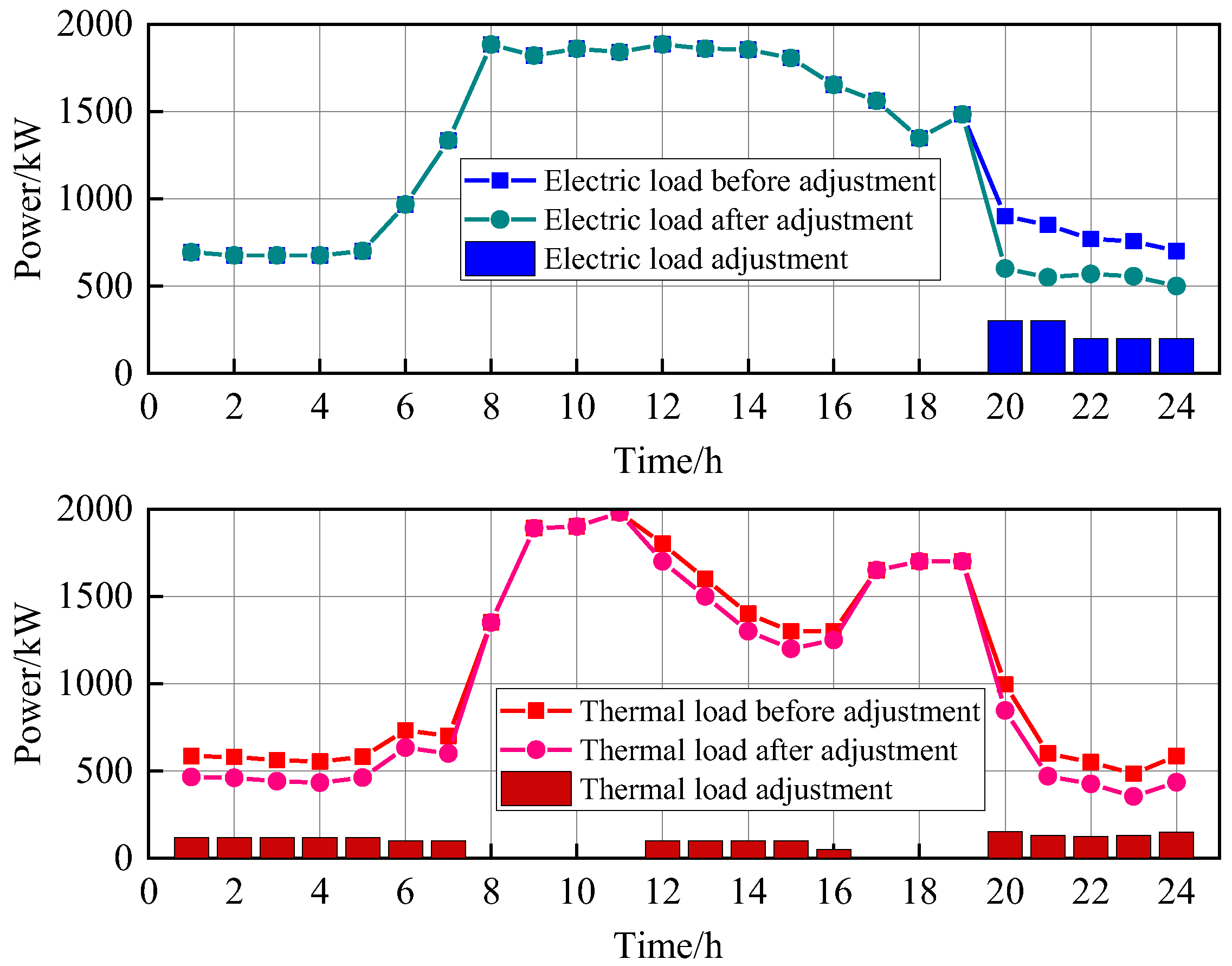
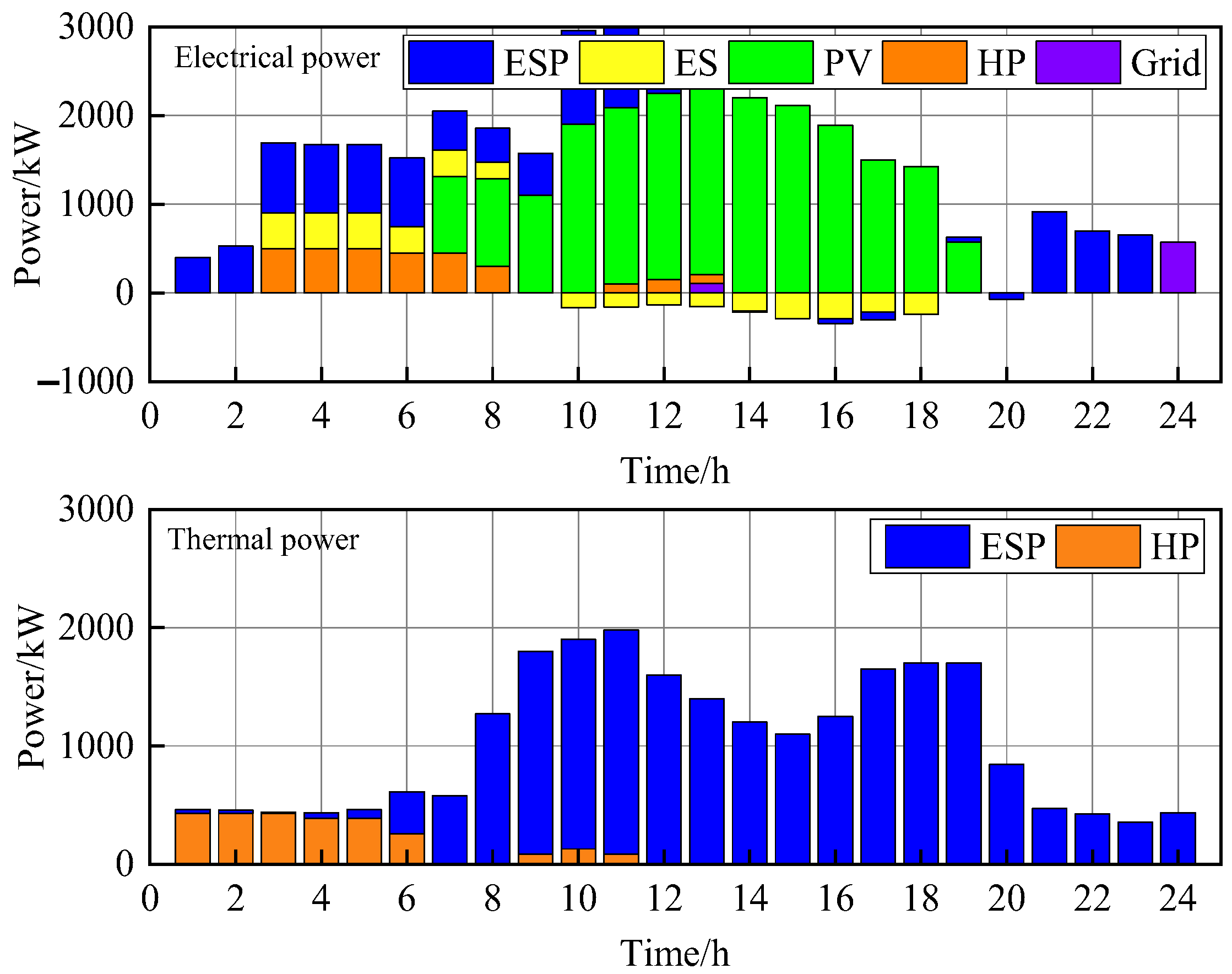

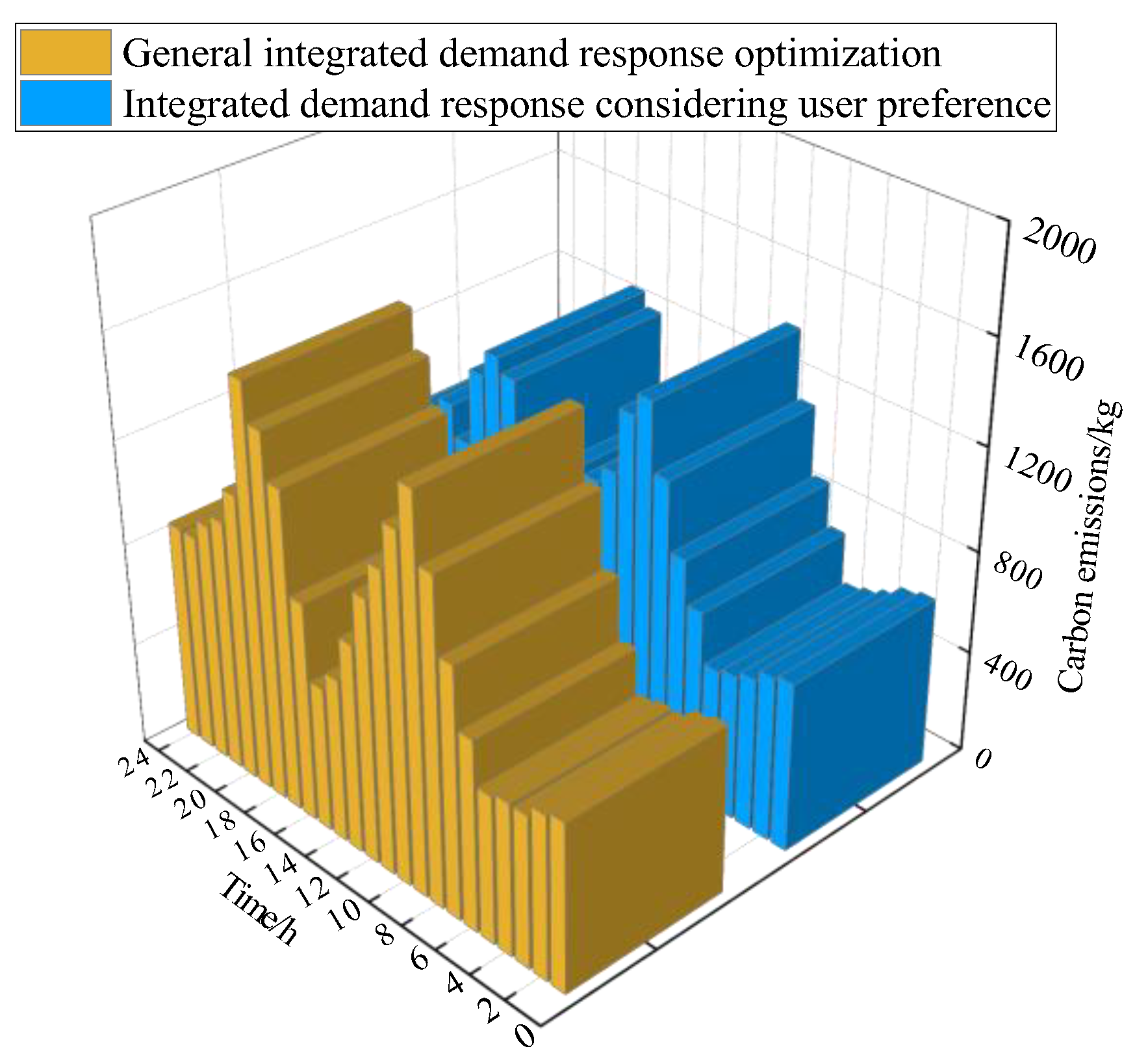
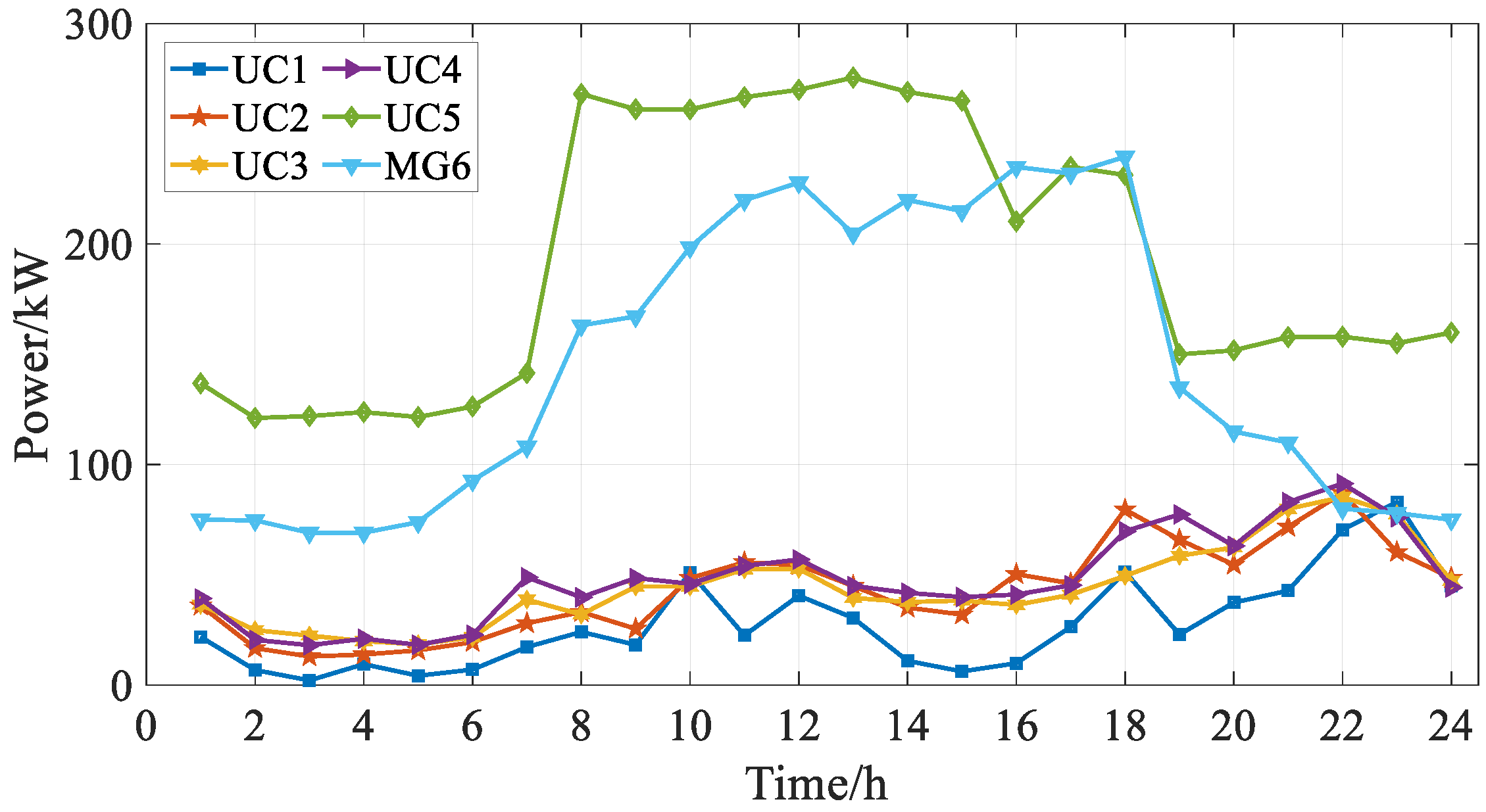
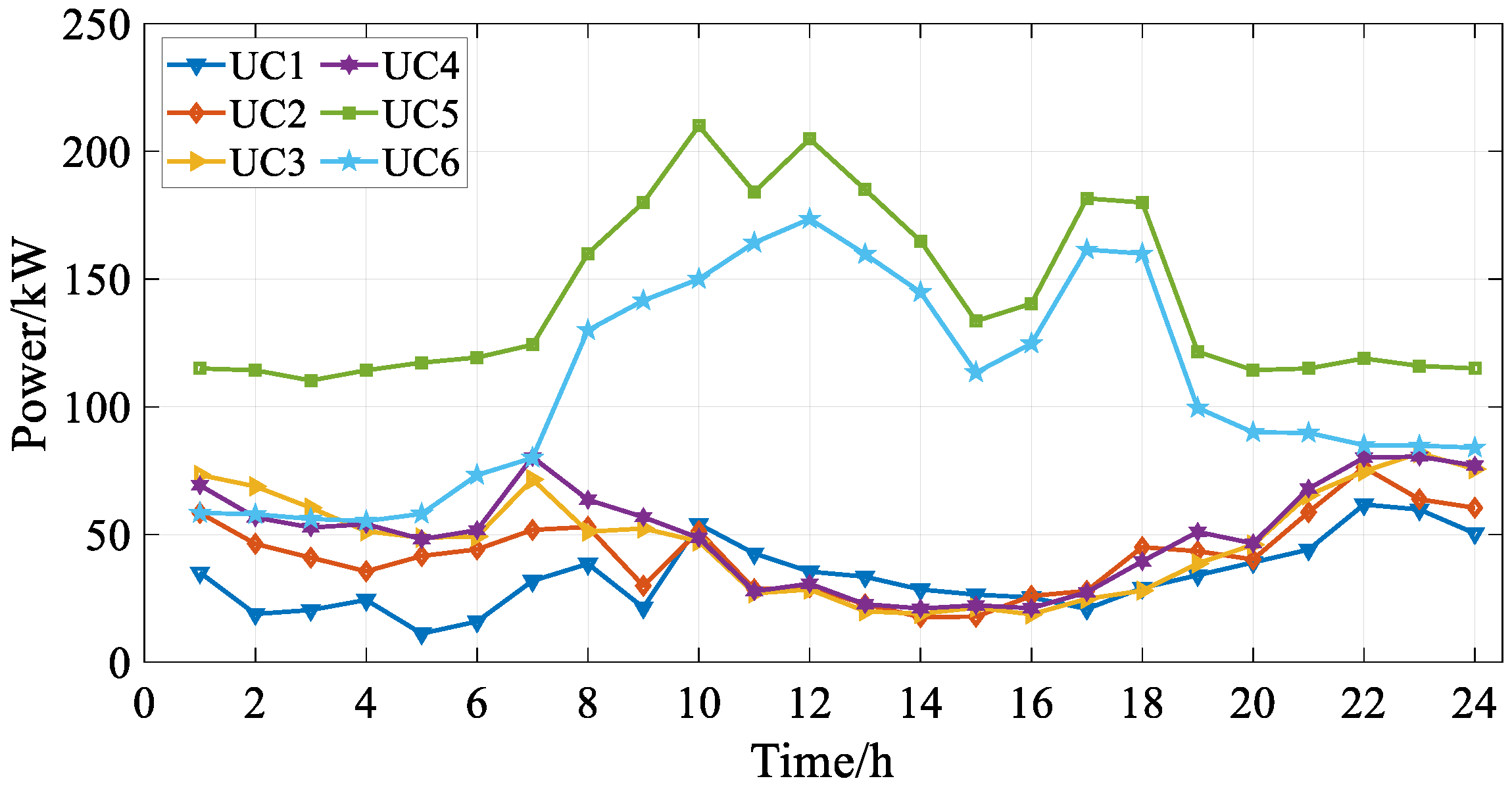

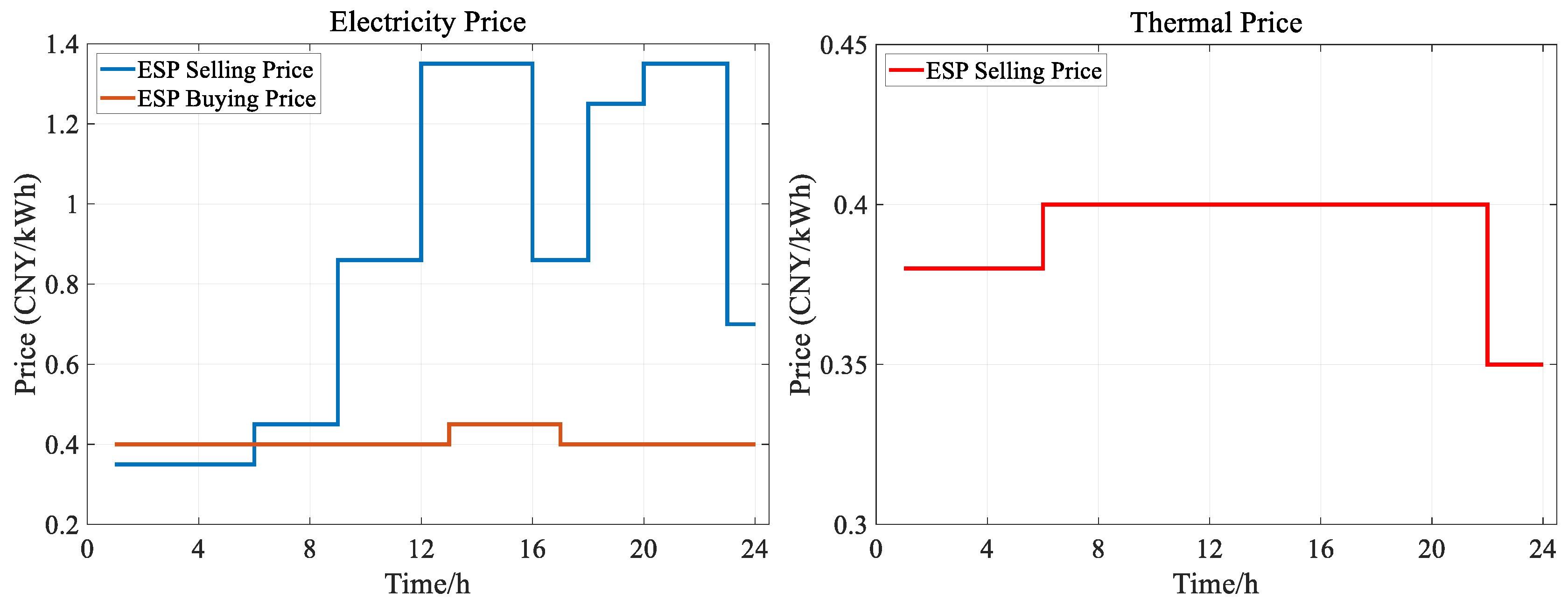
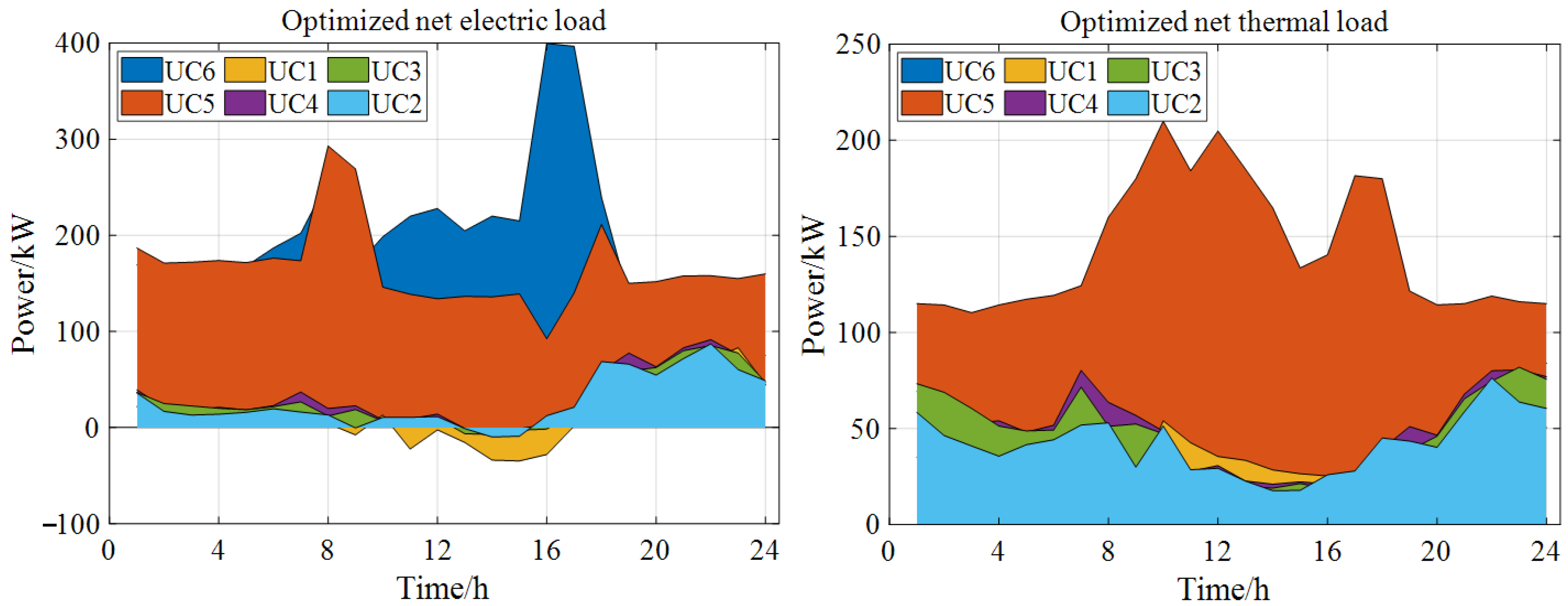
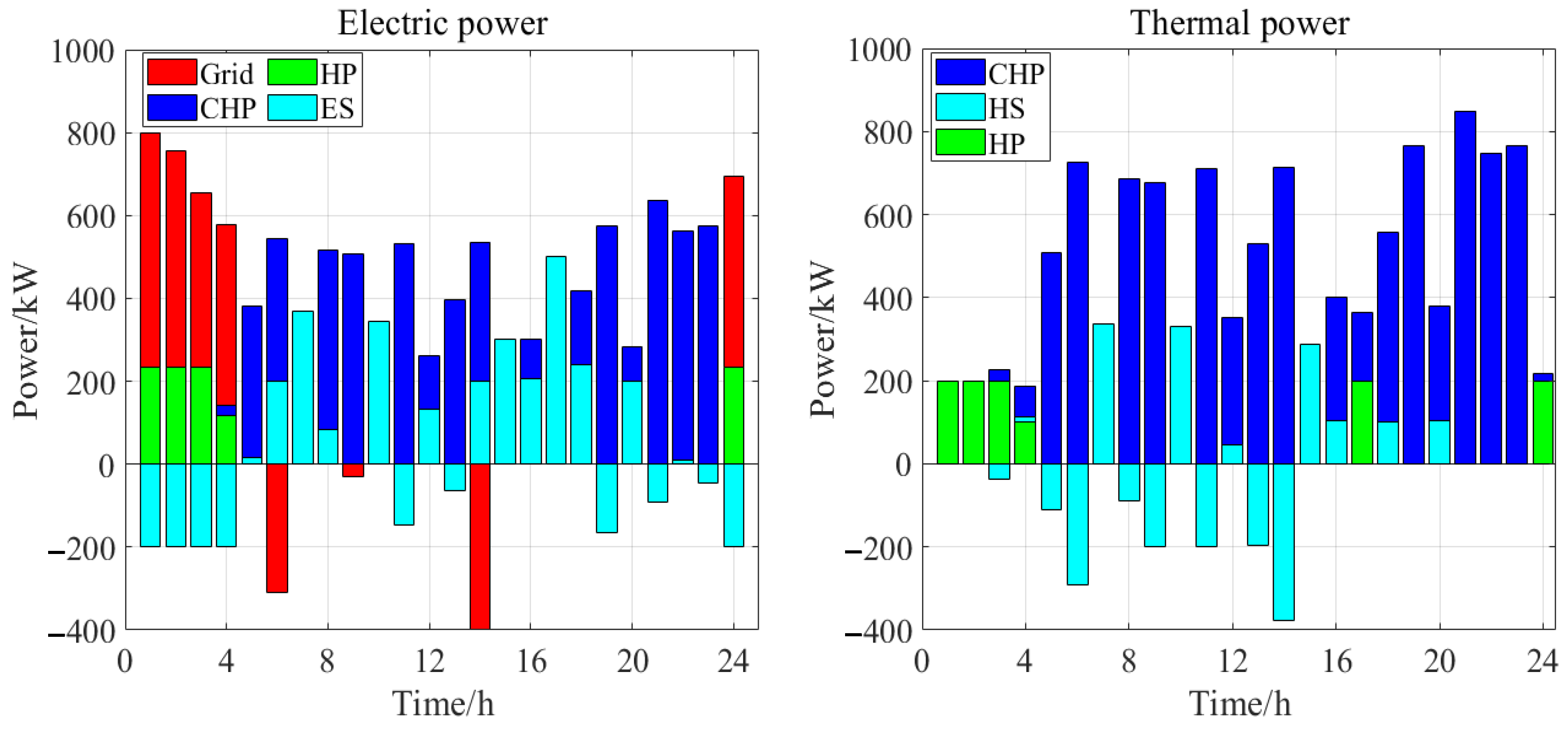
| Equipment | Parameters | ESP | User Cluster 1 | User Cluster 2 |
|---|---|---|---|---|
| CHP | Capacity | 1500 kW | - | - |
| Operating cost coefficient | 0.05 CNY/kWh | - | - | |
| Thermal–electric ratio | 1.35 | - | - | |
| HP | Capacity | - | 1500 kW | 1000 kW |
| Operating cost coefficient | - | 0.026 CNY/kWh | 0.026 CNY/kWh | |
| Heating efficiency | - | 0.90 | 0.86 | |
| GB | Capacity | 1500 kW | - | - |
| Operating cost coefficient | 0.15 CNY/kWh | - | - | |
| Heating efficiency | 0.85 | - | - | |
| PV | Capacity | - | 1000 kW | 2500 kW |
| Operating cost coefficient | - | 0.025 CNY/kWh | 0.025 CNY/kWh | |
| ES | Capacity | 1000 kW | - | 2000 kW |
| Operating cost coefficient | 0.02 CNY/kWh | - | 0.02 CNY/kWh | |
| HS | Capacity | 1000 kW | - | - |
| Operating cost coefficient | 0.02 CNY/kWh | - | - |
| Price Type | Off-Peak | Mid-Peak | On-Peak |
|---|---|---|---|
| Time | 1:00–8:00 | 9:00–11:00; 16:00–17:00; 23:00–24:00 | 12:00–15:00 20:00–22:00 |
| Selling Price | 0.45 CNY/kWh | 0.86 CNY/kWh | 1.35 CNY/kWh |
| Buying Price | 0.40 CNY/kWh | ||
| User Cost/CNY | General Integrated Demand Response Optimization | Optimization of Integrated Demand Response Considering User Preference | ||
|---|---|---|---|---|
| User Cluster 1 | User Cluster 2 | User Cluster 1 | User Cluster 2 | |
| Electricity transaction cost with ESP | 13,322.06 | 5968.64 | 13,489.56 | 4892.61 |
| Thermal transaction cost with ESP | 10,244.04 | 8644.99 | 8536.97 | 8536.97 |
| Electricity transaction cost with power grid | 0.00 | 2044.99 | 0.00 | 3793.04 |
| Satisfaction loss | 2780.52 | 3892.95 | 2462.21 | 3224.27 |
| Operation and maintenance cost | 269.77 | 707.12 | 269.77 | 735.72 |
| Total operating cost | 26,616.39 | 21,258.70 | 24,758.50 | 21,182.61 |
| ESP Benefit Composition/CNY | General Integrated Demand Response Optimization | Optimization of Integrated Demand Response Considering User Preference |
|---|---|---|
| Revenue from electricity interaction with power grid | 3601.02 | 3245.98 |
| Revenue from electricity interaction with users | 19,290.70 | 18,382.17 |
| Revenue from thermal energy interaction with users | 18,889.03 | 17,073.93 |
| Natural gas cost | 29,778.75 | 28,274.97 |
| Operation and maintenance cost | 3464.13 | 1876.47 |
| Environmental cost | 5736.60 | 5446.91 |
| Total operating benefit | 2801.27 | 3103.72 |
| Carbon Emission | General Integrated Demand Response Optimization | Optimization of Integrated Demand Response Considering User Preference |
|---|---|---|
| Carbon emission of CHP | 15,080.48 | 14,426.84 |
| Carbon emission of GB | 7865.91 | 7360.80 |
| Total carbon emission | 22,946.39 | 21,787.64 |
| Equipment | Parameters | Value |
|---|---|---|
| CHP | Capacity | 700 kW |
| Operating cost coefficient | 0.05 CNY/kWh | |
| Thermal–electric ratio | 1.35 | |
| HP | Capacity | 200 kW |
| Operating cost coefficient | 0.026 CNY/kWh | |
| Heating efficiency | 0.90 | |
| ES | Capacity | 500 kW |
| Operating cost coefficient | 0.02 CNY/kWh | |
| HS | Capacity | 500 kW |
| Operating cost coefficient | 0.02 CNY/kWh |
| Equipment | Parameters | UC 1–UC 4 | UC 5 | UC 6 |
|---|---|---|---|---|
| HP | Capacity | - | - | 150 kW |
| Operating cost coefficient | - | - | 0.026 CNY/kWh | |
| Heating efficiency | - | - | 0.86 | |
| PV | Capacity | 50 kW | 100 kW | 100 kW |
| Operating cost coefficient | 0.025 CNY/kWh | 0.025 CNY/kWh | 0.025 CNY/kWh | |
| ES | Capacity | - | 100 kW | - |
| Operating cost coefficient | - | 0.02 CNY/kWh | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Yang, S.; Sun, S.; Yu, P.; Xing, J. Energy Management for Integrated Energy System Based on Coordinated Optimization of Electric–Thermal Multi-Energy Retention and Reinforcement Learning. Processes 2025, 13, 2693. https://doi.org/10.3390/pr13092693
Cheng Y, Yang S, Sun S, Yu P, Xing J. Energy Management for Integrated Energy System Based on Coordinated Optimization of Electric–Thermal Multi-Energy Retention and Reinforcement Learning. Processes. 2025; 13(9):2693. https://doi.org/10.3390/pr13092693
Chicago/Turabian StyleCheng, Yan, Song Yang, Shumin Sun, Peng Yu, and Jiawei Xing. 2025. "Energy Management for Integrated Energy System Based on Coordinated Optimization of Electric–Thermal Multi-Energy Retention and Reinforcement Learning" Processes 13, no. 9: 2693. https://doi.org/10.3390/pr13092693
APA StyleCheng, Y., Yang, S., Sun, S., Yu, P., & Xing, J. (2025). Energy Management for Integrated Energy System Based on Coordinated Optimization of Electric–Thermal Multi-Energy Retention and Reinforcement Learning. Processes, 13(9), 2693. https://doi.org/10.3390/pr13092693





