Measuring the Effects of Gas Pressure and Confining Pressures on Coal: In the View of Time–Frequency Evolutionary Properties and Crack Propagation Behavior

Abstract

As coal mining progresses to greater depths, the complex geological conditions significantly increase the risk of compound disasters. With increasing mining depth, elevated ground stress and gas pressure exacerbate the coupling effects of rockburst and gas outburst. This study employs laboratory tests and theoretical analysis to investigate gas disasters under varying gas and confining pressures. The experimental results are analyzed in terms of mechanical parameters, crack propagation, and acoustic emission (AE) time–frequency evolution. Under conventional compression, coal failure exhibits shear damage with axial splitting or debris ejection. The peak strength demonstrates a clear confining pressure strengthening effect and gas pressure weakening effect. At constant gas pressure, the elastic modulus increases with confining pressure, whereas at constant confining pressure, it decreases with rising gas pressure.

1. Introduction

Considered as an important part of the primary energy structure, coal resources have an irreplaceable strategic position in promoting the industrialization process and securing the economic development. However, with the extension of mining depth to kilometers, mining engineering is facing increasingly severe technical bottlenecks and scientific problems [1,2] which seriously restrict the safe and efficient development of deep coal resources. The intricate geological conditions at greater depths contribute to the heightened frequency of coal–rock dynamic disasters, with major hazards such as gas outburst and rockburst posing critical challenges for mining engineering worldwide [3,4,5]. Research indicates that most underground engineering disasters are intrinsically linked to the progressive failure and instability of coal and rock masses. Particularly, deep coal seams exist under unique mechanical conditions characterized by high stress, high gas pressure, high temperature, and mining-induced disturbances. Consequently, understanding their deformation and failure mechanisms requires a comprehensive analysis of gas–solid coupling effects, where gas seepage interacts with coal deformation. Thus, given the distinctive high-stress and high-gas-pressure conditions prevalent in deep coal seams, any comprehensive analysis of coal deformation and damage mechanisms must incorporate considerations of gas–solid coupling effects. Consequently, systematic investigation of the deformation characteristics and damage evolution processes in coal under the coupled influence of external stress and gas pressure holds critical importance. Such research not only contributes to the mitigation of underground disasters but also enhances the mining efficiency of deep coal resources.

To elucidate the mechanical response mechanisms and damage evolution characteristics of coal–rock masses under mining-induced disturbances, extensive experimental and theoretical investigations have been conducted. Liu et al. [6,7] used a solid–gas coupled micromechanical testing device they developed themselves to obtain real-time images of crack changes in coal samples during triaxial compression under conditions containing methane gas, and studied the damage evolution characteristics of cracks in coal bodies. Yao et al. [8] established a gas–solid coupling model integrating coal seam deformation, gas diffusion–seepage dynamics, and adsorption–desorption processes, thereby delineating gas transport behavior during protective seam mining. Chen et al. [9] identified that energy-dissipation-induced damage manifests as a decelerated increase in bulk modulus prior to strain reversal, followed by accelerated degradation. Through triaxial compression experiments, Zhang et al. [10] demonstrated that confining pressure enhances energy input intensity, while Zhang et al. [11] observed an S-shaped evolution trend in dissipated energy versus axial strain under varying confining and gas pressures. Liu et al. [12] further quantified the confining pressure effect: increasing effective confinement reduces Poisson’s ratio but elevates peak strength. Employing AE monitoring. Xu et al. [13] pioneered the quantitative characterization of critical deformation thresholds for coal–rock failure precursors, establishing a theoretical framework for dynamic hazard early warning in deep mines. Xie et al. [14] revealed a distinct platform effect in axial, lateral, and volumetric strains near peak stress, indicative of energy accumulation during damage progression. Zhao et al. [15] and Zhang et al. [16] derived a linear constitutive relationship between coal–rock peak strength and confining pressure, providing critical insights for deep mining mechanical modeling. Xiao et al. [17] proposed a novel permeability model capturing permeability evolution across pore pressure regimes under coupled effective stress and slip effects. Liu et al. [18] developed a gas–solid coupling model incorporating adsorption-induced strain, and introduced a hybrid PSO-LM optimization algorithm for precise coal seam permeability determination. Wei et al. [19] quantitatively analyzed permeability rebound in tectonically deformed and intact coals via gas transport modeling, elucidating underlying evolution mechanisms. Tang et al. [20] experimentally validated coal seam seepage dynamics and slip effects during CBM extraction using a customized triaxial servo-permeability apparatus under constant stress–gas pressure conditions. Wang et al. [21,22,23] investigated the mechanical permeability characteristics and damage constitutive model of composite coal–rock masses under different gas pressures.

The effects of gas pressure and confining pressure on the time–frequency evolution characteristics and crack propagation behavior of coal are studied, which are mainly manifested in the following ways: gas pressure reduces the effective stress, promotes crack propagation, advances the AE activity, and increases the low-frequency component, while confining pressure inhibits crack extension, improves the strength, transforms the coal to ductile, and delays the AE activity with an increase in the high-frequency component. Both of them, through effective stress coupling, jointly determine the damage mode of coal, the morphology of crack network, and the time–frequency characteristics of the accompanying AE signals. These theoretical mechanisms together constitute a three-field coupling model of “stress field–absorption field–damage field”, which provides a theoretical basis for the prediction of instability in deep coal seams.

2. Test Setups and Systems

2.1. Test Systems

In order to study the influence of gas pressure and confining pressure on the mechanical properties and time–frequency evolution of coal, the conventional triaxial compression tests were carried out on coal samples on the rock triaxial test system (RTR-4600), as shown in Figure 1. Produced by GCTS, the test system’s functions consist of a uniaxial test, triaxial test, Brazilian splitting test, hydraulic fracturing test, adjusting temperature, and an HDDP pulse attenuation permeation test. Its maximum axial force is 4600 kN, confining pressure reaches 140 MPa, osmotic pressure difference is 800 kPa, and the maximum is 1.5 MPa.

2.2. Coal Sample Preparation and Determination of Basic Mechanical Parameters

Cylindrical coal samples measuring 50 mm in diameter × 100 mm in height were fabricated in accordance with conventional triaxial compression (CTC) test standards [24]. The experimental coal exhibited an average density of 1.38 g/cm³ and a uniaxial compressive strength of 8.8 MPa.

2.3. Experimental Procedure

In this study, the confining pressures were set to 3.5 MPa, 4.4 MPa, and 5.3 MPa. At the same time, the gas pressures were selected as 0 MPa, 1 MPa, 2 Mpa, and 3 MPa. During unloading, the gas pressure should be unloaded first, followed by the confining pressure. The specific experimental process was as follows. (1) The confining pressure was increased to the designed value with a loading rate of 0.5 MPa/min. (2) The coal samples were evacuated for 2 h and then the gas was charged at the design pressure and maintained for more than 4 h to saturate the samples with adsorption. CO₂ was used instead of CH₄. (3) The axial stress was administered in a strain-controlled pattern at a rate of 0.001%/s until the samples reached the residual stage. Test schemes of conventional triaxial compression are shown in

Table 1. Test schemes.

Experimental Mode	Confining Pressure (MPa)	Gas Pressure (MPa)
Conventional triaxial compression	3.5	0
		1
		2
		3
	4.4	0
		1
		2
		3
	5.3	0
		1
		2
		3

.

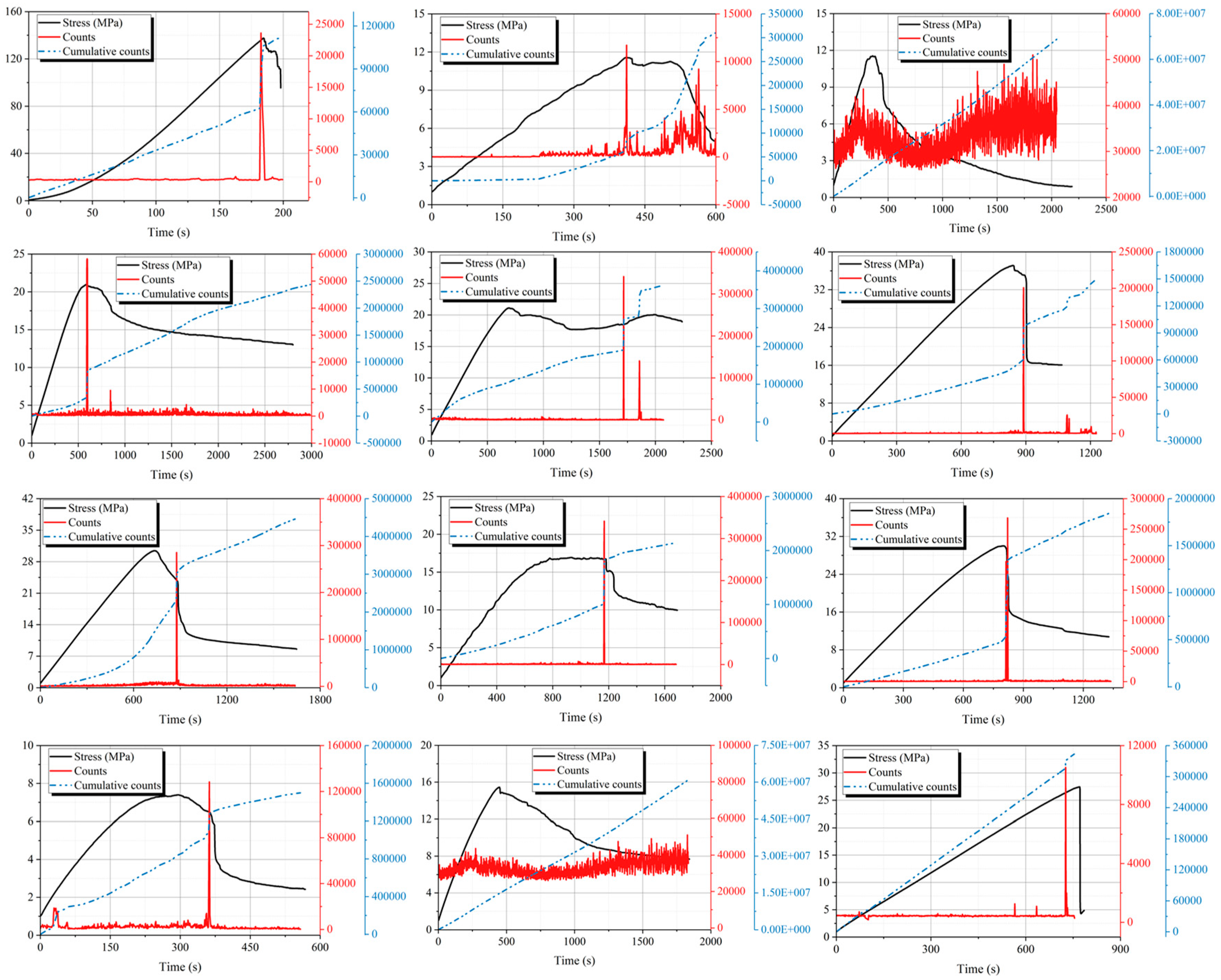
3. Results and Discussion

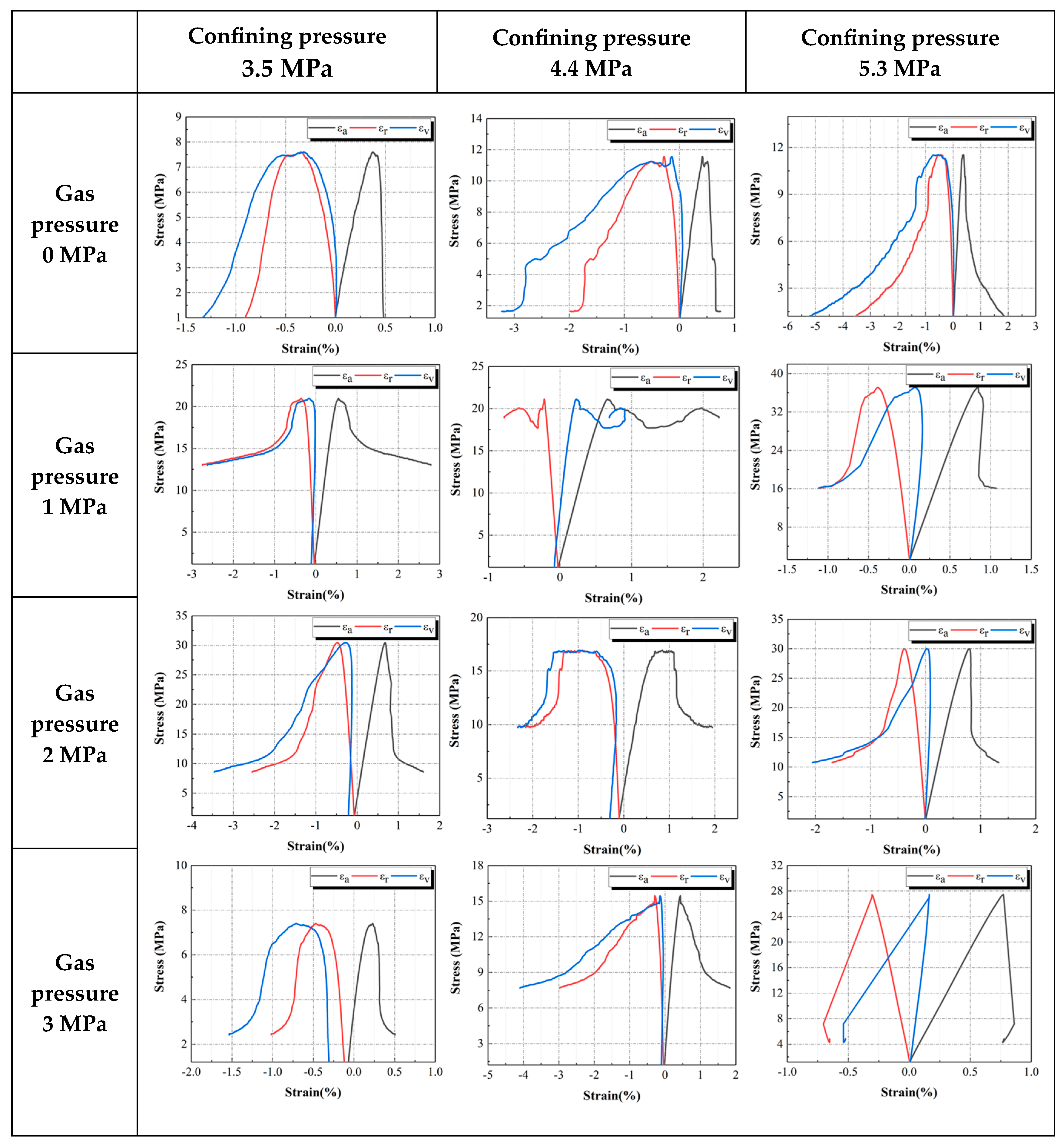
3.1. Stress–Strain Relationships and Failure Characterization

In order to analyze the fracture mode and failure mechanism of deep coal under the combined effect of gas pressure and confining pressure, the stress–strain curves of the coal samples are given in Figure 2 and the failure fracture pictures of the coal samples are given in Figure 3.

The stress–strain curve can be divided into four typical deformation stages: (1) The initial compaction stage: under the joint action of circumferential pressure σ₃ and axial stress σ₁, the primary pore and fissure system inside the coal body undergoes progressive closure, which is manifested by the monotonically increasing trend of volumetric strain εV and ε_V > 0, which is in line with the compression characteristics of porous media. (2) The linear elastic deformation stage: Axial stress–strain shows a good linear relationship, consistent with Hooke’s law. In this stage, the internal structure of the coal body remains stable, and the volumetric strain reaches the extreme point (ε_V_max) when the volumetric compression of the coal body reaches the maximum. (3) The plastic yielding stage: As the bias stress (σ₁-σ₃) continues to increase, microscopic damage begins to sprout inside the coal body, and newborn microcracks expand anisotropically. This stage is significantly characterized by the inflection point of volumetric strain and a negative growth trend (ε_V < 0), i.e., obvious dilatancy phenomenon, which is a typical mechanical response of crack expansion leading to volume expansion. (4) The post-peak damage stage: When the bias stress reaches the peak intensity, the coal body enters the strain softening stage. On the microscopic scale, the crack network undergoes three stages of evolution: (a) the exponential growth of microcrack density; (b) crack penetration to form a macroscopic fracture surface; (c) the eventual formation of a penetrating shear zone. Macroscopic damage morphology analysis (Figure 3) showed that the coal samples under triaxial stress showed a typical single shear damage pattern, with the normal direction of the damage surface at an angle of 45°–60° to the direction of the maximum principal stress, which is in line with the prediction of the Mohr–Coulomb strength theory.

In addition, at different gas pressures (0 MPa, 1 MPa, and 2 MPa), the coal samples still showed some residual strength after their peak strength, indicating that they still had some load-bearing capacity. However, when the gas pressure was increased to 3 MPa, the coal samples almost completely lost their load-bearing capacity after damage, showing typical characteristics of brittle failure.

This phenomenon can be attributed to the effect of gas pressure on the effective stress: higher gas pressure (3 MPa) significantly reduces the radial effective stress (σ₃′ = σ₃-P_p, where σ₃ is the circumferential pressure and P_p is the gas pressure), which weakened the restraining effect of radial deformation in the coal samples. During axial loading, the coal body undergoes significant lateral expansion due to the unloading effect of the internal gas pressure, which leads to the rapid expansion and penetration of microcracks, and ultimately to the complete loss of structural stability of the coal sample. This mechanism is in accordance with the Terzaghi effective stress principle and explains the mechanical behavior of brittle damage in coal bodies under high-gas-pressure conditions.

3.2. Characteristic Parameter Analysis of Damage

According to the theory of the gas adsorption–mechanical coupling effect, the presence of gas in the peri-pressure environment will significantly change the mechanical response characteristics of the coal body. In this study, through a series of triaxial compression experiments, we comprehensively analyzed the changes in coal’s mechanical behavior under different gas pressure conditions and loading paths, focusing on revealing the influence of gas pressure on key mechanical parameters such as the peak strength and elastic modulus of coal.

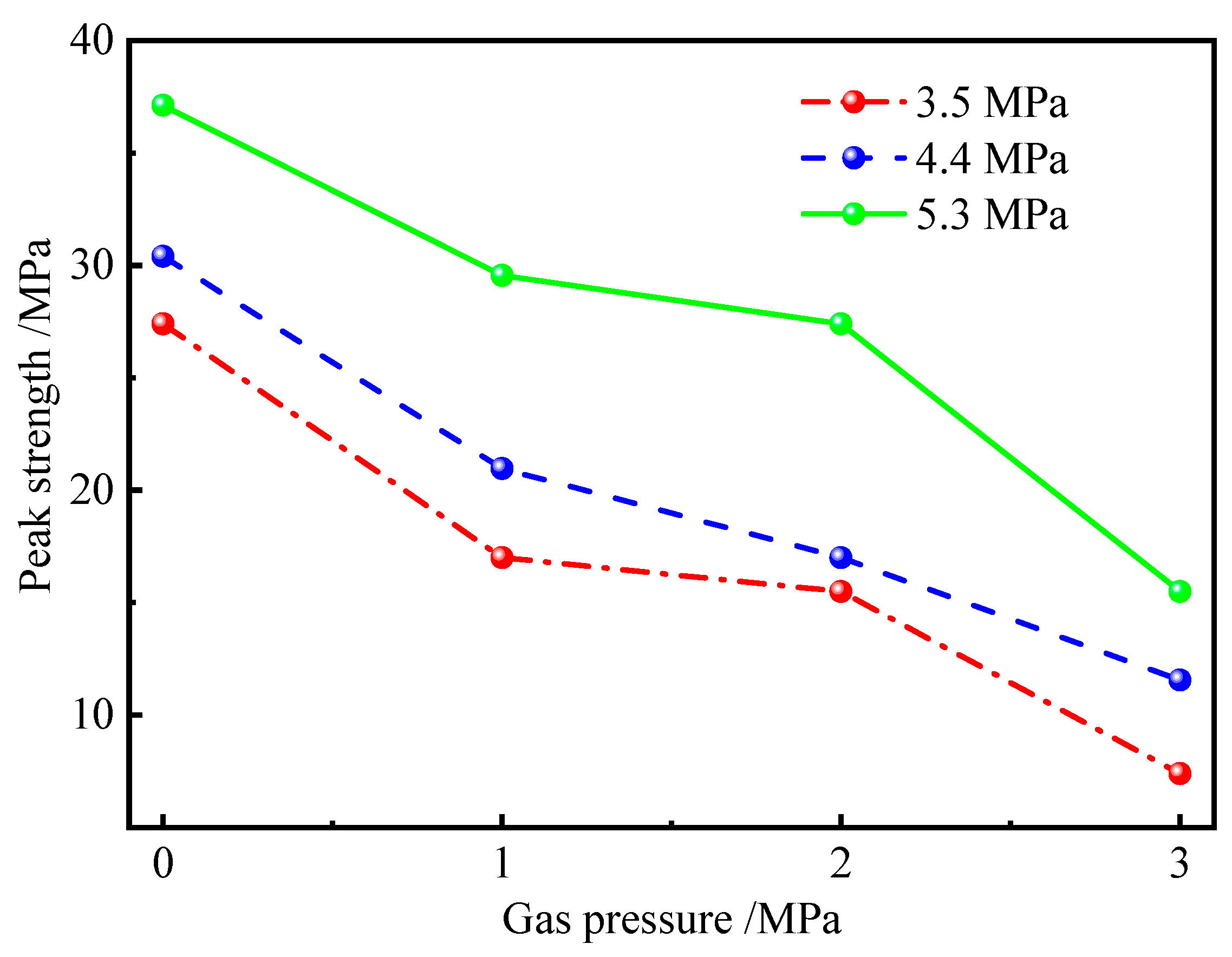
3.2.1. Peak Strength

Under different circumferential pressure conditions, the peak strength of the coal rock shows significant non-linear characteristics with the change in gas pressure. As shown in Figure 4, the experimental results show that the bearing capacity of the coal body gradually deteriorates with the increase in gas pressure, and this weakening effect is more obvious in higher-surrounding-pressure environments.

In the conventional triaxial compression test, the mechanical properties of the coal samples showed an obvious coupling effect of enclosure pressure–gas pressure. When the circumferential pressure was constant, the peak strength decreased significantly with increasing gas pressure, a phenomenon mainly caused by a dual mechanism: firstly, according to the effective stress principle, an increase in pressure reduces the effective circumferential pressure, thus weakening the axial load-bearing capacity of the coal; secondly, an increase in the amount of adsorption of gas weakens the surface bonding between the coal matrix particles, which further deteriorates the mechanical properties of the coal. On the contrary, under the condition of fixed gas pressure, the peak strength increases with the increase in the enclosure pressure, which is due to the fact that the high enclosure pressure promotes the densification of the internal structure of the coal body, improves the friction and occlusion between the particles, and ultimately strengthens the overall load-bearing capacity.

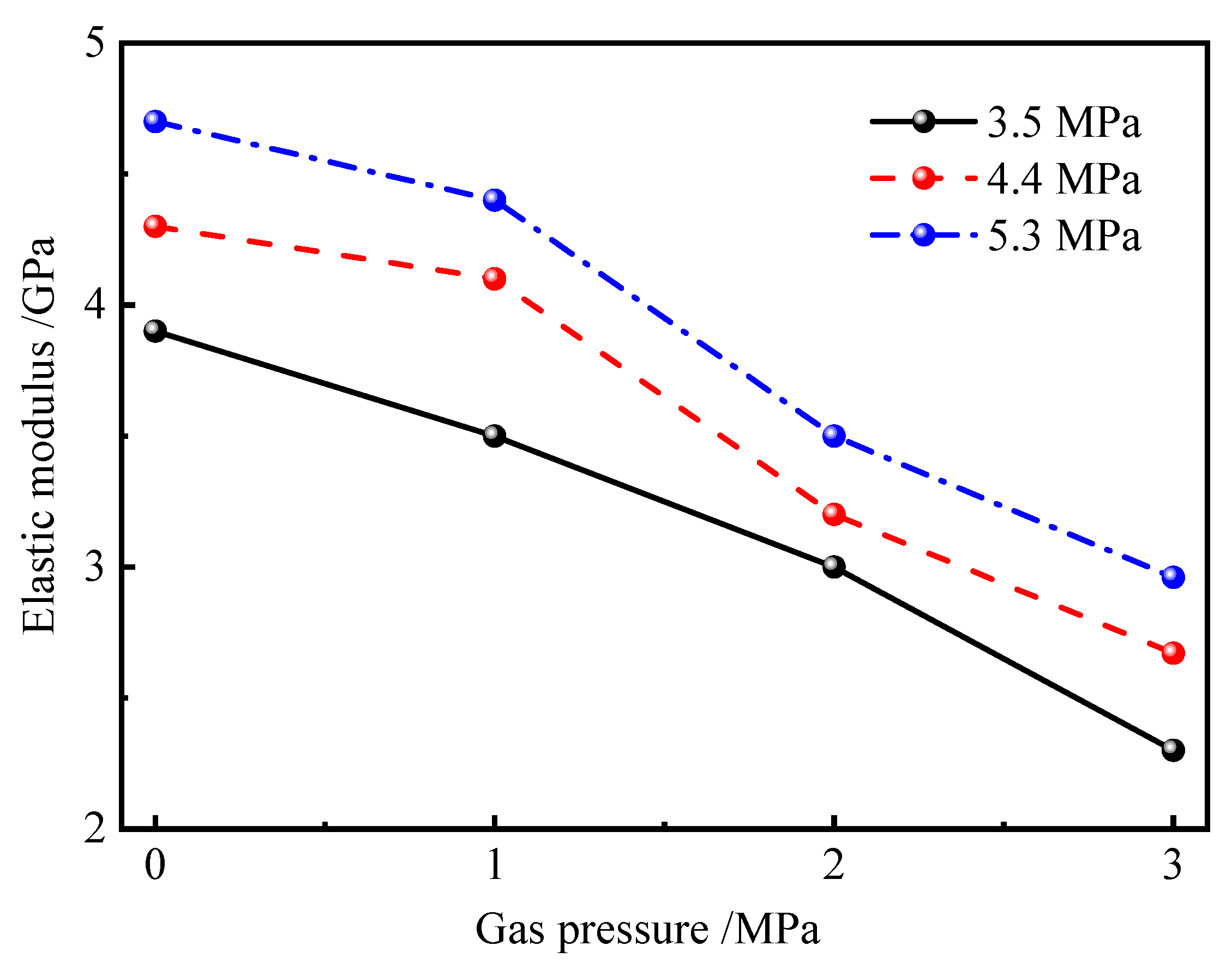
3.2.2. Elastic Modulus

The modulus of elasticity is an important index to characterize the mechanical characteristics of coal, reflecting the ability of coal to resist elastic deformation. Based on the tests in this study, the slope of the line segment of the stress–strain curve was used in this study to derive the modulus of elasticity. As shown in Figure 5, the experimental results show that the modulus of elasticity decreases from 3.9 GPa to 2.3 GPa with the increase in gas pressure to 3.5 MPa; the corresponding values are 4.3–2.67 GPa when the pressure increases to 4.4 MPa and 4.7–2.96 GPa at 5.3 MPa. This degradation effect is mainly due to the adsorption effect of the gas: on the one hand, the adsorption of gas molecules on the surface of the coal matrix weakens the inter-particle interaction force; on the other hand, the adsorption-induced expansion strain increases the particle spacing, which together leads to the reduction in the material stiffness. The modulus of elasticity increases significantly with increasing confining pressure under constant gas pressure, which is attributed to the fact that high confining pressure promotes densification of the coal body (decrease in porosity), which enhances the mechanical occlusion between the particles, and thus improves the overall deformation resistance.

3.3. Time–Frequency Evolution Analysis of AE

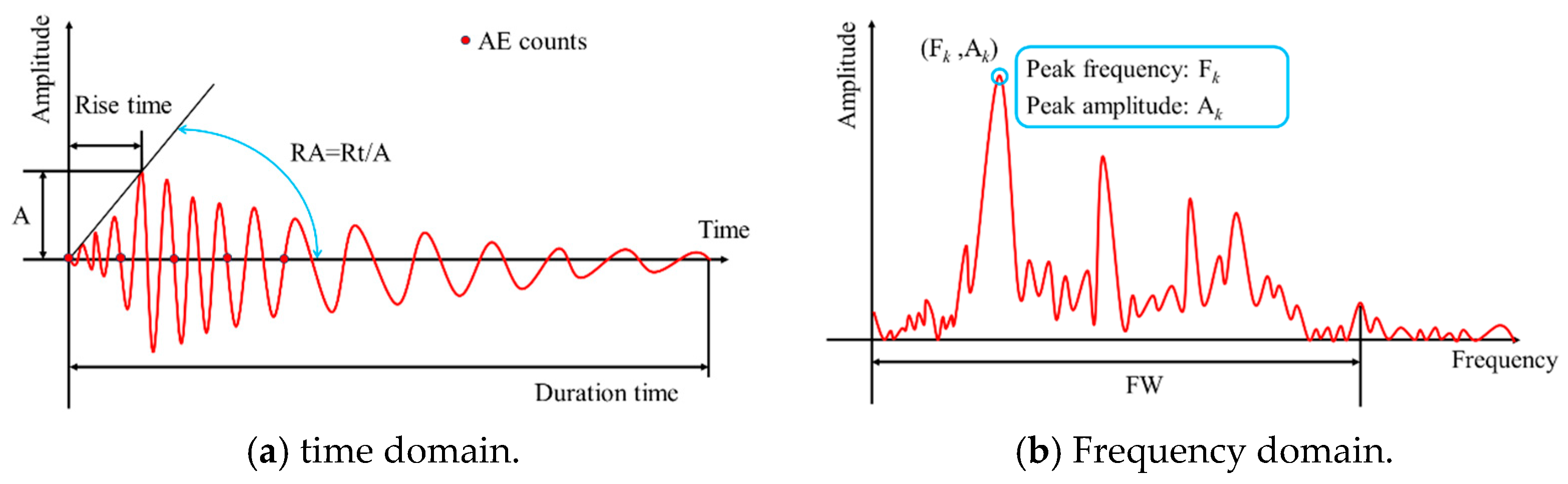
3.3.1. Introduction of AE Parameters

AE technology is capable of effectively monitoring the damage evolution of brittle materials during stress. When microcracks develop and expand inside the specimen, AE sensors can capture the elastic wave signals dynamically released by the cracks, thus realizing a non-destructive characterization of the internal microscopic damage mechanism of the material.

Elastic waves propagating in a homogeneous medium have a relatively stable dominant frequency distribution; when elastic waves travel through a non-homogeneous medium (e.g., rocks with particle interfaces, pores or micro-defects), their frequency domain characteristics will show significant time-dependent frequency modulation due to the scattering, reflection, and refraction effects caused by the difference in impedance modulation.

The selection of AE parameters is crucial to accurately characterize the dynamics of crack evolution and to quantitatively assess the crack scale. It has been shown that reliable damage assessment results can only be obtained when the AE parameters are selected to match the damage mechanism.

Table 2. Introduction to common AE parameters.

ID	Feature	Units	Description
1	Amplitude	dB, V	The maximum voltage peak in the waveform
2	Energy	J	The measurement area of waveform envelope
3	Counts	/	The number of times the transient voltage exceeds the threshold in the duration
4	Rise time	μs	Tine from start of signal to maximum amplitude
5	Rise angle	/	tan−1 (Amplitude/Rise time)
6	RA value	V × μs−1	Rise time/amplitude
7	Duration time	μs	Signal duration time
8	Average frequency	kHz	${\displaystyle \int F\left[x\right]}\left(k\right)dk/{\displaystyle \int kdk}$
9	Peak frequency	kHz	The point with the highest amplitude measured in the frequency distribution
10	Frequency centroid	kHz	${\displaystyle \int kF\left[x\right]}\left(k\right)dk/{\displaystyle \int kdk}$
11	Initiation frequency	kHz	Average frequency from signal onset to maximum amplitude
12	Weighted peak frequency	kHz	$f_{wp}=\sqrt{f_{centroid}\cdot f_{peak}}$

systematically lists the key time–frequency domain feature parameters that can be extracted from AE waveforms. Common time–frequency parameters are shown in Figure 6.

3.3.2. AE b-Value Analysis

In conventional triaxial compression tests of gas-containing coal, the AE b-value serves as a precursor indicator of damage. The dynamic evolution of the b-value quantitatively characterizes the cumulative damage degree, and its rapid decline typically signifies imminent macroscopic rupture. This b-value analysis provides a quantitative assessment of coal body stability, offering significant engineering relevance and scientific value.

The acoustic characterization of crack development trends during rock fracture processes predominantly employs the calculation of the b-value for assessment [25]. The b-value quantifies the size distribution of fracture events within a specific time interval. This parameter originates from seismology, where B. Gutenberg and C.F. Richter established the Gutenberg–Richter (G-R) relationship describing earthquake frequency–magnitude distributions [26,27]. Subsequent researchers extended this theoretical framework to the fields of AE and microseismics. Its mathematical expression is

$$lg(N)=a-bM$$

(1)

The amplitude in the formula is $M=A_{dB}/20$, where M is the magnitude, a and b are constants, and N is the seismic frequency, which is equivalent to the number of AE events.

The evolution of b-values in this experiment is shown in Figure 7. As can be seen from Figure 7, the confining pressure significantly inhibits crack extension, which is manifested in the fact that the confining pressure provides lateral constraints, significantly increases the strength and post-peak residual strength of the coal, inhibits the crack opening and extension, and transforms the coal from brittle to ductile. Moreover, the confining pressure changes the damage mode of the specimen, which is manifested by the fact that axial cleavage or monoclinic shear damage occurs more often at low confining pressures, while it transforms to conjugate shear damage or more homogeneous plastic flow at high confining pressures. At the same time, the increase in the confining pressure usually leads to higher b-values (relative increase in the proportion of small events), reflecting more dispersed damage.

The coupling effect of gas pressure and confining pressure is specifically manifested in the fact that they jointly determine the effective stress state of the coal body, also controlling the strength, deformation, and damage behavior of the coal body at the same time, and the increase in gas pressure and the decrease in confining pressure are equivalent in the sense of effective stress. Moreover, the time–frequency response of gas pressure and enclosure pressure to crack propagation presents an asymmetric state. In this case, the gas pressure affects the fracture of the specimen through the reduction in effective stress and fluid-driven action, while the confining pressure affects the damage through mechanical constraints. The combined effect of gas pressure and peripheral pressure determines whether the cracking of the specimen tends to tensile or shear damage. Specifically, tensile cracking is more pronounced at high gas pressure or low confining pressure, while shear cracking dominates at high confining pressure.

3.3.3. AE Count and Cumulative Count Analysis

The parameters of AE based on waveform analysis can effectively capture the characteristics associated with the source, while the energy detected by AE sensors represents the response to the energy release from the source. In general, a higher magnitude of damage results in a greater release of energy, leading to an increased presentation of AE energy. Additionally, the AE count rate indicates the frequency of AE events within a specific time frame and serves as a quantitative measure for assessing microcrack activity.

The occurrence of AE events in brittle rocks shares many similarities with seismic events in mechanics and statistics [28]. Laboratory-scale fracture experiments are an important method of crustal fracture and fracture extension mechanism investigation [29,30,31,32]. Count is one of the important parameters for analyzing rock AE activity.

Figure 8 shows the evolution of stress, ringing counts, and cumulative counts with time. The AE ringing counts are relatively small in the pre-compaction stage. This indicates that in the early stage, a gradual compaction process occurs inside the sample, generating more AE events, but the ringing counts are low, indicating that the rupture degree is relatively small in this stage. As the stress increases further, the rupture of the coal samples begins to occur and the ringing counts gradually increase. Especially when the stress is close to the peak, the ringing counts reach the most active state. This indicates that the AE ringing counts are most active during the rupture of the coal samples, reflecting the increased damage of the material.

Figure 9 shows the evolution of stress, events, and energy with time. The changes in the AE energy follow a similar pattern, with the energy remaining essentially unchanged at the beginning of the stress increase, which is due to the fact that the material has not yet released any significant energy from the compaction process at the initial stage. As the stress continues to increase and the coal sample ruptures, the AE energy begins to increase. The density of energy is most concentrated near the peak stress, indicating that the coal sample releases the most energy at this time and has the highest degree of damage. However, when the stress reached its peak, both the AE energy and the ringing counts decreased rapidly, indicating that many small ruptures had occurred and that there was an overall decrease in the level of damage to the material, but that some degree of internal rupture activity still existed.

4. Conclusions

In this study, the mechanical response characteristics of gas-containing coal bodies under complex stress states and their AE time–frequency evolution laws were investigated in depth through systematic conventional triaxial compression experiments. The main findings are as follows:

(1) Under conventional triaxial compression, coal damage in this study predominantly manifests as monoclinic shear failure, accompanied by axial splitting or debris ejection. The stress–strain curve evolution can be categorized into four distinct stages: (i) pore compaction, (ii) elastic deformation, (iii) stable fracture propagation, (iv) unstable fracture development leading to failure.

(2) The peak strength of coal demonstrates a significant strengthening effect under confining pressure but a weakening effect under gas pressure. At a constant confining pressure, the peak strength exhibits an exponential decay with increasing gas pressure, confirming that gas pressure substantially reduces coal strength.

(3) The elastic modulus exhibits a positive correlation with confining pressure and a negative correlation with gas pressure. Specifically, for a given gas pressure, the elastic modulus increases with higher confining pressure, whereas for a fixed confining pressure, it decreases with increasing gas pressure.

(4) AE b-value analysis reveals that elevated gas pressure promotes a transition from brittle to ductile failure modes. Additionally, time–frequency analysis indicates that high-frequency AE signals diminish with increasing gas pressure, while the energy release rate shows an inverse relationship with gas pressure.