Abstract
The accurate and effective prediction of PM2.5 concentrations is crucial for mitigating air pollution, improving environmental quality, and safeguarding public health. To address the challenge of strong temporal correlations in PM2.5 concentration forecasting, this paper proposes a novel hybrid model that integrates the Particle Optimization Algorithm (POA) and Variational Mode Decomposition (VMD) with the Long Short-Term Memory (LSTM) network. First, POA is employed to optimize VMD by adaptively determining the optimal parameter combination [k, α], enabling the decomposition of the original PM2.5 time series into subcomponents while reducing data noise. Subsequently, an LSTM model is constructed to predict each subcomponent individually, and the predictions are aggregated to derive hourly PM2.5 concentration forecasts. Empirical analysis using datasets from Beijing, Tianjin, and Tangshan demonstrates the following key findings: (1) LSTM outperforms traditional machine learning models in time series forecasting. (2) The proposed model exhibits superior effectiveness and robustness, achieving optimal performance metrics (e.g., MAE: 0.7183, RMSE: 0.8807, MAPE: 4.01%, R2: 99.78%) in comparative experiments, as exemplified by the Beijing dataset. (3) The integration of POA with serial decomposition techniques effectively handles highly volatile and nonlinear data. This model provides a novel and reliable tool for PM2.5 concentration prediction, offering significant benefits for governmental decision-making and public awareness.
1. Introduction
With the acceleration of urbanization and industrialization, environmental pollution has become a global problem, seriously threatening human production and life [1]. Among the various pollutants, PM2.5 (aerodynamic equivalent diameter ≤ 2.5 microns in ambient air) of lung-accessible particulate matter is a particularly dangerous air pollutant because its fine particles are easily inhaled by humans and deposited in the lungs, leading to respiratory and cardiovascular health problems. Airborne PM can attach to both bacteria and viruses, which has a significant negative impact on the human immune system and poses a serious threat to people’s lives and health, and high levels of PM2.5 may also have a variety of effects on the physical and chemical processes of the atmosphere, leading to the formation of extreme weather [2]. PM2.5 concentrations are not only related to direct emissions of air pollutants but also chemical and physical reactions between air pollutants such as SO2, NO2, CO, and O3, which in turn generate new air pollutants as well as fine particulate matter to further influence PM2.5 concentrations [3].
PM2.5 originates from dual pathways: natural geochemical processes and anthropogenic activities, with the latter posing greater environmental risks. Natural sources comprise three primary mechanisms: terrestrial–aerosol mobilization (wind-driven dispersion of soil-derived mineral oxides and marine-generated sea salt aerosols), biogenic emissions (seasonal release of pollen–spore complexes and microbial bioaerosols), and geophysical disturbances (transient events including volcanic eruptions, biomass combustion, and dust storms that generate episodic particulate loading). Anthropogenic sources exhibit distinct spatiotemporal patterns, categorized as follows: stationary sources (emissions from fossil fuel combustion in power generation, metallurgical operations, and industrial manufacturing) and mobile sources (combustion byproducts from transportation systems, dominated by carbonaceous particulates with heterogeneous size distributions). Notably, industrial processes contribute significantly to secondary aerosol formation through complex chemical transformations, particularly sulfate and organic particulate generation [4]. The mobile sources are mainly exhaust gases emitted into the atmosphere from the use of fuel in the operation of various types of transportation.
On 17 October 2013, the International Agency for Research on Cancer, an agency of the World Health Organization (WHO), released a report that found for the first time that PM2.5 causes cancer. Globally, about 2.1 million people die each year due to rising concentrations of particulate matter such as PM2.5. On 22 September 2021, the WHO released the Global Air Quality Guidelines 2021. Following the Global Air Quality Guideline Values (2005), the WHO has adopted a systematic approach to the review and assessment of new evidence on the impact of global air pollution on population health in recent years and has made new recommendations on air quality control from the perspective of avoiding the impact of air pollution on population health.
PM2.5 is an important indicator of air pollution, and its high concentration can have a great impact on human health and environmental quality. In recent years, with the accelerated urbanization and industrialization, the emission of PM2.5 is also increasing year by year. For example, in the northern part of China, air pollution is more serious in the winter because it is more affected by pollution emissions during the heating period. People in the haze environment, whether for daily travel or health conditions, are greatly affected, including in the Beijing, Tianjin, and Tangshan areas—China’s important economic centers—where PM2.5 concentration is high, causing a great threat to the ecological environment and the health of residents [5,6,7]. High-resolution PM2.5 predictive modeling delivers dual societal benefits through a multi-stakeholder framework. Primarily, it establishes an evidence base for data-driven decision support systems in environmental governance, enabling policymakers to optimize emission control protocols across energy, industrial, and urban sectors. Simultaneously, the spatiotemporal resolution of such models empowers precision public health interventions by forecasting particulate exposure hotspots, allowing populations to strategically adjust mobility patterns and occupational schedules [8,9].
The mainstream PM2.5 prediction methods in the current research mainly include statistical models, machine learning models, and hybrid models. Some researchers have used traditional statistical methods based on multivariate statistical analysis to achieve PM2.5 prediction [10,11]; however, PM2.5 time series are highly nonlinear and non-stationary, and the use of traditional statistical methods to predict PM2.5 is limited. Some researchers have also analyzed historical PM2.5 data obtained from ground-based monitoring stations to study the trend of its concentration over time [12].
Machine learning approaches have demonstrated significant potential in PM2.5 forecasting, with architecture including Back Propagation (BP) Neural Networks [13,14], Extreme Learning Machines (ELM) [15], Support Vector Regression [16], and deep learning variants like Convolutional Neural Networks [17] and LSTM being extensively applied [18,19]. Nevertheless, the inherent nonlinearity and non-stationarity of air pollutant time series pose fundamental challenges to prediction accuracy, as evidenced by persistent residual errors in multi-model comparative studies [20].
Emerging methodological frameworks address the non-stationarity of PM2.5 time series through adaptive decomposition algorithms (e.g., EMD, VMD), which decouple complex pollutant signals into intrinsic mode functions (IMFs) with improved stationarity characteristics [21,22]. For instance, scholars effectively quantified the reduction in PM2.5 concentration attributable to air quality assurance measures during the Beijing Winter Olympics by employing an AI-based BSTS approach in conjunction with the RF–LSTM hybrid model. This process involved multi-scale feature extraction of the PM2.5 time series, enabling the capture of potential transient pollution episodes while maintaining the robustness and reliability of the results under complex meteorological and emission conditions [23]. EMD is used to decompose PM2.5 into a set of smooth modes [24,25], but EMD is prone to modal mixing [26], which seriously affects the decomposition effect. VMD is a new adaptive decomposition method that can handle nonlinear and non-stationary sequences well, and has been widely used in fault diagnosis and time series prediction since it was proposed [27]. The novel VMD is used to smooth out the sequences, and the VMD adds a bandwidth constraint to effectively solve the modal mixing problem. However, how to automatically select the number of intrinsic mode functions and penalty parameters is still a problem to be solved [28].
Guo H. et al. developed a novel prediction framework that integrates VMD with an improved whale optimization algorithm, effectively decomposing PM2.5 concentration sequences and optimizing weight coefficients through intelligent parameter adjustment, ultimately achieving enhanced forecasting accuracy through refined series reconstruction [29]. Similarly, Yu M. et al. proposed a hybrid methodology for wind power prediction by implementing whale optimization algorithm-enhanced VMD processing, which enables the adaptive determination of optimal decomposition parameters [k, α] through iterative population-based optimization, thereby effectively mitigating noise interference in original wind power sequences [30]. From an algorithmic evolution perspective, the POA presents distinct advantages in complex optimization tasks. This metaheuristic technique mimics the cooperative hunting strategies of pelican populations, demonstrating superior global search capability through its unique dynamic exploration–exploitation balance mechanism [5]. Compared to conventional optimization methods, POA exhibits enhanced solution precision and robustness against local optima convergence, particularly in high-dimensional nonlinear optimization scenarios.
Although existing hybrid models significantly enhance PM2.5 prediction performance through the integration of signal decomposition and machine learning techniques, their core limitations remain concentrated in parametric optimization bottlenecks and insufficient decomposition adaptability. Specifically, conventional VMD relies on empirical parameter settings, requiring manual presets for mode number (k) and penalty parameter (α) due to the absence of adaptive mechanisms. This subjects decomposition outcomes to subjective influences. Furthermore, optimization algorithms exhibit tendencies toward local optima convergence during parameter searches, yielding suboptimal solutions that constrain decomposition quality. Residual mode-mixing risks also persist: while VMD alleviates EMD-inherent mode mixing via bandwidth constraints, improper parameter selection may retain high-frequency noise, thereby undermining subsequence stationarity.
To overcome these constraints, the proposed POA–VMD–LSTM model introduces a novel intelligent optimizer employing the recently developed POA to autonomously identify optimal VMD parameters (k, α). Leveraging POA’s superior global search capability prevents local optima convergence, fundamentally enhancing decomposition precision. The resultant stationary sub-modes from POA–VMD are fed into LSTM networks to simultaneously capture long-term and short-term dependencies, thereby overcoming single-model deficiencies in characterizing nonlinear, non-stationary features. This integrated optimization–decomposition–prediction framework systematically reduces sequence uncertainty through its adaptive architecture.
In this paper, a hybrid PM2.5 hourly concentration prediction model based on the combination of POA–VMD and LSTM is proposed to empirically analyze three areas in Beijing, Tianjin, and Tangshan, and the selected evaluation indexes are compared with the prediction results of the other four PM2.5 prediction models. The improved VMD model for PM2.5 prediction reduces the uncertainty of the series and improves the accuracy of the prediction.
The main innovations of this paper are as follows:
(1) An improved decomposition method is proposed on the basis of POA and VMD. POA is used to adaptively optimize the VMD parameters, i.e., the number of intrinsic mode functions and penalty parameters, in order to optimize the decomposition effect of VMD, improve the input quality of the prediction model, and improve the complexity of PM2.5 series.
(2) It is determined that the LSTM deep learning model has higher prediction accuracy and better prediction performance in PM2.5 concentration prediction. Compare the evaluation indexes of BP, ELM, and LSTM to determine the deep learning model to improve the PM2.5 prediction accuracy.
(3) Different evaluation metrics are used to assess the performance of the proposed model. The POA–VMD–LSTM model has the best evaluation metrics and the highest prediction accuracy compared to the other models.
The following are the other subsections of this paper: In Section 2, the review describes the methods and theories applied in this paper. In Section 3, the established PM2.5 hourly concentration prediction framework, including data preprocessing, POA–VMD decomposition, machine learning, and prediction result modules, is presented. In Section 4, the data sources of this paper are introduced, and the model evaluation indicators are selected. In Section 5, an empirical analysis is conducted to verify the validity of the prediction model in this paper. Finally, Section 6 summarizes the work of this paper, considers the shortcomings of the study, and puts forward the prospect.
2. Method and Models
2.1. VMD
Modern signal processing methodologies address the decomposition of nonlinear and non-stationary signals through constrained variational optimization frameworks. These advanced approaches iteratively resolve model parameters to adaptively characterize the spectral attributes of signal components, demonstrating enhanced robustness against noise interference and superior mode separability compared to conventional techniques [31]. The systematic integration of filter bank design with optimization theory establishes a novel paradigm for resolving complex environmental signals, particularly in scenarios requiring high-fidelity feature extraction.
VMD can decompose the original signal sequence into several intrinsic mode functions (IMF), i.e., amplitude-modulated and frequency-modulated sub-signals . The calculation method is as follows:
where is the number of intrinsic mode functions; is the time; is the instantaneous amplitude and satisfies ; is the instantaneous frequency; is the non-decreasing function.
In order to ensure sparsity, VMD can be used to decompose the original input signal into a series of amplitude-modulated frequency modulated sub-signals ; the resulting intrinsic mode functions should satisfy the constraint that they are approximately equal to the original input sequence after reconstruction, and the sum of the estimated bandwidths of each mode should be minimized.
The process of constructing the variational problem requires the following three steps:
(1) Hilbert transformation of the modal function to obtain its corresponding analytic signal, which in turn yields the one-sided spectrum.
(2) To adjust the central band of the modal function to the fundamental band, multiply the exponential function of the central frequency with the one-sided spectrum.
(3) Gaussian smoothing is performed on the demodulated signal to obtain the bandwidth of each segment. The objective function of the band-constrained variational problem required to be solved at this point is as follows:
where is the first IMF component after VMD decomposition; is the instantaneous frequency of the first IMF component; is the partial derivative function; is the unit impulse function; is the imaginary unit; is the convolution; is the Hilbert transform.
In solving the optimal solution of the constrained variational model, it is necessary to convert the constrained variational problem in Equation (2) into an unconstrained variational problem by introducing the penalty parameters α and the Lagrangian operator . At this point, the expression of the constructed augmented Lagrangian function is as follows:
From Equation (3), it can be seen that k and α affect the decomposition performance of VMD. If k is small, multiple components of the signal may be contained in one mode at the same time; if k is large, it will result in one component contained in multiple intrinsic mode functions, and the center frequencies obtained from iterations will overlap. For α, if α is large, the bandwidth limit will be narrow, which leads to the elimination of useful frequency components; conversely, redundant frequency components will be retained. Therefore, this paper proposes the Pelican optimization algorithm to optimally determine the optimal combination of parameters (k, α).
2.2. POA
The proposed algorithm draws inspiration from the cooperative foraging behavior observed in pelican colonies. Three key biological characteristics are abstracted into computational operators:
- Nonlinear Trajectory Exploration: Pelicans employ spiral flight patterns with altitude-dependent turning radii to survey three-dimensional spaces.
- Adaptive Swarm Density Control: Visual signal propagation regulates inter-individual distances based on prey distribution density.
- Probabilistic Plunge-diving: Stochastic gradient descent guided by local prey concentration gradients.
The pelican population initialization is mathematically described as follows:
where is the position of i-th pelican in the j-th dimension; is the population size; is the problem dimensionality (number of decision variables); , , and are the feasible bounds for the j-th dimension.
The population matrix is constructed as follows:
with a corresponding objective function vector:
Phase I: Prey Approaching (Global Exploration).
The algorithm simulates pelicans’ hunting behavior through two distinct phases. During global exploration, pelicans locate and approach randomly generated prey positions:
where is the randomly generated prey position; is the convergence coefficient; is the social learning factor; , is the stochastic scaling parameter.
The position update follows greedy selection:
Phase II: Surface Flight (Local Exploitation).
During local exploitation, pelicans perform an intensive search through wing-flapping dynamics:
where is the neighborhood radius in j-th dimension; is the maximum iteration; is the mean position in the j-th dimension.
The final position update follows:
2.3. POA–VMD
The VMD method enables the decomposition of raw PM2.5 concentration sequences into multiple intrinsic mode functions (IMFs) characterized by distinct frequency bands and enhanced regularity, thereby reducing sequence complexity. However, conventional VMD implementations require manual presetting of two critical hyperparameters: the number of IMF components (k) and the penalty factor (α). Suboptimal parameter selection may induce either over-decomposition (excessive k values) or under-decomposition (insufficient k values), while improper α configurations risk critical bandwidth information loss or redundant noise retention [32]. The current parameter determination methods, such as the empirical center frequency observation technique, exhibit notable limitations: they only empirically estimate k while failing to optimize α, introducing subjectivity and compromising decomposition fidelity.
To overcome these constraints, we propose an automated parameter optimization framework integrating the POA with minimum envelope entropy criteria. The envelope entropy metric quantifies signal sparsity characteristics, where higher entropy values correlate with noise-dominated IMFs, whereas lower entropy indicates feature-rich components. This relationship is formalized as follows:
where is the Hilbert-demodulated envelope of VMD-derived IMFs; is the normalized probability distribution sequence of ; corresponds to the sampling points.
By minimizing envelope entropy through a POA-driven parameter search (see Figure 1), the POA–VMD hybrid algorithm achieves dual optimization of both k and α, effectively balancing decomposition granularity with feature preservation.

Figure 1.
Flow chart of the prediction system.
2.4. LSTM
The LSTM network, a neural network algorithm, is widely employed for processing sequential data. It effectively resolves the gradient vanishing and explosion issues inherent in traditional Recurrent Neural Networks when handling long-sequence data [33]. The core mechanism of LSTM lies in its introduction of three gate controllers—the input gate, forget gate, and output gate—to regulate information flow, thereby enabling effective management of long- and short-term memory. Specifically, at time step t, xt denotes the input value of the memory cell and ht represents the current state value of the hidden layer. The initial values of the input gate (it), forget gate (ft), and output gate (ot) are defined as follows:
where at moment , is the input value of the memory unit; is the current value of the hidden layer of the memory unit; is the sigmoid activation function, which maps input values to probability values between 0 and 1; is the weight matrix; is the parameter matrices from the input layer to the hidden layer; corresponds to parameter matrices from the hidden layer to the output layer; is the bias term; is the candidate value of the memory unit.
where subscripts represent memory cells.
3. Construction of the Proposed Hybrid Model
The combined PM2.5 hourly concentration prediction model constructed in this paper is shown in Figure 1. The model consists of the following parts:
In the first part, data preprocessing, the original data sequence is input, the parameter range of the neutralization of the VMD algorithm is set, and the parameters in the POA model, including the population size and the maximum number of iterations, are initialized.
In the second part, the VMD parameters are optimized by the POA algorithm. The VMD is optimized using the pelican optimization algorithm to find the number of intrinsic mode functions and penalty parameters that make the VMD decomposition optimal in a limited number of iterations. The minimal value of the envelope entropy is used as the fitness function of the pelican optimization algorithm, and several iterations are performed to compare the fitness values, continuously update the pelican position, and save the current solution of the optimal parameter combination left. The original data sequence is decomposed by POA–VMD to generate subsequences.
In the third part, machine learning, determine the training set and test set, input the POA–VMD decomposed subsequence into the LSTM model, and perform prediction, respectively.
In the fourth part, the prediction results are output. The prediction results output from the LSTM model are summed to obtain the PM2.5 hourly concentration prediction. Based on the selected evaluation index, the effectiveness of the proposed hybrid prediction model is demonstrated.
4. Data Sources and Evaluation Index
4.1. Data Sources
Since there are many cities in the Beijing–Tianjin–Hebei region, three cities, Beijing, Tianjin, and Tangshan, were mainly selected as examples for analysis in this paper based on factors such as geographical location (Figure 2) and urban background. In this paper, the PM2.5 hourly concentration data of Beijing, Tianjin, and Tangshan from 1 February 2023 to 30 April 2023 were selected, and the original data are shown in Figure 3. The PM2.5 hourly concentration data used were obtained from the website, which encompasses air quality data for each city in China. For each city, the samples of 2136 time points were divided into a training set and a test set, as shown in Table 1.
Figure 2.
Location of Beijing–Tianjin–Tangshan.

Figure 3.
Original hourly PM2.5 concentration time series of Beijing–Tianjin–Tangshan.

Table 1.
Detailed data for three samples.
4.2. Evaluation Indicators of Prediction Model Results
In order to further validate the predictive performance of the model and its effectiveness, this study will evaluate the performance of the model using four classical error metrics—the mean absolute error (MAE), the root mean square error (RMSE), the mean absolute percentage error (MAPE), and the goodness of fit (R2)—which were adopted to implement error checks in the data test.
In addition, this paper introduces the improvement rates of the above four indicators to compare the advantages and disadvantages of different models, i.e., the improvement rates of , , and .
where subscript 1 denotes the comparison model and subscript 2 denotes the baseline model.
5. Case Analysis
The prediction analysis and comparison of the measured PM2.5 concentration data for 2023 in Beijing, Tianjin, and Tangshan were conducted to verify the effectiveness and superiority of the combined model. The actual PM2.5 concentration data from 1 February to 30 April were sampled, at an interval of 60 min, i.e., 24 sampling points per day, for a total of 2136 sampling points, with the first 2000 sampling points as the training set and 136 sampling points as the test set.
5.1. POA–VMD Decomposition
The number of modalities, k, and penalty parameters, α, of VMD are optimized using the method in Section 2.3. In order to determine the optimal settings for the population size and the number of iterations, we conducted a sensitivity analysis. The results indicated that for the problem dimension addressed in this study, a population size of 20 iterations provides a good balance between computational efficiency and the ability to effectively explore the solution space. Given the relatively lower dimensionality of the problem, these settings allow for a more efficient computation of the optimized parameter values. Based on the assessment of signal decomposition quality and references to prior studies [34], the range of the number of modalities k is set to (2,15), and the range of the penalty parameter α is set to (10,1000). All other parameters of the VMD are taken as default values.
Regarding the convergence curves of the VMD decomposition of the PM2.5 dataset in Beijing, Tianjin, and Tangshan using the POA algorithm, the optimization process curves of the number of intrinsic mode functions k and the optimization process curves of the penalty parameter α are shown in Figure 4. The optimal parameter combinations [k, α] of VMD decomposition for the Beijing–Tianjin–Tangshan PM2.5 data set optimized by the POA algorithm are (8,672), (8,711), and (8,910), in order. Taking the Beijing PM2.5 dataset as an example, the results of the POA–VMD decomposition are shown in Figure 5.
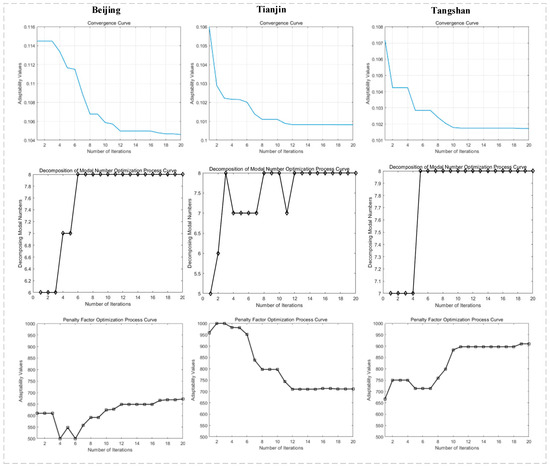
Figure 4.
POA–VMD parameter optimization process.

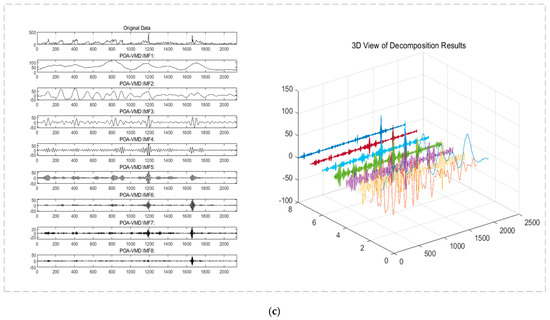
Figure 5.
POA–VMD decomposition results of Beijing–Tianjin–Tangshan. (a) POA–VMD decomposition result of Beijing; (b) POA–VMD decomposition result of Tianjin; (c) POA–VMD decomposition result of Tangshan.
5.2. PM2.5 Hourly Concentration Prediction
5.2.1. Model Input
In this paper, the time series of PM2.5 concentrations in Beijing, Tianjin, and Tangshan are selected as samples. Based on a combination of preliminary experiments and a literature review [35], the number of iterations of the LSTM model is set to 100, and the initial learning rate is 0.008. With the increase of the number of LSTM hidden layers, although the fitting ability of the prediction model will be further improved, if the model is not limited, there will be problems such as too long prediction time and overfitting, so this paper sets the LSTM hidden layers as two layers—the number of layers is 100 and 50, respectively.
5.2.2. Predicted Results
The time series of PM2.5 concentrations in Beijing, Tianjin, and Tangshan were input into BP, ELM, and LSTM models, respectively, to obtain the corresponding predicted results.
The traditional BP neural network in the field of machine learning is a forward feedback network, which requires setting the number of network layers and using a back propagation algorithm for weight update during training. In this paper, we set the number of layers of the network to 7 (Hiddennum = 7), the number of iterations to 80 (Iteration = 80), the learning rate to 0.05 (Learning rate = 0.05), and the mean square error to 0.0001. The ELM is a single-layer forward network that has an arbitrary number of hidden layer neurons and uses least squares for weight calculation during training, and the number of nodes in the hidden layer of ELM is set to 30 in this paper. The LSTM in the field of deep learning is a recurrent neural network that can effectively process time series data with strong memory capability, and the number of LSTM iterations in this paper is set to 100.
The BP, ELM, LSTM, VMD–LSTM, and POA–VMD–LSTM models were used to predict PM2.5 in Beijing, Tianjin, and Tangshan, respectively. The predicted PM2.5 values of each model were compared with the real PM2.5 values, scatter plots were plotted as shown in Figure 6, and the errors between the predicted results and the actual values were calculated. Figure 7 shows the five prediction models for the Beijing, Tianjin, and Tangshan error values. The prediction effect of the model is judged by observing the distribution trend in the scatter plot. If the distribution trend of the points is close to the diagonal, the difference between the predicted value and the true value is smaller, indicating that the model has a better prediction effect, and vice versa.

Figure 6.
Predicted results of each model.
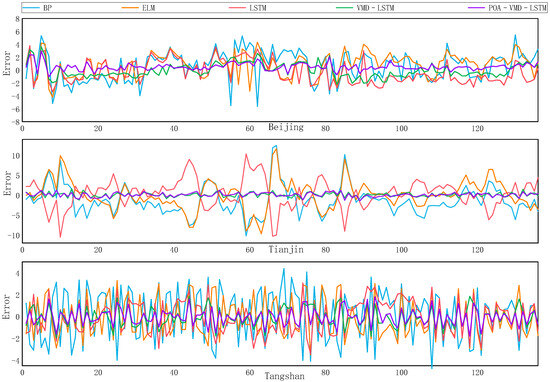
Figure 7.
Predicted errors of each model.
Figure 6 and Figure 7 show that the predicted values of the BP, ELM, and LSTM models are relatively different from the true values, the distribution is relatively scattered, the overall trend is similar to that of the true values but fluctuates more, and the prediction error is larger. The VMD–LSTM model has a more concentrated distribution of prediction results, and the overall trend is similar to that of the real value but less volatile than the BP, ELM, and LSTM models, with relatively small prediction errors, and is able to capture the long-term trend of PM2.5. In comparison, the POA–VMD–LSTM model proposed in this paper has the strongest predictive power, and the overall trend is similar and less volatile than the trend of the true values, proving the predictive accuracy of the POA–VMD–LSTM model.
Overall, in terms of the error between the predicted and true values, the model proposed in this paper has a smaller and more concentrated error float than other models, and the prediction is more accurate.
There are also some differences in the prediction accuracy of the POA–VMD–LSTM model between different cities in the same time dimension, with relatively small fluctuations in prediction errors in Tianjin.
To better demonstrate the good performance of POA–VMD–LSTM in PM2.5 concentration prediction, this paper compares the performance of BP (M1), ELM (M2), LSTM (M3), VMD–LSTM (M4), and POA–VMD–LSTM (M5) according to the four classical error metrics selected. The results are shown in Table 2.

Table 2.
Results of each model.
Different indicators can reflect the predictive power of a model from different perspectives, and different models evaluated with different indicators show different strengths and weaknesses. MAE, RMSE, and MAPE are common measures of prediction error, with smaller MAE and RMSE indicating better model performance and smaller MAPE indicating better prediction accuracy. The goodness of fit indicator reflects the degree of correlation between the model and the true value, and its value ranges from 0 to 1. The closer it is to 1, the better the fit between the model and the true value.
It can be intuitively seen from Figure 8 that the MAE values, RMSE values, and MAPE values of LSTM are generally lower than those of BP and ELM in PM2.5 prediction, and the R2 values of LSTM are relatively high, which proves that LSTM has better prediction accuracy and prediction fitting performance for this PM2.5 prediction sample. In addition, VMD–LSTM outperforms LSTM in all metrics, which illustrates the need to optimize the learning capability of LSTM using VMD, which can reduce the complexity and non-linear characteristics of the PM2.5 concentration time series and improve the prediction accuracy of the model. Compared to VMD-LSTM, the POA–VMD–LSTM model performs better in MAE, RMSE, MAPE, and R2 indicators, which indicates the effectiveness of the POA algorithm in improving the model.
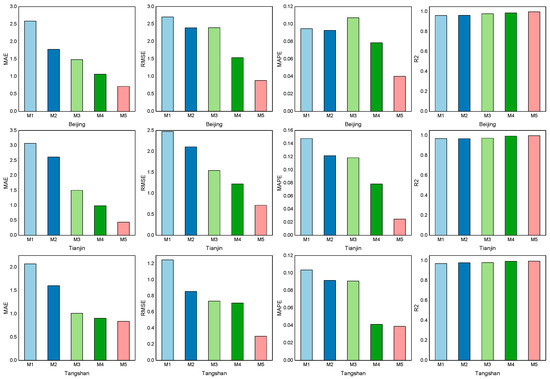
Figure 8.
Comparison of prediction errors of each model.
In reference to Ref. [35], we conducted a comparative analysis of the WOA–VMD–LSTM and POA–VMD–LSTM models using the Beijing dataset to demonstrate the effectiveness of POA optimization. The results of this comparison provide empirical evidence of the superior performance of the POA in optimizing the parameters of the VMD algorithm, thereby enhancing the accuracy and robustness of PM2.5 concentration predictions. The prediction results are shown in Figure 9.

Figure 9.
Comparison of prediction of WOA–VMD–LSTM and POA–VMD–LSTM.
5.3. Model Performance Discussion
This section discusses and analyzes the improvement rates of the indicators of BP (M1), ELM (M2), LSTM (M3), VMD–LSTM (M4), and POA–VMD–LSTM (M5) in the prediction process and analyzes the data on the prediction performance of the models to accurately compare the performance. The improvement rates of the model comparison indicators are shown in Figure 10 and Table 3.
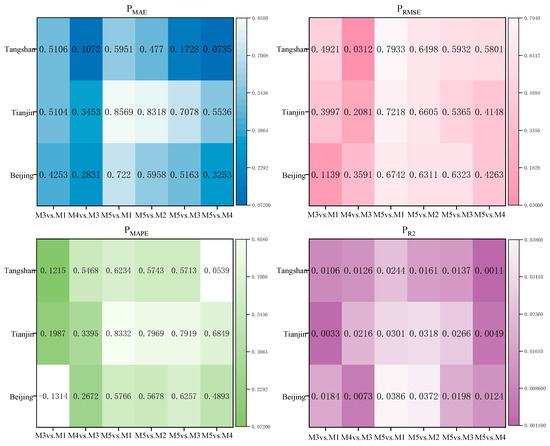
Figure 10.
Model performance comparison.

Table 3.
The percentage improvement of contrast models.
LSTM has higher prediction accuracy and better prediction performance for the PM2.5 concentration time series. Taking the Beijing city series as an example, this paper uses BP (M1) as the baseline model and LSTM (M3) as the comparison model. is 0.4253, indicating a 42.53% reduction in the MAE of the predicted value series, and similarly indicate that the improved prediction model reduces the prediction error, and is 0.0184, indicating a 1.84% improvement in the fit.
VMD can reduce the complexity of the PM2.5 time series. Taking the Tianjin city series as an example, this paper uses LSTM (M3) as the baseline model and VMD–LSTM (M4) as the comparison model. After the VMD improvement, the MAE and RMSE indicators are reduced by 34.53% and 20.81%, respectively, the MAPE indicator is reduced by 33.95%, and the goodness of fit is improved by 2.16%.
The POA algorithm improves the algorithm model with good results, and the prediction accuracy is significantly improved after improving on the VMD–LSTM model. Taking the city of Tangshan as an example, the POA–VMD–LSTM model decreased by 7.35%, 58.01%, and 5.39% in MAE, RMSE, and MAPE, respectively, and improved the goodness of fit by 0.11% compared with VMD–LSTM, which indicates that the POA algorithm can effectively improve the prediction accuracy of the model.
6. Conclusions
This study proposes a novel POA–VMD–LSTM hybrid model for hourly PM2.5 concentration prediction. Utilizing historical PM2.5 data, the framework integrates variational mode decomposition optimized by pelican optimization algorithm (POA–VMD) with LSTM networks to enhance prediction accuracy through noise reduction, feature decomposition, and adaptive sequence learning. Experimental validation across three cities (Beijing, Tianjin, and Tangshan) demonstrates the model’s generalization capability. The key findings are summarized as follows:
(1) The LSTM-based prediction framework outperforms conventional machine learning models in handling long-term PM2.5 time series. Unlike traditional algorithms that plateau in performance with increasing data volume, LSTM adaptively captures temporal dependencies, corrects anomalies, and maintains robustness in large-scale datasets.
(2) VMD decomposition effectively mitigates noise and disentangles multiscale features from nonlinear non-stationary PM2.5 sequences. For the Beijing dataset, VMD integration reduced MAE, RMSE, and MAPE by 28.31%, 35.91%, and 26.72%, respectively, while improving R2 by 0.73% compared to standalone LSTM.
(3) POA optimization further enhances VMD by adaptively determining optimal decomposition parameters, generating distinct subsequences with improved interpretability. Compared to VMD–LSTM, the POA–VMD–LSTM hybrid model achieved additional reductions of 32.53% (MAE), 42.63% (RMSE), and 48.93% (MAPE), with a 1.24% increase in R2.
Despite its high accuracy and stability, this study focuses solely on historical PM2.5 concentrations without incorporating meteorological variables (e.g., temperature, humidity, wind speed) or finer temporal resolutions. Future work should expand the model’s input dimensions and validate its scalability across broader spatiotemporal contexts.
Author Contributions
Conceptualization, methodology, software, X.Z.; validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing, X.M.; visualization, supervision, project administration, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used or analyzed during this current study are available from the corresponding author on reasonable request.
Conflicts of Interest
Author Xiaoqing Zhou was employed by the State Grid Jibei Zhangjiakou Wind and Solar Energy Storage and Transportation New Solar Energy Company and author Xiaoran Ma was employed by the State Grid Hebei Construction Company. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VMD | Variational modal decomposition |
| EMD | Empirical Mode Decomposition |
| LSTM | Long Short-Term Memory networks |
| POA | Pelican Optimization Algorithm |
References
- Zhang, Q.; Wu, S.; Wang, X.; Sun, B.; Liu, H. A PM2.5 concentration prediction model based on multi-task deep learning for intensive air quality monitoring stations. J. Clean. Prod. 2020, 275, 122722. [Google Scholar] [CrossRef]
- Zoran, M.A.; Savastru, R.S.; Savastru, D.M.; Tautan, M.N. Assessing the relationship between surface levels of PM2.5 and PM10 particulate matter impact on COVID-19 in Milan, Italy. Sci. Total Environ. 2020, 738, 139825. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Liu, K.; Ren, J. Seasonal characteristics of PM2.5 and its chemical species in the northern rural China. Atmos. Pollut. Res. 2020, 11, 11. [Google Scholar] [CrossRef]
- Tetsuya, T.; Shunsuke, M. Health-related and non-health-related effects of PM2.5 on life satisfaction: Evidence from India, China and Japan. Econ. Anal. Policy 2020, 67, 114–123. [Google Scholar]
- Li, G.; Wu, H.; Zhong, Q.; He, J.; Yang, W.; Zhu, J.; Zhao, H.; Zhang, H.; Zhu, Z.; Huang, F. Six air pollutants and cause-specific mortality: A multi-area study in nine counties or districts of Anhui Province, China. Environ. Sci. Pollut. Res. 2022, 29, 468–482. [Google Scholar] [CrossRef]
- Luo, F.; Guo, H.; Yu, H.; Li, Y.; Feng, Y.; Wang, Y. PM2.5 organic extract mediates inflammation through the ERβ pathway to contribute to lung carcinogenesis in vitro and vivo. Chemosphere 2021, 263, 127867. [Google Scholar] [CrossRef] [PubMed]
- Kuldeep, S.R.; Manish, K.G. Modelling health implications of extreme PM2.5 concentrations in Indian sub-continent: Comprehensive review with longitudinal trends and deep learning predictions. Technol. Soc. 2025, 81, 102843. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.J.; Chang, L.C.; Kao, I.F.; Wang, Y.S. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2018, 209, 134–145. [Google Scholar] [CrossRef]
- Guo, D.; Chen, H.; Long, R.; Zou, S. Who avoids being involved in personal carbon trading? An investigation based on the urban residents in eastern China. Environ. Sci. Pollut. Res. 2021, 28, 43365–43381. [Google Scholar] [CrossRef]
- Cobourn, W.G. An enhanced PM2.5 air quality forecast model based on nonlinear regression and back-trajectory concentrations. Atmos. Environ. 2010, 44, 3015–3023. [Google Scholar] [CrossRef]
- Qiao, J.; He, Z.; Du, S. Prediction of PM2.5 concentration based on weighted bagging and image contrast-sensitive features. Stoch. Environ. Res. Risk Assess. 2020, 34, 561–573. [Google Scholar] [CrossRef]
- Dong, L.; Yang, J.; Shi, W.; Zhang, L. Investigating the performance of satellite-based models in estimating the surface PM2.5 over China. Chemosphere 2020, 256, 127051. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM 2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, W. Prediction of Air Pollutants Concentration Based on an Extreme Learning Machine: The Case of Hong Kong. Int. J. Environ. Res. Public Health 2017, 14, 114. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Lian, X.; Wei, L.; Che, J.; Shen, X.; Yang, L.; Qiu, X.; Liu, X.; Gao, W.; Ren, X.; et al. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, G ELM and GCA considering meteorological factors. Atmos. Environ. 2018, 183, 20–32. [Google Scholar] [CrossRef]
- Li, T.; Hua, M.; Wu, X. A Hybrid CNN-LSTM Model for Forecasting Particulate Matter (PM2.5). IEEE Access 2020, 8, 26933–26940. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, H.; Xu, X.; Han, M.; Zuo, P. A balanced social LSTM for PM 2.5 concentration prediction based on local spatiotemporal correlation. Chemosphere 2021, 291, 133124. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Lu, Y.; Li, M.-Z.; Yang, R.; Pan, J.; Kou, Z. Air Pollutant Diffusion Trend Prediction Based on Deep Learning for Targeted Season—North China as an Example. Expert Syst. Appl. 2023, 232, 120718. [Google Scholar] [CrossRef]
- Zhou, Q.; Jiang, H.; Wang, J.; Zhou, J. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liang, W.; Li, Y.; Liu, X.; Dai, Q.; Feng, Y. AI-based Bayesian structural time series modeling for assessing PM2.5 air quality improvements during the Beijing 2022 Winter Olympics. Atmos. Environ. 2025, 358, 121328. [Google Scholar] [CrossRef]
- Yu, Q.; Yuan, H.W.; Liu, Z.L.; Xu, G.M. Spatial weighting EMD-LSTM based approach for short-term PM2.5 prediction research. Atmos. Pollut. Res. 2024, 15, 102256. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 Concentration Forecasting at Surface Monitoring Sites Using GRU Neural Network Based on Empirical Mode Decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Cheng, J.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeng, Y.; Yan, K. A hybrid deep learning technology for PM2.5 air quality forecasting. Environ. Sci. Pollut. Res. 2021, 28, 39409–39422. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Chen, B.; Han, J.; Zhao, Y.; Zhang, C. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]
- Guo, H.; Guo, Y.; Zhang, W.; He, X.; Qu, Z. Research on a Novel Hybrid Decomposition–Ensemble Learning Paradigm Based on VMD and IWOA for PM2.5 Forecasting. Int. J. Environ. Res. Public Health 2021, 18, 1024. [Google Scholar] [CrossRef]
- Yu, M.; Niu, D.; Gao, T.; Wang, K.; Sun, L.; Li, M.; Xu, X. A novel framework for ultra-short-term interval wind power prediction based on RF-WOA-VMD and Bi-GRU optimized by the attention mechanism. Energy 2023, 269, 126738. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Li, P.; Li, M.; He, Q.; Chao, H.; Zhang, J.; Hou, J. Load Prediction Based on Hybrid Model of VMD-m-RMR-BPNN-LSSVM. Complexity 2020, 2020, 6940786. [Google Scholar]
- Wang, D.; Liu, Y.; Luo, H.; Yue, C.; Cheng, S. Day-Ahead PM2.5 Concentration Forecasting Using WT-VMD Based Decomposition Method and Back Propagation Neural Network Improved by Differential Evolution. Int. J. Environ. Res. Public Health 2017, 14, 764. [Google Scholar] [CrossRef]
- Kim, Y.; Park, S.B.; Lee, S.; Park, Y.K. Comparison of PM2.5 prediction performance of the three deep learning models: A case study of Seoul, Daejeon, and Busan. J. Ind. Eng. Chem. 2023, 120, 159–169. [Google Scholar] [CrossRef]
- Zeng, T.; Xu, L.; Liu, Y.; Liu, R.; Luo, Y.; Xi, Y. A hybrid optimization prediction model for PM2.5 based on VMD and deep learning. Atmos. Pollut. Res. 2024, 15, 7. [Google Scholar] [CrossRef]
- Tran, H.D.; Huang, H.Y.; Yu, J.Y.; Wang, S.H. Forecasting hourly PM2.5 concentration with an optimized LSTM model. Atmos. Environ. 2023, 315, 15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).