Abstract
The large-scale integration of renewable energy into power systems poses significant challenges to reactive power and voltage stability. To enhance system stability, this work proposes a cluster partitioning and distributed control strategy for distribution networks with high-penetration distributed PV integration. Firstly, a comprehensive clustering index system, including electrical distance, voltage sensitivity, and regulation ability, is established. Considering the voltage and reactive power support capability of regional clusters, the distribution network is divided into clusters. Subsequently, based on the results of cluster division, a hierarchical partition optimization model is constructed with voltage and reactive power as the optimization objectives. Finally, a distributed optimization algorithm based on ADMM is proposed to solve the optimization model and maximize the utilization of distribution network control resources. The simulation results based on the IEEE 33-node distribution system verify the effectiveness of the proposed distributed optimization strategy.
1. Introduction
Compared to transmission networks, distribution networks exhibit a higher ratio of line resistance to reactance [1], making them more prone to voltage deviations due to power injection variations [2]. With the increasing penetration of renewable energy sources in power systems, their output fluctuations, combined with the limited reactive power support capability in distribution networks [3,4], pose significant voltage regulation challenges. Uncontrolled power fluctuations from large-scale distributed generation (DG) units may severely degrade power quality [5].
Currently, the voltage and reactive power control methods in power systems mainly comprise centralized and distributed approaches [6,7]. Centralized control strategies gather all network data and solve a global optimization problem [8,9]. Reference [10] proposed a centralized voltage optimization strategy considering the attack scenario in DER control. Reference [11] proposed a real-time centralized voltage control method based on a grid-forming converter. However, although centralized strategies can comprehensively consider the overall grid operation status, they impose significant computational and communication burdens in large-scale distribution networks [12]. Similarly, rule-based or heuristic schemes may be easy to implement but cannot guarantee optimal performance or fast convergence under varying conditions [13].
In contrast, distributed and hierarchical control strategies decompose the problem into regional sub-problems, enhancing the scalability and robustness [14,15]. By sharing only limited information across neighboring clusters, distributed algorithms can exploit parallel computation and reduce communication burden [16]. Reference [17] proposed an adaptive distributed voltage control strategy based on a hierarchical two-layer control model. Reference [18] proposed a cluster voltage control method based on an improved differential evolution algorithm, which improved the photovoltaic (PV) consumption capacity of a distribution network. Reference [19] proposed a voltage drop mitigation method based on graph theory, which divides dynamic voltage restorers in a radial distribution network into clusters to address the voltage drop problem.
However, with the increasing integration of heterogeneous DERs in distribution networks [20], the differences in regional control capacity and energy structure characteristics have become more pronounced [21]. Most existing distributed voltage and reactive power control strategies are based on fixed cluster division results, making them unable to adapt to the complex and dynamic operational conditions of distribution networks or meet the varying voltage and reactive power support requirements [22].
While the integration of DERs may affect distribution network stability, their controllability can actively support voltage regulation and power flow management [23,24]. Reference [25] proposed a distributed voltage control scheme based on a multi-input multi-output model, which realizes the voltage regulation of a distribution network through the response and power injection of a DER. Reference [26] proposed a voltage control strategy of a virtual power plant with a DER based on voltage sensitivity analysis.
To address the limitations in existing distribution network control strategies, this work focuses on PV-integrated distribution networks and explores the use of controllable distributed generation (DG) to mitigate PV integration impacts. A hierarchical cluster partitioning and coordinated reactive power optimization strategy is proposed. First, considering the voltage sensitivity as well as the operating characteristics and distribution features of distributed PVs and DG, a cluster partitioning strategy for distribution networks based on the K-means algorithm is proposed to generate cluster partitioning schemes. Subsequently, based on the cluster partitioning schemes, a distributed reactive power optimization control method based on the ADMM algorithm is presented, enabling rapid and efficient system optimization. The effectiveness of the hierarchical and zonal optimization strategy proposed in this paper is verified through simulations. The main contributions of this work are as follows.
- Hierarchical and zonal coordinated optimization framework: a novel two-layer hierarchical optimization framework that systematically integrates adaptive network partitioning with distributed cooperative control to address voltage regulation challenges in distribution networks with high renewable penetration.
- Dynamic cluster formation: a novel multi-criteria partitioning strategy that simultaneously considers nodal voltage coupling characteristics, DER regulation capacities, and spatial resource distribution patterns, enabling adaptive clustering for multiple scenarios.
- Coordinated distributed control strategy: a novel ADMM-based optimization framework is proposed that achieves inter-cluster voltage stability through the implementation of boundary consensus constraints, while simultaneously preserving computational efficiency.
The overall structure of the article is shown in Figure 1.
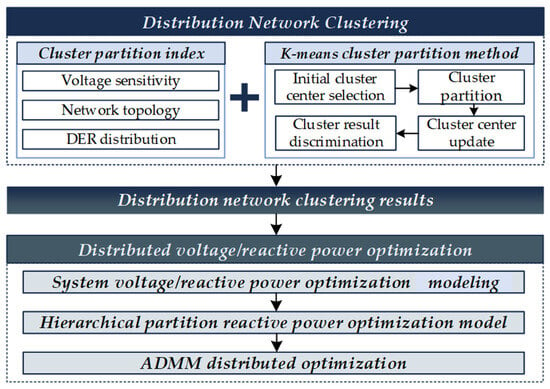
Figure 1.
Research structure and flow chart.
2. Distribution Network Clustering Strategy
The primary objective of cluster partitioning is to classify individual units based on specific characteristics, achieving strong internal coupling within clusters while maintaining approximate decoupling between them. Existing grid clustering methods typically rely on geographical distribution and network topology. Targeting voltage regulation in distribution networks with high PV penetration, this study proposes a K-means cluster partitioning strategy that incorporates voltage sensitivity, electrical distance, and the spatial distribution of distributed PVs, DGs, and ESSs.
2.1. K-Means Clustering Algorithm
The K-means method is to divide agents into uncoupled clusters, with the index set of each agent. The objective function of the algorithm is constructed with the cluster center index set , which can be characterized as follows:
where the index set of each agent is an n-dimensional vector, which contains the parameters of each index of this agent. together constitute the set of subjects of cluster partition. represents the number of entities in each cluster, and represents the number of clusters to be divided.
2.2. Clustering Strategy
In distribution networks with a high penetration of distributed PVs, this work employs a K-means clustering approach using electrical distance, voltage sensitivity, and resource type as partitioning criteria. By formulating a novel objective function, we achieve cluster partitioning that accounts for the spatial distribution of distributed PVs, ESSs, and DGs in the grid.
2.2.1. Cluster Index
This work proposes a voltage-sensitivity-based clustering approach, where nodes with strong coupling (high voltage–power sensitivity) are grouped into the same cluster, while weakly coupled nodes are assigned to different clusters. This partitioning strategy enables the efficient implementation of voltage regulation within each cluster while mitigating inter-cluster voltage interference.
In power systems, both active and reactive power injections affect nodal voltages, with varying degrees of inter-node coupling. Therefore, this study employs the sensitivity of voltage variations at other nodes to power injection changes at a given node as the clustering criterion.
Firstly, considering the topology structure, the sensitivity matrix of each node voltage and the active and reactive power changes of other nodes is as follows:
where , , , and are the elements of the Jacobi matrix, is the variation in the active power of a bus, and is the variation in the reactive power of a bus. Through simplification of the power flow equations, we derive the reactive voltage sensitivity matrix and active voltage sensitivity matrix , which characterize the nodal voltage responses to reactive and active power injections, respectively.
Therefore, the variation in voltage at each node in the distribution network can be expressed as
where is the number of buses in the distribution network.
(1) Electrical distance
Electrical distance directly shows the voltage coupling strength between nodes in a distribution network. It is calculated from the sensitivity matrix. Strongly coupled nodes are grouped together for local voltage control, while weakly coupled nodes are separated to reduce interference between clusters. This is the key principle behind voltage partitioning control. Based on the voltage, active power, and reactive power sensitivity matrix, an electrical distance clustering index is created. A higher index value means stronger coupling within the cluster.
where represents the electrical distance between bus and bus .
(2) DER regulation ability
This parameter represents the reactive power support capability of distributed generation (DG/PV) nodes, calculated based on their adjustable reactive power range. Nodes with high regulation capability serve as cluster cores, providing sufficient reactive power reserves to ensure independent voltage regulation within each partitioned cluster. To quantify the power regulation capability of distribution networks, we propose a bus flexibility index , defined as the ratio of a distributed generator’s (DG) adjustable active/reactive power range to the total nodal power injection:
where and are the adjustable range of the active and reactive power of DG on bus , respectively, and and are the active and reactive loads on bus , respectively.
(3) DER spatial distribution
Spatially proximate DERs exhibit stronger electrical coupling and greater potential for coordinated control, aligning with the ‘localized balancing’ principle in distribution network operation. To characterize the spatial concentration of PVs and DGs, we employ kernel density estimation (KDE) to quantify their aggregation levels at each distribution network bus.
where and are the aggregation parameters of bus i to the surrounding distributed PVs and DGs, respectively, is the total number of distributed PVs in the distribution network, and is the total number of DGs in the distribution network. is the Kernel function, and is the bandwidth parameter controlling spatial smoothing.
2.2.2. Cluster Objective Function
The K-means clustering algorithm aims to minimize the intra-cluster Euclidean distance between nodes and their cluster centroids. For distribution network partitioning tailored to voltage regulation, we formulate the objective function as
where is the distance function from bus to cluster center , is the number of clusters, and is the number of samples in each cluster. To facilitate the tunable control of metric preferences in the clustering algorithm, we implemented weighting coefficients , , and that govern the relative emphasis on different clustering objectives. The weighting coefficients were determined through sensitivity analysis on the IEEE 33-node system, optimizing for minimal SSE and voltage deviation. Electrical distance ( = 0.5) received higher priority due to its direct impact on intra-cluster voltage coupling, while DER regulation ( = 0.3) and spatial distribution ( = 0.2) were balanced to reflect reactive power support and resource localization.
2.2.3. Cluster Center
This work proposes an electrical-distance-based centroid selection criterion for K-means clustering, where the new cluster center is chosen as the node with the minimal total electrical distance to all other nodes within the emerging cluster.
where represents the cluster center of cluster .
2.2.4. Cluster Number K Value Selection
The quality of cluster partitioning is evaluated using the Sum of Squared Errors (SSE) metric, which quantifies the total squared electrical distance between nodes and their assigned cluster centroids. For a distribution network partitioned into K clusters, the SSE is defined as
Based on the preceding analysis, Figure 2 presents the comprehensive workflow for the proposed cluster partition strategy.
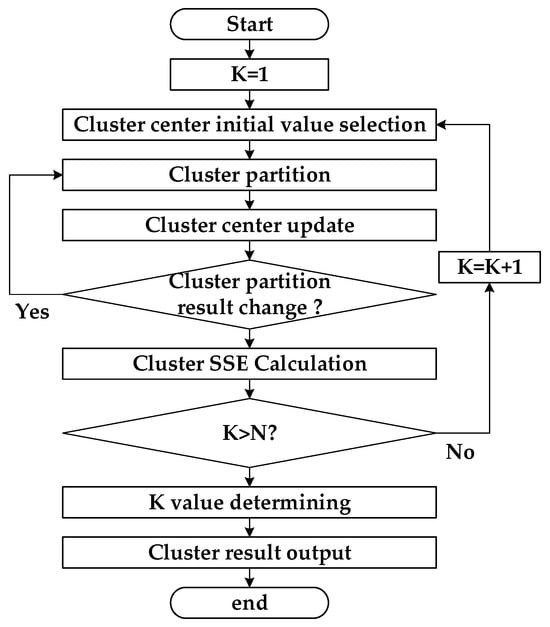
Figure 2.
Comprehensive workflow for proposed cluster partition strategy.
3. Hierarchical Partition Reactive Power Optimization Model
3.1. Reactive Power Optimization Model
The distribution network system can be modeled by graph theory as , where is the set of buses in the whole distribution network and is the set of transmission lines in the whole distribution network.
3.1.1. Objective Function
In this work, the objective function aims to minimize both the network active power losses and the voltage deviations during system operation. The mathematical formulation is given below:
where is the total load loss of the distribution network, is the voltage deviation of the system, is the resistance of line , and and represent the active and reactive power injections at the sending end of line , respectively.
3.1.2. Constraints
(1) Power flow constraint
where represents the transmission power at the sending end of line , denote the active and reactive load power at bus , respectively, and and correspond to the active and reactive output power of the PV and DG units connected to bus .
(2) Voltage constraint
where is the allowable range of voltage deviation of the distribution network.
(3) DG operation constraint
where is the reactive power output of the -th DG, is the maximum reactive power output of the -th DG, and is the rated capacity of the -th DG.
3.2. Hierarchical Partition Reactive Power Optimization Control Model
Based on the cluster partition results of the distribution network, its hierarchical partition control can be realized. The distribution network system can be expressed by the graph theory model as follows:
where is the set of buses in the distribution network system and is the set of transmission lines in the distribution network system. Based on the distribution network cluster partition results, the set of distribution network clusters is K. Adjacent clusters are coupled through branches on the cluster boundary.
To ensure that the solution of the cluster partition sub-problem is equivalent to the original problem, the state variables of the coupled branches derived from the solutions of the adjacent cluster sub-problems must remain consistent. Specifically, the coupling branch state variable obtained from the solution of the sub-problem for cluster must be exactly equal to the corresponding coupling branch state variable obtained from the solution of the adjacent cluster sub-problem. Therefore, the cluster coupling constraint is added to the reactive power optimization model.
4. ADMM Distributed Optimization
The parallel ADMM method is used to solve the distributed reactive power and voltage optimization. The original problem is decomposed into a sub-optimization problem coordinated by and regions, and the distributed solution process of ADMM is clarified [27].
4.1. Construction of Lagrange Objective Function
Firstly, based on the basic constraints of the optimization model, the sub-optimization problems of each region are established, and the objective functions of region and region are constructed as follows:
where is the number of iterations; and are the vectors of dual variables of clusters and , respectively; and are the fixed reference values of the t + 1th iteration of clusters and , respectively; and is the penalty parameter of the algorithm [28].
4.2. Cluster Constraint Condition Division
Taking cluster as an example, its optimization constraints are as follows:
By integrating the optimization model of the aforementioned clusters, the ADMM-based distributed optimization solution is implemented following the proposed solution procedure. The detailed solution process is illustrated below [29].
4.3. Distributed Optimization Solution Process
(1) In the t + 1th iteration, the sub-optimization problems in the region are solved in clusters K1 and K2, respectively, and the decision variable value in the region is minimized by parallel computing so as to obtain the state of the coupling branches between clusters and .
(2) The interaction relationship between the coupling path state of cluster K1 and K2 is constructed as follows, which is used as the reference value of the next iteration.
(3) The control variables of cluster K1 and K2 are updated as follows:
(4) Taking the boundary residual as the convergence criterion of the algorithm, the convergence criterion of the algorithm is set as follows:
where (1.2) is the penalty parameter, represents the discrepancy in branch states between clusters and , is the change in cluster ’s state between iterations t and , and (10−4) and (10−3) are the numerical threshold for dual convergence, respectively. The specific process of distributed voltage optimization solution is shown in Figure 3 below.
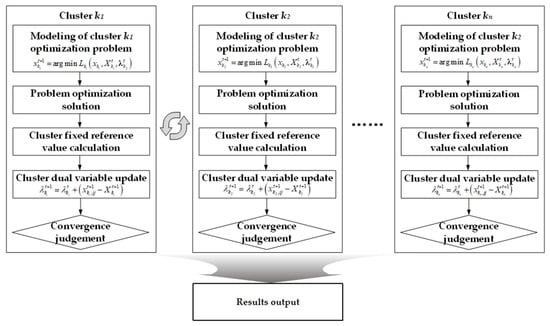
Figure 3.
Distributed voltage optimization solution flowchart.
5. Example Analysis
5.1. Simulation Example Construction
Based on the IEEE33-node distribution network, distributed PVs and DGs are connected to each bus of the distribution network, and a simulation example model is constructed, as shown in Figure 4. The load change of the distribution network is shown in Figure 5, and the 11 photovoltaic units connected are shown in Figure 6. The specific distributed PV data is shown in Table 1 below.
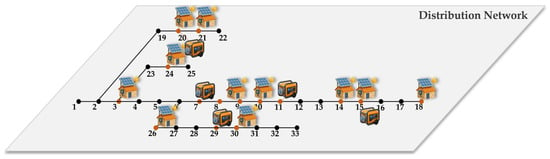
Figure 4.
IEEE-33 distribution network simulation system.
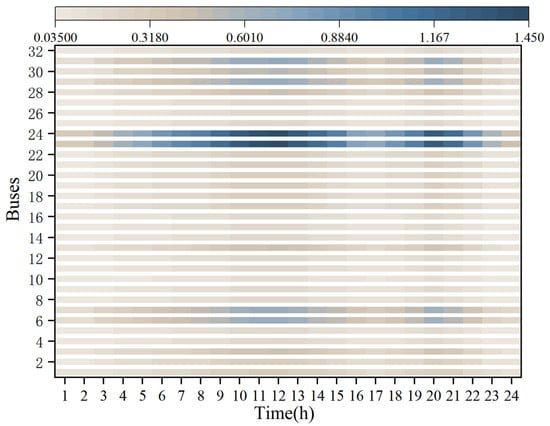
Figure 5.
Bus load fluctuation.
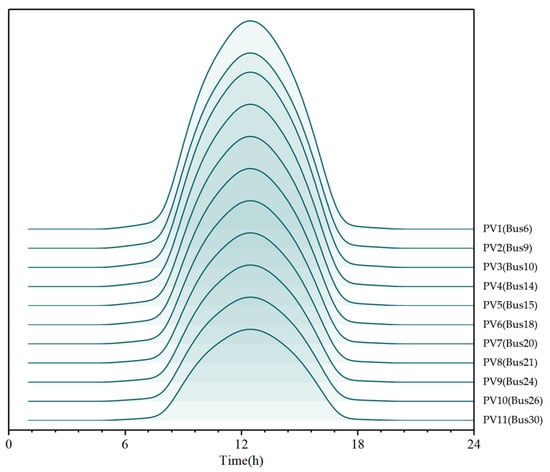
Figure 6.
Distributed PV output curve.

Table 1.
Distributed PV capacity.
The time resolution of our data is aggregated to 15 min intervals for control updates. The parameters of DG are shown in Table 2 below.

Table 2.
DG reactive power support capacity.
Based on the above simulation system, two simulation scenarios are set up to verify the effectiveness of the reactive power control strategy proposed in this paper.
- Scenario 1: Without voltage and reactive power optimization, the voltage distribution of the distribution network is output.
- Scenario 2: The centralized reactive power and voltage control strategy is used to optimize the reactive power and voltage of the distribution network.
- Scenario 3: Based on the hierarchical partition reactive power optimization method proposed in this paper, the reactive power and power grid of the distribution network are optimized.
All scenarios use identical input data: the same load profiles, PV generation curves, and DG parameters. This ensures a fair comparison by isolating the impact of the control strategies.
5.2. Result Analysis and Discussion
The multi-scene simulation results are shown in Table 3, and the cluster partition results are shown in Figure 7 and Figure 8. The simulation results of distributed reactive power and voltage control are shown in Figure 9 and Figure 10 below.

Table 3.
Multi-scenario simulation optimization results.
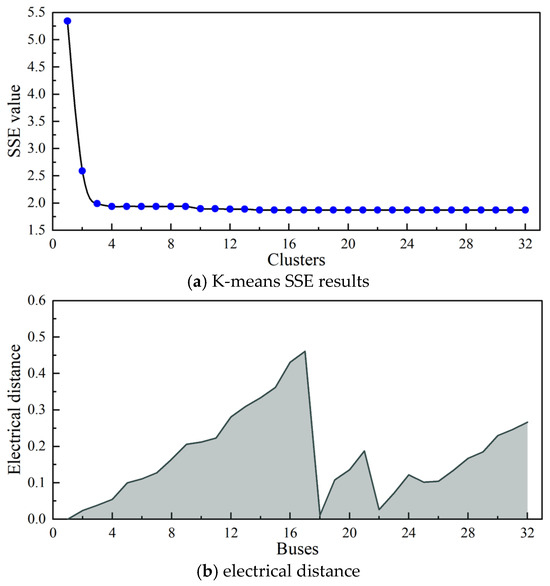
Figure 7.
K-means clustering analysis parameters.
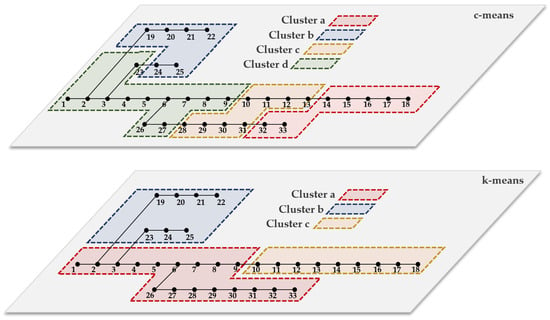
Figure 8.
Distribution network cluster division results.
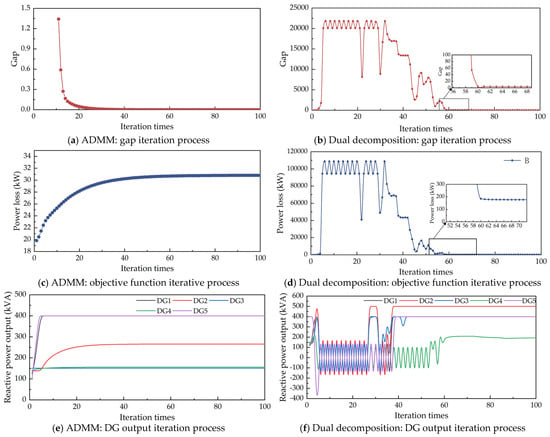
Figure 9.
Comparison of distributed optimization algorithms for solving process in Scenario 3.
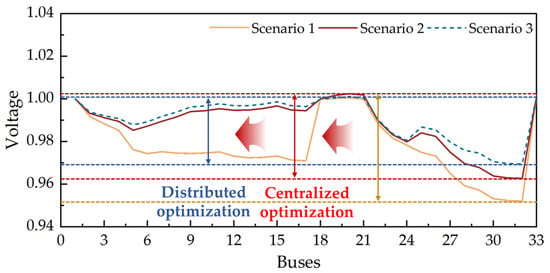
Figure 10.
Scenario 3 AMDD solving process.
As shown in Table 3, the implementation of centralized optimization control for voltage and reactive power with the full participation of DERs across the entire distribution network yields a substantial 63.4% reduction in load losses. Furthermore, when applying the cluster division strategy coupled with the distributed reactive voltage optimization control methodology proposed in this study (Scenario 3), an additional 14.6% decrease in overall load losses is achieved. These quantitative results provide conclusive verification of the operational efficacy and performance superiority of the proposed optimization control strategy.
To validate the effectiveness of the proposed clustering method, the distribution network was partitioned using a c-means-based clustering algorithm under identical simulation conditions, with the comparative results presented in Figure 8.
As shown in Figure 7, during the distribution network clustering process, the final SSE value exhibits minimal variation beyond k = 3, with fluctuation amplitudes remaining below 10%. Therefore, this study selects three clusters as the optimal partitioning target. Based on the proposed clustering method, the partitioning results for the distribution network with integrated PV and DG systems are presented in Figure 8.
As shown in Figure 8, the c-means algorithm divides the distribution network into four zones, which increases the computational demands during iterative solving. Moreover, the correlation between buses in Cluster b and Cluster c is weak, and the PV-to-DG ratio is unbalanced within each zone. In contrast, the K-means algorithm achieves a more rational clustering distribution: Cluster a contains five PV units and three DG units, Cluster b has four PV units and two DG units, and Cluster c includes three PV units and one DG unit. This ensures a balanced allocation of the regulation capacity.
For a comparative evaluation of the algorithm’s performance, we implemented the dual decomposition distributed optimization method under identical scenarios. The comparative results between the two approaches are presented in Figure 9.
As shown in Figure 9, the proposed ADMM-based reactive power optimization method demonstrates superior convergence performance compared to the dual decomposition distributed optimization algorithm. Figure 9c,d reveal that the ADMM algorithm requires 20 fewer iterations to achieve convergence, while exhibiting faster stabilization and smaller fluctuations in the distributed DG reactive power outputs. The simulation results indicate that all DG reactive power outputs stabilize by the 42nd iteration, with the duality gap reaching its minimum value. The objective function initially produces smaller values when the boundary constraints remain inactive, and then gradually approaches optimality as the constraints take effect, ultimately achieving the optimal solution by the 46th iteration. This case study verifies that the parallel ADMM algorithm not only effectively generates local control strategies but also substantially reduces inter-regional communication requirements. By dividing the distribution network into microgrid blocks, the proposed method attains rapid convergence at external boundaries, thereby efficiently solving the voltage–reactive power optimization problem.
The voltage stability performance under different optimization approaches is systematically compared in Figure 10. The proposed distributed optimization strategy demonstrates superior voltage regulation capability, exhibiting the minimum fluctuation amplitude among all scenarios. The quantitative analysis reveals that compared to (i) the non-optimized case, the proposed method achieves a 36% reduction in voltage fluctuations, and compared to (ii) the centralized optimization approach, it provides a further 20% improvement in voltage stability. More specifically, the distributed control strategy successfully eliminates the voltage sag phenomenon occurring at buses 6–17, while significantly mitigating the voltage dip issues at buses 30–32, with respective fluctuation amplitude reductions of 35% and 18% being attained. These experimental results provide comprehensive validation for both (a) the effectiveness of the novel cluster partitioning methodology in enabling targeted voltage control and (b) the technical advantages of the distributed optimization framework in maintaining superior voltage profiles across different network locations. The demonstrated performance improvements in addressing both voltage sags and dips confirm the practical viability of the proposed solution for enhancing power quality in distribution networks.
To analyze the adaptability of the proposed distributed method to variations in system operating conditions, the load power at each bus was varied according to the fluctuations shown in Figure 5. The resulting system network losses under both centralized and distributed optimal control are compared in Figure 11.
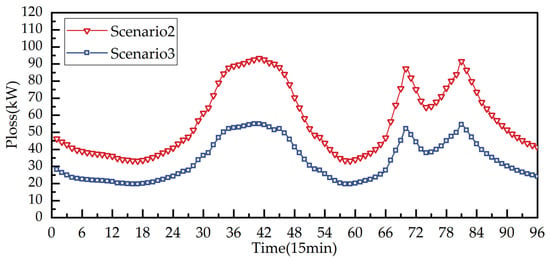
Figure 11.
Comparison of network loss of centralized and distributed optimization.
The results demonstrate that the proposed method achieves distributed reactive power optimization control at each time point under varying load conditions, significantly reducing network losses. This indicates the strong adaptability of the proposed distributed control approach to system operational state variations, including power fluctuations at distribution network buses with a high PV penetration.
A comparison of the optimization strategies reveals distinct trade-offs between the centralized and distributed approaches. While centralized control achieves global optimality with a 63.4% reduction in power losses, its computational demands grow significantly with the system scale. The proposed distributed framework improves upon this by reducing losses by an additional 14.6% through parallel cluster-level optimization, converging in just 42 iterations. Although distributed control shows marginally higher voltage deviations than the centralized methods, it offers compelling advantages: the computation time per iteration is 75% faster, and the communication overhead is reduced by 80% through boundary-constrained ADMM coordination. Furthermore, the distributed approach demonstrates superior adaptability to load fluctuations, as evidenced in Figure 11. These results confirm the scalability benefits of the distributed architecture.
Compared to existing studies, the optimization method proposed in this paper demonstrates certain advantages over the method in the referenced literature in terms of computational efficiency, communication overhead, and system performance. The proposed method achieves convergence in 42 iterations for the IEEE 33-node test system, demonstrating superior convergence speed compared to the method proposed in reference [30], which requires 289 iterations. By limiting data exchange to boundary variables between adjacent clusters, the proposed method reduces communication volume by 80%. This localized communication strategy significantly outperforms the method proposed in reference [30], which requires system-wide information sharing for fitness evaluation. Meanwhile, the method proposed in reference [30] achieves a minimum power loss of 100 kW, whereas the hierarchical and partitioned optimization approach presented in this paper can maintain power losses below 60 kW. The proposed optimization method exhibits clear advantages over the method proposed in reference [30] regarding convergence speed, communication efficiency, and dynamic performance. These improvements make it particularly suitable for modern distribution networks with high renewable penetration, where fast response and decentralized control are critical.
6. Conclusions
This work proposes a voltage–reactive power coordinated control strategy based on cluster partitioning, aiming to fully leverage the regulatory potential of distribution network resources for voltage support and network loss optimization, demonstrating three key advances:
(1) A comprehensive clustering method combining electrical distance, DER regulation capability, and spatial distribution that reduced power losses by 14% versus conventional approaches.
(2) An ADMM-based distributed optimization framework achieving convergence within 42 iterations while maintaining voltage stability under high-variability conditions.
(3) A hierarchical control architecture enabling coordinated local optimization.
While the current validation focused on typical operational scenarios, we recognize that further testing under extended temporal scales, more diverse operational scenarios, and larger network configurations could provide additional insights—these represent valuable directions for future research to complement the core methodology established here. The proposed approach offers a practical foundation for decentralized voltage control in renewable-integrated distribution systems. Future work will quantify performance under communication constraints and measurement uncertainties and extend the framework to larger metropolitan distribution networks. The hierarchical architecture inherently supports such scaling through cluster-level autonomy.
Author Contributions
Conceptualization, B.Z. and K.L.; methodology, K.L.; software, Y.L.; validation, B.Z. and Z.J.; formal analysis, P.Q.; investigation, P.Q.; resources, Z.J.; data curation, Y.L.; writing—original draft preparation, B.Z.; writing—review and editing, W.Z. and P.Q.; visualization, K.L.; supervision, P.Q.; project administration, B.Z.; funding acquisition, B.Z. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the science and technology project of State Grid Jibei Electric Power Company Limited (520101240002).
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
During the preparation of this manuscript/study, the author(s) used Matlab 2020b and cplex 12.1 for the purposes of simulation. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
Authors Bingxu Zhai, Yuanzhuo Li and Zhilin Jiang were employed by the company State Grid Jibei Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funding entities played no role in study design, data handling, or publication decisions.
References
- Wang, Z.; Huang, B.; Zhou, B.; Chen, J.; Wang, Y. An Enhanced Fault Localization Technique for Distribution Networks Utilizing Cost-Sensitive Graph Neural Networks. Processes 2024, 12, 2312. [Google Scholar] [CrossRef]
- Qian, T.; Ming, W.; Shao, C.; Hu, Q.; Wang, X.; Wu, J.; Wu, Z. An Edge Intelligence-Based Framework for Online Scheduling of Soft Open Points With Energy Storage. IEEE Trans. Smart Grid 2024, 15, 2934–2945. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, C.; Du, X.; Chen, T.; Hu, Q.; Wang, Z.; Lu, J. Capacity Configuration of Hybrid Energy Storage System for Ocean Renewables. J. Energy Storage 2025, 116, 116090. [Google Scholar] [CrossRef]
- Qian, T.; Fang, M.; Hu, Q.; Shao, C.; Zheng, J. V2Sim: An Open-Source Microscopic V2G Simulation Platform in Urban Power and Transportation Network. IEEE Trans. Smart Grid 2025, 16, 3167–3178. [Google Scholar] [CrossRef]
- Hu, Q.; Han, R.; Quan, X.; Wu, Z.; Tang, C.; Li, W.; Wang, W. Grid-Forming Inverter Enabled Virtual Power Plants With Inertia Support Capability. IEEE Trans. Smart Grid 2022, 13, 4134–4143. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef]
- Almazroui, A.; Mohagheghi, S. Coordinated Control of Photovoltaic Resources and Electric Vehicles in a Power Distribution System to Balance Technical, Environmental, and Energy Justice Objectives. Processes 2025, 13, 1979. [Google Scholar] [CrossRef]
- Naderi, E.; Narimani, H.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Marzband, M.; Lehtonen, M. State-of-the-Art of Optimal Active and Reactive Power Flow: A Comprehensive Review from Various Standpoints. Processes 2021, 9, 1319. [Google Scholar] [CrossRef]
- Liu, X.; Tang, J.; Zhou, Q.; Peng, J.; Huang, N. Coordinated Optimization Scheduling Method for Frequency and Voltage in Islanded Microgrids Considering Active Support of Energy Storage. Processes 2025, 13, 2146. [Google Scholar] [CrossRef]
- Majumdar, A.; Agalgaonkar, Y.P.; Pal, B.C.; Gottschalg, R. Centralized Volt–Var Optimization Strategy Considering Malicious Attack on Distributed Energy Resources Control. IEEE Trans. Sustain. Energy 2018, 9, 148–156. [Google Scholar] [CrossRef]
- Wagle, R.; Sharma, P.; Sharma, C.; Amin, M.; Gonzalez-Longatt, F. Real-Time Volt-Var Control of Grid Forming Converters in DER-Enriched Distribution Network. Front. Energy Res. 2023, 10, 1–18. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Chen, Y.; Ren, Q.; Zhao, J.; Qiu, S.; Zhao, Y.; Zhang, H. A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks. Processes 2025, 13, 1633. [Google Scholar] [CrossRef]
- Xiao, C.; Ren, Y.; Cao, Q.; Wang, L.; Yin, J. A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction. Processes 2024, 12, 2586. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Wang, Y.; Dong, Z.Y.; Zhang, R. Three-Stage Hierarchically-Coordinated Voltage/Var Control Based on PV Inverters Considering Distribution Network Voltage Stability. IEEE Trans. Sustain. Energy 2022, 13, 868–881. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, P.; Qu, H.; Liu, N.; Zhao, K.; Xiao, C. Optimal Placement and Sizing of Distributed PV-Storage in Distribution Networks Using Cluster-Based Partitioning. Processes 2025, 13, 1765. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Wu, Q.; Zhang, K.; Li, X.; Zhao, B. Research on Power Stability of Wind-Solar-PEM Hydrogen Production System Based on Virtual Synchronous Machine Control. Processes 2025, 13, 1733. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Yan, Q.; Li, Y. Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration. Energies 2025, 18, 2093. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T.; Chen, J.; Liao, Z.; Shu, J. Cluster Voltage Control Method for “Whole County” Distributed Photovoltaics Based on Improved Differential Evolution Algorithm. Front. Energy 2023, 17, 782–795. [Google Scholar] [CrossRef]
- Majumder, S.; Khaparde, S.A.; Agalgaonkar, A.P.; Kulkarni, S.V.; Perera, S. Graph Theory Based Voltage Sag Mitigation Cluster Formation Utilizing Dynamic Voltage Restorers in Radial Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 18–28. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, W.; Ye, Y.; Li, Y.; Tang, Y.; Long, Y.; Duan, M. A Novel Non-Intrusive Load Monitoring Method Based on ResNet-Seq2seq Networks for Energy Disaggregation of Distributed Energy Resources Integrated with Residential Houses. Appl. Energy 2023, 349, 121703. [Google Scholar] [CrossRef]
- Hu, Q.; Liang, Y.; Ding, H.; Quan, X.; Wang, Q.; Bai, L. Topological Partition Based Multi-Energy Flow Calculation Method for Complex Integrated Energy Systems. Energy 2022, 244, 123152. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, B.; Jin, X.; Luo, Y.; Song, M.; Ye, Y.; Hu, Q.; Chen, Q.; Zambroni, A.C. Mitigating Power Grid Impact from Proactive Data Center Workload Shifts: A Coordinated Scheduling Strategy Integrating Synergistic Traffic—Data—Power Networks. Appl. Energy 2025, 377, 124697. [Google Scholar] [CrossRef]
- Alshehri, M.; Yang, J. Voltage Optimization in Active Distribution Networks—Utilizing Analytical and Computational Approaches in High Renewable Energy Penetration Environments. Energies 2024, 17, 1216. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, T.; Chen, T.; Hu, Q.; Chen, H.; Hu, X.; Jiang, Z. A High-Resolution Electric Vehicle Charging Transaction Dataset with Multidimensional Features in China. Sci. Data 2025, 12, 643. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. A Decentralized Approach for Voltage Control by Multiple Distributed Energy Resources. IEEE Trans. Smart Grid 2021, 12, 3115–3127. [Google Scholar] [CrossRef]
- Hyun, S.; Kim, G.; Park, J.; Choi, Y. Optimal Virtual Power Plant Control Algorithm Considering the Electrical Characteristics of Distributed Energy Resources. Appl. Sci. 2025, 15, 127. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, F.; Ma, P.; Yan, H. Study of Cooperative Management Strategies in Interconnected Microgrid Clusters Via ADMM-Based Optimization. In Proceedings of the 2025 7th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 March 2025; pp. 1131–1136. [Google Scholar]
- Wang, Z.; Zhang, Z.; Luo, F.; Mu, R.; Wu, X.; Zhang, X.; Duan, J. Coordinated Optimal Operation Method for Snow-Shaped Distribution Networks Based on Game Theory. Energies 2024, 17, 5470. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yang, L.; Wang, Y. Active and Reactive Power Collaborative Optimization for Active Distribution Networks Considering Bi-Directional V2G Behavior. Sustainability 2021, 13, 6489. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, J.; Xie, P.; Zhai, P.; Tao, Y. Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage. Processes 2025, 13, 831. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).