Numerical Simulation of Fracture Sequence on Multiple Hydraulic Fracture Propagation in Tight Oil Reservoir
Abstract
1. Introduction
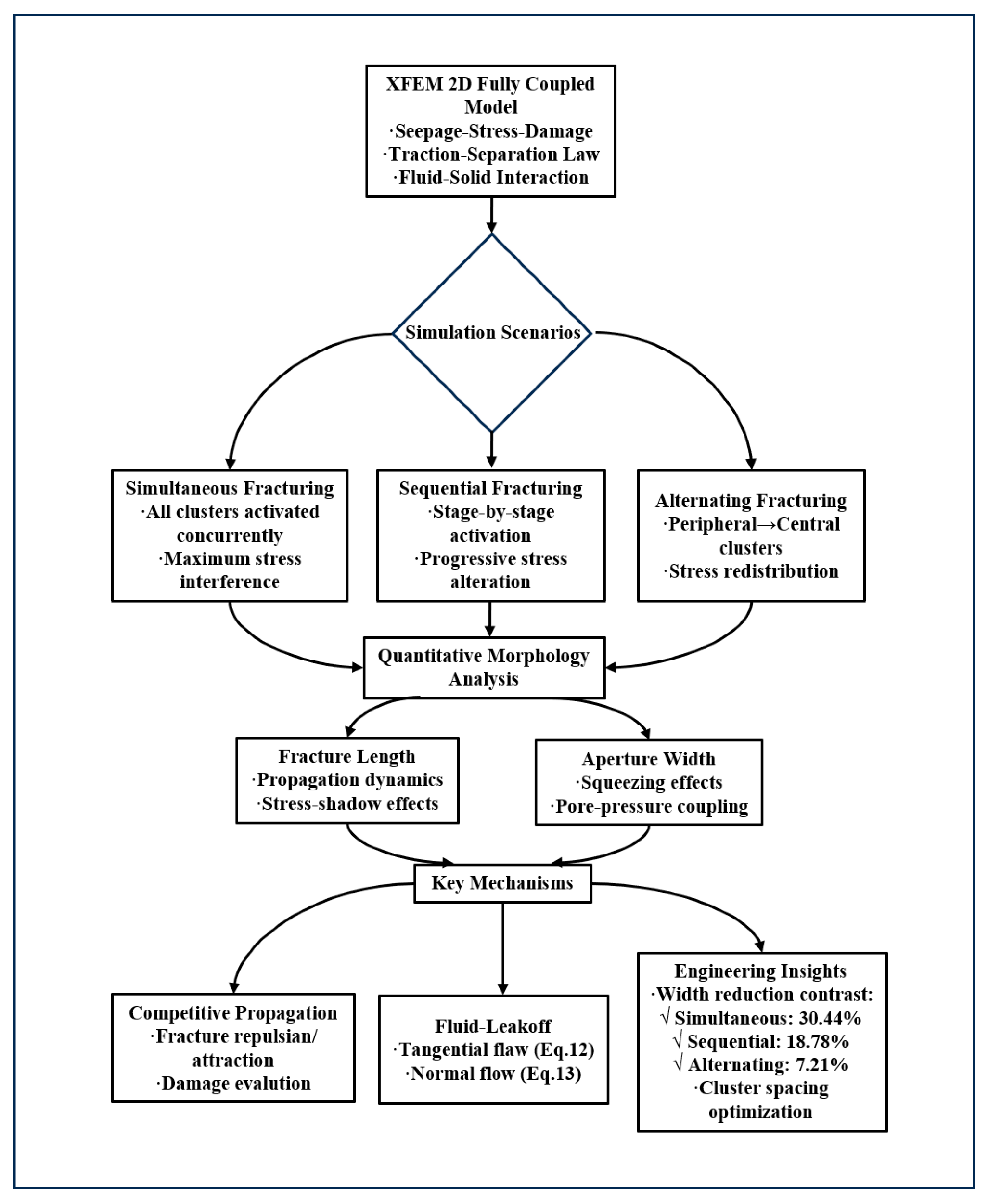
- Simultaneous fracturing: All fractures propagate concurrently;
- Sequential fracturing: Fractures propagate sequentially;
- Alternating fracturing: Peripheral fractures initiate first, followed by central clusters.
2. Methodology
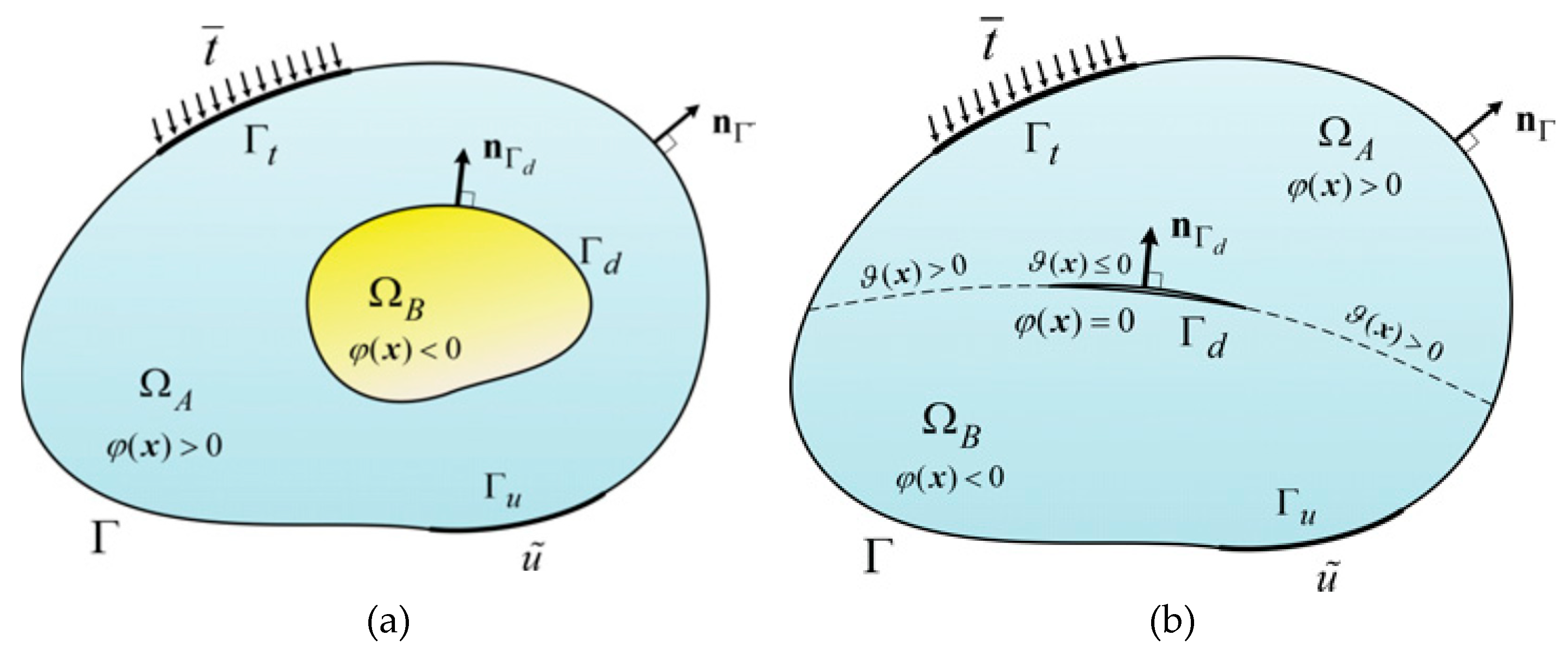
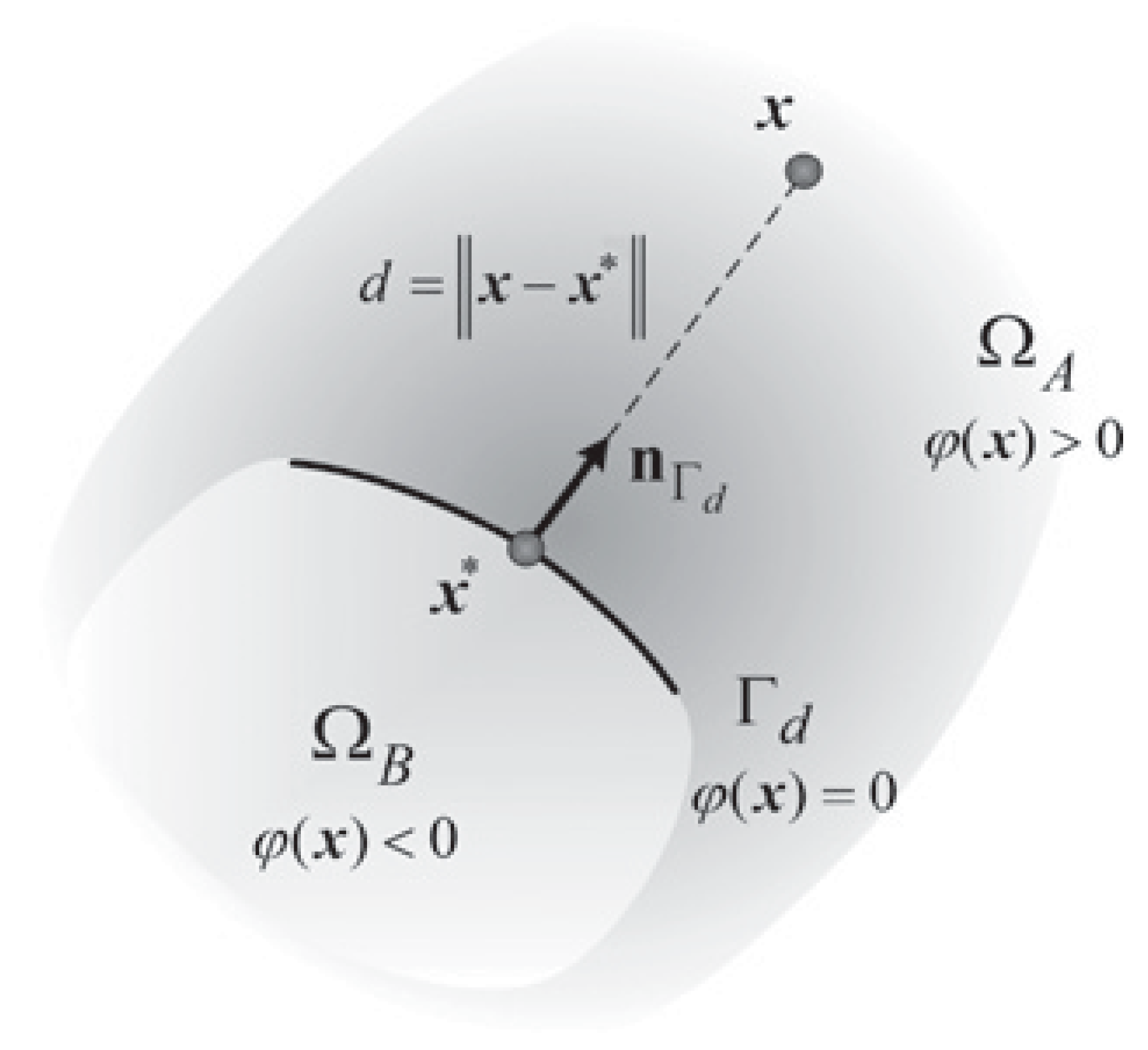
2.1. XFEM Approximation
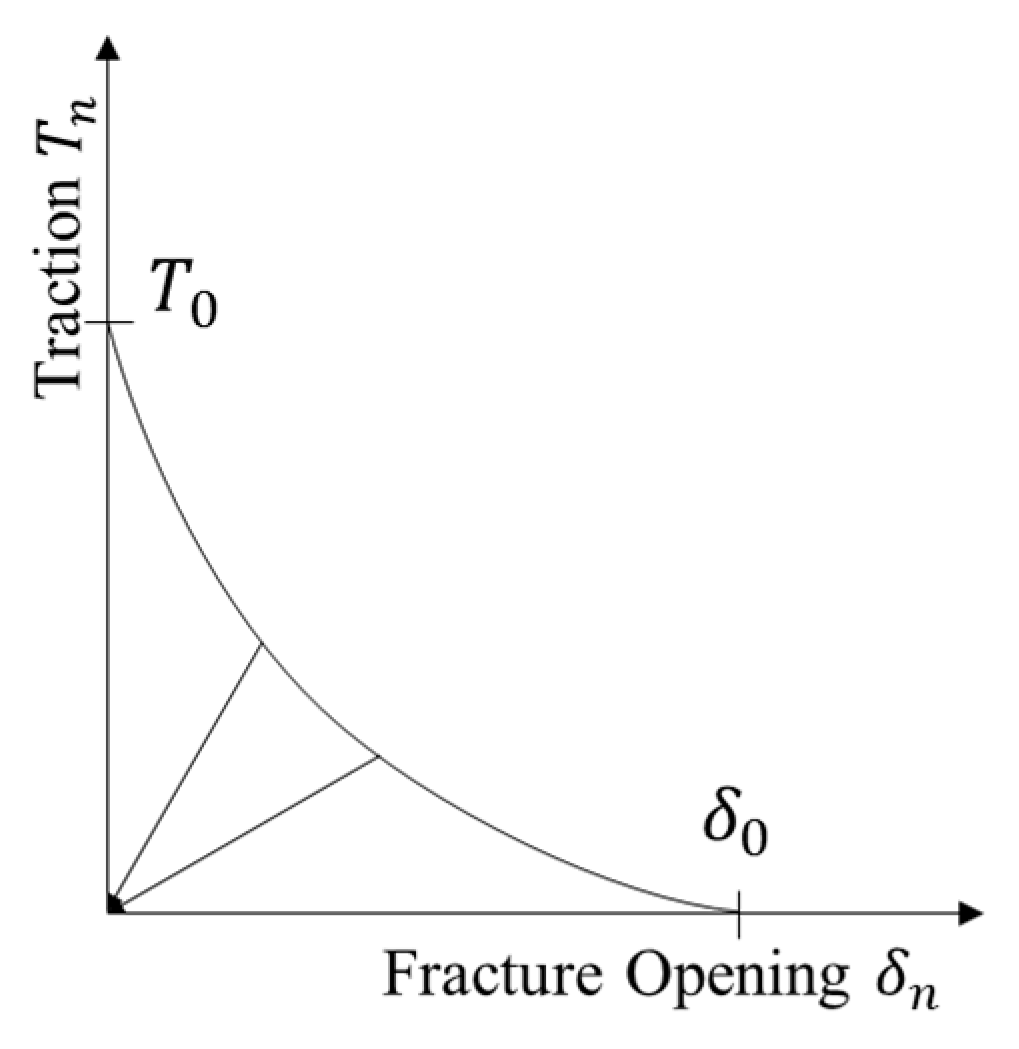
2.2. Modeling Fractures with the Cohesive Zone Method
2.3. Damage Evaluation
2.4. Fluid Flow Within the Fractures
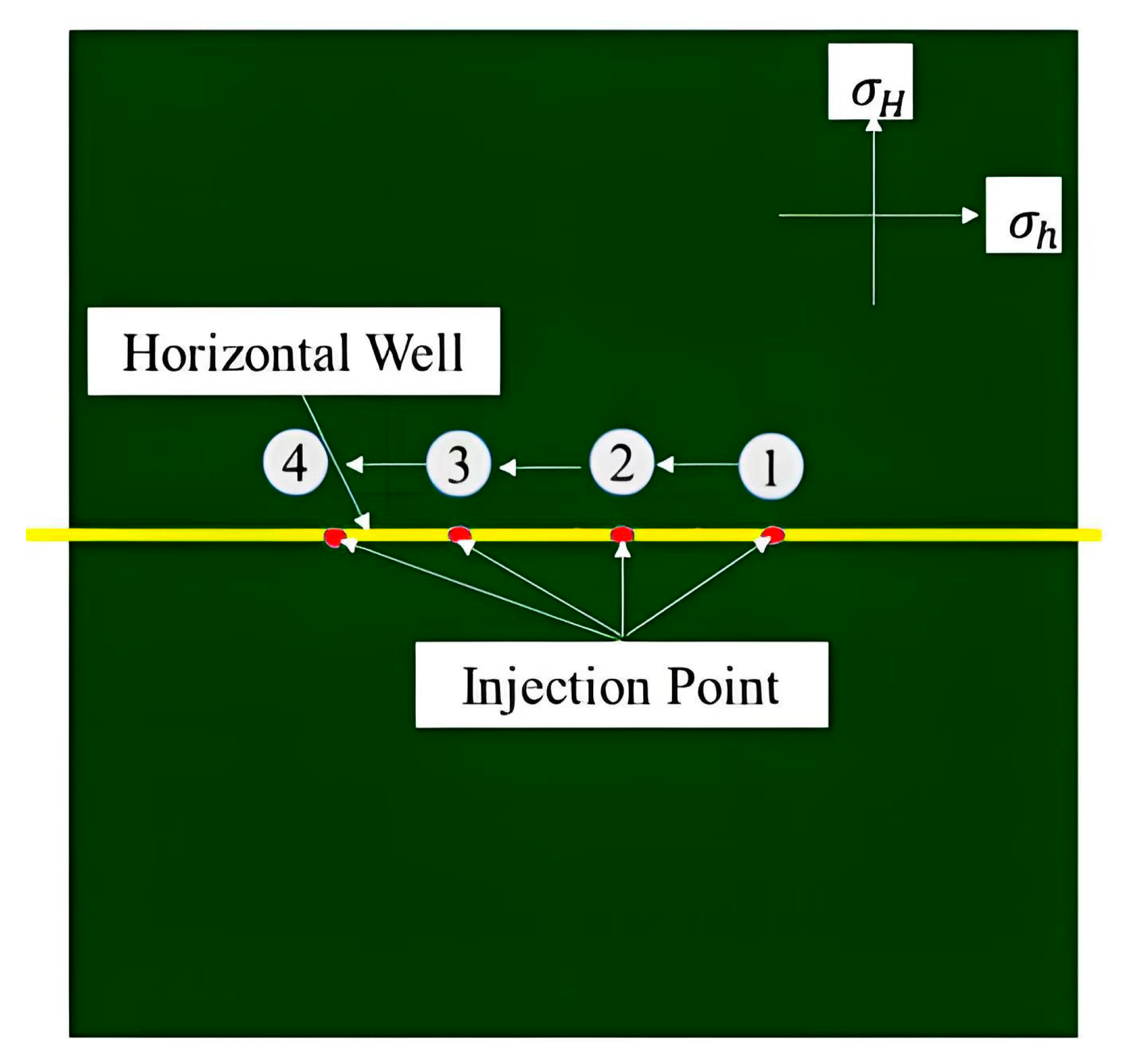
3. Modeling and Simulation
3.1. Results and Discussion
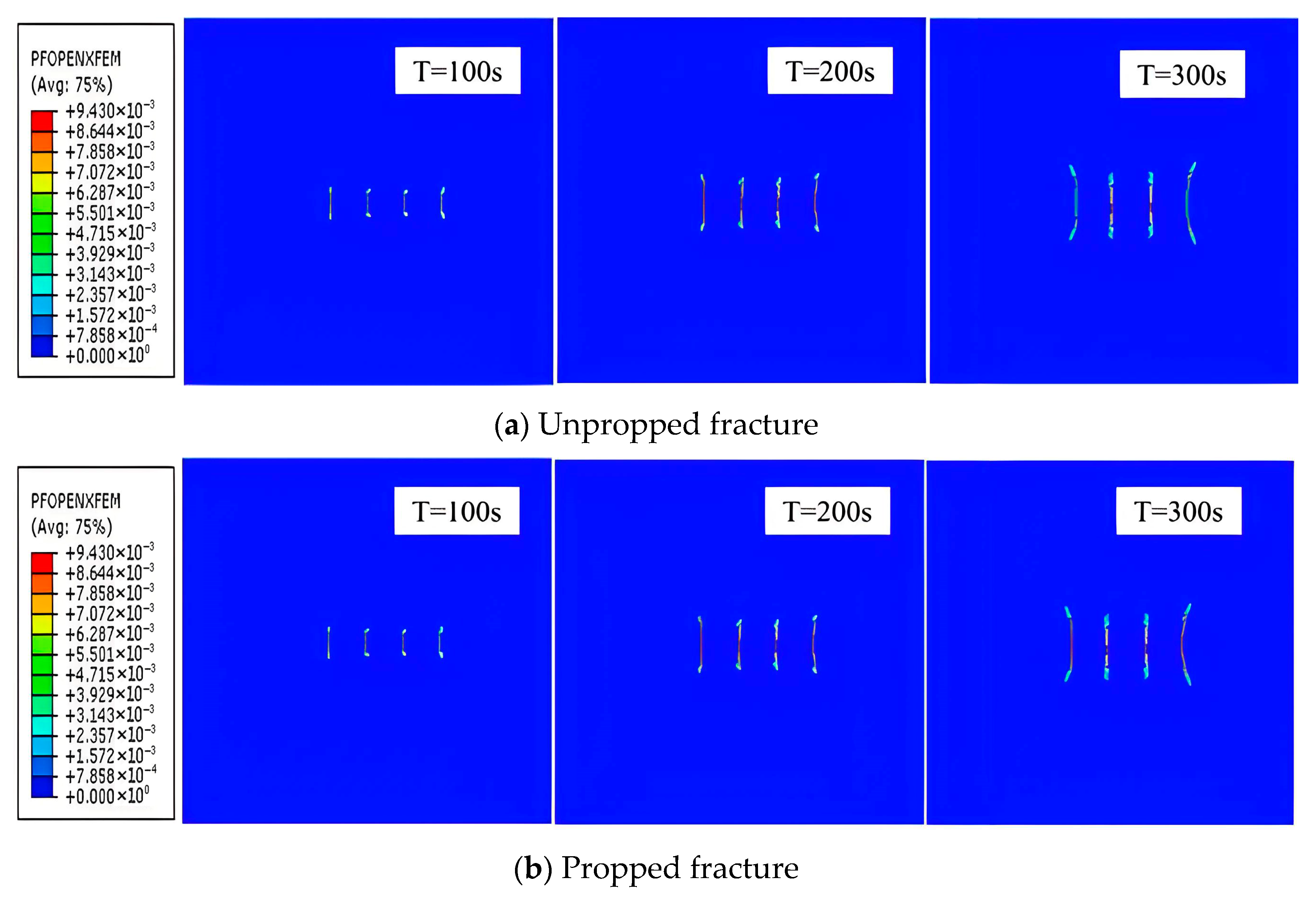
3.1.1. Simultaneous Fracturing
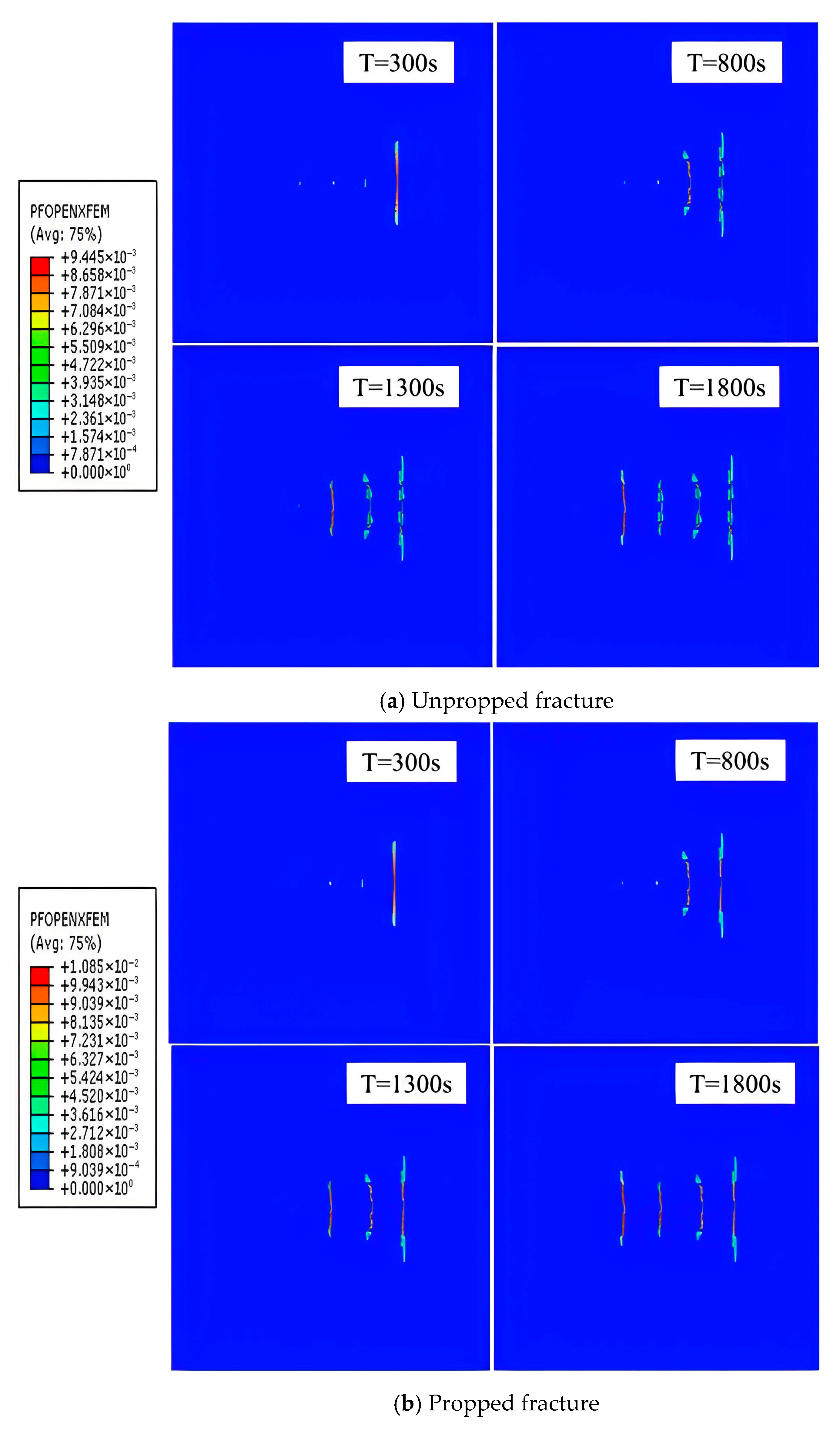
3.1.2. Sequential Fracturing
3.1.3. Alternating Fracturing
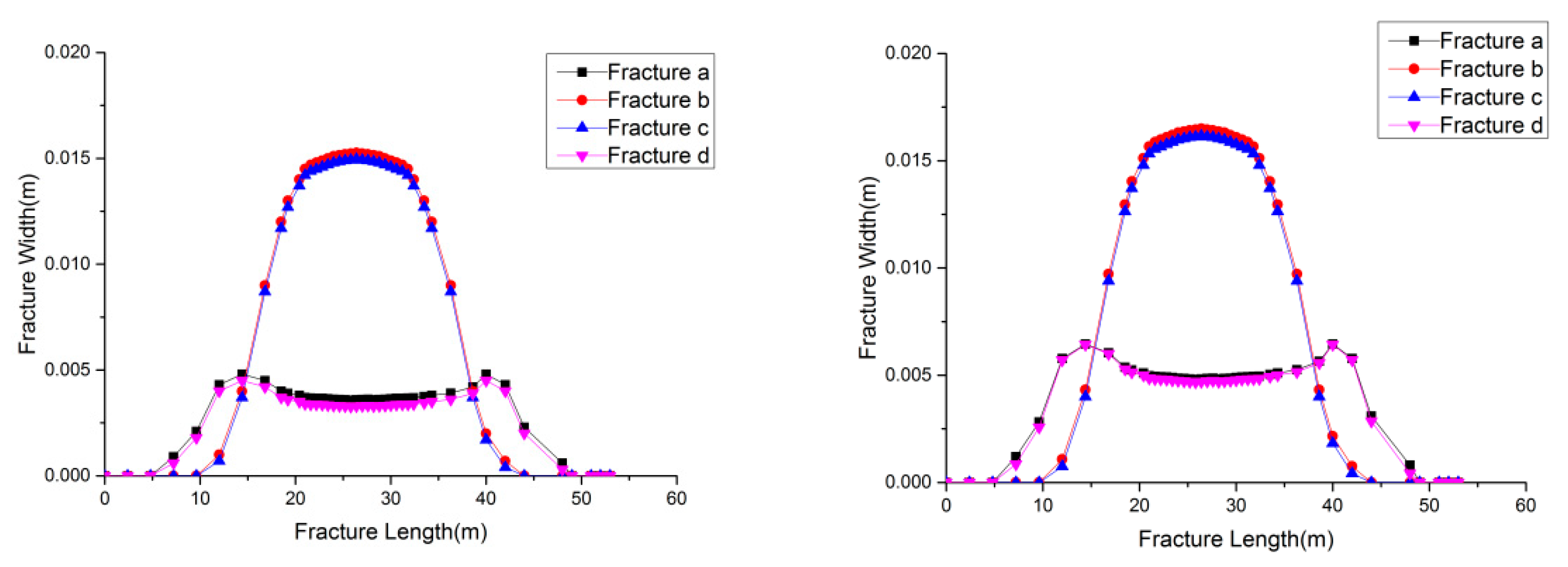
3.2. Analysis
4. Conclusions
- Fracture Length Enhancement: Sequential and alternating fracturing increased total fracture length by 20.6% (222 m) and 26.1% (232 m), respectively, versus simultaneous fracturing (184 m);
- Width Preservation Superiority: Alternating fracturing minimized pore-pressure-driven squeezing effects, reducing width reduction to 7.21% (vs. 30.44% in simultaneous), optimizing fracture conductivity;
- Deflection Control: Alternating fracturing maintained near-linear propagation (0° deflection), contrasting with 18° and 11° deflections in simultaneous/sequential methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| XFEM | Extended Finite Element Method |
| LEFM | Linear Elastic Fracture Mechanics |
| CZM | Cohesive Zone Method |
References
- Cheng, Y. Mechanical Interaction of Multiple Fractures—Exploring Impacts of the Selection of the Spacing/Number of Perforation Clusters on Horizontal Shale-Gas Wells. SPE J. 2012, 17, 992–1001. [Google Scholar] [CrossRef]
- Crosby, D.G.; Yang, Z.; Rahman, S.S. Methodology to Predict the Initiation of Multiple Transverse Fractures from Horizontal Wellbores. J. Can. Pet. Technol. 2001, 40, PETSOC-01-10-04. [Google Scholar] [CrossRef]
- Mortazavi, A.; Molladavoodi, H. A numerical investigation of brittle rock damage model in deep underground openings. Eng. Fract. Mech. 2012, 90, 101–120. [Google Scholar] [CrossRef]
- Meyer, B.R.; Bazan, L.W. A Discrete Fracture Network Model for Hydraulically Induced Fractures—Theory, Parametric and Case Studies. SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011. SPE-140514-MS. [Google Scholar]
- Izadi, G.; Settgast, R.; Moos, D.; Baba, C.; Jo, H. Fully 3D Hydraulic Fracture Growth within Multi-Stage Horizontal Wells. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Guo, J.; Lu, Q.; Zhu, H.; Wang, Y.; Ma, L. Perforating cluster space optimization method of horizontal well multi-stage fracturing in extremely thick unconventional gas reservoir. J. Nat. Gas Sci. Eng. 2015, 26, 1648–1662. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Dryden, H.L., von Kármán, T., Kuerti, G., van den Dungen, F.H., Howarth, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1962; pp. 55–129. [Google Scholar]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-Symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Elasticity and Consolidation for a Porous Anisotropic Solid. J. Appl. Phys. 1955, 26, 4. [Google Scholar] [CrossRef]
- Zhang, G.M.; Liu, H.; Zhang, J.; Wu, H.A.; Wang, X.X. Three-dimensional finite element simulation and parametric study for horizontal well hydraulic fracture. J. Pet. Sci. Eng. 2010, 72, 310–317. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Stegent, N.A.; Wagner, A.L.; Mullen, J.; Borstmayer, R.E. Engineering a Successful Fracture-Stimulation Treatment in the Eagle Ford Shale. In Proceedings of the Tight Gas Completions Conference, Society of Petroleum Engineers, San Antonio, TX, USA, 2–3 November 2010. [Google Scholar]
- Sone, H.; Zoback, M.D. Visco-plastic Properties of Shale Gas Reservoir Rocks. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, American Rock Mechanics Association, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Mokryakov, V. Analytical solution for propagation of hydraulic fracture with Barenblatt’s cohesive tip zone. Int. J. Fract. 2011, 169, 159–168. [Google Scholar] [CrossRef]
- Réthoré, J.; de Borst, R.; Abellan, M.-A. A two-scale model for fluid flow in an unsaturated porous medium with cohesive cracks. Comput. Mech. 2008, 42, 227–238. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Shah, S.; Lamb, A.R.; Bordas, S.P.A. Enriched finite elements for branching cracks in deformable porous media. Eng. Anal. Bound. Elem. 2015, 50, 435–446. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput. Methods Appl. Mech. Eng. 2013, 253, 305–322. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Implicit level set schemes for modeling hydraulic fractures using the XFEM. Comput. Methods Appl. Mech. Eng. 2013, 266, 125–143. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Enrichment strategies and convergence properties of the XFEM for hydraulic fracture problems. Comput. Methods Appl. Mech. Eng. 2015, 283, 474–502. [Google Scholar] [CrossRef]
- Khoei, A.R.; Haghighat, E. Extended finite element modeling of deformable porous media with arbitrary interfaces. Appl. Math. Model. 2011, 35, 5426–5441. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A.R. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elem. Anal. Des. 2013, 73, 77–95. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E.; Balhoff, M.T. Study of Multiple Fracture Interaction Based on An Efficient Three-Dimensional Displacement Discontinuity Method. In Proceedings of the 49th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Wu, K.; Olson, J.; Balhoff, M.T.; Yu, W. Numerical Analysis for Promoting Uniform Development of Simultaneous Multiple Fracture Propagation in Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Cipolla, C.L.; Lolon, E.P.; Mayerhofer, M.J. Resolving Created, Propped, and Effective Hydraulic-Fracture Length. SPE Prod. Oper. 2009, 24, 619–628. [Google Scholar] [CrossRef]
- Haddad, M.; Du, J.; Vidal-Gilbert, S. Integration of Dynamic Microseismic Data with a True 3D Modeling of Hydraulic-Fracture Propagation in the Vaca Muerta Shale. SPE J. 2017, 22, 1714–1738. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Y.; Chen, M.; Qu, Z.; Tang, S.; Wen, D. Multi-stage and multi-well fracturing and induced stress evaluation: An experiment study. Geoenergy Sci. Eng. 2023, 230, 212271. [Google Scholar] [CrossRef]
- Zhao, H.; Tannant, D.D.; Ma, F.; Guo, J.; Feng, X. Investigation of Hydraulic Fracturing Behavior in Heterogeneous Laminated Rock Using a Micromechanics-Based Numerical Approach. Energies 2019, 12, 3500. [Google Scholar] [CrossRef]
- Chang, C.; Tao, S.; Wang, X.; Liu, C.; Yu, W.; Miao, J. Post-frac evaluation of deep shale gas wells based on a new geology-engineering integrated workflow. Geoenergy Sci. Eng. 2023, 231, 212228. [Google Scholar] [CrossRef]
- Yang, L.; Sheng, X.; Zhang, B.; Yu, H.; Wang, X.; Wang, P.; Mei, J. Propagation behavior of hydraulic fractures in shale under triaxial compression considering the influence of sandstone layers. Gas Sci. Eng. 2023, 110, 204895. [Google Scholar] [CrossRef]
- Yoshioka, K.; Sattari, A.; Nest, M.; Günther, R.-M.; Wuttke, F.; Fischer, T.; Nagel, T. Numerical models of pressure-driven fluid percolation in rock salt: Nucleation and propagation of flow pathways under variable stress conditions. Environ. Earth Sci. 2022, 81, 139. [Google Scholar] [CrossRef]




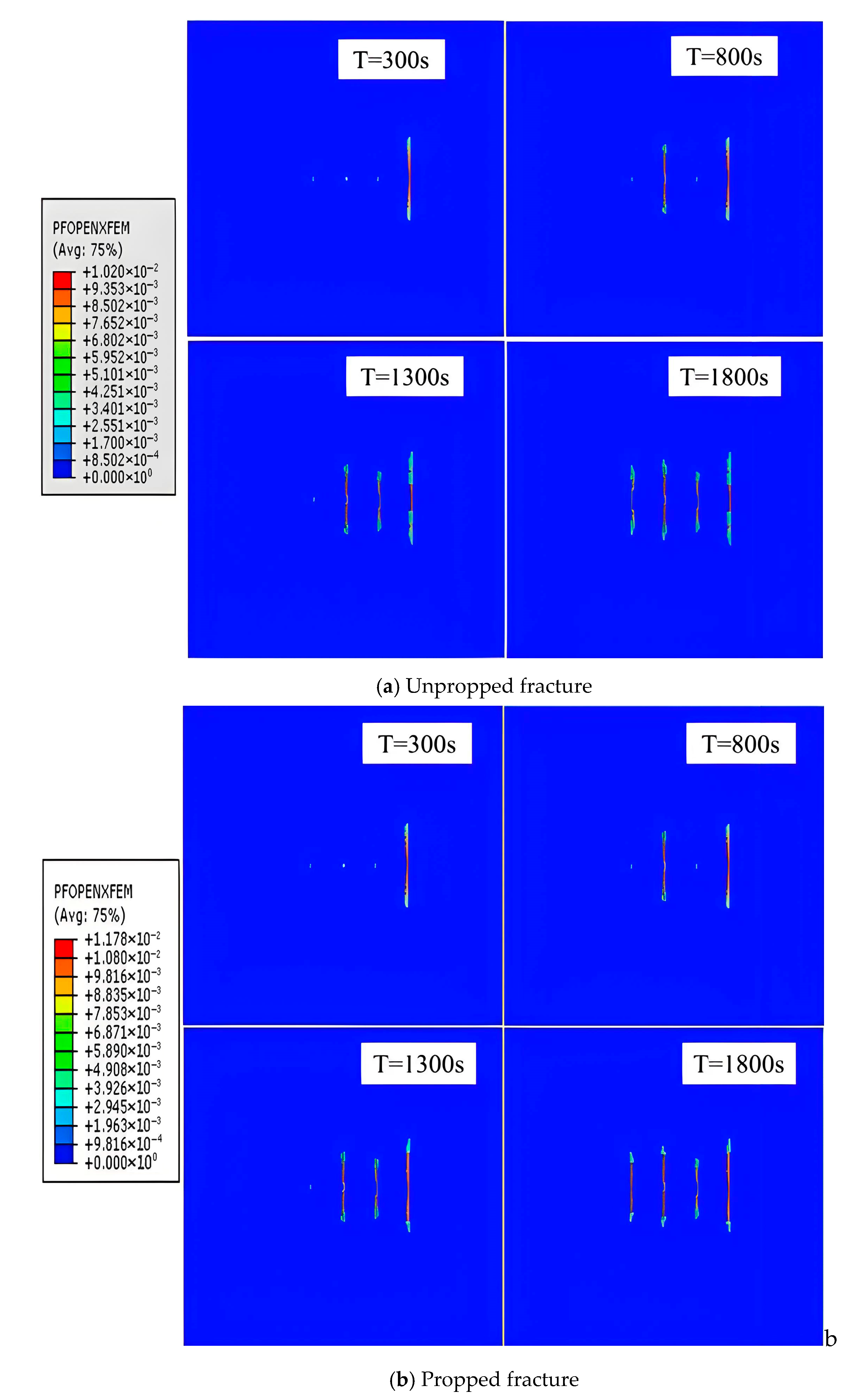
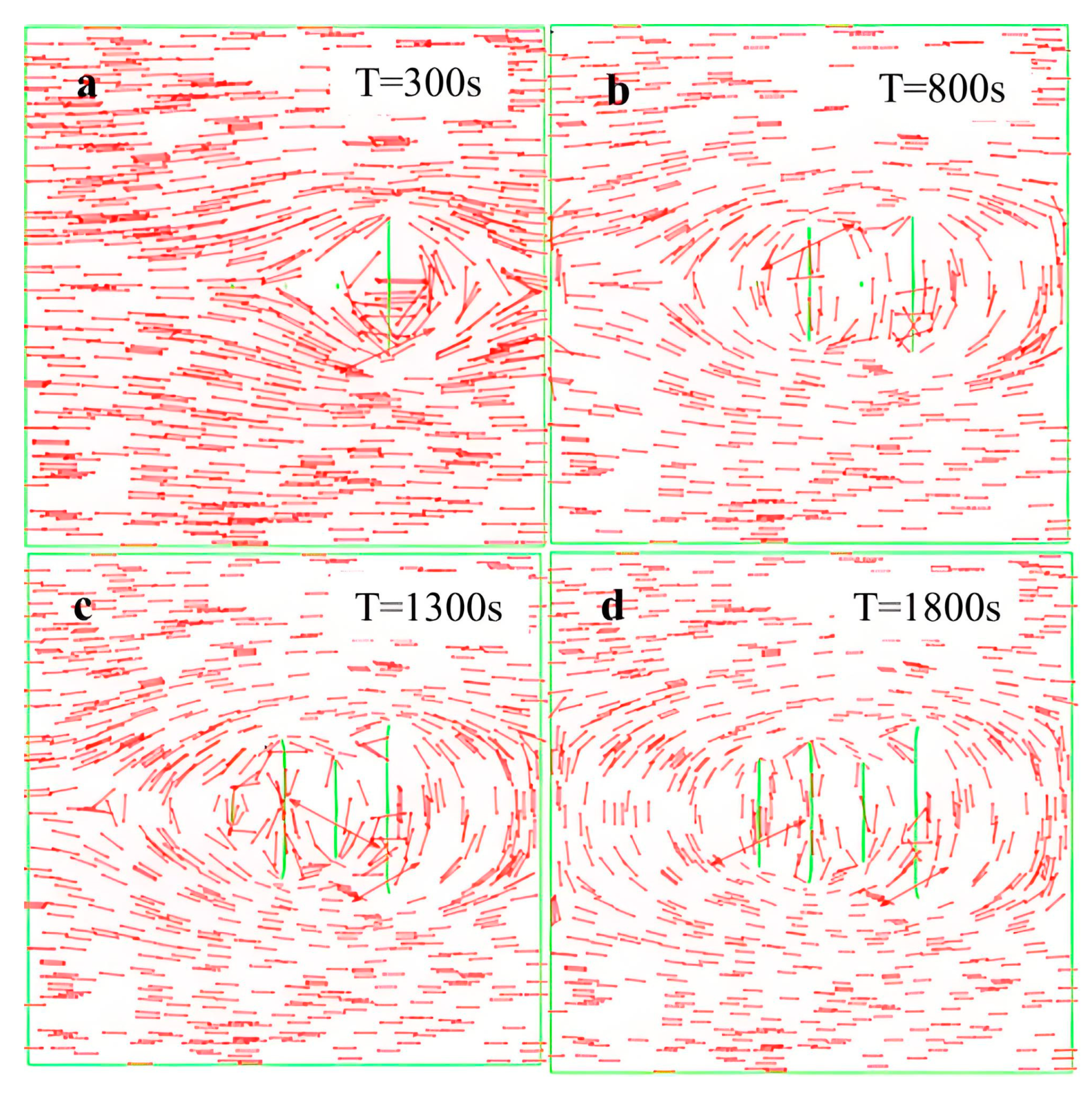
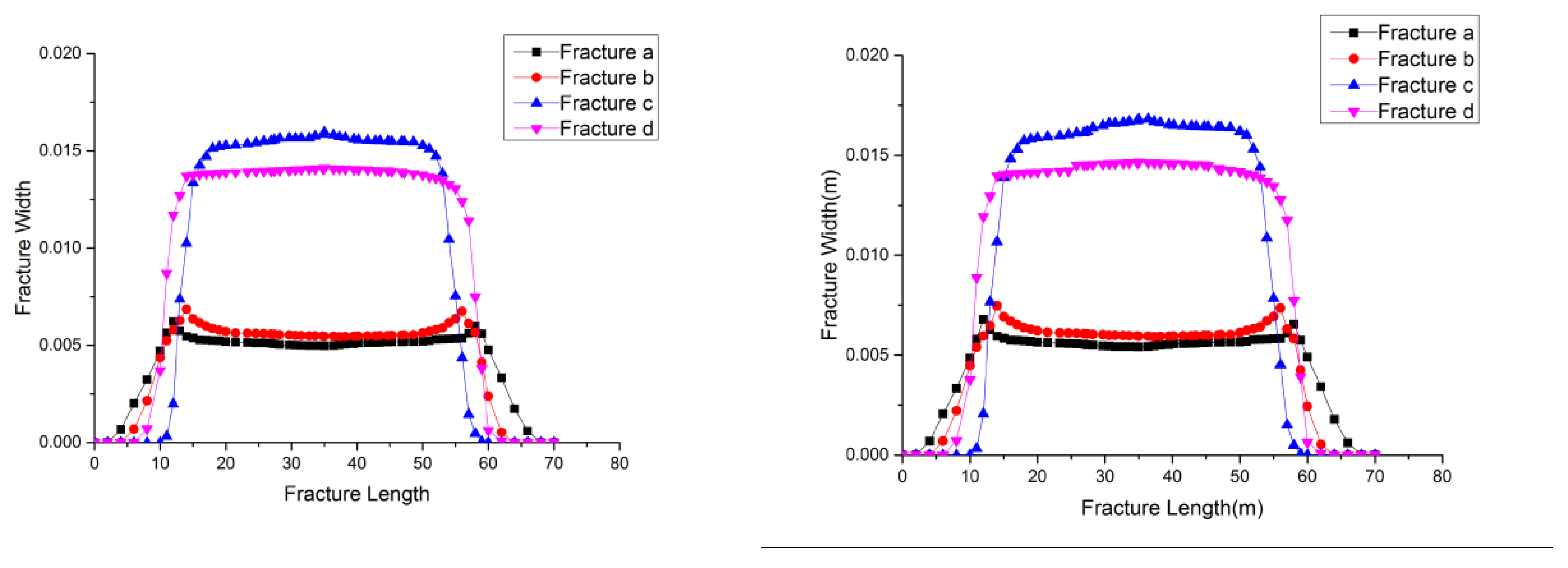


| Parameter | Unit | Value |
|---|---|---|
| Young’s modulus | ×103 MPa | 28.6 |
| Poisson’s ratio | Dimensionless | 0.215 |
| Porosity | % | 2.7 |
| Permeability | 10−3 μm2 | 0.014 |
| Initial pore pressure | MPa | 38.41 |
| Vertical stress | MPa | 74.42 |
| Minimum Horizontal Principle stress | MPa | 57.43 |
| Maximum Horizontal Principle stress | MPa | 66.53 |
| Fracture | Unpropped Fracture | Propped Fracture | ||
|---|---|---|---|---|
| The Maximum Fracture Width | The Average Fracture Width | The Maximum Fracture Width | The Average Fracture Width | |
| Fracture a | 0.0048 | 0.0031 | 0.0062 | 0.0041 |
| Fracture b | 0.0160 | 0.0100 | 0.0164 | 0.0130 |
| Fracture c | 0.0150 | 0.0096 | 0.0161 | 0.0120 |
| Fracture d | 0.0045 | 0.0029 | 0.0059 | 0.0039 |
| Fracture | Unpropped Fracture | Propped Fracture | ||
|---|---|---|---|---|
| The Maximum Fracture Width | The Average Fracture Width | The Maximum Fracture Width | The Average Fracture Width | |
| Fracture a | 0.0059 | 0.0043 | 0.0064 | 0.0051 |
| Fracture b | 0.0064 | 0.0049 | 0.0072 | 0.0059 |
| Fracture c | 0.0067 | 0.0052 | 0.0076 | 0.0067 |
| Fracture d | 0.0156 | 0.0133 | 0.0162 | 0.0143 |
| Fracture | Unpropped Fracture | Propped Fracture | ||
|---|---|---|---|---|
| The Maximum Fracture Width | The Average Fracture Width | The Maximum Fracture Width | The Average Fracture Width | |
| Fracture a | 0.0062 | 0.0048 | 0.0068 | 0.0052 |
| Fracture b | 0.0068 | 0.0053 | 0.0074 | 0.0058 |
| Fracture c | 0.0159 | 0.0120 | 0.0169 | 0.0130 |
| Fracture d | 0.0140 | 0.0110 | 0.0146 | 0.0113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhang, J.; Zheng, H.; Shi, B.; Liao, R. Numerical Simulation of Fracture Sequence on Multiple Hydraulic Fracture Propagation in Tight Oil Reservoir. Processes 2025, 13, 2409. https://doi.org/10.3390/pr13082409
Tang Y, Zhang J, Zheng H, Shi B, Liao R. Numerical Simulation of Fracture Sequence on Multiple Hydraulic Fracture Propagation in Tight Oil Reservoir. Processes. 2025; 13(8):2409. https://doi.org/10.3390/pr13082409
Chicago/Turabian StyleTang, Yu, Jin Zhang, Heng Zheng, Bowei Shi, and Ruiquan Liao. 2025. "Numerical Simulation of Fracture Sequence on Multiple Hydraulic Fracture Propagation in Tight Oil Reservoir" Processes 13, no. 8: 2409. https://doi.org/10.3390/pr13082409
APA StyleTang, Y., Zhang, J., Zheng, H., Shi, B., & Liao, R. (2025). Numerical Simulation of Fracture Sequence on Multiple Hydraulic Fracture Propagation in Tight Oil Reservoir. Processes, 13(8), 2409. https://doi.org/10.3390/pr13082409





